Abstract
The matter of neutron stars is characterised by the density of the order of typical nuclear densities; hence, it can be described with methods of nuclear physics. However, at high densities, some effects that are absent in nuclear and hypernuclear physics can appear, and this makes neutron stars a good place for studying the properties of baryonic interactions. In the present work, we consider neutron stars consisting of nucleons, leptons and hyperons with Skyrme baryonic forces. We study the character of the interactions taking place in neutron stars at high densities. In particular, we show the difference between three-body and density-dependent forces. We also demonstrate that the Skyrme forces proportional to nuclear density are better suited for the modelling of neutron stars than the forces proportional to fractional powers of density. Finally, we emphasize the importance of the point of appearance of hyperons in a further search for parameterizations which are suitable for describing neutron stars.
1. Introduction
Neutron stars are stars in hydrostatic equilibrium that consist mostly of neutrons and have the density of the order of typical nuclear densities. Currently, neutron stars are observed in all parts of the electromagnetic spectrum. The vast majority of measurements of neutron star masses were conducted using radio observations of rotating pulsars in binary systems. At present, more than 2500 pulsars are known in the galaxy, but about 90% of them are isolated, and their masses cannot be measured using current methods. Among the neutron stars with masses measured reliably, the majority fall into the range of 1.3 to 1.5 [1,2]. However, there are neutron stars with masses about 2 . The most massive of these are currently the pulsars PSR J1614-2230 [3,4], PSR J0348+0432 [5] and PSR J0740+6620 [6,7] with masses of (1.908 ± 0.016) , (2.01 ± 0.04) and (2.08 ± 0.07) , respectively, at 68.3% credibility. Additionally, PSR J0952-0607 [8] with a mass of (2.35 ± 0.17) was observed recently, and it is currently the fastest known spinning neutron star in the galaxy. Thus, the latest observational data indicate that the maximum mass of 2 should be reached in theoretical models. The construction of such models appears to be a difficult task due to the reduction in the maximum mass in models with hyperons. This problem will be discussed below in more detail.
Another measured characteristic of neutron stars is their radii. The majority of methods for their measurement are based on the analysis of thermal radiation from the surface of the star. Such measurements require detailed theoretical modelling of this radiation and careful selection of its sources, considering that the surface radiation of a star can be distorted due to the accretion of matter from the companion star or from a strong magnetic field. Therefore, it is difficult to measure the radii of neutron stars in binary systems, and it is rarely possible to simultaneously measure both the mass and the radius of a neutron star. However, relatively accurate radius values were obtained, for instance, for pulsar PSR J0740+6620 (which was mentioned above) by two independent groups: km (68 % credible interval) in [9] and in [10]. Later, these results were revised in [11], where the value of km was reported (68% credible interval).
A wide range of extreme states of matter that cannot be studied in terrestrial conditions are realized in neutron stars, making them a source of information on the properties of baryonic interactions and nuclear matter. Additional sensitivity to certain properties of baryonic interactions can arise in these states; thus, the study of neutron stars is of great importance for nuclear physics. Alternatively, the development of the theory of many-body nuclear systems is required for a better understanding of neutron star physics. In the present work, we do not pretend to conduct a comprehensive description of the observed data; rather, we study the influence of certain properties of hyperonic interactions on the characteristics of neutron stars.
At densities that are close to the normal nuclear density, the matter of neutron stars presumably consists of neutrons, protons, electrons and muons. At densities that are several times higher, hyperons may also appear. As the density increases, -hyperons are expected to appear first; thus, in the present work, we consider neutron stars to consist of nucleons, leptons and -hyperons. Although the appearance of hyperons in neutron star matter seems to be the most likely option today, it also is the cause of the problem known as the “hyperon puzzle”. In particular, the models incorporating hyperons predict maximum masses smaller than the masses in models without hyperons, and also smaller than the masses obtained from observations. This phenomenon arises due to the fact that the presence of hyperons considerably softens the equations of state of neutron star matter. To stand up to this challenge, a deeper study of the hyperon–nucleon and hyperon–hyperon interactions, as well as a search for more stiff equations of state, are required [12,13].
Various attempts to resolve the hyperon puzzle have been reported in the literature (for a recent brief review, see [14]). In [15], the so-called universal three-baryon interaction was shown to potentially resolve the puzzle. An important role of the three-baryon interactions was discussed later in [13,16,17,18]. More exotic explanations like deconfined quark matter in the central region or in the whole star (see [13,14]), as well as dark matter particles in neutron stars [19], have also been proposed.
Since the pioneering paper of [20], the relativistic mean field theory in its various versions has become one of the most frequently used approaches in this field. After [20], our knowledge of hypernuclear properties was enhanced substantially; thus, the parameters of the corresponding relativistic energy density functional are constrained more strictly. However, it is yet possible to come up with many sets of parameters that are compatible with hypernuclear data. Additional theoretical refinements were suggested in the last few decades, e.g., nonlinearities in the scalar and vector fields, the addition of the hidden-strangeness scalar and vector fields, the density dependence of the coupling constants, etc. The current progress in this approach has been reviewed recently [21]. Within the relativistic mean field theory, various attempts to solve the hyperon puzzle are known, e.g., refs. [22,23,24,25,26,27,28,29,30,31,32]. Essentially, a sufficient repulsion at short baryon–baryon distances due to usual and/or hidden strangeness vector fields is introduced to resolve the puzzle.
However, there is no commonly accepted solution thus far. The main reason for this is that the properties of the baryonic interactions occurring at high densities that play a crucial role in this problem have been studied insufficiently; thus, it is difficult to independently check any of the explanations of the hyperon puzzle.
To describe the baryonic matter of neutron stars, we used an approach based on the Skyrme interaction, which is a self-consistent non-relativistic mean field model that was developed for nuclear systems. Skyrme potential parameterizations include a large set of parameters that are obtained from the empirical data of atomic nuclei and hypernuclei, which allow for the description of nucleon–nucleon, nucleon–hyperon and hyperon–hyperon interactions in a single approach. There is a wide variety of Skyrme potential parametrizations that describe the matter equally well at nuclear densities, but these same parametrizations can lead to completely different results at higher densities.
The Skyrme model was widely used in various works in order to study the properties of nuclei and nuclear matter [18]. It was applied to the description of neutron stars [33,34], including those with -hyperons, where the authors attempted to solve the hyperon puzzle [35] and explore different properties of baryonic interactions [36]. In this work, we focus on examining the properties of the interactions which have been studied relatively well for hypernuclei. By construction, the Skyrme interaction contains three-body forces or density-dependent, repulsive two-body forces.
It is worth noting that the Skyrme model is non-relativistic, which leads to limitations in the high-density region, but its flexibility and a large number of different parameterizations make it a good choice for realizing the goals of this work.
Renewed interest in neutron stars physics was induced by one of the most important discoveries in this area. On 17 August 2017, gravitational waves from a neutron star merger were registered for the first time by the detector system LIGO-Virgo (GW170817) [37]. Information about electromagnetic and gravitational waves can be used, in particular, to obtain restrictions on the equation of state of dense nuclear matter. Nowadays, neutron star mergers are considered to be an important factor in the nucleosynthesis of heavy elements in the universe. In 2019, the first astrophysical confirmation of such process was obtained when the spectrum of strontium was identified in the data from GW170817 [38]. Moreover, it became the first experimental evidence that the matter of neutron stars is indeed neutron-rich. Among other things, the registration of GW170817 provided us with the first experimental estimates of such a characteristic, the tidal deformability of a neutron star.
Later, the GW190425 event [39] was observed, but its assignment as the neutron star merger remains ambiguous.
Tidal deformability shows how the shape of a star changes under the influence of external gravitational forces. In the present work, following the majority of works on tidal deformability, we consider only quadrupole deformations. Tidal deformability coefficient is defined as the ratio of the quadrupole moment of the star to the external tidal field [40,41]:
We use a dimensionless tidal deformability coefficient:
where M is the mass of the neutron star. The tidal deformability coefficient provides us with an additional instrument for the selection of equations of state and parameters of interactions.
2. Methods
2.1. Skyrme Potential
We use the nucleon–nucleon [42]
and the hyperon–nucleon [43]
Skyrme potentials in the standard form. In (3) and (4), is the operator of the relative momentum acting on the ket while acts on the bra, is the spin exchange operator and are the Pauli spin matrices. For the interaction, the 1 and 2 indices should be replaced by and N.
The two-body interaction depends on the parameters and . Parameters and correspond to the terms acting on relative even states (in fact, only s-states), and governs the term acting in relative odd states (p-states). Using the parameters allows one to influence the proton–neutron asymmetry properties. Parameter determines the one-body spin–orbit strength. Numerous parametrizations of nucleon–nucleon forces have been obtained by fitting certain characteristics of atomic nuclei and nuclear matter. Parameters , and of the two-body hyperon–nucleon interaction are introduced in a similar way; their values are also obtained mainly by fitting the experimental spectra of the hypernuclei. The spin–orbit terms in (3) and (4) vanish in uniform non-polarized nuclear matter and will not be considered further.
Reliable (and scarce) information on the interaction has been obtained from the data on hypernuclei [44]. Since the hypernuclei were so far observed only in the ground states with both hyperons in the 1s state, there is no information on the p-wave interaction. Thus, we use the simplified Skyrme potential from [45].
Many-body effects other than (3) and (4) should also be included. For nucleonic interaction, they may be represented as the three-body force:
or the density-dependent force:
where n is the nucleon density. Forces (6) and (7) lead to equivalent results in matter at and [42].
Similarly, for hyperonic interactions the three-body force
or density-dependent force
are introduced [43,46].
At and , (8) and (9) are almost equivalent for hypernuclei and exactly equivalent for symmetric (with equal numbers of protons and neutrons) nuclear matter. The issue of equivalence is discussed in more detail in [47]. However, neutron stars are neutron-rich nuclear systems, and said equivalence is violated. Moreover, the force (9) at apparently is not equivalent to (8). We study how different hyperonic many-body forces manifest in neutron stars.
2.2. Neutron Star Matter and Tidal Deformability
We consider the chemically equilibrated matter consisting of nucleons, leptons and -hyperons. Usual conditions of the chemical equilibrium in terms of chemical potentials are used (see, e.g., ref. [20]). Using Skyrme potentials (3)–(9), we calculate in the standard way the energy density, pressure and chemical potentials, and determine the particle fractions from the equilibrium conditions. Repeating these calculations at various densities, we obtain the equation of state of the neutron star matter.
With the equation of state, we are in position to solve the Tolman–Oppenheimer–Volkov equation [48,49] at various central densities, which gives the dependence and, particularly, the maximum mass of the neutron star. We follow the methodology used in [34,36] in the equation of state and calculations. We also employ the equation of state of the neutron star crust using approximations obtained in [50].
Tidal deformability is represented [51] in terms of the Love tidal number and compactness parameter
while is derived from the following expression [52,53,54]:
where is the value of the function at the edge of the star. This function satisfies the equation
where
In (12) and (13), r is the radial variable measured from the centre of the star, and are energy per baryon and pressure at r, and is the mass inside the sphere of radius r. We use here the geometric unit system with . Starting at the centre of the star, for a given EOS, equation (12) is integrated self-consistently together with the Tolman–Oppenheimer–Volkoff equation, at various central densities with the boundary condition at the centre , to obtain the dependence. This together with expression (10) and the mass–radius dependence give us the dependences of tidal deformability on mass M and radius R.
From the GW170817 event, the LIGO-Virgo collaboration has extracted [37,55,56]:
where [57] and [41,58] are averaged quantities determined by the individual of the two stars merged:
If one of the stars has the ”standard” mass , its deformability and radius satisfy the following constraints [37,55,56]:
We use these constraints as well as the condition in the selection of the equation of state.
3. Results and Discussion
As a first step, we consider nucleon matter without hyperons and employ six parametrizations of the interaction: SLy230a [34], SLy4 [59], SkI3 [60], SkO [61], SkM* [62] and SkX [63].
The choice of Skyrme -forces relevant for studying neutron star matter has been considered earlier. It was shown in [33] that in the case of interactions SkM* and SkX, the proton fraction disappears at densities above and the state of pure neutron matter becomes more energetically favourable. In [36], the density at the point of transition to the ferromagnetic state is used as a selection criterion, and the SkO parameter set is excluded by this criterion, although the equation of state in this case is in good agreement with other models [33]. Earlier in [64], we considered the correlations between the characteristics of nuclear matter equation of state and the neutron star properties on the example of 42 parametrizations of the Skyrme -force. The maximum mass of neutron star and its corresponding radius are most strongly related to the first and second derivatives of the symmetry energy with respect to density, which characterize the behaviour of the symmetry energy at high densities. Parameterization SkI3 leads to one of the highest values of among the sets considered in [64].
Figure 1 shows the calculations of equation of state and dependencies of neutron star mass on the radius for the six listed parameters sets, including the results for the previously excluded SkX, SkM* and SkO. Parameterizations SkX and SkM* lead to overly soft equations of state and, as a result, the corresponding values of do not reach 2 even without hyperons. For other parametrizations, the differences in the equations of state are not so significant and the dependence turns out to be more sensitive to the properties of the interaction.
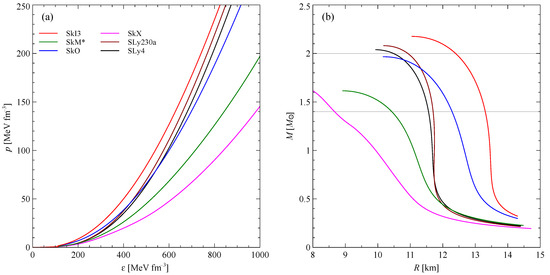
Figure 1.
Neutron stars without hyperons with different parameterizations of interaction: (a) equation of state, (b) dependence of mass on radius.
Figure 2 shows the dependencies of the tidal deformability on the star radius and mass. Although the first experimental estimates of make it possible to impose new restrictions on the model predictions (18) and (19), at this stage, these limits are quite wide and most of the interactions satisfy them or lay on the boundary.
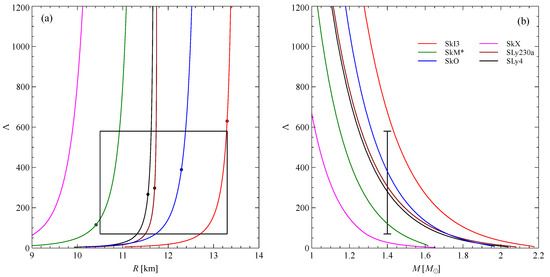
Figure 2.
Dependence of tidal deformability for neutron star matter without hyperons for different parameterizations of interaction (a) on neutron star radius; (b) on neutron star mass. Dots in figure (a) correspond to neutron stars with . The rectangle in (a) and interval in (b) represent restrictions (18) and (19).
For further considerations, we adopt the SkI3 and SLy230a parameter sets, which give the greatest maximum masses. Several predictions of bulk properties of nuclear matter made with parametrizations under consideration are summarized in Table 1.

Table 1.
Symmetric nuclear matter saturation properties obtained with different -force Skyrme parametrizations (energy per particle at saturation (MeV), incompressibility (MeV), the symmetry energy (MeV) and its first and second derivatives at saturation L (MeV) and (MeV), effective mass (data are taken from [18]), and characteristics of neutron stars: maximum mass and corresponding radius (km).
Let us now include hyperons. The parameters of interactions we use are presented in Table 2. Parameterizations YMR [65], LYI [66] and SLL4’ [67] provide the best description of the hypernuclear experimental data and can be considered realistic. Earlier parametrizations from [68] also describe the experiment satisfactorily. We use parameterizations YBZ2 with the largest three-body force and YBZ6 with especially strong non-locality.

Table 2.
Parameters of employed interactions ( is given in , and in , in ; other parameters are dimensionless).
The YBZ2 and YBZ6 sets were constructed with the three-body force (8), while the other sets involve the density-dependent force (9). For hypernuclei, the difference is insignificant. Below, we employ form (9), unless explicitly stated otherwise.
To describe the interaction, we use three sets of parameters, namely S1, S2 and S3. The parameters of interactions we use are shown in Table 3.

Table 3.
Parameters of employed interactions ( is given in , in ).
The S1, S2 and S3 sets were obtained [45] using the fit to the data accepted at that time. These three sets effectively conform to a small, moderate and large interaction range, correspondingly. All the sets reproduce a strong attraction, as believed before the famous Nagara event [69].
When the attraction became much weaker, the S1 and S3 sets were modified accordingly and the S1 and S3 sets were obtained [70]. Note that S2 set was not modified and the attraction remains strong in this case.
The equations of state with interaction SkI3 for nucleonic interaction and interactions SLL4 and LYI for hyperon–nucleon interaction are depicted in Figure 3.
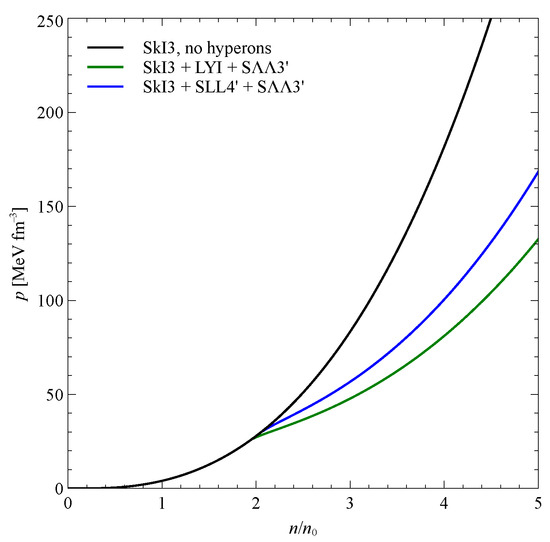
Figure 3.
Equation of state without hyperons (black) and with hyperons for (SLL4, blue) and (LYI, green). The nucleon interaction is SkI3 and the interaction is S3.
Figure 3 illustrates the “hyperon puzzle”. It is seen that the equation of state becomes substantially softer when the hyperons are added. However, the softening with the LYI interaction is much larger than that obtained with the SLL4 parameter set. The reason is that in the first case and in the second (for definition, see (9)). These two interactions give equally good descriptions of hypernuclear spectra [66,67], but the repulsion at high densities grows faster for . Therefore, we can suggest that the neutron star studies require the interaction with or three-body interactions. This point will be further discussed below.
In Figure 4, fractions of nucleons, hyperons and leptons are presented as functions of the density. It is seen that the fraction grows rapidly with density.
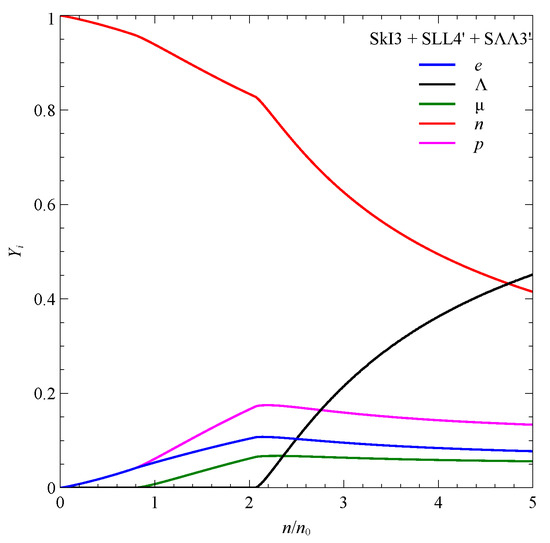
Figure 4.
Dependence of fractions () of different particles on density for a certain combination of parameterizations of , and forces.
One may naively suppose that never exceeds and since . However, at high densities is a typical result, which is also encountered in other studies performed within other (not Skyrme) approaches. The reason is that repulsive forces become dominant at high densities. Repulsive forces are parameterized here via (8) and (9) (for comparison, coupling is used to describe repulsive forces in the relativistic mean field theory). All the forces compatible with hypernuclear spectra contain the many-body force (8) or (9), which is much weaker than (6) and (7) in nucleon interaction. Due to the stronger repulsive forces (6) and (7), the neutron chemical potential grows with density more rapidly than the hyperon chemical potential, and so the neutron fraction is depleted. Therefore, the system prefers more and more hyperons, which repel relatively weakly.
We stress that the softening of the equation of state, the “hyperon puzzle” and the hyperon excess at high densities have the same origin. The weaker the hyperonic repulsion (many-body effect in our approach) is, the more abundant hyperons are and the softer the equation of state is.
Figure 5 displays the dependence. We compare three cases here: the non-interacting hyperons, hyperons interacting with nucleons, but not with each other, and the full set of interactions.
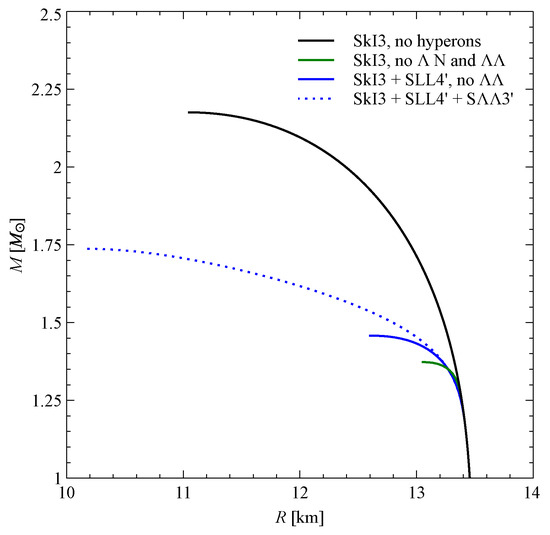
Figure 5.
Dependence of neutron star mass on radius for different cases: without hyperons (black), with non-interacting hyperons (green), hyperons interacting with nucleons, but not with each other (solid blue), and with a full set of interactions (dotted blue).
It is interesting that non-interacting hyperons result in the smallest maximum mass and, therefore, the softest equation of state. At nuclear densities, the hyperon–nucleon interaction is presumably attractive, as known from hypernuclear studies. Switching off the interaction, we cancel not only this attraction, but also the short-range repulsion. It appears that the second point is more important for neutron stars, and the omission of interaction leads to a softer equation of state.
In Figure 6, we compare the density-dependent interactions with and the three-body forces.
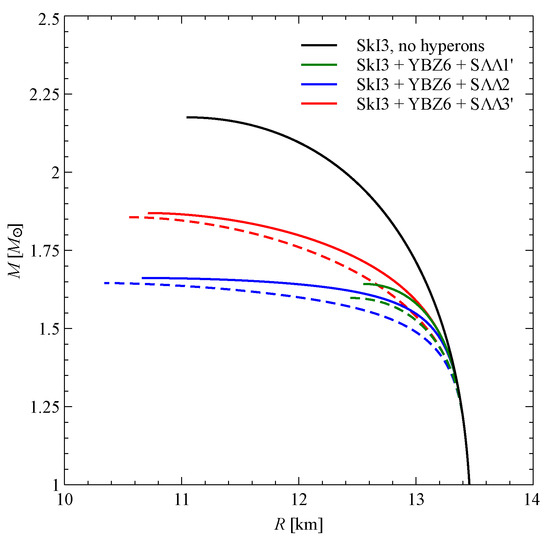
Figure 6.
Dependence of neutron star mass on radius obtained with different parameterizations of interaction. Dashed lines correspond to calculations with three-body forces; solid lines correspond to calculations with density-dependent forces.
We recall that (8) and (9) are equivalent in the symmetric matter at and . The maximum mass for the density-dependent force is always larger than that for the three-body force. Skyrme three-body interactions (8) in the (and ) system acts only on a singlet pair, while the density-dependent force does not discriminate between various spin states. Therefore, the repulsion in the first case weakens. However, the effect is not large, as seen from Figure 6.
In the same figure, we demonstrate the differences between the dependencies for different forces. It should be noted that the interaction is known rather poorly and the S1, S2 and S3 sets are rather simplified since they contain neither the p-wave contribution nor any many-body effects. However, it may still be instructive to verify some interesting features even with these simplified potentials.
The short-range S1 interaction does not affect the maximum mass strongly, but increases the corresponding (minimal) radius considerably. Since the interaction becomes rather strong at high densities in this case, further contraction leads to instability. At the same time, the strong attraction of the moderate range (the S2 set) leads to smaller minimal radii, but does not significantly change the maximum mass. The long-range S3 set results in larger maximum masses. However, we recall that the interaction employed here is incomplete and the results should be interpreted with caution.
In Figure 7, the dependence for all the hyperonic interactions used is shown.
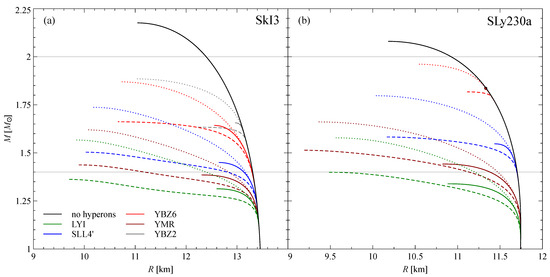
Figure 7.
Dependence of neutron star mass on radius with different parameterizations of the and forces and the SkI3 parameterization (a), the SLy230a (b) parameterization of the force. Different line types correspond to the different parameterizations of interaction: S1 (solid), S2 (dashed), S3 (dotted). In Figure (b), the dot shows the maximum mass of a neutron star obtained with the combinations of parameter sets SLy230a + YBZ6 + S1. In the SLy230a+YBZ2 case, hyperons do not appear so the curves for the YBZ2 set in panel (b) coincide with the curve for the pure nucleonic matter.
The interactions with evidently result in larger maximum masses, in accordance with the discussion above. We see once again that hyperons in the case of S1 interaction extend to neutron stars, i.e., the radius corresponding to the maximum mass (the minimal radius) becomes larger.
No combination of interactions yields the maximum mass of . For the SkI3 interaction, the addition of hyperons lowers the maximum mass substantially. The YBZ2 set with a high-density-dependent term produces relatively better results.
On the other hand, lowering the maximum mass via hyperons is weaker for the SLy230a interaction. In this case, the hyperons appear at higher densities than in the SkI3 case, and in combination with YBZ2, hyperons do not appear at all. As a result, the equation of state is softened to a smaller degree.
To describe this situation in more detail, we introduce the binding energy of -hyperon in the pure nucleonic matter:
From hypernuclear studies, is known to be about 30 MeV at the normal nuclear density. At higher densities, decreases and becomes negative due to the three-body or density-dependent forces.
We also introduce the critical energy of -hyperons in the nucleonic matter:
Hyperons appear when the following condition is fulfilled: [71]
Note that does not depend on the choice of the interaction if the density-dependent force (9) is employed (for the three-body force (8), the dependence is weak), and does not depend on the hyperonic interaction otherwise.
Figure 8 depicts the density dependence of for different parameterizations of the interaction and for two parameterizations of the interaction (SkI3 and SLy230a) in nucleonic matter. The intersection point of and corresponds to the point of appearance of hyperons.
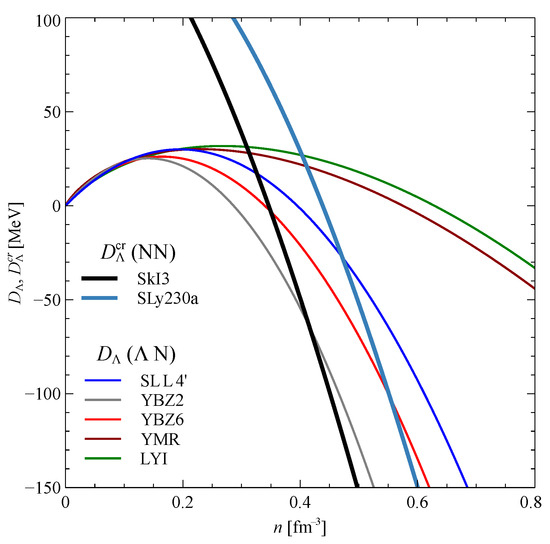
Figure 8.
The density dependence of for different parameterizations of the interaction and for two parameterizations of the interaction in nucleonic matter.
We see from Figure 8 that in the case of YBZ2 and SLy230a, does not cross and hyperons do not appear. Note also that for each parameterization of the interaction, there is a clear correlation between the density of the appearance of hyperons and the maximum mass of a neutron star: a higher density corresponds to a higher maximum mass.
Seemingly, the simplest way to resolve the hyperon puzzle is to prove that hyperons cannot appear in neutron stars. It can be shown that large three-body or density-dependent forces can support such a conjecture, which was already noted in [13,15,17]. However, the majority of realistic hyperon–nucleon interactions employed here include the three-body or density-dependent forces not strong enough to prevent hyperon appearance, as seen from Figure 8. The single exception is the YBZ2 set when used together with SLy230a. Parameter set YBZ2, with the largest three-body force, should be considered “borderline realistic”. The description of hypernuclear spectra with this set is acceptable, but somewhat worse [66] than with the other employed sets. Therefore, it seems unlikely, but not fully improbable, that the interactions compatible with hypernuclear data can exclude hyperons from neutron star matter. This straightforward solution is probably inappropriate.
As seen from Figure 7, the SLy230a + YBZ6 + S3 combination results in a maximum mass rather close to . We cannot state that this combination should be treated as a ”genuine” one, but we pinpoint the directions in which to search for suitable parameterizations.
In Figure 9, the tidal deformability as a function of radius is displayed.
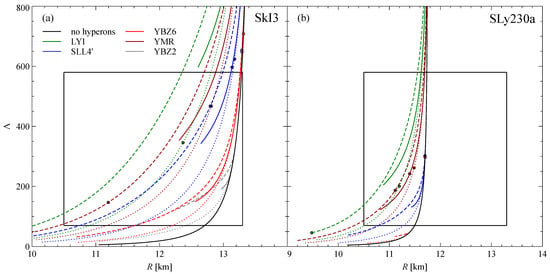
Figure 9.
Tidal deformability dependence on neutron star radius with different parameterizations of the and forces with the SkI3 parameterization (a), SLy230a parameterization (b) of the force. Different line types correspond to different parameterizations of the interaction: S1 (solid), S2 (dashed), S3 (dotted). The rectangles are the same as in Figure 2a. The dots correspond to .
It is interesting that the combinations of interactions providing good results for the tidal deformability produce rather low maximum masses in the SkI3 case. At the same time, the combinations offering large maximum masses also provide acceptable tidal deformabilities in the SLy230a case.
Characteristics of neutron stars for all used interactions are also presented in Table 4. Note that for certain combinations of and interactions, namely SkI3+YBZ2 and SLy230a+YBZ6, hyperons appear at densities higher than those corresponding to , which was already illustrated in Figure 7. For these combinations, Table 4 includes values of and corresponding to nucleonic matter. Moreover, for SLy230a+YBZ2, all values correspond to nucleonic matter, since hyperons do not appear in this case.

Table 4.
Characteristics of neutron stars with different parameterizations of and forces and SkI3 and SLy230a interactions. Table contains the following characteristics: radius of neutron star with (, km) and corresponding tidal deformability , maximum mass of the star , and corresponding radius , km.
4. Conclusions
A very popular instrument in nuclear physics, the approach based on Skyrme interactions is not used as widely in neutron star studies, probably due to its non-relativistic nature. Naturally, relativistic mean field theory and similar approaches have advantages. However, the rich experience gathered in nuclear and hypernuclear theory with Skyrme interactions can also be rather helpful in the field of neutron stars. We note that superluminosity certainly does not manifest in full in our calculations. Here, we study the implications of various features of Skyrme interactions, mainly the one.
Density-dependent and three-body forces are a necessary part of Skyrme interactions. or forces proportional to various powers of nuclear densities are usually treated as equally possible in hypernuclear physics. However, different s lead to substantially different equations of state in neutron stars. Moreover, density-dependent forces even at become no longer equivalent to the forces.
Properties of neutron star matter at high densities play a crucial role for maximum neutron star mass and resolution in the hyperon puzzle. Therefore, while various parameters of the Skyrme interaction are equally important at normal nuclear densities (in hypernuclei), the density-dependent or three-body forces dominate in neutron stars. They determine the point of hyperon appearance, hyperon abundance and the stiffness of the equation of state. We show that the best interactions from hypernuclear studies do not prevent hyperon appearance, so the hyperon puzzle still stands.
We used an oversimplified interaction since the empirical information in this field is rather scarce. At large abundances, this interaction may be too crude. Note that three-body zero-range force results in exactly zero due to the Pauli principle, but forces are possible. The force, depending on the nucleon density, has been derived in [66] and already has been used in [72] for the equation of state of neutron star matter.
We restricted ourselves here with hyperons since hypernuclei are studied much better than the other ones. However, the Skyrme interaction has also been derived previously [73,74,75], so our consideration can be extended to a more realistic composition of neutron star matter.
Author Contributions
Conceptualization, D.L.; methodology, D.L. and T.T.; software, S.M. and A.N.; investigation, S.M. and A.N.; data curation, S.M. and A.N.; writing—original draft preparation, S.M. and A.N.; writing—review and editing, D.L. and T.T.; supervision, D.L. and T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available upon reasonable request.
Acknowledgments
Authors thank the Interdisciplinary Scientific and Educational School of Moscow University «Fundamental and Applied Space Research» for support. S.A. Mikheev expresses gratitude to the Theoretical Physics and Mathematics Advancement Foundation «BASIS». We would like to thank the organizers of the conference Infinite and Finite Nuclear Matter (INFINUM-2023), where the results of this paper were reported. We are also grateful to S.V. Sidorov for his help in editing the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952–0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Salmi, T.; Vinciguerra, S.; Choudhury, D.; Riley, T.E.; Watts, A.L.; Remillard, R.A.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Arzoumanian, Z.; et al. The Radius of PSR J0740+6620 from NICER with NICER Background Estimates. Astrophys. J. 2022, 941, 150. [Google Scholar] [CrossRef]
- Bombaci, I. The Hyperon Puzzle in Neutron Stars. J. Phys. Soc. Jpn. Conf. Proc. 2017, 17, 101002. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. Constraints from Λ hypernuclei on the ΛNN content of the Λ-nucleus potential. Phys. Lett. B 2023, 837, 137669. [Google Scholar] [CrossRef]
- Vidaña, I. Neutron stars and the hyperon puzzle. EPJ Web Conf. 2022, 271, 09001. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Yamamoto, Y. Necessity of extra repulsion in hypernuclear systems: Suggestion from neutron stars. Eur. Phys. J. A 2002, 13, 213–215. [Google Scholar] [CrossRef]
- Lonardoni, D.; Lovato, A.; Gandolfi, S.; Pederiva, F. Hyperon Puzzle: Hints from Quantum Monte Carlo Calculations. Phys. Rev. Lett. 2015, 114, 092301. [Google Scholar] [CrossRef]
- Gerstung, D.; Kaiser, N.; Weise, W. Hyperon–nucleon three-body forces and strangeness in neutron stars. Eur. Phys. J. A 2020, 56, 175. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Martins, S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Del Popolo, A.; Deliyergiyev, M.; Le Delliou, M. Solution to the hyperon puzzle using dark matter. Phys. Dark Universe 2020, 30, 100622. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Sedrakian, A.; Li, J.J.; Weber, F. Heavy baryons in compact stars. Prog. Part. Nucl. Phys. 2023, 131, 104041. [Google Scholar] [CrossRef]
- Bednarek, I.; Manka, R. The role of nonlinear vector meson interactions in hyperon stars. J. Phys. G Nucl. Part. Phys. 2009, 36, 095201. [Google Scholar] [CrossRef]
- Bednarek, I. Hyperon puzzle in compact stars. Phys. Part. Nucl. 2015, 46, 816–820. [Google Scholar] [CrossRef]
- Oertel, M.; Providência, C.; Gulminelli, F.; Raduta, A. Hyperons in neutron star matter within relativistic mean-field models. J. Phys. G Nucl. Part. Phys. 2014, 42, 075202. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Making a soft relativistic mean-field equation of state stiffer at high density. Phys. Rev. C 2015, 92, 052801. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802. [Google Scholar] [CrossRef]
- van Dalen, E.N.E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with Λ-hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef]
- Fortin, M.; Avancini, S.S.; Providência, C.; Vidaña, I. Hypernuclei and massive neutron stars. Phys. Rev. C 2017, 95, 065803. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Sedrakian, A. Hypernuclear stars from relativistic Hartree-Fock density functional theory. Eur. Phys. J. A 2018, 54, 133. [Google Scholar] [CrossRef]
- Lim, Y.; Lee, C.-H.; Oh, Y. Effective interactions of hyperons and mass-radius relation of neutron stars. Phys. Rev. D 2018, 97, 023010. [Google Scholar] [CrossRef]
- Li, Z.; Ren, Z.; Hong, B.; Lu, H.; Bai, D. Neutron stars within a relativistic mean field theory compatible with nucleon-nucleon short-range correlations. Nucl. Phys. A 2019, 990, 118–136. [Google Scholar] [CrossRef]
- Fu, H.R.; Li, J.J.; Sedrakian, A.; Weber, F. Massive relativistic compact stars from SU(3) symmetric quark models. Phys. Lett. B 2022, 834, 137470. [Google Scholar] [CrossRef]
- Rikovska Stone, J.; Miller, J.C.; Koncewicz, R.; Stevenson, P.D.; Strayer, M.R. Nuclear matter and neutron-star properties calculated with the Skyrme interaction. Phys. Rev. C 2003, 68, 034324. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Lim, Y.; Hyun, C.H.; Kwak, K.; Lee, C.-H. Hyperon puzzle of neutron stars with Skyrme force models. Int. J. Mod. Phys. E 2015, 24, 1550100. [Google Scholar] [CrossRef]
- Mornas, L. Neutron stars in a Skyrme model with hyperons. Eur. Phys. J. A 2005, 24, 293–312. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Watson, D.; Hansen, C.J.; Selsing, J.; Koch, A.; Malesani, D.B.; Andersen, A.C.; Fynbo, J.P.U.; Arcones, A.; Bauswein, A.; Covino, S.; et al. Identification of strontium in the merger of two neutron stars. Nature 2019, 574, 497–500. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Thorne, K.S. Tidal stabilization of rigidly rotating, fully relativistic neutron stars. Phys. Rev. D 1998, 58, 124031. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Rayet, M. Skyrme parametrization of an effective Λ-nucleon interaction. Nucl. Phys. A 1981, 367, 381–397. [Google Scholar] [CrossRef]
- Hiyama, E.; Nakazawa, K. Structure of S =−2 Hypernuclei and hyperon-hyperon interactions. Annu. Rev. Nucl. Part. Sci. 2018, 68, 131–159. [Google Scholar] [CrossRef]
- Lanskoy, D.E. Double-Λ hypernuclei in the Skyrme-Hartree-Fock approach and nuclear core polarization. Phys. Rev. C 1998, 58, 3351–3358. [Google Scholar] [CrossRef]
- Millener, D.J.; Dover, C.B.; Gal, A. Λ-nucleus single-particle potentials. Phys. Rev. C 1988, 38, 2700–2708. [Google Scholar] [CrossRef]
- Lanskoi, D.E.; Tret’yakova, T.Y. Skyrme interactions in calculations of hypernuclei by the Hartree–Fock method. Sov. J. Nucl. Phys. (Engl. Transl.) 1989, 49, 987–991. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Krastev, P.G.; Li, B.-A. Imprints of the nuclear symmetry energy on the tidal deformability of neutron stars. J. Phys. Nucl. Part. Phys. 2019, 46, 074001. [Google Scholar] [CrossRef]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Cutler, C.; Flanagan, É.É. Gravitational waves from merging compact binaries: How accurately can one extract the binary’s parameters from the inspiral waveform? Phys. Rev. D 1994, 49, 2658–2697. [Google Scholar] [CrossRef]
- Favata, M. Systematic Parameter Errors in Inspiraling Neutron Star Binaries. Phys. Rev. Lett. 2014, 112, 101101. [Google Scholar] [CrossRef] [PubMed]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Part II. Nuclei far from stablities. Nucl. Phys. A 1998, 635, 231–256, Erratum: Nucl. Phys. A 1998, 643, 441–441. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Flocard, H. Nuclear effective forces and isotope shifts. Nucl. Phys. A 1995, 584, 467–488. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Dean, D.J.; Nazarewicz, W.; Dobaczewski, J.; Maruhn, J.A.; Strayer, M.R. Shape coexistence and the effective nucleon-nucleon interaction. Phys. Rev. C 1999, 60, 014316. [Google Scholar] [CrossRef]
- Bartel, J.; Quentin, P.; Brack, M.; Guet, C.; Håkansson, H.-B. Towards a better parametrisation of Skyrme-like effective forces: A critical study of the SkM force. Nucl. Phys. A 1982, 386, 79–100. [Google Scholar] [CrossRef]
- Brown, B.A. New Skyrme interaction for normal and exotic nuclei. Phys. Rev. C 1998, 58, 220–231. [Google Scholar] [CrossRef]
- Mikheev, S.A.; Lanskoy, D.E.; Tretyakova, T.Y. Correlations between Properties of Nuclear Matter and Characteristics of Neutron Stars. Phys. Part. Nucl. 2022, 53, 409–414. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Motoba, T.; Rijken, T.A. G-Matrix Approach to Hyperon-Nucleus Systems. Prog. Theor. Phys. Suppl. 2010, 185, 72–105. [Google Scholar] [CrossRef]
- Lanskoy, D.E.; Yamamoto, Y. Skyrme-Hartree-Fock treatment of Λ and ΛΛ hypernuclei with G-matrix motivated interactions. Phys. Rev. C 1997, 55, 2330–2339. [Google Scholar] [CrossRef]
- Schulze, H.-J.; Hiyama, E. Skyrme force for light and heavy hypernuclei. Phys. Rev. C 2014, 90, 047301. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Bandō, H.; Žofka, J. On the Λ-Hypernuclear Single Particle Energies. Prog. Theor. Phys. 1988, 80, 757–761. [Google Scholar] [CrossRef]
- Takahashi, H.; Ahn, J.K.; Akikawa, H.; Aoki, S.; Arai, K.; Bahk, S.Y.; Baik, K.M.; Bassalleck, B.; Chung, J.H.; Chung, M.S.; et al. Observation of a Double Hypernucleus. Phys. Rev. Lett. 2001, 87, 212502. [Google Scholar] [CrossRef]
- Minato, F.; Chiba, S. Fission barrier of actinide nuclei with double-Λ particles within the Skyrme–Hartree–Fock method. Nucl. Phys. A 2011, 856, 55–67. [Google Scholar] [CrossRef]
- Imasheva, L.T.; Lanskoy, D.E.; Tretyakova, T.Y. Neutron Star Matter and Baryonic Interactions. Phys. At. Nucl. 2019, 82, 402–407. [Google Scholar] [CrossRef]
- Balberg, S.; Barnea, N. S-wave pairing of Λ hyperons in dense matter. Phys. Rev. C 1998, 57, 409–416. [Google Scholar] [CrossRef]
- Sun, T.T.; Hiyama, E.; Sagawa, H.; Schulze, H.-J.; Meng, J. Mean-field approaches for Ξ− hypernuclei and current experimental data. Phys. Rev. C 2016, 94, 064319. [Google Scholar] [CrossRef]
- Jin, Y.; Zhou, X.-R.; Cheng, Y.-Y.; Schulze, H.-J. Study of Ξ− hypernuclei in the Skyrme-Hartree-Fock approach. Eur. Phys. J. A 2020, 56, 135. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, X.-R.; Schulze, H.-J. Skyrme force for all known Ξ− hypernuclei. Phys. Rev. C 2021, 104, L061307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).