Abstract
We present a combination of two quick guides aimed at summarizing relevant information about the CompOSE nuclear equation of state repository. The first is aimed at nuclear physicists and describes how to provide standard equation of state tables. The second quick guide is meant for users and describes the basic procedures to obtain customized tables with equation of state data. Several examples are included to help providers and users to understand and benefit from the CompOSE database.
1. Introduction: The CompOSE Data Base
The main purpose of the online service CompOSE (https://compose.obspm.fr) is to provide information and data for different equations of states (EoSs) ready for further use in astrophysical applications, nuclear physics, and beyond, see the review [1] for a general introduction. To that end, CompOSE contains a repository of EoS data in tabulated form following a common format with information on a large number of thermodynamic properties and, if available, on the chemical composition of dense matter and on microphysical properties of the constituents. CompOSE not only allows direct downloading of data together with a bibliography on data-related publications, but also provides several tools to handle and customize data, for instance for extracting selected quantities, interpolation of tabulated data, or calculation of additional related quantities. A full documentation with detailed instructions can be found in the full manual [2,3]. Here, we present quick guides for potential providers of EoS data and for users of the CompOSE service. One word of caution is in order: CompOSE is designed to evolve and to be extended over time; thus, the presentation below shows the current status (July 2022) and will not be adapted in the future upon the adding of new features to the service.
If you make use of the tables provided by CompOSE, please cite the publications describing the respective EoS models (available on the CompOSE web page for each EoS data table), together with the original CompOSE publications [1,2,3] and the CompOSE website https://compose.obspm.fr.
2. Instructions for Providers of EoS Data
The success of CompOSE depends on the support of nuclear physicists providing their data. A collection of EoS models is already incorporated in the CompOSE database, however, a larger set of EoS from different models is highly desirable. Please contact the CompOSE core team (develop.compose@obspm.fr) if you wish to contribute.
2.1. Preparation of Tables
In the CompOSE database, the EoS is assumed to describe dense matter in thermodynamic equilibrium, i.e., thermal and mechanical equilibrium. In addition, it is assumed that all the constituents are in chemical equilibrium with respect to reactions mediated by the strong and electromagnetic interactions. Whether equilibrium with respect to weak -type reactions is assumed depends on the particular table. Tables designated for application to core-collapse supernovae or binary neutron star mergers do not, whereas the tables constructed to describe cold neutron star matter do, reducing in this case the number of independent particle number densities, i.e., thermodynamic parameters. For EoS models with strangeness-bearing particles, it is assumed that strangeness-changing weak interactions have enough time to equilibrate, in which case there is no constraint related to the strangeness density and the strangeness chemical potential vanishes. Except for the tables of pure hadronic and/or quark matter (without leptons), charge neutrality is assumed to hold. Neutrinos are never included in the present tables, since they are usually treated independently from the EoS in astrophysical simulations, not assuming thermodynamic equilibrium. Photons can be included in finite-temperature tables. In the case of EoS for pure-neutron matter, however, it is supposed that photons are not included.
Quantities in CompOSE are given in natural units (for details on unit conversion see the NIST (https://physics.nist.gov/cuu/Constants/index.html) or CODATA (https://www.codata.org) websites). Particle number densities of all particles i are given by , where is the particle number inside the volume V. For particles with half-integer spin at finite temperature, represents the net particle density, i.e., the difference between the number density of particles and antiparticles (see full CompOSE manual [2,3] for the possibility of entering particles and antiparticles separately). For particles with integer spin, particle and antiparticle number densities are given separately. The baryon number density is given by , where is the total baryonic number and the baryon number of a given particle, e.g., the baryon number for a quark is .
The hadronic (and quark) charge density is given by , where Q is the total electric charge and is the electric charge of a given particle. The prime indicates that the summation excludes leptons. For a nucleus , the baryon number and electric charge are the mass number and atomic number , respectively. Particle fractions are defined as [dimensionless].
The hadronic (and quark) charge fraction, from hereon simply charge fraction, is defined as [dimensionless]. In models with electrons and muons, charge neutrality requires , where is the lepton fraction (not considering neutrinos). Because of the imposed physical conditions, the state of the system is uniquely characterized by the three quantities temperature T [MeV], baryon number density [fm], and charge fraction . The latter variable is used because it is also defined in pure hadronic EoS models that do not include charged leptons.
Table 1 introduces an indexing scheme for the most relevant particles that identifies them uniquely (more can be added upon request—see the full manual). For a nucleus , the index is and, for the photon , the index is 600. Note that it should be stated in the accompanying information if a given EoS includes photon contributions. This should appear in a pdf file (the so-called ‘data sheet’) that includes a short characterisation of the EoS model, relevant references, the meaning of an index for the phases that appear in the tables, considered particle species, parameter ranges, additional quantities provided, etc.

Table 1.
Particle indices.
2.2. EoS Tables and Data Format
There are at least four files with numerical data required for an EoS to be included in the CompOSE repository: three files that specify the discretization scheme of the independent variables temperature, baryon number density, and charge fraction (eos.t, eos.nb, and eos.yq), and a file (eos.thermo) with the table of thermodynamic quantities. Additional data on the chemical composition and on microscopic quantities can be collected in two additional files (eos.compo and eos.micro).
The variables T, , and are given on a provider-defined grid in which each point is identified by three indices. The values corresponding to these indices are given in separate files (and should ideally have at least eight significant digits):
- temperatureT [MeV] in file eos.t, recommended to increase logarithmically (at least at large temperatures),
- baryon number density [fm] in file eos.nb, recommended to increase logarithmically,
- charge fraction [dimensionless] in file eos.yq, recommended to increase linearly in .
In Section 2.2.5 we list recommended ranges of these parameters for the different types of tables. In these files, the first two lines should be the minimum and maximum indices (representing the respective minimum and maximum values that are given). The following lines give the numerical values of the variables for the indices in ascending order. Each line of the data files eos.thermo, eos.compo, and eos.micro, except the first line in eos.thermo, starts with the indices corresponding to the three variables in the order T, , . In the particular case of equilibrium and zero temperature, the files eos.t and eos.yq are simply
0 1
0 1
0.00000000E+00 0.00000000E+00
2.2.1. Thermodynamic Properties
These are listed in the file eos.thermo. It contains three entries in the first line, namely, the masses of the neutron and proton in MeV, and an integer that indicates if the EoS contains leptons (1) or not (0). The remaining lines contain the following entries
corresponding to the indices for temperature, baryon number density, and charge fraction, followed by seven mandatory thermodynamic quantities. These are
- pressure divided by baryon number density (MeV),
- entropy per baryon (or entropy density per baryon number density) s,
- scaled and shifted baryon chemical potential ,
- scaled charge chemical potential ,
- scaled effective lepton chemical potential (set to zero in models without leptons) ,
- scaled and shifted free energy per baryon ,
- scaled and shifted energy per baryon .
An integer follows, indicating the absence (0) or presence () of additional optional thermodynamic quantities to be specified in the data sheet. If the table contains repeated rows with identical indices , , , only the last row is used.
From thermodynamic identities, the free energy density is , with particle chemical potentials and lepton numbers that do not distinguish between electrons and muons. In pure hadronic (and quark) models without leptons, it can be written as . In the case that charged leptons are present, charge neutrality requires . The condition of (neutrinoless) equilibrium corresponds to (assuming identical lepton chemical potentials of electrons and muons ) and .
2.2.2. Composition of Matter (Optional)
This is listed in the file eos.compo containing in all lines the entries
corresponding again to the indices for temperature, baryon number density, and charge fraction, followed by an index encoding the type of phase (chosen by provider and identified in the data sheet), number of particles (pairs) for which the composition is given, particle pairs in no particular order (particle indices from Table 1 followed by the respective particle charge fractions), number of particle quadruples, particle quadruples (particle indices from Table 1 followed by the respective average mass and charge numbers of the representative nucleus and respective combined charge fraction). In each quadruple, the index specifies a group of nuclei with average mass number , average charge number , and combined charge fraction . In the case that there are no quadruples to report, . The correlation between and should appear in the data sheet.
2.2.3. Stellar Information (Optional)
This is listed in the file eos.mr containing in all lines the entries
corresponding to the radius (in km), mass (in solar masses), and dimensionless tidal deformability of a family of cold -equilibrated spherical neutron stars obtained from the provided equation of state. The third column is optional.
2.2.4. Microscopic Information (Optional)
This is listed in the file eos.micro containing in all lines the entries
corresponding again to the indices for temperature, baryon number density, and charge fraction, followed by the number of stored quantities (pairs), the composite correlation indices that identify uniquely the particle or correlation with the physical quantity ( found in Table 1 and Table 2), and the microscopic quantity index ( found in Table 3). The microscopic quantities available so far are the Landau mass , the effective Dirac mass , the single-particle potential , the vector self-energy , the scalar self-energy , and the size of superconductivity or superfluidity pairing gaps (see full manual for more details).

Table 2.
Two-body correlation indices (with most relevant channel).

Table 3.
Indices for microscopic quantities.
2.2.5. Dimensionality of Tables
The recommended dimensions of the EoS data grids are:
- 3D: general-purpose EoS table with 1,462,860 data points, not including points with MeV when increasing logarithmically or . The temperature should start at MeV and the baryon number density at fm or below,
- 2D: zero-temperature EoS table with 18,361 data points. The baryon number density should start at fm or below,
- 2D: symmetric-matter EoS table with 24,381 data points, not including points with MeV when increasing logarithmically all the way. The temperature should start at MeV and the baryon number density at fm or below,
- 2D: neutron-matter EoS table with = 24,381 data points, not including points with MeV when increasing logarithmically all the way. The temperature should start at MeV and the baryon number density at fm or below,
- 2D: EoS table of -equilibrated matter with = 24,381 data points, not including points with MeV when increasing logarithmically all the way. The charge fraction is determined by the condition of charge neutrality and weak chemical equilibrium. The temperature should start at MeV and the baryon number density at fm or below,
- 1D: EoS table of cold-symmetric matter with data points with and MeV. The baryon number density should start at fm or below,
- 1D: EoS table of cold-neutron matter with data points with and . The baryon number density should start at fm or below,
- 1D: EoS table of cold -equilibrated matter with data points with T = 0 MeV. The baryon number density should start at fm or below. Charge fraction is determined by the conditions of charge neutrality and weak chemical equilibrium. This table can be used directly by the library LORENE (https://lorene.obspm.fr) to generate neutron-star models, and among others extract the maximum mass.
3. Instructions for Users
There are two equivalent ways to handle and customize data provided by the CompOSE website. Both are based on the compose software, which is free and anyone can download it. A very convenient way to handle and customize data is thus to use it directly. Alternatively, there is a web interface to the software, accesible via the “Compute” button for each EoS table, which is free but password restricted. This quick guide describes the basic procedures to obtain a table with EoS data with the help of a number of examples by direct use of the software. It is prepared in particular for first-time users in order to get familiar with the files, the program and the handling. See Appendix A for a summary of the notation we use.
In this quick guide only the preparation of data tables in ASCII format is described using a LINUX based operation system. For an output of data in the HDF5 format, please refer to the full CompOSE manual [2,3].
3.1. Preparation of Program and Files
Download the compose code from the software section on the CompOSE web page, where a link to the CompOSE gitlab can be found (To clone the git repository, please use the https protocol). You will need the files compose.f90, composemodules.f90 and Makefile. Copy them to the same directory. Generate the executable by typing
make compose
The provided version of the Makefile employs the gfortran compiler, available on many LINUX systems. For another compiler, you have to modify the Makefile accordingly.
If during compilation an error related to HDF5 appears, check line 49 of the file Makefile. Ensure that it reads
HDF5 = 0
3.1.1. EoS Data
There are presently four families of EoS tables available in CompOSE, i.e., General Purpose EoS, Neutron Matter EoS, Cold Neutron Star EoS, and Cold Matter EoS. You will see this option when clicking on “EoS” and then on “Families” in the left column of the CompOSE web page. The code should run with each of them. Alternatively, you can find the EoS model of your preferred author with the help of the bibliography search on the web page. The files for download can be found by clicking on ’Details’ for each EoS model. Download the files for your preferred EoS table and move them to the same directory as the code. Note that, by default, the data from all EoS models have the same name. Thus, you should either remove all previous EoS data files before running a new model or create a different directory for each model.
3.1.2. Input Parameters
The code allows calculation of many different quantities, and surely not every user needs all of them. In addition, some of them are only available for selected EoS tables. Therefore, before running the code, the grid in thermodynamic variables (temperature T, baryon number density , and charge fraction ), as well as the desired output quantities have to be specified. This is done with two input parameter files, eos.parameters for the grid and eos.quantities for the output. Three examples, described below, are available on the web page in the ’software’ section. Note that if you do not remove the older versions of the input files eos.parameters and eos.quantities, you will be prompted to overwrite them upon creating new versions.
3.1.3. Generating the Parameter Files
Run the code by typing
./compose
in a terminal. You will then be prompted to select from three options. Selecting task ‘1’ will guide you to the generation of the eos.quantities file, specifying the needed output. Task ‘2’ will guide you to the generation of the eos.parameters file, specifying the grid in thermodynamic variables. Just follow the instructions. Keep in mind that the code is interpolating the EoS data, it is thus not possible to calculate outside the ranges given by your EoS data tables. You can check the ranges for each table on the web page, or in the files eos.t, eos.nb, and eos.yq.
3.2. Running the Code
Once eos.parameters and eos.quantities are present in your directory, you can run the code with option ‘3’
./compose
3
This should generate in particular a file eos.table. The first three columns contain the thermodynamic grid in the order T (MeV), (fm), and with the followings columns providing the quantities specified in eos.quantities in the same order and recalled by the terminal output.
Up to seven other files are generated, eos.init, eos.report, eos.beta, eos.errdistr, eos.info.json, eos.nb.ns, and eos.thermo.ns. These files are usually not of interest for the first-time user, see the full manual for details.
3.3. Examples
Download the example files from the CompOSE web page ‘software’ section. They contain four distinct examples for running the compose code.
3.3.1. Generating a Table for -Equilibrated Matter from a General Purpose EoS
The following steps will allow you to run the compose code and generate a table containing the energy per baryon, pressure, and scaled baryon chemical potential () for -equilibrated matter at a temperature of keV. This table can be used for solving the equations describing cold -equilibrated neutron stars. The example has been obtained with the FOP(SFHoY) EoS, see http://compose.obspm.fr/eos/118/. Download eos-beta.zip from the software section and unpack it. Then enter,
cp eos.parameters.beta eos.parameters
cp eos.quantities.beta eos.quantities
./compose
3
You can find a snapshot when running compose for this particular case in Appendix B.
The file eos.table should then contain the columns
for -equilibrated matter, where the units are given in parentheses. You can compare the output with the provided data in eos.table.beta. The result for the electron fraction as function of baryon number density is shown in Figure 1.
| T | p | ||||
| [MeV] | [fm] | [MeV] | [MeV fm] | [MeV] |
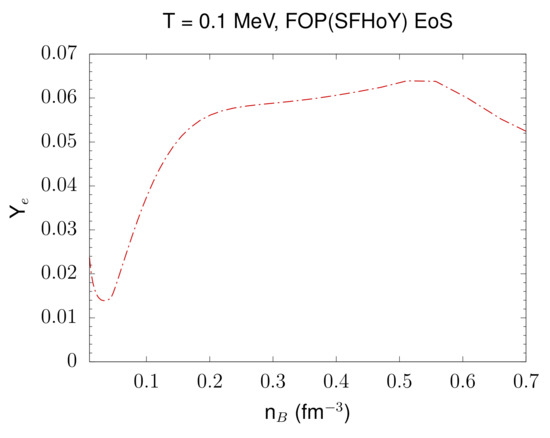
Figure 1.
The electron fraction in -equilibrium for the FOP(SFHoY) EoS at MeV as function of baryon number density.
Please note that -equilibrium is defined here via vanishing lepton chemical potential and obtained by simple root finding. At finite temperature or for trapped neutrinos, it does not necessarily correspond to the physical -equilibrium.
You can run the present example with any general purpose table containing electrons. Please note that potentially you have to adapt the temperature to the lowest entry in the respective table and the range in baryon number density in the file eos.parameters in lines 8 (minimum values, order ) and 9 (maximum values, order ). Output is generated in this case only if a solution for -equilibrium is found within the ranges in of the table.
3.3.2. Generating a Table at Fixed Entropy per Baryon from a General Purpose EoS
The following steps will allow you to run the compose code and generate a table containing the energy par baryon, pressure, and scaled baryon chemical potential () at a constant fixed entropy per baryon, and , as function of baryon number density. The example has been obtained with the OMHN(DD2Y) EoS, see http://compose.obspm.fr/eos/104/. Download eos-s.zip from the software section and unpack it. Then enter,
cp eos.parameters.s eos.parameters
cp eos.quantities.s eos.quantities
./compose
3
You can find a snapshot when running compose for this particular case in Appendix C.
The file eos.table should then contain the columns
with the units given in parentheses. Figure 2 displays the result for the temperature as function of baryon number density. You can compare the ouput with the provided data in eos.table.s. You can run the present example with any general purpose table. If the option of fixed entropy per baryon is chosen, the first entries in lines 8–11 of eos.parameters concern the minimum and maximum value of s, the number of points, and logarithmic/linear scaling in entropy. Since the EoS tables are generated as a function of temperature, and depend on baryon number density and hadronic charge fraction. Output is generated in this case only if a solution for the given value of fixed entropy is found within the ranges in temperature of the table for the given value of and .
| T | s | p | ||||
| [MeV] | [fm] | [] | [MeV] | [MeV fm] | [MeV] |
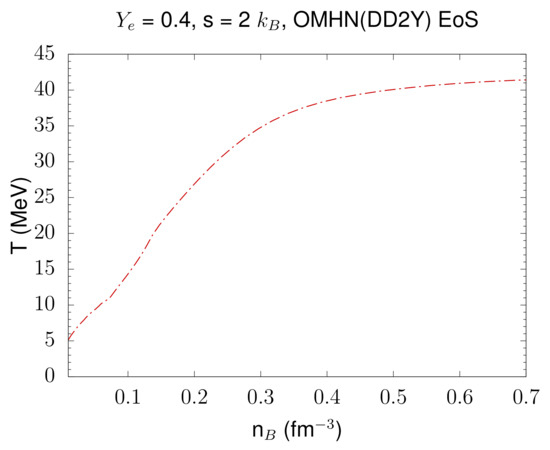
Figure 2.
The temperature at constant entropy per baryon and electron fraction for the OMHN(DD2Y) EoS as function of baryon number density.
3.3.3. Extracting Composition Information from a General Purpose Table
The following steps will allow you to run the compose code and generate a table containing the energy per baryon and pressure, as well as all particle fractions as a function of temperature for a general purpose EoS. In the present example, particle fractions for electrons, nucleons, and hyperons are listed, as well as light nuclei and one average heavy nucleus. The Dirac effective mass for neutrons is given too. The example has been obtained with the FOP(SFHoY) EoS, see http://compose.obspm.fr/eos/118/. If you did not yet download it, get eos-3d.zip from the software section and unpack it. Then enter,
cp eos.parameters.3d eos.parameters
cp eos.quantities.3d eos.quantities
./compose
3
You can find a snapshot when running compose for this particular case in Appendix D.
The file eos.table should then contain in the columns
at and fm for different values of the temperature. The symbol denotes the occurrence of 12 columns of this quantity, in the order , p, , , , , , , , , , .
| T | p | |||||||||
| [MeV] | [fm] | [MeV] | [MeV fm] |
You can compare the output with the provided data in eos.table.3d, from which some particle fractions are shown in Figure 3. You can run the present example with any general purpose table. Please note that you will potentially need to adapt the temperature to the lowest entry in the respective table and the range in baryon number density in the file eos.parameters in lines 8 (minimum values) and 9 (maximum values). If you employ a table not containing hyperons, then the number of pairs in line 6 has to be adapted and the indices starting with 100 in line 8 have to be removed. In the same way, if your table does not contain information about individual nuclei, then in line 6 the number of pairs has to be adapted and the four-digit entries in line 8 have to be removed. If the Dirac effective mass is not available, line 10 should contain a 0 and line 12 should be empty. If you run compose with task ‘1’, you will be guided through the generation of a new eos.quantities file.
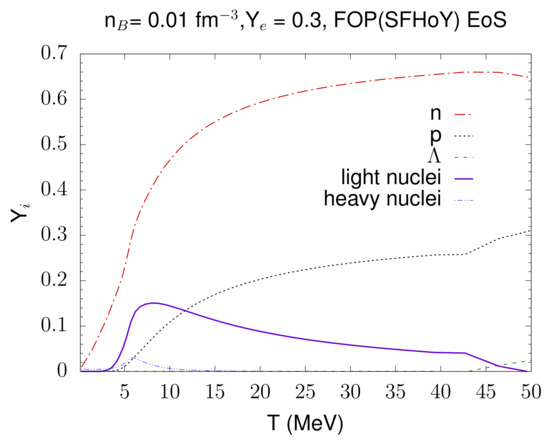
Figure 3.
Different particle fractions as function of temperature for the FOP(SFHoY) EoS at = 0.01 fm and .
3.3.4. Extracting Sound Speed and Adiabatic Index from a Cold Neutron Star Table
The following steps will allow you to run the compose code and generate a table containing the energy per baryon, pressure, and scaled baryon chemical potential (), as well as squared speed of sound, adiabatic index, and entropy per baryon as a function of baryon number density for a cold neutron star EoS. The example has been obtained with the RG(SkA) EoS, see http://compose.obspm.fr/eos/96/. Download eos-ns.zip from the software section and unpack it. Then enter,
cp eos.parameters.ns eos.parameters
cp eos.quantities.ns eos.quantities
./compose
3
You can find a snapshot when running compose for this particular case in Appendix E.
The file eos.table should then contain the columns
at MeV for -equilibrated matter. You can compare the output with the provided data in eos.table.ns, the result for the sound speed is shown in Figure 4. You can run the present example with any cold neutron star table. Please note that you will potentially need to adapt to the lowest entry in the respective table in the file eos.parameters in line 8 and the maximum value in line 9.
| T | p | s | ||||||
| [MeV] | [fm] | [MeV] | [MeV fm] | [MeV] | [] | [] |
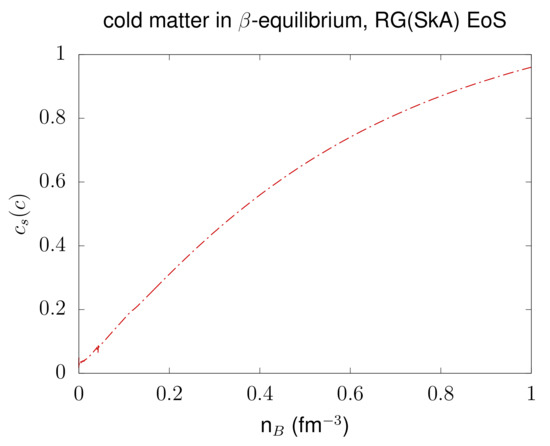
Figure 4.
Sound speed as function of baryon number density for the cold -equilibrated RG(SkA) EoS.
Author Contributions
Set up of the data base and compose software—M.O. and S.T.; web site and web tools—M.M. and M.O.; writing—V.D. and L.T.; review and editing—V.D., M.M., M.O., C.P., L.T. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
CompOSE would not be possible without the financial and organisatorial support from a large number of institutions and individual contributors. We gratefully acknowledge support by the CompStar network of the European Science Foundation (ESF), the birthplace of the CompOSE project, the COST actions NewCompStar, and PHAROS, a grant from the Polish Ministry for Science and Higher Education (MNiSW) supporting the “CompStar” activity, by the Instytut Fizyki Teoretycznej of the Uniwersytet Wrocławski, the National Science Centre Poland (Narodowe Centrum Nauki, NCN) within the “Maestro” programme under contract No. DEC-2011/02/A/ST2/00306, by the “hadronphysics3” network within the seventh framework program of the European Union, by the GSI Helmholtzzentrum für Schwerionenforschung GmbH, by the Helmholtz International Center for FAIR within the framework of the LOEWE program launched by the state of Hesse via the Technical University Darmstadt, by the Helmholtz Association (HGF) through the Nuclear Astrophysics Virtual Institute (VH-VI-417), by the ExtreMe Matter Institute EMMI in the framework of the Helmholtz Alliance “Cosmic Matter in the Laboratory”, by the DFG cluster of excellence “Origin and Structure of the Universe”, by the DFG through grant SFB 1245, by the SN2NS project ANR-10-BLAN-0503. L.T. also acknowledges support from CEX2020-001058-M (Unidad de Excelencia “María de Maeztu”), PID2019-110165GB-I00 financed by the spanish MCIN/AEI/10.13039/501100011033/, as well as by the EU STRONG-2020 project, under the program H2020-INFRAIA-2018-1 grant agreement no. 824093, and the CRC-TR 211 “Strong-interaction matter under extreme conditions”- project No. 315477589—TRR 211. V.D. acknowledges support from the National Science Foundation under grants PHY1748621, MUSES OAC-2103680, and NP3M PHY-2116686. C.P. acknowledges support from the Fundação para a Ciência e Tecnologia under the Projects UIDP/04564/2020 and UIDB/04564/2020.
Data Availability Statement
All data are publicly available on https://compose.obspm.fr.
Acknowledgments
We thank Jean-Yves Giot for creating the first version of the CompOSE web site.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Notations

Table A1.
Notations used in the Quick Guides.
Table A1.
Notations used in the Quick Guides.
| Symbol | Quantity | Unit |
|---|---|---|
| T | temperature | MeV |
| baryon number density | fm | |
| number density fraction of particle i | - | |
| hadronic (and quark) charge fraction | - | |
| p | pressure | MeV fm |
| energy per baryon | MeV | |
| neutron mass | MeV | |
| baryon chemical potential | MeV | |
| speed of sound | c | |
| s | entropy per baryon |
Appendix B. Example of a Table for -Equilibrated Matter from a General Purpose EoS

Figure A1.
Snapshot when running compose for generating a table for -equilibrated matter from a general purpose EoS.
Appendix C. Example of a Table at Fixed Entropy per Baryon from a General Purpose EoS

Figure A2.
Snapshot when running compose for generating a table at fixed entropy per baryon from a general purpose EoS.
Appendix D. Example of the Composition Information from a General Purpose Table

Figure A3.
Snapshot when running compose for extracting compositional information from a general purpose table.
Appendix E. Example of the Sound Speed and Adiabatic Index from a Cold Neutron Star Table

Figure A4.
Snapshot when running compose for computing sound speed and adiabatic index from a cold neutron star EoS.
References
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Typel, S.; Oertel, M.; Klähn, T. CompOSE CompStar online supernova equations of state harmonising the concert of nuclear physics and astrophysics compose.obspm.fr. Phys. Part. Nucl. 2015, 46, 633. [Google Scholar] [CrossRef]
- Typel, S.; Oertel, M.; Klähn, T.; Chatterjee, D.; Dexheimer, V.; Ishizuka, C.; Mancini, M.; Novak, J.; Pais, H.; Providência, C.; et al. CompOSE Reference Manual. arXiv 2022, arXiv:2203.03209. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
