Colliding and Fixed Target Mode in a Single Experiment—A Novel Approach to Study the Matter under New Extreme Conditions
Abstract
1. Introduction
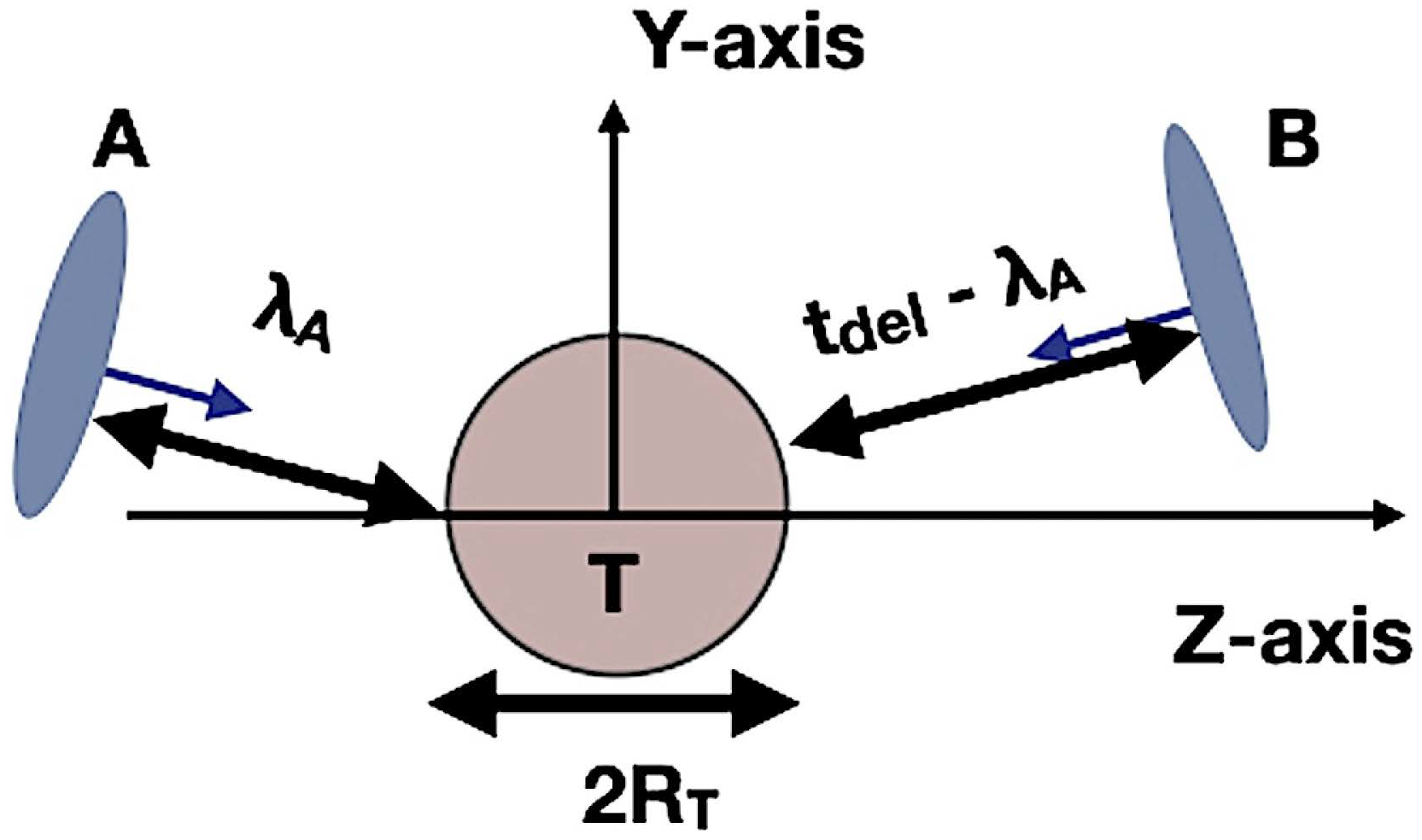
2. The Triple Nuclear Collisions Method
2.1. Rate Estimates of the Triple Nuclear Collisions
2.2. Discussion of Different Types of Fixed Targets
3. Possible Signatures of TNC
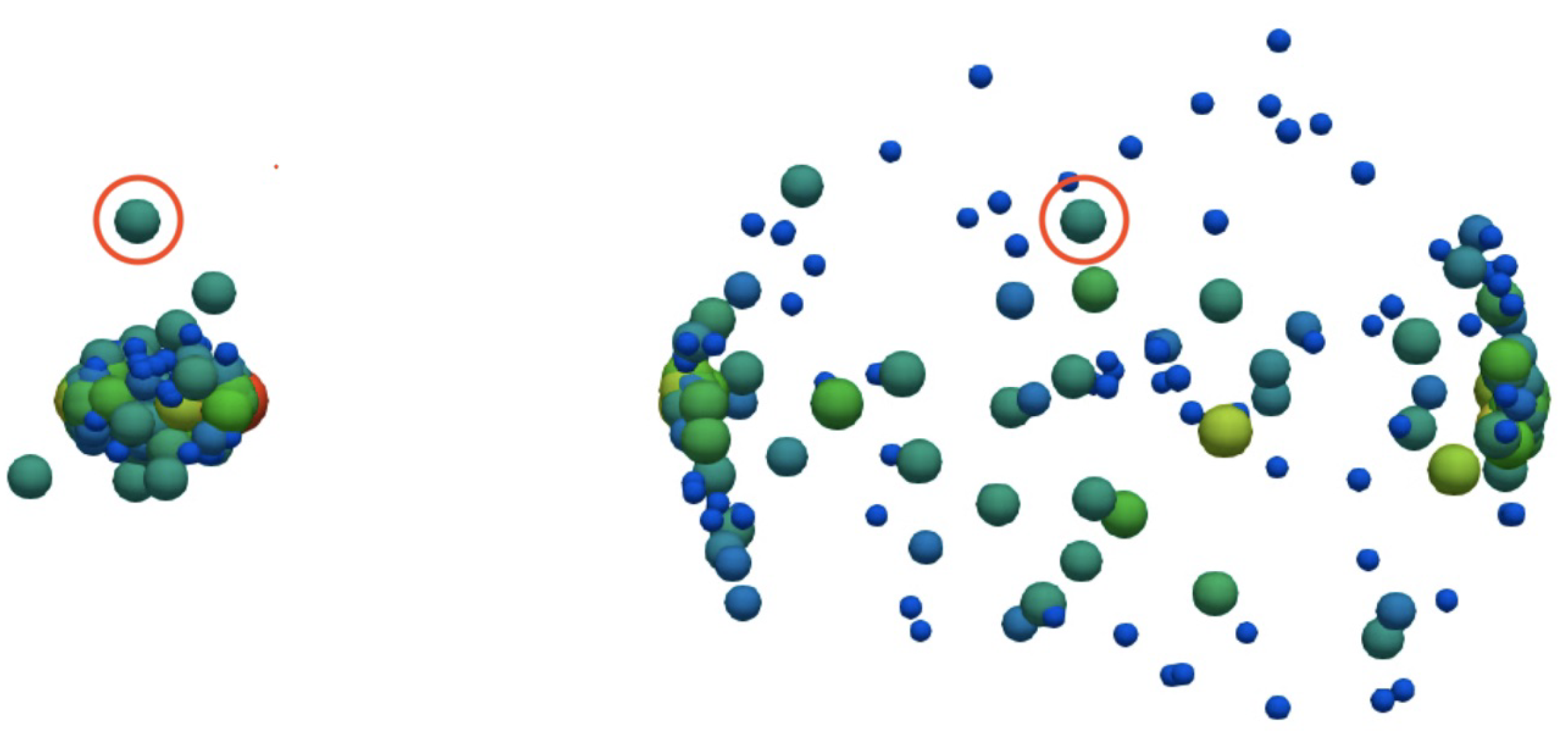
4. Evolution of Matter in Central Cell in Pb+Pb+Pb Collisions
5. Conclusions and Perspectives
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Cassing, W.; Palmese, A.; Moreau, P.; Bratkovskaya, E.L. Chiral symmetry restoration versus deconfinement in heavy-ion collisions at high baryon density. Phys. Rev. C 2016, 93, 014902. [Google Scholar] [CrossRef]
- Palmese, A.; Cassing, W.; Seifert, E.; Steinert, T.; Moreau, P.; Bratkovskaya, E.L. Chiral symmetry restoration in heavy-ion collisions at intermediate energies. Phys. Rev. C 2016, 94, 044912. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Ivanytskyi, A.I.; Oliinychenko, D.R.; Sagun, V.V.; Mishustin, I.N.; Rischke, D.H.; Satarov, L.M.; Zinovjev, G.M. Thermodynamically anomalous regions and possible new signals of mixed-phase formation. Eur. Phys. J. A 2016, 52, 175. [Google Scholar] [CrossRef]
- Sun, K.-J.; Sun, K.J.; Chen, L.W.; Ko, C.M.; Xu, Z. Probing QCD critical fluctuations from light nuclei production in relativistic heavy-ion collisions. Phys. Lett. B 2017, 774, 103. [Google Scholar] [CrossRef]
- Moreau, P.; Soloveva, O.; Grishmanovskii, I.; Voronyuk, V.; Oliva, L.; Song, T.; Kireyeu, V.; Coci, G.; Bratkovskaya, E. Properties of the quark-gluon plasma created in heavy-ion collisions. Astron. Nachr. 2021, 342, 715. [Google Scholar] [CrossRef]
- Adolfsson, J.; Andronic, A.; Bierlich, C.; Bozek, P.; Chakraborty, S.; Christiansen, P.; Chinellato, D.D.; Fries, R.J.; Gustafson, G.; van Hees, H.; et al. QCD challenges from p–p to A–A collisions. Eur. Phys. J. A 2020, 56, 288. [Google Scholar] [CrossRef]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron-star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef]
- Orsaria, M.G.; Malfatti, G.; Mariani, M.; Ranea-Sandoval, I.F.; García, F.; Spinella, W.M.; Contrera, G.A.; Lugones, G.; Weber, F. Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G 2019, 46, 073002. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic Models for Ultrarelativistic Heavy Ion Collisions. Prog. Part. Nucl. Phys. 1998, 41, 225. [Google Scholar] [CrossRef]
- Bleicher, M.; Zabrodin, E.; Spieles, C.; Bass, S.A.; Ernst, C.; Soff, S.; Bravina, L.; Belkacem, M.; Weber, H.; Stocker, H.; et al. Relativistic Hadron-Hadron Collisions in the Ultra-Relativistic Quantum Molecular Dynamics Model. J. Phys. G 1999, 25, 1859. [Google Scholar] [CrossRef]
- Hillmann, P.; Steinheimer, J.; Reichert, T.; Gaebel, V.; Bleicher, M.; Sombun, S.; Herold, C. and Limphirat, A. First, second, third and fourth flow harmonics of deuterons and protons in Au+Au reactions at 1.23 AGeV. J. Phys. G Nucl. Part. Phys. 2020, 47, 055101. [Google Scholar] [CrossRef]
- Petersen, H.; Steinheimer, J.; Burau, G.; Bleicher, M.; Stöcker, H. A Fully Integrated Transport Approach to Heavy Ion Reactions with an Intermediate Hydrodynamic Stage. Phys. Rev. C 2008, 78, 044901. [Google Scholar] [CrossRef]
- Batyuk, P.; Blaschke, D.; Bleicher, M.; Ivanov, Y.; Karpenko, I.; Merts, S.; Nahrgang, M.; Petersen, H.; Rogachevsky, O. Event simulation based on three-fluid hydrodynamics for collisions at energies available at the Dubna Nuclotron-based Ion Collider Facility and at the Facility for Antiproton and Ion Research in Darmstadt. Phys. Rev. C 2016, 94, 044917. [Google Scholar] [CrossRef]
- Karpenko, I.; Huovinen, P.; Petersen, H.; Bleicher, M. Estimation of the shear viscosity at finite net-baryon density from A+A collision data at = 7.7–200 GeV. Phys. Rev. C 2015, 91, 064901. [Google Scholar] [CrossRef]
- ALICE Collaboration. Centrality dependence of the pseudorapidity density distribution for charged particles in Pb–Pb collisions at =2.76 TeV. Phys. Lett. B 2013, 726, 610. [Google Scholar] [CrossRef]
- Gutierrez, G.; Reyes, M.A. Fixed target experiments at the Fermilab Tevatron. Int. J. Mod. Phys. A 2014, 29, 1446008. [Google Scholar] [CrossRef]
- Massacrier, L.; Trzeciak, B.; Fleuret, F.; Hadjidakis, C.; Kikola, D.; Lansberg, J.P.; Shao, H.S. Feasibility Studies for Quarkonium Production at a Fixed-Target Experiment Using the LHC Proton and Lead Beams (AFTER@LHC). Adv. High Energy Phys. 2015, 2015, 986348. [Google Scholar] [CrossRef]
- Massacrier, L.; Anselmino, M.; Arnaldi, R.; Brodsky, S.J.; Chambert, V.; Den Dunnen, W.; Didelez, J.P.; Genolini, B.; Ferreiro, E.G.; Fleuret, F.; et al. Studies of Transverse-Momentum-Dependent distributions with A Fixed-Target ExpeRiment using the LHC beams (AFTER@LHC). Int. J. Mod. Phys. Conf. Ser. 2016, 40, 1660107. [Google Scholar] [CrossRef]
- Massacrier, L.; Anselmino, M.; Arnaldi, R.; Brodsky, S.J.; Chambert, V.; Da Silva, C.; Didelez, J.P.; Echevarria, M.G.; Ferreiro, E.G.; Fleuret, F.; et al. Physics perspectives with AFTER@LHC (A Fixed Target ExpeRiment at LHC). EPJ Web Conf. 2018, 171, 10001. [Google Scholar] [CrossRef]
- Meehan, K.C.; STAR Collaboration. Fixed Target Collisions at STAR. Nucl. Phys. A 2016, 956, 878. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Amarian, M.; Andrus, A.; Aschenauer, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetissian, E.; et al. The HERMESsm polarized hydrogen and deuterium gas target in the HERA electron storage ring. Nucl. Instrum. Meth. A 2005, 540, 68. [Google Scholar] [CrossRef]
- Vassiliev, Y.; Aushev, V.; Ehret, K.; Funcke, M.; Sever, S.I.; Pavlenko, Y.; Pugatch, V.; Spratte, S.; Symalla, M.; Tkatch, N.; et al. Multi-target operation at the HERA-B experiment. AIP Conf. Proc. 2000, 512, 359. [Google Scholar]
- Hast, C.; Ehret, K.; Hofmann, W.; Khan, S.; Knöpfle, K.T.; Reber, M.; Rieling, J.; Spahn, M.; Spengler, J.; Lohse, T.; et al. Test of the internal halo targets in the HERA proton ring. Nucl. Instrum. Meth. A 1995, 354, 224. [Google Scholar] [CrossRef]
- LHCb Collaboration. The LHCb Detector at the LHC. JINST 2008, 3, S08005. [Google Scholar]
- Bursche, A.; Manca, G.; Neri, N.; Fleuret, F.; Schmelling, M.; Robbe, P.; Dembinski, H.P.; Graziani, G.; Pappalardo, L.L.; Ferro-Luzzi, M.; et al. Physics Opportunities with the Fixed-Target Program of the LHCb Experiment Using an Unpolarized Gas Target; Tech. Rep. LHCb-PUB-2018-015. CERN-LHCb-PUB-2018-015; CERN: Geneva, Switzerland, 2018. [Google Scholar]
- Ferro-Luzzi, M. Proposal for an absolute luminosity determination in colliding beam experiments using vertex detection of beam-gas interactions. Nucl. Instrum. Meth. A 2005, 553, 388. [Google Scholar] [CrossRef][Green Version]
- The LHCb Collaboration. LHCb SMOG Upgrade; CERN-LHCC-2019-005, LHCB-TDR-020; (Technical design report. LHCb); CERN: Geneva, Switzerland, 2019. [Google Scholar]
- LHCb Collaboration; Aaij, R. First measurement of charm production in fixed-target configuration at the LHC. Phys. Rev. Lett. 2019, 122, 132002. [Google Scholar] [CrossRef]
- Pugatch, V. Heavy-ion and fixed-target physics in LHCb. Ukr. J. Phys. 2019, 64, 619. [Google Scholar] [CrossRef]
- Fedorovich, O.; Kovalchuk, O.; Pugatch, V.; Okhrimenko, O.; Storozhyk, D.; Kyva, V. Metal micro-detectors: Development of ‘transparent’ position sensitive detector for beam diagnostics. Voprosy Atomnoj Nauki i Tekhniki 2012, 82, 196. [Google Scholar]
- Pugatch, V. Physics and Techniques of the Fixed Metal Microstrip Target for the LHCb Experiment. In Proceedings of the Int. Conference CERN-Ukraine Cooperation: Current State and Prospects, Kharkiv, Ukraine, 15 May 2018; Available online: https://cds.cern.ch/record/2658000 (accessed on 8 May 2019).
- Vitiuk, O.V.; Pugatch, V.M.; Bugaev, K.A.; Panasiuk, P.P.; Yakovenko, N.S.; Grinyuk, B.E.; Zherebtsova, E.S.; Bleicher, M.; Bravina, L.V.; Taranenko, A.V.; et al. Triple nuclear collisions—A new method to explore the matter properties under new extreme conditions. Eur. Phys. J. Web Conf. 2022, 259, 13012. [Google Scholar] [CrossRef]
- Bediaga, I.; LHCb Collaboration; LHCb SMOG Upgrade. LHCb Technical Design Report-020. 2019. Available online: https://cds.cern.ch/record/2673690/files/LHCB-TDR-020.pdf (accessed on 8 May 2019).
- Hartmann, N.; Hartmann, G.; Heider, R.; Wagner, M.S.; Ilchen, M.; Buck, J.; Lindahl, A.O.; Benko, C.; Grünert, J.; Krzywinski, J.; et al. Attosecond time-energy structure of X-ray free-electron laser pulses. Nat. Photonics 2018, 12, 215. [Google Scholar] [CrossRef]
- Barschel, C.; Bernhard, J.; Bersani, A.; Boscolo Meneguolo, C.; Bruce, R.; Calviani, M.; Carassiti, V.; Cerutti, F.; Chiggiato, P.; Ciullo, G.; et al. LHC Fixed Target Experiments: Report from the LHC Fixed Target Working Group of the CERN Physics Beyond Colliders Forum; CERN Yellow Reports: Monographs, CERN-2020-004; CERN: Geneva, Switzerland, 2020. [Google Scholar]
- Pugatch, V.; Sivtsov, G.; Glushko, A.; Pitatelev, G.; Popov, S.; Voitsechovsky, B.; Toporkov, D. Superthin internal target for storage rings. In Proceedings of the Cyclotrons and Their Applications. Proceedings of the 13th International Conference, Vancouver, BC, Canada, 6–10 July 1992; Available online: https://accelconf.web.cern.ch/c92/papers/vii-07.pdf (accessed on 1 August 1992).
- Pugatch, V.; Sivtsov, G.; Glushko, A.; Pitatelev, G.; Popov, S.; Voitsechovsky, B.; Toporkov, D. Laser diagnostics system for a super-thin internal target for storage rings. Hyperfine Interaction. Hyperfine Interact. 1992, 74, 314. [Google Scholar] [CrossRef]
- Sombun, S.; Tomuang, K.; Limphirat, A.; Hillmann, P.; Herold, C.; Steinheimer, J.; Yan, Y.; Bleicher, M. Deuteron production from phase-space coalescence in the UrQMD approach. Phys. Rev. C 2019, 99, 014901. [Google Scholar] [CrossRef]
- ALICE Collaboration. Charged-particle multiplicities in proton–proton collisions at = 0.9 to 8 TeV. Eur. Phys. J. C 2017, 77, 33. [Google Scholar] [CrossRef]
- ALICE Collaboration. Centrality dependence of π, K, and p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- ALICE Collaboration. Production of charged pions, kaons and protons at large transverse momenta in pp and Pb–Pb collisions at =2.76 TeV. Phys. Lett. B 2014, 736, 196. [Google Scholar] [CrossRef]
- ALICE Collaboration. Centrality dependence of the nuclear modification factor of charged pions, kaons, and protons in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2016, 93, 034913. [Google Scholar] [CrossRef]
- Deb, S.; Sahu, D.; Sahoo, R.; Pradhan, A.K. Bose-Einstein condensation of pions in proton-proton collisions at the Large Hadron Collider using non-extensive Tsallis statistics. Eur. Phys. J. A 2021, 57, 158. [Google Scholar] [CrossRef]
- Chodos, A.J.R.L.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. New extended model of hadrons. Phys. Rev. D 1974, 9, 3471. [Google Scholar] [CrossRef]
- Wong, C.Y. Introduction to High-Energy Heavy Ion Collisions; World Scientific: Singapore, 1994. [Google Scholar]
- Florkowski, W. Phenomenology of Ultra-Relativistic Heavv-Ion Collisions; World Scientific: Singapore, 2010. [Google Scholar]
- Borsanyi, S.; Fodor, Z.; Guenther, J.N.; Kara, R.; Katz, S.D.; Parotto, P.; Pasztor, A.; Ratti, C.; Szabó, K.K. QCD crossover at finite chemical potential from lattice simulations. Phys. Rev. Lett. 2020, 125, 052001. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Sagun, V.V.; Ivanytskyi, A.I.; Yakimenko, I.P.; Nikonov, E.G.; Taranenko, A.V.; Zinovjev, G.M. Going beyond the second virial coefficient in the hadron resonance gas model. Nucl. Phys. A 2018, 970, 133. [Google Scholar] [CrossRef]
- Sagun, V.V.; Bugaev, K.A.; Ivanytskyi, A.I.; Yakimenko, I.P.; Nikonov, E.G.; Taranenko, A.V.; Greiner, C.; Blaschke, D.B.; Zinovjev, G.M. Hadron resonance gas model with induced surface tension. Eur. Phys. J. A 2018, 54, 6–100. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Vitiuk, O.V.; Grinyuk, B.E.; Sagun, V.V.; Yakovenko, N.S.; Ivanytskyi, O.I.; Zinovjev, G.M.; Blaschke, D.B.; Nikonov, E.G.; Bravina, L.V.; et al. Second virial coefficients of light nuclear clusters and their chemical freeze-out in nuclear collisions. Eur. Phys. J. A 2020, 56, 293. [Google Scholar] [CrossRef]
- Shiltsev, V.; Zimmermann, F. Modern and Future Colliders. Rev. Mod. Phys. 2021, 93, 015006. [Google Scholar] [CrossRef]
- Herr, W.; Muratori, B. Contribution to: CERN Accelerator School and DESY Zeuthen, Germany; Brandt, D., Ed.; CERN: Geneva, Switzerland, 2003. [Google Scholar] [CrossRef]
- Iida, K.; Kohama, A.; Oyamatsu, K. Formula for Proton-Nucleus Reaction cross Section at Intermediate Energies and Its Application. J. Phys. Soc. Jpn. 2007, 76, 044201. [Google Scholar] [CrossRef]
- Tanabashi, M. Particle Data Group. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Krane, K.S. Introductory Nuclear Physics; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC:Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitiuk, O.V.; Pugatch, V.M.; Bugaev, K.A.; Yakovenko, N.S.; Panasiuk, P.P.; Zherebtsova, E.S.; Dobishuk, V.M.; Chernyshenko, S.B.; Grinyuk, B.E.; Sagun, V.; et al. Colliding and Fixed Target Mode in a Single Experiment—A Novel Approach to Study the Matter under New Extreme Conditions. Particles 2022, 5, 245-264. https://doi.org/10.3390/particles5030022
Vitiuk OV, Pugatch VM, Bugaev KA, Yakovenko NS, Panasiuk PP, Zherebtsova ES, Dobishuk VM, Chernyshenko SB, Grinyuk BE, Sagun V, et al. Colliding and Fixed Target Mode in a Single Experiment—A Novel Approach to Study the Matter under New Extreme Conditions. Particles. 2022; 5(3):245-264. https://doi.org/10.3390/particles5030022
Chicago/Turabian StyleVitiuk, Oleksandr V., Valery M. Pugatch, Kyrill A. Bugaev, Nazar S. Yakovenko, Pavlo P. Panasiuk, Elizaveta S. Zherebtsova, Vasyl M. Dobishuk, Sergiy B. Chernyshenko, Borys E. Grinyuk, Violetta Sagun, and et al. 2022. "Colliding and Fixed Target Mode in a Single Experiment—A Novel Approach to Study the Matter under New Extreme Conditions" Particles 5, no. 3: 245-264. https://doi.org/10.3390/particles5030022
APA StyleVitiuk, O. V., Pugatch, V. M., Bugaev, K. A., Yakovenko, N. S., Panasiuk, P. P., Zherebtsova, E. S., Dobishuk, V. M., Chernyshenko, S. B., Grinyuk, B. E., Sagun, V., & Ivanytskyi, O. (2022). Colliding and Fixed Target Mode in a Single Experiment—A Novel Approach to Study the Matter under New Extreme Conditions. Particles, 5(3), 245-264. https://doi.org/10.3390/particles5030022






