Abstract
We present the current status of the performance studies of hyperon directed flow measurement with the CBM experiment at the future FAIR facility in Darmstadt. Kalman Filter mathematics is used to reconstruct weak decay kinematics, while the Particle Finder Simple package is used to optimize criteria for hyperon candidate selection. Directed flow of hyperons is studied as a function of rapidity, transverse momentum and collision centrality. The effects on flow measurement due to non-uniformity of the CBM detector response in the azimuthal angle, transverse momentum and rapidity are corrected using the QnTools analysis framework.
1. Introduction
The main goal of the Compressed Baryonic Matter (CBM) experiment at the future Facility for Antiproton and Ion Research (FAIR) in Darmstadt is to study highly compressed baryonic matter produced by heavy-ion collisions. The SIS-100 accelerator will provide heavy-ion beams with momentum of GeV/ and an interaction rate of up to Hz. This will allow investigation of the QCD matter at temperatures up to approximately 120 MeV and net baryon densities 5–6 times the normal nuclear density. Experimental studies under these conditions are also important for understanding the properties of the neutron stars and evolution of the neutron star mergers [1].
Strange quarks are produced at the early stage of the collision of heavy ions. They provide information about the equation of state of the QCD matter in the high baryon density phase where the yield of strange quarks is expected to be comparable with that of light quarks [2,3]. According to hadronic transport models, (multi)-strange hyperons are produced in sequential collisions involving kaons and s and, therefore, are sensitive to the density of the hot matter created in the nuclei overlap. This sensitivity is largest at beam energies close to the production threshold in elementary collisions, and it is expected to shed light on the compressibility of nuclear matter [4,5].
The measurement of produced particles’ anisotropic flow is important for understanding the dynamics and evolution of the QCD matter created in the collision. The collective flow of strange hadrons is driven by the pressure gradients in the early dense phase of the collision evolution and, as such, allows the study of the dynamics of the strange quark production. In particular, an important aspect to observe is the directed flow, which is caused by the interaction of produced particles in the nuclei overlap region with the nuclei spectator fragments and is sensitive to the equation of state of created matter. Directed flow of strange hadrons ( and kaons) in the collision energy range of a few GeV was measured by experiments at RHIC [6,7], AGS [8,9] and SIS-18 [10] and is a part of the physics program of experiments at the future FAIR and NICA facilities. Due to the high interaction rate, the CBM experiment will allow multi-differential analysis of the anisotropic flow of rarely produced multi-strange particles such as , and hypernuclei. The main goal is to develop and optimize the measurement procedure for multi-strange particle flow. In the current work, we validate the procedure with hyperons as the most abundantly produced and we study possible biases due to the CBM reconstruction algorithms.
2. CBM Experiment and Simulation Setup
The CBM is a multipurpose fixed-target experiment which will be capable to measure the production of hadrons, electrons and muons in proton-ion and heavy-ion collisions over the full FAIR beam momentum range [5]. The main subsystems of the CBM experiment relevant to the measurement of the hyperon flow are the Silicon Tracking System (STS) and Micro-Vertex Detector (MVD) for charged hadron tracking, the Time Of Flight (TOF) detector for charged particle identification and the Projectile Spectator Detector (PSD) for centrality and reaction plane estimation. The MVD and STS are located inside the dipole magnet with a magnetic field bending power of 1 Tm and allow the reconstruction of strange hyperon decay products with a momentum resolution of and decay vertex resolution of m [11]. The z axis of the CBM coordinate system is directed along the beam line, while the magnetic field is directed along the y axis.
A sample of 5M Au + Au collisions at = 12 GeV/ was generated with the DCM-QGSM-SMM model [12,13], which includes coalescence, fragmentation of nuclei recoil and hypernuclei production. In particular, modeling of fragmentation is important for centrality and reaction plane determination and flow studies [14]. The GEANT4 [15,16] package was used to transport generated particles through the CBM detector material. The resulting signals were used to reconstruct collision products using the CBMROOT [17] software.
Centrality was estimated using track multiplicity following the procedure described in [18] and implemented in [19]. For multiplicity calculation, the reconstructed tracks with vertex , number of hits , reduced track and pseudorapidity range were used.
3. Hyperon Reconstruction
The kinematics of the strange neutral hadrons, such as hyperons, can only be reconstructed in CBM via their weak decay products. Figure 1 (left) shows the CBM event display as an illustration of the multi-particle environment, which complicates the hyperon decay reconstruction. The event display is shown for one of the central (impact parameter ) Au + Au collisions at beam momentum 12 GeV/ generated with the DCM-QGSM-SMM event generator. The red (blue) line represents the trajectory of the daughter pion (proton) originating from the weak decay. The red dot indicates the vertex of the the Au + Au collision and the black dot represents the decay vertex, which are called the primary and secondary vertex, respectively. The black line represents the straight line trajectory of the hyperon before decay.
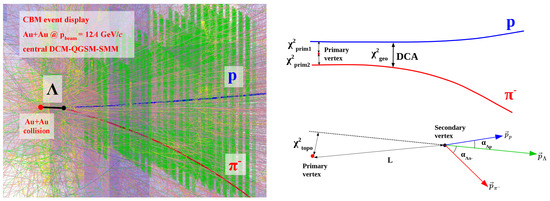
Figure 1.
(left) The CBM event display illustrating the multi-particle environment which complicates the hyperon decay reconstruction. (right) Schematic view of the decay which indicates parameters used for the candidate selection. See text for description of notations.
The following information is used for the decay reconstruction: the primary vertex position; the reconstructed parameters of the daughter tracks, such as charge, momentum and covariance matrix calculated at the first hit position of the daughter track; and the particle type hypothesis. To construct the candidates, each reconstructed negatively charged track ( candidate) is combined with each positively charged track (proton candidate), with particle type used as track preselection. For the presented analysis, the particle types were taken from matching the reconstructed tracks with true particle trajectories in GEANT4 simulations.
Figure 1 (right) illustrates the parameters which determine the decay topology and are used for the candidate selection optimization. The parameters are:
- —a distance of the closest approach between two daughter tracks (in cm);
- —a cosine of the angle between the candidate and proton momenta;
- —a distance (L) between the primary and secondary vertices divided by its error ();
- —a square of the distance between the proton (negatively charge pion) track and the primary vertex position divided by its error;
- —a square of the distance between the daughter proton and negatively charged pion divided by its error;
- —a square of the distance between the candidate trajectory and primary vertex divided by its error.
The , , and are calculated as the matrix convolution of the respective distance with elements of the corresponding inverted covariance matrix :
The Kalman Filter implementation of the decay parameter calculation is described in [20] and the corresponding mathematics is implemented in the Kalman Filter Particle (KFParticle) package [21,22]. The KFParticle mathematics is interfaced via the Particle Finder Simple (PFSimple) code [23] for optimized and efficient hyperon reconstruction and background rejection. Numerical values of the candidate selection criteria are listed in Table 1.

Table 1.
Numerical values of the candidate selection criteria.
Figure 2 (left) shows as an example the distribution of the for the candidates constructed from daughters of the true decay (signal) and combinatorial background normalized to the integral of the signal.
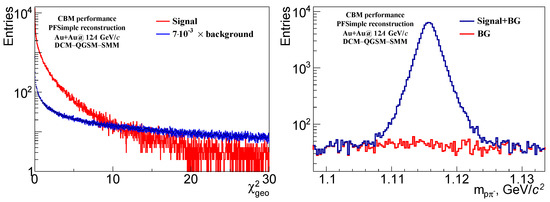
Figure 2.
(left) Distribution of the for candidates selected using criteria for listed in Table 1. No event or candidate kinematical selection. (right) Invariant mass distribution for all (blue) and combinatorial background (red) candidates.
Figure 2 (right) and Figure 3 illustrate the performance of PFSimple code. The signal to background ratio calculated within five standard deviations from the invariant mass peak is around 30 and the reconstruction efficiency in the midrapidity region is for the decay channel .
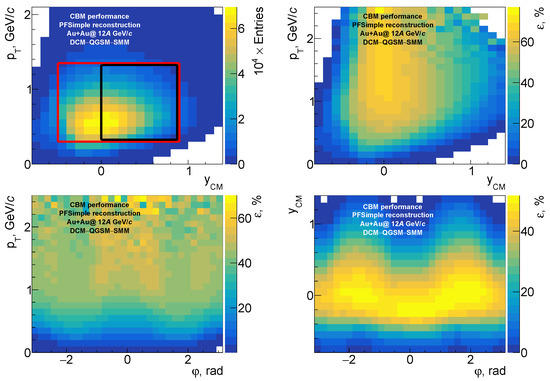
Figure 3.
(top left) Population of reconstructed hyperons vs. and . The kinematic ranges for which vs. ( and centrality) were calculated are indicated by the red (black) rectangle. Reconstruction efficiency for the decay channel (top right) vs. and , (bottom left) vs. and and (bottom right) vs. and .
4. Anisotropic Flow Measurement Technique
Anisotropic flow is characterized by coefficients in a Fourier decomposition of the produced particles’ azimuthal distribution relative to the reaction (symmetry) plane:
where n is the harmonic number, is the azimuthal angle of the particle and is the reaction (symmetry) plane angle. The flow coefficients can be calculated as follows:
The first harmonic coefficient represents the directed flow.
The reaction plane angle in Equation (3) is not known. A data-driven procedure for the reaction plane estimation and corresponding resolution correction extraction using the spectators’ energy registered with the PSD [24] is discussed in [14]. The focus of the current work is on the CBM performance for hyperon directed flow measurements, and we used the reaction plane angle from the event generator, assuming that it can be reconstructed reliably with the PSD. Signal and background candidates reconstructed with PFSimple were separated by matching their daughters to the true particle trajectories in GEANT4 simulations.
Non-uniformity of the reconstruction in the azimuthal angle , transverse momentum and rapidity may bias the measurement of the directed flow. To study detector biases in the directed flow measurement, we use two independent estimates from projections in the x and y direction of the laboratory frame:
Effects of the azimuthal non-uniformity can be corrected with the procedure described in [25]. For this, a vector is introduced, which is corrected via three main consecutive steps:
- Recenter the distribution by subtracting the corresponding average values;
- Twist the vector distribution;
- Rescale the vector distribution along x and y directions.
Figure 4 illustrates the transformation of the vector distribution after different correction steps.
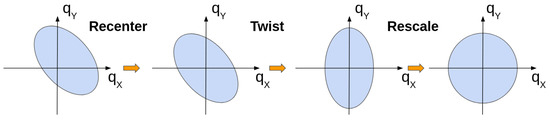
Figure 4.
Schematic illustration of recenter, twist and rescale correction steps.
The correction procedure is implemented in the QnTools [26] and QnAnalysis [27] software packages.
Figure 3 illustrates the asymmetric CBM detector response in , and , which provides input for the QnTools package. Non-uniformity of the reconstruction in and is taken into account by weighting the candidates in the calculation with the inverse value of efficiency for a given and region.
5. Results
Figure 5 shows the CBM performance for the hyperon directed flow measurement. is presented as a function of hyperon’s rapidity, transverse momentum and centrality. The integration region over the kinematical phase space is indicated in Figure 3 (top left) by red (black) boxes for the calculation of vs. y ( and centrality). Blue and green open circles in Figure 5 show, respectively, the uncorrected and defined by Equation (4). Red full circles show an average value of and after applying both azimuthal non-uniformity corrections and ()-dependent efficiency weights. The red solid line shows the Monte Carlo true value of the directed flow. The lighter red-shaded areas show the systematical uncertainty estimated from the remaining difference between and after all corrections are applied.
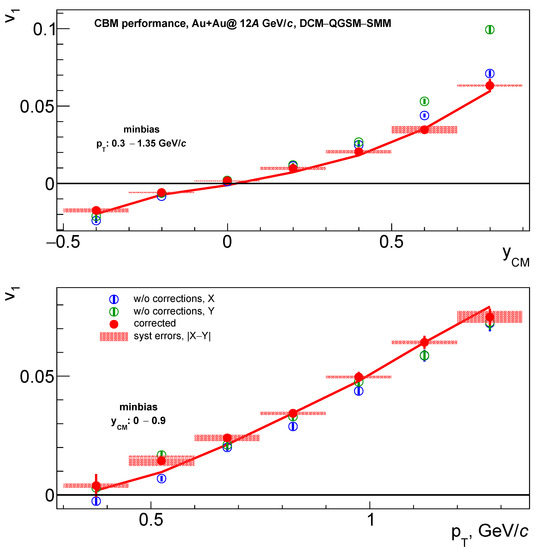
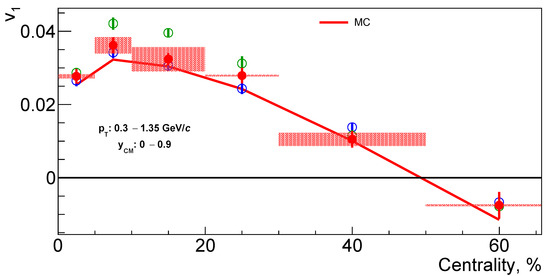
Figure 5.
Directed flow of hyperons as a function of (top) rapidity for minbias collisions, , (middle) transverse momentum for minbias collisions, , and (bottom) centrality, .
A positive slope of is reproduced, with being consistent within the statistical precision with the Monte Carlo input values (see Figure 5, top). The dependence of is shown in the middle panel of Figure 5. There is a small discrepancy between evaluated and true values of at small GeV/c, which requires further investigation with higher statistics. Figure 5 (bottom) illustrates dependence on centrality. The sign change of with centrality around is reproduced. Peripheral collisions with centrality >70% are not considered in this analysis because of the very poor statistics of the produced hyperons.
6. Conclusions
In summary, the performance of the CBM experiment for the measurements of the directed flow of hyperons is presented. After applying corrections for azimuthal non-uniformity and and rapidity-dependent efficiency weights, the Monte Carlo input is reproduced within the statistical precision. The future plans are to use the data-driven procedure for the reaction plane estimation with the PSD, deploy the invariant mass fit method for signal–background separation in the hyperon reconstruction and perform multi-differential , y and centrality analysis.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Carlo and Karin Giersch Stiftung, HGS-HIRe Graduate School by HIC for FAIR, the Ministry of Science and Higher Education of the Russian Federation, Project “Fundamental properties of elementary particles and cosmology” No 0723-2020-0041, the Russian Foundation for Basic Research (RFBR) funding within the research project no. 18-02-40086, the European Union’s Horizon 2020 research and innovation program under grant agreement No. 871072, the National Research Nuclear University MEPhI in the framework of the Russian Academic Excellence Project (contract no. 02.a03.21.0005, 27 August 2013).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M.; et al. Probing dense baryon-rich matter with virtual photons. Nat. Phys. 2019, 15, 1040–1045. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Vidaña, I.; Wei, J.B. A Modern View of the Equation of State in Nuclear and Neutron Star Matter. Symmetry 2021, 13, 400. [Google Scholar] [CrossRef]
- Friman, B.; Höhne, C.; Knoll, J.; Leupold, S.; Randrup, J.; Rapp, R.; Senger, P. (Eds.) The CBM Physics Book: Compressed Baryonic Matter in Laboratory Experiments; Springer: Berlin/Heidelberg, Germany, 2011; Volume 814, pp. 1–980. [Google Scholar] [CrossRef]
- Ablyazimov, T.; Abuhoza, A.; Adak, R.P.; Adamczyk, M.; Agarwal, K.; Aggarwal, M.M.; Ahammed, Z.; Ahmad, F.; Ahmad, N.; Ahmad, S.; et al. Challenges in QCD matter physics—The scientific programme of the Compressed Baryonic Matter experiment at FAIR. Eur. Phys. J. A 2017, 53, 60. [Google Scholar] [CrossRef]
- Wu, Y.; STAR Collaboration. Recent results for STAR sNN=4.9 GeV Al+Au and sNN=4.5 GeV Au + Au Fixed-Target Collisions. Nucl. Phys. A 2019, 982, 899–902. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Aggarwal, Z.; Ahammed, I.; Alekseev, D.M.; Anderson, A.; et al. Flow and interferometry results from Au + Au collisions at sNN=4.5 GeV. Phys. Rev. C 2021, 103, 034908. [Google Scholar] [CrossRef]
- Zhang, B.; Ko, C.M.; Li, B.A.; Sustich, A.T. Directed flow of neutral strange particles at AGS. J. Phys. G 2000, 26, 1665–1670. [Google Scholar] [CrossRef]
- Ko, C.M. Medium effects on the flow of strange particles in heavy ion collisions. J. Phys. G 2001, 27, 327–336. [Google Scholar] [CrossRef]
- Chlad, L. Strangeness Flow in Au + Au Collisions at 1.23AGeV Measured with HADES. Springer Proc. Phys. 2020, 250, 221–224. [Google Scholar] [CrossRef]
- Heuser, J.; Müller, W.; Pugatch, V.; Senger, P.; Schmidt, C.J.; Sturm, C.; Frankenfeld, U.; CBM Collaboration. [GSI Report 2013–4], Technical Design Report for the CBM Silicon Tracking System (STS). Available online: https://repository.gsi.de/record/54798 (accessed on 30 April 2021).
- Baznat, M.; Botvina, A.; Musulmanbekov, G.; Toneev, V.; Zhezher, V. Monte-Carlo Generator of Heavy Ion Collisions DCM-SMM. Phys. Part. Nucl. Lett. 2020, 17, 303–324. [Google Scholar] [CrossRef]
- Botvina, A.S.; Mishustin, I.N.; Begemann-Blaich, M.; Hubele, J.; Imme, G.; Iori, I.; Kreutz, P.; Kunde, G.J.; Kunze, W.D.; Lindenstruth, V.; et al. Multifragmentation of spectators in relativistic heavy ion reactions. Nucl. Phys. A 1995, 584, 737–756. [Google Scholar] [CrossRef]
- Golosov, O.; Klochkov, V.; Kashirin, E.; Selyuzhenkov, I.; CBM Collaboration. Physics Performance Studies for Anisotropic Flow Measurements with the CBM Experiment at FAIR. Phys. Part Nucl. 2020, 51, 297–300. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270. [Google Scholar] [CrossRef]
- The CBM Collaboration. Available online: https://git.cbm.gsi.de/computing/cbmroot (accessed on 30 April 2021).
- Segal, I.; Lubynets, O.; Selyuzhenkov, I.; Klochkov, V.; CBM Collaboration. Using multiplicity of produced particles for centrality determination in heavy-ion collisions with the CBM experiment. J. Phys. Conf. Ser. 2020, 1690, 012107. [Google Scholar] [CrossRef]
- Klochkov, V.; Segal, I.; Lubynets, O.; Selyuzhenkov, I. CBM-GSI gitlab. Available online: https://git.cbm.gsi.de/pwg-c2f/analysis/centrality (accessed on 30 April 2021).
- Gorbunov, S. On-line reconstruction algorithms for the CBM and ALICE Experiments. GSI-2017-01227. Available online: https://core.ac.uk/download/pdf/14529239.pdf (accessed on 30 April 2021).
- Zyzak, M. Online Selection of Short-Lived Particles on Many-Core Computer Architectures in the CBM Experiment at FAIR. GSI-2017-00683. Available online: http://repository.gsi.de/record/201581?ln=de (accessed on 30 April 2021).
- Zyzak, M.; Kisel, I. github. Available online: https://github.com/cbmsw/KFParticle.git (accessed on 30 April 2021).
- Lubynets, O.; Klochkov, V.; Selyuzhenkov, I.; Glaessel, S.; Blume, C. CBM-GSI gitlab. Available online: https://git.cbm.gsi.de/pwg-c2f/analysis/pf_simple (accessed on 30 April 2021).
- Guber, F.; Selyuzhenkov, I.; CBM Collaboration. [GSI Report 2015-02020], Technical Design Report for the CBM Projectile Spectator Detector (PSD). Available online: https://repository.gsi.de/record/109059 (accessed on 30 April 2021).
- Selyuzhenkov, I.; Voloshin, S. Effects of non-uniform acceptance in anisotropic flow measurement. Phys. Rev. C 2008, 77, 034904. [Google Scholar] [CrossRef]
- Kreis, L.; Selyuzhenkov, I. github. Available online: https://github.com/HeavyIonAnalysis/QnTools (accessed on 30 April 2021).
- Kashirin, E.; Selyuzhenkov, I. github. Available online: https://github.com/HeavyIonAnalysis/QnAnalysis (accessed on 30 April 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).