Abstract
One of the common methods to measure the centrality of nucleus-nucleus collision events consists of detecting forward spectator neutrons. Because of non-monotonic dependence of neutron numbers on centrality, other characteristics of spectator matter in Au–Au collisions at NICA must be considered to improve the centrality determination. The numbers of spectator deuterons and -particles and the forward–backward asymmetry of the numbers of free spectator nucleons were calculated with the Abrasion–Ablation Monte Carlo for Colliders (AAMCC) model as functions of event centrality. It was shown that the number of charged fragments per spectator nucleon decreases monotonically with an increase of the impact parameter, and thus can be used to estimate the collision centrality. The conditional probabilities that a given event with specific spectator characteristics belongs to a certain centrality class were calculated by means of AAMCC. Such probabilities can be used as an input to Bayesian or other machine-learning approaches to centrality determination in Au–Au collisions.
1. Introduction
It is expected that hot and dense matter is created in the domain of overlap of colliding relativistic nuclei. The remnants of colliding nuclei outside the overlap represent relatively cold spectator matter. The volume, shape and excitation energy of spectator matter correlate with the distance of the closest approach of the centers of colliding nuclei, defined as impact parameter b. The determination of b and the initial collision geometry for each detected event is a key point in the analysis of nucleus-nucleus collision data, in particular, in ALICE experiment at the LHC [1]. In such studies collision events are typically classified into centrality classes representing certain fractions of the total reaction cross sections corresponding to specific intervals of b [1]. The detection of all spectator nucleons and nuclear fragments in forward calorimeters would be the most straightforward method of estimating b from the total volume of spectator matter. However, in collider experiments some spectators propagate very close to circulating beams and thus cannot be intercepted by forward detectors due to their limited acceptance. In particular, some of spectator nucleons and nuclear fragments will remain undetected by Forward Hadron Calorimeters (FHCal) designed for the MPD experiment at NICA facility [2]. This is because of void central sections of FHCal which make possible the passage of collider beams. The Projectile Spectator Detector (PSD) of the CBM experiment at FAIR [3] also has a central hole to reduce radiation damage to the detector from primary beam nuclei. As a result, very forward heavy spectator fragments will escape PSD. Because of this, a procedure of collision centrality determination in the CBM experiment [3] will include information on particles produced in the participant zone in addition to PSD signals. Forward nuclear fragments remain undetectable in the ALICE experiment at the LHC. ALICE is equipped with neutron and proton Zero Degree Calorimeters (ZDC) [4] designed to detect, respectively, unbound neutrons and protons, but not fragments.
As known, see, in particular [5], equally small numbers of free spectator nucleons are expected in central as well as in peripheral collisions, while the maximum of nucleon multiplicity is expected in semi-central collisions. By studies of multifragmentation of spectator matter in collisions of Au with light and heavy nuclei [6] it was demonstrated that the multiplicity of intermediate-mass fragments (IMF) with is also large in semi-central events in contrast to central and peripheral ones. This all means that the measurements of multiplicities of unbound spectator nucleons as well as IMF are not sufficient for unambiguous centrality determination in the whole range of b. Therefore, it is necessary to search for additional characteristics of spectator matter associated with centrality. First, it is reasonable to consider the characteristics of spectator nucleons and light fragments with , because they will be detected more effectively by the forward calorimeters of the MPD and CBM experiments in comparison to fragments with . Secondly, since some spectator deuterons and -particles were detected in PHOBOS experiment at RHIC [7], the considered characteristics can be proposed also for measurements at RHIC.
Several event characteristics, in particular, the multiplicity of produced particles and spectator neutrons, were used as input to machine-learning (ML) algorithms to associate a measured event with a certain centrality or impact parameter interval [8,9,10]. In particular, the Bayesian approach to the data analysis has been used [11]. Within the framework of the present study Bayes’ theorem is used to calculate the posterior probability that a detected event with measured multiplicity of spectators, in particular, neutrons, H or He, belongs to a certain centrality interval . It is calculated as
from the conditional probability that an event of a given centrality is characterized by multiplicity and unconditional prior probabilities and . As shown [8,10], it is very promising to use a set of characteristics rather than a single one for centrality determination. Processing multiple observables leads to a multidimensional problem that needs to be solved with efficient ML algorithms. However, the success of such algorithms depends on the proper choice of observables as well as on reliable calculations of the respective conditional probabilities by a model. In contrast to conventional methods which map a single observable such as neutron multiplicity to a centrality bin, ML algorithms for centrality determination can be based on a set of observables, including several characteristics of spectator matter, not limiting to the neutron multiplicity.
In this work we use our Abrasion–Ablation Monte Carlo for Colliders (AAMCC or AMC) model [5] to calculate several characteristics of spectator matter which can be potentially used as input to multidimensional ML algorithms for centrality determination in nucleus-nucleus collisions. By means of Equation (1) we calculate individually for each characteristic to evaluate the extent of its specificity to . AAMCC modeling is based on the abrasion–ablation mechanism to produce spectator fragments. At the first abrasion stage AAMCC employs Glauber Monte Carlo model [12] to calculate the numbers of interacting (participant) neutrons and protons which are knocked out from each of the colliding nuclei. Other nucleons are considered to be spectators and compose prefragments which decay at the ablation stage into spectator nucleons and fragments. Such decays are simulated with statistical models from Geant4 toolkit [13]. More details on AAMCC modeling are given in Section 2, and simulation results for Au–Au collisions at GeV are presented in Section 3. In particular, the probabilities that an event with given numbers of spectator deuterons or -particles belongs to a certain centrality class are presented in this section. In Section 4 our results are summarized.
2. AAMCC Model
Within AAMCC model [5] the production of spectator matter in nucleus-nucleus collisions is considered to be a two-stage abrasion–ablation process as described below. Each simulation event starts with a creation of a pair of nuclei by sampling positions of intranuclear neutrons and protons according to the individual distributions of their densities in colliding nuclei. The flowchart of AAMCC is presented in Figure 1.
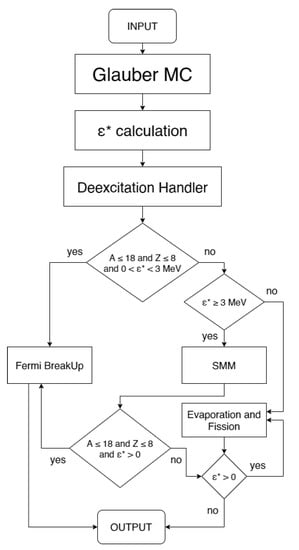
Figure 1.
AAMCC flowchart.
2.1. Abrasion Stage
The propagation of nucleons from one nucleus towards another nucleus is simulated by means of Glauber Monte Carlo model (GlauberMC) [12]. The history of the Glauber model, its theoretical background, main assumptions and Monte Carlo implementation were reviewed in Ref. [14]. This model is widely used for estimating the initial geometry in collisions of relativistic nuclei. Nucleons undergoing interactions are explicitly marked as participants, while other nucleons in each of the colliding nuclei are considered to be spectator nucleons which form two pieces of exited spectator matter (prefragments). It is assumed that all participant nucleons are separated (abraded) from spectator matter because of large transverse momenta obtained in the interactions. Since neutrons and protons are distinguished in GlauberMC, the charges of prefragments are unambiguously defined in each event.
2.2. Excitation Energy of Spectator Matter
Because of the stochasticity of nucleus-nucleus collisions it is expected that prefragment excitation energy vary from one event to another. A key point in modeling consists of a proper assignment of to a prefragment with a given mass number created after the abrasion stage of a nucleus-nucleus collision event. There are several methods to estimate for prefragments representing spectator matter. Three methods were compared and discussed in Ref. [15] for a version of abrasion–ablation model similar to AAMCC. The first method is based on the Ericson formula [16]. It calculates the prefragment excitation energy as the sum of energies of hole states left in the core of initial nucleus after the removal of all participating nucleons. An equidistant level scheme with constant level density is assumed in this method in contrast to another method proposed in Ref. [17] with a linear correlation between the level density and level energy. Typically, following these two methods each removed nucleon adds 20–40 MeV to the prefragment excitation energy . As a result, becomes extremely large in central collisions characterized by large numbers of removed nucleons, but small . A phenomenological correlation between and extracted by ALADIN collaboration from experimental data [6] is assumed in the third method, which is used in the present work. In this case, is restricted by ∼8 MeV even for the most central collisions.
2.3. Ablation Stage
At the second ablation stage decays of prefragments into unbound spectator nucleons and nuclear fragments are modeled by means of statistical decay models from Geant4 toolkit [13]. Depending on the value of estimated for a prefragment either the Weisskopf–Eving evaporation model [18] at MeV, or the Statistical Multifragmentation Model (SMM) [19,20] at MeV are used to model its decays, see Figure 1. It is assumed that secondary fragments produced in multifragmentation can be also excited. The Fermi break-up model [19] is employed at any to simulate decays of prefragments with and or light secondary fragments resulting from multifragmentation, see Figure 1. The Fermi break-up model has been developed to describe first multiple pion production in proton-proton collisions [21], but later it was successfully applied to decays of light excited nuclei [19,20]. It is assumed that only nuclei in their ground states or in low-lying discrete states can be produced in decays simulated with the Fermi break-up model. The statistical decay models from Geant4 of version 10.4 were used, except for the Fermi break-up model taken from the version 9.2. This is because the version 9.2 demonstrates the best agreement with the FORTRAN version of the Fermi break-up model described in Refs. [19,20].
2.4. Calculations of Posterior Probabilities
To calculate the posterior probabilities given by Equation (1), a large set of minimum bias collision events has been generated with AAMCC. Then, frequency distributions for the considered characteristics of spectators were filled in from the events of certain centrality 0–20%, 20–40%, 40–60%, 60–80% or 80–100%. After that, all functions were divided by the respective frequency distributions obtained from minimum bias events.
3. Results
It is expected that light spectator fragments, in particular, deuterons and -particles can be registered in addition to spectator nucleons in the forward calorimeters FHCal designed for the MPD experiment at NICA [2]. In the present FHCal design only the total energy of spectators in each event can be measured and, say, the response of the calorimeter to two neutrons cannot be distinguished from the response to a deuteron. However, providing that scintillator detectors will be installed in front of FHCal, charged spectators can be distinguished from spectator neutrons following such an upgrade. Therefore, a correlation between the numbers of spectator deuterons or -particles and event centrality can be also considered in addition to the relation between the total spectator energy and centrality in Au–Au collisions at NICA.
3.1. Numbers of Spectator Deuterons and -Particles
The posterior probabilities and were calculated with AAMCC as the probabilities of event with a given number of spectator deuterons or -particles , respectively, to belong to specific centrality interval: 0–20%, 20–40%, 40–60%, 60–80% or 80–100%. Such probabilities which are presented in Figure 2 were calculated for Au–Au collisions at GeV using the ALADIN parameterization, see Section 2. With these probabilities in hands one can try to classify an event with given and as central, semi-peripheral or peripheral.
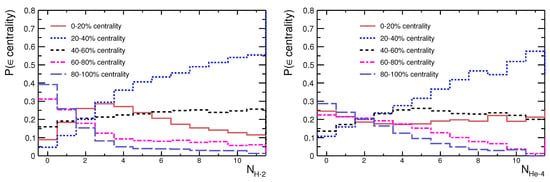
Figure 2.
Probability of event with a given number of spectator deuterons (left) or -particles (right) to belong to certain centrality interval: 0–20%, 20–40%, 40–60%, 60–80% or 80–100% calculated with AAMCC for Au–Au collisions at GeV.
AAMCC predicts that up to 11 spectator deuterons can be produced in Au–Au collisions at GeV. As seen from the left panel of Figure 2, it is most likely that an event with 6–11 deuterons belongs to 20–40% centrality interval. As also seen, it is very improbable that this event is a peripheral one. According to AAMCC, an event with 6 to 11 -particles can be either central (0–20%), semi-central (20–40%) or semi-peripheral (40–60%). Similarly, it is difficult to classify with confidence an event with 1–3 spectator deuterons or -particles because such small numbers of these light nuclei can be produced at any centrality, see Figure 2. Nevertheless, it is most probable that events with and are peripheral ones. In general, while a high multiplicity of deuterons or -particles in a detected event suggests that this event belongs to 20–40% or 40–60% centrality intervals, and are not suitable as robust centrality indicators for all kinds of events. This is because of the rise and fall of production of these light nuclei with the increase of b from central to peripheral collisions predicted by AAMCC. The maxima of the multiplicities of deuterons and -particles are expected in semi-peripheral collisions in the middle of the range of b corresponding to hadronic interactions of Au nuclei.
3.2. Number of Charged Fragments per Spectator Nucleon
The number of charged fragments calculated per spectator nucleon for Au–Au collisions at GeV is shown in Figure 3 as a function of impact parameter b. As mentioned above, in the MPD experiment at NICA the scintillator detectors are planned to be installed between the interaction point and FHCal. With these scintillator hodoscopes spectator protons and nuclear fragments can be distinguished from spectator neutrons. The segmentation of the hodoscopes in the transverse plane will make possible to read independent signals from charged spectators emitted at different forward angles. In this way, the number of charged spectators will be also measured in addition to extracted from the total forward energy measured in FHCal.
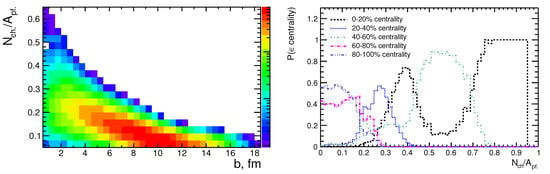
Figure 3.
Number of charged fragments per spectator nucleon as a function of impact parameter b (left), and the probability of event with given to belong to certain centrality interval: 0–20%, 20–40%, 40–60%, 60–80% or 80–100% (right) calculated with AAMCC for Au–Au collisions at GeV.
As seen in the left panel of Figure 3, calculated with AAMCC monotonically decreases with the increase of impact parameter b. This kind of correlation between and b is specific for collisions of equal heavy nuclei, and it is caused by the following effects. The total volume of spectator matter increases with the increase of b. In central or semi-central collisions is small because of large numbers of nucleons involved in collisions with small b. The excitation energy of spectator matter per nucleon is high in such collisions, MeV, thus leading to abundant production of unbound spectator protons and light nuclear fragments in decays of spectator matter. As a result, fluctuates significantly with the average value of and can reach 0.6–0.8 in rare central events with an occasionally high content of protons in spectator matter. This is reflected in the posterior probability of events with high values of to belong to 0–20% centrality interval, see the right panel of Figure 3. It is very probable that events with measured for spectators belong to 40–60% centrality interval characterized by multifragment decays of prefragments. In contrast, heavy prefragments produced in peripheral collisions (60–80% or 80–100%) are less excited ( MeV) and mostly evaporate neutrons accompanied by a few protons. This dominance of neutrons in decay products naturally leads to low . Therefore, it can be expected that events with must be considered to be peripheral Au–Au collisions, see Figure 3.
3.3. Forward–Backward Asymmetry of the Numbers of Spectator Nucleons
The neutron and proton Zero Degree Calorimeters (ZDC) [4] in the ALICE experiment at the LHC detect spectator nucleons from both colliding nuclei, A and B. The MPD experiment at NICA [2] will be also capable of detecting spectators at both sides. Therefore, it is interesting to consider the forward–backward (A–B) asymmetry of the numbers and of spectator neutrons [22] defined as
and the asymmetry of the numbers and of spectator nucleons (protons and neutrons):
The posterior probabilities and of a Au–Au collision event at GeV with a given value of forward–backward asymmetry of spectator neutrons or unbound spectator nucleons to belong to specific centrality interval: 0–20%, 20–40%, 40–60%, 60–80% or 80–100% were calculated with AAMCC. They are presented in Figure 4 as functions of and . Due to a very limited total volume of spectator matter in central collisions, noticeable statistical fluctuations are expected in the numbers of a few spectator nucleons emitted by each of the colliding nuclei. Indeed, as seen in the left panel of Figure 4, it is most probable that an event with large neutron asymmetry is central (0–20%). However, as seen from the right panel, a large asymmetry of total numbers of unbound nucleons at each side is possible not only in central events, but also in peripheral ones (60–80% or 80–100%). This is because of limited numbers of spectator nucleons evaporated from heavy prefragments with low excitation energy which are created in peripheral collisions. In contrast, spectator asymmetry in semi-central collisions (20–40%) is rather small. According to AAMCC, it is quite probable that an event with and belongs to 20–40% interval of centrality, see Figure 4. In general, while an event with large spectator asymmetry is most probably a central one, the discrimination of events of other centrality intervals based on their and is not straightforward.
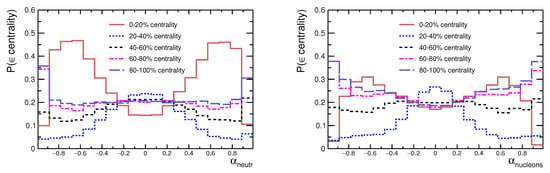
Figure 4.
Probability of Au–Au collision event at GeV with a given value of forward–backward asymmetry of the numbers of free spectator neutrons (left) and nucleons (right) to belong to specific centrality interval: 0–20%, 20–40%, 40–60%, 60–80% or 80–100%.
4. Conclusions
Several characteristics of spectator matter produced in Au—Au collisions at NICA were calculated with AAMCC model as functions of impact parameter using ALADIN parameterization for excitation energy of prefragments. The numbers of deuterons and -particles , the numbers of charged fragments per nucleon and also the forward–backward asymmetry of the numbers of unbound neutrons and nucleons were considered to assist the determination of event centrality. The calculation results were expressed in terms of the posterior probabilities of an event with a given characteristic to belong to a certain centrality interval. The specificity of each characteristic to event centrality was evaluated from these results. It was found that events with large numbers of deuterons () or alpha-particles () mostly belong to mid-centrality intervals 20–40% and 40–60%, while events with or are most probably central ones. Events with large neutron asymmetry are expected to be central (0–20%). It was demonstrated by calculations that in contrast to , , and , the number of charged spectator fragments per spectator nucleon monotonically depends on the collision impact parameter. As shown, for certain values of only events with centrality 0–20% or 40–60% are possible, while events with are peripheral ones. This makes suitable for the determination of centrality in the whole range of b in addition to more common measurements of multiplicities of spectator neutrons.
The considered characteristics of spectators were evaluated as centrality indicators based on AAMCC. These results are model-dependent and it is recommended to confirm them with other models and future measurements. However, for the moment, the considered characteristics of spectators look promising for their implementation in multidimensional machine-learning algorithms to determine centrality in future experiments at NICA and at the LHC.
Author Contributions
Methodology I.P. and A.S.; software A.S. and R.N.; analysis A.S.; model validation R.N.; supervision I.P.; writing—original draft preparation A.S.; writing—review and editing R.N. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RFBR grant number 18-02-40035-mega.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAMCC | Abrasion–Ablation Monte Carlo for Colliders |
| AMC | Abrasion–Ablation Monte Carlo for Colliders |
| SMM | Statistical model of multifragmentation |
References
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality determination of Pb-Pb collisions at TeV with ALICE. Phys. Rev. C 2013, 88, 044909. [Google Scholar] [CrossRef]
- Golubeva, M.B.; Ivashkin, A.P.; Kurepin, A.B. Study of nuclear fragmentation at MPD/NICA. EPJ Web Conf. 2017, 138, 11001. [Google Scholar] [CrossRef]
- Klochkov, V.; Selyuzhenkov, I. Centrality determination in heavy-ion collisions with the CBM experiment. J. Phys. Conf. Ser. 2017, 798, 012059. [Google Scholar] [CrossRef]
- Oppedisano, C.; Arnaldi, R.; Chiavassa, E.; Cicalò, C.; Cortese, P.; De Falco, A.; Dellacasa, G.; De Marco, N.; Ferretti, A.; Floris, M.; et al. Physics performance of the ALICE Zero Degree Calorimeter. Nucl. Phys. B Proc. Suppl. 2009, 197, 206–210. [Google Scholar] [CrossRef]
- Svetlichnyi, A.O.; Pshenichnov, I.A. Formation of Free and Bound Spectator Nucleons in Hadronic Interactions between Relativistic Nuclei. Bull. Russ. Acad. Sci. Phys. 2020, 84, 911–916. [Google Scholar] [CrossRef]
- Botvina, A.S.; Mishustin, I.N.; Begemann-Blaich, M.; Hubele, J.; Imme, G.; Iori, I.; Kreutz, P.; Kunde, G.J.; Kunze, W.D.; Lindenstruth, V.; et al. Multifragmentation of spectators in relativistic heavy-ion reactions. Nucl. Phys. Sect. A 1995, 584, 737–756. [Google Scholar] [CrossRef]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. Participant and spectator scaling of spectator fragments in Au + Au and Cu + Cu collisions at = 19.6 and 22.4 GeV. Phys. Rev. C 2016, 94, 1–16. [Google Scholar] [CrossRef]
- David, C.; Freslier, M.; Aichelin, J. Impact parameter determination for heavy-ion collisions by use of a neural network. Phys. Rev. C 1995, 51, 1453–1459. [Google Scholar] [CrossRef]
- Sanctis, J.D.; Masotti, M.; Bruno, M.; D’Agostino, M.; Geraci, E.; Vannini, G.; Bonasera, A. Classification of the impact parameter in nucleus–nucleus collisions by a support vector machine method. J. Phys. G Nucl. Part. Phys. 2008, 36, 015101. [Google Scholar] [CrossRef]
- Altsybeev, I.; Kovalenko, V. Classifiers for centrality determination in proton-nucleus and nucleus-nucleus collisions. EPJ Web Conf. 2017, 137, 11001. [Google Scholar] [CrossRef]
- Pang, L.G. Machine learning for high energy heavy ion collisions. Nucl. Phys. Sect. A 2021, 1005, 121972. [Google Scholar] [CrossRef]
- Loizides, C.; Kamin, J.; D’Enterria, D. Improved Monte Carlo Glauber predictions at present and future nuclear colliders. Phys. Rev. C 2018, 97. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in GEANT 4. Nucl. Instrum. Methods Phys. Res. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber Modeling in High-Energy Nuclear Collisions. Annu. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Scheidenberger, C.; Pshenichnov, I.A.; Sümmerer, K.; Ventura, A.; Bondorf, J.P.; Botvina, A.S.; Mishustin, I.N.; Boutin, D.; Datz, S.; Geissel, H.; et al. Charge-changing interactions of ultrarelativistic Pb nuclei. Phys. Rev. C 2004, 70, 14902. [Google Scholar] [CrossRef]
- Ericson, T. The statistical model and nuclear level densities. Adv. Phys. 1960, 9, 425–511. [Google Scholar] [CrossRef]
- Gaimard, J.J.; Schmidt, K.H. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction. Nucl. Phys. Sect. A 1991, 531, 709–745. [Google Scholar] [CrossRef]
- Weisskopf, V. Statistics and Nuclear Reactions. Phys. Rev. 1937, 52, 295–303. [Google Scholar] [CrossRef]
- Bondorf, J.; Donangelo, R.; Mishustin, I.N.; Schulz, H. Statistical multifragmentation of nuclei. (II). Application of the model to finite nuclei disassembly. Nucl. Phys. Sect. A 1985, 444, 460–476. [Google Scholar] [CrossRef]
- Bondorf, J.; Botvina, A.; Iljinov, A.; Mishustin, I.; Sneppen, K. Statistical multifragmentation of nuclei. Phys. Rep. 1995, 257, 133–221. [Google Scholar] [CrossRef]
- Fermi, E. High Energy Nuclear Events. Prog. Theor. Phys. 1950, 5, 570–583. [Google Scholar] [CrossRef]
- Raniwala, R.; Raniwala, S.; Loizides, C. Effects of longitudinal asymmetry in heavy-ion collisions. Phys. Rev. C 2018, 97, 024912. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).