Abstract
The “Facility for Antiproton and Ion Research” (FAIR) in Darmstadt, Germany, and the “Nuclotron-based Ion Collider Facility” (NICA) in Dubna, Russia, are two accelerator centers under construction. FAIR will provide beams and experimental setups to perform forefront research in hadron, nuclear, atomic, and plasma physics, as well as in radiation biology and material science. At NICA, a unique research program on nuclear matter and spin physics will be conducted. Both facilities will execute experiments to explore the properties of QCD matter at neutron star core densities, in order to study the high-density equation of state, and to shed light on the quark degrees-of-freedom emerging in QCD matter at high densities. The research programs will be performed at FAIR with the CBM experiment, and at NICA with the MPD setup at the collider, and with the BM@N experiment at the Nuclotron. These three experiments are complementary, with respect to the beam energy. The physics programs and the relevant experimental observables will be discussed.
1. FAIR and NICA
The “Facility for Antiproton and Ion Research” (FAIR) is an accelerator center under construction in Darmstadt, Germany, which will provide unique experimental conditions for fundamental and applied research with particle beams [1,2]. The superconducting synchrotron accelerator SIS100 at FAIR has a maximum magnetic rigidity of 100 Tm, and will deliver high-intensity proton and ion beams, which can be converted into intense secondary beams of antiprotons and rare isotopes. Unstable neutron-rich or neutron-deficient nuclei will be produced in collisions of a high-intensity primary beam with a target, then selected by the Superconducting Fragment Separator, and finally analyzed by subsequent experimental setups operated by the NUSTAR collaboration. An important goal of these measurements is to unravel the origin of heavy elements by determination of the mass and lifetime of short-lived isotopes, which participate in the nucleosynthesis of heavy nuclei in supernova explosions and neutron star mergers. Intense beams of antiprotons will be produced, collected, and finally injected into and accelerated by the High-Energy Storage Ring, where hadron physics experiments will be performed by the PANDA collaboration. Intense ion beams also will be directed to various instruments, where experiments on atomic physics, plasma physics, radiation biology, and material science will be conducted by the APPA collaboration. Finally, heavy-ion beams up to kinetic energies of 11 A·GeV and with an intensity of 109 ions/s will be delivered to the first cave downstream SIS100, where the Compressed Baryonic Matter (CBM) experiment will be located. The layout of FAIR is illustrated in Figure 1. The blue lines sketch the existing accelerators at GSI, the linear accelerator UNILAC, and the ring accelerator SIS18 with subsequent experimental setups and two storage rings. The red lines represent the future facility: the ring accelerator SIS100, the beam lines to the various experiments, the production targets for new nuclei and antiprotons, the Super Fragment Separator, and the collector and storage rings.
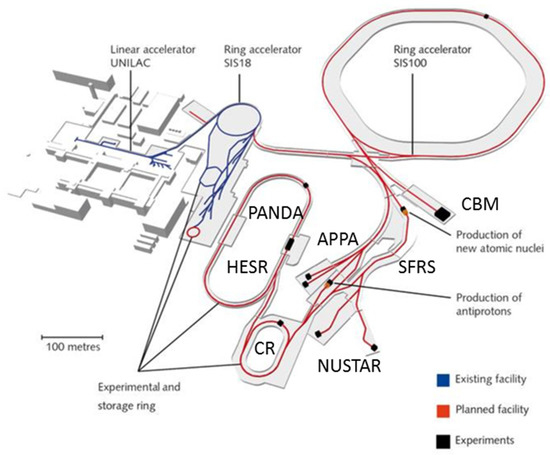
Figure 1.
Layout of the Facility for Antiproton and Ion Research (FAIR) (see text) [1,2].
The “Nuclotron-based Ion Collider Facility” (NICA) at the Joint Institute for Nuclear Research (JINR) in Dubna is one of the mega-science projects in Russia [3,4]. At NICA, the new superconducting booster synchrotron accumulates and accelerates the ions for efficient stripping, and then injects the ions into the Nuclotron synchrotron, which finally accelerates the beams up a magnetic rigidity of 45 Tm. For example, Au beams up to kinetic energies of 4.5 A·GeV and with intensities of up to about 109 ions/s will be either used for fixed target experiments, or injected into the NICA collider, where collision energies of up to √sNN = 11 GeV and luminosities of 1027 cm−2s−1 can be reached. Polarized protons and deuterons will be injected from an ion source directly into the Nuclotron. The layout of NICA is displayed in Figure 2. In the Nuclotron experimental hall, setups with a fixed target are located, for example the Baryonic Matter at Nuclotron (BM@N) experiment. In the collider, two detector stations will be established, the Multiple Purpose Detector (MPD), which will be used for dense matter studies, and the Spin Physics Detector (SPD).
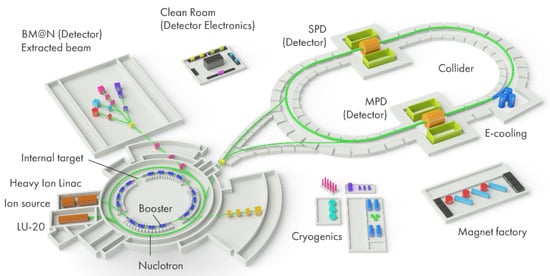
Figure 2.
Layout of the NICA facility at JINR in Dubna (see text) [3,4].
The investigation of the properties of dense QCD matter represents an important field of research at FAIR and NICA. The experimental setups used for these measurements are CBM at FAIR, and MPD and BM@N at NICA. These experiments are complementary, concerning two important features: the collision energy and the reaction rate. These two parameters are plotted in Figure 3 for experiments under construction, such as CBM, MPD, and BM@N, and for running experiments, which also study QCD matter at high baryon densities: HADES at GSI, NA61/SHINE at the CERN-SPS, and STAR at the Relativistic Heavy Ion Collider (RHIC) in Brookhaven, the latter in both collider and fixed target mode [5]. As illustrated in Figure 3, the reaction rates at the NICA and RHIC colliders decrease with decreasing collision energy as the luminosities fade away, while the reaction rates of the fixed target experiments are essentially limited by the rate capability of the detector setups. In particular, the detectors and the data acquisition of the CBM experiment are optimized for extremely high reaction rates, of up to 10 MHz, in order to collect high statistics data for rare probes and multi-different observables. In contrast, MPD at NICA covers the energy range accessible by CBM and STAR. For Au ions, SIS18 (HADES) reaches beam kinetic energies of up to 1.23 A·GeV, while the Nuclotron (BM@N) covers energies up to 3.8 A·GeV.
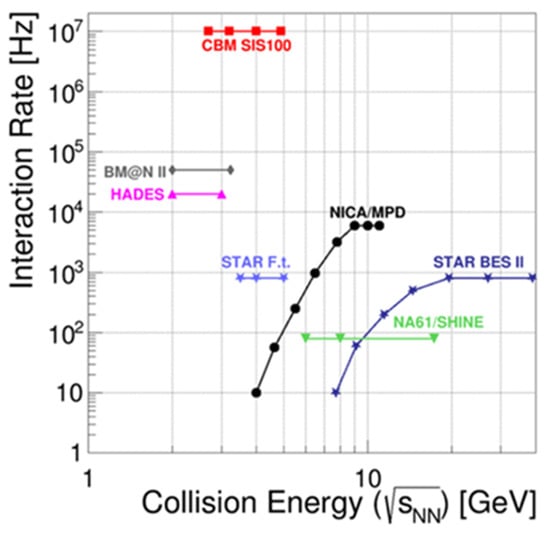
Figure 3.
Interaction rates versus Au + Au collision energies for existing and emerging experiments (see text, taken from [5]).
The most fascinating aspect of the laboratory measurements with heavy-ion beams at intermediate energies is the possibility of producing and to studying nuclear matter at densities like those in compact stellar objects. Although the size and lifetime of the compressed reaction volume of a heavy-ion collision differs dramatically from the reaction zone of two colliding neutron stars, the dynamics of both events is governed by the same high-density equation-of-state (EOS). Even the temperatures reached in both types of collision are not very different [6]. The isospin dependence of the EOS can also be determined in heavy-ion collisions. The high-density EOS for symmetric matter, together with the symmetry energy, both determined in heavy-ion collisions, would allow predicting the mass-radius relation of neutron stars via the Tolman–Oppenheimer–Volkoff equation. Another important property of high-density QCD matter is its microscopic structure. At densities at about five times saturation density, ρ0, the nucleons are expected to melt, and quark degrees of freedom will emerge. Whether this transition is a smooth crossover, or of the first order with a critical endpoint, is a fundamental problem being addressed by ongoing experimental and theoretical efforts. In the following, experimental observables in heavy-ion collisions will be discussed, which may shed light on the properties of high-density QCD matter.
2. Exploring the Equation-of-State of Dense Nuclear Matter with Heavy-Ion Collisions
The nuclear-matter equation of state (EOS) describes the pressure as a function of density, volume, temperature, energy, and isospin. For a constant temperature, the pressure can be written as:
with ρ the density and the binding energy per nucleon.
with the (isospin) symmetry energy Esym and the asymmetry parameter δ = (ρn − ρp)/ρ. For symmetric nuclear matter, E/A has a minimum at saturation density ρ0 and a curvature given by the nuclear incompressibility Knm = 9ρ2·δ2(E/A)/δρ2. In order to contribute to our understanding of neutron stars, both E/A for symmetric matter and the symmetry energy has to be determined up to densities of about 5 ρ0. A very important observable, which is sensitive to the EOS and can be measured in heavy ion collisions, is the collective flow of nucleons and light fragments, because it is directly related to the pressure gradient built up in the dense volume of the reaction. Such flow measurements have been performed both at GSI with beams from SIS18, and at BNL using beams from AGS. At SIS18, gold ions have been accelerated up to kinetic beam energies of 1.5 A GeV, where average densities of about 2 ρ0 are reached. The FOPI collaboration at GSI measured the elliptic flow of protons, deuterons, tritons, and 3He in Au + Au collisions at beam kinetic energies from 0.4 A to 1.5 A·GeV [7]. The data could be reproduced by IQMD transport calculations with a nuclear incompressibility of Knm = 190 ± 30 MeV. Values of Knm from about 160 to 220 MeV indicate a “soft” EOS, whereas Knm values around 300 MeV and higher denote a “hard” EOS.
P = ρ2 d(E/A)/dρ
E/A(ρ,δ) = E/A(ρ,0) + Esym(ρ)·δ2 + O(δ4)
An alternative approach towards the study of the EOS for symmetric matter has been pursued by the KaoS collaboration, which measured the excitation function of K+ production in Au + Au collisions at subthreshold beam energies, i.e., from 0.8 A·GeV to 1.5 A·GeV [8]. In proton–proton collisions, the threshold energy for K+ production is 1.6 GeV. In heavy-ion collisions at subthreshold beam energies, K+ mesons are created in multiple step collisions of nucleons, resonances, and pions, which happen more frequently at high densities. Therefore, the K+ yield is sensitive to the density of the fireball, and, hence, to the EOS. In order to correct for other effects that might also contribute to subthreshold K+ production, such as the Fermi energy of the nucleons and short-range correlations, C + C collisions have been studied as a reference system. The KaoS data have been also explained by transport model calculations assuming a soft EOS with a nuclear incompressibility of Knm ≈ 200 MeV [9,10].
The transverse and elliptic flow of protons has been also measured in Au + Au collisions at beam kinetic energies between 2 A·GeV and 11 A·GeV at the AGS in Brookhaven [11]. At these beam energies, baryon densities of more than 5 ρ0 can be reached, like in the core of neutron stars. The data have been analyzed by relativistic transport model calculations, which found the transverse flow data are in agreement with a soft EOS (Knm = 210 MeV), while the elliptic flow data are compatible with a stiff EOS (Knm = 300 MeV) [12]. The resulting constraint for the high-density EOS for symmetric nuclear matter, plotted as pressure versus density, is depicted in Figure 4 by the grey shaded area. For comparison, a soft (blue line) and a hard (red line) EOS are also shown, together with the FOPI and KaoS results (yellow area). The figure clearly demonstrates that the EOS for symmetric matter is well constrained up to densities of about 2 ρ0, but much less for higher densities, where only very soft or very hard EOS are excluded. Future flow measurements to further reduce the uncertainties are already underway at STAR in the fixed target mode, and will be performed with high precision in future experiments, like CBM at FAIR and MPD and BM@N at NICA.
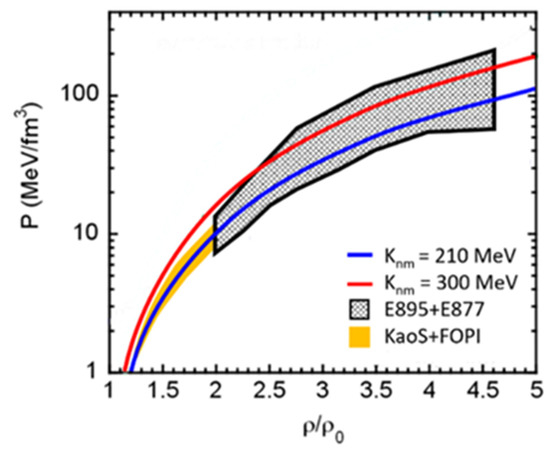
Figure 4.
Pressure versus baryon density for symmetric nuclear matter. Grey hatched area: constraint provided by proton flow data taken at the AGS [11,12]. Yellow area: constraint from kaon data and fragment flow measured at GSI [7,8]. Red line: hard EOS, blue line: soft EOS [12].
In addition to the flow measurements, the high-density EOS of symmetric nuclear matter can be also studied by subthreshold particle production. While at baryon densities up to 2 ρ0, i.e., at beam energies up to 1.5 A GeV, K+ mesons serve as a diagnostic probe of the density, at higher beam energies up to about 10 A·GeV, multi-strange (anti-hyperons) are promising candidates for probing the high-density EOS. According to preliminary calculations of Au + Au collisions at a beam energy of 4 A·GeV, performed with the PHQMD transport code, the yield of Ξ± and Ω± hyperons increases by a factor of about 2 for a soft EOS as compared to a hard EOS [13].
In order to define the EOS for pure neutron matter, the symmetry energy, Esym, has to be determined at high densities by measuring the elliptic flow of neutrons in comparison to protons. This experiment has been performed by the ASY–EOS collaboration at GSI for Au + Au collisions at a beam energy of 0.4 A GeV, where densities well above ρ0 could be reached [14]. The result of this measurement could be reproduced by an UrQMD transport code, assuming a value of Esym = 55 ± 5 MeV. Another observable sensitive to Esym is the ratio of particles with opposite isospin, which reflects the density of neutrons and protons. However, the π+/π− ratio turned out to be not very sensitive to the Esym, because the beam energies investigated were well above the pion production threshold [15]. A more promising observable might be hyperons with different isospin projections I3 = ±1, such as sigma hyperons, which have a higher production threshold. The measured Σ− (dds)/Σ+(uus) ratio serve as a proxy of the n(ddu)/p(uud) ratio. Experimentally, more easily accessible is the Σ*−(dds)/Σ*+(uus) ratio, because these resonances decay into Λπ pairs, in contrast to the Σ± hyperons, which have one neutral decay daughter. However, in both cases the determination of the decay vertex requires a high-resolution tracking detector.
3. The Microscopic Structure of QCD Matter at High Densities
Various neutron star calculations predict a transition from hadronic to quark matter above baryon densities of 4–5 ρ0, when the nucleons start to overlap. Whether this transition is of first order with a mixed phase, as suggested by a non-local 3-flavor Nambu Jona-Lasinio model [16], or a smooth crossover into quark matter, according to the picture of hadron–quark continuity [17,18], is one of the most important open questions in the field of QCD matter under extreme conditions. A hypothetical QCD phase diagram is sketched in Figure 5 as a function of temperature T, baryon-chemical potential μB, and isospin-chemical potential μI. The only known features of this diagram are the locations of stable nuclei, of neutron stars, neutron star mergers, and supernovae. Moreover, the fundamental theory of strong interaction, Quantum Chromo Dynamics (QCD), predicts a smooth crossover from hadronic to quark matter at vanishing baryon-chemical potential at a pseudo-critical temperature of about 156 MeV [19,20]. All the other structures in the phase diagram are conjectures based on model calculations, in particular the existence of a critical endpoint, together with the corresponding first order transition lines separating various phases.
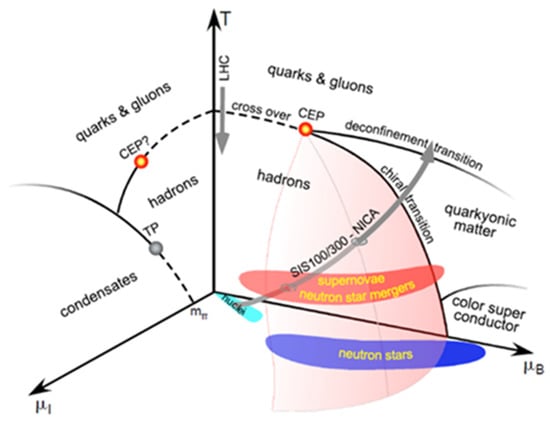
Figure 5.
Sketch of the conjectured QCD phase diagram as a function of temperature T, baryon-chemical μB, and isospin-chemical potential μI [23].
Recently, lattice QCD calculations have determined a value of Tc0 = 132 MeV with an uncertainty of +3 MeV and −6 MeV as an upper bound for the temperature of the chiral critical point for μB = 0 in the chiral limit, i.e., for vanishing quark masses [21,22]. The authors stated that the temperature of the critical endpoint for non-zero quark masses at finite μB must be lower than this value, if it exists at all. This result restricts the possible location of the critical endpoint to large baryon-chemical potentials, which can be reached at relatively low beam energies, as will be discussed below.
The experimental information from heavy-ion collisions on the QCD phase diagram is shown in Figure 6, plotted as chemical freeze-out temperature versus baryon-chemical potential [24]. The parameters T and μb have been calculated by a statistical hadronization model based on the measured particle yields for different collision energies. For very small values of the baryon-chemical potential, i.e., at LHC collision energies, a freeze-out temperature of 156.5 ± 1.5 MeV (with μB = 0.7 ± 3.8 MeV) was measured by the ALICE collaboration [25]. As mentioned above, this freeze-out temperature agrees with the pseudo-critical temperature calculated by lattice QCD. The data points at finite μb have been extracted from particle yields measured at RHIC, SPS, AGS, and GSI. A parameterization of the freeze-out curve, assuming an average kinetic energy of 1 GeV per nucleon, is drawn as a dotted line [26]. The horizontal blue-shaded area illustrates the above-mentioned upper bound for the temperature of a possible chiral critical point of Tc0 = 132 + 3 − 6 MeV, as calculated by lattice QCD [21,22]. This result is supported by calculations based on the Functional Renormalization Group (FRG), which exclude a critical endpoint for values of μb/T < 4, as illustrated by the red line in Figure 6 [27]. Recent FRG calculations even predict a critical endpoint at TCEP = 107 MeV and μb = 635 MeV [28]. In this case, the critical endpoint would be accessible in heavy-ion collisions with a beam kinetic energy of about 6 A·GeV, as available at FAIR and NICA. The following sections present a selection of observables that are expected to provide information about the properties of dense QCD matter as it is formed in heavy-ion reactions.
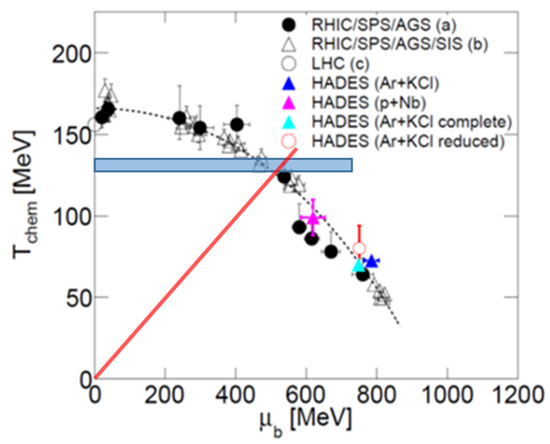
Figure 6.
Chemical freeze-out temperatures Tchem as a function of the baryon chemical potential μb extracted from particle yields measured at different energies [24]. The black dashed line is calculated assuming a fixed energy per nucleon of 1 GeV [26]. Blue-shaded area: upper limit for the chiral critical point T0c = 132 + 3 − 6 MeV [21,22]. According to FRG calculations, the location of the chiral critical endpoint is excluded for values smaller than μb/T = 4 (below the red line) [27].
3.1. The Collective Flow of Particles
An intriguing observation made by the STAR collaboration at RHIC was the scaling of the elliptic flow signal v2 with the number of constituent (valence) quarks nq of the hadrons. When plotting v2/nq versus the transverse kinetic energy per quark (mT − m0)nq, the flow signal of the measured baryons and mesons fell on one curve. This result was interpreted as evidence that the collective flow was generated in the early Quark-Gluon Plasma phase. In order to search for the disappearance of the QGP signal, the STAR collaboration studied the elliptic flow over a large range of collision energies down to √sNN = 7.7 GeV, where the reaction rate of the collider was reduced to several Hz [29]. In the fixed target mode, the measurements could be continued down to collisions energy of √sNN = 4.5 GeV, where the quark number scaling still could be observed [30]. Preliminary results of flow measurements at a collision energy of √sNN = 3 GeV indicate that the scaling law is broken. However, the interpretation of the quark number scaling signal at collision energies below √sNN = 3 GeV is complicated by the fact that the v2 signal changes sign at this energy, because the reaction zone is shadowed by the spectator nucleons. This situation produces the so called squeeze-out phenomenon, where the elliptic flow of particles expands perpendicularly to the reaction plane, and the quark number scaling might be violated by rescattering effects of the hadrons. Future high-precision flow measurements of many hadron species at the different beam energies accessible at FAIR and NICA will help to clarify the situation.
3.2. Event-by-Event Fluctuations of Net-Proton Multiplicity Distributions
Critical opalescence occurs in classical systems due to increased density fluctuations in the vicinity of the critical point. In central heavy-ion collisions, a corresponding phenomenon is predicted for the multiplicity distribution of conserved quantities, such as the baryon number. The STAR collaboration used the net-protons as a proxy for the baryons, and measured the beam energy dependence of the kurtosis (4th order cumulant times variance) of the net-proton multiplicity event-by-event for very central Au + Au reactions [31]. Within the statistical errors, no fluctuation signal was observed down to a collision energy of √sNN = 7.7 GeV. This observation agrees with the result of the lattice QCD calculations, which exclude the existence of a critical endpoint for temperatures above about 130 MeV, corresponding to a collision energy of about √sNN = 6 GeV. Future experiments with STAR using a fixed target, with BM@N and MPD at NICA, and CBM at FAIR, will scan the low energy range, and either discover or exclude the existence of a critical endpoint of a first order phase transition in QCD matter within the experimentally accessible range.
3.3. Chemical Equilibration of Multi-Strange (Anti-) Hyperons
As illustrated in Figure 6, the location of the freeze-out of particles produced in heavy-ion collisions in the QCD phase diagram can be determined by statistical hadronization models, which reproduce the measured particle yields for each collision energy by one freeze-out temperature and a baryon chemical potential. At high collision energies, the multi-strange (anti-) hyperons are also found to be chemically equilibrated. Due to the small hyperon–nucleon scattering cross section and the short lifetime of the dense hadronic phase, it was concluded that these hyperons must be driven into equilibration by multi-particle collisions, which are strongly enhanced due to the high particle density during hadronization [32]. Hence, the chemical equilibration of multi-strange hyperons may serve as indication of a quark-hadron phase transition. Ξ and Ω hyperons were also found in chemical equilibrium in heavy-ion collisions down to a beam energy of 30 A·GeV [33]. However, in Ar + KCl collisions at a beam kinetic energy of 1.76 A GeV, the yield of the double-strange Ξ− hyperon drops out of equilibration: while the yields of all the other particles agree with a statistical model calculation for a chemical freeze-out temperature of 70 ± 3 MeV and a baryon chemical potential of μb = 748 ± 8 MeV, the yield of Ξ− hyperon yield exceeds the statistical model value by a factor of 24 ± 9 [34]. This high hyperon yield is the result of deep-subthreshold production mechanisms, such as multi-step hadron collisions including strangeness-exchange reactions [35]. Future measurements at FAIR and NICA will study the excitation functions of Ξ± and Ω± hyperons and search for the beam energy, where multi-strange (anti-) hyperons are driven into chemical equilibration, which might indicate the onset of deconfinement.
3.4. Probing Deconfinement with Charmonium
The first “smoking gun” proposed as experimental proof for deconfinement in heavy-ion collisions was the suppression of J/ψ mesons (cpairs), which were predicted to melt in the Quark-Gluon Plasma [36]. More than 20 years later, an alternative charm production mechanism was suggested within the statistical hadronization model (SHM) [37]. Within this scheme, c and quarks are created in initial hard collisions, then equilibrate within the Quark-Gluon Plasma, and finally form J/ψ mesons, D mesons, and Λc hyperons during hadronization. These charm production processes differ from hadronic scenarios, such as the ones implemented in the Hadron-String-Dynamics (HSD) transport code, which includes reactions like pp → J/ψ pp, pp → Λc p, and pp → D pp with different threshold energies of Ethr = 11.3 GeV, 11.9 GeV, and 14.9 GeV, respectively [38]. In contrast, charm production in the QGP, as considered in the SHM, does not exhibit different energy thresholds for J/ψ and D mesons. Therefore, the yields of these particles should differ for the two scenarios, particularly at threshold beam energies, as illustrated in Figure 7, where the (J/ψ)/(D + ) ratio is shown as function of collision energy for central Au + Au reactions. The red dots represent the results of the HSD code, while the blue squares stem from the SHM. The HSD results exhibit a strong increase of the ratio towards lower beam energies, because in a hadronic scenario the threshold for J/ψ production is lower than for D meson production. The SHM model results depend only weakly on collision energy. To date, no charm production in heavy-ion collisions has been measured below the highest SPS energies. Future experiments at NICA and FAIR close to the charm threshold are needed, to unravel the production mechanisms and the microscopic structure of dense QCD matter.
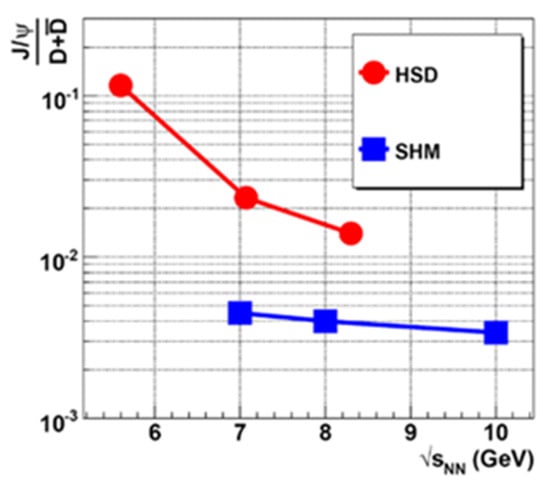
Figure 7.
(J/ψ)/(D + ) ratio as function of collision energy for central Au + Au reactions. Blue symbols: SHM code [37]. Red symbols: HSD model [38].
In heavy ion collisions at beam energies very close to or even below the production threshold, J/ψ and D mesons may also be produced via multi-step processes. Such a scenario has been proposed within UrQMD calculations of central Au + Au reactions, where heavy N* resonances are excited by sequential hadron–hadron collisions. These resonances then decay via processes like N* → J/ψ + N + N and N* → Λc + into charmed particles [39]. The identification of such decays in heavy-ion collisions would strongly challenge the proposed signal of deconfinement within the scanned beam energy range.
3.5. Investigating Dense Matter with Lepton Pairs
Electrons and muons are very promising probes of hot and dense matter as it is created in heavy-ion collisions, since they carry undisturbed information out of the fireball, because they are not affected by the rescattering and absorption due to strong interaction. For example, in-medium modifications of vector mesons decaying into lepton pairs can be studied by lepton spectroscopy. Moreover, the invariant mass distribution of lepton pairs directly reflects the average temperature of the fireball, because it is not blue-shifted by the collective flow, as it is the case for hadron spectra. In particular, the slope of the invariant dilepton mass distribution between 1 GeV/c2 and 2 GeV/c2 is a perfect measure of the fireball temperature, as in this invariant mass range the contributions of vector meson decays are strongly reduced. This is illustrated in Figure 8, which depicts a calculation of the various contributions to the dilepton invariant mass spectrum for central Au + Au collisions at a beam energy of 20 A·GeV [5]. The solid red curve shows the contribution of the thermal radiation, which includes in-medium ρ and ω spectral functions, and a QGP spectrum calculated using a many-body approach [40]. The NA60 collaboration has measured μ+μ− pairs in In-In collisions at 158 A GeV, and extracted a temperature of about 200 MeV from the invariant mass spectrum above 1 GeV/c2 [41]. The HADES collaboration measured electron–positron pairs up to invariant masses of about 1 GeV/c2 in Au + Au collisions at 1.25 A GeV. Nevertheless, they managed to subtract contributions from known vector meson decays, and extracted an average fireball temperature of about 72 MeV from the resulting e+e− invariant mass spectrum [42]. It is worthwhile to note that the dilepton invariant mass spectra include the radiation over the fireball evolution, and, hence, reflect an average temperature. Nevertheless, the measurement of dileptons as a function of beam energy in heavy-ion collisions at FAIR and NICA offers the unique possibility of determining the caloric curve of dense QCD matter and discovering the first order phase transition with its critical endpoint, if it exists at all.
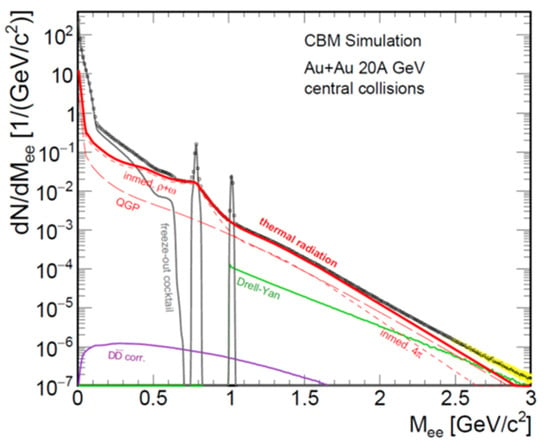
Figure 8.
Di-electron invariant mass spectrum simulated for central Au + Au collisions at 20 A·GeV [5].
4. Exploring the Strange Dimension of the Nuclear Chart
Heavy-ion collisions in the FAIR/NICA energy range are ideally suited to producing and studying hypernuclei. This is illustrated in Figure 9, which depicts the yield of light hypernuclei produced in heavy-ion reactions versus the collision energy, as predicted by the Statistical Hadronization Model (SHM) [43]. The yield of the (double-) lambda hypernuclei exhibit a maximum around √sNN = 5 − 6 GeV, which can be explained by folding the lambda yield with the yield of deuterons, tritons, and helium. While the lambda yield increases with increasing collision energy up to about √sNN = 8 GeV, the yield of light nuclei increases with decreasing collision energy. Similar results have been obtained with a UrQMD-hydro hybrid model and with a coalescence mechanism from a hadronic cascade model [44]. According to the SHM calculations, double-lambda hypernuclei will be measurable in high-rate heavy-ion collision experiments.
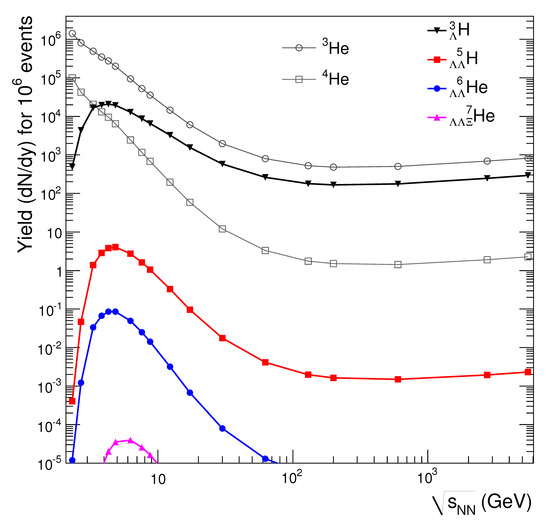
Figure 9.
Yields of hypernuclei at midrapidity for 106 central Au + Au collisions as a function of energy calculated with the Statistical Hadronization Model [43,46]. 3He and 4He nuclei together with the corresponding anti-nuclei (dashed lines) are shown for comparison.
The identification of (double-) lambda hypernuclei, together with a precise determination of their lifetimes and masses, will improve our knowledge on the interactions between neutrons N and hyperons Y, including the 3-body forces NNY and NYY. These interactions play an important role at high densities in neutron star cores with respect to the so called “hyperon puzzle”. For example, in chiral effective field theory, which takes into account only hadron degrees-of-freedom and repulsive 3-body ΛNN interactions, the hyperon chemical potential is kept above the neutron chemical potential up to densities of about 5 ρ0. In this scenario, the weak decay of neutrons into hyperons and, hence, the softening of the EOS is prevented, and neutron stars are stabilized up to 2 solar masses [45]. In conclusion, the future heavy-ion collision experiments at FAIR and NICA will provide important new information on hypernuclei and on our understanding of neutron stars.
5. Summary
Heavy-ion collisions at FAIR and NICA energies are ideally suited to studying the properties and degrees-of-freedom of QCD matter at neutron star core densities. An important research program will be devoted to the investigation of the high-density equation of state (EOS). The relevant diagnostic observables for the investigation of the EOS of symmetric matter are the collective flow of identified particles and fragments, and the subthreshold production of multi-strange (anti-) hyperons. The symmetry energy can be studied by measuring the collective flow of neutrons, and the yields of particles with opposite isospin, such as Σ± hyperons. At baryonic densities above around 5 ρ0, it is expected that quark degrees of freedom emerge. Whether such a transition is smooth, or of first order, is still an open question. According to recent lattice calculations, the critical endpoint of a first order transition should be located at temperatures below about 130 MeV, if it exist at all. Such fireball temperatures are reached in central heavy-ion collisions at energies below √sNN = 5 GeV, i.e., at FAIR–NICA energies. This might be the reason why experiments at SPS and at the RHIC collider did not find indications for a critical endpoint. A promising signal is the higher-order cumulants of the net-proton multiplicity, which should start to fluctuate in the vicinity of the critical endpoint. Experiments at FAIR and NICA will search for such fluctuations. Moreover, observables like the quark number scaling of the elliptic flow, the chemical equilibration of multi-strange hyperons, and charm production will be investigated as function of beam energy, as these probes are expected to be sensitive to a transition from quark to hadronic matter. A key observable of a first-order phase transition is provided by lepton pairs, which allows us to directly measure the temperature of the fireball as a function of beam energy, and, hence, to discover or to exclude a caloric curve that is specific for QCD matter. Finally, the determination of lifetimes and masses of (double-)lambda hypernuclei in heavy-ion collisions at FAIR and NICA will improve our understanding of 2 and 3 body interactions between hyperons and nucleons, and will shed light on the ”hyperon puzzle” in neutron stars.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author is supported by the Europeans Union’s Horizon 2020 research and innovation programme under grant agreement No. 871072, and via RFBR according to the research project No. 18-02-40086 by the Ministry of Science and Higher Education of the Russian Federation, Project “Fundamental properties of elementary particles and cosmology” No 0723-2020-0041.
Conflicts of Interest
The author declares no conflict of interest.
References
- Available online: https://fair-center.de (accessed on 1 March 2021).
- Durante, M.; Indelicato, P.J.; Jonson, B.; Koch, V.; Langanke, K.; Meissner, U.-G.; Nappi, E.; Nilsson, T.; Stöhlker, T.; Widmann, E.; et al. All the fun of the FAIR: Fundamental physics at the facility for antiproton and ion research. Phys. Scr. 2018, 94, 033001. [Google Scholar] [CrossRef]
- Available online: https://nica.jinr.ru/ (accessed on 1 March 2021).
- Senger, P. Studies of dense nuclear matter at NICA. arXiv 2020, arXiv:2005.13856. [Google Scholar]
- Ablyazimov, T.; Abuhoza, A.; Adak, R.P.; Adamczyk, M.; Agarwal, K.; Aggarwal, M.M.; Ahammed, Z.; Ahmad, F.; Ahmad, N.; Ahmad, S.; et al. Challenges in QCD matter physics—The Compressed Baryonic Matter experiment at FAIR. Eur. Phys. J. A 2017, 53, 60. [Google Scholar]
- Hanauske, M.; Steinheimer, J.; Bovard, L.; Mukherjee, A.; Schramm, S.; Takami, K.; Papenfort, J.; Wechselberger, N.; Rezzolla, L.; Stöcker, H. Concluding Remarks: Connecting Relativistic Heavy Ion Collisions and Neutron Star Mergers by the Equation of State of Dense Hadron- and Quark Matter as signalled by Gravitational Waves. J. Phys. Conf. Ser. 2017, 878, 012031. [Google Scholar] [CrossRef]
- Le Fèvre, A.; Leifels, Y.; Reisdorf, W.; Aichelin, J.; Hartnack, C. Constraining the nuclear matter equation of state around twice saturation density. Nucl. Phys. A 2016, 945, 112–133. [Google Scholar] [CrossRef]
- Sturm, C.; Böttcher, I.; Dȩbowski, M.; Förster, A.; Grosse, E.; Koczoń, P.; Kohlmeyer, B.; Laue, F.; Mang, M.; Naumann, L.; et al. Evidence for a Soft Nuclear Equation-of-State from Kaon Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.-M. Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 1974–1977. [Google Scholar] [CrossRef] [PubMed]
- Hartnack, C.; Aichelin, J. Analysis of kaon production around the threshold. J. Phys. G Nucl. Part. Phys. 2002, 28, 1649–1656. [Google Scholar] [CrossRef]
- Pinkenburg, C.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L.; et al. Elliptic Flow: Transition from Out-of-Plane to In-Plane Emission in Au+ Au Collisions. Phys. Rev. Lett. 1999, 83, 1295–1298. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Aichelin, J.; Bratkovskaya, E.; Fevre, A.L.; Kireyeu, V.; Kolesnikov, V.; Leifels, Y.; Voronyuk, V. Parton Hadron Quantum Molecular Dynamics (PHQMD)—A Novel Microscopic N-Body Transport Approach for Heavy-Ion Collisions, Dynamical Cluster Formation and Hypernuclei Production. In Proceedings of the XVIII International Conference on Strangeness in Quark Matter (SQM 2019), Bari, Italy, 10–15 June 2019. [Google Scholar]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F. Results of the ASY-EOS experiment at GSI: The symmetry energy at supra-saturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Cozma, M. The impact of energy conservation in transport models on the π−/π+ multiplicity ratio in heavy-ion collisions and the symmetry energy. Phys. Lett. B 2016, 753, 166–172. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutronstars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Fukushima, K.; Kojo, T.; Weise, W. Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter. Phys. Rev. D 2020, 102, 096017. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrődi, G.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. Chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Lahiri, A.; Li, S.T.; Mukherjee, S.; Ohno, H.; Petreczky, P.; Schmidt, C.; et al. Chiral Phase Transition Temperature in (2 + 1)-Flavor QCD. Phys. Rev. Lett. 2019, 123, 062002. [Google Scholar] [CrossRef] [PubMed]
- Karsch, F. Critical behavior and net-charge fluctuations from lattice QCD. In Proceedings of the Corfu Summer Institute 2018 “School and Workshops on Elementary Particle Physics and Gravity”—PoS(CORFU2018), Corfu, Greece, 31 August–28 September 2018. [Google Scholar]
- NUPECC Long Range Plan 2017. Available online: http://www.nupecc.org/lrp2016/Documents/lrp2017.pdf (accessed on 1 March 2021).
- Agakishiev, G.; Arnold, O.; Balanda, A.; Belver, D.; Belyaev, A.; Berger-Chen, J.C.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Cabanelas, P.; et al. Statistical model analysis of hadron yields in proton-nucleus and heavy-ion collisions at SIS 18 energies. Eur. Phys. J. A 2016, 52, 178. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nat. Cell Biol. 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Fu, W.; Luo, X.; Pawlowski, J.M.; Rennecke, F.; Wen, R.; Yinet, S. Hyper-order baryon number fluctuations at finite temper-ature and density. arXiv 2021, arXiv:2101.06035. [Google Scholar]
- Fu, W.; Pawlowski, J.M.; Rennecke, F. The QCD phase structure at finite temperature and density. Phys. Rev. D 2020, 101, 054032. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Elliptic flow of identified hadrons in Au+Au collisions at √sNN=7.7–62.4 GeV. Phys. Rev. C 2013, 88, 014902. [Google Scholar] [CrossRef]
- Abdallah, M.S.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Kiselev, A.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I. Flow and interferometry results from Au+Au collisions at √sNN = 4.5 GeV. Phys. Rev. C 2021, 103, 034908. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aparine, A.; et al. Net-proton number fluctuations and the Quantum Chromodynamics critical point. arXiv 2020, arXiv:2001.02852. [Google Scholar]
- Braun-Munzinger, P.; Stachel, J.; Wetterich, C. Chemical freeze-out and the QCD phase transition temperature. Phys. Lett. B 2004, 596, 61–69. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions: The hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 2009, 673, 142–145. [Google Scholar] [CrossRef]
- Agakishiev, G.; Balanda, A.; Bannier, B.; Bassini, R.; Belver, D.; Belyaev, A.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Zumbruch, P.; et al. Hyperon production in Ar + KCl collisions at 1.76A GeV. Eur. Phys. J. A 2011, 47, 21. [Google Scholar] [CrossRef]
- Graef, G.; Steinheimer, J.; Li, F.; Bleicher, M. Deep sub-threshold Ξ and Λ production in nuclear collisions with the UrQMD transport model. Phys. Rev. C 2014, 90, 064909. [Google Scholar] [CrossRef]
- Matsui, T.; Satz, H. J/ψ Suppression by Quark-Gluon Plasma Formation. Phys. Lett. B 1986, 178, 416. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Charmonium and open charm production in nuclear collisions at SPS/FAIR energies and the possible influence of a hot hadronic medium. Phys. Lett. B 2008, 659, 149–155. [Google Scholar] [CrossRef]
- Linnyk, O.; Bratkovskaya, E.L.; Cassing, W.; Stöcker, H. Charmonium dynamics in heavy ion collisions. J. Phys. G Nucl. Part. Phys. 2008, 35, 4. [Google Scholar] [CrossRef][Green Version]
- Steinheimer, J.; Botvina, A.; Bleicher, M. Sub-threshold charm production in nuclear collisions. Phys. Rev. C 2017, 95, 014911. [Google Scholar] [CrossRef]
- Rapp, R.; Wambach, J. Low-mass dileptons at the CERN-SPS: Evidence for chiral restoration? Eur. Phys. J. A 1999, 6, 415. [Google Scholar] [CrossRef][Green Version]
- Specht, H.J.; Nieves, J.M.; Oset, E.; Vicente-Vacas, M.J. Na60 Collaboration Thermal Dileptons from Hot and Dense Strongly Interacting Matter. In Proceedings of the AIP Conference Proceedings, Chonburi, Thailand, 18–20 July 2018. [Google Scholar]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M. Probing baryon-rich matter with virtual photons, The HADES Collaboration. Nat. Phys. 2019, 15, 1040–1045. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stöcker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Steinheimer, J.; Gudima, K.; Botvina, A.; Mishustin, I.; Bleicher, M.; Stöcker, H. Hypernuclei, dibaryon and antinuclei production in high energy heavy ion collisions: Thermal production vs. Coalescence. Phys. Lett. B 2012, 714, 85. [Google Scholar] [CrossRef]
- Weise, W. Dense Baryonic Matter and Strangeness in Neutron Stars. In Proceedings of the 8th International Conference on Quarks and Nuclear Physics (QNP2018), Tsukuba, Japan, 12–17 November 2018. [Google Scholar]
- Andronic, A. (Westfälische Wilhelms-Universität Münsterdisabled, Munster, Germany). Personal communication, 2021.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).