A Vector Finder Toolkit for Track Reconstruction in MPD ITS

Abstract

As a part of the future upgrade program of the Multi-Purpose Detector (MPD) experiment at the Nuclotron-Based Ion Collider Facility (NICA) complex, an Inner Tracking System (ITS) made of Monolitic Active Pixel Sensors (MAPSs) is proposed between the beam pipe and the Time Projection Chamber (TPC). It is expected that the new detector will enhance the experimental potential for the reconstruction of short-lived particles—in particular, those containing the open charm particle. To study the detector performance and select its best configuration, a track reconstruction approach based on a constrained combinatorial search was developed and implemented as a software toolkit called Vector Finder. This paper describes the proposed approach and demonstrates its characteristics for primary and secondary track finding in ITS, ITS-to-TPC track matching and hyperon reconstruction within the MPD software framework. The results were obtained on a set of simulated central gold–gold collision events at $\sqrt{s_{NN}}=9$ GeV with an average multiplicity of ∼1000 charged particles in the detector acceptance produced with the Ultra-Relativistic Quantum Molecular Dynamics (UrQMD) generator.

1. Introduction

The Nuclotron-Based Ion Collider Facility (NICA) and the Multi-Purpose Detector (MPD) at the NICA collider, which are currently under construction at the Joint Institute for Nuclear Research (JINR) in Russia [1,2], are expected to strengthen the experimental investigation of the high-density baryonic matter produced in heavy-ion collisions. New experiments will be performed to collect measurements of the bulk properties of the nuclear matter and study different probes with relatively high production rates. These are also planned during the upgrade of the detector to enhance its capabilities to study rear probes such as multi-strange (anti)hyperons and charmed particles.

The investigation of the formation and propagation of particles containing charm and/or anticharm quarks in heavy-ion collisions opens the possibility of exploring the early phase of the fireball due to the large mass of the charm quarks, which can be produced in hard processes only. The elliptic flow of charm quarks is an important diagnostic aspect of the early fireball and its prevailing degrees of freedom. The propagation of open charm particles in the fireball provides information about the transport properties of hot and dense matter [3,4].

The NICA energy region of $\sqrt{s_{NN}}=4-11$ GeV for heavy-ion collisions is at the kinematic threshold for the production of charmed mesons $D^{\pm },D^0,D_s$ and baryons ${\Lambda }_c,{\Xi }_c$ [5]. Therefore, the study of charmed particles in the MPD experiment could provide valuable information on their production mechanisms (such as subthreshold production, for instance).

The MPD upgrade plan foresees the installation of the Inner Tracking System (ITS) based on the next-generation silicon pixel detectors known as Monolitic Active Pixel Sensors (MAPSs) [6] between the beam pipe and the Time Projection Chamber (TPC). Such a detector will increase the research potential of the experiment in terms of both the high-luminosity proton–proton and high-multiplicity nucleus–nucleus interactions. The main purpose of the ITS is to improve the quality and precision of track, primary and secondary vertex reconstruction in MPD in the region close to the interaction point.

In order to optimize the ITS configuration and study the performance of the upgraded detector, a dedicated ITS track reconstruction method based on a constrained combinatorial search was developed and implemented as a Vector Finder toolkit [7,8]. The approach is described below, and some results of its application to track and hyperon decay reconstruction in the MPD ITS are presented.

2. MPD Tracking System Configuration

The MPD detector at the NICA collider has been designed to detect hadrons, electrons and photons over a large phase-space at the high event rate achieved at NICA. At the designed luminosity of L = 10²⁷ cm⁻²s⁻¹ for Au + Au, the collision rate will be ∼7 kHz.

Figure 1a shows a three-dimensional view of the MPD setup. All the subdetectors are located inside a superconducting solenoid, which produces a magnetic field along the beam axis with a nominal strength of 0.5 T. The detailed description of the MPD detector can be found in [9]. Here, only the tracking system is presented.

The MPD TPC is the main tracking device for the reconstruction of charged particle trajectories over the pseudorapidity range of $\left|\eta \right|<1.5$. It provides the momentum measurement for charged particles with a precision better than 3.5% at a transverse momentum $p_T$ below 2 GeV/c and particle identification via the specific energy loss measurement ($dE/dx$) in the TPC gas with a resolution better than 8%. The track reconstruction quality outside the midrapidity region is enhanced by a straw-tube End Cap Tracker (ECT). The Inner Tracker (IT) system, made of five layers of silicon pixel detectors (Figure 1b,c), is intended for the very precise determination of the position of primary and secondary vertices and improvement of the track reconstruction performance for low-$p_T$ tracks. These goals are achieved due to the higher acceptance of the ITS at pseudorapidity ($\left|\eta \right|<2.0$) and transverse momentum of tracks because of its close proximity to the beam line (∼3 cm instead of ∼40 cm in the TPC) and excellent spatial resolution (<10 μm in each direction as compared with 0.5 mm and 1 mm in transverse and longitudinal directions, respectively, for the TPC).

3. Vector Finder Toolkit Algorithms

The track finding method is based on the combinatorial search for detector hit combinations that can potentially belong to the same particle. Here, a hit is a reconstructed point of a particle trajectory crossing of a detector layer. Possible hit combinations are selected on detector layers using prior constraints defined by the detector geometry and event characteristics, such as the momentum and angular spectra of particles to be reconstructed.

The collected hit combinations, forming sequences of joint vectors connecting pairs of hits on different detector layers, are further fitted by the Kalman filter to verify hit-to-track associations via the track quality values defined by the ${\chi }^2$-metrics and to obtain track parameters.

3.1. Primary Track Reconstruction

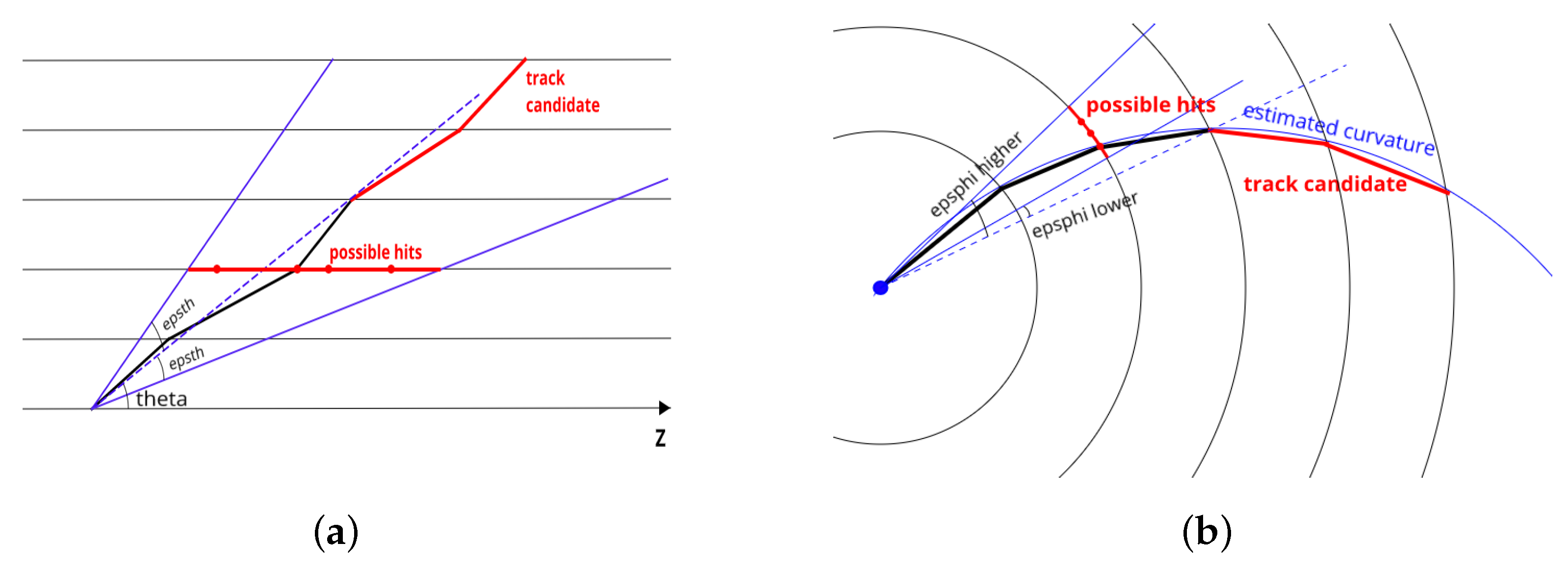
Primary tracks are produced in the collision point of two particle beams, called the primary vertex. Therefore, the acceptance window determination for hits on each detector layer can utilize hit azimuthal and polar angles in the coordinate system with the Z-axis directed along the beam line, the Y-axis vertically upward and X-axis horizontally.

In the longitudinal projection, the particle track is not affected by the magnetic field, so it can be considered as a straight line. Therefore, the track candidate can be extended on each detector layer by adding hits with sufficiently close polar angle theta (Figure 2).

In the transverse projection, the charged particle track is close to a circle arc because of the magnetic field. Therefore, hits added to a track candidate on each layer should correspond to the estimated track curvature. Thus, the area of interest can be defined by two angles epsphi lower and epsphi higher shifted from the track candidate’s last accepted hit azimuthal angle phi in the direction defined by the particle charge.

The size of the hit acceptance window on each detector layer can be evaluated from the Monte Carlo-simulated event samples. For example, Figure 3 shows the distributions of the angular position differences of hits on adjacent layers from the same particle as functions of $p_T$. From the plots, one can select optimal cuts which are usually taken to be dependent on the processing iteration. Running the reconstruction procedure in several passes allows one to relax the acceptance criteria, with the number of remaining hits decreasing after previous iterations, resulting in the acceleration of the processing. From Figure 3b, one can also see that to determine the proper shift of the transverse angle window, it is necessary to evaluate $p_T$ (by taking two first hits and the primary vertex nominal position, for example). More details can be found in [11].

3.2. Secondary Track Reconstruction

Secondary tracks can be produced by decay products of short-lived particles; therefore, they do not pass through the primary vertex. Thus, the primary vertex cannot be used to define good constraints, and the utilization of longitudinal and transverse angles theta and phi is no longer optimal. Thus, an alternative solution should be used; e.g., based on estimated track parameters at the earlier steps of its propagation.

In the longitudinal projection, the particle track is still close to a straight line, because it is not affected by the magnetic field. Thus, linear extrapolation can be used to find possible hits to extend track candidates to detector layers (Figure 4). In the transverse projection, the particle track is close to a circle arc, so the circle arc propagation is used. Initial acceptance windows and $p_T$ estimates still can be taken as for the case of primary tracks with some adjustment to account for the approximation.

3.3. Track Matching

Separate track reconstruction procedures in ITS and TPC require a method to combine tracks from both detectors to achieve optimal track reconstruction quality. The implemented track-matching procedure propagates tracks from both detectors to a cylinder surface lying between them to find a set of corresponding TPC tracks for each ITS track, as shown in Figure 5. The best possible match is chosen using a special quality function that takes into account both the number of hits and ${\chi }^2$ of the resulting track, defined as

$$quality=N_{hits}+(100.0-min({\chi }^2,100.0))/101.0,$$

where $N_{hits}$ is the number of hits in the combined track and ${\chi }^2$ is the total ${\chi }^2$ value.

4. Results

The algorithms described were implemented as a Vector Finder toolkit within the MpdRoot software framework [12] and tested on a simulated 200-event set of central Au + Au collisions produced with the Ultra-Relativistic Quantum Molecular Dynamics (UrQMD) generator [13]. Produced particles were transported through the detector setup with the Geant3 code [14]. To have better defined conditions for track reconstruction (namely, a cleaner track matching environment), TPC response simulation was performed using a simplified approach based on a Gaussian-smeared-hit approximation; i.e., effects of track multiplicity in the TPC on the results were mostly excluded.

Results for track reconstruction efficiencies as functions of pseudorapidity $\eta$ and transverse momentum $p_T$ can be seen in Figure 6. The efficiency is defined with respect to particles having produced hits in at least three layers of the ITS. One can see that the efficiency remained close to 100% up to the geometric acceptance limit of $\left|\eta \right|=2$ and down to ∼0.05 GeV/c in $p_T$. Some decrease for secondary tracks below 0.25 GeV/c can be explained by the particle specie composition; i.e., there was a relatively large fraction of protons in this momentum region. They experienced non-negligible energy loss in the outer two silicon layers with relatively large thickness and changed their curvature in the magnetic field, which was not accounted for in the algorithm, since there was no particle identification at this reconstruction stage. This explanation is supported by earlier results obtained for a detector configuration with all 50 μm layers [11], where no such efficiency decrease was observed.

The track matching efficiency remained above ∼90% up to $\left|\eta \right|=2$ for $p_T$-values above ∼0.1 GeV/c (Figure 7).

To demonstrate the effect of the ITS on the short-lived particle decay reconstruction quality, a Monte Carlo event set of 250,000 central Au + Au collisions at $\sqrt{s_{NN}}=9$ GeV was produced and processed to reconstruct and select $\Lambda$ and ${\Omega }^{-}$ hyperons via their weak decays into $p+{\pi }^{-}$ and $\Lambda +K^{-}$, respectively. The simulation and reconstruction were done for two detector configurations—with and without the ITS. For this study, the TPC simulation package included the part realistically describing the detector response to properly take into account high-multiplicity effects [15], although decay products were identified using Monte Carlo truth information. To ensure a fair comparison of the results, the hyperon selection criteria were chosen to obtain the maximum significance of the decay product invariant mass peak [16]. The significance was defined as $S/\sqrt{S+B}$, where the signal S and background B were calculated as integrals within the $\pm 2\sigma$ interval of the peak position of the signal and background distributions, obtained from the invariant mass fit to a sum of gaussian (signal) and polynomial (background) functions. From Figure 8, one can see that the ITS gives a significant improvement in hyperon reconstruction quality, especially for objects with a shorter decay length (decay length $c\tau$ = 7.9 cm for $\Lambda$ and 2.5 cm for ${\Omega }^{-}$), and the presented track reconstruction approach improves the results as compared with the method based on a Kalman filter extension of tracks from the TPC to the ITS (Figure 8a).

5. Conclusions

A track reconstruction approach based on a constrained combinatorial search was developed and implemented as a software toolkit called Vector Finder for the optimization of studies of the future inner tracking system of the MPD experiment.

It demonstrated good performance results for simulated high-multiplicity events of Au + Au collisions, showing improvements in the reconstruction quality of short-lived particles over the existing method.

The role of the ITS for future studies of short-lived particles has been also demonstrated, and this research direction will be further followed by evaluating the reconstruction feasibility of open charm particles.