Techniques for Reconstruction of Strange Objects at MPD
Abstract
1. Introduction
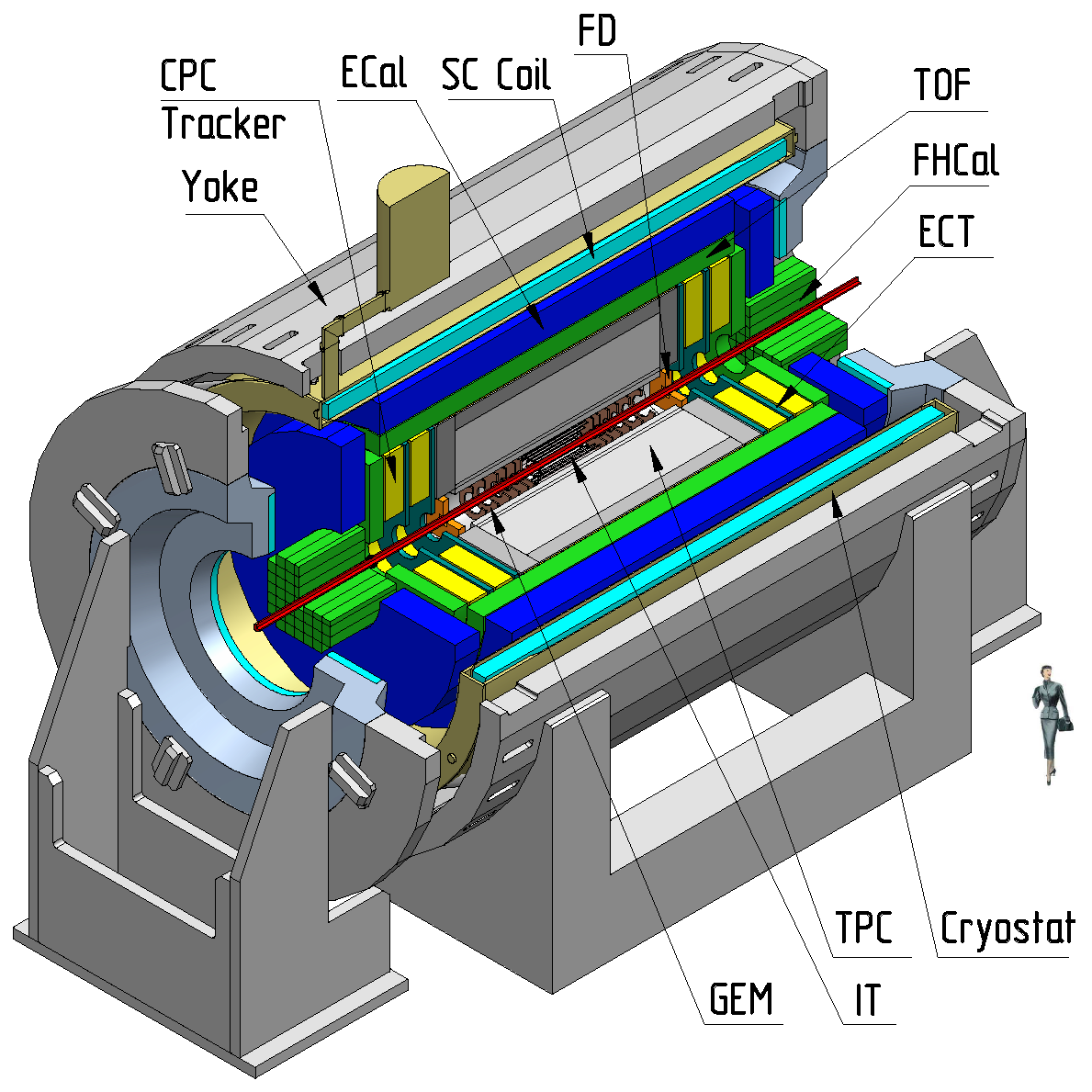
2. MPD Detector Configuration
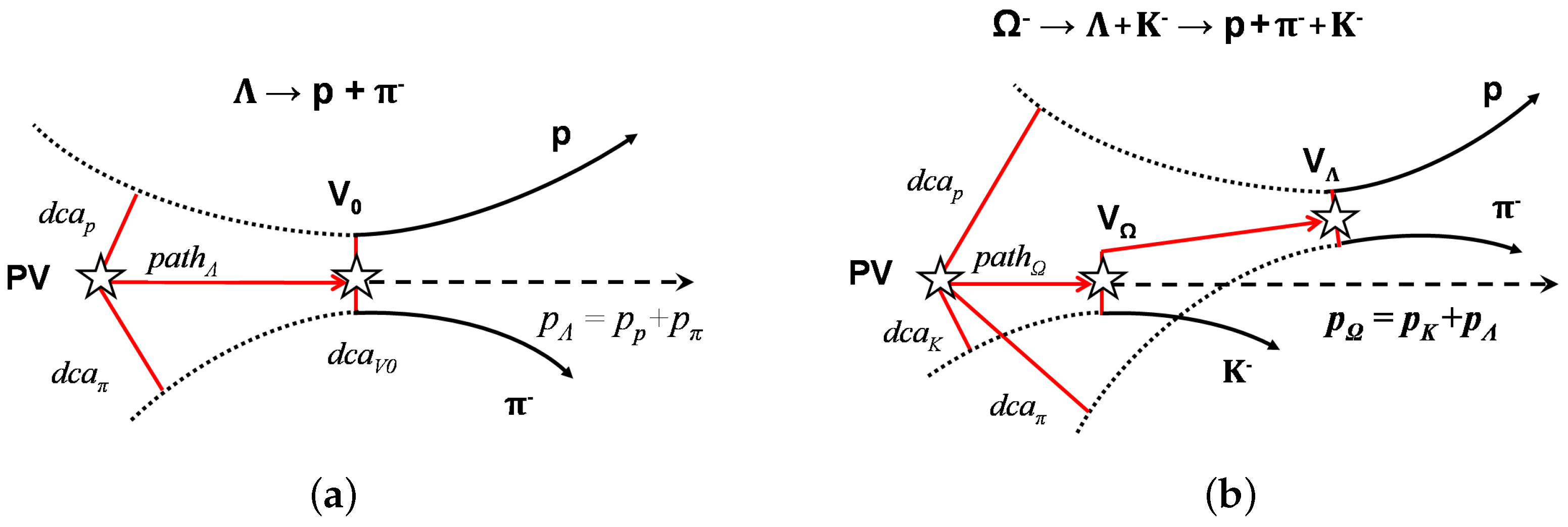
3. Reconstruction of Decays
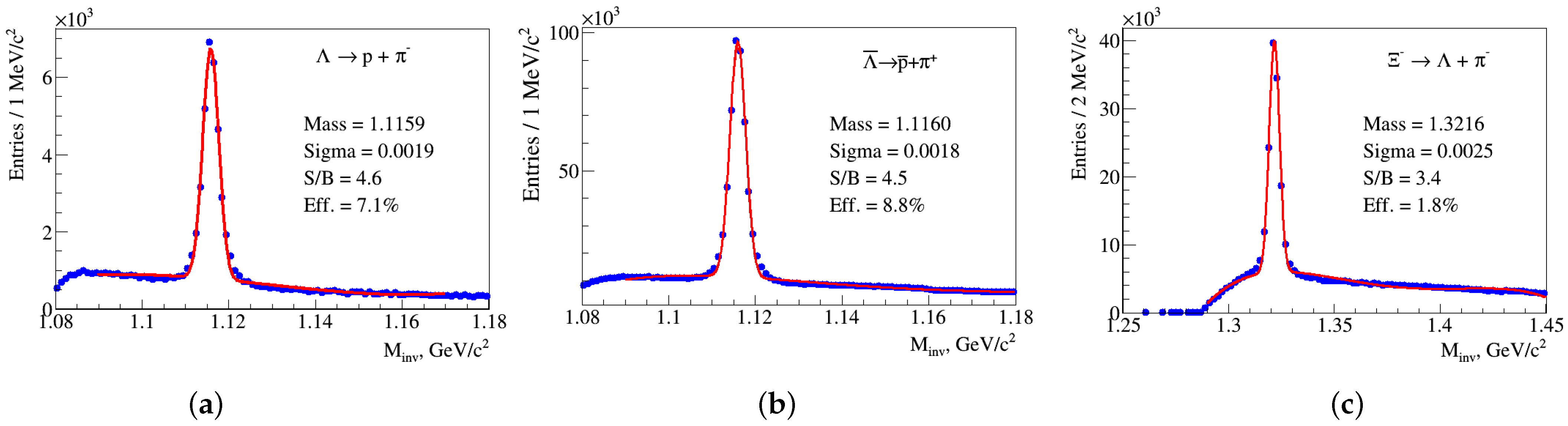
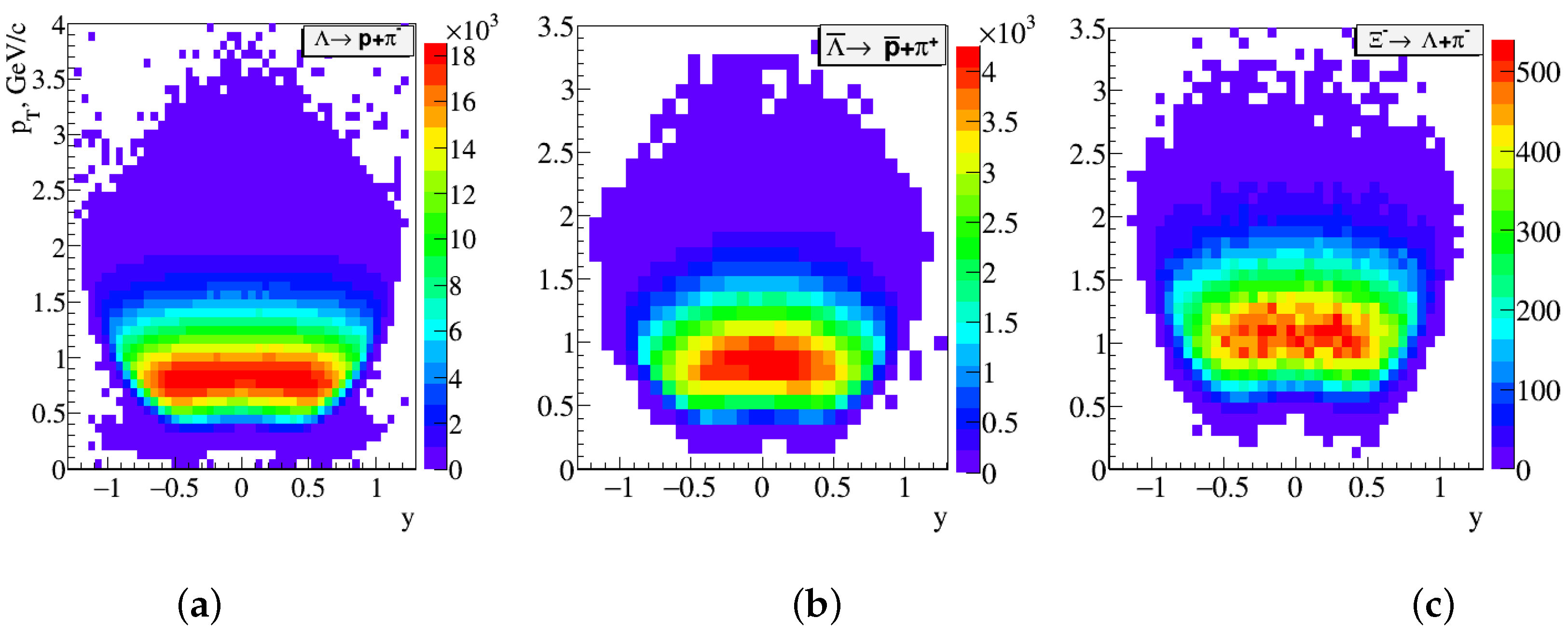
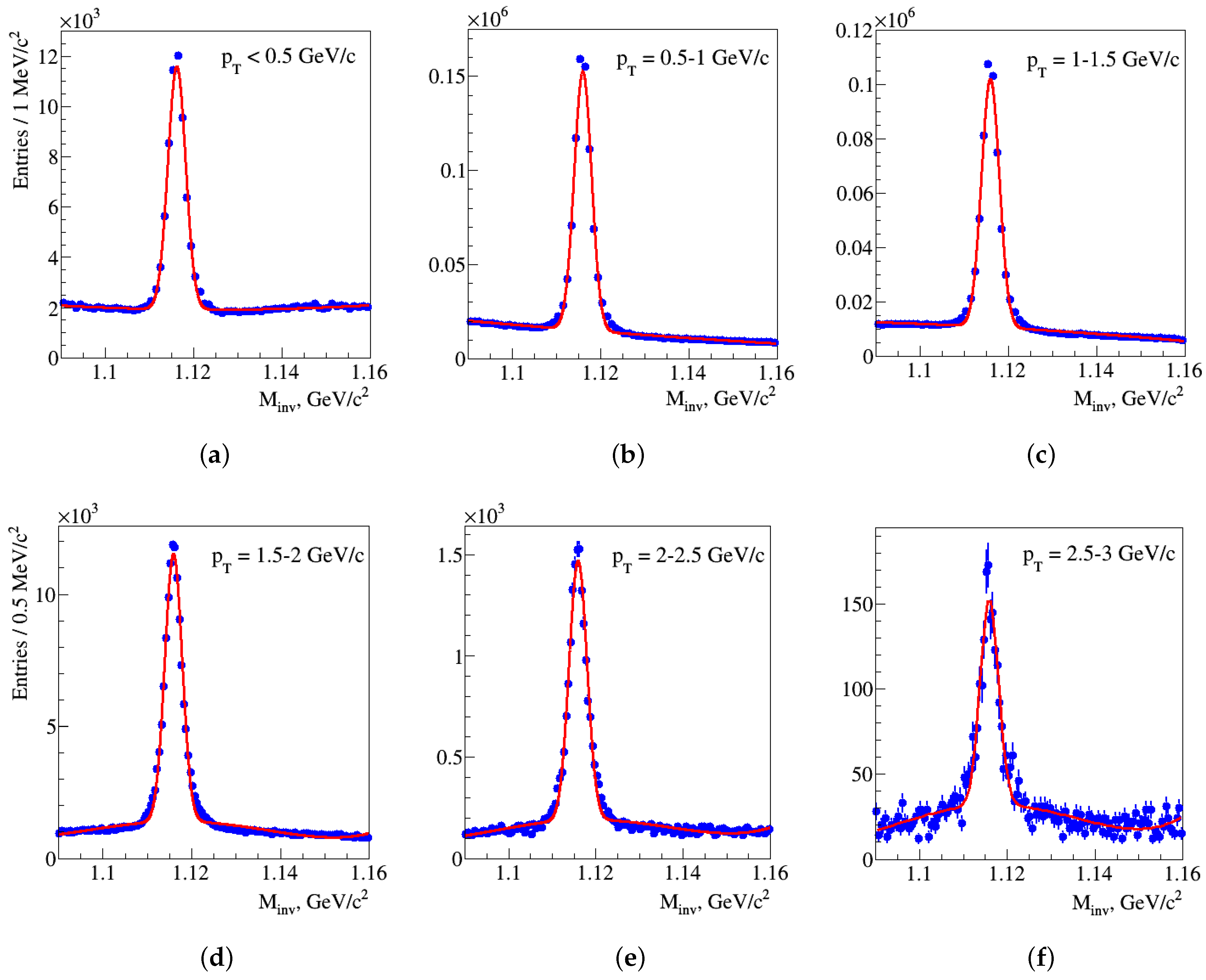
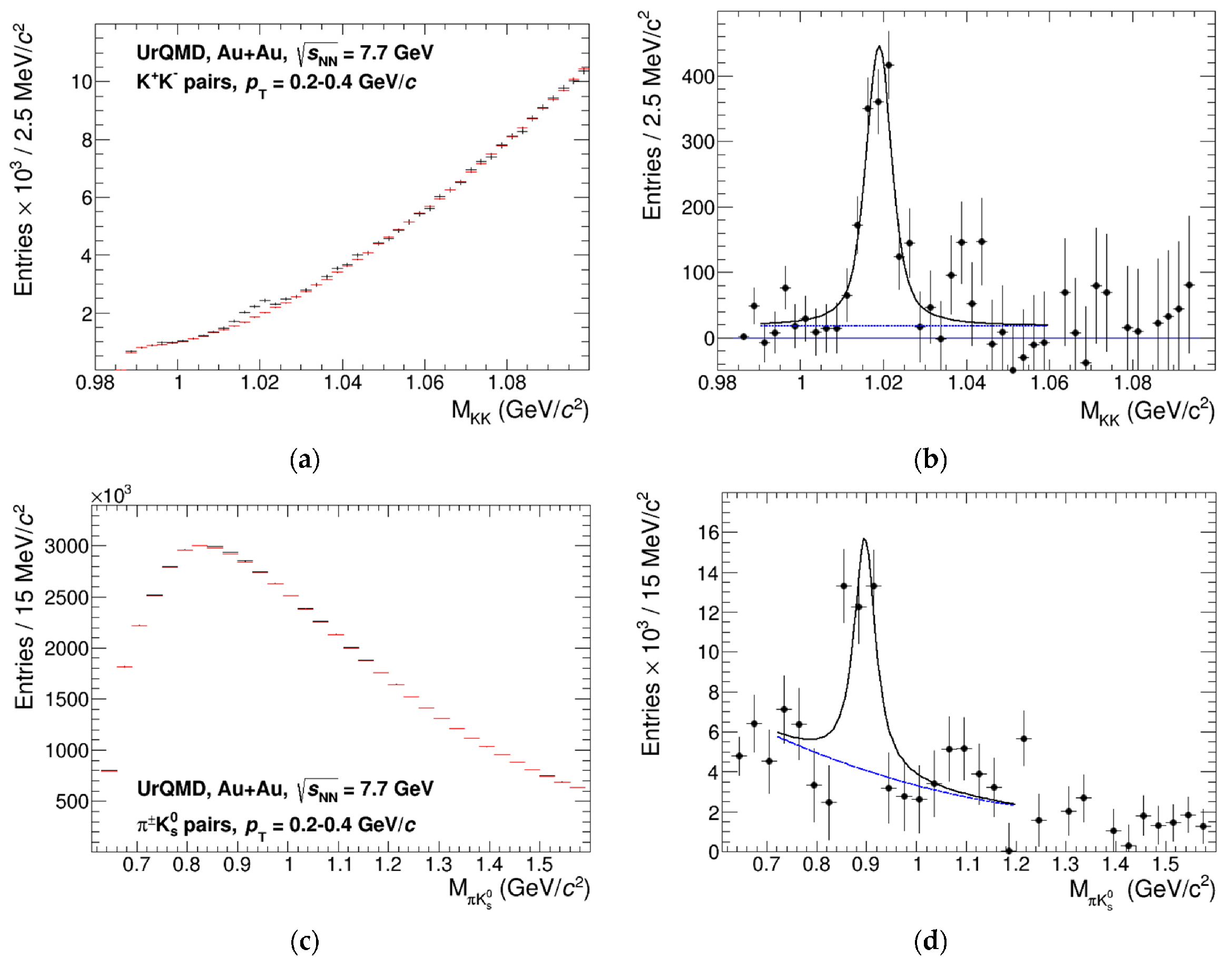
4. Results
5. Conclusions
Funding
Conflicts of Interest
References
- Kekelidze, V.D.; Lednicky, R.; Matveev, V.A.; Meshkov, I.N.; Sorin, A.S.; Trubnikov, V.G. Three stages of the NICA accelerator complex. Eur. Phys. J. A 2016, 52, 211. [Google Scholar] [CrossRef]
- Golovatyuk, V.; Kekelidze, V.; Kolesnikov, V.; Rogachevsky, O.; Sorin, A. The multi-purpose detector (MPD) of the collider experiment. Eur. Phys. J. A 2016, 52, 212. [Google Scholar] [CrossRef]
- Antinori, F.; Bacon, P.A.; Badala, A.; Barbera, R.; Belogianni, A.; Bloodworth, I.J.; Bombara, M.; Bruno, G.E.; Bull, S.A.; Caliandro, R.; et al. [NA57 Collaboration.] Strangeness enhancements at central rapidity in 40 A GeV/c Pb–Pb collisions. J. Phys. G 2010, 37, 045105. [Google Scholar]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. [STAR Collaboration] Enhanced strange baryon production in Au+Au collisions compared to p + p at = 200 GeV. Phys. Rev. C 2008, 77, 044908. [Google Scholar] [CrossRef]
- Rafelski, J.; Muller, B. Strangeness production in the quark–gluon plasma. Phys. Rev. Lett. 1982, 48, 1066. [Google Scholar] [CrossRef]
- Becattini, F.; Manninen, J. Centrality dependence of strangeness production in heavy-ion collisions as a geometrical effect of core-corona superposition. Phys. Lett. B 2009, 673, 19–23. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of Quark-Hadron Phase Transitions in General-Relativistic Neutron-Star Mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef] [PubMed]
- Kerman, A.K.; Weiss, M.S. Superstrange Nuclei. Phys. Rev. C 1973, 8, 408. [Google Scholar] [CrossRef]
- Wakai, M.; Bando, H.; Sano, M. Hypernucleus Formation in High-energy Nuclear Collisions. Phys. Rev. C 1998, 38, 748. [Google Scholar] [CrossRef] [PubMed]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stocker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Steinheimer, J.; Gudima, K.; Botvina, A.; Mishustin, I.; Bleicher, M.; Stocker, H. Hypernuclei, dibaryon and antinuclei production in high energy heavy ion collisions: Thermal production versus Coalescence. Phys. Lett. B 2012, 714, 85–91. [Google Scholar] [CrossRef]
- Riabov, V. Short-Lived Resonances as Probes of the Medium Produced in Heavy-Ion Collisions. Particles 2020, 4, 1. [Google Scholar] [CrossRef]
- Abraamyan, K.U.; Afanasiev, S.V.; Alfeev, V.S.; Anfimov, N.; Arkhipkin, D.; Aslanyan, P.Z.; Babkin, V.A.; Baznat, M.I.; Bazylev, S.N.; Blaschke, D.; et al. [MPD Collaboration] The MPD detector at the NICA heavy-ion collider at JINR. Nucl. Instrum. Methods A 2011, 628, 99–102. [Google Scholar] [CrossRef]
- Luchsinger, R.; Grab, C. Vertex reconstruction by means of the method of Kalman filter. Comput. Phys. Commun. 1993, 76, 263–280. [Google Scholar] [CrossRef]
- Gertsenberger, K.; Merts, S.; Rogachevsky, O.; Zinchenko, A. Simulation and analysis software for the NICA experiments. Eur. Phys. J. A 2016, 52, 214. [Google Scholar] [CrossRef]
- Gorbunov, S.; Kisel, I. Reconstruction of decayed particles based on the Kalman filter. CBM SOFT Note 2007 003 2007, 7. Available online: https://www.star.bnl.gov/bouchet/KFParticle/DOC-2007-May-14-1.pdf (accessed on 21 April 2021).
- Hulsbergen, W.D. Decay chain fitting with a Kalman filter. Nucl. Instrum. Meth. A 2005, 552, 566–575. [Google Scholar] [CrossRef]
- Ilieva, M.; Kolesnikov, V.; Murin, Y.; Suvarieva, D.; Vasendina, V.; Zinchenko, A.; Litvinenko, E.; Gudima, K. Evaluation of the MPD Detector Capabilities for the Study of the Strangeness Production at the NICA Collider. Phys. Part. Nucl. Lett. 2015, 12, 100–112. [Google Scholar] [CrossRef]
- Ilieva, M.; Kolesnikov, V.; Suvarieva, D.; Vasendina, V.; Zinchenko, A. Reconstruction of Multistrange Hyperons with the MPD Detector at the NICA Collider: A Monte Carlo Feasibility Study. Phys. Part. Nucl. Lett. 2015, 12, 618–627. [Google Scholar] [CrossRef]
- Drnojan, J.; Levterova, E.; Vasendina, V.; Zinchenko, A.; Zinchenko, D. Perspectives of Multistrange Hyperon Study at NICA/MPD from Realistic Monte Carlo Simulation. Phys. Part. Nucl. Lett. 2020, 17, 32–43. [Google Scholar] [CrossRef]
- Kolesnikov, V.I.; Zinchenko, A.I.; Vasendina, V.A. Prospects for Studying Hyperons and Hypernuclei on the NICA Collider. Bull. Russ. Acad. Sci. Phys. 2020, 84, 451–454. [Google Scholar] [CrossRef]
- Bass, S.A. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Toneev, V.D.; Amelin, N.S.; Gudima, K.K.; Sivoklokov, S.Y. Dynamics of relativistic heavy ion collisions. Nucl. Phys. A 1990, 519, 463–478. [Google Scholar] [CrossRef]
- Cassing, W.; Bratkovskaya, E.L. Parton-hadron-string dynamics: An off-shell transport approach for relativistic energies. Nucl. Phys. A 2009, 831, 215–242. [Google Scholar] [CrossRef]
- Kamada, H.; Golak, J.; Miyagawa, K.; Witala, H.; Gloeckle, W. Pi mesonic decay of the hypertriton. Phys. Rev. C 1998, 57, 1595. [Google Scholar] [CrossRef]
- Kumagai-Fuse, I.; Okabe, S.; Akaishi, Y. Pionic decay spectra of few body Lambda hypernuclei. Phys. Rev. C 1996, 54, 2843. [Google Scholar] [CrossRef]
- Ivanishchev, D.; Kotov, D.; Malaev, M.; Riabov, V.; Ryabov, Y. Resonance Reconstruction in the MPD. Particles 2021, 4, 3. [Google Scholar] [CrossRef]


| Decay Channel | Branching Ratio, % |
|---|---|
| H He | 24.7 |
| H + p + d + | 36.7 |
| H He | 75.0 |
| He He + p + | 32.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zinchenko, A. Techniques for Reconstruction of Strange Objects at MPD. Particles 2021, 4, 178-185. https://doi.org/10.3390/particles4020016
Zinchenko A. Techniques for Reconstruction of Strange Objects at MPD. Particles. 2021; 4(2):178-185. https://doi.org/10.3390/particles4020016
Chicago/Turabian StyleZinchenko, Alexander. 2021. "Techniques for Reconstruction of Strange Objects at MPD" Particles 4, no. 2: 178-185. https://doi.org/10.3390/particles4020016
APA StyleZinchenko, A. (2021). Techniques for Reconstruction of Strange Objects at MPD. Particles, 4(2), 178-185. https://doi.org/10.3390/particles4020016






