Constraints on CP-Odd ALP Couplings from EDM Limits of Fermions

Abstract

We discuss constraints on soft CP-violating couplings of axion-like particles with photon and fermions by using data on electric dipole moments of standard model particles. In particular, for the axion-like particle (ALP) leptophilic scenario, we derive bounds on CP-odd ALP-photon-photon coupling from data of the ACME collaboration on electron EDM. We also discuss prospects of the storage ring experiment to constrain the ALP–photon–photon coupling from data on proton EDM for the simplified hadrophilic interactions of ALP. The resulting constraints from experimental bounds on the muon and neutron EDMs are weak. We set constraint on the CP-odd ALP coupling with electron and derive bounds on combinations of coupling constants, which involve soft CP-violating terms.

1. Introduction

Since resolving strong CP violation problem using the Peccei–Quinn (PQ) mechanism [1,2], the axion-like particles (ALPs) proposed by Weinberg and Wilczek [3,4] play an important role in hadron phenomenology and searching for new physics (NP) beyond standard model (SM) [5,6]. In this vein, the important step was formulation of the effective Lagrangian approach with an explicit manifestation of the invisible axion [7]. In particular, Lagrangian involving couplings of axion with SM gauge fields and fermions has been proposed. It was shown that the couplings of axion with SM gauge fields ($G=g,W,B$) are generated using the anomalous coupling of the ALP to $G\tilde{G}$ gauge field currents, where G and $\tilde{G}$ are generic strength of gauge field and its dual. In particular, the part describing the coupling of ALPs with photons and fermions $\psi =e,\mu ,p$ reads [7,8]

$$\begin{array}{ccc}\hfill \mathcal{L}& \supset & \frac{1}{2}{\left({\partial }^{\mu }a\right)}^2-\frac{m_a^2}{2}{a}^2+\frac{g_{a\gamma \gamma }}{4}a{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }+\sum _{\psi =e,\mu ,p}a{g}_{a\psi \psi }\overline{\psi }i{\gamma }_5\psi ,\hfill \end{array}$$

(1)

where $g_{a\gamma \gamma }=c_{a\gamma \gamma }/\Lambda$ and $g_{a\psi \psi }=c_{\psi \psi }{m}_f/\Lambda$ are the couplings of ALP with photons and fermions, $\Lambda$ is the NP scale, which is much larger than the electroweak scale ${\Lambda }_{\mathrm{EW}}$: $\Lambda \gg {\Lambda }_{\mathrm{EW}}$. One should stress that the coupling of axion with SM fermions is suppressed by $1/\Lambda$. Such coupling can be generated from the coupling of axion to the scalar fields (dimension-5 operator) after the spontaneous breaking of electroweak symmetry [9]. We demonstrate the inducing of that coupling in Appendix A.

In addition to this CP-even coupling, let us consider the CP-odd coupling of ALP with photons

$$\begin{array}{c}\hfill {\mathcal{L}}_{a\gamma \gamma }^{C\backslash P}\supset \frac{{\overline{g}}_{a\gamma \gamma }}{4}a{F}_{\mu \nu }{F}^{\mu \nu },\end{array}$$

(2)

where ${\overline{g}}_{a\gamma \gamma }$ has dimension of GeV${}^{-1}$. Such coupling was recently discussed in  [10]. On the other hand, ALP is accompanied by a scalar field, dilaton $\varphi$, in extra dimension theories. In particular, these degrees of freedom play an important role in phenomenology of black holes and hadrons [11,12,13,14]. Coupling of the dilaton with photons has a similar structure as the CP-odd one for the axion: $\mathcal{L}\supset \frac{g_{\varphi \gamma \gamma }}{4}\varphi F_{\mu \nu }{F}^{\mu \nu }$. Note, analogous couplings with two photons, in case of light scalar mesons $f_0\left(600\right)$ and $a_0/f_0\left(980\right)$, have been studied in  [15,16,17]. The coupling of the dilaton with fermions has Yukawa type, which is manifestly CP-invariant: $\mathcal{L}\supset {\overline{g}}_{\varphi \psi \psi }\varphi \overline{\psi }\psi$. Note, the dilaton plays the role of the Nambu–Goldstone-like boson responsible for the spontaneous breaking of conformal/scale invariance [18]. Its mass is expected below the typical conformal symmetry breaking scale $m_{\varphi }\lesssim 1/g_{\varphi \gamma \gamma }$.

Constraints on $\varphi \gamma \gamma$ coupling from collider experiments are widely discussed in the literature [19,20,21,22,23,24,25,26,27] for the mass range 1 GeV$\lesssim m_{\varphi }\lesssim 1$ TeV. In addition, the authors of  [28] provided a detailed analysis of light dilaton scenarios (1 KeV$\lesssim m_{\varphi }\lesssim 10$ GeV) and estimated the bounds on radion–photon–photon coupling $g_{\varphi \gamma \gamma }$ from Supernova SN1987a, cosmology, horizontal branch stars, and beam-dump experiments. The latter analysis reveals an unconstrained window below $g_{\varphi \gamma \gamma }\lesssim {10}^{-5}$ GeV${}^{-1}$ for the regarding mass range. However, we note that emerging a CP violating coupling in the dilaton model $\mathcal{L}\supset g_{\varphi \psi \psi }\varphi \overline{\psi }i{\gamma }_5\psi$ will require a proper recasting of the relevant bounds. That task however is beyond the scope of present paper. Instead, we study the CP-violating scenario (2) for light sub-GeV pseudo-scalar particle and analyze in detail its implication for EDM physics of charged leptons and nucleons. In addition, for the certain ALP mass range, we also set the limits on soft the CP-violating coupling of ALP with electron:

$$\begin{array}{c}\hfill {\mathcal{L}}_{aee}^{CP\setminus }\supset {\overline{g}}_{aee}a\overline{e}e.\end{array}$$

(3)

In our previous paper [29], we discussed the NP phenomenology of hidden scalar, pseudoscalar, vector, and axial-vector particles coupled to nucleons and leptons, which could give contributions to different puzzles in particle physics (like proton charge radius, ${(g-2)}_{\mu }$, ${}^8$Be-${}^4$He anomaly, electric dipole moments (EDMs) of SM particles).

In the present paper, we derive new limits on the couplings of ALPs with SM fermions using data on fermion EDMs. In particular, we consider the contribution of diagrams to fermion EDMs generated by the CP-even coupling of ALP with fermions and CP-odd coupling of ALP with photons. In this vein, we do not require a universality of the coupling of ALP with leptons and quarks, which means that the limits on quark couplings with ALP are not necessarily applicable to corresponding couplings in lepton sector. We note that constraints on a combination of CP-violating couplings from EDM physics are widely discussed in the literature. In particular, in [30,31], authors derived constraints on scalar and pseudoscalar coupling constant combinations $|g_{aee}{\overline{g}}_{aee}|$ and $|g_{aee}{\overline{g}}_{app}|$ from atomic and molecular EDM experiments for the relatively wide range masses of ALP 10${}^{-6}$ eV $\lesssim m_a\lesssim {10}^6$ eV. In  [32,33,34,35] authors discuss constraints on CP-violating effective interactions $\overline{e}e\overline{N}N$ from data on EDM of atoms and molecules.

The paper is structured as follows. In Section 2, we discuss the constraints on CP-even ALP-lepton couplings for the mass range of interest from 1 MeV to 1 GeV for leptophilic scenario of ALP interaction. We also obtain the limits on ALP-photon-photon couplings using data on electron and muon EDM. The expected bounds on ALP couplings from proton EDM are derived in Section 3 for the hadrophilic scenario of ALP interaction. In Section 4, we discuss bounds on CP-odd couplings associated with $a\gamma {\mathrm{Z}}^0$ and $aee$ interaction. Combined bounds on products of ALP couplings are discussed in Section 5.

2. Constraints for Leptophilic Scenario

Let us consider Lagrangian describing the CP-odd coupling of ALP with SM photons and CP-even leptophilic interaction

$$\mathcal{L}\supset \frac{{\overline{g}}_{a\gamma \gamma }}{4}a{F}_{\mu \nu }{F}^{\mu \nu }+\sum _{l=e,\mu }i{g}_{all}a\overline{l}{\gamma }_{5}l.$$

(4)

These operators induce a finite contribution to the EDM of lepton. In the left panel of Figure 1, we show the contribution of 1-loop diagram to the operator of fermion EDM. It must be pointed out that CP-even couplings $\mathcal{L}\supset \frac{g_{a\gamma \gamma }}{4}a{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }$ do not generate lepton EDM operators at the one-loop level. In [29], authors showed that the ALP Lagrangian (4) induces the lepton EDM, which has the following form

$$|d_l/e|=\frac{1}{16{\pi }^2}{\overline{g}}_{a\gamma \gamma }{g}_{all}J\left(m_a/m_l\right),$$

(5)

where function $J\left(m_a/m_l\right)$ for $m_a/m_l\gg 1$ can be approximated as

$$J\left(m_a/m_l\right)\simeq \frac{m_l^2}{3m_a^2}log\frac{m_a^2}{m_l^2},$$

(6)

and for light ALP, $m_a/m_l\ll 1$, it is given by

$$J\left(m_a/m_l\right)\simeq \frac{1}{2}.$$

(7)

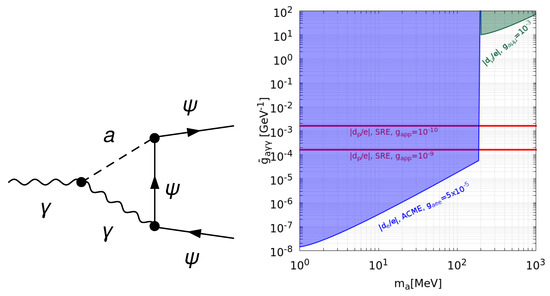
Figure 1. (Left): fermion EDM operator associated with CP-odd coupling of photon with axion-like particle (ALP) and CP-even interaction of ALP with standard model (SM) fermions $\psi$, see, e.g., Equation (1). (Right): Limits on ${\overline{g}}_{a\gamma \gamma }-m_a$ from various experiments. Blue region shows the parameter space of ALP at $90\%$ CL constrained by ACME, that corresponds to the electron EDM limits $|d_e/e|<1.1\times {10}^{-29}$ cm and $g_{aee}\simeq 5.0\times {10}^{-5}$ ($c_{ee}/\Lambda \simeq {10}^{-1}$ GeV${}^{-1}$). Green region represents the current constraints on ${\overline{g}}_{a\gamma \gamma }$ from muon EDM, $|d_{\mu }/e|\lesssim 1.5\times {10}^{-19}$ cm, and benchmark coupling $g_{a\mu \mu }\simeq {10}^{-3}(c_{\mu \mu }/\Lambda \simeq {10}^{-2})$. Red solid lines are expected bounds on ${\overline{g}}_{a\gamma \gamma }$ for planned sensitivity of SRE to the proton EDM at the level of $|d_p/e|<{10}^{-29}$ cm.

Now, let us discuss existing constraints on CP-even ALP-fermion coupling $\mathcal{L}\supset i{g}_{all}a\overline{l}{\gamma }_{5}l$ for the mass range of interest 1 MeV $\lesssim m_a\lesssim 1$ GeV. In particular, we refer to the analysis of  [8] on leptophilic coupling of ALP

$$\mathcal{L}\supset \sum _{l=e,\mu ,\tau }\frac{c_{ll}}{2\Lambda }\left({\partial }_{\mu }a\right)\overline{l}{\gamma }^{\mu }{\gamma }^{5}l$$

(8)

It is appropriate to rewrite coupling $g_{all}$ in Equation (4) through the Yukawa-like term as follows $g_{all}=c_{ll}{m}_l/\Lambda$. Indeed, Equation (8) on lepton mass shell implies that

$$\begin{array}{c}\hfill \mathcal{L}\supset \sum _{l=e,\mu }\frac{c_{ll}}{\Lambda }{m}_l\overline{l}i{\gamma }_{5}l.\end{array}$$

(9)

An author of  [8] provided current limits on $c_{ll}/\Lambda$ from beam-dump experiments [36] and BaBar facility [37] as well as from astro-particle physics and cosmological observations [38], assuming  lepton universality of couplings, $c_{ee}\simeq c_{\mu \mu }\simeq c_{\tau \tau }$. In particular, in our estimate, we use a benchmark conservative value $c_{ee}/\Lambda \simeq {10}^{-1}$ GeV${}^{-1}$ from coupling loop hole in the ALP mass range 1 MeV $\lesssim m_a\lesssim 200$ MeV. Finally, this implies $g_{aee}\simeq 5\times {10}^{-5}$ for electron-ALP coupling. In addition, for the muon-ALP interaction, we take $g_{a\mu \mu }={10}^{-3}$ as an unconstrained benchmark coupling in the mass range 200 MeV $\lesssim m_a\lesssim 1$ GeV; it corresponds to $c_{\mu \mu }/\Lambda ={10}^{-2}$GeV${}^{-1}$.

We note that ACME collaboration [39] sets a severe constraint on electron EDM at $90\%$ CL, $|d_e/e|<1.1\times {10}^{-29}$ cm, or equivalently,

$$|d_e/e|\lesssim 5.5\times {10}^{-16}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}.$$

(10)

Therefore, for $g_{aee}\simeq 5\times {10}^{-5}$, it follows from Equations (5), (7), and (10) that ${\overline{g}}_{a\gamma \gamma }\lesssim 3.3\times {10}^{-9}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}$ for $m_a\lesssim m_e$. Moreover, for $m_a\gg m_e$, one has the following allowed limit on ALP–photon–photon coupling

$${\overline{g}}_{a\gamma \gamma }\lesssim 5\times {10}^{-9}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}\times \frac{m_a^2}{m_e^2}\times \frac{1}{log(m_a^2/m_e^2)}.$$

(11)

We note that existing the limit on muon EDM, $|d_{\mu }/e|<1.5\times {10}^{-19}$ cm, provides relatively weak bound

$${\overline{g}}_{a\gamma \gamma }\lesssim 3.6{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}\times \frac{m_a^2}{m_{\mu }^2}\times \frac{1}{log(m_a^2/m_{\mu }^2)}.$$

(12)

for the benchmark coupling $g_{a\mu \mu }\simeq {10}^{-3}$ and ALP masses in the range $200\mathrm{M}\mathrm{e}\mathrm{V}\lesssim m_a\lesssim 1$ GeV. In the right panel of Figure 1, we show ALP parameter space constrained by the experiments which are sensitive to EDMs of leptons.

However, one remark should be added. For concreteness in our study, we consider non-universal ALP coupling with leptons and quarks, $c_{ll}\ne c_{qq}$, which means that limits on $c_{qq}/\Lambda$ coming from meson decays [36,40] are not directly applicable to $c_{ll}/\Lambda$ bounds. We address hadrophilic constraints in Section 3.

3. Constraints for Hadrophilic Scenario

In this section, we discuss the constraints on the CP-even ALP-photon-photon couplings for the following simplified hadrophilic scenario

$$\mathcal{L}\supset \frac{{\overline{g}}_{a\gamma \gamma }}{4}a{F}_{\mu \nu }{F}^{\mu \nu }+\sum _{h=p,n}i{g}_{ahh}a\overline{h}{\gamma }_{5}h.$$

(13)

Let us consider first the prospects of the storage ring experiment (SRE) (see, e.g.,  [41]) to probe ALP scenario with coupling to proton $\mathcal{L}\supset i{g}_{app}a\overline{p}{\gamma }_{5}p$. In particular, in our analysis, we consider the following typical bound on ALP–proton–proton coupling $g_{app}\lesssim {10}^{-10}-{10}^{-9}$ for the mass range of interest $1\mathrm{M}\mathrm{e}\mathrm{V}\lesssim m_a\lesssim 1$ GeV. In addition, the limit on $g_{app}$ is expected to be reasonable due to ruled out limits on light pseudoscalar universal coupling with quarks [40] at the level of $g_{aqq}\lesssim {10}^{-8}$. The storage ring experiment is expected to be sensitive to the proton EDM at the order of $|d_p/e|\lesssim {10}^{-29}$ cm. This implies the following conservative bound on ALP-photon-photon interaction

$${\overline{g}}_{a\gamma \gamma }\lesssim 1.6\times ({10}^{-4}-{10}^{-3}){\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}.$$

(14)

The relevant expected limits for SRE are shown in the right panel of Figure 1. The current limit on neutron electric charge, ${\overline{g}}_{\gamma nn}<(-2\pm 8)\times {10}^{-22}e$ and its coupling to ALP at the level of $g_{ann}\lesssim {10}^{-10}$ do not induce experimentally favored constraints on ${\overline{g}}_{a\gamma \gamma }$ at one-loop level.

4. Constraints on ALP Coupling with ${\mathrm{Z}}^0$-Boson and Electron

It is worth mentioning that one can also consider dimension-5 operator of ALP coupling with photon and ${\mathrm{Z}}^0$-boson

$$\mathcal{L}\supset \frac{{\overline{g}}_{a\gamma \mathrm{Z}}}{2}a{F}_{\mu \nu }{\mathrm{Z}}^{\mu \nu },$$

(15)

which provides a finite contribution to fermion EDM in association with CP-even, $\mathcal{L}\supset i{g}_{a\psi \psi }a\overline{\psi }{\gamma }_5\psi$, and CP-odd, $\mathcal{L}\supset {\overline{g}}_{a\psi \psi }a\overline{\psi }\psi$, ALP interaction with fermions. In the left panel of Figure 2, corresponding 1-loop diagrams are labeled by (3), (4), (5), and (6). However, these diagrams generate sub-leading contributions to the EDM of fermions due to suppression factor $\sim 1/m_{\mathrm{Z}}^2$, which is associated with ${\mathrm{Z}}^0$-boson internal line. Therefore, CP-odd interaction (15) does not induce viable constraint on ${\overline{g}}_{a\gamma \mathrm{Z}}$ from the EDM of fermions.

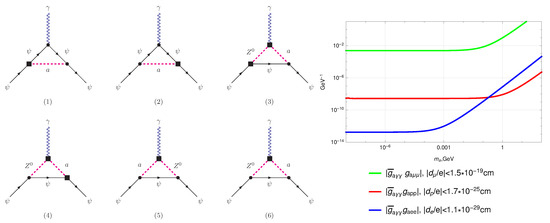
Figure 2. (Left): diagrams describing contribution of new particles to fermion EDMs. Black boxes and dots represent CP-odd and CP-even vertices, respectively. In particular, in diagrams (1) and (2) black boxes correspond to ${\overline{g}}_{a\psi \psi }a\overline{\psi }\psi$ vertices, black rounds denote $i{g}_{a\psi \psi }a\overline{\psi }{\gamma }_5\psi$ vertices. In diagrams (3–6), black box (the $a\gamma \mathrm{Z}$ vertex) corresponds to the interaction (15). (Right): limits on $|{\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }|-m_a$ ruled out at $90\%$ CL by experiments which are sensitive to measurements of EDM of SM fermions. We address to [42,43] for experimental constraints on muon and proton EDM respectively (for recent review see, e.g., [44]).

In our previous paper [29], we derived constraints on the product of the couplings ${\overline{g}}_{aee}$ and $g_{aee}$ from EDM bounds of the electron. Corresponding 1-loop diagrams, which induce electron EDM, are labeled by (1) and (2) in the left panel of Figure 2. However, it is instructive to obtain limits on CP-odd coupling ${\overline{g}}_{aee}$ for certain values of benchmark coupling $g_{aee}$ and ALP mass $m_a$. Indeed, one has the following estimate for the electron EDM [45]

$$\left|d_e/e\right|=\frac{{\overline{g}}_{aee}{g}_{aee}}{8{\pi }^2{m}_e}I(m_a/m_e),$$

(16)

where $I(m_a/m_e)$ can be approximated as

$$I(m_a/m_e)=\left\{\begin{array}{cc}\frac{2m_{\psi }^2}{m_a^2}log\left(\frac{m_a}{m_e}\right),& m_a/m_e\gg 1,\\ 1,& m_a/m_e\ll 1.\end{array}\right.$$

(17)

Therefore, for  $g_{aee}=5\times {10}^{-5}$ and the ALP mass range $1\mathrm{M}\mathrm{e}\mathrm{V}\lesssim m_a\lesssim 200$, the MeV one has the following conservative limits on ${\overline{g}}_{aee}$ at 90% CL

$${\overline{g}}_{aee}\lesssim \left\{\begin{array}{cc}2.1\times {10}^{-13}{\left(\frac{m_a}{m_e}\right)}^2{log}^{-1}\left(\frac{m_a}{m_e}\right),& m_e\ll m_a,\\ 4.3\times {10}^{-13},& m_a\ll m_e.\end{array}\right.$$

(18)

It is worth mentioning that the limit ${\overline{g}}_{aee}\lesssim 4.3·{10}^{-13}$ for $m_a\gtrsim 20$ MeV is better than the bound on ${\overline{g}}_{aee}$ from non-resonant production of new scalars in horizontal branch star core during helium burning (for detail, see, e.g.,  [46] and corresponding left panel in Figure 5).

5. Bounds on Combination of Couplings

In this section, for completeness, we summarize current reasonable constraints on a combination of couplings, which are ruled out by the EDM of SM fermions. In the right panel of Figure 2, we show limits associated with muon, proton, and electron EDM. In particular, for relatively light ALP, $m_a\ll m_{\psi }$, one has the following scaling of the limit

$${\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }\lesssim 1.6\times {10}^{16}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}\times \left|\frac{d_{\psi }/e}{\mathrm{c}\mathrm{m}}\right|.$$

(19)

In addition, for heavy ALP, $m_a\gg m_{\psi }$ one has

$${\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }\lesssim 2.4·{10}^{16}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}\frac{m_a^2}{m_{\psi }^2}{log}^{-1}\left(\frac{m_a^2}{m_{\psi }^2}\right)\left|\frac{d_{\psi }/e}{\mathrm{c}\mathrm{m}}\right|$$

(20)

One can see from Figure 2 that most stringent constraints follow from the electron EDM bound, ${\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }\lesssim {10}^{-13}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}$, as expected for $m_a\lesssim 1$ GeV. On the other hand, the limit on ${\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }$ is ruled out from proton EDM for $m_a\gtrsim 1$ GeV at the level of ${\overline{g}}_{a\gamma \gamma }{g}_{a\psi \psi }\lesssim {10}^{-8}{\mathrm{G}\mathrm{e}\mathrm{V}}^{-1}$. Finally, the combination of couplings associated with muon is feebly constrained due to the weak bounds on the muon EDM.

To conclude this section, we discuss known results on limits for the couplings from EDM bounds. In particular, we note that in [30], authors derived similar constraints on scalar and pseudoscalar coupling constant combinations $|g_e^p{g}_N^s|\lesssim {10}^{-16}$ from ${}^{199}$ Hg EDM experiments for the typical masses $m_a\lesssim {10}^6$ eV. These couplings are associated with the following Lagrangian $\mathcal{L}\supset i{g}_e^{p}a\overline{e}{\gamma }_{5}e+g_N^{s}a\overline{N}N$. This combination connected with the exchange of an axion between the atomic electrons and the nucleus. Moreover, one can translate these couplings to our notations as follows, $g_e^p\equiv g_{aee}$ and $g_N^s\equiv {\overline{g}}_{app}$. In addition, authors of [31] provided constraints on $|g_e^p{g}_e^s|\lesssim {10}^{-19}$ from atomic and molecular EDM experiment for $m_a\lesssim {10}^6$ eV. In our notation, these couplings are $g_e^s\equiv {\overline{g}}_{aee}$ and $g_e^p\equiv g_{aee}$. The relevant combination of the coupling constant corresponds to diagrams (1) and (2) in the left panel of Figure 2. In [32,33,34,35], authors provided constraints on CP-violating contact interactions $\overline{e}e\overline{N}N$ from data on EDM of atoms and molecules.

6. Conclusions

In the present paper, we derive constraints on soft CP-violating couplings of ALP from experimental data on the EDM bounds of SM fermions. In particular, we derive $90\%$ CL limit on CP-odd ALP coupling with photons, by taking into account EDM limits for leptons. This analysis is based on the simplified phenomenological scenario of leptophilic ALPs in the mass range $1\mathrm{M}\mathrm{e}\mathrm{V}\lesssim m_a\lesssim 1$ GeV. We also obtain expected limits on CP-odd $a\gamma \gamma$ coupling for the SRE experiment on proton EDM, which is associated with hadrophilic ALP interactions. We calculate bounds on soft CP-violating ALP coupling with electron.