Abstract
The relativistic mean field (RMF) model of the nuclear matter equation of state was modified by including the effect of Pauli-blocking owing to quark exchange between the baryons. Different schemes of a chiral enhancement of the quark Pauli blocking was suggested according to the adopted density dependence of the dynamical quark mass. The resulting equations of state for the pressure are compared to the RMF model DD2 with excluded volume correction. On the basis of this comparison a density-dependent nucleon volume is extracted which parameterizes the quark Pauli blocking effect in the respective scheme of chiral enhancement. The dependence on the isospin asymmetry is investigated and the corresponding density dependent nuclear symmetry energy is obtained in fair accordance with phenomenological constraints. The deconfinement phase transition is obtained by a Maxwell construction with a quark matter phase described within a higher order NJL model. Solutions for rotating and nonrotating (hybrid) compact star sequences are obtained, which show the effect of high-mass twin compact star solutions for the rotating case.
Keywords:
pauli blocking; six-quark state; quark exchange; nucleon excluded volume; symmetry energy; high-mass twin stars PACS:
12.38.Mh; 12.39.Jh; 13.75.Cs; 21.65.-f; 26.60.Kp
1. Introduction
The behavior of baryons in a dense, strongly interacting medium and the resulting properties of dense baryonic matter are highly interesting questions because of their relevance for explaining the interior of compact astrophysical objects like pulsars and their mergers as well as heavy-ion collision experiments in the NICA-FAIR energy range. The main problem, which awaits a better theoretical formulation and understanding, is to treat the baryon as a bound state of quarks and to study the effects of this quark substructure as a function of density. In particular, it is expected that at a critical value of the density the many-baryon system will change its character and get transformed to the new state of deconfined quark matter. Already before this transition occurs, the effective interaction between baryons will be strongly modified due to the fact that the effects of quark exchange between different baryons need to be taken into account as a requirement following from the Pauli principle on the quark level of description. These quark substructure effects will eventually dominate over other effects due to, e.g., the meson exchange interaction. The resulting quark exchange contribution to the baryon self-energy entails an increase of the energy per baryon and thus lead to a stiffening of dense baryonic matter. On the other hand, the quark exchange between two baryons involves already a six-quark wave function, which is a partial delocalization of quarks and can be seen as a precursor of the transition to deconfined (i.e., delocalized) quark matter. In this transition from a many-baryon to a many-quark system, the matter is effectively softened, due to the appearance of a mean field emerging from the attractive two-quark interactions. The value of the critical density for deconfinement is crucial for applications in heavy-ion collisions and compact stars.
The aspect we wanted to consider in this work was to investigate the influence of quark exchange on the self energies of baryons and the equation of state of dense baryonic matter on the one hand and on the phase transition to delocalized quark matter on the other. For quantitative estimates we employed a relativistic mean field theory for baryonic matter (the linear Walecka model) as well as for quark matter (the NJL-type model with higher order quark interactions) and superimpose the quark exchange contribution to the baryon self-energy obtained within a nonrelativistic quark potential model of the baryon structure and the six-quark wave function. The quark mass in this calculation has a density dependence (even inside the baryon) and is taken, e.g., from the NJL model calculation.
The effect of Pauli blocking in systems of composite particles can be discussed from the quark and nuclear level to that of atomic clusters. The relationship between Pauli blocking and excluded volume is known from the fact that the hard-sphere model of molecular interactions is based on the electron exchange interaction among atoms (see, e.g., Ebeling et al. [1]) which is captured, e.g., in the Carnahan–Starling EoS [2]. Note that the Carnahan–Starling form of the EoS for multicomponent mixtures [3] has recently been reproduced for a hadron resonance gas model with induced surface tension when the packing fraction is not too large [4]. A recent application of the Pauli blocking effect has been found in [5] where its role for explaining the ionization potential depression accessible in high-pressure experiments with warm dense plasmas has been demonstrated. The temperature, density and momentum dependence of the Pauli blocking depends on the generic form of bound state wave functions and therefore concepts developed for atomic systems could thus be taken over to the case of dense hadronic systems. Detailed parameterizations of the Pauli shift for nuclear clusters in warm, dense nuclear matter are given in [6] (see also references therein). In [7] it has been demonstrated that the repulsive part of effective density-dependent nucleon–nucleon interactions of the Skyrme type (e.g., the one by Vautherin and Brink [8]) can be reproduced by the quark exchange interaction between nucleons.
On the other hand, for the description of repulsive interactions in dense hadronic systems the concept of an excluded volume has been successfully applied [9] and extended to the case of light nuclear clusters [10], but this application requires a medium dependence of the excluded volume parameter [11] and thus hints to a microscopic origin from the composite nature of hadrons and clusters. We therefore use the present approach to quantify such a relationship between quark Pauli blocking in dense nuclear matter and the medium dependence of the excluded volume parameter by comparing the EoS of the present approach to the relativistic mean field approach DD2 with excluded volume [12]. We would like to point out that the inclusion of the Pauli-blocking effect within a quantum statistical description of light cluster formation and dissociation in nuclear matter at subsaturation densities [13,14,15] has important consequences for the equation of state and the composition of matter as seen, e.g., in the nuclear symmetry energy [16] that is successfully compared to experiments and in the description of supernova matter [17,18] where otherwise excluded volume approaches are commonly used [19].
In the present investigation, we also consider the role that the quark exchange interaction can play for the nuclear symmetry energy. Here the interesting question arises inasmuch the quark exchange contribution can make the contribution from isovector meson exchange obsolete. Our present study suggests that the -meson mean field may not have any contribution for densities up to the onset of baryon dissociation.
Recently, the question of the softening of dense baryonic matter due to the appearance of strange baryons became very popular and led to the hyperon puzzle: a lowering of the maximum mass of compact stars so that the existence of pulsars with masses as high as could not be explained. In principle, the approach can be extended to obtain results on the baryon self-energy shifts also in the case that the strange quark flavor will be included. In that case the presented approach can make a contribution to solving the question: Which effect will dominate when increasing the density: the occurrence of strange baryons or of deconfined strange quark matter? In this present work we want to consider as a first step only the question of nonstrange quark-nucleon matter.
2. Quark Exchange in Nuclear Matter
2.1. Quark Substructure Effect on the Self-Energy of the Nucleons
The quark substructure of nucleons becomes apparent for higher densities, when the nucleon wave functions have a finite overlap so that the effects of quark exchange between nucleons due to the Pauli principle on the quark level are no longer negligible. A quantitative estimate for this effect has been made within a potential model for the nucleons as three-quark bound states [7,20], see the Appendix for details of the derivation, and we employ the resulting contribution to the nucleon self-energy as the basis for our work. The result has been obtained in the form of a Pauli blocking energy shift for a nucleon with momentum P, given spin and the isospin projection in nuclear matter at ,
where is the Fermi momentum of a medium nucleon with the isospin projection , which is directly related to the medium density by . The coefficients for the are given in Table 1, and their superscript index indicates whether they apply for the one-quark or the two-quark exchange in the two-nucleon system. The functions are the contributions due to the Pauli-shift in the energy spectrum of three quark bound states. Their analytic derivation within a harmonic oscillator confinement model for the ground state nucleons according to the [20] is detailed in the Appendix A. The resulting expression for is

Table 1.
Quark exchange coefficients in spin-flavor-color space. These coefficients entail the symmetry relation .
Here m is the constituent quark mass and b is the width parameter of the nucleon wave function that describes the quark substructure by a product of two Gaussian functions of the relative (Jacobi) coordinates in the three-quark system with ; denote the ranges for one- and two-quark exchange processes. Values for b and are given below.
We want to consider as examples the two special cases:
- Symmetric nuclear matter (SNM), for which andThe Pauli shift for protons is obtained using the symmetry relation that is encoded in the coefficients of Table 1. With these coefficients and the low-density expansion (A29) up to fifth order in the Fermi momentum, we obtainThis energy shift can be identified with a shift in the chemical potential and thus be used to derive a contribution to the equation of state, see [7].In order to give numerical results for the Pauli shift (4), we adopt the values MeV and fm according to [20], which reproduce quite well the single nucleon properties. With the relation , the Pauli blocking shift can be given as a function of the nuclear matter densitywith MeV fm3 and MeV fm5. As has been discussed already in [7], this density dependent energy shift is in good agreement with the repulsive part of the Skyrme Hartree–Fock shift in nuclear matter obtained by Vautherin and Brink [8].
- Pure neutron matter (PNM), for which , andInserting the coefficients from Table 1 and the low-density expansion (A29) up to fifth order in the Fermi momentum, we obtainInserting the relation between Fermi momentum and density for PNM, we obtain the energy shift in the form (5) with the coefficients MeV fm3 and MeV fm5.
Figure 1 shows the Pauli blocking shift for the SNM and PNM cases as function of the Fermi momentum.
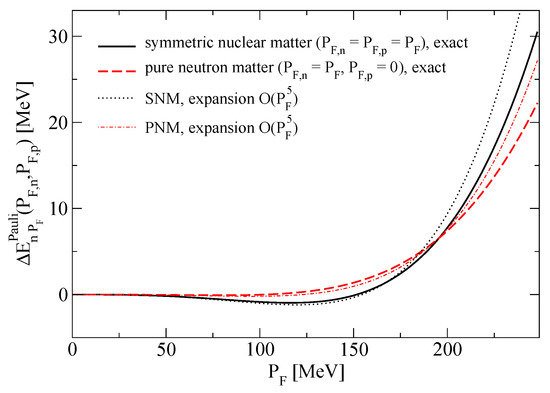
Figure 1.
Exact Pauli-shifts for symmetric nuclear matter (solid line) and pure neutron matter (dashed line) as function of the Fermi momentum, together with their power law expansion up to (dotted and dash-dotted thin lines, resp.).
2.2. Chiral Improvement of the Quark Pauli Blocking
One of the main shortcomings when applying the results for the quark Pauli blocking obtained within the nonrelativistic quark model to the equation of state of dense nuclear and neutron star matter up to the deconfinement phase transition is the fact that the quark mass is a medium-independent constant in this model. From chiral perturbation theory it is known that the chiral condensate melts in a dense hadronic matter environment so that the constituent quark mass shall be reduced towards its value in the QCD Lagrangian which obeys approximate chiral symmetry.
Effective chiral quark models for the low-energy sector of QCD are capable of addressing the aspect of dynamical chiral symmetry breaking and its restoration in a hot and dense medium, but have a problem with modeling confinement of quarks in hadrons. Here we suggest a compromise. We adopt a density dependence for the dynamically generated quark mass and thus achieve a chiral improvement of the quark Pauli blocking shift. We discuss in the following three schemes for this density-dependent quark mass: (i) a constant quark mass, (ii) a linear density dependence (called Brown–Rho scaling [21]) and (iii) a density dependence according to the calculation within a higher order Nambu–Jona-Lasinio model [22]. These density dependences of the quark mass are illustrated in Figure 2. In Figure 3 we show the energy shifts resulting from the insertion of the density dependencies for the Fermi momenta and the quark mass as shown in Figure 2 into Equations (4) and (7) for SNM and PNM, respectively.
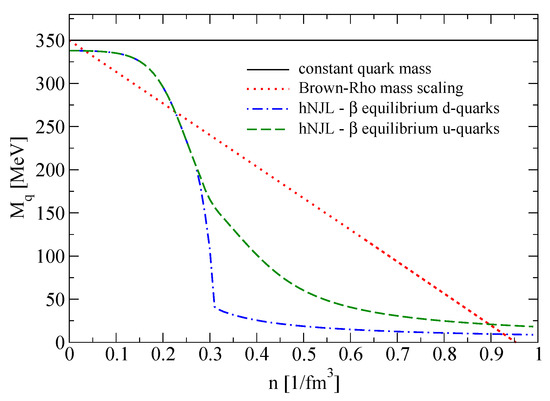
Figure 2.
Dependence of the quark masses on density: constant quark mass (solid line), Brown–Rho scaling (dotted line), Nambu–Jona-Lasinio (hNJL) model in -equilibrium for u-quarks (dashed line) and for d-quarks (dash-dotted line).
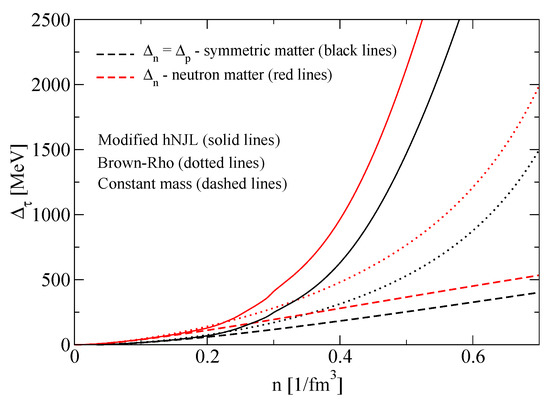
Figure 3.
The quark exchange contributions to self-energy for symmetric nuclear matter (black lines) and for pure neutron matter (red lines) as a function of the baryon density. Constant quark mass case (dashed lines), Brown–Rho scaling (dotted lines) and hNJL model case (solid lines).
In order to arrive at a model for dense (asymmetric) nuclear matter with quark substructure effects at supranuclear densities, we adopt a combined approach consisting of a relativistic mean-field (RMF) approach to nuclear matter which in its simplest form is the well-known linear Walecka (LW) model [23,24], to which we add the repulsive quark Pauli blocking interaction, which should then partly replace the vector meson exchange at high densities and play the role of a precursor of the delocalization of the nucleon wave functions in the quark deconfinement transition. Such a combined approach has been very successfully employed before in the description of light nuclear clusters in nuclear matter by Typel et al. [15], where self-energy effects for nucleons were treated within a relativistic mean-field theory while the cluster formation is described within a nonrelativistic quantum statistical approach that allowed to account for the reduction of the binding energy of the clusters due to nucleonic Pauli blocking, leading to the Mott dissociation of the clusters and the formation of uniform nuclear matter around the saturation density.
In the present work, the role of the clusters is played by the nucleons as three-quark bound states, subject to a quark Pauli blocking effect that triggers their Mott dissociation into deconfined quark matter described in a relativistic mean-field model for which we adopt the higher order Nambu–Jona-Lasinio (hNJL) model of [22]. At lower densities, in order to make contact with the phenomenology of nuclear matter saturation properties, the Fermi gas model of nucleons three-quark bound states with a hard core repulsion from quark Pauli blocking has to be augmented with additional attraction and repulsion as described, e.g., by the coupling to scalar and vector mean fields in the (LW) model.
3. Equation of State of Cold, Dense Matter with Deconfinement Transition
3.1. Relativistic Mean Field Model with Quark Exchange Contribution
The modification of the LW model to account for quark exchange (Pauli blocking) effects among nucleons is introduced by additional contributions to the pressure () and to the energy density () as
where is the baryon density, the scalar density, and for each baryon species we have
The effective coupling constants and are adjusted in order to fit the saturation point of symmetric nuclear matter with the phenomenological binding energy per nucleon, see Table 2 and the section with the results.

Table 2.
Parameter sets for vector () and scalar () meson couplings, the compressibility K and symmetry energy at the nuclear saturation density as well as radius of the neutron star with mass for the relativistic mean-field (RMF) linear Walecka (LW) model and for modified LW models with quark exchange contributions for different density-dependences of the quark mass: constant quark mass (LW + Qex), Brown–Rho scaling (LW + MQex) and hNJL model (LW + MhNJL).
In the relativistic mean-field EoS of Equations (8) and (9) we also introduce the contribution to the thermodynamical quantities that originate from the quark exchange self-energy via
where () denotes the proton (neutron) density and is the proton fraction.
3.2. NJL Model with Higher Order Quark Interactions
In order to describe cold quark matter that is significantly stiffer than the ideal gas, we employ a recently developed generalization of the NJL model, which includes higher order quark interactions in both Dirac scalar and Dirac vector channels (hNJL), see [22] and references therein. The thermodynamic potential density of the 2-flavor hNJL model for a homogeneous quark matter system in the mean-field approximation is given by
where
is the potential energy density and the quark quasiparticle dispersion relation is , with
The model parameters are the 4-quark scalar and vector couplings , and , the 8-quark scalar and vector couplings and as well as the current quark mass m and the momentum cutoff placed on the divergent zero-point energy. Furthermore, the subtraction of the constant ensures zero pressure in the vacuum.
The model is solved by minimizing the thermodynamic potential density with respect to the mean-fields , i.e.,
and the pressure is obtained from the relation .
In this work we use the parameter set of [25] with , , MeV, and MeV. The vector channel strengths are quantified by
We concentrate on the parameter space where is small and use to control the stiffness of the EoS. With small we do not delay the onset of quark matter. Additionally, we put [22].
This approach allows us to calculate partial pressures and partial densities for . In a cold stellar environment, the processes and result in the -equilibrium relation for the chemical potentials , since the neutrinos leave the star and do not take part in the chemical equilibration. Local charge neutrality requires
The total pressure in the quark phase is given as , where is the electron pressure given by the relativistic ideal gas formula. The baryon chemical potential in the quark phase can be calculated from
and the respective baryon number density is
3.3. Quark Deconfinement Phase Transition
To construct a thermodynamically consistent hybrid EoS, we use the Maxwell construction, which is tantamount to assuming a large surface tension at the hadron–quark interface. The critical baryon chemical potential is obtained by matching the pressures from the low density and the high density phase. The first order phase transition obtained by the Maxwell construction generates a jump in the density and the energy density. Illustrative examples for this are shown and discussed in the following Section for the parametrization that is introduced there.
4. Results
4.1. Parameterization of the Model
For the calculations, we fixed the parameters of our models on the properties of symmetric nuclear matter at the saturation density = 0.153 fm−3, at which the binding energy is = = MeV. The parameters are given in the Table 2.
In Figure 4, we demonstrate the properties of symmetric nuclear matter as a function of the baryon density. As it can be seen from the values of coupling constants of mesons in Table 2 in comparison with those of the LW model the repulsion of the -meson is partially replaced by the inclusion of Pauli-blocking via quark exchange mechanism. At low densities, the binding energy per baryon goes to zero since no nuclear cluster formation is included here. For a detailed discussion of this aspect, see [15,16].
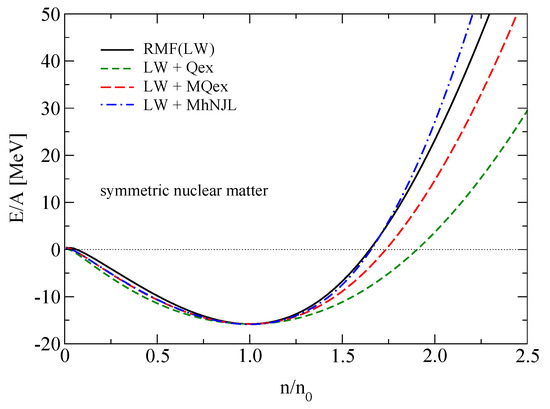
Figure 4.
Energy per nucleon of symmetric matter for relativistic mean-field (RMF) (LW) (solid lines), LW + Qex (dashed lines) and LW + MQex (long-dashed lines) models.
4.2. Equation of State
The EoS for the nuclear matter is obtained and in Figure 5 the pressure as a function of the density is shown for symmetric matter (left panel) and for pure neutron matter (right panel). The symmetry energy is shown and discussed below in Section 4.4 for all our models.
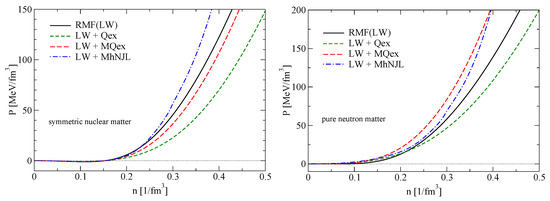
Figure 5.
(Left panel): Pressure as a function of number density for symmetric nuclear matter. (Right panel): EoS for pure neutron matter for all models.
4.3. Comparison with Nucleonic Excluded Volume
It is interesting to compare the effect of accounting for the compositeness and finite extension of the nucleon wave function by the Pauli blocking effect with the phenomenological improvement of nuclear matter models by implementing a nucleonic excluded volume like in the van-der-Waals gas. In Figure 6 we show the equations of state for pressure vs. density that results from our LW model with chirally enhanced Pauli blocking and the RMF model DD2 for different values of the nucleonic excluded volume parameter [12].
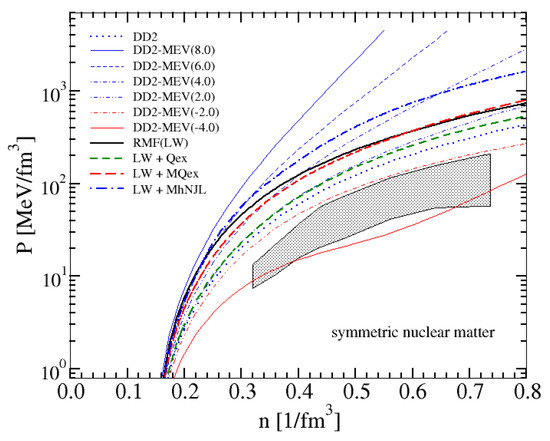
Figure 6.
Same as the left panel of Figure 5 on a logarithmic pressure scale and compared to a set of EoS for the DD2 EoS with excluded volume corrections from [12]. From this comparison one could read-off a density dependent excluded volume corresponding to the quark Pauli blocking effect in the equation of state. The hatched region corresponds to the constraint derived from the analysis [26] of flow data from heavy ion collision experiments.
Also shown is the flow constraint derived from the analysis of heavy ion collision experiments [26]. From comparing the Pauli-blocking improved LW models with excluded-volume corrected DD2 models, we extracted a density-dependent excluded volume parameter and the corresponding hard-core radius for nucleons. We note that these results compare very well with nucleonic hard-core radii obtained within the induced surface tension approach reported in [9]. A thorough analysis of the critical temperature of symmetric nuclear matter, the incompressibility of the normal nuclear matter and the proton flow constraint clearly shows [9,27] that a hard-core radius of nucleons up to 0.45 fm is still consistent with the available experimental data. Therefore, the short dashed curve in Figure 7 is perfectly consistent with the known symmetric nuclear matter properties.
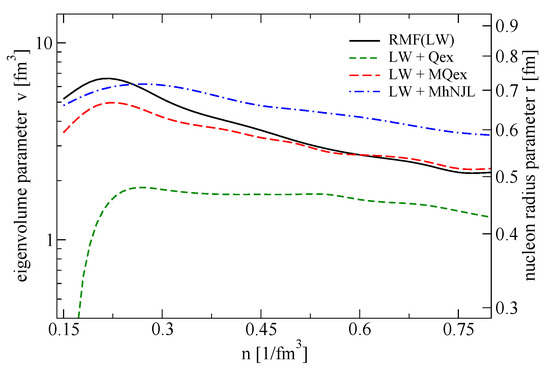
Figure 7.
Density dependence of the nucleonic eigenvolume parameter that would reproduce the quark Pauli blocking EoS of the present approach for the DD2 EoS with excluded volume from [12]. Identifying the eigenvolume parameter with the van-der-Waals excluded volume one can extract a nucleon radius parameter r shown on the alternative axis.
It should be stressed that smaller values of fm for the nucleon hard-core radius are obtained from fits to heavy-ion collision data for hadron production at LHC and RHIC energies so that a dependence of the hard-core radius on the chemical freezeout temperature was conjectured in [9]. Extending the present approach to finite temperatures, such a temperature dependence is expected to result from the temperature dependence of the quark Pauli-blocking energy shift.
4.4. Applications for Neutron Stars
In the left panel of Figure 8, we show the symmetry energy as a function of the density for all considered models. In the right panel of Figure 8, we show the proton fraction as a function of the density which results from accounting for the -equilibrium with electrons for all considered models.
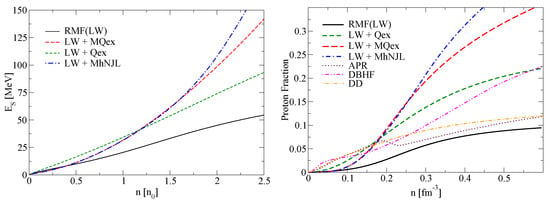
Figure 8.
(Left panel): Symmetry energy as a function of density for RMF (LW) (solid lines), LW + Qex (dashed lines), LW + MQex (long-dashed lines) and LW + MhNJL models. (Right panel): Proton fraction as a function of density for these models (same line styles) in comparison to standard neutron star EoS: APR, DBHF and the DD RMF model.
For all three models we construct the thermodynamics of stellar matter in -equilibrium fulfilling the charge neutrality condition with electrons and protons. In Figure 9 we show the EoS in -equilibrium for all considered models in comparison with the LW EoS.
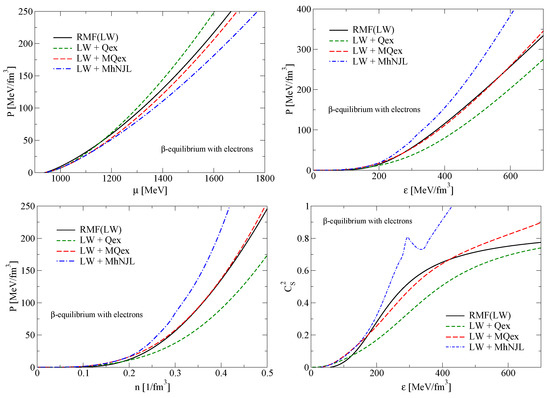
Figure 9.
EoS in -equilibrium with electrons for all considered models. Clockwise: pressure as function of baryo-chemical potential ; pressure as function of baryon density ; squared speed of sound ; pressure as function of energy density .
We consider the problem of causality in our modeling and show in the lower right panel of Figure 9 the dependence of the squared speed of sound on density. As it is shown for models LW, LW + Qex and LW + MQex for all relevant densities the causality holds since . For the model LW + MhNJL the causality is violated for high densities where already the transition to quark matter has to happen. This fact is consistent with our modeling because as a mass function for the quarks we took the behavior corresponding to hNJL model, see Figure 2.
Having defined the hadronic EoS with three different scenarios of the chiral enhancement of the quark Pauli blocking effect, and four choices for pair of free parameters of the quark matter EoS: and , we perform four Maxwell constructions for each hadronic model, see Figure 10.
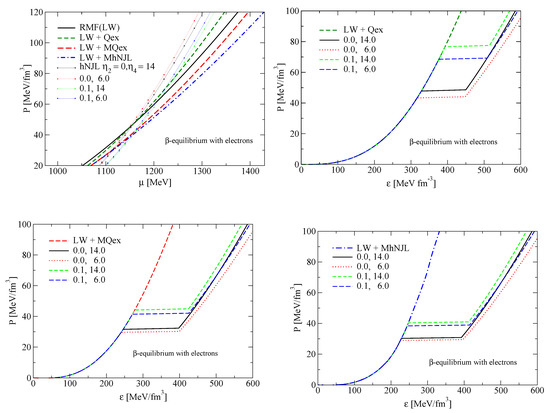
Figure 10.
Upper left panel: Maxwell construction of the first-order phase transition in the pressure-chemical potential plane. The crossing points of the parameterizations of the hNJL quark matter model with the hadronic EoS models define the values for the critical pressure and the critical chemical potential where the system switches from the hadronic to the quark matter phase, described by the corresponding EoS. Upper right panel: first order phase transitions from the hadronic model LW + Qex to hNJL quark matter with four parametrizations in the pressure-energy density plane. Lower left (right) panel: same as upper right panel, but for the hadronic model LW + MQex (LW+MhNJL).
In the upper left panel of that figure, we illustrate the Maxwell construction in the pressure-chemical potential plane. Each crossing point of a hadronic EoS with a quark matter one fulfills the Gibbs conditions for phase equilibrium at because the chemical potentials are equal to the critical value (chemical equilibrium) where the pressures coincide (mechanical equilibrium). According to the principles of equilibrium thermodynamics, the system is at each value of the chemical potential in the phase with the highest pressure. Therefore, at the crossing point the system switches from the hadronic to the quark matter EoS. Since at the corresponding pressures have a different slope, this transition is accompanied with a jump in the baryon number density and energy density .
In the remaining three panels of Figure 10 we show the pressure as a function of the energy density for the 12 hybrid EoS models resulting from the combination of the three hadronic EoS: LW + Qex (upper right panel), LW + MQex (lower left panel) and LW + MhNJL (lower right panel) with the four quark matter EoS for the model parameters of the hNJL model: and The other parameters of the hNJL model are fixed to values of [25], see also Section 3.2 above.
In Figure 11 we show the mass-radius relation for compact star configurations considering two models for the density dependence of the quark mass: constant quark mass (LW + Qex, green short-dashed line) and Brown-Rho scaling (LW + MQex, red long-dashed line) without and with the possible phase transition to quark matter. We do not show the M-R curves for LW + MhNJL here because, as we mentioned earlier when discussing Figure 9, this scenario violates causality () at large densities in the hadronic phase and makes sense only with a phase transition that prevents this problem to occur. The phase transition, however, is the same for LW + MQex and LW + MhNJL, so that the lines for the latter results are indistinguishable from those for the former ones and are not displayed separately. From the calculation we choose the hybrid EoS where quark matter is modeled with the parameters and . As it is shown in the figure, the differences between all three models for the masses of stars are small, and all of them satisfying the observational constraint from the Shapiro-delay based mass measurement on PSR J0740 + 6220 [28].
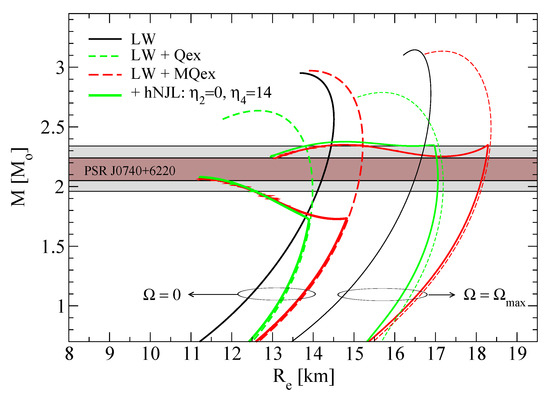
Figure 11.
Mass-radius relation for neutron stars within the LW model (black dotted lines) modified by quark exchange effects within two different schemes for the density dependence of the quark mass: constant quark mass (LW + Qex, green short-dashed line) and Brown-Rho scaling (LW + MQex, red long-dashed line). The bold lines are for nonrotating star sequences and the thin lines for the rigidly rotating ones with maximal angular velocity. Results for a deconfinement phase transition to hNJL quark matter core sequences are shown by solid lines.
Moreover, with this particular hybrid EoS the third family of compact stars [29] is possible because the three conditions are fulfilled [30]: (i) a sufficiently stiff hadronic EoS, (ii) a large jump in energy density at the transition which occurs at a low pressure MeV/fm3, (iii) a sufficiently stiff quark matter EoS to reach a maximum mass of . Such a third family of compact stars, if it would be discovered, would signal a strong first-order phase transition and therefore support the existence of a critical endpoint in the QCD phase diagram [30,31]. Recently, it was shown within a Bayesian analysis that the existence of such a class of hybrid EoS is in accordance with modern constraints from multi-messenger astronomy [32].
We like to remark that a similar calculation, with quark Pauli blocking as a repulsive interaction in the nuclear matter phase (for constant quark mass) and with the string-flip model for quark matter has been performed as early as in 1989 with a similar result that stable hybrid stars with quark matter core are possible and have a maximum mass above [33]. At that time, measured pulsar masses were below .
In the same plot we also show the relationship between mass and equatorial radius for stars rotating with the maximum possible angular velocity. These calculations have been performed within the slow-rotation approximation described in detail in [34,35].
5. Conclusions
The relativistic mean field model of the nuclear matter equation of state was modified by including the effect of Pauli-blocking owing to quark exchange between the baryons. Different schemes of a chiral enhancement of the quark Pauli blocking due to a density-dependent reduction of the value of the dynamical quark mass were considered. The resulting equations of state for the pressure were compared to the RMF model DD2 with excluded volume correction.
On this basis a density-dependent nucleon excluded volume is extracted which parameterizes the quark Pauli blocking effect in the respective scheme of chiral enhancement. The dependence on the isospin asymmetry of the quark Pauli blocking was investigated and the corresponding density dependent nuclear symmetry energy was obtained in fair accordance with phenomenological constraints.
The deconfinement phase transition was obtained by a Maxwell construction with a quark matter phase described within a higher order NJL model. Solutions for rotating and nonrotating (hybrid) compact star sequences were obtained, which show the effect of high-mass twin compact star solutions for the rotating case. This result is a consequence of the stiffening of the nuclear equation of state due to the quark Pauli blocking effect which at the same time is a precursor of the delocalization of the quark wave function in the deconfinement transition that leads to a strong softening and thus a large enough density jump at the phase transition to induce a gravitational instability as one of the necessary conditions for the occurrence of a third family solution for hybrid star sequences in the neutron star mass-radius diagram. The other one is the sufficient stiffness of deconfined quark matter at high densities which is provided by the 8-quark interactions in the scalar and vector channels of the higher order NJL model.
Author Contributions
Conceptualization, D.B. and H.G.; methodology, G.R.; software, H.G.; validation, D.B., H.G. and G.R.; formal analysis, D.B.; data curation, H.G.; writing—original draft preparation, D.B. and H.G.; writing—review and editing, D.B. and G.R.; visualization, D.B. and G.R.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation under grant number 17-12-01427.
Acknowledgments
The authors thank Kyrill Bugaev for discussions and comments on the manuscript and Steven Moszkovski for his continued and stimulating interest in this work. Stefan Typel is acknowledged for providing the data of the DD2 equation of state with modified excluded volume that are shown in Figure 6. H.G. is grateful for the hospitality that was extended to him during his visits at the University of Rostock and at the University of Wroclaw.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Pauli Quenching for Nucleons in Nuclear Matter-a Quark Substructure Effect
At the present there is a growing interest to understand the properties of nuclear matter on the basis of the underlying quark substructure. As long as a first principle QCD-approach to this problem cannot be realized, semi-phenomenological quark potential mode approaches can be successfully applied to work out the description of hadronic properties within a quark picture. Nonrelativistic quark models have been proven remarkably useful in describing the hadron spectroscopy [36,37,38]. Many efforts have been made to derive the hadron–hadron interaction from say the 6-quark problem. Phase shifts obtained from a nonrelativistic quark potential model give a good fit to the scattering data of the nucleon–nucleon [39,40,41,42,43,44,45,46] meson–nucleon [47] and meson–meson [48,49,50,51] interaction.
Another interesting problem is the investigation of nuclear matter as a many quark system at finite temperature and density. As a consequence of their quark substructure the nucleons are affected by the surrounding nuclear medium. In contrast to the few-quark problem, where we have to solve the Schrödinger equation for the isolated three-quark system, a quantum statistical approach is needed to treat the many-quark system at finite temperature. Because of the confinement property of the quark interaction potential, this quantum statistical approach must be modified if compared with usual classical many-particle systems.
To formulate the Hamiltonian we consider nonrelativistic massive quarks so that the kinetic energy is given by
The potential energy PE is constructed in the following way [7]. The configuration is decomposed into color-neutral clusters or , respectively. The confining two-body interaction among quarks is assumed here in the form of a harmonic oscillator potential
and shall act only within these color-neutral clusters (saturation property of the interaction). Within all possible decompositions of the quark configurations one has to take the cluster configuration with the minimum potential energy, this minimum value of the potential energy will be denoted by PE. The Hamiltonian is then given by
Of course, this Hamiltonian is able to describe isolated hadrons where the quark interaction is confined within the color-neutral hadronic cluster. With respect to the two-nucleon problem [46], color van-der-Waals forces do not arise because of the saturation property of the quark interaction [52]. A massive quark matter phase can be described where the potential energy is given by the distribution function of the next neighbors [53,54].
We consider nuclear matter as the hadronized phase where the interaction strings are confined within the nucleons and string flips like in the quark matter phase are not likely to occur. However, the color-neutral three-quark cluster is influenced by the surrounding clusters by reason of the Pauli principle what demands the antisymmetrization of the hadronic quark wave functions. The corresponding shift of the nucleon energy which may be considered as the self-energy of the three-quark cluster should contribute to the binding energy of nuclear matter. It is the aim of this appendix to evaluate this self-energy contribution due to Pauli blocking and to provide it in a simple analytic form that can be used in phenomenological approaches in order to account for this quark substructure effect when comparing with empirical values for the properties of nuclear matter.
Within a Green function approach [7] the lowest order diagram with respect to the density gives the Pauli shift of the three-quark cluster
This Pauli blocking shift has already been evaluated for finite temperatures and densities of the nuclear environment and leads to temperature and density dependent nucleonic properties, such as the effective nucleon mass [55], and corresponds to the hard-core part of the effective Skyrme interaction for nuclear matter [7].
However, at zero temperature the Pauli quenching shift (A4) obtained within a quantum statistical treatment of the completely hadronized quark plasma may be interpreted as a contribution due to an appropriately chosen antisymmetrization of the six-quark wave function of the two-nucleon problem. In this appendix we want to show this correspondence in detail thus coacting few-body approaches which deal with the problem of effective NN-interactions on the quark level using the resonating-group method [41,42,43,44,45,56].
In the spirit of a perturbation theory, we want to represent the six-quark wave function as a product of two nucleonic wave functions that behaves antisymmetrically with respect to each exchange of quantum numbers belonging to quarks () or to nucleons () thus fulfilling the Pauli principle on the nucleonic as well as on the quark level. Following this prescription and considering only the two nucleon channel, all those permutations leading to color nonsinglet clusters have to be excluded and we obtain
where the numbers stand for the momentum, spin, flavor and color indices of the i-th quark and n denotes the center-of-mass momentum as well as one of the spin-isospin orientations of the ground state nucleon (). The wave function of the nucleon can be found as the ground state solution of the three-quark Hamiltonian
with the harmonic oscillator confinement potential (A2). Since the Hamiltonian (A6) is independent of spin, flavor and color (SFC) of the constituent quarks, the SFC-part can be separated from the orbital part of the nucleon wave function according to
The property of antisymmetry of the three-quark wave function determines the symmetry properties of the and the part. In a systematic way, this decomposition can be done by using the technique of Young tableaux. The lowest energy eigenvalue corresponds to a total symmetric orbital part, with respect to spin and flavor the wave function has a mixed symmetry, whereas for the color part a total antisymmetric function is needed, see also [10]. With explicit notation of the spin (), flavor () and color () degrees of freedom, the SFC-part of the nucleon wave function reads
By alternating the spin or isospin orientations in (A8), the four species of ground state nucleons () are described. The orbital part of the nucleonic wave function is obtained by solving the Schrödinger equation
yielding for the ground state
Here we have used the Jacobi coordinates
and the width parameter of the Gaussian wave function , V is the normalization volume.
Now, the antisymmetrized two-nucleon wave function follows from (A5) with (A7), (A8) and (A10). The normalization is given by
Here, the and reflect the scalar products of the SFC-part with exchange according to and
The color degrees of freedom are immediately elaborated by rearranging the color variables, a factor 2 arises from two different variants of if the non exchanged variables are transposed. The remaining SF-variables are explicitly written down and evaluated. The results for are given in Table A1, the equivalent results hold also for the other nucleon states, if the interaction is invariant with respect to the isospin variables.

Table A1.
The values of the matrix elements and for .
Table A1.
The values of the matrix elements and for .
| 31/243 | −31/243 | ||
| 14/243 | −17/243 | ||
| 14/243 | −17/243 | ||
| 22/243 | −25/243 | ||
| 1/3 | −10/27 |
The momentum variables are integrated taking into account that the exchange operator is different from zero only for . The result can be given in a closed form
The antisymmetrization of the two-nucleon wave function with respect to the quark degrees of freedom leads to a shift in the two-nucleon energy according to
with given by Equation (A11). The Hamiltonian contains the kinetic part, Equation (A1), and the potential part, Equation (A2). Neglecting the antisymmetrization of the wave function with respect to quark exchange, the kinetic energy which is in Jacobi coordinates
and the potential energy
are immediately evaluated for the two-nucleon system with the result
so that no energy shift arises.
Orthogonalization of the wave function by antisymmetrization will lead to a change in the kinetic energy. In contrast to the kinetic energy, the potential energy (A2) is not determined by the wave function but by the density distribution of the quarks. In particular, the probability of a given quark configuration is determined by the density distribution function. It is well-known from the Hartree–Fock theory that antisymmetrization will not change the particle density distribution . For two nucleons we obtain an overlap of the quark density distributions, and the potential energy in not significantly changed by the antisymmetrization procedure, as long as string flip processes are not of importance. As discussed below, a variation of the wave function beyond the scope of a Hartree–Fock type antisymmetrization will also lead to a variation of the potential energy.
Expanding the normalization factor up to the first order with respect to the overlap integral, see Equation (A13), the expression (A4) for the Pauli shift is recovered.
The interpretation of the energy shift due to the Pauli blocking can be given in correspondence to atomic physics. At short interatomic distances, the energy of the two-atom system is sharply increasing what is usually represented by a repulsive, hard core like interaction potential. Indeed, the physical reason of this increase of energy is not the Coulombic electron–electron interaction, but the increase of kinetic energy because of the Pauli principle which demands the orthogonalization of the electron wave functions.
Now, let us proceed to the explicit evaluation of the Pauli-blocking shift (A21) which may be given using the Jacobi coordinates (A12) as follows:
Whereas this quantity (A23) measures the surplus energy arising from the antisymmetrization of the wave function with respect to the two-nucleon problem, we are especially interested in the energy shift for a single nucleon in a many-nucleon system which can be obtained from (A23) by summation over the second nucleonic index , whereby at the respective distribution function (see (A4)) is a step function restricting the momentum summation to the range of the Fermi sphere . The sum over may then be evaluated as an integral yielding
where the abbreviations and have been used. We introduce dimensionless momenta and analogous for the primed momentum as well as the Fermi momentum and perform the angular integration over the z-variable
For the applications to symmetric nuclear matter and to pure neutron matter we just need the case that both arguments are equal to the same Fermi momentum, i.e.,
where
is the Pauli blocking function that described the momentum dependence of the quark exchange between three-quark clusters and is depicted in Figure A1 together with its power law expansion up to a given order,
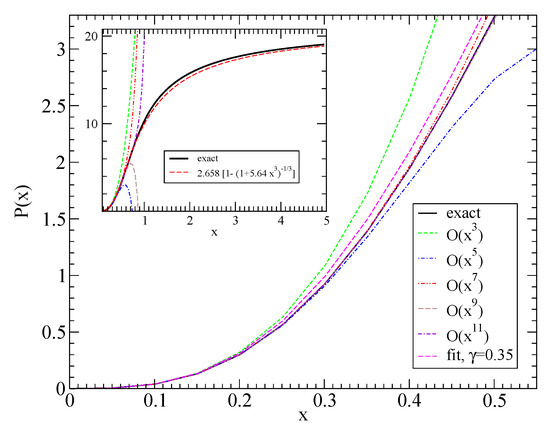
Figure A1.
The function P(x) defined in Equation (A28) with its polynomial expansions in different lowest orders, as well as a fit that obeys both limits of and . In the main panel the range of applicability of the low-density approximation is shown, a larger picture is shown in the inset.
This divergent series is useful only in the low-density (i.e., low-momentum) limit, but it does not display the fact that this function asymptotically approaches the constant .
An excellent fit to the exact result (A28) is given by
which is a sufficiently simple function of the nucleon density . Note that we need to use this function with different arguments for the one-quark () and two-quark () exchange contributions to the nucleon self-energy which have a different range in momentum space.
This function is used in the main text when the effect of quark Pauli blocking between nucleons on the nuclear equation of state is numerically evaluated and discussed.
References
- Ebeling, W.; Blaschke, D.; Redmer, R.; Reinholz, H.; Röpke, G. The Influence of Pauli blocking effects on the properties of dense hydrogen. J. Phys. A 2009, 42, 214033. [Google Scholar] [CrossRef]
- Carnahan, N.F.; Starling, K.E. Equation of State for Nonattracting Rigid Spheres. J. Chem. Phys. 1969, 51, 635–636. [Google Scholar] [CrossRef]
- Mansoori, G.A.; Carnahan, N.F.; Starling, K.E.; Leland, T.W.J. Equilibrium Thermodynamic Properties of the Mixture of Hard Spheres. J. Chem. Phys. 1971, 54, 1523–1525. [Google Scholar] [CrossRef]
- Sagun, V.; Bugaev, K.; Ivanytskyi, A.; Yakimenko, I.; Nikonov, E.; Taranenko, A.; Greiner, C.; Blaschke, D.; Zinovjev, G. Hadron Resonance Gas Model with Induced Surface Tension. Eur. Phys. J. A 2018, 54, 100. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Döppner, T.; Lin, C.; Kraeft, W.D.; Redmer, R.; Reinholz, H. Ionization potential depression and Pauli blocking in degenerate plasmas at extreme densities. Phys. Rev. E 2019, 99, 033201. [Google Scholar] [CrossRef] [PubMed]
- Röpke, G. Parametrization of light nuclei quasiparticle energy shifts and composition of warm and dense nuclear matter. Nucl. Phys. A 2011, 867, 66–80. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Schulz, H. Pauli Quenching Effects in a Simple String Model of Quark/Nuclear Matter. Phys. Rev. 1986, D34, 3499–3513. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D. Hartree-Fock calculations with Skyrme’s interaction. 1. Spherical nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Ivanytskyi, A.I.; Sagun, V.V.; Grinyuk, B.E.; Savchenko, D.O.; Zinovjev, G.M.; Taranenko, A.V. Hard-core Radius of Nucleons within the Induced Surface Tension Approach. Universe 2019, 5, 63. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Vitiuk, O.V.; Grinyuk, B.E.; Sagun, V.V.; Yakovenko, N.S.; Ivanytskyi, O.I.; Zabrodin, E.E. Second virial coefficients of light nuclear clusters and their chemical freeze-out in nuclear collisions. arXiv 2020, arXiv:2005.01555. [Google Scholar]
- Vovchenko, V.; Motornenko, A.; Gorenstein, M.I.; Stoecker, H. Beth-Uhlenbeck approach for repulsive interactions between baryons in a hadron gas. Phys. Rev. C 2018, 97, 035202. [Google Scholar] [CrossRef]
- Typel, S. Variations on the excluded-volume mechanism. Eur. Phys. J. A 2016, 52, 16. [Google Scholar] [CrossRef]
- Röpke, G.; Münchow, L.; Schulz, H. Particle clustering and Mott transitions in nuclear matter at finite temperature. Nucl. Phys. A 1982, 379, 536–552. [Google Scholar] [CrossRef]
- Röpke, G.; Schmidt, M.; Münchow, L.; Schulz, H. Particle clustering and Mott transition in nuclear matter at finite temperature (II). Nucl. Phys. A 1983, 399, 587–602. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Natowitz, J.B.; Röpke, G.; Typel, S.; Blaschke, D.; Bonasera, A.; Hagel, K.; Wada, R. Symmetry energy of dilute warm nuclear matter. Phys. Rev. Lett. 2010, 104, 202501. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Röpke, G. Appearance of light clusters in post-bounce evolution of core-collapse supernovae. Phys. Rev. C 2008, 77, 055804. [Google Scholar] [CrossRef]
- Röpke, G. Light p-shell nuclei with cluster structures (4 ≤ A ≤ 16) in nuclear matter. arXiv 2020, arXiv:2004.09773. [Google Scholar]
- Lattimer, J.M.; Swesty, F. A Generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Blaschke, D.; Röpke, G. Pauli Quenching for Hadrons in Nuclear Matter: A Quark Substructure Effect; Report JINR-E2-88-77; JINR Dubna: Dubna, Russia, 1988. [Google Scholar]
- Brown, G.; Rho, M. Scaling effective Lagrangians in a dense medium. Phys. Rev. Lett. 1991, 66, 2720–2723. [Google Scholar] [CrossRef]
- Benic, S. Heavy hybrid stars from multi-quark interactions. Eur. Phys. J. A 2014, 50, 111. [Google Scholar] [CrossRef][Green Version]
- Chin, S.; Walecka, J. An Equation of State for Nuclear and Higher-Density Matter Based on a Relativistic Mean-Field Theory. Phys. Lett. B 1974, 52, 24–28. [Google Scholar] [CrossRef]
- Walecka, J. A Theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Kashiwa, K.; Kouno, H.; Sakaguchi, T.; Matsuzaki, M.; Yahiro, M. Chiral phase transition in an extended NJL model with higher-order multi-quark interactions. Phys. Lett. B 2007, 647, 446–451. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Ivanytskyi, A.; Bugaev, K.; Sagun, V.; Bravina, L.; Zabrodin, E. Influence of flow constraints on the properties of the critical endpoint of symmetric nuclear matter. Phys. Rev. C 2018, 97, 064905. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Ferdman, R.D. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Gerlach, U.H. Equation of State at Supranuclear Densities and the Existence of a Third Family of Superdense Stars. Phys. Rev. 1968, 172, 1325–1330. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Benic, S.; Blaschke, D.; Han, S.; Typel, S. Neutron star mass limit at 2M⊙ supports the existence of a CEP. Eur. Phys. J. A 2016, 52, 232. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez-Castillo, D.E.; Benic, S. Mass-radius constraints for compact stars and a critical endpoint. arXiv 2013, arXiv:1310.3803. [Google Scholar]
- Blaschke, D.; Ayriyan, A.; Alvarez-Castillo, D.; Grigorian, H. Was GW170817 a canonical neutron star merger? Bayesian analysis with a third family of compact stars. Universe 2020, 6, 81. [Google Scholar] [CrossRef]
- Blaschke, D.; Tovmasian, T.; Kämpfer, B. Predicting Stable Quark Cores in Neutron Stars From a Unified Description of Quark - Hadron Matter. Sov. J. Nucl. Phys. 1990, 52, 675–678. [Google Scholar]
- Chubarian, E.; Grigorian, H.; Poghosyan, G.S.; Blaschke, D. Deconfinement phase transition in rotating nonspherical compact stars. Astron. Astrophys. 2000, 357, 968–976. [Google Scholar]
- Blaschke, D.; Alvarez-Castillo, D.E.; Ayriyan, A.; Grigorian, H.; Largani, N.K.; Weber, F. Astrophysical aspects of general relativistic mass twin stars. In Topics in Strong Gravity; Zen Vasconcellos, C.A., Ed.; World Scientific: Singapore, 2020; pp. 207–256. [Google Scholar] [CrossRef]
- Isgur, N.; Karl, G. P Wave Baryons in the Quark Model. Phys. Rev. 1978, D18, 4187. [Google Scholar] [CrossRef]
- Isgur, N.; Karl, G. Positive Parity Excited Baryons in a Quark Model with Hyperfine Interactions. Phys. Rev. 1979, D19, 2653. [Google Scholar] [CrossRef]
- Isgur, N.; Karl, G. Ground State Baryons in a Quark Model with Hyperfine Interactions. Phys. Rev. 1979, D20, 1191–1194. [Google Scholar] [CrossRef]
- Barnes, T.; Capstick, S.; Kovarik, M.; Swanson, E. N N core interactions and differential cross-sections from one gluon exchange. Phys. Rev. C 1993, 48, 539–552. [Google Scholar] [CrossRef]
- Oka, M.; Yazaki, K. Nuclear Force in a Quark Model. Phys. Lett. 1980, 90B, 41–44. [Google Scholar] [CrossRef]
- Oka, M.; Yazaki, K. Short Range Part of Baryon Baryon Interaction in a Quark Model. 1. Formulation. Prog. Theor. Phys. 1981, 66, 556–571. [Google Scholar] [CrossRef]
- Oka, M.; Yazaki, K. Short Range Part of Baryon Baryon Interaction in a Quark Model. 2. Numerical Results for S-Wave. Prog. Theor. Phys. 1981, 66, 572–587. [Google Scholar] [CrossRef]
- Burov, V.V.; Dorkin, S.M.; Lukyanov, V.K.; Titov, A.I. On the Six Quark Structure in the Deuteron Form-factor. Z. Phys. 1982, A306, 149. [Google Scholar] [CrossRef]
- Faessler, A.; Fernandez, F.; Lübeck, G.; Shimizu, K. The Quark Model and the Nature of the Repulsive Core of the Nucleon Nucleon Interaction. Phys. Lett. 1982, 112B, 201–205. [Google Scholar] [CrossRef]
- Faessler, A.; Fernandez, F.; Lübeck, G.; Shimizu, K. The Nucleon Nucleon Interaction and the Role of the (42) Orbital Six Quark Symmetry. Nucl. Phys. 1983, A402, 555–568. [Google Scholar] [CrossRef]
- Oka, M.; Horowitz, C.J. Hadron interaction in the string flipflop model of quark confinement with color, spin and flavor degrees of freedom. 2. Nucleon-nucleon interaction. Phys. Rev. 1985, D31, 2773–2779. [Google Scholar] [CrossRef]
- Barnes, T.; Swanson, E. Kaon-nucleon scattering amplitudes and Z* enhancements from quark Born diagrams. Phys. Rev. C 1994, 49, 1166–1184. [Google Scholar] [CrossRef]
- Oka, M. Hadron interaction in the string flipflop model of quark confinement with color, spin and flavor degrees of freedom. 1. Meson-meson interaction. Phys. Rev. 1985, D31, 2274–2287. [Google Scholar] [CrossRef]
- Barnes, T.; Swanson, E. A Diagrammatic approach to meson meson scattering in the nonrelativistic quark potential model. Phys. Rev. D 1992, 46, 131–159. [Google Scholar] [CrossRef]
- Barnes, T.; Swanson, E.; Weinstein, J.D. I = 3/2 K pi scattering in the nonrelativistic quark potential model. Phys. Rev. D 1992, 46, 4868–4872. [Google Scholar] [CrossRef] [PubMed]
- Blaschke, D.; Röpke, G. Quark exchange contribution to the effective meson meson interaction potential. Phys. Lett. B 1993, 299, 332–337. [Google Scholar] [CrossRef]
- Horowitz, C.; Moniz, E.; Negele, J.W. Hadron structure in a simple model of quark/nuclear matter. Phys. Rev. D 1985, 31, 1689–1699. [Google Scholar] [CrossRef]
- Blaschke, D.; Reinholz, F.; Röpke, G.; Kremp, D. Mott Mechanism and the Hadronic to Quark Matter Phase Transition. Phys. Lett. 1985, 151B, 439–443. [Google Scholar] [CrossRef]
- Schulz, H.; Röpke, G. A Note on the Massive Quark Matter Phase. Z. Phys. 1987, C35, 379–382. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Schulz, H. Quark substructure contribution to the temperature dependent effective nucleon mass. Phys. Lett. 1986, B174, 5–9. [Google Scholar] [CrossRef]
- Storm, M.H.; Watt, A. Clustering in many quark systems: The two nucleon problem. J. Phys. 1985, G11, 217–230. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).