Abstract
In this paper, we discuss the damping of density oscillations in dense nuclear matter in the temperature range relevant to neutron star mergers. This damping is due to bulk viscosity arising from the weak interaction “Urca” processes of neutron decay and electron capture. The nuclear matter is modelled in the relativistic density functional approach. The bulk viscosity reaches a resonant maximum close to the neutrino trapping temperature, then drops rapidly as temperature rises into the range where neutrinos are trapped in neutron stars. We investigate the bulk viscous dissipation timescales in a post-merger object and identify regimes where these timescales are as short as the characteristic timescale ∼10 ms, and, therefore, might affect the evolution of the post-merger object. Our analysis indicates that bulk viscous damping would be important at not too high temperatures of the order of a few MeV and densities up to a few times saturation density.
1. Introduction
The recent detections of gravitational waves by the LIGO-Virgo collaboration, in particular, the multimessenger binary-neutron star (BNS) merger event GW170817 [1], motivate studies of the transport properties of dense nuclear matter at temperatures and densities relevant to BNS mergers [2,3,4,5,6,7]. The mass of the post-merger object typically would exceed the maximum mass of a neutron star and, as a consequence, it would collapse to a black hole on the timescales ranging from tens of milliseconds up to seconds depending on the mass of the post-merger object [8,9,10]. While gravitational waves in the post-merger phase have not been observed in the GW170817 event due to lack of detector sensitivity at high frequencies, numerical relativity studies of BNS mergers in their highly non-linear regime predict intense emission of gravitational waves in the kHz frequency range during the initial phase of post-merger phase lasting typically 10 ms (for recent simulations see, for example, [11,12,13,14]). Improvements at least by a factor of 2 compared to advanced LIGO design sensitivity are necessary to measure the dominant frequency component of the signal of GW170817-like event and by factors of 4–5 to observe sub-dominant features of post-merger signal [15]. It is expected that dissipation or damping of matter flows in the merged stars could influence the gravitational waves emitted during the post-merger phase. Recent estimates of the role of the thermal conduction and shear and bulk viscosities indicate that, of these, damping of density oscillations via bulk viscosity has the strongest influence [2,6,7]. After a brief introduction to the problem of computation of the bulk viscosity, we present an extension of our recent work [7] on the bulk viscosity of nucleonic matter which includes the estimates of timescales of the damping of the oscillations by the bulk viscosity. The relevance of the bulk viscosity will be assessed by comparing the damping timescales of density oscillations to the characteristic timescales of the initial phase of post-merger ∼10 ms (over which the post-merger object is expected to emit intense gravitational waves) as well as the longer-term phase ∼1 s.
The bulk viscosity of nuclear matter at temperatures up to about 1 MeV has been studied extensively [16,17,18,19,20,21,22,23,24,25,26] in the context of oscillations of neutron stars and, in particular, as a source of damping of (unstable) r-mode oscillations; for reviews see [27,28]. More recently, interest in neutron star mergers has motivated studies of bulk viscosity of nucleonic matter at temperatures up to several tens of MeV, covering both the regime where neutrinos escape from neutron stars and the regime where they are trapped [6,7]. Such high temperatures significantly affect the phase space occupation of the fermions and, therefore, the rates of the weak-interaction processes [29]. Once the temperature becomes high enough for neutrinos to be trapped, they affect the composition of matter and ensure that direct Urca processes are always kinematically possible, and modified Urca is a subleading correction.
In this contribution, we extend recent work [7] to compute the timescales associated with bulk-viscous damping of oscillations. We use two models of the equation of state (EoS) and associated composition of dense matter which are based on the relativistic density functional theory of nuclear matter. The overall picture is that, at densities from around (nuclear saturation density) to around , the bulk viscosity reaches a maximum at temperature MeV, which is in the regime where neutrinos are not (or not completely) trapped. At these temperatures, therefore, the damping timescale is at a minimum, with values ranging from about 10 ms at low densities down to milliseconds (or even tenths of milliseconds depending on the EoS) at . This means that bulk viscous damping can have noticeable effects during the ∼10 ms of initial (gravitational-wave-emission) phase of the post-merger. At higher temperatures where the neutrino-trapping occurs the bulk viscosity falls by orders of magnitude, which implies much longer damping timescales which are larger than the characteristic timescales involved.
This paper is organized as follows. In Section 2 we discuss the formalism for computing the bulk viscosity and the approximations involved in such a computation. Our focus is on the beta equilibration processes of neutron decay and electron capture and the microscopic relaxation rates associated with these processes. Section 3 starts with a brief discussion of the thermodynamic properties of nuclear matter derived from density functional theory in Section 3.1. Bulk viscosity and the oscillation damping timescale are discussed in Section 3.2 and Section 3.3. Our main results are summarized in Section 4. We use natural units () and the metric signature .
2. Urca Processes and Bulk Viscosity
We start with a brief reminder of the bulk viscosity of nuclear matter composed of neutrons, protons, electrons, muons; for more details see [6,7]. For simplicity, we will neglect the muonic contribution to equilibration rates, although we include their contribution to static thermodynamic quantities such as susceptibilities.
Above the trapping temperature MeV, the neutrino mean-free-path is smaller than the size of a neutron star, so neutrinos are trapped in the merger region. Under these conditions beta equilibrium is established via neutron decay and electron capture, and their inverse processes
In -equilibrium the chemical potentials of particles obey the relation
The particle fractions of baryonic matter for any given temperature T, baryon number density and lepton densities (since we ignore muon reactions, the lepton fractions need to be fixed for each flavor separately) are found by imposing the beta-equilibrium condition (3), a similar condition for muons and the charge neutrality condition .
At lower temperatures the neutrino mean free path is larger than the size of a neutron star so the system is neutrino-transparent. Neutrinos cannot occur in initial states, therefore the reactions (1) and (2) proceed only in one direction (from left to right). To determine the composition of matter in this case we use the ordinary zero-temperature -equilibrium conditions and . Reference [29] found that there are significant corrections to these conditions at MeV; nevertheless the bulk viscosity in the neutrino transparent regime is not affected significantly [6].
If the matter is driven out of -equilibrium, for example by compression and rarefaction, the left and right-hand sides of Equation (3) do not balance anymore. The deviation from -equilibrium is then measured by a quantity
As a result, the Urca processes (1) and (2) will go faster in one direction than in the other until the beta equilibrium of matter is restored.
Consider now small-amplitude density oscillations in nuclear matter with a frequency . The baryon and lepton conservation implies for periodic perturbations
where and are the unperturbed background densities of baryons and leptons, and is the divergence of fluid velocity. The compression and rarefaction of matter implies perturbations in particle densities which can be separated into instantaneous equilibrium and non-equilibrium parts
where are the static values of particle densities. The variations stand for the shifts of the equilibrium state for the instantaneous values of and , whereas are the deviations of the particle densities from those equilibrium values. There exist two choices of the instantaneous equilibrium state. Below, we follow our recent work [7], for the alternative see reference [30]. We compare below these two approaches and explain why they give the same result for the bulk viscosity.
The non-equilibrium perturbations drag matter out of chemical equilibrium by leading to a small chemical potential shift (4) which can be written in terms of particle densities as
where , , and , with
The off-diagonal elements and are non-zero because of the cross-species strong interaction between neutrons and protons. For small amplitude density oscillations we only need to evaluate the derivatives in Equation (8) at .
If there were no flavor-changing weak processes, then the particle densities would just oscillate around their static equilibrium values according to
The weak interactions lead to an imbalance between the rates of direct and inverse Urca processes which in the “subthermal regime” () can be written as [18,19,30]
with and being the production rates of protons and neutrons, respectively. The production rate (10) should be added to the right hand sides of Equation (9) with a plus sign for and a minus sign for , for example,
Substituting here Equation (7), exploiting the conditions , and , and using Equation (5) for , and an analogous equation for (as muons are assumed not to participate in any reactions, their fraction is conserved) one finds
with a “beta-disequilibrium–proton-fraction” susceptibility given by
Equations (12)–(15) are the extensions of Equations (37)–(39) of reference [7] as we included non-zero muon density here, which was previously neglected. The final formula for the bulk viscosity, however, remains the same after this addition.
In the next step we find using the definition of the instantaneous -equilibrium state: , which gives
Note that these expressions are the solutions of the balance Equation (11) in the limit of infinite relaxation rate , which implies necessarily . One can check this also by pushing to infinity directly in general solutions (12)–(15) which will reduce then to Equations (17)–(20).
Now the non-equilibrium density perturbations can be found according to Equation (6)
where has a dimension of frequency and measures the relaxation rate of particle densities to their equilibrium values, and
is the “beta-disequilibrium-baryon-density” susceptibility, with being the neutron fraction. The non-equilibrium part of the pressure—the so-called bulk viscous pressure, can be now computed as
where we used the Gibbs-Duhem relation . Substituting the solutions (21) in Equation (23) one finds the bulk viscosity from the definition
The susceptibility prefactor is a pure thermodynamic quantity and depends only on the EoS, whereas the relaxation rate (Equation (10)) depends on the microscopic scattering amplitudes of weak interactions. It is seen from Equations (10) and (16) that is actually the derivative
Thus, the quantity measures how the proton net production rate increases when the neutron fraction increases at fixed baryon density, i.e., measures how fast the system reacts to a change in the chemical composition of matter. The quantity has a dimension of time and can be interpreted as a relaxation time of the system to its beta-equilibrium state.
The bulk viscosity in Equation (24) has the classic resonant form and for density oscillations of a given frequency, attains a resonant maximum at the temperature where the relaxation rate matches the oscillation frequency, .
The value of the bulk viscosity at that maximum is
which is independent of the microscopic interaction rates.
In the regime of slow equilibration, where , the bulk viscosity takes the form
In the fast equilibration regime , and the bulk viscosity, in this case, reduces to
The physical reason for this resonant maximum is easy to understand. In the limit where the relaxation rate is much smaller than the oscillation frequency there would effectively be an additional conserved quantity since both proton number and neutron number would be conserved. The proton fraction would be independent of density, so density oscillations would not drive the system out of chemical equilibrium. There would then be no bulk viscosity.
In the opposite limit of fast equilibration or slow density oscillations, , weak interactions are able to restore the chemical equilibrium of matter on timescales much smaller than the oscillation period. This means that the matter is practically always beta-equilibrated while undergoing compression and rarefaction and, therefore, will not experience any bulk viscosity.
Above we computed the bulk viscous pressure using its standard definition
where is the shift of the pressure from its static equilibrium value for arbitrary perturbations , and is the instantaneous shift of the equilibrium pressure, which depends on and does not contribute to the bulk viscous pressure.
According to the two limiting cases of vanishing bulk viscosity discussed above the bulk viscous pressure can be defined also in an alternative way
where is the instantaneous shift of the pressure in a certain non-equilibrium state with conserved particle fractions which corresponds to the limit . According to Equation (30) we can take as alternatives of the beta-equilibrium shifts the shifts given by Equation (9), as these are the solutions of exact balance Equation (11) in the limit . This was just the choice of the equilibrium state in reference [30]. Then instead of Equation (21) we will have
Computing the bulk viscous pressure from Equation (23) we obtain the same result for , as expected.
Urca Process Rates
As it was shown in reference [7] the equilibration rate of the neutrino-trapped matter is dominated by the electron capture process because the neutron decay rate is exponentially damped at low temperatures as ∼. The microscopic -equilibration rate of the electron capture process is given by [7]
where , GeV is the Fermi coupling constant, is the Cabibbo angle with , and is the axial-vector coupling constant; the index j runs over the four participating particles , are the Fermi distributions of particles and . The inverse process will be given by an analogous expression by replacing all functions with .
For small departures from -equilibrium the imbalance between the direct and inverse rates can be linearized in with the coefficient of the linear expansion given by [7]
where is the effective nucleon mass, , are the effective chemical potentials of particles, and are the Fermi and the Bose distributions, respectively, , , and
In the case of neutrino-transparent matter the equilibration rate is given by a similar expression, see references [6,7] for details. The low-temperature limit of in neutrino-trapped matter is given by [7]
and in the neutrino-transparent matter [6,7,20]
where are the Fermi-momenta of the particles. The -function in Equation (36) blocks the direct Urca processes at low densities where the proton and electron Fermi momenta are not sufficiently large to guarantee the momentum conservation. In the case where neutrinos are trapped in matter the momentum conservation can be always satisfied for certain particle momenta and the rate is always finite.
3. Numerical Results
We start with the thermodynamics of nuclear matter, which is derived from the relativistic density functional theory based on phenomenological baryon-meson Lagrangians, for reviews see [31,32]. We use the density-dependent baryon-meson coupling model DDME2 [33] as applied to finite-temperature nucleonic matter, see for details reference [34,35,36].
3.1. Thermodynamics of Nuclear Matter
The Lagrangian density of the model considered reads
where N sums over nucleons, —over the leptons, and are the fermionic Dirac fields with masses . The meson fields , and are the effective mediators of strong interaction between baryons, and are the field strength tensors of and mesons, respectively, , , and are meson masses, and are the baryon-meson coupling constants with .
The density dependence of the particle fractions is shown in Figure 1. The left panel is for a low temperature MeV where the system is neutrino-transparent, and the right panel shows the results for neutrino-trapped matter at temperature MeV for lepton fraction fixed at . In the first case muons appear only above a certain baryon density , where the condition MeV is satisfied, whereas in the neutrino-trapped case the muons’ threshold disappears.
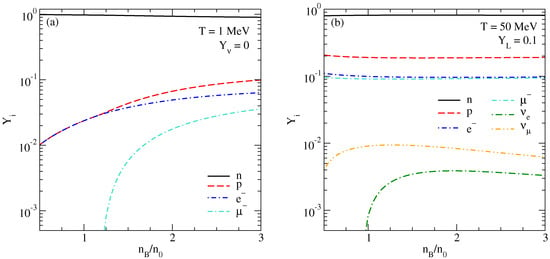
Figure 1.
Particle fractions as functions of the baryon density for (a) neutrino-transparent matter () at MeV; (b) neutrino-trapped matter at and MeV.
Within the framework of the model above the susceptibilities A and C in the non-relativistic limit for nucleons are given by (see reference [7] for details)
where
is the meson mean field and is the meson mean field which is non-zero in asymmetric nuclear matter. These expressions for susceptibilities are derived for isothermal density perturbations, which is the case only if the thermal conduction is fast enough to smoothen the temperature gradients during one period of oscillation [2,7]. This might happen, e.g., in the presence of turbulent flows in the merger region which could generate temperature and density variations on distance scales of the order of a few hundred meters. An order-of-magnitude estimate of thermal relaxation timescale is given in reference [2], which is 1 s , where is the typical length scale of thermal gradients. Assuming m and temperatures MeV (this is the temperature range where the bulk viscosity is relevant to mergers, see below), the thermal relaxation time will lie in the interval 0.1–10 ms, which is below the characteristic timescale of binary neutron star mergers. Thus, for thermal gradients on this distance scale the assumption of isothermal matter is the relevant one. On the scales over which thermal conduction is inefficient the matter should be treated as iso-entropic. The isothermal and adiabatic susceptibilities differ at most by a factor of 2 in the relevant density and temperature range, see reference [6] for further details.
Figure 2 shows the ratio of susceptibilities as a function of density for three values of the temperature. The susceptibility C is an increasing function of density. At sufficiently high temperatures MeV, it is negative at low density and crosses zero at a temperature-dependent critical density where the proton fraction reaches a minimum as a function of the density. At that point, the system becomes scale-invariant, as the compression does not drive the matter out of beta equilibrium, and the bulk viscosity vanishes at that critical point.
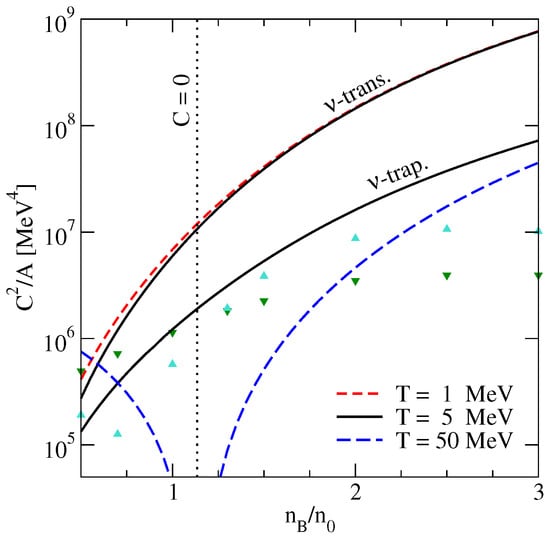
Figure 2.
The susceptibility prefactor as a function of the baryon density for three values of the temperature for the neutrino-transparent matter (upper curves labelled as -trans.) and neutrino-trapped matter (lower curves labelled as -trap.). The upper and lower triangles show the results of reference [6] for models IUFSU and DD2, respectively.
The ratio grows rapidly with the density in both cases of neutrino-transparent and neutrino-trapped matter and is sensitive to the temperature only close to the point where . We see that is approximately an order of magnitude smaller in the neutrino-trapped matter the reason being much larger values of A dominated by the contribution of neutrinos as compared to neutrino-transparent matter.
3.2. Beta Relaxation Rates and Bulk Viscosity
Figure 3 shows the relaxation rate (Equations (10) and (25)) as a function of temperature for various densities. The equilibration rate of the neutrino-trapped matter is dominated by the electron capture process because the neutron decay rate is exponentially damped at low temperatures as , whereas has approximately a quadratic increase with the temperature as suggested by Equation (35). It is seen from Figure 3b that the relaxation rate of the neutrino-trapped matter is several orders of magnitude larger than the oscillation frequencies kHz which are typical to neutron star mergers. This means that the neutrino-trapped matter is always in the fast equilibration regime where the bulk viscosity is independent of the oscillation frequency and is given by Equation (28).
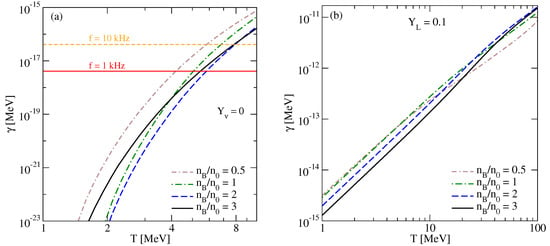
Figure 3.
The beta-relaxation rate as a function of the temperature for (a) neutrino-transparent and (b) neutrino-trapped regimes for several values of baryon density. Note the very different y-axis scales. The horizontal lines in panel (a) correspond to the fixed values of oscillation frequency kHz (solid line) and kHz (dashed line).
In the neutrino-transparent regime, in contrast, the relaxation rate is much slower, reaching values in the kHz range where it can resonate with typical density oscillations in mergers. We see this in Figure 3a where the relaxation rate crosses the kHz (corresponding to kHz) line at temperatures MeV indicating that the neutrino-transparent matter possesses a resonant maximum at those temperatures, as it was found also in references [2,6].
The density dependence of the bulk viscosity is shown in Figure 4. The oscillation frequency is fixed at kHz in the case of neutrino-transparent matter whereas the neutrino-trapped matter features a frequency-independent bulk viscosity, as discussed above. The bulk viscosity of neutrino-transparent matter mainly increases with the density, the increase being faster at low temperatures MeV where , as seen from Figure 3.
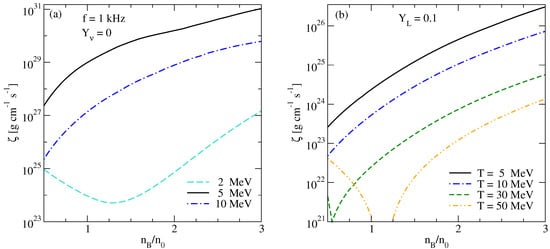
Figure 4.
The density dependence of the bulk viscosity for (a) neutrino-transparent matter; (b) neutrino-trapped matter at for various values of the temperature. The oscillation frequency is kHz in panel (a); the bulk viscosity in panel (b) is frequency independent. Note the very different y-axis scales.
The density dependence of the bulk viscosity of neutrino-trapped matter mainly follows that of the susceptibility because depends weakly on the baryon density in this case. At sufficiently high temperatures MeV there are sharp drops of the bulk viscosity to zero related to the fact that the matter becomes scale-invariant at certain critical values of density. Note that for temperature range MeV we show the results for both neutrino-transparent and neutrino-trapped cases to account for the uncertainty in the exact value of neutrino trapping temperature which is supposed to lie in that range.
Figure 5 plots the dependence of the bulk viscosity on the temperature. As already discussed above, the bulk viscosity of neutrino-transparent matter attains its maximum at the temperature where , whereas the temperature dependence of the bulk viscosity in the neutrino-trapped matter is mainly decreasing (up to point where the matter becomes scale-invariant) because the relaxation rate is already too fast: The resonant maximum would be at lower temperatures. Since the relaxation rate rises as (Equation (35)) we expect (from Equation (28)) that in this regime.
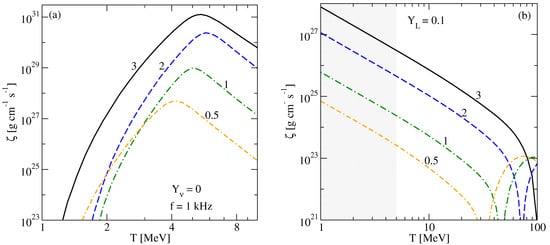
Figure 5.
The temperature dependence of the bulk viscosity for several values of the baryon density marked on the plots for (a) neutrino-transparent matter; (b) neutrino-trapped matter at . The oscillation frequency is kHz in panel (a); the bulk viscosity in panel (b) is frequency independent. Note the very different y-axis scales. The shaded region in panel (b) indicates that the results therein are extrapolations to the regime where they are not applicable.
In Figure 6, panel (a), we combine the results obtained for neutrino-transparent and neutrino-trapped matter by interpolating the results between these two regimes in the temperature range MeV which is regarded as the transition region. Close to the transition temperature, the bulk viscosity is much larger in the neutrino transparent regime because of much lower beta relaxation rate and larger susceptibility as well. As a result, the resonant peak of the bulk viscosity occurs always at or below the neutrino-trapping temperature. Hence we can already anticipate that the bulk viscosity is going to play an important role in the dynamics of neutron star mergers in the regime of neutrino-transparent rather than neutrino-trapped matter.
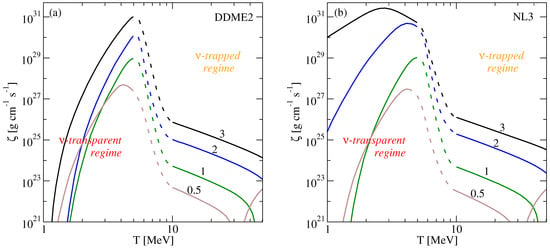
Figure 6.
The bulk viscosity as a function of temperature for several values of the baryon density marked on the plots for (a) model DDME2; (b) model NL3. In the temperature range MeV the bulk viscosity is obtained by interpolating between the results of neutrino-transparent and neutrino-trapped matter. The oscillation frequency is fixed at kHz, and the lepton fraction is fixed at .
For comparison, we show also the bulk viscosity of nuclear matter for an alternative model NL3 [37] in panel (b) of Figure 6. This model has density-independent meson-nucleon couplings but contains non-linear terms in the -meson field. The results obtained within the two models differ mainly in the low-temperature regime, where the model NL3 features much higher viscosities than the model DDME2 above the saturation density. The reason for this is that NL3 model has a threshold of direct Urca opening at around whereas the model DDME2 does not have a threshold up to densities . Because of the threshold, the model NL3 has much faster relaxation rates at than the model DDME2, and, as a consequence, the maximum of bulk viscosity is shifted to lower values of the temperature as compared to the DDME2 model.
3.3. Estimating Damping Timescales
In this subsection we examine the characteristic timescales of damping of density oscillations by the bulk viscosity in neutron star mergers. The energy density stored in baryonic oscillations with amplitude is given by
where
is the isothermal incompressibility of nuclear matter. The energy dissipation rate by the bulk viscosity per unit volume is
The characteristic timescale required for damping of oscillations is then given by
The incompressibility of nuclear matter is shown in Figure 7 for the two parametrizations discussed above. It is an increasing function of the density and at low densities decreases from its value at zero temperature as the temperature is increased.
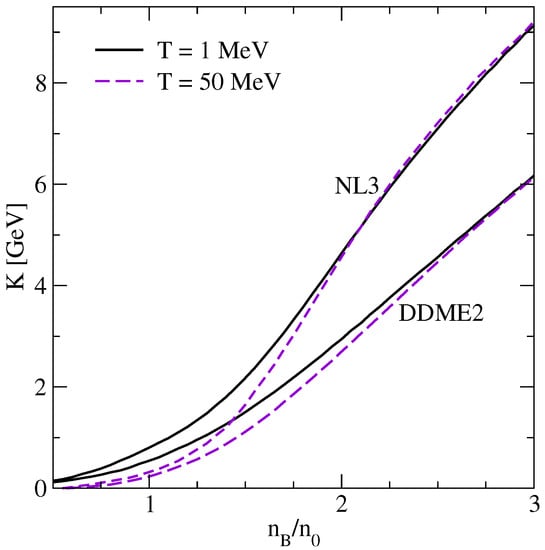
Figure 7.
The isothermal incompressibility of nuclear matter as a function of density for several temperatures for models DDME2 and NL3.
Figure 8a,b show, for two EoSs, the damping timescales of oscillations with frequency kHz. We use the interpolation of bulk viscosity between neutrino-transparent and neutrino-trapped regimes shown in Figure 6. As nuclear incompressibility depends weakly on the temperature, the temperature dependence of the damping timescale closely follows that of the bulk viscosity. As a result, the damping timescale attains a minimum at the temperature where the bulk viscosity has a maximum for a fixed value of the density. The minimal value of the damping timescale is
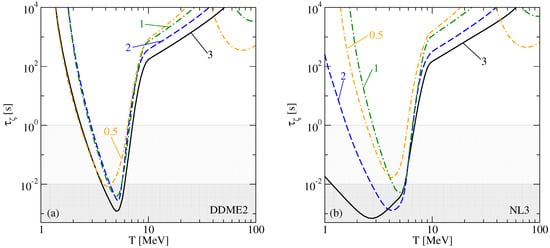
Figure 8.
The oscillation damping timescale as a function of temperature for various densities and for frequency fixed at kHz. We interpolate between the neutrino-transparent and neutrino-trapped regime, as in Figure 6; (a) model DDME2; (b) model NL3.
In the limits of slow and fast equilibration the damping timescale is given by
Thus, in contrast to the bulk viscosity, the damping timescale becomes frequency-independent in the low-temperature (slow equilibration) regime, and decreases with the frequency at high temperature (fast equilibration) regime.
The density dependence of reflects the density dependence of the ratio of nuclear incompressibility and the bulk viscosity. The density dependence of these two quantities almost compensates each other in the neutrino-transparent regime of the DDME2 model. In the case of NL3 model the density dependence of the bulk viscosity dominates and the damping timescale mainly decreases with density. The reason for this is the increase of the reaction rates with density as a result of fast opening of phase space for direct Urca reactions in the NL3 model.
The gray shaded areas in Figure 8 show the temperature regions where the damping timescale is smaller than the characteristic timescales for the early (≃10 ms, dark shaded areas) and long-term (≃1 s, light shaded areas) post-merger evolution, respectively. It is seen that in massive neutron star mergers, bulk viscosity strongly damps density oscillations at densities in the temperature range 3 6 MeV for model DDME2 and 1 6 MeV for model NL3. On the timescale of long-term evolution the damping is efficient also at lower densities, and the whole range of temperatures where the bulk viscosity is relevant is 2 7 MeV for model DDME2 and 1 7 MeV for model NL3.
Comparing the two panels of Figure 8 we observe that at low temperatures MeV and at densities the damping timescales are much shorter for the EoS model NL3 which has a direct Urca threshold. Thus, the dynamics and observational signatures of post-merger objects potentially contain information on whether the direct Urca processes are operative in the high-density domain of the neutron stars.
The temperature where the damping timescale reaches its minimum for kHz is located around MeV at densities below the direct Urca threshold and around MeV above the threshold. These results agree well with the results of reference [6] obtained within the Fermi-surface approximation. The exact computation, however, obtained using exact beta-equilibrium condition for the neutrino-transparent matter at finite temperatures [29] suggests that the minimum of is shifted to lower temperatures at densities which are below the direct Urca threshold, and, as a result, the minimum always appears around MeV [6] (note that the authors of reference [6] included also the modified Urca processes in their calculations, which, however, do not change the location of the maximum of bulk viscosity as their contribution is subdominant above MeV).
The density-dependence of the damping timescale found here differs from that of reference [6] where was found to reach its minimum at low densities . Apart from this, we find much lower values for the damping timescale at the minimum. This discrepancy arises because of the non-relativistic approximation for nucleon susceptibilities used in this work. This approximation works well at low densities, but strongly overestimates the susceptibility at higher densities .
The triangles in Figure 2 show the values of the susceptibility obtained in reference [6] for the models DD2 and IUFSU. We see that, although the relativistic corrections to the spectrum of nucleonic excitations are about at , they need to be included in the susceptibilities. This will require also a fully relativistic study of the beta-equilibration rates which is relegated to a future work.
In Figure 9 we show the damping timescale for 10 kHz density oscillations. The minimum value of , in this case, is smaller than in the case of kHz by factors between 2 and 10, and the values of in the neutrino-trapped regime are smaller by two orders of magnitude. However, the damping timescales of neutrino-trapped matter always remain larger than a second, since the bulk viscosity is not high enough to affect the evolution of mergers in this regime.
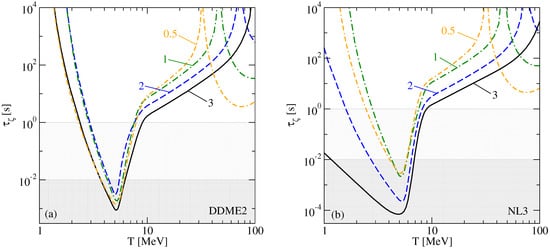
Figure 9.
The oscillation damping timescale as a function of temperature for various densities, interpolating between the neutrino-transparent and neutrino-trapped regimes as in Figure 8 but for kHz; (a) model DDME2; (b) model NL3.
Figure 10 and Figure 11 show the dependence of the bulk viscous damping timescale on the density and temperature colormap for the oscillation frequency fixed at kHz and kHz, respectively. The white solid and blue dashed lines show where the damping timescale becomes equal to the timescales of 10 ms and 1 s, respectively. In the areas shaded in dark red the bulk viscous damping timescale is ms, therefore, the damping of density oscillations by the bulk viscosity is very efficient in those regimes. In the regions shaded in blue the role of the bulk viscosity in damping of oscillations is negligible, as the damping timescale s there.
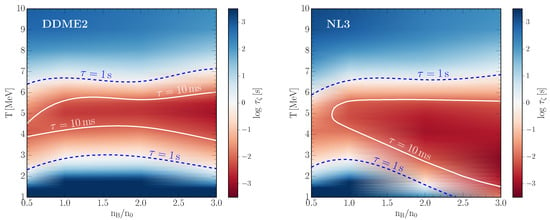
Figure 10.
Bulk viscous damping timescale as a function of the density and temperature for model DDME2 (left panel) and model NL3 (right panel). The density oscillation frequency is fixed at kHz. The white solid lines correspond to the characteristic timescale ms, the blue dashed lines - to the timescale s. The areas colored in red are the regions where the bulk viscous dissipation becomes important in the dynamics of neutron star mergers.
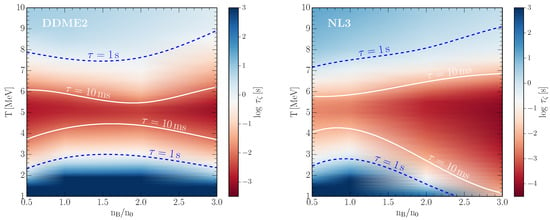
Figure 11.
Same as Figure 10 but for frequency kHz.
For completeness we comment also on how our results will change if larger lepton fractions are considered. The case was studied in our previous work, reference [7], where the bulk viscosity was shown to be reduced by factors from 1 to 3 as compared to the case. The pressure, and, therefore, also the nuclear incompressibility is only slightly sensitive to the lepton fraction. As a consequence, the damping timescales in the case will be larger than in the case by factors of a few, but the overall quantitative picture will remain the same.
In closing, we stress again that at densities the relativistic corrections to the spectrum of nucleonic excitations become important for the computation of the bulk viscosity, and our results at high densities need to be improved accordingly. Moreover, the appearance of hyperons and other heavy baryons needs to be taken into account. Finally, we note that in the case of hybrid stars with quark cores, the bulk viscosity of quark matter can be important for damping of density oscillations (for computations in the case of cold compact stars see [30,38,39,40,41,42,43,44,45,46]).
4. Summary
We have reviewed the computation, ingredients, and approximations involved in computations of bulk viscosity of nuclear matter at finite temperatures relevant to binary neutron star mergers. The bulk viscosity arises from the direct Urca -equilibration reactions. A novel ingredient relative to the studies of cold neutron stars is the trapped neutrino component coexisting with the nuclear matter at temperatures MeV. The concrete computations were carried out with the relativistic density functional approach to the EoS of nuclear matter with two different parametrizations.
At a given value of oscillation frequency the bulk viscosity shows the standard resonant form (24), with a maximum where the beta relaxation rate matches . This resonant maximum is achieved in the temperature range where neutrinos escape from the merger region, since the relaxation rate at temperatures of a few MeV is sufficiently low to match the density oscillation frequency. The reason for lower relaxation rates as compared to the neutrino-trapped case is the suppression of the direct Urca processes at the relevant temperatures and densities.
When the temperature rises to the threshold for neutrino trapping () the bulk viscosity experiences a sharp fall by several orders of magnitude as the relaxation rate rises and the material enters the fast beta-equilibration regime with . In this regime the bulk viscosity is independent of the frequency and decreases with the temperature approximately as . At temperatures of about 30 MeV a new feature appears: The bulk viscosity drops to zero at the temperature where the beta-disequilibrium-baryon-density susceptibility C vanishes, and then rises again at higher temperatures. The susceptibility vanishes because the particle fractions become independent of the density and the material becomes scale-invariant.
The main new result of this work concerns the timescales of damping of density oscillations in neutron star mergers by the bulk viscous dissipation. As an input we used the results for the bulk viscosity in reference [7]. We find that the damping timescale has a minimum as a function of temperature, which is located at temperatures in the range 3 ÷ 6 MeV for various densities. Assuming oscillation frequency of 1 kHz we find that the damping timescale at its minimum is of the order of ms, i.e., much shorter in the entire density range considered than the characteristic timescales of initial (∼10 ms) and long-term (∼1 s) post-merger evolution. We further find that the timescales of damping of density oscillations are shorter at the higher densities. If the temperature is above the neutrino trapping temperature, the damping timescales are much longer as the bulk viscosity is strongly suppressed. Finally, we note that bulk viscous dissipation could be of interest in the context of hydrodynamics simulations of supernovas, where electron capture rates on protons and nuclei could be out of equilibrium (for recent numerical simulations, see [47,48,49,50]).
Author Contributions
All authors have contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
The research of M.A. was funded by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Award Number #DE-FG02-05ER41375. The research of A.H. and A.S. was funded by the Volkswagen Foundation (Hannover, Germany) grant No. 97029 and the European COST Action “PHAROS” (CA16214). The research of A.S. was funded by Deutsche Forschungsgemeinschaft Grant No. SE 1836/5-1.
Acknowledgments
We thank Steven Harris, Kai Schwenzer, Alex Haber for discussions. M.A. and A.H. acknowledge the hospitality of Frankfurt Institute for Advanced Studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Alford, M.G.; Bovard, L.; Hanauske, M.; Rezzolla, L.; Schwenzer, K. Viscous Dissipation and Heat Conduction in Binary Neutron-Star Mergers. Phys. Rev. Lett. 2018, 120, 041101. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Sedrakian, A. Electrical conductivity of a warm neutron star crust in magnetic fields. Phys. Rev. C 2016, 94, 025805. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Sedrakian, A. Electrical conductivity tensor of dense plasma in magnetic fields. arXiv 2016, arXiv:1607.04541. [Google Scholar]
- Harutyunyan, A.; Nathanail, A.; Rezzolla, L.; Sedrakian, A. Electrical resistivity and Hall effect in binary neutron star mergers. Eur. Phys. J. A 2018, 54, 191. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. Damping of density oscillations in neutrino-transparent nuclear matter. Phys. Rev. C 2019, 100, 035803. [Google Scholar] [CrossRef]
- Alford, M.; Harutyunyan, A.; Sedrakian, A. Bulk viscosity of baryonic matter with trapped neutrinos. Phys. Rev. D 2019, 100, 103021. [Google Scholar] [CrossRef]
- Faber, J.A.; Rasio, F.A. Binary Neutron Star Mergers. Living Rev. Relativ. 2012, 15, 8. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron-star mergers: A review of Einstein’s richest laboratory. Rept. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Endrizzi, A.; Logoteta, D.; Giacomazzo, B.; Bombaci, I.; Kastaun, W.; Ciolfi, R. Effects of chiral effective field theory equation of state on binary neutron star mergers. Phys. Rev. D 2018, 98, 043015. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Rezzolla, L. Beyond second-order convergence in simulations of magnetized binary neutron stars with realistic microphysics. MNRAS 2019, 490, 3588–3600. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Kalinani, J.V.; Giacomazzo, B. First 100 ms of a long-lived magnetized neutron star formed in a binary neutron star merger. Phys. Rev. D 2019, 100, 023005. [Google Scholar] [CrossRef]
- Tsokaros, A.; Ruiz, M.; Paschalidis, V.; Shapiro, S.L.; Uryū, K. Effect of spin on the inspiral of binary neutron stars. Phys. Rev. D 2019, 100, 024061. [Google Scholar] [CrossRef]
- Torres-Rivas, A.; Chatziioannou, K.; Bauswein, A.; Clark, J.A. Observing the post-merger signal of GW170817-like events with improved gravitational-wave detectors. Phys. Rev. D 2019, 99, 044014. [Google Scholar] [CrossRef]
- Sawyer, R.F.; Soni, A. Transport of neutrinos in hot neutron-star matter. ApJ 1979, 230, 859–869. [Google Scholar] [CrossRef]
- Sawyer, R.F. Damping of neutron star pulsations by weak interaction processes. ApJ 1980, 237, 187–197. [Google Scholar] [CrossRef]
- Sawyer, R.F. Bulk viscosity of hot neutron-star matter and the maximum rotation rates of neutron stars. Phys. Rev. D 1989, 39, 3804–3806. [Google Scholar] [CrossRef]
- Haensel, P.; Schaeffer, R. Bulk viscosity of hot-neutron-star matter from direct URCA processes. Phys. Rev. D 1992, 45, 4708–4712. [Google Scholar] [CrossRef]
- Haensel, P.; Levenfish, K.; Yakovlev, D. Bulk viscosity in superfluid neutron star cores. I. direct urca processes in npeμ matter. Astron. Astrophys. 2000, 357, 1157–1169. [Google Scholar]
- Haensel, P.; Levenfish, K.; Yakovlev, D. Bulk viscosity in superfluid neutron star cores. 2. Modified Urca processes in npe mu matter. Astron. Astrophys. 2001, 327, 130–137. [Google Scholar] [CrossRef]
- Haensel, P.; Levenfish, K.; Yakovlev, D. Bulk viscosity in superfluid neutron star cores. 3. Effects of sigma-hyperons. Astron. Astrophys. 2002, 381, 1080–1089. [Google Scholar] [CrossRef]
- Dong, H.; Su, N.; Wang, Q. Bulk viscosity in nuclear and quark matter. J. Phys. G Nucl. Phys. 2007, 34, S643–S646. [Google Scholar] [CrossRef]
- Alford, M.G.; Mahmoodifar, S.; Schwenzer, K. Large amplitude behavior of the bulk viscosity of dense matter. J. Phys. G Nucl. Phys. 2010, 37, 125202. [Google Scholar] [CrossRef]
- Alford, M.G.; Good, G. Leptonic contribution to the bulk viscosity of nuclear matter. Phys. Rev. 2010, C82, 055805. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Voskresensky, D.N. Viscosity of neutron star matter and r-modes in rotating pulsars. Phys. Rev. C 2015, 91, 025805. [Google Scholar] [CrossRef]
- Schmitt, A.; Shternin, P. Reaction rates and transport in neutron stars. arXiv 2017, arXiv:1711.06520. [Google Scholar]
- Kokkotas, K.D.; Schwenzer, K. r-mode astronomy. Eur. Phys. J. A 2016, 52, 38. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. β equilibrium in neutron-star mergers. Phys. Rev. C 2018, 98, 065806. [Google Scholar] [CrossRef]
- Huang, X.G.; Huang, M.; Rischke, D.H.; Sedrakian, A. Anisotropic hydrodynamics, bulk viscosities, and r-modes of strange quark stars with strong magnetic fields. Phys. Rev. D 2010, 81, 045015. [Google Scholar] [CrossRef]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; Institute of Physics: Bristol, UK, 1999. [Google Scholar]
- Sedrakian, A. The physics of dense hadronic matter and compact stars. Prog. Part. Nucl. Phys. 2007, 58, 168–246. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meso n-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Colucci, G.; Sedrakian, A. Equation of state of hypernuclear matter: Impact of hyperon-scalar- meson couplings. Phys. Rev. C 2013, 87, 055806. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Implications from GW170817 for Δ-isobar Admixed Hypernuclear Compact St ars. ApJ 2019, 874, L22. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Madsen, J. Bulk viscosity of strange quark matter, damping of quark star vibration, and the maximum rotation rate of pulsars. Phys. Rev. D 1992, 46, 3290–3295. [Google Scholar] [CrossRef] [PubMed]
- Drago, A.; Lavagno, A.; Pagliara, G. Bulk viscosity in hybrid stars. Phys. Rev. D 2005, 71, 103004. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A. Bulk viscosity in 2SC quark matter. J. Phys. 2007, G34, 67–102. [Google Scholar] [CrossRef]
- Alford, M.G.; Braby, M.; Reddy, S.; Schäfer, T. Bulk viscosity due to kaons in color-flavor-locked quark matter. Phys. Rev. 2007, C75, 055209. [Google Scholar] [CrossRef]
- Manuel, C.; Llanes-Estrada, F.J. Bulk viscosity in a cold CFL superfluid. JCAP 2007, 0708, 001. [Google Scholar] [CrossRef]
- Sa’d, B.A.; Shovkovy, I.A.; Rischke, D.H. Bulk viscosity of spin-one color superconductors with two quark flavors. Phys. Rev. D 2007, 75, 065016. [Google Scholar] [CrossRef]
- Sa’d, B.A.; Shovkovy, I.A.; Rischke, D.H. Bulk viscosity of strange quark matter: Urca versus nonleptonic processes. Phys. Rev. D 2007, 75, 125004. [Google Scholar] [CrossRef]
- Alford, M.G.; Braby, M.; Schmitt, A. Bulk viscosity in kaon-condensed color-flavor locked quark matter. J. Phys. 2008, G35, 115007. [Google Scholar] [CrossRef]
- Wang, X.; Shovkovy, I.A. Bulk viscosity of spin-one color superconducting strange quark matter. Phys. Rev. D 2010, 82, 085007. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Lentz, E.J.; Bruenn, S.W.; Hix, W.R.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N.; et al. A Neutrino-Driven Core Collapse Supernova Explosion of a 15 M Star. arXiv 2015, arXiv:1507.05680. [Google Scholar]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cierniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The State of Matter in Simulations of Core-Collapse supernovae—Reflections and Recent Developments. PASA 2017, 34, e067. [Google Scholar] [CrossRef]
- O’Connor, E.P.; Couch, S.M. Exploring Fundamentally Three-dimensional Phenomena in High-fidelity Simulations of Core-collapse Supernovae. ApJ 2018, 865, 81. [Google Scholar] [CrossRef]
- Burrows, A.; Radice, D.; Vartanyan, D.; Nagakura, H.; Skinner, M.A.; Dolence, J.C. The overarching framework of core-collapse supernova explosions as revealed by 3D F ORNAX simulations. MNRAS 2020, 491, 2715–2735. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).