Abstract
With the aim of understanding the phase structure of nuclear matter created in high-energy nuclear collisions at finite baryon density, a beam energy scan program has been carried out at Relativistic Heavy Ion Collider (RHIC). In this mini-review, most recent experimental results on collectivity, criticality and heavy flavor productions will be discussed. The goal here is to establish the connection between current available data and future heavy-ion collision experiments in a high baryon density region.
1. Introduction
Most of the visible matter in our universe can be described by the Quantum Chromdynamics (QCD), the standard theory of strong interactions. In the beginning of the century, the new form of matter, the quark-gluon plasma (QGP) in which quarks and gluons are ‘freed’ in a much larger volume compared to that of nucleon’s, was discovered in the largest heavy-ion colliders RHIC and LHC [1,2,3,4] at vanishing baryonic density. Soon after the discovery, a serious question was asked: what is the structure of the nuclear matter at high baryonic density?
Tremendous efforts from both experimental and theoretical sides have launched in order to address the question. Figure 1 summarizes the current status of the studies. At the zero baryonic density, the transition from QGP to hadronic matter is a smooth-crossover at T = MeV [5,6,7,8,9], see dashed-line in the figure. These results are extracted from the state of the art Lattice gauge theory calculations. At high baryonic density, on the other hand, one would expect a first-order phase transition, shown as a black solid-line. Thermodynamically the first-order phase boundary line must end at finite baryonic density, this is the illusive QCD critical point (CP). Again, recent Lattice calculations have concluded that the QCD critical is ‘unfavored’ [10,11] when . The red-line is the chemical freeze-out curve extracted from the measured hadron yields. The collision energies with the corresponding accelerator complex are indicated at the top of the figure.
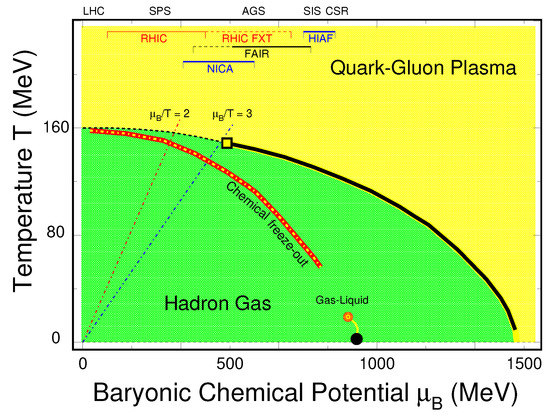
Figure 1.
(Color online) Schematic Quantum Chromdynamics (QCD) phase diagram in the thermodynamic parameter space spanned by the temperature T and baryonic-chemical potential . Experimentally extracted chemical freeze-out parameters are shown as the red-line [12]. The dashed-line near 0 indicates the crossover transition from the Quark-Gluon-Plasma to Hadron Gas [5,6,7,8,9]. The solid-line and the square show the expected 1st-order phase boundary and its end point: critical point. The regions of and are shown as red and blue dot-dashed lines, respectively. The Lattice QCD calculations have concluded that the QCD critical point is unlikely to exist at [10,11]. The red-circle and the yellow-line represent the liquid-gas transition [13]. Regions for physics programs of RHIC beam energy scan and fixed-target (US) [14], NICA (Russia) [15], FAIR (Germany) [16] as well as the HIAF (China) [17] are indicated at the top of the plot.
Experimental status on the beam energy scan (BES) is highlighted in Figure 2. Plot (a) shows the chemical freeze-out temperature as a function of the baryonic chemical potential . Both ALICE at LHC and STAR at RHIC results clearly show that at the vanishing baryon density, i.e., at high collision energy, the data driven freeze-out temperature is consistent with the Lattice calculation, MeV. Many authors have tried to analyze the chemical freeze-out conditions. Those include the results fluctuations analysis from Lattice QCD [18,19,20,21,22], HRG model [12] and other methods [23,24]. In the low baryon density region, MeV, the dependence of the freeze-out temperature is quite weak and the value of the freeze-out temperature is around 150–160 MeV. More dramatic drop of the temperature is seen in the high baryon density region. Plot (b) is the kaon over pion yield ratios, extracted from central heavy-ion collisions, as a function of the collision energies. While one observes the smooth increase of the negative kaon over pion ratio with the collision energy, the positive ratio shows a broad peak around GeV and eventually merged with the negative ratios at high collision energy, GeV, where the pair production becomes dominant. Due to the associate channel, , positive kaons carry information on baryon density. The peak in plot (b) implies the maximum freeze-out density reached at 8 GeV. Later in the discussions, we attribute the region of GeV as the high baryon density region (HBDR) as indicated by the yellow-area in the plot.
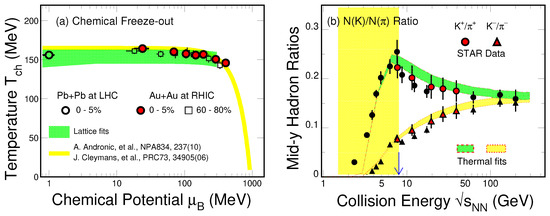
Figure 2.
(Color online) (a) Experimental results of chemical freeze-out temperature as a function of the baryonic chemical potential from the RHIC BES-I [12] and LHC [25,26]. Red-circles and black-squares represent results from the top and 60–80% Au+Au collisions at RHIC, respectively. Open-circle is from the 2.76 TeV 0–5% Pb+Pb collisions at LHC. The hatched green-band represents the Lattice results [7,27]. The yellow-line shows the empirical thermal fits results [28,29]. (b) Mid-rapidity particles of positive and negative kaons over pions shown as circles and triangles, respectively. The results [30] of thermal model fits are shown as hatched-bands in the plot and the high-baryon-density region is highlighted in yellow.
Collective flow (collectivity) and the critical behavior (criticality) are important aspects in high-energy nuclear collisions. In this short review, we will discuss the experimental status including the results on collectivity and criticality from high-energy nuclear collisions. RHIC has provided most recent data so we will focus on the information. At the end we will address the importance of the future fixed-target experiments such as STAR fixed-target program in BES-II, CBM at FAIR [16] as well the CEE at HIAF [17].
2. Beam Energy Dependence of the Collectivity
The main goal of high energy heavy-ion collisions, such as collisions at LHC and top energy collisions at RHIC, is to study the properties of new form of matter QGP. QGP is a thermalized (or nearly) system with partonic degree of freedom. The elliptic flow measurement of multi-strange hadrons and mesons indicates the partonic collectivity has been built up at the top energy heavy-ion collisions at RHIC [31,32,33,34,35,36,37]. The Heavy Flavor Tracker, a high resolution silicon detector system, which was installed in the year of 2013, provides high vertex position resolution. The significance of charmed hadron reconstruction is significantly improved. Thus the precise measurement of becomes possible. Figure 3 shows the results for , , and [38]. A number of constituent quark () is tested by scaling both and with . A simple quark coalescence or recombination model suggests the baryon would be 1.5 times of the meson assuming the collectivity has been attained in the partonic stage, as the number of constituent quarks for baryons is 3 where it is 2 for mesons. When discussing the scaling, we usually focus on the intermediate range in which the value saturates. The follows the scalings with selected multi-strange and strange hadrons in Figure 3. It indicates the collectivity of parton level has been built up from light flavor u, d quarks to strange and charm quarks. Since the mass of the charm-quark is much larger than the temperature reached in the system, the observed strong charm-quark collectivity can be interpreted as the thermalization of the medium created in the 200 GeV Au+Au collisions at RHIC [38]. To some extent, this result justified the phase diagram sketched in Figure 1.
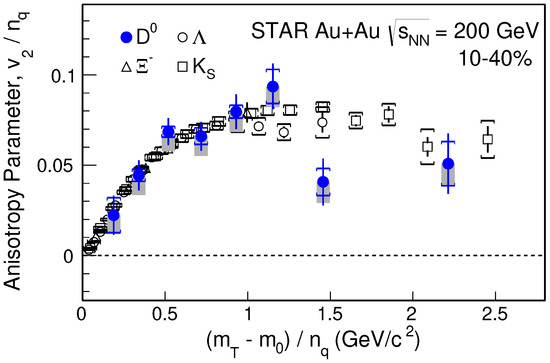
Figure 3.
(Color online) The number of constituent quark () scaled as a function of in 10%–40% Au+Au collisions for , , and (from [38]). Where is square root of the rest mass squared plus transverse momentum squared.
The main motivation of BES program is to explore the QCD phase boundary and critical point. The logic is straightforward: as the collision energy decreases, the conditions of QGP formation are no longer satisfied at some point. It offers us a unique experimental way to investigate the QCD phase structure. The transverse radial flow velocity is obtained by fitting the transverse momentum spectra with a blast wave model [39]:
where and are the modified Bessel functions and . The model assumes a radially boosted thermalized source with two key parameters, kinetic freeze-out temperature and a transverse collective flow velocity .
Plot (a) of Figure 4 shows the extracted parameter as a function of collision energy. The data points are taken from E802 [40,41,42,43], E866 [44,45], E877 [46], E895 [47], NA49 [48,49,50,51], STAR [12,52,53] and ALICE experiments [54] and references therein. The spectra of , , p and are fitted simultaneously with the blast wave model. The range for simultaneous fitting are similar across all RHIC BES and LHC energies. A rapid increase of is observed at low energies (<5 GeV), then a steady increase follows up to LHC energy. The six points from RHIC BES (7.7–39 GeV) are almost flat within uncertainties.
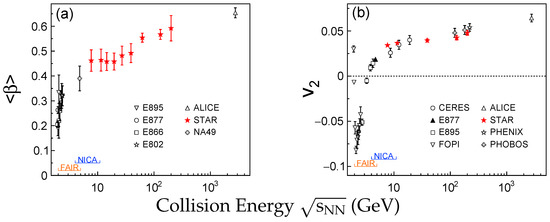
Figure 4.
(Color online) (a) The transverse radial flow velocity as a function of collision energy from central heavy-ion collisions. The data points are taken from E802 [40,41,42,43], E866 [44,45], E877 [46], E895 [47], NA49 [48,49,50,51], STAR [12,52,53] and ALICE experiments [54] and references therein. The data points of RHIC and LHC are from 0–5% central collisions. AGS and SPS energies are mostly from 0–5% and 0–7% central collisions respectively. (b) The -integrated in 20%–30% most central collisions (or similar centrality) from various collision energies. The data points are from E895 [55] for protons, NA49 [56] for pions and FOPI [57], E877 [58], CERES [59], STAR and ALICE [60] for charged hadrons. The RHIC results of inclusive charged particles for 130 and 200 GeV are from refs. [61,62,63,64,65]. The RHIC BES data are from refs. [66,67]. The energy regions of future collider and fix-target experiments, NICA and FAIR, are indicated in both plots.
The parameter extracted from blast wave model reflects the transverse radial flow built-up in the collision system. The second order coefficient of final azimuth distribution in the momentum space, , is sensitive to the initial geometry and interactions of early stage of the collisions. It suggests that a non-monotonic variation could be observed around the so-called, “softest point of EOS” [68,69]. The “softest point of EOS” is usually defined as a strong drop of speed of sound (a minimum value) or a reduction in the pressure of the system during the dynamic evolution. Plot (b) of Figure 4 shows the -integrated from 20%–30% or similar centrality as a function of collision energy. The data points are from E895 [55] for protons, NA49 [56] for pions and FOPI [57], E877 [58], CERES [59], STAR and ALICE [60] for charged hadrons. The RHIC results of inclusive charged particles for 130 and 200 GeV are from refs. [61,62,63,64,65]. The RHIC BES data are from refs. [66,67]. The negative (3 GeV) is known due to the “squeeze-out” effect [57]. An increasing trend is observed for integrated from AGS to LHC. It appears that the slope of with collision energy is steeper for 3–7.7 GeV compared to 7.7–2760 GeV, which is consistent with that we observe for parameter. The of charged hadrons as a function of does not change significantly at RHIC BES and LHC energies. Due to the rise in mean which is expected from larger radial flow, the -integrated increases. It is consistent with the collision energy dependence of parameter, as discussed in panel (a) of Figure 4. Non-monotonic behavior which is predicted by the softening of the equation of state for a system close to the critical temperature [68] is not observed.
The first order coefficient of final azimuth distribution in the momentum space, (rapidity-odd), as a function of rapidity is sensitive to the system expansion during the early stage of collisions. Both hydrodynamic and nuclear transport models indicate that in the midrapidity region offers sensitivity to details of the expansion of the participant matter during the early collision stages [70,71,72]. Hydrodynamic plus first-order phase transition calculations suggest a minimum of net-baryon slope () near mid-rapidity is a signal of phase transition between QGP and hadronic matter [73,74]. Net-particle is defined as the excess yield of a particle type over its anti-particle [75,76]. The of net-particle is defined as: , where X represents particle, represents the corresponding anti-particle, is the ratio of particle to anti-particle yield. Plot (a) of Figure 5 shows the slope relative to rapidity for net-proton, net- and net-kaon. Similar energy dependence is observed for net-proton and net-. The non-monotonic behavior is consistent with the hydrodynamical calculations with first-order phase transition [73,74]. Large divergence between of net-kaon and net-proton (net-) is observed below GeV, whereas all three agrees well at and above 20 GeV. More theoretical inputs are needed to understand the difference. At the same time the measurements of centrality dependence in the future BES program will further verify the energy dependence and constrain model calculations. In Ref. [76], the of mesons shows larger magnitude than pions and kaons at and above 14.5 GeV, and more interesting, the meson slope seems to increase sharply at 11.5 GeV. Because of the large statistical uncertainties, it is still not conclusive. It opens a new direction for both experimental and theoretical investigation on directed flow [77].
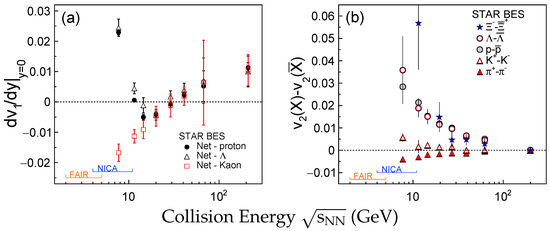
Figure 5.
(Color online) (a) The slope of at mid-rapidity () as a function of collision energy in 10%–40% Au+Au collisions for net-proton, net- and net-kaon [75,76]. (b)The difference between particles and the corresponding anti-particles as a function of collision energy [78,79,80]. The energy regions of future collider and fix-target experiments, NICA and FAIR, are indicated in both plots.
As discussed above, the of multi-strange hadrons and mesons are more sensitive to the parton level collectivity as their hadronic cross sections are smaller than light flavor hadrons [81,82,83]. The results from RHIC BES I suggest a possible drop of meson compared to other hadrons in Au+Au collisions at = 11.5 and 7.7 with ∼2 effect [78,79,80]. Data of high precision will be available with RHIC BES II. A significant difference in the values between particles and the corresponding anti-particles is observed at low energy heavy-ion collisions at RHIC. As shown in plot (b) of Figure 5, the difference is more pronounced for of baryons and anti-baryons when the collision energy is less than 20 GeV [78,79,80]. These differences naturally break the scaling discussed previously, as the number of constituent quarks are same for particle and the corresponding anti-particle. Several models try to explain the data [84,85,86,87,88]: the hydro + transport (UrQMD) calculation can reproduce the proton data, but not the meson data [84]; A analytic hydro model can quantitatively reproduce the , K and proton data, but the flavor dependence () is not consistent with data [85]; A Nambu-Jona-Lasino (NJL) model incorporating partonic and hadronic potentials can describe the data qualitatively, but not quantitatively [86,87]. New data from RHIC BES II, especially data of multi-strange hadrons, could offer more constrains on the model calculation.
3. Beam Energy Dependence of the Higher-Order Cumulants of Net-Particle Multiplicity Distributions and Light Nuclei Productions
Fluctuations of conserved quantities, such as net-baryon (B), net-charge (Q) and net-strangeness (S), are sensitive observables to search for the QCD critical point in heavy-ion collisions [89,90,91,92,93]. The higher-order cumulants (, the order cumulants), which can be used to quantify the fluctuations and describe the shape of the event-by-event multiplicity distributions, are predicted to be sensitive to the correlation length () of the system as and [90,94]. The various order cumulants and cumulant ratios can be expressed in terms of moments as , , and , , , where , S and are variance, skewness and kurtosis, respectively [95]. The various order cumulants are extensive quantities and are proportional to the system volume, which is difficult to be measured in heavy-ion collisions. By taking the ratio between various order cumulants, the system volume can be cancelled to the first order and are directly related to the ratios of the thermodynamic susceptibilities () as [89,93,96].
Figure 6 (left) shows the density plot of fourth order cumulant of order parameter as a function of temperature and baryon chemical potential (T and ) by mapping the Ising equation of state onto the QCD equation of state near the critical point [97]. The red and blue regions in the density plot denote the negative and positive contributions to the fourth order cumulant, respectively. Experimentally, by tuning the beam energy, the T and at chemical freeze-out are varied accordingly. The green dashed line represents the chemical freeze-out points (T, ) passing through the critical region when one varies the beam energies. Figure 6 (right) shows fourth order fluctuation as a function of baryon chemical potential (). Due to the negative and positive critical contributions near the critical point, the will show a non-monotonic energy or dependence with respect to the non-critical baseline. This is the characteristic experimental signature of the critical point we are looking for in the heavy-ion collision experiment. Theoretically, the properties of QCD phase diagram at finite baryon density and the signatures of conserved charge fluctuations near the QCD critical point have been extensively studied by various model calculations, such as Lattice QCD [10,18,19,20,21,22,98], NJL, PNJL model [99,100,101,102,103,104,105,106], PQM, FRG model [107,108,109], Dyson-Schwinger Equation (DSE) method [110,111,112,113], chiral hydrodynamics [114] and other effective models [94,115,116,117,118,119]. However, one should keep in mind that the above results are under the assumption of thermal equilibrium with infinite and static medium. In the real heavy-ion collisions, there exists the effects of finite size/time [120,121,122], non-equilibrium [123,124,125,126,127] and thermal blurring effects [128]. Dynamical modeling of heavy-ion collisions by implementing both the critical and those background effects are ongoing [129,130,131].
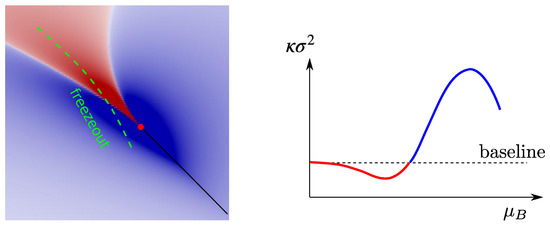
Figure 6.
(Color online) (Left) Density plot of fourth order cumulant of order parameter as a function of temperature and baryon chemical potential (T and ) by mapping the Ising equation of state onto the QCD equation of state near the critical point [97]. The red and blue regions in the density plot denote the negative and positive contributions to the fourth order cumulant, respectively. The green dashed line is the chemical freeze-out points (T, ) passing through the critical region when we scan the beam energies. (Right) Normalized fourth order proton cumulant as a function of collision energy or along the chemical freeze-out line.
Before turning to the experimental status, we would like to stress that there is a long history of using the higher-order cumulants to extract the information on that state created in high-energy nuclear collisions. As extensively discussed in Ref. [26], hadron yields or their ratios, which are the first order moment of the multiplicity distributions, have been used for determine the nature of thermalization in such collisions. Once the thermalization is established [132], on the other hand, the higher-orders cumulants of the very same distributions can be used to study the fine structures of the QCD matter. For example, the critical point [94], the nature of the crossover transition [5,107] and the phase boundary [133] at vanishing and large net-baryon region, respectively.
Experimentally, the fluctuation of the net-proton and net-kaon are used as a proxy of net-baryon and net-strangeness fluctuations, respectively. The STAR experiment has measured the higher-order cumulants (–) and second-order off-diagonal cumulants of net-proton [134,135,136,137,138,139], net-charge [140] and net-kaon [141] multiplicity distributions in Au+Au collisions at = 7.7, 11.5, 14.5, 19.6, 27, 39, 62.4 and 200 GeV, which are collected during the first phase of RHIC beam energy scan program (2010–2014) [142]. To make precise measurements, various corrections and techniques have been applied in the data analysis, those include: (1) Select proper collision centralities to avoid auto-correlations and suppress volume fluctuations [143,144], (2) Detector Efficiency Correction [145,146,147,148,149], (3) Centrality Bin Width Correction (CBWC) [143], (4) Statistical error estimation with Delta theorem and/or Bootstrap [143,150]. Figure 7 shows the measured event-by-event net-charge, net-kaon and net-proton multiplicity distributions of three different centralities in Au+Au collisions at = 14.5 GeV. Those are raw distributions and not corrected for detector efficiency and acceptance. One should apply the efficiency correction and CBWC to obtain the final efficiency corrected cumulants. In Ref. [150], we have shown that the statistical uncertainties of the cumulants () strongly depend on the width of the distributions (). In general, the widths of the distributions in central collisions are wider and with larger mean values than those from peripheral collisions. Further, the widths of the net-charge distributions are much wider than those of net-proton and net-kaon in the same centrality. That’s the reason why we observe larger statistical uncertainties in central collisions than those from peripheral. Assuming the measured particles are emitted from many independent sources in the fire ball, the multiplicity distributions in central collisions would be more symmetric and close to Gaussian distribution than the peripheral based on the central limit theorem (CLT). If those sources are identical and uncorrelated, the cumulant ratios are expected to be a constant as a function of collision centralities.
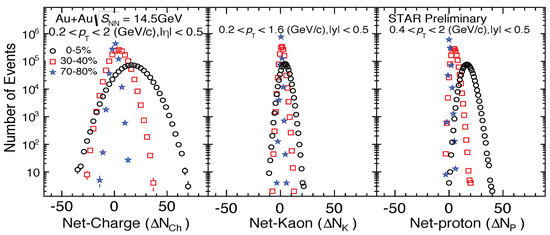
Figure 7.
(Color online) The STAR measured raw event-by-event net-charge, net-kaon and net-proton distributions of three centralities (0–5%, 30%–40% and 70%–80%) in Au+Au collisions at = 14.5 GeV [151].
Figure 8 shows the energy dependence of cumulant ratios (, Skellam, ) of net-charge, net-kaon and net-proton multiplicity distributions in Au+Au collisions measured by STAR. The blue bands are the results obtained from UrQMD model calculations without including the physics of critical point [92,152,153]. The values are normalized by the Skellam expectations, which are constructed with the measured mean values of proton and anti-proton by assuming they are distributed as independent Poisson distributions. The deviation of /skellam from unity would indicate the deviation of from Poisson statistical fluctuations (Poisson baseline). For /Skellam and , their Poisson baselines are unity, which are plotted as the dashed lines. We found that the of net-charge, net-kaon and net-proton monotonically increase when increasing the collision energy. The Skellam and show weak energy dependence for net-charge and net-kaon measurements. We didn’t observe significant deviations of net-charge and net-kaon cumulant ratios Skellam and from the Poisson expectations and UrQMD calculations within uncertainties. However, a clear non-monotonic energy dependence of net-proton was observed in top 0–5% central Au+Au collisions. The 0–5% net-proton values are close to unity for energies above 39 GeV and show large deviations below unity around 19.6 and 27 GeV, and then increasing above unity below 19.6 GeV. The UrQMD calculations of net-proton displaying a strong suppression below unity at lower energies is due to the effects of baryon number conservation [154,155,156,157]. However, this suppression is not observed at low energies in the STAR data. Another transport model (JAM model) study further demonstrates that the resonance weak decay and hadronic re-scattering have very small effects on the proton number fluctuations (–) at low energies [158].
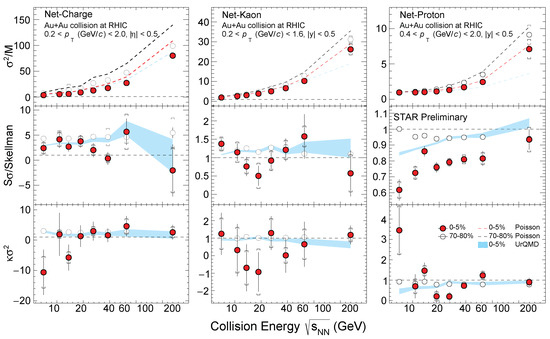
Figure 8.
(Color online) Energy dependence of cumulant ratios (, Skellam, ) of net-charge, net-kaon and net-proton multiplicity distributions for top 0–5% and 70%–80% peripheral collisions. The Poisson expectations are denoted as dotted lines and UrQMD calculations are shown as bands. The statistical and systematical errors are shown in bars and brackets, respectively.
In Figure 9, we summarize the energy dependence of of net-charge, net-kaon and net-proton multiplicity distributions in Au+Au collisions measured by the STAR experiment. For comparison, the net-charge results in Au+Au collisions at = 7.7, 19.6, 27, 39, 62.4 and 200 GeV measured by the PHENIX experiment [159] are shown in the panel (b). We found that the of the net-charge and net-kaon multiplicity distributions measured by the STAR experiment show larger statistical uncertainties than those of net-proton . This can be understood as the statistical uncertainties of depend on the width () of the multiplicity distributions and the particle detecting efficiencies () in the detector as [146]. The width of the net-charge distributions are larger than those of net-proton and net-kaon. Meanwhile, due to decays, the efficiency of kaon (∼40%) is much lower than proton (∼80%). It is the reason why we observe larger statistical uncertainties for net-kaon fluctuations than net-proton. For the net-charge and net-kaon from STAR, we observe weak energy dependence within current statistical uncertainties. The PHENIX net-charge are with much smaller statistical uncertainties than the results from STAR. This is due to smaller acceptance of PHENIX detector than the STAR detector, thus the width of the net-charge multiplicity distributions measured by the PHENIX experiment is much narrower than those measured by STAR. We observe a clear non-monotonic energy dependence for net-proton in the most central (0–5%) Au+Au collisions with a minimum around 19.6 GeV. This non-monotonic behavior cannot be described by various model calculations without the physics of phase transition and critical point.
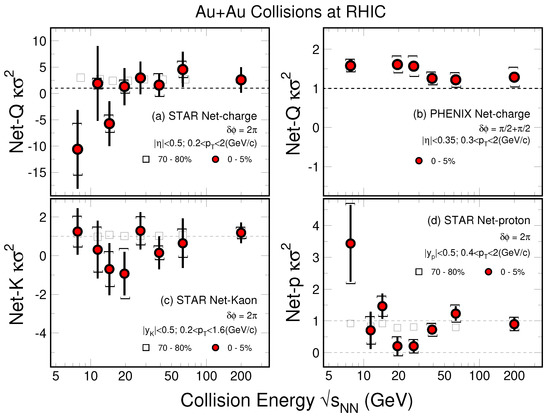
Figure 9.
(Color online) The STAR measured energy dependence of of net-charge (top left), net-kaon and net-proton distributions in Au+Au collisions at = 7.7, 11.5, 14.5, 19.6, 27, 39, 62.4 and 200 GeV. The net-charge fluctuations measured by the PHENIX experiment in Au+Au collisions at = 7.7, 19.6, 27, 39, 62.4 and 200 GeV are shown in top right panel.The statistical and systematical errors are shown in bars and brackets, respectively.
Figure 10 shows the energy dependence of the fourth-order fluctuations () of net-proton from the top 5% central Au+Au collisions measured by STAR experiment [139]. Recent result from the HADES experiment is also shown in the figure. Note that there are differences in the data shown in Figure 10: while STAR data points are from the top 5% central collisions and GeV/c, the HADES data is from the top 10% central Au+Au collisions and GeV/c. From 200 GeV to 7.7 GeV, non-monotonic energy dependence is clearly shown in the of net-proton multiplicity distributions and one can observe a strong enhancement at the highest MeV, corresponding to the Au+Au central collisions at = 7.7 GeV. This might indicate attractive correlations between nucleons in nature at the large baryon density region. However, interestingly, the strong enhancement in the fourth-order fluctuation seems disappeared as shown by the HADES result at = 2.4 GeV [160]. Indeed, in the high baryon density region, between = 2 GeV and 8 GeV, there might be a peak in the fourth order fluctuations as speculated in Ref. [92,97,133]. If the peak structure is confirmed, that would be the experimental indication of the QCD critical point and/or the first order phase transition created in such high-energy nuclear collisions. On the other hand, it is possible that from = 2 GeV to 8 GeV data points are smoothly connected without any peaks or dips. Results from the future experiments like NICA, CBM, and CEE will certainly provide the answer.
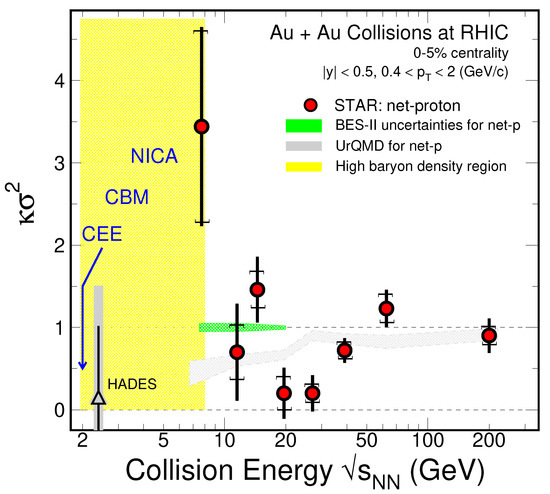
Figure 10.
(Color online) Energy dependence of the mid-rapidity net-proton 4th order cumulants ratios from central 0–5% Au+Au collisions, STAR experiment ( GeV/c: filled-circles) [139] and 0–10% Au+Au collision, HADES experiment ( GeV/c: open-triangle) [160]. The statistical uncertainties of the second RHIC beam-energy-scan (BES-II) are shown as the green-band while the UrQMD results are shown as gray-band. The energy region covered by the future experiments is shown as yellow.
In Figure 10, the results from the transport model UrQMD (grey band) show a monotonic decrease from low to high baryon density region, which is due to the effect of baryon number conservation in high-energy nuclear collisions. Note that in the Poisson limit, the absence of criticality or other dynamical correlations, the is expected to be unity. The green band in the figure is the projected statistical error of the fourth-order fluctuations of net-protons in the second phase of the RHIC Beam Energy Scan (BES-II, 2019–2021) program [161]. The BES-II program, which is scheduled between 2019 and 2021 for the Au+Au collisions at 7.7–19.6 GeV, will take about 10 to 20 times higher statistics (depending on energy) to confirm the non-monotonic behavior observed in the fourth order fluctuations () of net-proton and proton in Au+Au collisions in the BES-I at RHIC. Assuming the data in the figure is related to the critical region, one must study the net-proton fluctuations at even higher baryon density region, i.e., at lower collision energies. The yellow band shown in the figure represents the high baryon density region ( = 2–8 GeV) covered by future FAIR/CBM fixed target (FXT) experiment ( = 2–5 GeV) [162] and the NICA/MPD collider experiment ( = 4–11 GeV) [163]..
Besides the conserved charge fluctuations, the light nuclei production is predicted to be sensitive to the baryon density fluctuations assuming that the light nuclei is formed from the nucleon coalescence. Model calculations show that the yield ratio between deuteron, triton and proton, is related to the neutron density fluctuations, thus can be used to search for the QCD critical point in heavy-ion collisions [164,165]. Experimentally, the STAR experiment has measured the production of deuteron (d) and triton (t) in the Au+Au collisions at = 7.7, 11.5, 14.5, 19.6, 27, 39, 54.4, 62.4 and 200 GeV. As shown in Figure 11, non-monotonic energy dependence is observed for the yield ratio, , in 0–10% central Au+Au collisions with a peak around 20–30 GeV [166,167,168]. The yield ratios measured by STAR experiment below 20 GeV are consistent with the results calculated from NA49 experiment [164]. Since there is no critical physics implemented in the JAM model, the results of central ( fm) Au+Au collisions from JAM model is also plotted as blue band in Figure 11 for comparison [166]. The model results show a flat energy dependence and cannot describe the non-monotonic trend observed in the STAR data. The current STAR results shown in Figure 11 is for 0–10% centrality, it is also worthwhile to perform centrality dependence study on this yield ratio. On the other hand, more theoretical studies and dynamical modeling of heavy-ion collisions with critical physics are needed to understand whether this non-monotonic behavior is related to the QCD critical fluctuations.
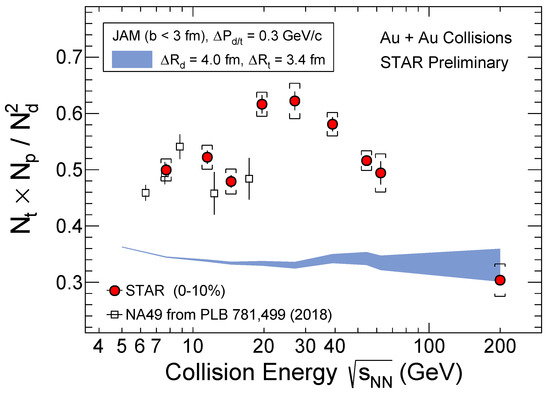
Figure 11.
(Color online) Energy dependence of the light nuclei yield ratio in central (0–10%) heavy-ion collisions. The red solid circles are the results measured in central (0–10%) Au+Au collisions at BES energies by the STAR experiment and the open squares are the results calculated from the Pb+Pb data of NA49 experiment. The blue band represents the results of central Au+Au collisions ( fm) from the JAM model calculations [166].
4. Beam Energy Dependence of the Heavy-Flavor Production
Since the masses of heavy flavor quarks are much larger than the temperature of the system created in the high-energy nuclear collisions, they can be used as clean probes of the medium properties at early stage of the collisions. As shown in Figure 12, heavy flavor quark masses are all generated in the electro-weak sector while light quarks (u, d, and s) are dominated by the spontaneous breaking of chiral symmetry in QCD. Thus heavy quarks keep massive when participating in strong interactions. Due to their large masses, these heavy flavor quarks are primarily pair-created in initial hard pQCD processes. These facts making heavy quark hadrons are ideal for studying the medium effects including the thermalization of the system. One example has already discussed in previous section, see Figure 3.
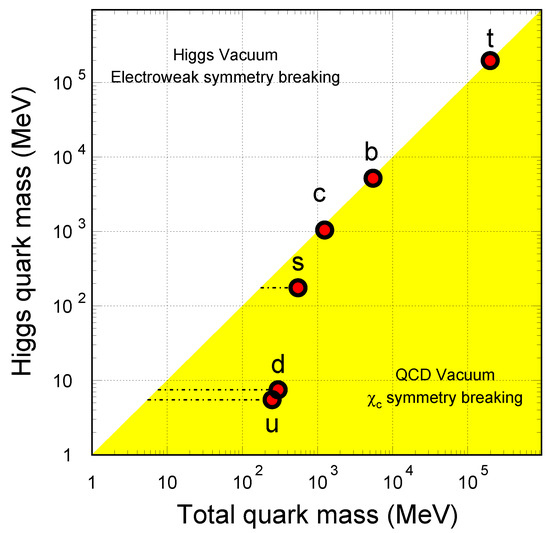
Figure 12.
(Color online) Quark masses in the QCD vacuum and the Higgs vacuum. A large fraction of the light quark mass is due the the chiral symmetry breaking in the QCD vacuum. The numerical values were taken from reference [169]. The plot is taken from Ref. [170].
The QCD calculations can evaluate the charm production cross sections at high energies via a perturbation scheme in p+p collisions [171,172]. Figure 13 shows the charm production cross sections at midrapidity as a function of in p+p collisions at 7 TeV, 1.96 TeV, 500 GeV and 200 GeV from ALICE [173], CDF [174] and STAR [175,176] experiments, respectively. Within uncertainties the Fixed-Order-Next-to-Leading-Logarithm (FONLL) calculations [172] agree with data. The data points are more on top of the upper limit of the theoretical uncertainties for all of the collision energies.
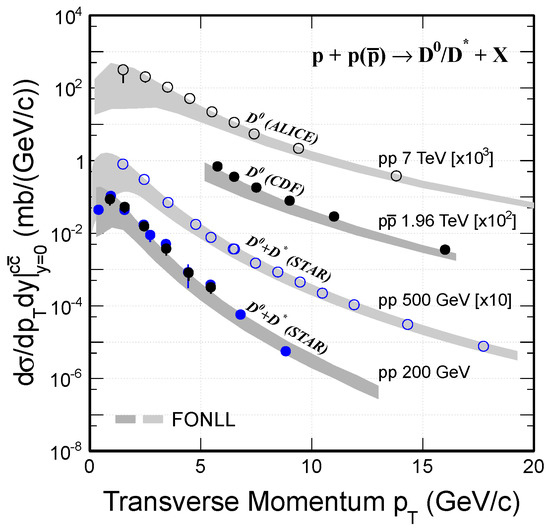
Figure 13.
(Color online) Charm production cross sections at midrapidity as a function of . Symbols from top to bottom are experiment results at 7 TeV [173], 1.96 TeV [174], 500 GeV [176] and 200 GeV [175] from ALICE, CDF and STAR experiments, respectively. The gray bands are FONLL calculations with uncertainties.
In heavy-ion collisions, charm quark interacts with the QGP matter when traversing in the medium. The transverse momentum of charm quark is modified by the medium via energy loss or collective flow. However, the total number of charm quarks may keep conserved since they are produced in initial hard processes before the QGP formation and there is no more charm quark created later via thermal production at RHIC energies. Figure 14 shows the -integrated cross section for production per nucleon-nucleon collision from different centrality bins in = 200 GeV Au+Au collisions for the full range (a) and for > 4 GeV/c (b), respectively [177]. The result from the p+p measurement at the same collision energy is also shown in both panels [175].
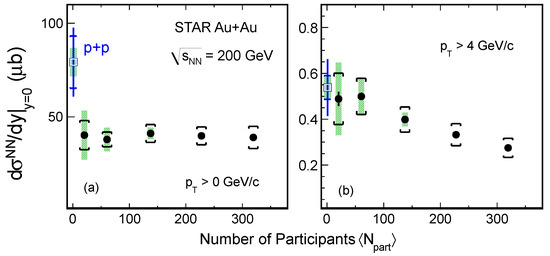
Figure 14.
(Color online) Integrated cross section per nucleon-nucleon collision at mid-rapidity in 200 GeV Au+Au collisions for > 0 (a) and > 4 GeV/c (b) as a function of centrality . The statistical and systematic uncertainties are shown as bars and brackets on the data points. The green boxes on the data points depict the overall normalization uncertainties in p+p and Au+Au data respectively.
The high (> 4 GeV/c) shows a clear decreasing trend from peripheral to mid-central and central collisions and the result in peripheral collisions is consistent with p+p collisions within uncertainties. This is consistent with charm quarks lose more energy in more central collisions at high . However, for the integrated over full range shows approximately a flat distribution as a function of . The values for the full range in mid-central to central Au+Au collisions are smaller than that in p+p collisions with ∼1.5 effect considering the large uncertainties from the p+p measurements. The total charm quark yield in heavy-ion collisions is expected to follow the number-of-binary-collision scaling since charm quarks are conserved at RHIC energies. However, the cold nuclear matter (CNM) effect including shadowing could also play an important role. In addition, hadronization through coalescence could alter the hadrochemistry distributions of charm quark in various charmed-hadron states which may lead to the reduction in the observed yields in Au+Au collisions [178]. For instance, hadronization through coalescence can lead to an enhancement of the charmed baryon over yield [179,180,181], and together with the strangeness enhancement in the hot QCD medium and sequential hadronization, can also lead to an enhancement in the charmed strange meson yield relative to [180,181,182].
The STAR Heavy Flavor Tracker (HFT) with a silicon pixel detector achieved ∼30 μm spacial resolution of the track impact parameter to the primary vertex allows a topological reconstruction of the decay vertices of open charm hadrons. Figure 15 left panels show the charmed baryon over meson ratio compared with light and strange baryon over meson ratios [183,184] (a) and various models (b). The ratio is comparable in magnitude to the and p/ ratios and shows a similar dependence in the measured region. A significant enhancement is seen compared to the calculations from the latest PYTHIA 8.24 release (Monash tune [185]) without (green solid curve) and without (magenta dot-dashed curve) color reconnections (CR) [186]. The implementation with CR is found to enhance the baryon production with respect to mesons. However, both calculations fail to fully describe the data and its dependence. Figure 15b also shows the comparison to various models with coalescence hadronization of charm quarks [179,180,181,182]. The comparisons suggest coalescence hadronization plays an important role in charm-quark hadronization in the presence of QGP. Also, the data can be used to constrain the coalescence model calculations and their model parameters.
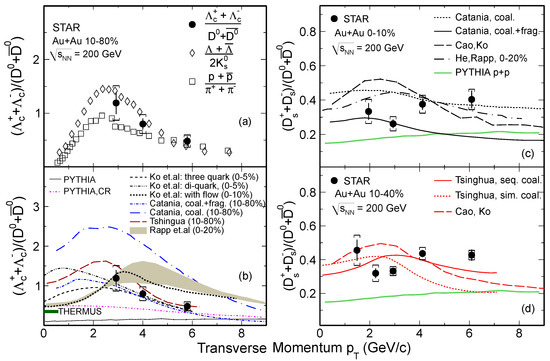
Figure 15.
(Color online) Left panels: The measured ratio at midrapidity ( 1) as a function of for Au+Au collisions at = 200 GeV in 10%–80% centrality, compared to the baryon-to-meson ratios for light and strange hadrons (a) and various model calculations (b). The -integrated ratio from the THERMUS [187] model calculation with a freeze-out temperature of MeV is shown as a horizontal bar on the left axis of the plot. Right panels: (c) The integrated ratio (black solid circles) of 1.5 << 8 GeV/c as a function of compared to model calculation (curves) in 0–10%Au+Au collisions at = 200 GeV. (d) Same ratio as (c) but with 10–40% centrality. The vertical lines and brackets on the data points indicate statistical and systematic uncertainties respectively.
Figure 15 right panel shows the ratio as a function of compared to coalescence model calculations for 0–10% (c) and 10%–40% (d) collision centralities. Several models incorporating coalescence hadronization of charm quarks and strangeness enhancement are used to describe the dependence of ratio. Those models assume that mesons are formed by recombination of charm quarks with equilibrated strange quarks in the QGP [179,180,181,182]. In particular, the sequential coalescence model together with charm quark conservation [180] considers that more charm quarks are hadronized to mesons than since the former is created earlier in the QGP, which results in further enhancement of ratio in Au+Au collisions relative to collisions.
D meson and have been observed similar as light flavor hadrons in 200 GeV Au+Au collisions [177], which indicates charm is thermalized in the system with 170 MeV. In low energy region, such as the energies in RHIC beam energy scan program, it is of particular interest to measure open charm hadron production in a relative smaller and colder system compared to top energy at 200 GeV. This may provide a chance to tell us in what temperature charm behaves different from light flavors. However, in low energy region, the perturbation algorithm in theoretical calculations of charm production cross section becomes invalid, which may result in large theoretical uncertainties. Meanwhile the charm production cross section drops rapidly when collision energy decreases, it is very challenging to measure open charm production at low energies. The previous measurements at SPS energies are with large uncertainties [188,189]. Since the HFT detector was taken out from STAR for the BES-II runs together with low cross section, it is impossible to reconstruct open charm hadrons via hadronic decay channels, the electron production from heavy flavor semi-leptonic decays becomes the unique way to measure heavy flavor productions at low energy.
Figure 16 shows the of electrons from heavy flavor decays as a function of in 54 and 200 GeV Au+Au collisions [190] as solid circles and open stars, respectively. A semi-empirical exponential function [191] is used to fit all the data points and the ratios of data over the fit function are shown in the bottom panel. The result in 54 GeV agrees with that in 200 GeV within uncertainties, which may suggest charm quarks are still thermalized in 54 GeV Au+Au collisions. On the other hand, it is of interest to repeat the same measurement in lower energies, such as 27 GeV from STAR BESII experiment.
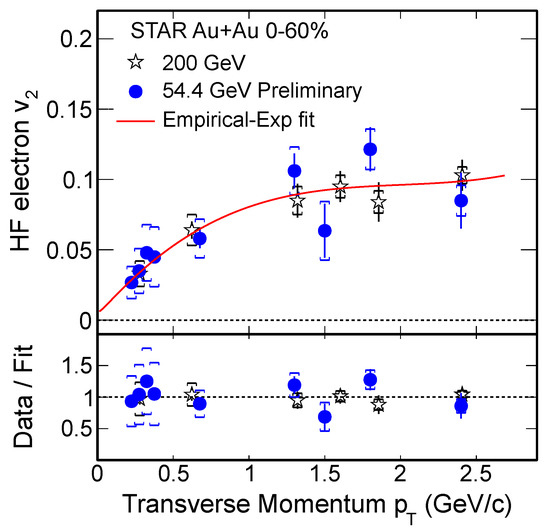
Figure 16.
(Color online) Upper panel: of electrons from heavy flavor decays as a function of in 54 (blue solid circles) and 200 (open stars) GeV Au+Au collisions [190]. Red curve denotes an empirical reversed exponential fit [191] to all the data points. Bottom panel: The ratios of data over the fit function. Vertical bars and brackets denote statistical and systematic uncertainties, respectively.
STAR experiment extracted the total charm production cross section per binary nucleon collision at midrapidity in 200 GeV Au+Au collisions by summing all yields of the open charm hadron states and reported as = 152 ± 13 (stat) ± 29 (sys) [192], which is consistent with that in p+p collisions = 130 ± 30 (stat) ± 26 (sys) [175] within uncertainties. This result is consistent with charm quark conservation in heavy-ion collisions at RHIC top energy.
The total charm production cross section in full rapidity region can be calculated from above charm cross section at midrapidity multiplying an equivalent correction factor (4.7 ± 0.7) assuming charm quark rapidity distribution from PYTHIA calculations [193]. Figure 17 shows the charm total production cross section over a wide collision energy region from a few ten GeV to TeV. Open symbols are the experimental results taken from Ref. [188,189,194]. STAR p+p [175] and Au+Au [192] results are shown as blue solid square and red star, respectively. As for comparison, the total cross section of charmonium measured from CERN-PS [195], WA39 [196], IHEP [197], E288 [198], E331 [199], E444 [200], E595 [201], E672 [202], E705 [203], E706 [202], E771 [204], E789 [205], NA3 [206], NA38 [207], NA50 [208], NA51 [209], UA6 [210], HERA-B [211], ISR [212], PHENIX [213] experiments (open diamonds) and NRQCD (long-dashed curve) are shown as well over a broad collision energy region [214].
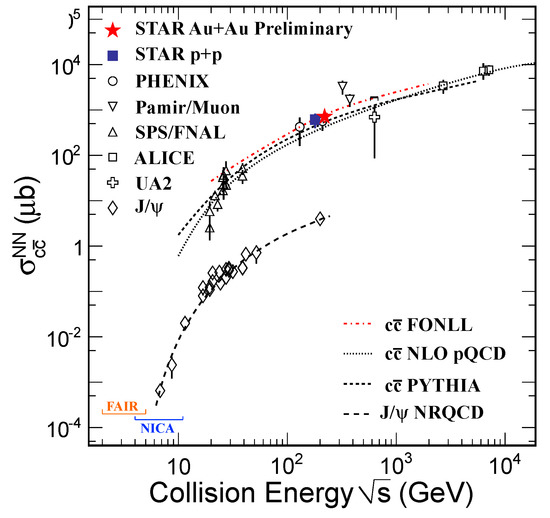
Figure 17.
(Color online) Charm and J/ total production cross sections per nucleon-nucleon as a function of collision energy. The open diamonds denote the charmonium cross section from worldwide experiments [195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213]. The other open symbols are the experiment results of charm total cross section taken from Ref. [188,189,194]. STAR p+p [175] and Au+Au [192] results are shown as blue solid square and red star, respectively. Model calculations from FONLL [172], NLO pQCD [215], PYTHIA [193] and NRQCD [214] are represented as dot-dashed, dotted, dashed and long-dashed curves, respectively.
5. Future Upgrades and Physics Program at High Baryon Density Region
The RHIC BES program II and future FAIR and NICA experiments will focus on collision energy below 20 GeV offering us a unique opportunity to explore the QCD phase structure at high baryon density region. In Figure 18, interaction rates from both collider experiments and fixed-target experiments are shown. The region for the high baryon density, largely covered by the fixed-target experiments, is highlighted with yellow. In the following, we discuss few key measurements with the future experimental facilities. Again the discussions are arranged around the headlines of Collectivity, Criticality and Heavy Flavor Productions.
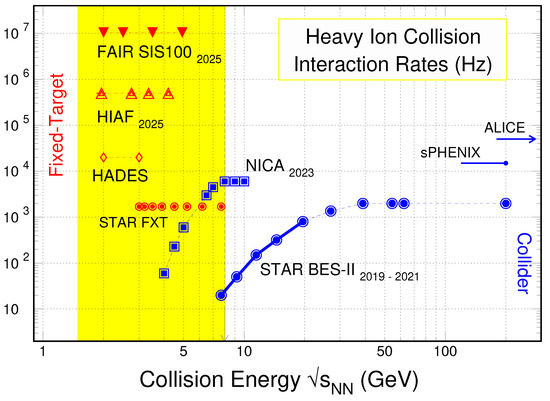
Figure 18.
(Color online) Interaction rates for high-energy nuclear collision facilities: the second phase RHIC beam energy scan (filled blue circles: BES-II, GeV), NICA (squares: GeV) as well as the fixed-target projects including HADES (diamonds), HIAF (triangles) and FAIR (filled triangles). STAR fixed-target range is indicated with filled red circles.
Collectivity: The flow results from top energy heavy-ion collisions at RHIC indicate that the partonic collectivity has been built up from light u, d and s quarks to heavy c quark as well. This is one of the most important experimental evidences for the creation of the QGP in high-energy nuclear collisions [1,2,3,4]. As a function of the collision energy, both radial and elliptic flow show an increasing trend, say above GeV (Figure 4). Above that energy, the slope of net-particles for both baryons and mesons, is observed to be almost the same, the difference between particle and anti-particle also becomes similar (Figure 5). While the shows large divergence between net-kaon and net-proton (and net-), the particle and anti-particle difference splits between baryons and mesons dramatically below GeV, see Figure 5. All of these observations imply that the medium properties created in heavy-ion collisions would be different above/below GeV.
In collectivity, two noticeable observations are the splitting between baryon’s and meson’s and in the low energy. Mesons such as kaons and –mesons are important, especially the –meson as it has the similar mass of proton. The precise results of –meson’s and will reveal the origin of collectivity at the high baryon density region. In addition, the ratio of will shed light on the production mechanism. It could be treated as a micro-laboratory for understanding the quarkonia productions in nucleus-nucleus collisions.
Criticality: One of the main goal of RHIC Beam Energy Scan program is to search for the QCD critical point, which is the end point of the first order phase boundary in the QCD phase diagram. The experimental confirmation of the existence of the CP will be a landmark of exploring the QCD phase structure. Near the QCD critical point, the density fluctuations and correlation length will diverge. The conserved charge fluctuations and light nuclei productions have been proposed as sensitive observables to search for the signature of QCD phase transition and the QCD critical point. Experimentally, the STAR experiment has measured the higher order cumulants of net-particle distributions and light nuclei productions (deuteron and triton) in Au+Au collisions at = 7.7 to 200 GeV. In Figure 10 and Figure 11, it has been observed that both fourth order fluctuations of net-proton () and light nuclei yield ratio show non-monotonic energy dependence in central Au+Au collisions, with a minimum and peak around 20 GeV, respectively. Although the two measurements are of different order of fluctuations, the two observations are consistent with the expectation of model calculations with CP physics and might suggest that the created system skims close by the CP receiving the contributions from critical fluctuations. To confirm the above two observed non-monotonic energy dependence trends in BES-I, the second phase of Beam Energy Scan (BES-II) has been planned at RHIC (2019–2021). It will allow us to have 10–20 times more statistics at energies = 7.7–19.6 GeV. In addition, one observes large changes between 19.6 and 14.5 GeV in the energy dependence of net-proton kurtosis (Figure 10) and light nuclei yield ratio (Figure 11) measured in the RHIC BES-I data. This could indicate that the QCD critical point is put by nature between the thermodynamic condition () of 19.6 and 14.5 GeV. Thus, it is important to conduct a finer beam energy scan between these two energies, i.e., 19.6 GeV ( MeV) and 14.5 GeV ( MeV). Therefore, we propose to take the data of a new energy point of Au+Au collisions at = 16.7 GeV ( MeV), which is just between 19.6 and 14.5 GeV with equal gap, on each side. Based on the net-proton fluctuations measured from HADES and STAR experiments, and the model calculations, there might be a peak in the fourth order net-proton fluctuations in Au+Au collisions between = 2 GeV and 8 GeV. In order to experimentally map out the QCD phase diagram at the higher baryon density region, the future heavy-ion collision experiments like MPD/NICA, CBM/FAIR and CEE/CSR are certainly necessary and important.
On the other hand, it is predicted that the higher order conserved charge fluctuations, such as sixth order () or eighth order () cumulants, should be more sensitive to the phase transition. If the chemical freeze-out temperature in heavy-ion collisions are close enough to the phase boundary, the sixth and eighth order fluctuations could show negative values [98,107]. STAR experiment has measured the centrality dependence of sixth order () of net-proton distributions in Au+Au collisions at = 54.4 and 200 GeV. Negative values are observed for net-proton from mid-central to central collisions at 200 GeV, while positive values are observed at 54.4 GeV [216,217]. The negative sign of net-proton observed at 200 GeV could be an experimental evidence of smooth crossover at small baryon chemical potential [98,107]. In future fixed target experiments, with much more statistics of low energy data, we can perform precise measurements of those higher order cumulants of conserved charges at the high baryon density region.
Heavy Flavor Production: FAIR-CBM and NICA-MPD experiments with advanced fast detector technology under high luminosity beam condition will provide unique chance to measure open and hidden charm hadrons with large statistics close to the production energy threshold [162,218]. It is expected that this measurements will improve the precision of the total charm cross section at low energies and will provide constraints on pQCD calculations, as well as the unknown interactions between charmed particles and cold hadronic medium. Taking the prediction of the HSD model [219], the yield obtained in one week of running of CBM detectors with 10 MHz event rate would be about 300 J/ for central Au+Au collisions at 10A GeV, and about 600 J/ for central Ni+Ni collisions at 15A GeV. In the latter case, also open charm production can be studied at a rate of 300 kHz with a silicon vertex detector MVD in operation for charmed hadron decay vertex reconstruction. As a result, the expected yield in central Ni+Ni collisions at 15A GeV will be about 30 D mesons per week. This would be sufficient for cross section measurement and an analysis of charmonium propagation and absorption in dense baryonic matter based on the ratio of hidden to open charm at low energy.
In order to extend the coverage to even larger baryon density region, STAR has developed a fixed-target (FXT) program. As shown in Figure 18, a gold-target (1% interaction length) is placed at the right entrance of TPC. The end cap time-of-flight wall will be constructed at approximately the other side of the TPC entrance. The time-of-flight detectors are on loan from the CBM experiment at FAIR [220,221]. In addition, the inner-TPC upgrade [222] will extend the rapidity coverage, essential for the search for the QCD critical point measurement. STAR will be setup in such a way that data taking from both colliding and FXT modes will take place concurrently. With this configuration, STAR detector system will measure particle productions and correlations in Au+Au collisions from = 3–19.6 GeV, extending its coverage of baryon chemical potential from about = 400 MeV to 750 MeV. The center of mass energy from the highest energy of the FXT mode is overlay with the lowest colliding mode at = 7.7 GeV and the lower part of the FXT energies overlap with the future collision energies provided by CBM at FAIR [16]. These allow systematic crosschecks on many of the observables in STAR experiment, for both colliding and FXT modes, and CBM experiment for the FXT mode. The BES program II and future FAIR and NICA experiments will focus on the high baryon density region (<20 GeV), offer us a unique opportunity to explore the QCD phase structure.
In summary, the precise flow measurements of mesons and multi-strange hadrons with STAR BES-II and future fixed-target experiments will reveal the degree of freedom originates from partonic or hadronic level at the high baryon density region. The confirmation of non-monotonic energy dependence in central Au+Au collisions for net-proton and/or light nuclei yield ratio with STAR BES-II and future fixed-target experiments will provide crucial experimental evidences for establishing the case for the discovery of the QCD critical point. The energy dependence of heavy flavor measurements will provide crucial information on thermalization of the system and provide unique opportunity to study the unknown interactions between heavy quark and the cold nuclear matter. A great deal of new information on the QCD phase diagram will be extracted with current and planned heavy-ion collision programs.
Author Contributions
X.L., S.S., N.X. and Y.Z. contribute equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key Research and Development Program of China (2018YFE0205200), the National Natural Science Foundation of China (No. 11890711, 11890712, 11828501 and 11861131009).
Acknowledgments
We thank Xin Dong, ShinIchi Esumi, Lokesh Kumar, Volker Koch, Bedangadas Mohanty for discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arsene, I.; Bearden, I.; Beavis, D.; Besliu, C.; Budick, B.; Boggild, H.; Chasman, C.; Christensen, C.; Christiansen, P.; Cibor, J.; et al. Quark-gluon plasma and color glass condensate at RHIC? The perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1. [Google Scholar] [CrossRef]
- Back, B.B.; Baker, M.; Ballintijn, M.; Barton, D.; Becker, B.; Betts, R.; Bickley, A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.; Ahammed, Z.; Amonett, J.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Badyal, S.; Bai, Y.; Balewski, Q.; et al. Experimental and theoretical challenges in the search for the quark–gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102. [Google Scholar]
- Adcox, K.; Adler, S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus–nucleus collisions at RHIC: Experimental evaluation by the PHENIX Collaboration. Nucl. Phys. A 2005, 757, 184. [Google Scholar]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.; Szabo, K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; Li, S.; et al. Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 2019, 795, 15–21. [Google Scholar] [CrossRef]
- Bellwied, R.; Borsanyi, S.; Fodor, Z.; Günther, J.; Katz, S.D.; Ratti, C.; Szabo, K.K. The QCD phase diagram from analytic continuation. Phys. Lett. B 2015, 751, 559–564. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Guenther, J.; Kara, R.; Katz, S.; Parotto, P.; Pasztor, A.; Ratti, C.; Szabo, K. The QCD crossover at finite chemical potential from lattice simulations. arXiv 2020, arXiv:2002.02821. [Google Scholar]
- Bazavov, A.; Ding, H.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Ohno, H.; Petreczky, P.; Rinaldi, E.; et al. Skewness and kurtosis of net baryon-number distributions at small values of the baryon chemical potential. Phys. Rev. D 2017, 96, 074510. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. QCD equation of state to O(mu(6)(B)) from lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; Anderson, D.; Aoyama, R.; Aparin, A.; et al. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 2017, 96, 044904. [Google Scholar]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rept. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Available online: https://drupal.star.bnl.gov/ (accessed on 28 February 2020).
- Available online: http://nica.jinr.ru/ (accessed on 28 February 2020).
- Available online: https://fair-center.eu/ (accessed on 28 February 2020).
- Available online: http://hiaf.impcas.ac.cn/ (accessed on 28 February 2020).
- Bazavov, A.; Ding, H.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Smith, D.; et al. Freeze-out Conditions in Heavy Ion Collisions from QCD Thermodynamics. Phys. Rev. Lett. 2012, 109, 192302. [Google Scholar] [CrossRef] [PubMed]
- Borsanyi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Freeze-out parameters from electric charge and baryon number fluctuations: Is there consistency? Phys. Rev. Lett. 2014, 113, 052301. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Ding, H.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Ohno, H.; Petreczky, P.; Schmidt, C.; et al. Curvature of the freeze-out line in heavy-ion collisions. Phys. Rev. D 2016, 93, 014512. [Google Scholar] [CrossRef]
- Alba, P.; Alberico, W.; Bellwied, R.; Bluhm, M.; Sarti, V.; Nahrgang, M.; Ratti, C. Freeze-out conditions from net-proton and net-charge fluctuations at RHIC. Phys. Lett. B 2014, 738, 305. [Google Scholar] [CrossRef]
- Bluhm, M.; Nahrgang, M. Freeze-out conditions from strangeness observables at RHIC. Eur. Phys. J. C 2019, 79, 155. [Google Scholar] [CrossRef]
- Poberezhnyuk, R.; Vovchenko, V.; Motornenko, A.; Gorenstein, M.I.; Stoecker, H. Chemical freeze-out conditions and fluctuations of conserved charges in heavy-ion collisions within quantum van der Waals model. Phys. Rev. C 2019, 100, 054904. [Google Scholar] [CrossRef]
- Alba, P.; Sarti, V.M.; Noronha-Hostler, J.; Parotto, P.; Portillo-Vazquez, I.; Ratti, C.; Stafford, J.M. Influence of hadronic resonances on the chemical freeze-out in heavy-ion collisions. arXiv 2020, arXiv:2002.12395. [Google Scholar]
- Acharya, S.; Adamova, D.; Adolfsson, J.; Aggarwal, M.; Aglieri, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.; Aiola, S.; et al. Production of 4He and 4He− in Pb+Pb collisions at 2.76 TeV at the LHC. Nucl. Phys. A 2018, 971, 1c. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarek, O.; Karsch, F.; Laermann, E.; Miao, C.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Soeldner, W.; Unger, W. Phase boundary for the chiral transition in (2+1) -flavor QCD at small values of the chemical potential. Phys. Rev. D 2011, 83, 014504. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. The horn, the hadron mass spectrum and the QCD phase diagram? The statistical model of hadron production in central nucleus-nucleus collisions. Nucl. Phys. A 2010, 834, 237c. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Chatterjee, S.; Godbole, R.M.; Gupta, S. Stabilizing hadron resonance gas models. Phys. Rev. C 2010, 81, 044907. [Google Scholar]
- Adler, C.; Ahammed, Z.; Allgower, C.; Amonett, J.; Anderson, B.; Anderson, M.; Averichev, G.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Azimuth Anisotropy of and Λ + Production at Midrapidity from Au+Au Collisions at = 130 GeV. Phys. Rev. Lett. 2002, 89, 132301. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.; Ahammed, Z.; Amonett, J.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Badyal, S.; Bai, Y.; Balewski, Q.; et al. Multistrange Baryon Elliptic Flow in Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2005, 95, 122301. [Google Scholar] [CrossRef]
- Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; Armendariz, R.; Aronson, S.; et al. Elliptic Flow for ϕ Mesons and (Anti)deuterons in Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2007, 99, 052301. [Google Scholar] [CrossRef]
- Abelev, B.; Aggarwal, M.; Ahammed, Z.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Partonic Flow and ϕ-Meson Production in Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2007, 99, 112301. [Google Scholar] [CrossRef]
- Abelev, B.; Aggarwal, M.; Ahammed, Z.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Centrality dependence of charged hadron and strange hadron elliptic flow from = 200 GeV Au + Au collisions. Phys. Rev. C 2008, 77, 054901. [Google Scholar] [CrossRef]
- Abelev, B.; Aggarwal, M.; Ahammed, Z.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Charged and strange hadron elliptic flow in Cu + Cu collisions at = 62.4 and 200 GeV. Phys. Rev. C 2010, 81, 044902. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.; Averichev, G.; et al. Centrality and Transverse Momentum Dependence of Elliptic Flow of Multistrange Hadrons and ϕ Meson in Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2016, 116, 062301. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; Anderson, D.; Aoyama, R.; Aparin, A.; et al. Measurement of D0 Azimuthal Anisotropy at Midrapidity in Au + Au Collisions at = 200 GeV. Phys. Rev. Lett. 2017, 118, 212301. [Google Scholar] [CrossRef]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200A GeV S+S collisions. Phys. Rev. C 1993, 48, 2462. [Google Scholar] [CrossRef]
- Akiba, Y.; Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Britt, H.; Chang, J.; Chasman, C.; Chen, Z.; et al. Particle production in Au + Au collisions from BNL E866. Nucl. Phys. A 1996, 610, 139c. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Britt, H.; Chang, J.; Chasman, C.; Chen, Z.; Chi, C.; et al. Particle production at high baryon density in central Au+Au reactions at 11.6A GeV/c. Phys. Rev. C 1998, 57, R466. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Britt, H.; Chang, J.; Chasman, C.; Chen, Z.; Chi, C.; et al. Proton and deuteron production in Au+Au reactions at 11.6A GeV/c. Phys. Rev. C 1999, 60, 064901. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Beery, P.; Britt, H.; Budick, B.; Chang, J.; Chasman, C.; et al. Centrality dependence of kaon yields in Si+A and Au+Au collisions at relativistic energies. Phys. Rev. C 1999, 60, 044904. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Budick, B.; Chang, J.; Chasman, C.; Chen, Z.; Chu, Y.; et al. Excitation function of K+ and π+ production in Au+Au reactions at 2-10 AGeV. Phys. Lett. B 2000, 476, 1. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.; Beavis, D.; Budick, B.; Chang, J.; Chasman, C.; Chen, Z.; Chu, Y.; et al. An excitation function of K- and K+ production in Au+Au reactions at the AGS. Phys. Lett. B 2000, 490, 53. [Google Scholar] [CrossRef]
- Barrette, J.; Bellwied, R.; Bennett, S.; Bersch, R.; Braun-Munzinger, P.; Chang, W.; Cleland, W.; Clemen, M.; Cole, J.; Cormier, T.; et al. Proton and pion production in Au+Au collisions at 10.8A GeV/c. Phys. Rev. C 2000, 62, 024901. [Google Scholar] [CrossRef]
- Klay, J.; Ajitanand, N.; Alexander, J.; Anderson, M.; Best, D.; Brady, F.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.; et al. Longitudinal Flow of Protons from (2-8)A GeV Collisions. Phys. Rev. Lett. 2002, 88, 102301. [Google Scholar] [CrossRef]
- Afanasiev, S.; Anticic, T.; Barna, D.; Bartke, J.; Barton, R.; Behler, M.; Betev, L.; Bialkowska, H.; Billmeier, A.; Blume, C.; et al. Energy dependence of pion and kaon production in central Pb+Pb collisions. Phys. Rev. C 2002, 66, 054902. [Google Scholar] [CrossRef]
- Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Behler, M.; Betev, L.; Bialkowska, H.; Billimeier, A.; Blume, C.; Boimska, B.; et al. Energy and centrality dependence of deuteron and proton production in Pb+Pb collisions at relativistic energies. Phys. Rev. C 2004, 69, 024902. [Google Scholar] [CrossRef]
- Alt, C.; Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Betev, L.; Bialkowska, H.; Blume, C.; Boimska, B.; Botje, M.; et al. Energy and centrality dependence of p and production and the / ratio in Pb+Pb collisions between 20A GeV and 158A GeV. Phys. Rev. C 2006, 73, 044910. [Google Scholar] [CrossRef]
- Alt, C.; Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Betev, L.; Bialkowska, H.; Blume, C.; Boimska, B.; Botje, M.; et al. Pion and kaon production in central Pb+Pb collisions at 20A and 30A GeV: Evidence for the onset of deconfinement. Phys. Rev. C 2008, 77, 024903. [Google Scholar] [CrossRef]
- Abelev, B.; Aggarwal, M.; Ahammed, Z.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Systematic measurements of identified particle spectra in pp, d+Au, and Au+Au collisions at the STAR detector. Phys. Rev. C 2009, 79, 034909. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Anderson, D.; Aparin, A. Bulk Properties of the System Formed in Au+Au Collisions at = 14.5 GeV at STAR. arXiv 2019, arXiv:1908.03585v1. [Google Scholar]
- Abelev, B.; Adam, J.; Adamova, D.; Adare, A.; Aggarwal, M.; Aglieri, G.; Agnello, M.; Agocs, A.; Agostinelli, A.; Ahammed, Z.; et al. Centrality dependence of π, K and p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Pinkenburg, C.; Ajitanand, N.; Alexander, J.; Anderson, M.; Best, D.; Brady, F.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.; et al. Elliptic Flow: Transition from Out-of-Plane to In-Plane Emission in Au+Au Collisions. Phys. Rev. Lett. 1999, 83, 1295. [Google Scholar] [CrossRef]
- Alt, C.; Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Behler, M.; Betev, L.; Bialkowska, H.; Billimeier, A.; Blume, C.; et al. Directed and elliptic flow of charged pions and protons in Pb+Pb collisions at 40A and 158A GeV. Phys. Rev. C 2003, 68, 034903. [Google Scholar] [CrossRef]
- Andronic, A.; Barret, V.; Basrak, Z.; Bastid, N.; Benabderrahmane, L.; Berek, G.; Caplar, R.; Cordier, P.; Crochet, P.; Dupieux, P.; et al. Excitation function of elliptic flow in Au + Au collisions and the nuclear matter equation of state. Phys. Lett. B 2005, 612, 173. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J. Dynamics of ultra-relativistic nuclear collisions with heavy beams: An experimental overview. Nucl. Phys. A 1998, 638, 3c. [Google Scholar] [CrossRef]
- Appelshauser, H. New results from CERES. Nucl. Phys. A 2002, 698, 253c. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Abrahantes, A.; Adamova, D.; Adare, A.; Aggarwal, M.; Aglieri, G.; Agocs, A.; Aguilar, S.; Ahammed, Z.; et al. Elliptic Flow of Charged Particles in Pb+Pb Collisions at = 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef]
- Voloshin, S.A.; Poskanzer, A.M.; Snellings, R. Collective phenomena in non-central nuclear collisions. In Relativistic Heavy Ion Physics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 293–333. [Google Scholar]
- Adams, J.; Aggarwal, M.; Ahammed, Z.; Amonett, J.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Badyal, S.; Bai, Y.; Balewski, Q.; et al. Azimuthal anisotropy in Au+Au collisions at = 200 GeV. Phys. Rev. C 2005, 72, 014904. [Google Scholar] [CrossRef]
- Adler, C.; Ahammed, Z.; Allgower, C.; Amonett, J.; Anderson, B.; Anderson, M.; Averichev, G.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Elliptic flow from two- and four-particle correlations in Au+Au collisions at = 130 GeV. Phys. Rev. C 2002, 66, 034904. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Scaling Properties of Azimuthal Anisotropy in Au+Au and Cu+Cu Collisions at = 200 GeV. Phys. Rev. Lett. 2007, 98, 162301. [Google Scholar] [CrossRef] [PubMed]
- Alver, B.; Back, B.; Baker, M.; Ballintijn, M.; Barton, D.; Betts, R.; Bickley, A.; Bindel, R.; Busza, W.; Carroll, A.; et al. System Size, Energy, Pseudorapidity, and Centrality Dependence of Elliptic Flow. Phys. Rev. Lett. 2007, 98, 242302. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alakhverdyants, A.; Alekseev, I.; Alford, J.; Anderson, B.; Anson, C.; Arkhipkin, D.; et al. Inclusive charged hadron elliptic flow in Au+Au collisions at = 7.7–39 GeV. Phys. Rev. C 2012, 86, 054908. [Google Scholar] [CrossRef]
- Shi, S. Event anisotropy v2 in Au+Au collisions at = 7.7–62.4 GeV with STAR. Nucl. Phys. A 2013, 904-905, 895c. [Google Scholar] [CrossRef][Green Version]
- Kolb, P.F.; Sollfrank, J.; Heinz, U. Anisotropic transverse flow and the quark-hadron phase transition. Phys. Rev. C 2000, 62, 054909. [Google Scholar] [CrossRef]
- Sorge, H. Highly Sensitive Centrality Dependence of Elliptic Flow: A Novel Signature of the Phase Transition in QCD. Phys. Rev. Lett. 1999, 82, 2048. [Google Scholar] [CrossRef]
- Heinz, U.W. Relativistic Heavy Ion Physics; Stock, R., Ed.; Landolt- Bornstein Data Collection Series; Springer: New York, NY, USA, 2010; Volume I/23. [Google Scholar]
- Bass, S.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255. [Google Scholar] [CrossRef]
- Bleicher, M.; Zabrodin, E.; Spieles, C.; Bass, S.; Ernst, C.; Soff, S.; Bravina, L.; Belkacem, M.; Weber, H.; Stocker, H.; et al. Relativistic Hadron-Hadron Collisions in the Ultra-Relativistic Quantum Molecular Dynamics Model (UrQMD). J. Phys. G 1999, 25, 1859. [Google Scholar] [CrossRef]
- Rischke, D.; Maruhn, J.; Stocker, H.; Greiner, W. The phase transition to the quark-gluon plasma and its effect on hydrodynamic flow. Heavy Ion Phys. 1996, 1, 309. [Google Scholar]
- Stocker, H. Collective flow signals the quark gluon plasma. Nucl. Phys. A 2005, 750, 121. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.; Aparin, A.; Arkhipkin, D.; et al. Beam-Energy Dependence of the Directed Flow of Protons, Antiprotons, and Pions in Au+Au Collisions. Phys. Rev. Lett. 2014, 112, 162301. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; et al. Beam-Energy Dependence of Directed Flow of Λ, , K±, , and ϕ in Au+Au Collisions. Phys. Rev. Lett. 2018, 120, 062301. [Google Scholar] [CrossRef]
- Nayak, K.; Shi, S.; Xu, N.; Lin, Z.-W. Energy dependence study of directed flow in Au+Au collisions using an improved coalescence in a multiphase transport model. Phys. Rev. C 2019, 100, 054903. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.; Aparin, A.; Arkhipkin, D.; et al. Observation of an Energy-Dependent Difference in Elliptic Flow between Particles and Antiparticles in Relativistic Heavy Ion Collisions. Phys. Rev. Lett. 2013, 110, 142301. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.; Aparin, A.; Arkhipkin, D.; et al. Elliptic flow of identified hadrons in Au + Au collisions at = 7.7–62.4 GeV. Phys. Rev. C 2013, 88, 014902. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.; Averichev, G.; et al. Centrality dependence of identified particle elliptic flow in relativistic heavy-ion collisions at = 7.7–62.4 GeV. Phys. Rev. C 2016, 93, 014907. [Google Scholar] [CrossRef]
- Shor, A. ϕ-Meson production as a probe of the quark-gluon plasma. Phys. Rev. Lett. 1985, 54, 1122. [Google Scholar] [CrossRef]
- Van Hecke, H.; Sorge, H.; Xu, N. Evidence of early mul- tistrange hadron freeze-out in high energy nuclear collisions. Phys. Rev. Lett. 1998, 81, 5764. [Google Scholar] [CrossRef]
- Shi, S. An Experimental Review on Elliptic Flow of Strange and Multistrange Hadrons in Relativistic Heavy Ion Collisions. Adv. High Energy Phys. 2016, 2016, 1987432. [Google Scholar] [CrossRef]
- Steinheimer, J.; Koch, V.; Bleicher, M. Hydrodynamics at large baryon densities: Understanding proton versus anti-proton v2 and other puzzles. Phys. Rev. C 2012, 86, 044903. [Google Scholar] [CrossRef]
- Hatta, Y.; Monnai, A.; Xiao, B.-W. Flow harmonics vn at finite density. Phys. Rev. D 2015, 92, 114010. [Google Scholar] [CrossRef]
- Xu, J.; Song, T.; Ko, C.; Li, F. Elliptic flow splitting as a probe of the QCD phase structure at finite baryon chemical potential. Phys. Rev. Lett. 2014, 112, 012301. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F.; Sun, K.; Xu, J.; Ko, C. Isospin splitting of pion elliptic flow in relativistic heavy-ion collisions. Phys. Lett. B 2019, 798, 135002. [Google Scholar] [CrossRef]
- Biao, T.; Shi, S.; Liu, F. Elliptic flow of transported and produced protons in Au+Au collisions with the UrQMD model. Chin. Rhys. C 2019, 43, 054106. [Google Scholar]
- Ejiri, S.; Karsch, F.; Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. B 2006, 633, 275–283. [Google Scholar] [CrossRef]
- Stephanov, M.A. Non-Gaussian fluctuations near the QCD critical point. Phys. Rev. Lett. 2009, 102, 032301. [Google Scholar] [CrossRef]
- Asakawa, M.; Ejiri, S.; Kitazawa, M. Third moments of conserved charges as probes of QCD phase structure. Phys. Rev. Lett. 2009, 103, 262301. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Xu, N. Search for the QCD Critical Point with Fluctuations of Conserved Quantities in Relativistic Heavy-Ion Collisions at RHIC: An Overview. Nucl. Sci. Tech. 2017, 28, 112. [Google Scholar] [CrossRef]
- Gupta, S.; Luo, X.; Mohanty, B.; Ritter, H.G.; Xu, N. Scale for the Phase Diagram of Quantum Chromodynamics. Science 2011, 332, 1525. [Google Scholar] [CrossRef]
- Stephanov, M.A. On the sign of kurtosis near the QCD critical point. Phys. Rev. Lett. 2011, 107, 052301. [Google Scholar] [CrossRef]
- Kitazawa, M.; Luo, X. Properties and uses of factorial cumulants in relativistic heavy-ion collisions. Phys. Rev. C 2017, 96, 024910. [Google Scholar] [CrossRef]
- Ding, H.T.; Karsch, F.; Mukherjee, S. Thermodynamics of strong-interaction matter from Lattice QCD. Int. J. Mod. Phys. E 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Bzdak, A.; Esumi, S.; Koch, V.; Liao, J.; Stephanov, M.; Xu, N. Mapping the Phases of Quantum Chromodynamics with Beam Energy Scan. arXiv 2019, arXiv:1906.00936. [Google Scholar]
- Bazavov, A.; Bollweg, D.; Ding, H.; Enns, P.; Goswami, J.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Larsen, R.; Mukherjee, S.; et al. Skewness, kurtosis and the 5th and 6th order cumulants of net baryon-number distributions from lattice QCD confront high-statistics STAR data. arXiv 2020, arXiv:2001.08530. [Google Scholar]
- Fu, W.J.; Liu, Y.X.; Wu, Y.L. Fluctuations and Correlations of Conserved Charges in QCD at Finite Temperature with Effective Models. Phys. Rev. D 2010, 81, 014028. [Google Scholar] [CrossRef]
- Fu, W.J.; Wu, Y.L. Fluctuations and Correlations of Conserved Charges near the QCD Critical Point. Phys. Rev. D 2010, 82, 074013. [Google Scholar] [CrossRef]
- Lu, Y.; Du, Y.; Cui, Z.F.; Zong, H.S. Critical behaviors near the (tri-)critical end point of QCD within the NJL model. Eur. Phys. J. C 2015, 75, 495. [Google Scholar] [CrossRef]
- Chen, J.W.; Deng, J.; Kohyama, H.; Labun, L. Robust characteristics of nongaussian fluctuations from the NJL model. Phys. Rev. D 2016, 93, 034037. [Google Scholar] [CrossRef]
- Fan, W.; Luo, X.; Zong, H.S. Mapping the QCD phase diagram with susceptibilities of conserved charges within Nambu–Jona-Lasinio model. Int. J. Mod. Phys. A 2017, 32, 1750061. [Google Scholar] [CrossRef]
- Fan, W.; Luo, X.; Zong, H. Probing the QCD phase structure with higher order baryon number susceptibilities within the NJL model. Chin. Phys. C 2019, 43, 033103. [Google Scholar] [CrossRef]
- Li, Z.; Xu, K.; Wang, X.; Huang, M. The kurtosis of net baryon number fluctuations from a realistic Polyakov–Nambu–Jona-Lasinio model along the experimental freeze-out line. Eur. Phys. J. C 2019, 79, 245. [Google Scholar] [CrossRef]
- Yang, L.K.; Luo, X.; Zong, H.S. QCD phase diagram in chiral imbalance with self-consistent mean field approximation. Phys. Rev. D 2019, 100, 094012. [Google Scholar] [CrossRef]
- Friman, B.; Karsch, F.; Redlich, K.; Skokov, V. Fluctuations as probe of the QCD phase transition and freeze-out in heavy-ion collisions at LHC and RHIC. Eur. Phys. J. C 2011, 71, 1694. [Google Scholar] [CrossRef]
- Fu, W.J.; Pawlowski, J.M.; Rennecke, F.; Schaefer, B.J. Baryon number fluctuations at finite temperature and density. Phys. Rev. D 2016, 94, 116020. [Google Scholar] [CrossRef]
- Fu, W.J.; Pawlowski, J.M.; Rennecke, F. The QCD phase structure at finite temperature and density. arXiv 2019, arXiv:1909.02991. [Google Scholar] [CrossRef]
- Fischer, C.S.; Luecker, J. Propagators and phase structure of Nf=2 and Nf=2+1 QCD. Phys. Lett. B 2013, 718, 1036. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y.L.; Jiang, Y.; Cui, Z.F.; Zong, H.S. Locate QCD Critical End Point in a Continuum Model Study. JHEP 2014, 1407, 14. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Y.X. QCD phase transitions via a refined truncation of Dyson-Schwinger equations. Phys. Rev. D 2016, 94, 076009. [Google Scholar] [CrossRef]
- Fischer, C.S. QCD at finite temperature and chemical potential from Dyson–Schwinger equations. Prog. Part. Nucl. Phys. 2019, 105, 1. [Google Scholar] [CrossRef]
- Herold, C.; Nahrgang, M.; Yan, Y.; Kobdaj, C. Dynamical net-proton fluctuations near a QCD critical point. Phys. Rev. C 2016, 93, 021902. [Google Scholar] [CrossRef]
- Chen, J.W.; Deng, J.; Labun, L. Baryon susceptibilities, non-Gaussian moments, and the QCD critical point. Phys. Rev. D 2015, 92, 054019. [Google Scholar] [CrossRef]
- Vovchenko, V.; Anchishkin, D.V.; Gorenstein, M.I.; Poberezhnyuk, R.V. Scaled variance, skewness, and kurtosis near the critical point of nuclear matter. Phys. Rev. C 2015, 92, 054901. [Google Scholar] [CrossRef]
- Jiang, L.; Li, P.; Song, H. Correlated fluctuations near the QCD critical point. Phys. Rev. C 2016, 94, 024918. [Google Scholar] [CrossRef]
- Mukherjee, A.; Steinheimer, J.; Schramm, S. Higher-order baryon number susceptibilities: Interplay between the chiral and the nuclear liquid-gas transitions. Phys. Rev. C 2017, 96, 025205. [Google Scholar] [CrossRef]
- Zhang, H.; Hou, D.; Kojo, T.; Qin, B. Functional renormalization group study of the quark-meson model with ω meson. Phys. Rev. D 2017, 96, 114029. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S.; Kodama, T. Finite-size effects and signatures of the QCD critical endpoint. J. Phys. G 2010, 37, 094031. [Google Scholar] [CrossRef]
- Fraga, E.S.; Palhares, L.F.; Sorensen, P. Finite-size scaling as a tool in the search for the QCD critical point in heavy ion data. Phys. Rev. C 2011, 84, 011903. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, Z.F.; Chang, C.H.; Zong, H.S. Finite-volume effects on phase transition in the Polyakov-loop extended Nambu–Jona-Lasinio model with a chiral chemical potential. Int. J. Mod. Phys. A 2017, 32, 1750067. [Google Scholar] [CrossRef]
- Mukherjee, S.; Venugopalan, R.; Yin, Y. Universal off-equilibrium scaling of critical cumulants in the QCD phase diagram. Phys. Rev. Lett. 2016, 117, 222301. [Google Scholar] [CrossRef]
- Bluhm, M.; Nahrgang, M.; Kalweit, A.; Arslandok, M.; Braun-Munzinger, P.; Floerchinger, S.; Fraga, E.; Gazdzicki, M.; Hartnack, C.; Herold, C.; et al. Dynamics of critical fluctuations: Theory – phenomenology – heavy-ion collisions. arXiv 2020, arXiv:2001.08831. [Google Scholar]
- Wu, S.; Wu, Z.; Song, H. Universal scaling of the σ field and net-protons from Langevin dynamics of model A. Phys. Rev. C 2019, 99, 064902. [Google Scholar] [CrossRef]
- Nahrgang, M.; Bluhm, M.; Schaefer, T.; Bass, S. Diffusive dynamics of critical fluctuations near the QCD critical point. Phys. Rev. D 2019, 99, 116015. [Google Scholar] [CrossRef]
- Asakawa, M.; Kitazawa, M.; Müller, B. Note on Search for Critical Point in QCD with Relativistic Heavy Ion Collisions. arXiv 2019, arXiv:1912.05840. [Google Scholar]
- Ohnishi, Y.; Kitazawa, M.; Asakawa, M. Thermal blurring of event-by-event fluctuations generated by rapidity conversion. Phys. Rev. C 2016, 94, 044905. [Google Scholar] [CrossRef]
- Stephanov, M.; Yin, Y. Hydrodynamics with parametric slowing down and fluctuations near the critical point. Phys. Rev. D 2018, 98, 036006. [Google Scholar] [CrossRef]
- Rajagopal, K.; Ridgway, G.; Weller, R.; Yin, Y. Hydro+ in Action: Understanding the Out-of-Equilibrium Dynamics Near a Critical Point in the QCD Phase Diagram. arXiv 2019, arXiv:1908.08539. [Google Scholar]
- An, X.; Basar, G.; Stephanov, M.; Yee, H.U. Fluctuation dynamics in a relativistic fluid with a critical point. arXiv 2019, arXiv:1912.13456. [Google Scholar]
- Mohanty, B. (National Institute of Science Education and Research, Odisha, India). Private Communications, 2019.
- Bzdak, A.; Koch, V.; Oliinychenko, D.; Steinheimer, J. Large proton cumulants from the superposition of ordinary multiplicity distributions. Phys. Rev. C 2018, 98, 054901. [Google Scholar] [CrossRef]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.; Alekseev, I.; Alford, J.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Balewski, J.; Barnby, L.; et al. Higher Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2010, 105, 022302. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.; Aparin, A.; Arkhipkin, D.; et al. Energy Dependence of Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2014, 112, 032302. [Google Scholar] [CrossRef]
- Luo, X. Energy Dependence of Moments of Net-Proton and Net-Charge Multiplicity Distributions at STAR. PoS CPOD 2015, 2014, 19. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Anderson, D.; Aoyama, R.; et al. Collision-energy dependence of second-order off-diagonal and diagonal cumulants of net-charge, net-proton, and net-kaon multiplicity distributions in Au + Au collisions. Phys. Rev. C 2019, 100, 014902. [Google Scholar] [CrossRef]
- Luo, X. Exploring the QCD Phase Structure with Beam Energy Scan in Heavy-ion Collisions. Nucl. Phys. A 2016, 956, 75. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Anderson, D.; Aparin, A.; et al. Net-proton number fluctuations and the Quantum Chromodynamics critical point. arXiv 2020, arXiv:2001.02852. [Google Scholar]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.; Aparin, A.; Arkhipkin, D.; et al. Beam energy dependence of moments of the net-charge multiplicity distributions in Au+Au collisions at RHIC. Phys. Rev. Lett. 2014, 113, 092301. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; et al. Collision Energy Dependence of Moments of Net-Kaon Multiplicity Distributions at RHIC. Phys. Lett. B 2018, 785, 551. [Google Scholar] [CrossRef]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.; Alekseev, I.; Alford, J.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Balewski, J.; Barnby, L.; et al. An Experimental Exploration of the QCD Phase Diagram: The Search for the Critical Point and the Onset of De-confinement. arXiv 2010, arXiv:1007.2613. [Google Scholar]
- Luo, X.; Xu, J.; Mohanty, B.; Xu, N. Volume fluctuation and auto-correlation effects in the moment analysis of net-proton multiplicity distributions in heavy-ion collisions. J. Phys. G 2013, 40, 105104. [Google Scholar] [CrossRef]
- Chatterjee, A.; Zhang, Y.; Zeng, J.; Sahoo, N.R.; Luo, X. Centrality selection effect on higher order cumulants of net-proton multiplicity distributions in relativistic heavy-ion collisions. Phys. Rev. C 2020, 101, 034902. [Google Scholar] [CrossRef]
- Bzdak, A.; Koch, V. Local Efficiency Corrections to Higher Order Cumulants. Phys. Rev. C 2015, 91, 027901. [Google Scholar] [CrossRef]
- Luo, X. Unified description of efficiency correction and error estimation for moments of conserved quantities in heavy-ion collisions. Phys. Rev. C 2015, 91, 034907, Erratum: [Phys. Rev. C 2016, 94, 059901]. [Google Scholar] [CrossRef]
- Kitazawa, M. Efficient formulas for efficiency correction of cumulants. Phys. Rev. C 2016, 93, 044911. [Google Scholar] [CrossRef]
- Nonaka, T.; Kitazawa, M.; Esumi, S. More efficient formulas for efficiency correction of cumulants and effect of using averaged efficiency. Phys. Rev. C 2017, 95, 064912. [Google Scholar] [CrossRef]
- Luo, X.; Nonaka, T. Efficiency correction for cumulants of multiplicity distributions based on track-by-track efficiency. Phys. Rev. C 2019, 99, 044917. [Google Scholar] [CrossRef]
- Luo, X. Error Estimation for Moments Analysis in Heavy Ion Collision Experiment. J. Phys. G 2012, 39, 025008. [Google Scholar] [CrossRef]
- Thäder, J. Higher Moments of Net-Particle Multiplicity Distributions. Nucl. Phys. A 2016, 956, 320. [Google Scholar] [CrossRef]
- Xu, J.; Yu, S.; Liu, F.; Luo, X. Cumulants of net-proton, net-kaon, and net-charge multiplicity distributions in Au + Au collisions at = 7.7, 11.5, 19.6, 27, 39, 62.4, and 200 GeV within the UrQMD model. Phys. Rev. C 2016, 94, 024901. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, J.; Luo, X.; Liu, F. Cumulants of event-by-event net-strangeness distributions in Au+Au collisions at = 7.7–200 GeV from UrQMD model. Phys. Rev. C 2017, 96, 014909. [Google Scholar] [CrossRef]
- Bzdak, A.; Koch, V.; Skokov, V. Baryon number conservation and the cumulants of the net proton distribution. Phys. Rev. C 2013, 87, 014901. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Rustamov, A.; Stachel, J. Bridging the gap between event-by-event fluctuation measurements and theory predictions in relativistic nuclear collisions. Nucl. Phys. A 2017, 960, 114. [Google Scholar] [CrossRef]
- He, S.; Luo, X.; Nara, Y.; Esumi, S.; Xu, N. Effects of Nuclear Potential on the Cumulants of Net-Proton and Net-Baryon Multiplicity Distributions in Au+Au Collisions at =5 GeV. Phys. Lett. B 2016, 762, 296. [Google Scholar] [CrossRef]
- He, S.; Luo, X. Proton Cumulants and Correlation Functions in Au + Au Collisions at = 7.7–200 GeV from UrQMD Model. Phys. Lett. B 2017, 774, 623. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Liu, H.; Yang, Z.; Luo, X. Effects of resonance weak decays and hadronic re-scattering on the proton number fluctuations in Au + Au collisions at =5 GeV from JAM model. Phys. Rev. C 2020, 101, 034909. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Al-Ta’ani, H.; Angerami, A.; et al. Measurement of higher cumulants of net-charge multiplicity distributions in Au+Au collisions at = 7.7–200 GeV. Phys. Rev. C 2016, 93, 011901. [Google Scholar] [CrossRef]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.; Biernat, J.; Blanco, A.; Blume, C.; Bohmer, M.; et al. Proton number fluctuations in = 2.4 GeV Au+Au collisions studies with HADES. arXiv 2020, arXiv:2002.08701. [Google Scholar]
- STAR Note 0598: BES-II. white paper. Available online: http://drupal.star.bnl.gov/STAR/starnotes/public/sn0598 (accessed on 28 February 2020).
- Ablyazimov, T.; Abuhoza, A.; Adak, R.; Adamczyk, M.; Agarwal, K.; Aggarwal, M.; Ahammed, Z.; Ahmad, F.; Ahmad, N.; Ahmad, S.; et al. Challenges in QCD matter physics –The scientific programme of the Compressed Baryonic Matter experiment at FAIR. Eur. Phys. J. A 2017, 53, 60. [Google Scholar] [CrossRef]
- NICA white paper. Available online: http://nica.jinr.ru/files/WhitePaper.pdf (accessed on 28 February 2020).
- Sun, K.J.; Chen, L.W.; Ko, C.M.; Pu, J.; Xu, Z. Light nuclei production as a probe of the QCD phase diagram. Phys. Lett. B 2018, 781, 499. [Google Scholar] [CrossRef]
- Yu, N.; Zhang, D.; Luo, X. Search for the QCD Critical Point by Transverse Velocity Dependence of Anti-deuteron to Deuteron Ratio. Chin. Phys. C 2020, 44, 014002. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; He, S.; Yu, N.; Luo, X. Light Nuclei Production in Au+Au Collisions at = 5–200 GeV from JAM model. arXiv 2019, arXiv:1909.09304. [Google Scholar]
- Zhang, D. Energy Dependence of Light Nuclei (d, t) Production at STAR. arXiv 2019, arXiv:1909.07028. [Google Scholar]
- Zhang, D. Light Nuclei (d, t) Production in Au + Au Collisions at = 7.7–200 GeV. arXiv 2020, arXiv:2002.10677. [Google Scholar]
- Eidelman, S.; Hayes, K.G.; Olive, K.E.; Aguilar-Benitez, M.; Amsler, C.; Asner, D.; Babu, K.S.; Barnett, R.M.; Beringer, J.; Burchat, P.R.; et al. Review of Particle Physics. Phys. Lett. B 2004, 592, 1. [Google Scholar] [CrossRef]
- Zhu, X.; Bleicher, M.; Huang, S.; Schweda, K.; Stocker, H.; Xu, N.; Zhuang, P. D correlations as a sensitive probe for thermalization in high energy nuclear collisions. Phys. Lett. B 2007, 647, 366. [Google Scholar] [CrossRef]
- Cacciari, M.; Nason, P.; Vogt, R. QCD predictions for charm and bottom production at RHIC. Phys. Rev. Lett. 2005, 95, 122001. [Google Scholar] [CrossRef] [PubMed]
- Vogt, R. The Total charm cross-section. Eur. Phys. J. ST 2008, 155, 213–222. [Google Scholar] [CrossRef]
- Abelev, B.; Abrahantes, A.; Adamova, D.; Adare, A.; Aggarwal, M.; Aglieri, G.; Agocs, A.; Agostinelli, A.; Aguilar, S.; Ahammed, Z.; et al. Measurement of charm production at central rapidity in proton-proton collisions at = 7 TeV. JHEP 2012, 2012, 128. [Google Scholar] [CrossRef]
- Acosta, D.; Affolder, T.; Ahn, M.; Akimoto, T.; Albrow, M.; Ambrose, D.; Amidei, D.; Anastassov, A.; Anikeev, K.; Annovi, A.; et al. Measurement of prompt charm meson production cross sections in p collisions at = 1.96 TeV. Phys. Rev. Lett. 2003, 91, 241804. [Google Scholar] [CrossRef]
- Adamczyk, L.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alakhverdyants, A.; Alekseev, I.; Alford, J.; Anderson, B.; Anson, C.; Arkhipkin, D.; et al. Measurements of D0 and D∗ production in p + p collisions at = 200 GeV. Phys. Rev. D 2011, 86, 072013. [Google Scholar] [CrossRef]
- Ye, Z. Open charm hadron production in p + p, Au + Au and U + U collisions at STAR. Nucl. Phys. A 2014, 931, 520–524. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adam, J.; Adamczyk, L.; Adams, J.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; et al. Observation of D0 meson nuclear modifications in Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2018, 121, 229901. [Google Scholar] [CrossRef]
- Greco, V.; Ko, C.; Rapp, R. Quark coalescence for charmed mesons in ultrarelativistic heavy-ion collisions. Phys. Lett. B 2004, 595, 202. [Google Scholar] [CrossRef]
- Oh, Y.; Ko, C.; Lee, S.; Yasui, S. Heavy baryon/meson ratios in relativistic heavy-ion collisions. Phys. Rev. C 2009, 79, 044905. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, S.; Xu, N.; Zhuang, P. Sequential coalescence with charm conservation in high energy nuclear collisions. arXiv 2018, arXiv:1805.10858. [Google Scholar]
- Plumari, S.; Minissale, V.; Das, S.K.; Coci, G.; Greco, V. Charmed hadrons from coalescence plus fragmentation in relativistic nucleus-nucleus collisions at RHIC and LHC. Eur. Phys. J. C 2018, 78, 348. [Google Scholar] [CrossRef]
- He, M.; Fries, R.J.; Rapp, R. Ds-meson as quantitative probe of diffusion and hadronization in nuclear collisions. Phys. Rev. Lett. 2013, 110, 112301. [Google Scholar] [CrossRef]
- Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Alakhverdyants, A.; Alekseev, L.; Alford, J.; Anderson, B.; Anson, C.; Arkhipkin, D.; Averichev, G.; et al. Strangeness enhancement in Cu+Cu and Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2012, 108, 072301. [Google Scholar] [CrossRef] [PubMed]
- Abelev, B.; Aggarwal, M.; Ahammed, Z.; Anderson, B.; Arkhipkin, D.; Averichev, G.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.; et al. Identified baryon and meson distributions at large transverse momenta from Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2006, 97, 152301. [Google Scholar] [CrossRef] [PubMed]
- Skands, P.; Carrazza, S.; Rojo, J. Tuning PYTHIA 8.1: The Monash 2013 Tune. Eur. Phys. J. C 2014, 74, 3024. [Google Scholar] [CrossRef]
- Bierlich, C.; Christiansen, J.R. Effects of color reconnection on hadron flavor observables. Phys. Rev. D 2015, 92, 094010. [Google Scholar] [CrossRef]
- Wheaton, S.; Cleymans, J.; Hauer, M. THERMUS: A Thermal model package for ROOT. Comput. Phys. Commun. 2009, 180, 84. [Google Scholar] [CrossRef]
- Adcox, K.; Adler, S.; Ajitanand, N.; Akiba, Y.; Alexander, J.; Aphecetche, L.; Arai, Y.; Aronson, S.; Averbeck, R.; Awes, T.; et al. Measurement of single electrons and implications for charm production in Au+Au collisions at = 130 GeV. Phys. Rev. Lett. 2002, 88, 192303. [Google Scholar] [CrossRef]
- Frixione, S.; Mangano, M.L.; Nason, P.; Ridolfi, G. Heavy quark production. Adv. Ser. Direct. High Energy Phys. 1998, 15, 609–706. [Google Scholar]
- Adamczyk, L.; Adkins, J.; Agakishiev, G.; Aggarwal, M.; Ahammed, Z.; Ajitanand, N.; Alekseev, I.; Anderson, D.; Aoyama, R.; Aparin, A.; et al. Elliptic flow of electrons from heavy-flavor hadron decays in Au + Au collisions at = 200, 62.4, and 39 GeV. Phys. Rev. C 2017, 95, 034907. [Google Scholar] [CrossRef]
- Si, F.; Chen, X.; Zhou, L.; Zhang, Y.; Zhang, S.; Ju, X.; Li, X.; Dong, X.; Xu, N. Charm and beauty isolation from heavy flavor decay electrons in Au+Au collisions at = 200 GeV at RHIC. arXiv 2019, arXiv:1906.08974. [Google Scholar]
- Xie, G. Measurements of open charm hadron production in Au+Au Collisions at = 200 GeV at STAR. PoS HardProbes2018 2018, 142. [Google Scholar]
- Sjöstrand, T.; Mrenna, S.; Skands, P. PYTHIA 6.4 Physics and Manual. JHEP 2006, 605, 26. [Google Scholar] [CrossRef]
- Tavernier, S.P.K. Charmed and bottom flavored particle production in hadronic interactions. Rep. Prog. Phys. 1987, 50, 1439–1489. [Google Scholar] [CrossRef]
- Bamberger, A.; Binon, F.; Bricman, C.; Bruning, H.; Duteil, P.; Gouanere, M.; Hartung, R.; Jansen, J.; Lagnaux, J.; Massas, G.; et al. J/psi production by 24 GeV/c protons. Nucl. Phys. B 1978, 134, 1. [Google Scholar] [CrossRef]
- Corden, M.J.; Dowell, J.; Garvey, J.; Homer, R.; Jobes, M.; Kenyon, I.; McMahon, T.; Owen, R.; Sumorok, K.; Vallance, R.; et al. Experimental results on J/ψ production by π±, K±, p and p¯ incident on hydrogen at 39.5 GeV/c. Phys. Lett. B 1981, 98, 220. [Google Scholar] [CrossRef]
- Antipov, Y.M.; Bessubov, V.; Budanov, N.; Bushnin, Y.; Denisov, S.; Gorin, Y.; Lebedev, A.; Lednev, A.; Mikhailov, Y.; Petrukhin, A.; et al. J/ψ particle production by 70 GeV/c protons. Phys. Lett. B 1976, 60, 309. [Google Scholar] [CrossRef]
- Snyder, H.D.; Hom, D.; Lederman, L.; Paar, H.; Weiss, J.; Yoh, J.; Appel, J.; Brown, B.; Brown, C.; Innes, W.; et al. Production of Ψ(3100) and Ψ′(3700) in p-Be collisions at 400 GeV. Phys. Rev. Lett. 1976, 36, 1415. [Google Scholar] [CrossRef]
- Anderson, K.J.; Henry, G.; McDonald, K.; Pilcher, J.; Rosenberg, E.; Branson, J.; Sanders, G.; Smith, A.; Thaler, J. Production of muon pairs by 150 GeV/cπ+ and protons. Phys. Rev. Lett. 1976, 36, 237. [Google Scholar] [CrossRef]
- Anderson, K.J.; Coleman, B.; Hogan, G.; Karhi, H.; McDonald, K.; Newman, C.; Pilcher, J.; Rosenberg, E.; Sanders, G.; Smith, A.; et al. Production of muon pairs by 225 GeV π±, K±, p± beams on nuclear targets. Phys. Rev. Lett. 1979, 42, 944. [Google Scholar] [CrossRef]
- Siskind, E.J.; Barish, B.; Bartlett, J.; Bodek, A.; Merritt, F.; Shaevitz, M.; Diamant-Berger, A.; Dishaw, J.; Faessler, M.; Liu, J.; et al. Production of Ψ(3100) in 400 GeV/c proton interactions. Phys. Rev. D 1980, 21, 628. [Google Scholar] [CrossRef]
- Gribushin, A.; Abramov, V.; Antipov, Y.; Baldin, B.; Crittenden, R.; Davis, C.; Dauwe, L.; Denisov, S.; Dyshkant, A.; Dzierba, A.; et al. Production of J/ψ mesons in p-Be collisions at 530 GeV/c and 800 GeV/c. Phys. Rev. D 2000, 62, 012001. [Google Scholar] [CrossRef]
- Antoniazzi, L.; Arenton, M.; Cao, Z.; Chen, T.; Conetti, S.; Cox, B.; Delchamps, S.; Fortney, L.; Guffey, K.; Haire, M.; et al. A measurement of J/ψ and ψ′ production in 300 GeV/c proton, anti-proton and π± nucleon interactions. Phys. Rev. D 1992, 46, 4828. [Google Scholar] [CrossRef]
- Alexopoulos, T.; Antoniazzi, L.; Arenton, M.; Ballagh, H.; Bingham, H.; Blankman, A.; Block, M.; Boden, A.; Bonomi, G.; Cao, Z.; et al. Differential cross-sections of J/ψ and ψ′ in 800 GeV/cp-Si interactions. Phys. Rev. D 1997, 55, 3927. [Google Scholar] [CrossRef]
- Schub, M.H.; Jansen, D.; Mishra, C.; Ho, P.; Brown, C.; Carey, T.; Chen, Y.; Childers, R.; Cooper, W.; Darden, C.; et al. Measurement of J/ψ and ψ′ production in 800 GeV/c proton-gold collisions. Phys. Rev. D 1995, 52, 1307. [Google Scholar] [CrossRef] [PubMed]
- Badier, J.; Boucrot, J.; Bourotte, J.; Burgun, G.; Callot, O.; Charpentier, P.; Crozon, M.; Decamp, D.; Delpierre, P.; Gandois, B.; et al. Experimental J/ψ hadronic production from 150 GeV/c to 280 GeV/c. Z. Phys. C 1983, 20, 101. [Google Scholar]
- Abreu, M.C.; Baglin, C.; Baldit, A.; Bedjidian, M.; Bordalo, P.; Bussiere, A.; Busson, P.; Castor, J.; Chambon, T.; Charlot, C.; et al. Charmonia production in 450 GeV/c proton induced reactions. Phys. Lett. B 1998, 444, 516. [Google Scholar] [CrossRef]
- Alessandro, B.; Alexa, C.; Arnaldi, R.; Atayan, M.; Baglin, C.; Baldit, A.; Beole, S.; Boldea, V.; Bordalo, P.; Borenstein, S.; et al. Charmonium production and nuclear absorption in p-A interactions at 450 GeV. Eur. Phys. J. C 2004, 33, 31. [Google Scholar]
- Abreu, M.C.; Alessandro, B.; Baldit, A.; Barriere, C.; Bedjidian, M.; Bordalo, P.; Castor, J.; Chambon, T.; Chaurand, B.; Chiavassa, E.; et al. J/ψ and ψ′ and Drell-Yan production in pp and pd interactions at 450 GeV/c. Phys. Lett. B 1998, 438, 35. [Google Scholar] [CrossRef]
- Morel, C.; Bernasconi, A.; Breedon, R.; Camilleri, L.; Cool, R.; Cox, P.; Cushman, P.; Dick, L.; Dukes, E.; Gabioud, B.; et al. Measurement of the inclusive J/ψ production cross-sections in p and pp collisions at = 24.3 GeV. Phys. Lett. B 1990, 252, 505. [Google Scholar] [CrossRef]
- Abt, I.; Adams, M.; Agari, M.; Albrecht, H.; Aleksandrov, A.; Amaral, V.; Amorim, A.; Aplin, S.; Aushev, V.; Bagaturia, Y.; et al. Measurement of the J/ψ production cross section in 920 GeV/c fixed-target proton-nucleus interactions. Phys. Lett. B 2006, 638, 407. [Google Scholar] [CrossRef][Green Version]
- Nagy, E.; Regler, M.; Schmidt-Parzefall, W.; Schubert, K.; Winter, K.; Brandt, A.; Dibon, H.; Flugge, G.; Niebergall, F.; Schumacher, P.; et al. Observation of high mass μ+μ- pairs at the ISR. Phys. Lett. B 1975, 60, 96. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.; Averbeck, R.; et al. J/ψ production from proton proton collisions at = 200 GeV. Phys. Rev. Lett. 2004, 92, 051802. [Google Scholar] [CrossRef] [PubMed]
- Maltoni, F.; Spengler, J.; Bargiotti, M.; Bertin, A.; Bruschi, M.; Castro, S.; Fabbri, L.; Faccioli, P.; Giacobbe, B.; Grimaldi, F.; et al. Analysis of charmonium production at fixed-target experiments in the NRQCD approach. Phys. Lett. B 2006, 638, 202–208. [Google Scholar] [CrossRef]
- Vogt, R. Phenomenology of charm and bottom production. Z. Phys. C 1996, 71, 475–481. [Google Scholar] [CrossRef][Green Version]
- Nonaka, T. Measurement of the Sixth-Order Cumulant of Net-Particle Distributions in Au+Au Collisions from the STAR Experiment. In Proceedings of the QM2019, Wuhan, China, 4–9 November 2019. [Google Scholar]
- Pandav, A. Measurement of cumulants of conserved charge multiplicity distributions in Au+Au collisions from the STAR experiment. In Proceedings of the QM2019, Wuhan, China, 4–9 November 2019. [Google Scholar]
- Geraksiev, N.S. The Nuclotron-based Ion Collider Facility Project. The Physics Programme for the Multi-Purpose Detector. J. Phys. Conf. Ser. 2019, 1390, 012121. [Google Scholar] [CrossRef]
- Cassing, W.; Bratkovskaya, E.; Sibirtsev, A. Open charm production in relativistic nucleus-nucleus collisions. Nucl. Phys. A 2001, 691, 753. [Google Scholar] [CrossRef]
- Available online: https://www.gsi.de/work/forschung/cbmnqm/cbm.htm (accessed on 28 February 2020).
- STAR Endcap TOF Proposal. Available online: https://drupal.star.bnl.gov/STAR/starnotes/public/sn0665 (accessed on 28 February 2020).
- STAR iTPC upgrade Proposal. Available online: https://drupal.star.bnl.gov/STAR/starnotes/public/sn0644 (accessed on 28 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).