Dense Baryonic Matter and Applications of QCD Phase Diagram Dualities

Abstract

Recently it has been found that quantum chromodynamics (QCD) phase diagram possesses a duality between chiral symmetry breaking and pion condensation. For the first time this was revealed in the QCD motivated toy model. Then it was demonstrated in effective models as well and new additional dualities being found. We briefly recap the main features of this story and then discuss its applications as a tool to explore the QCD phase structure. The most appealing application is the possibility of getting the results on the QCD phase diagram at large baryon density. Taking the idea from large $1/N_c$ universalities it was argued that the scenario of circumventing the sign problem with the help of dualities seems plausible. It is also discussed that there is a persistent problem about whether there should be catalysis or anti-catalysis of chiral symmetry breaking by chiral imbalance. One can probably say that the issue is settled after lattice results (first principle approach), where the catalysis was observed. But they used an unphysically large pion mass so it is still interesting to get additional indications that this is the case. It is shown just by the duality property that there exists catalysis of chiral symmetry breaking. So, having in mind our results and the earlier lattice simulations, one can probably claim that this issue is settled. It is demonstrated that the duality can be used to obtain new results. As an example, it is showcased how the phase structure of dense quark matter with chiral imbalance (with possibility of inhomogeneous phases) can be obtained from the knowledge of a QCD phase diagram with isopin asymmetry.

1. Introduction

It is believed now that the dynamics of mesons and baryons should be described by the quantum chromodynamics (QCD), non-Abelian gauge theory of quarks and gluons. The ultimate goal of QCD studies is to understand all the hadronic phenomena at the level of quarks and gluons. For very high energy processes, where the perturbation theory works, this paradigm has been very successful, for example, describing the deep inelastic scattering (DIS) of leptons and hadrons. The situation is different at low energies (of the order of low lying hadron masses (1 GeV)), where one needs non-perturbative description and analytic study is very complicated. Although QCD has been a central point of the high energy physics community from its inception, it remains one of the main topics today. Not only because it is still impossible to truly understand the mechanism of confinement and non-perturbative physics but also because of the increasing interest in the studies of QCD phase structure in extreme conditions.

One can easily think about at least two important external parameters for QCD in equilibrium, namely temperature T and baryon chemical potential ${\mu }_B$ (conjugated to baryon density $n_B$). Now let us try to guess the orders of magnitude of temperature and density that could cause interesting phenomena. Recall now that the intrinsic energy scale of QCD is ${\mathsf{\Lambda }}_{QCD}\sim 200$ MeV (the energy at which coupling constant blows up). So one can expect that the phase transition of thermal QCD should take place around the temperature $T\sim {\mathsf{\Lambda }}_{QCD}$ around 200 MeV (that is not that far from lattice simulation results) and a phase transition of dense QCD should happen at a baryon density of the order of $n_B\sim {\mathsf{\Lambda }}_{QCD}^3\sim 1$ fm⁻³.

Finite baryon density QCD has piqued huge interest in nuclear physics, high energy physics and even astrophysics. It is excepted that QCD has a very rich phase structure in (T, $\mu$) parameter space [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], and there are several heavy-ion collision experiments such as NICA, FAIR, RHIC (BES II), J-PARC, HIAF that will elucidate the properties of dense QCD matter in the near future. Especially awaited is the NICA (Nuclotron-based Ion Collider fAility) complex that is now under construction at the Joint Institute for Nuclear Research (Dubna, Russia) [19].

But it is not hard to believe that temperature and baryon density are not the only relevant parameters in various physical setups. These physical settings, for example, could be systems with a large isospin imbalance [1,20,21,22]. Consider, for instance, the initial state of heavy-ion collisions, the initial ions have twice as many neutrons as protons and this can be important in collisions of not that high energy. Moreover, neutron star matter is characterized by even larger isospin imbalance (it consists of mostly neutrons and the fraction of protons is rather small). More unexpected is the fact that, although it is believed that baryon density in the early Universe is typically small, a large lepton asymmetry (poorly constrained by observations) might lead to a large isospin imbalance [23].

There is another new interesting field of novel transport phenomena, so-called anomalous transport phenomena, that has caused a lot of excitement in the community. Heavy-ion collision experiments have exhibited intriguing hints of possible signals but due to background effects the situation is still unclear. One of the central players in this field is the so-called chiral imbalance $n_5$ (the difference between densities of right-handed and left-handed quarks) or the corresponding chiral chemical potential ${\mu }_5$. It is believed that the chiral imbalance can be created at high temperatures in the heavy-ion collisions due to the Adler-Bell-Jackiw anomaly and nontrivial gluon field configurations. Moreover, in strong magnetic field or under rotation, due to the so-called chiral separation [24] or chiral vortical [25] effects, chiral density can be produced in dense quark matter [26,27,28]. Chiral imbalance can also be generated in parallel electric and magnetic fields [29,30,31]. Moreover, there is another type of chiral imbalance, when chiral densities of u and d quarks are different, it is called chiral isospin imbalance $n_{I5}$. It can be shown that chiral isospin imbalance can be produced in magnetized or rotating dense quark matter [26]. Moreover, in parallel electric and magnetic fields chiral isospin imbalance can be generated as well. Let us also note that in the context of a QCD phase diagram, the formal inclusion of chiral isospin imbalance is more rigorous than the chiral one. There are a lot of studies on chiral imbalanced QCD [32,33,34,35,36,37,38,39,40,41,42].

In this letter we discuss the dualities of QCD phase structure and its possible uses and applications to the process of unraveling the puzzles of QCD phase diagram including the region of large baryon densities. First, the duality between chiral symmetry breaking (CSB) and charged pion condensation (PC) phenomena is considered in terms of QCD related toy models, namely the NJL₂ model, where it has been found for the first time. Then it is shown that duality holds in the framework of effective model for QCD that bolster our confidence that it can be valid in real QCD. It is also shown that the duality remains valid if one considers the phase diagram with all four possible imbalances, baryon density, isospin, chiral isospin and chiral imbalance (first, it was shown only for the first three of them). It can be considered as another indication that it is not a coincidence and there is something behind it. After that it is argued in the framework of effective model that there exist other dualities of phase structure not as strong as the main one but also rather interesting.

Then comes the main part of the paper; the discussion on how and where the dualities can be used and be helpful in understanding the phase structure of QCD.

(i)

First, there is a brief overview of dualities similar to ours (universalities) obtained in the so-called large $1/N_c$ orbifold equivalence principle. Then the idea of the possibility of circumventing the sign problem has been expanded to our dualities and it is argued that it is a feasible scenario.

(ii)

It is shown that a problem of catalysis or anti-catalysis of chiral symmetry breaking by chiral imbalance can be resolved just by duality and the rather well-established knowledge of pion condensation properties at isospin density.

(iii)

It is shown that the duality can be used to produce new results and new phase diagrams (different sections of the phase diagram). As an example, it is showcased how, from the phase structure of dense quark matter with non-zero isospin density (including the possibility of inhomogeneous condensates (phases)), one can obtain, based on the duality only, the phase structure of dense quark matter with chiral imbalance.

In this way, from the different regions studied in a number of works, whether one can assemble the whole picture of the phase structure of QCD at finite baryon and isospin density including inhomogeneous phases was explored.

Most of the studies in this paper are performed in the framework of the effective NJL model. It is one of the most widely used effective models for QCD, where one can explore the phase structure at non-zero baryon density. A lot of different phenomena have been successfully studied in this approach. Despite all that, the NJL model has a number of limitations and drawbacks, there are no gluons in the consideration and it is not confining, but this can be partially improved by including interaction with constant background gluon field and considering the Polyakov loop as an order parameter for deconfinement (the s- called PNJL model). Also, often the considerations are performed in the mean field approximation (ignoring the meson fluctuations). In this mean field approach one struggles to explain various phenomena. For example, the behaviour of chiral condensate is flat at its origin (it weakly depends on temperature). This behavior is drastically different from what is obtained from ChPT [43]. One can obtain the right low-temperature parabolic behaviour of chiral condensate only if one includes into consideration the meson loops (go beyond the mean field) [44]. In the simplest version of the NJL model in the mean field one also gets the wrong prediction for the influence of magnetic field on the chiral phase transition. It is shown on the lattice that there should be an inverse magnetic catalysis (IMC) effect [45], that is, it is found from all the observables that the pseudo-critical temperature decreases significantly with the increase of magnetic field. Mean field NJL consideration predicts the magnetic catalysis (MC) (increase of pseudo-critical temperature). The correct behaviour can be obtained only if one phenomenologically extends the model to include the dependence of the NJL model interaction coupling on the magnetic field [46,47,48] (it should decrease with the magnetic field and mimic the expected running of the coupling with the strength of the magnetic field). In this approach, one can obtain MC at low and high temperatures and IMC around the critical temperature. These results can also be obtained in the NJL model beyond mean field approximation [49], where meson contribution lead to the dependence of effective coupling on both the magnetic field and the temperature. Having all these remarks in mind one can see that, despite all the successes of the mean field NJL model, it has many limitations and one should always remember this.

Let us briefly overview the content of the paper and what is covered in each section. Section 1 outlines the introduction and the purpose of this paper. In Section 2 the Gross-Neveu model and its different extensions, including the NJL₂ model, are discussed. Section 3 contains the discussion of quark matter with non-zero baryon density, isospin, chiral and chiral isospin imbalances and corresponding charges. The phase structure and its duality in the framework of the (1+1)-dimensional QCD related toy model are discussed in Section 3.1. Then, in Section 3.2 duality is shown to be valid in the framework of the effective model. Section 3.3 contains the proof that the duality remains valid even if we include chiral imbalance (in addition to chiral isospin one) in the system. In Section 3.4 it is shown that there are other dualities. In Section 4 it is demonstrated how duality can be used and how it can help us study the phase structure of QCD at finite densities.

2. (1+1)-Dimensional Models: The GN Model and Its Extensions

In order to understand the phase structure of matter at finite temperature and baryon density, it is necessary to comprehend the non-perturbative vacuum of QCD and its properties. As has been pointed out, QCD is hard to deal with, which is why one can try to study the phase structure in a similar but simpler and hence tractable model (QCD related toy models).

2.1. GN Model

The Gross-Neveu (GN) model is a model with four-fermion interaction that consists of only a single quark flavour [50,51,52]. It is remarkable that it can be solved analytically in the limit of an infinite number of quark colours $N_c$. Interest in this model from the particle physics side stems from the fact that it in many respects resembles QCD. For example, it exhibits a lot of similar inherent features to QCD such as renormalizability, asymptotic freedom, dynamical chiral symmetry breaking (in vacuum) and its restoration (at finite temperatures), dimensional transmutation, and meson and baryon bound states [53]. In addition, the ${\mu }_B-T$ phase diagram is qualitatively the same.

Probably an even more unexpected fact is that (1+1)-dimensional GN type models have exhibited great success in the description of a variety of quasi-one-dimensional condensed matter systems [53,54,55,56,57], for example, polyacetylene [53,54] or similar models can be used in the description of planar systems [58,59,60,61], carbon nanotubes and fullerenes [62,63,64].

The Lagrangian of the GN model has the form

$$\begin{array}{c}L=\mathrm{i}\overline{q}{\gamma }^{\nu }{\partial }_{\nu }q+\frac{G}{N_c}{\left(\overline{q}q\right)}^2,\hfill \end{array}$$

(1)

where the quark field $q\left(x\right)\equiv q_{i\alpha }\left(x\right)$ is a colour $N_c$-plet ($\alpha =1,\dots ,N_c$) as well as a two-component Dirac spinor (the summation in (1) over color, and spinor indices is implied). The Dirac ${\gamma }^{\nu }$-matrices ($\nu =0,1$) and ${\gamma }^5$ in (1) are matrices in two-dimensional spinor space,

$$\begin{array}{c}\hfill {\gamma }^0=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right);{\gamma }^1=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right);{\gamma }^5={\gamma }^0{\gamma }^1=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).\end{array}$$

(2)

2.2. Chiral GN Model ($\chi$GN)

A straightforward extension of the GN model (1) can be obtained by adding to the Lagrangian a pseudo-scalar term [65,66]. It is called a chiral GN ($\chi$GN) model and its Lagrangian would take the following form

$$\begin{array}{c}L=\mathrm{i}\overline{q}{\gamma }^{\nu }{\partial }_{\nu }q+\frac{G}{N_c}\left[{\left(\overline{q}q\right)}^2+{\left(\mathrm{i}\overline{q}{\gamma }^{5}q\right)}^2\right],\hfill \end{array}$$

(3)

It can be shown that it is invariant under continuous chiral symmetry transformations $U_A\left(1\right)$: $\psi \to e^{i{\gamma }^5\theta }\psi$. There are also certain similarities between this model and one-flavour QCD, if one excludes the chiral anomaly from consideration.

2.3. NJL₂ Model

Let us even further generalize the GN model by considering, in addition to scalar channel, pion- like field combinations [67,68,69,70,71]. The Lagrangian of this so-called (1+1)-dimensional Nambu-Jona-Lasinio model (NJL₂ model) is

$$\begin{array}{c}L=\mathrm{i}\overline{q}{\gamma }^{\nu }{\partial }_{\nu }q+\frac{G}{N_c}\left({\left(\overline{q}q\right)}^2+{\left(\overline{q}\mathrm{i}{\gamma }^5\overrightarrow{\tau }q\right)}^2\right),\hfill \end{array}$$

(4)

In addition to all the similarities with QCD that were discussed for the GN model, this model can describe the interactions of pions and is similar to two-flavour QCD. We consider this model in order to mimic the phase structure of real dense quark matter with two massless quark flavors (u and d quarks). Below the phase diagram of dense quark matter with isospin and chiral isospin imbalance will be studied in the framework of this model.

3. Dense Quark Matter with Isospin and Chiral Imbalance

If one wants to describe quark matter with non-zero baryon (quark) density one needs to add to the Lagrangian the following term $\frac{{\mu }_B}{3}\overline{q}{\gamma }^{0}q$. So ${\mu }_B$ is baryon chemical potential which leads to the settings to describe the matter with a non-zero difference between number of baryons and anti-baryons. Sometimes different quantities and quark chemical potential $\mu =\frac{{\mu }_B}{3}$ are used, which describe the non-zero difference between number of quarks and anti-quarks. If in addition, one has the isospin imbalance in the system, that is, a different number of protons and neutrons (or equivalently u quarks and d quarks) one needs to add to the Lagrangian the following term $\frac{{\mu }_I}{2}\overline{q}{\tau }_3{\gamma }^{0}q$. The more exotic opportunity that will be considered in the following is chiral imbalance, the difference between left-handed and right-handed quarks in the system. In order to describe it one needs to add to the Lagrangian the following term ${\mu }_5\overline{q}{\gamma }^0{\gamma }^{5}q$. There still another imbalance that will be considered below, namely chiral isospin imbalance ${\mu }_{I5}$, that accounts for the difference between chiral imbalances of different flavours (u and d quarks), $n_{I5}=n_5^u-n_5^d\ne 0$ and it is introduced as the following term $\frac{{\mu }_{I5}}{2}\overline{q}{\tau }_3{\gamma }^0{\gamma }^{5}q$ in the Lagrangian.

3.1. Dense Isospin Asymmetric Quark Matter with Non-Zero Chirality: Phase Diagram in QCD Related Model

Bearing in mind all that has been said in the above two sections now let us consider the phase diagram of dense (${\mu }_B\ne 0$) quark matter with non-zero isospin (${\mu }_I\ne 0$) and chiral isospin (${\mu }_{I5}\ne 0$) imbalance in the framework of the (1+1)-dimensional QCD related toy model, namely the NJL₂ model. Let us also stress that here the chiral imbalance ${\mu }_5$ of the system is considered to be zero, so the Lagrangian in this case has the following form

$$\begin{array}{c}L=\overline{q}\left[{\gamma }^{\nu }\mathrm{i}{\partial }_{\nu }+\frac{{\mu }_B}{3}{\gamma }^0+\frac{{\mu }_I}{2}{\tau }_3{\gamma }^0+\frac{{\mu }_{I5}}{2}{\tau }_3{\gamma }^0{\gamma }^5\right]q+\frac{G}{N_c}\left[{\left(\overline{q}q\right)}^2+{\left(\overline{q}\mathrm{i}{\gamma }^5\overrightarrow{\tau }q\right)}^2\right].\hfill \end{array}$$

(5)

As said above, all these parameters (${\mu }_B,{\mu }_I,{\mu }_{I5}$) are introduced in order to investigate in the framework of the model quark matter with nonzero baryon $n_B$, isospin $n_I$ and axial isospin $n_{I5}$ densities, respectively.

It is evident that at zero ${\mu }_B={\mu }_I={\mu }_{I5}=0$ the Lagrangian is invariant with respect to $SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U_B\left(1\right)$ group. If one introduce non-zero ${\mu }_B\ne 0$ into the system the symmetries remain the same. But if we include non-zero isospin imbalance ${\mu }_I\ne 0$ then the symmetry of the model is $U_B\left(1\right)\times U_{I_3}\left(1\right)\times U_{A{I}_3}\left(1\right)$, where $U_{I_3}\left(1\right):q\to exp(\mathrm{i}\beta {\tau }_3/2)q$ and $U_{A{I}_3}\left(1\right):q\to exp(\mathrm{i}\omega {\gamma }^5{\tau }_3/2)q$.

If in addition, one introduces non-zero ${\mu }_{I5}$ then the symmetry group will not change.

So the quark bilinears $\frac{1}{3}\overline{q}{\gamma }^{0}q$, $\frac{1}{2}\overline{q}{\gamma }^0{\tau }^{3}q$ and $\frac{1}{2}\overline{q}{\gamma }^0{\gamma }^5{\tau }^{3}q$ are the zero components of corresponding to these groups conserved currents and their ground state expectation values are just the baryon, isospin and chiral isospin densities, that is, $n_B=\frac{1}{3}\langle \overline{q}{\gamma }^{0}q\rangle$, $n_I=\frac{1}{2}\langle \overline{q}{\gamma }^0{\tau }^{3}q\rangle$ and $n_{I5}=\frac{1}{2}\langle \overline{q}{\gamma }^0{\gamma }^5{\tau }^{3}q\rangle$. As usual, the quantities $n_B$, $n_I$ and $n_{I5}$ can also be found by differentiating the thermodynamic potential of the system with respect to the corresponding chemical potentials. For brevity we will use the following notations $\mu \equiv {\mu }_B/3$, $\nu \equiv {\mu }_I/2$ and ${\nu }_5\equiv {\mu }_{I5}/2$.

In order to find the thermodynamic potential of the system, it is more convenient to use a semi-bosonized version of the Lagrangian, which contains composite bosonic fields $\sigma \left(x\right)$ and ${\pi }_a\left(x\right)$$(a=1,2,3)$

$$\begin{array}{ccc}\hfill \tilde{L}& =& \overline{q}\left[{\gamma }^{\rho }\mathrm{i}{\partial }_{\rho }+\mu {\gamma }^0+\nu {\tau }_3{\gamma }^0+{\nu }_5{\tau }_3{\gamma }^0{\gamma }^5-\sigma -\mathrm{i}{\gamma }^5{\pi }_a{\tau }_a\right]q-\frac{N_c}{4G}\left[\sigma \sigma +{\pi }_a{\pi }_a\right].\hfill \end{array}$$

(6)

From the Lagrangian (6) one can get the Euler–Lagrange equations of the bosonic fields

$$\begin{array}{c}\hfill \sigma \left(x\right)=-2\frac{G}{N_c}\left(\overline{q}q\right);{\pi }_a\left(x\right)=-2\frac{G}{N_c}\left(\overline{q}\mathrm{i}{\gamma }^5{\tau }_{a}q\right).\end{array}$$

(7)

The composite bosonic field ${\pi }_3\left(x\right)$ can be identified with the physical ${\pi }_0$ meson, whereas the ${\pi }^{\pm }\left(x\right)$- meson fields with the following combinations of the composite fields, ${\pi }^{\pm }\left(x\right)=({\pi }_1\left(x\right)\mp i{\pi }_2\left(x\right))/\sqrt{2}$. In general, the phase structure is characterized by the behaviour of so-called order parameters (or condensates) with respect to external parameters such as temperature, chemical potentials, and so forth. In our case such order parameters are the ground state expectation values of the composite fields, $\langle \sigma \left(x\right)\rangle$ and $\langle {\pi }_a\left(x\right)\rangle$$(a=1,2,3)$.

If $M=\langle \sigma \left(x\right)\rangle \ne 0$ (or $\langle {\pi }_3\left(x\right)\rangle \ne 0$), then the axial isospin $U_{A{I}_3}\left(1\right)$ symmetry (remnant of chiral symmetry at non-zero ${\mu }_I$ and ${\mu }_{I5}$) is dynamically broken down and

$$U_B\left(1\right)\times U_{I_3}\left(1\right)\times U_{A{I}_3}\left(1\right)\to U_B\left(1\right)\times U_{I_3}\left(1\right).$$

Whereas if $\Delta =\langle {\pi }_1\left(x\right)\rangle \ne 0$ (or $\langle {\pi }_2\left(x\right)\rangle \ne 0$) we have a spontaneous breaking of the isospin symmetry $U_{I_3}\left(1\right)$ and

$$U_B\left(1\right)\times U_{I_3}\left(1\right)\times U_{A{I}_3}\left(1\right)\to U_B\left(1\right)\times U_{A{I}_3}\left(1\right).$$

Since in this case condensates of the fields ${\pi }^{+}\left(x\right)$ and ${\pi }^{-}\left(x\right)$ are not zero, this phase is usually called the charged pion condensation (PC) phase.

Starting from the linearized semi-bosonized model Lagrangian (6), one can obtain in the leading order of the large $N_c$-expansion (i.e., in the one-fermion loop approximation) the thermodynamic potential (TDP) $\mathsf{\Omega }(M,\Delta )$ of the system:

$$\begin{array}{c}\hfill \mathsf{\Omega }(M,\Delta )\equiv -\frac{{\mathcal{S}}_{\mathrm{eff}}(\sigma ,{\pi }_a)}{N_c\int d^{2}x}{|}_{\{\sigma ,{\pi }_1,{\pi }_2,{\pi }_3\}=\{M,\Delta ,0,0\}}=\frac{M^2+{\Delta }^2}{4G}+\mathrm{i}\int \frac{d^{2}p}{{\left(2\pi \right)}^2}ln{P}_4\left(p_0\right),\end{array}$$

(8)

where $P_4\left(p_0\right)={\eta }^4-2a{\eta }^2-b\eta +c$, $\eta =p_0+\mu$ and

$$\begin{array}{ccc}\hfill a& =& M^2+{\Delta }^2+p_1^2+{\nu }^2+{\nu }_5^2;b=8p_1\nu {\nu }_5;\hfill \\ \hfill c& =& a^2-4p_1^2({\nu }^2+{\nu }_5^2)-4M^2{\nu }^2-4{\Delta }^2{\nu }_5^2-4{\nu }^2{\nu }_5^2.\hfill \end{array}$$

(9)

One can see that the TDP is invariant with respect to the so-called duality transformation

$$\begin{array}{c}\hfill \mathcal{D}:M⟷\Delta ,\nu ⟷{\nu }_5.\end{array}$$

(10)

The duality tells us that we can simultaneously exchange chiral condensate and charged pion condensate and isospin and chiral imbalances and the results do not change. This means that chiral symmetry breaking phenomenon in the system with isospin (chiral) imbalance is the same as (equivalent to) charged pion condensation phenomenon in the system with chiral (isospin) imbalance. It is an interesting property of the phase structure of the toy model and possibly of real QCD.

It is clear from (8) that the effective potential is an ultraviolet (UV) divergent, so we need to renormalize it. This procedure can be found in References [68,69,70,71] and it is shown that it does not concern the duality property, which can be seen already at the level of unrenormalized TDP. The phase structure of the model is considered in detail in Reference [68,70,71].

3.2. Dense Isospin Asymmetric Quark Matter with Non-Zero Chirality: Effective Model Consideration

In the previous section it was shown in the framework of the NJL₂ model that there is a duality between chiral symmetry breaking and pion condensation phenomena. Although the NJL₂ model has a lot of features in common with QCD and one can probably argue that the duality is one of them, the NJL₂ model is not real QCD and one cannot guarantee that all the properties that it has can be transformed to QCD. So it is interesting to try to check whether there is a duality in effective models for QCD. At least they are (3+1) dimensional and they have many more connections with QCD.

Here in this section the same situation, that is, the quark matter with isospin and chiral isospin imbalance, has been considered in the framework of a more realistic effective model for QCD, namely the Nambu–Jona-Lasinio model. Its Lagrangian has the similar form

$$\begin{array}{c}L=\overline{q}\left[{\gamma }^{\nu }\mathrm{i}{\partial }_{\nu }+\frac{{\mu }_B}{3}{\gamma }^0+\frac{{\mu }_I}{2}{\tau }_3{\gamma }^0+\frac{{\mu }_{I5}}{2}{\tau }_3{\gamma }^0{\gamma }^5\right]q+\frac{G}{N_c}\left[{\left(\overline{q}q\right)}^2+{\left(\overline{q}\mathrm{i}{\gamma }^5\overrightarrow{\tau }q\right)}^2\right],\hfill \end{array}$$

(11)

where, in contrast to the (1+1)-dimensional case, the flavor doublet, $q={(q_u,q_d)}^T$, ($q_u$ and $q_d$ u and d quark fields) are four-component Dirac spinors (also color $N_c$-plets) and the gamma matrices are normal, familiar (3+1)-dimensional ones.

One can also use the semi-bosonized Lagrangian and the technique similar to that which was used above and to obtain the TDP of the model in this case. After a rather long but straightforward calculations one can show that in this case the TDP of the model reads

$$\begin{array}{c}\hfill \mathsf{\Omega }(M,\Delta )=\frac{M^2+{\Delta }^2}{4G}+\mathrm{i}\int \frac{d^{4}p}{{\left(2\pi \right)}^4}{P}_{-}\left(p_0\right)P_{+}\left(p_0\right),\end{array}$$

(12)

where $P_{-}\left(p_0\right)P_{+}\left(p_0\right)\equiv \left({\eta }^4-2a{\eta }^2-b\eta +c\right)\left({\eta }^4-2a{\eta }^2+b\eta +c\right)$ and $\eta =p_0+\mu$, $|\overrightarrow{p}|=\sqrt{p_1^2+p_2^2+p_3^2}$. We also used the same notations for $a,b$ and c just with a substitution $p_1\to \left|\overrightarrow{p}\right|$

$$\begin{array}{cc}\hfill a& =M^2+{\Delta }^2+|\overrightarrow{p}{|}^2+{\nu }^2+{\nu }_5^2;b=8\left|\overrightarrow{p}\right|\nu {\nu }_5;\hfill \\ \hfill c& =a^2-4{\left|\overrightarrow{p}\right|}^2({\nu }^2+{\nu }_5^2)-4M^2{\nu }^2-4{\Delta }^2{\nu }_5^2-4{\nu }^2{\nu }_5^2.\hfill \end{array}$$

(13)

One can see in a similar way that the duality (10) takes place in this case as well, meaning it can be found even in the more realistic effective model for QCD. So one can conclude that the duality is probably the property of the phase structure of real QCD.

The phase structure of the model (11) is discussed in [72].

3.3. Inclusion of ${\mu }_5$ Chiral Imbalance and the Consideration of the General Case

The duality property of the phase structure of quark matter was shown in the case of non-zero baryon density and isospin imbalance of the system as well as chiral isospin imbalance. But it is not obvious in any sense that this property holds in other situations and is universal. For example, there are a lot of studies (see Reference [73] and references therein) discussing the possibility of generation of chiral imbalance ${\mu }_5$ (in reality much more than the discussions on the generation of ${\mu }_{I5}$) and it is interesting to investigate whether the duality also holds for the general case of the phase structure of quark matter with all four chemical potentials (baryon density and three imbalances—isospin, chiral and chiral isospin). If the duality is valid for the phase structure of this general system then it is probably more deep quality of the phase structure.

Let us try to consider this situation in the framework of an effective model for QCD (NJL model), which Lagrangian has the form

$$\begin{array}{c}L=\overline{q}\left[{\gamma }^{\nu }\mathrm{i}{\partial }_{\nu }+\frac{{\mu }_B}{3}{\gamma }^0+\frac{{\mu }_I}{2}{\tau }_3{\gamma }^0+{\mu }_5{\gamma }^0{\gamma }^5+\frac{{\mu }_{I5}}{2}{\tau }_3{\gamma }^0{\gamma }^5\right]q+\frac{G}{N_c}\left[{\left(\overline{q}q\right)}^2+{\left(\overline{q}\mathrm{i}{\gamma }^5\overrightarrow{\tau }q\right)}^2\right].\hfill \end{array}$$

(14)

It is almost the same Lagrangian as (1) but containing the chiral chemical potential ${\mu }_5$ accounting for the chiral imbalance $n_5$.

One can obtain the TDP of the system in this rather general case and it was shown to have the form

$$\begin{array}{c}\hfill \mathsf{\Omega }(M,\Delta )=\frac{M^2+{\Delta }^2}{4G}+\mathrm{i}\int \frac{d^{4}p}{{\left(2\pi \right)}^4}{P}_{-}\left(p_0\right)P_{+}\left(p_0\right),\end{array}$$

(15)

where $P_{+}\left(\eta \right)P_{-}\left(\eta \right)\equiv \left({\eta }^4-2a_{+}{\eta }^2+b_{+}\eta +c_{+}\right)\left({\eta }^4-2a_{-}{\eta }^2+b_{-}\eta +c_{-}\right)$ and

$$\begin{array}{cc}\hfill a_{\pm }& =M^2+{\Delta }^2+\left(\right|\overrightarrow{p}|\pm {\mu }_5{)}^2+{\nu }^2+{\nu }_5^2;b_{\pm }=\pm 8\left(\right|\overrightarrow{p}|\pm {\mu }_5)\nu {\nu }_5;\hfill \\ \hfill c_{\pm }& =a_{\pm }^2-4{\nu }^2\left(M^2+\left(\right|\overrightarrow{p}{|\pm {\mu }_5)}^2\right)-4{\nu }_5^2\left({\Delta }^2+\left(\right|\overrightarrow{p}{|\pm {\mu }_5)}^2\right)-4{\nu }^2{\nu }_5^2.\hfill \end{array}$$

(16)

One can see that the duality property $\mathcal{D}:M⟷\Delta ,\nu ⟷{\nu }_5$ stays the same in this case of non-zero chiral imbalance (non-zero ${\mu }_5\ne 0$) as well. So the duality is the property of the phase structure of dense quark matter with isospin, chiral and chiral isospin imbalances (in the rather general case one can imagine) at least in terms of effective model.

3.4. Other Dualities

One can also note that there are more dualities aside from the one we have already mentioned. Although they are not as strong as the original one described above they are still pretty interesting and useful. These new dualities are valid only if there are some additional constraints, for example, there is no pion condensation in the system or chiral symmetry is restored. One should show additionally that these constraints are fulfilled dynamically in considered situation, for example, chiral symmetry is dynamically restored (high temperature or density).

Let us discuss it in more detail. One can show from Equations (15) and (16) that at the constraint $\Delta =0$ (if there is no charged pion condensation in the system)

$$\begin{array}{c}{P}_{+}\left(\eta \right)P_{-}\left(\eta \right){|}_{\Delta =0}=\left[M^2+\left(\right|\overrightarrow{p}{|+{\mu }_5+{\nu }_5)}^2-{(\eta +\nu )}^2\right]\left[M^2+\left(\right|\overrightarrow{p}{|+{\mu }_5-{\nu }_5)}^2-{(\eta -\nu )}^2\right]\hfill \\ \times \left[M^2+\left(\right|\overrightarrow{p}{|-{\mu }_5+{\nu }_5)}^2-{(\eta -\nu )}^2\right]\left[M^2+\left(\right|\overrightarrow{p}{|-{\mu }_5-{\nu }_5)}^2-{(\eta +\nu )}^2\right]\hfill \end{array}$$

(17)

and one can see that the TDP (15) in this case is invariant with respect to the following transformation

$$\begin{array}{c}\hfill {\mathcal{D}}_M:\Delta =0,{\mu }_5⟷{\nu }_5.\end{array}$$

(18)

This is another duality and it shows that chiral symmetry breaking phenomenon does not feel the difference between two types of chiral imbalance (chiral and chiral isospin imbalances).

Likewise, it is possible to demonstrate that the integrand in the expression for the TDP (15) with the constraint $M=0$ has the following form

$$\begin{array}{c}{P}_{+}\left(\eta \right)P_{-}\left(\eta \right){|}_{M=0}=\left[{\Delta }^2+\left(\right|\overrightarrow{p}{|+{\mu }_5+\nu )}^2-{(\eta +{\nu }_5)}^2\right]\left[{\Delta }^2+\left(\right|\overrightarrow{p}{|+{\mu }_5-\nu )}^2-{(\eta -{\nu }_5)}^2\right]\hfill \\ \times \left[{\Delta }^2+\left(\right|\overrightarrow{p}{|-{\mu }_5+\nu )}^2-{(\eta -{\nu }_5)}^2\right]\left[{\Delta }^2+\left(\right|\overrightarrow{p}{|-{\mu }_5-\nu )}^2-{(\eta +{\nu }_5)}^2\right].\hfill \end{array}$$

(19)

So at the constraint $M=0$ the TDP is invariant under the transformation

$$\begin{array}{c}\hfill {\mathcal{D}}_{\Delta }:M=0,{\mu }_5⟷\nu .\end{array}$$

(20)

That shows that charged pion condensation phenomenon is influenced in the same way by chiral and isospin imbalance. Systems with isospin and chiral imbalance are completely different systems and it is remarkable that some phenomena in these systems are entirely equivalent.

Additionally, one can notice that the dualities ${\mathcal{D}}_M$ and ${\mathcal{D}}_{\Delta }$ are themselves dual to each other with respect to the $\mathcal{D}$ duality (10). So one can conclude that there exists only one independent additional duality and one can get the other duality by making use of the main duality (10).

4. Use of Dualities

4.1. Circumventing the Sign Problem with Use of Dualities

One of the key open questions in the standard model of particle physics is the phase structure of QCD, especially at non-zero baryon density. However, the understanding of the properties of QCD phase diagram at finite baryon chemical potential is limited by the so-called sign problem. It consists of the fact that at ${\mu }_B\ne 0$ the fermion determinant is no longer real-valued and positive quantity and the conventional Monte-Carlo simulations are impossible in this case. There are a number of approaches to solve or at least alleviate the sign problem but it stands to this day in the way of obtaining the phase structure of dense matter from first principles. And it is quite likely that it will not be solved completely in the near future.

Here we will discuss a possibility to circumvent it in a way and possibly get some clues of phase structure at large baryon densities. It has been noticed that there is a whole class of gauge theories that have no sign problem even at nonzero baryon chemical potential and probably may resemble QCD ($SU\left(3\right)$ gauge theory). The examples include $SU\left(3\right)$ theory but with fermions in the adjoint representation, $SO\left(2N_c\right)$ gauge theory and $Sp\left(2N_c\right)$ gauge theory or two-colour QCD with even number of flavours $N_f$ (with the same mass). So one can study the properties of these theories not encountering the sign problem. But it is not clear how, if at all, these theories are connected with real QCD. Then it has been shown in References [74,75,76] by means of the orbifold equivalence technique that in the limit of large $N_c$ (large number of colours) the whole or at least part of the phase diagram of these theories are the same. This sameness of the phase structure is called universality. There exist pieces of evidence that this universality remains valid even for QCD with three-colour but only approximately [74,76]. These universalities are very similar to our dualities but they connect not only phase structure at different chemical potentials but also the phase structure of different gauge theories. If the gauge groups of two theories related by the universality are the same then they coincide with our dualities. For example, one of the universalities, namely the equivalence of phase structure of QCD at finite ${\mu }_5$ and at finite ${\mu }_I$ where the pion condensate and chiral condensate should be exchanged is very similar to the duality that can be obtained from our dualities for these cases.

It was also pointed out in References [74,76] that the universalities of phase structure can be used in circumventing the sign problem due to the fact that one gauge theory can be sign problem free. For example, universality can relate gauge theories with groups $G_1$ and $G_2$ at different chemical potentials ${\mu }_1$ and ${\mu }_2$, then assume that $G_1=SU\left(3\right)$ and and ${\mu }_1={\mu }_B$, so it is QCD at finite baryon density. If $G_2$ happens to be sign problem free (at non-zero ${\mu }_2$) theory then one can obtain the phase structure of QCD at ${\mu }_B$ by studying the $G_2$ gauge theory at ${\mu }_2$ using lattice simulations. The same idea can be applied to our dualities. For example, QCD at isospin chemical potential ${\mu }_I$ or QCD at chiral chemical potential ${\mu }_5$ has no sign problem. Phase structures of QCD at different chemical potentials are connected with each other by dualities and there are ideas that the dualities can concern also baryon chemical potential ${\mu }_B$ (connect ${\mu }_B$ with other chemical potentials). Here we only note that it is a viable option and the detailed discussion is left for the future.

Let us make another small remark here at the end of the section. As we have pointed out above there are hints that the universalities are also valid approximately for the case $N_c=3$. Let us note that some arguments (although, maybe not that strong) can be made from NJL model considerations. If the same (to the corresponding large $N_c$ equivalence) duality can be obtained in NJL model then one can conclude that it holds not only for large $N_c$ limit but in mean field approximation as well. In mean field approximation one can take $N_c=3$ (let us put aside the argument that mean field is a good approximation) and it supports the arguments that the duality (equivalence) is approximate in the case $N_c=3$.

4.2. Predicting the Catalysis of Chiral Symmetry Breaking

There have been a long debate if chiral symmetry breaking is enhanced by chiral imbalance, that is, there is catalysis of chiral symmetry breaking [40,75,77,78,79,80,81], or it is inhibited by chiral imbalance, that is, there is anti-catalysis of chiral symmetry breaking [37,38,39,40,82,83,84,85,86]. This question has been studied in a variety of approaches [37,38,39,40,75,77,78,79,80,81,82,83,84,85,86] and different studies came to opposite conclusions. One can say that the issue is settled after lattice simulations results [32,33,34,35], where it has been found that chiral imbalance catalyses chiral symmetry breaking in QCD. But they used unphysically large pion mass so it is still interesting to get additional indications that it is the case.

Let us discuss the possibility of using our considerations and dualities for establishing the catalysis of chiral symmetry breaking by chiral chemical potential. We have the main duality (10) connecting isospin chemical potential ${\mu }_I$ and chiral isospin chemical potential ${\mu }_{I5}$. But now we talk about the influence of chiral imbalance ${\mu }_5$ on QCD phase structure, not a chiral isospin one. Nevertheless, one can note that we have another duality (18). Using this duality one can argue that the effects of chiral isospin chemical potential ${\mu }_{I5}$ and chiral chemical potential ${\mu }_5$ on the phenomenon of chiral symmetry breaking are exactly the same. It can be objected that this duality holds only if there is no pion condensation phenomenon in the system and can be broken by pion condensate. However, one can show dynamically (at least in the framework of NJL model) that pions do not condense in the system with just chiral or chiral isospin imbalance and the condition of zero pion condensate holds in this case. So we can use the dualities (18), (10) and argue that $({\mu }_5,T)$ and $({\mu }_I/2,T)$ phase diagrams are dual to each other if one performs the transformation PC ↔ CSB. Thus one can use the duality to get the critical temperature of chiral symmetry breaking phase as a function of chiral chemical potential $T_c$(${\mu }_5$) from the phase structure at ${\mu }_I$. And the QCD phase structure at non-zero isospin imbalance is comparatively well-known [20,21,22,87,88,89] and one knows that the critical temperature of PC phase is an increasing function of isospin chemical potential at least to the values of several hundred MeV. One also knows that the duality is valid only in the chiral limit ($m_{\pi }=0$) and is a very good approximation but not exact in the physical point ($m_{\pi }\approx 140$ MeV) [26] (the duality is almost exact if $\nu >m_{\pi }/2$, at least from one hundred to several hundred MeV). So one can conclude using the duality and lattice QCD results at isospin imbalance that critical temperature of chiral symmetry breaking phase should be an increasing function of chiral chemical potential ${\mu }_5$. Meaning that the catalysis of chiral symmetry breaking takes place. One can also show that the chiral condensate increases with the chiral imbalance as well and it gets harder to melt it so the critical temperature increases. This is another example of the practical use of the duality and the physical results that can be obtained from it.

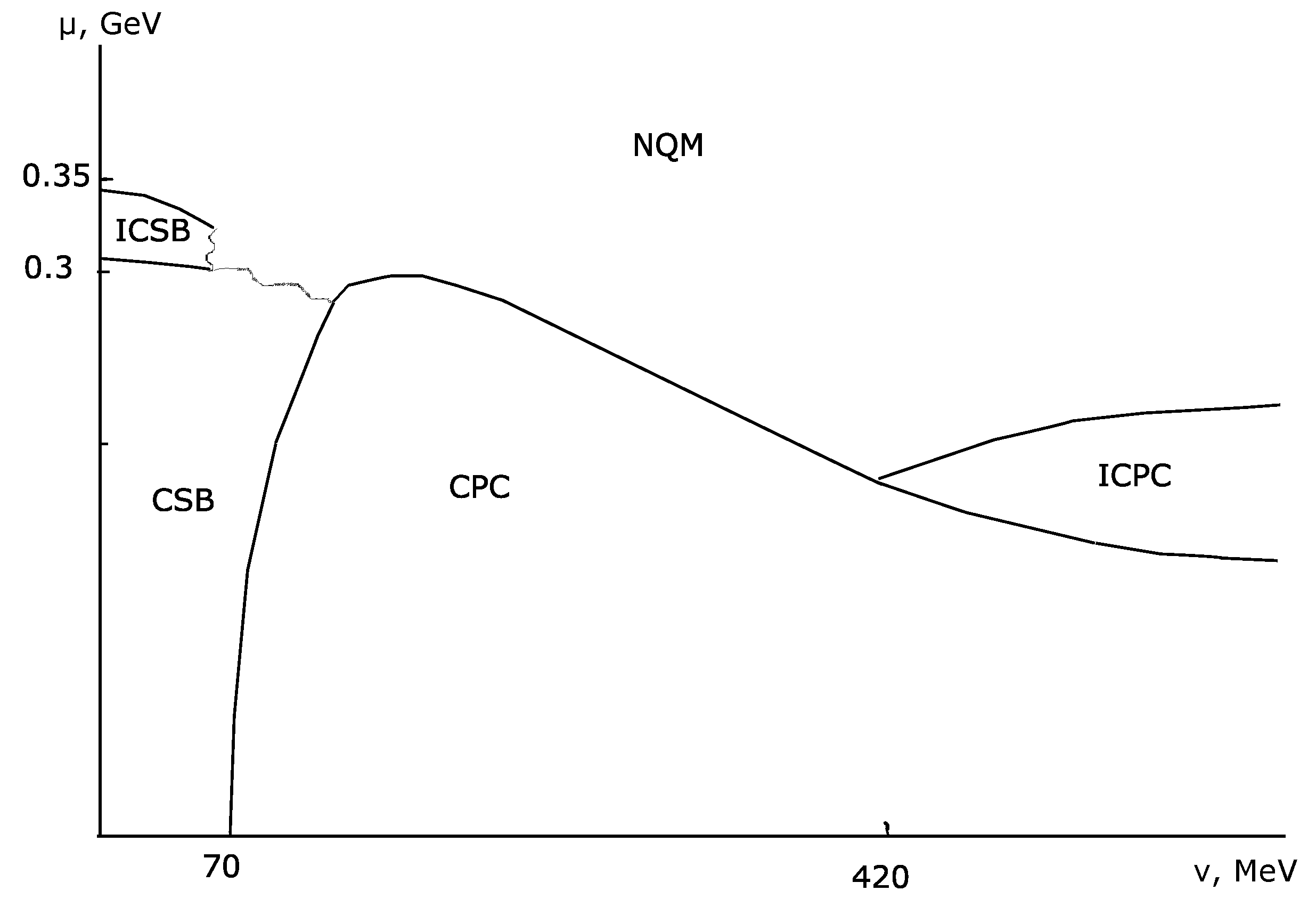
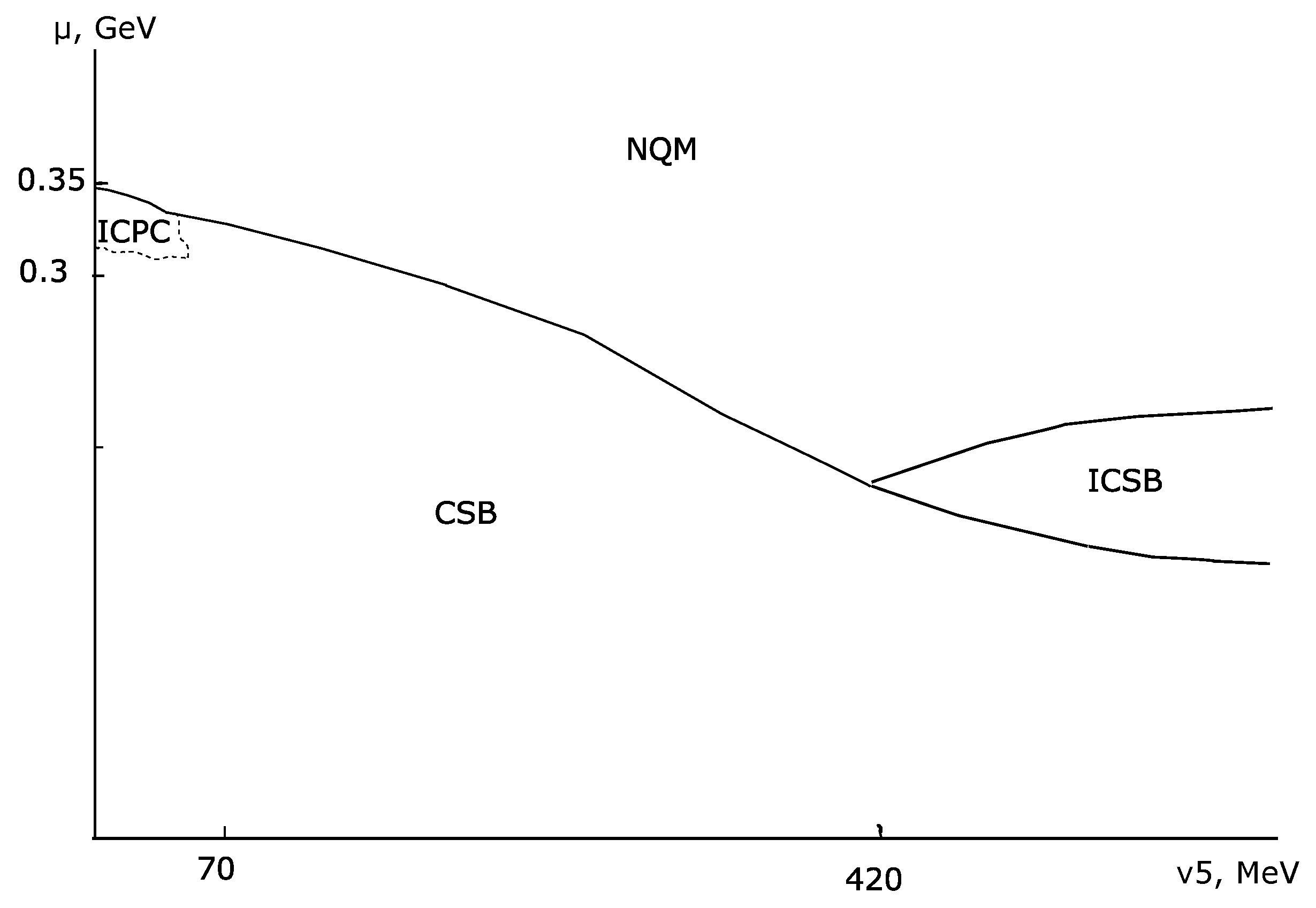
4.3. Generating the Phase Diagram without Any Calculations

Duality is an interesting property of the QCD phase structure in itself. But as has been shown in the previous sections one can also use it to get new results or even try to circumvent the sign problem. Here in this section we will add another example and show that it is possible to get the whole new phase diagram from duality only.

There are a number of strong arguments supported by model calculations that at large and intermediate densities in the QCD phase diagram there exist phases with spatially inhomogeneous condensates (order parameters) (see the reviews in References [90,91]).

The possible inhomogeneous phases in QCD phase structure at isospin imbalance have been studied in a number of papers. First, it was assumed that the pion condensate is homogeneous and only inhomogeneous chiral symmetry breaking phases are possible [92,93,94,95] and the QCD-phase diagram was obtained within NJL models, for example, in [92,93,94] (similar results was obtained in [95] in the quark- meson model).

It has been found that, at rather small values of isospin chemical potential $\nu ={\mu }_I/2$ ($\nu <60$ MeV) and for $\mu \gtrsim 300$ MeV, there might appear a region of inhomogeneous chiral symmetry breaking (ICSB) phase. The considerations were performed in the chiral limit for simplicity. But one can think that it is a good approximation because the case with zero isospin imbalance in physical point was considered in Reference [92] and it was shown that qualitative picture does not change with the non-zero current quark mass. With increase of the mass the region of the inhomogeneous phase only gets smaller in size. Probably the influence of quark mass stays qualitatively the same also in the case of non-zero isospin chemical potential.

Second, it was assumed in Reference [96] that chiral condensate is homogeneous and a spatially inhomogeneous charged pion condensation (ICPC) phase has been studied in the framework of NJL model. It was noted that inhomogeneous pion condensation phase is realized in the phase diagram at rather high isospin chemical potential $\nu \gtrsim 400$ MeV.

It is possible to connect these situations and obtain the full $(\nu ,\mu )$ phase diagram assuming the possibility of both inhomogeneous charged pion condensation and chiral symmetry breaking phases. It is possible due to the fact that the regions of inhomogeneous phases of different studies do not overlap at the phase diagram and the assumption that there is no mixed inhomogeneous phase. The latter assumption in principle can be lifted and what we can get is only a more rich picture of inhomogeneous phases. So one can envisage the full schematic $(\nu ,\mu )$-phase portrait of quark matter with baryon density and isospin imbalance, it is shown in Figure 1.

Now one can note that the phase diagram $(\nu ,\mu )$ that we have discussed above can be transformed by the main duality (10) to the phase diagram $({\nu }_5,\mu )$. And we get two phase diagrams $(\nu ,\mu )$ and $({\nu }_5,\mu )$ that are dual to each other. As was discussed above, the first one is more or less known at least in effective models but the latter is completely unexplored and one has no idea how it looks like. And by this dual transformation one can get completely yet not considered part of QCD phase diagram, namely, $({\nu }_5,\mu )$ phase diagram that is depicted in Figure 2. One can see that there is ICPC phase in the region corresponding to rather high values of $\mu$ and, probably, baryon density is non-zero in this region. It can also be noticed that there is ICSB phase at values of chemical potential $\mu$ around 200 MeV and rather large chiral isospin chemical potential ${\nu }_5$ (see Figure 2). Due to rather large chiral isospin chemical potential a part of this region might have non-zero baryon density. One can conclude that in inhomogeneous case phase diagram seems to be rather rich and (dense) quark matter with chiral isospin imbalance can have various inhomogeneous condensates, namely chiral or charged pion one.

The above has used the duality in inhomogeneous case but it is far from obvious that the duality is valid in this case as well. However, it has been demonstrated in Reference [97] that it is the case. It is rather nontrivial fact and it indicates that probably the duality is a more deep property of the QCD phase diagram. Let us also stress that the duality holds for the case of non-zero baryon density and it is, in particular, an interesting feature of dense quark matter.

Let us also note that at high baryon density a different phenomenon are expected to take place. At low temperatures and sufficiently large baryon chemical potential the colour interaction (in the color anti-symmetric channel) starts to favour the formation of non-zero diquark (quark-quark) condensate [98]. Due to the fact that this phenomenon breaks colour symmetry it is called colour superconductivity. There could be also interesting inhomogeneous structure of condensates [99,100]. Throughout this paper we neglect the possibility of colour superconductivity phase but it is also very interesting to study the dualities if it takes place. However, it is outside the scope of this paper and we leave it for the future.

5. Conclusions

The dualities of the QCD phase diagram, in particular, the duality between chiral symmetry breaking and pion condensation phenomena has been found in the framework of the (1+1)-dimensional QCD motivated toy model in Reference [68,69,70,71]. Then it was shown to exist in the framework of effective models in References [26,97,101,102,103,104,105].

In this paper we have endeavoured to show that the duality is not just an interesting mathematical fact in itself and an interesting feature intrinsic to the phase diagram of dense quark matter (that it surely is) but also a powerful tool that can be used to produce new results almost effortlessly. There are even ideas that it can help (not solve but circumvent) the sign problem (see Section 4.1). Moreover, it is known that there is a contradiction between the predictions of different studies of the influence of chiral imbalance on chiral symmetry breaking phenomenon. Some works predicted that there should be catalysis of chiral symmetry breaking, others that there is anti-catalysis. It is shown in the framework of duality that it is possible to, if not settle the issue completely, surely make a strong argument to favour the existence of catalysis of chiral symmetry breaking.

Another argument, an even more trustworthy one, is the lattice simulations [32,33,34,35] (first principle approach) that, however, performed not at physical pion mass, gives a decisive answer to this question. One can probably argue that our results, combined with the lattice simulations, can claim that there is not a lot of doubt that this effect indeed takes place. Then we showed that the duality can be used as a tool for plotting entirely new phase diagrams completely for free in terms of efforts. It is demonstrated by constructing the phase diagram of dense quark matter with chiral imbalance.

The basic features of the GN model and its extensions, including the question of why it might be interesting in the context of QCD, are summarised at the beginning of the paper. Then it is shown how to obtain the duality property with different approaches (including the above-mentioned toy model). After that, the picture with several additional dualities of dense quark matter has been discussed. Eventually, the possible applications of dualities have been considered.

Let us enlist the main applications of dualities that have been discussed in this paper.

• There has been discussed the possibility of circumventing the sign problem by constructing dualities between QCD phase diagrams with different chemical potentials.
• It is shown that a problem if there exists catalysis or anti-catalysis of chiral symmetry breaking by chiral imbalance, can be resolved just by duality property to the favour of catalysis. And bearing also in mind the lattice simulations results at unphysically large pion mass one can say that there is not much doubt that this issue is settled.
• The whole new phase diagram of dense quark matter with chiral imbalance with the possibility of different inhomogeneous phases has been obtained just by duality only and previously known results.

So the dualities can be used and can be very helpful in understanding the phase structure of QCD, including the large baryon density region.

Let us make another note on the possible applications of dualities in astrophysics. Dense matter with isospin imbalance can be easily found inside neutron stars. Chirality can be probably generated in heavy ion collisions, for example, due to strong electromagnetic fields (see introduction). It is demonstrated in this paper that (dense) matter with isospin imbalance is connected by duality with (dense) matter with chiral imbalance (chiral isospin chemical potential). So maybe one can think that using the main duality, phenomena in cores of neutron stars can be probed in the terrestrial heavy ion collision experiments. Besides, since in neutron stars the baryon density is rather high (huge) and main duality leave baryon density intact, one needs at the other side large baryon density in heavy ion collisions, which is possible only at not so high energy, for example, as at NICA complex or other projects discussed in the introduction. It is a rather interesting opportunity but there are a number of hindrances. For example, the conditions in this settings are different as in neutron stars there should be, for example, $\beta$-equilibrium condition. Also, since duality does not change temperature (let us note that it has been shown in Reference [26] that the duality is valid also in the case of non-zero or even high temperatures), at both sides of possibly connected by duality phenomena there should be similar temperatures. And even in the intermediate energy heavy ion collision experiments one talks about rather large temperatures that is not even closely realized in individual neutron stars (even in proto-neutron stars, where temperatures can reach 10 MeV, they are still smaller). But here one can think about recently observed mergers of neutron stars [106]. Since in neutron star mergers the temperature can reach values as high as 80 MeV [107,108] and they are not significantly different from the ones reached in intermediate energy heavy-ion collisions ($\beta$-equilibrium condition in this case is also slightly different from cold neutron star case [109]), it is a more plausible candidate to be mapped by duality to heavy ion collisions. Also let us note that supernova explosions, where temperatures can be rather high [110], and matter during the black hole formation from a gravitational collapse of a massive star, where temperatures could be even higher ($T\sim 90$ MeV [111] or even over 100 MeV [112]), are also viable for this role. If one assumes that all the above conditions are fulfilled, then the conditions dual to the ones during neutron star mergers can be realized and studied at intermediate energy heavy ion collision experiments such as NICA. It is also even more feasible to get interesting information by duality connecting baryon chemical potential (with the another one) that we talked about in Section 4.1, especially try to get information about equation of state from phase structure of QCD at non-zero isospin or chiral imbalances. It can be studied in the future.