Probes of Lepton Flavor Universality in b → u Transitions
Abstract
1. Introduction
2. Extended Effective Hamiltonian
3. and
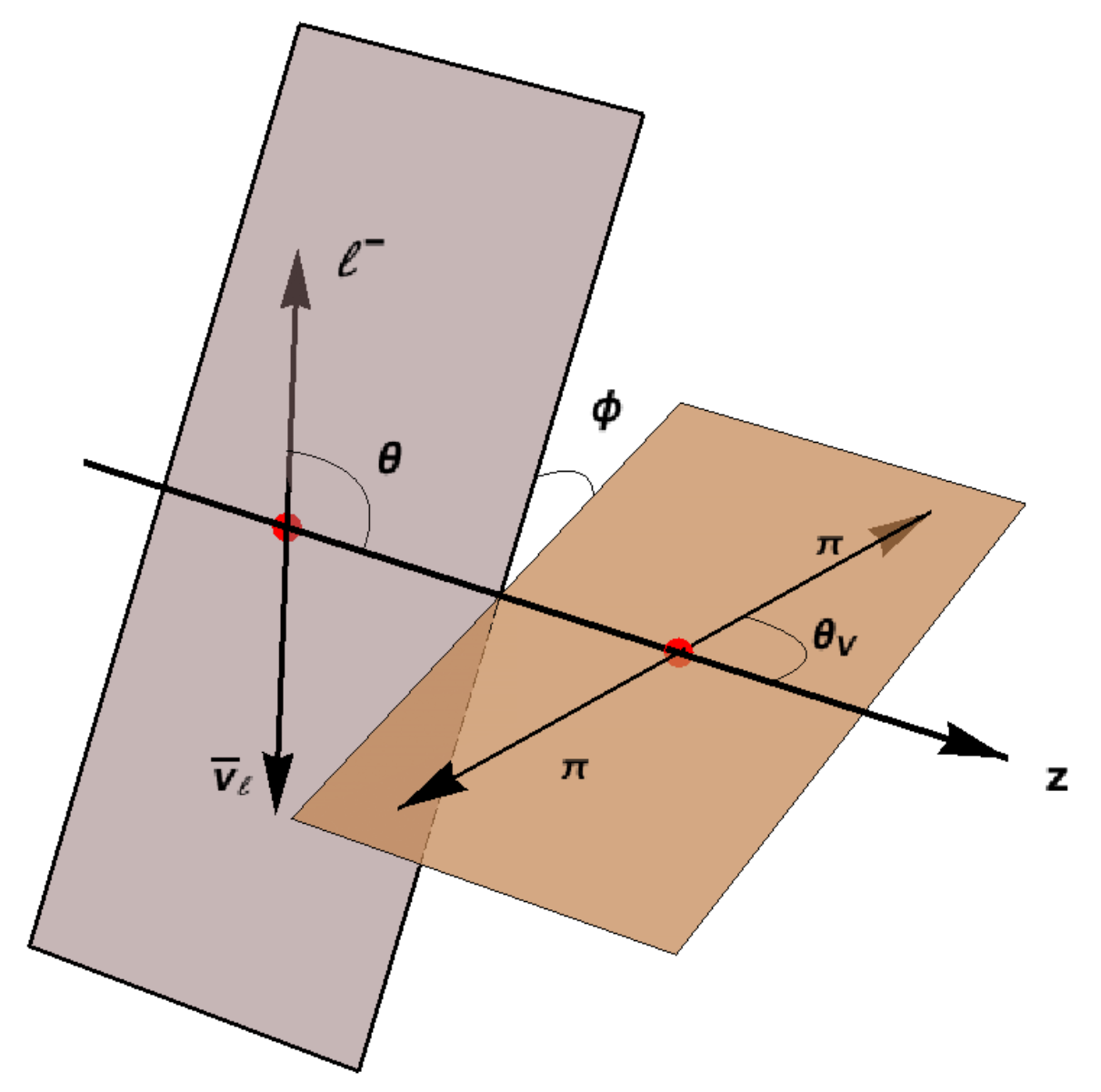
4. and Full Angular Distributions
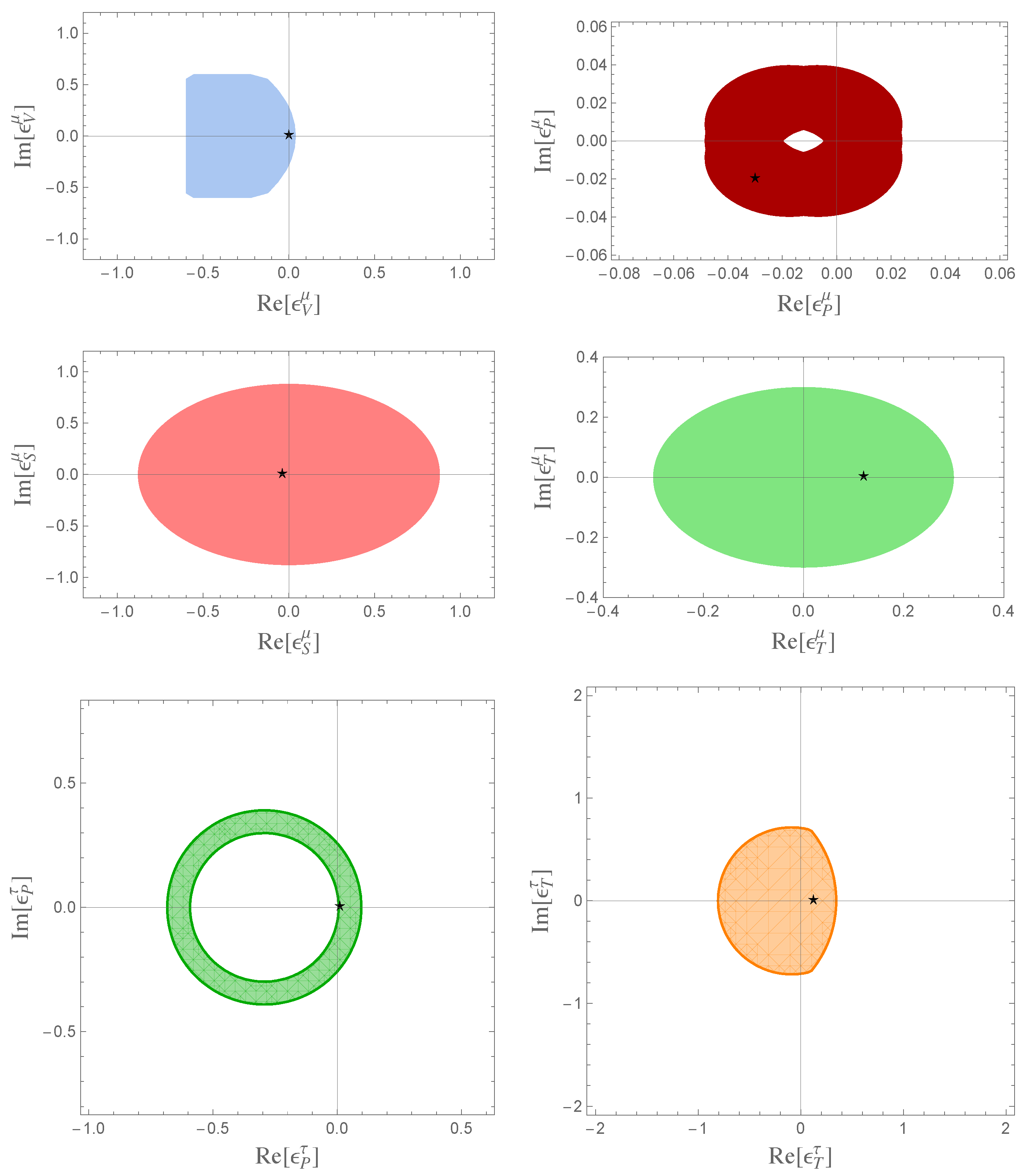
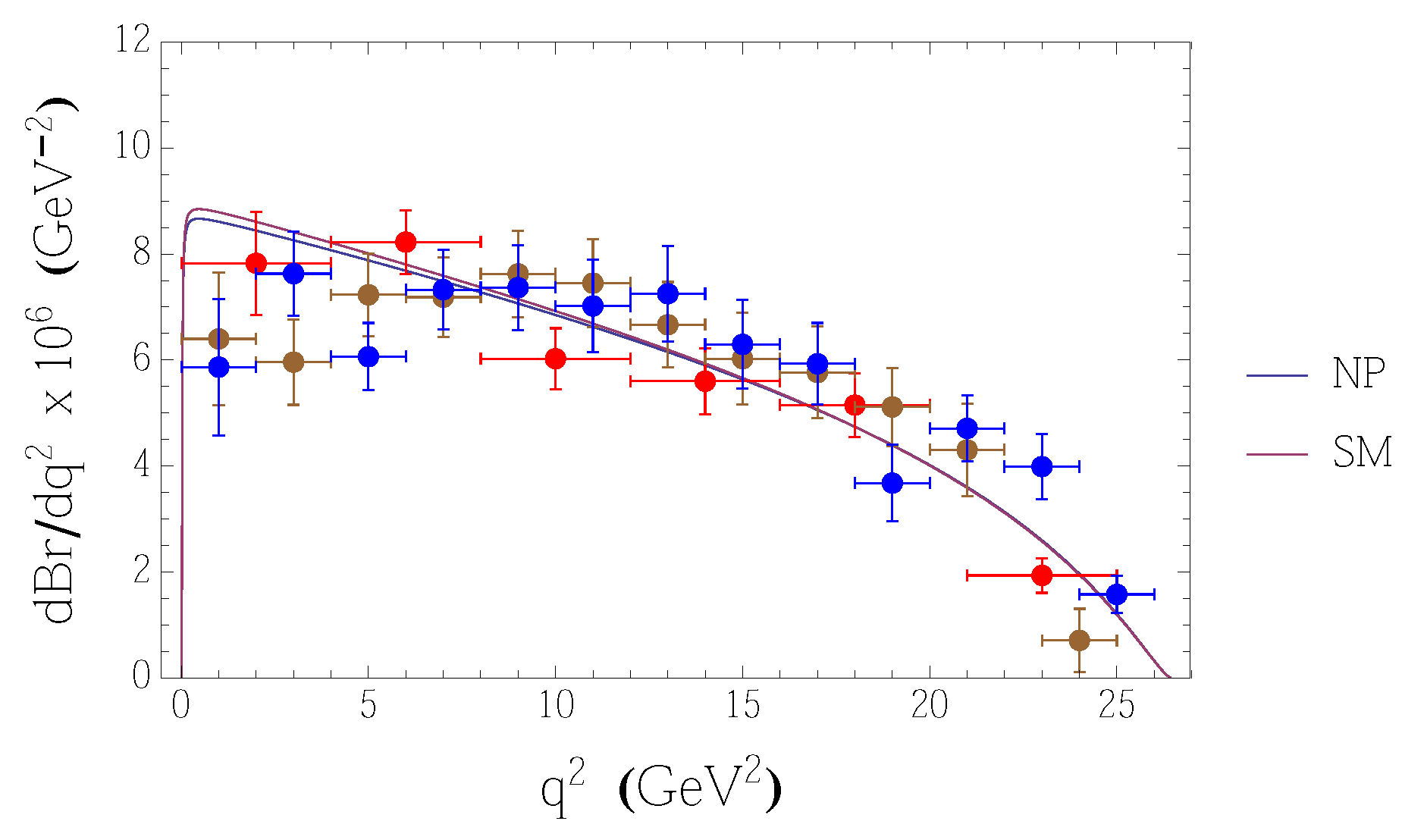
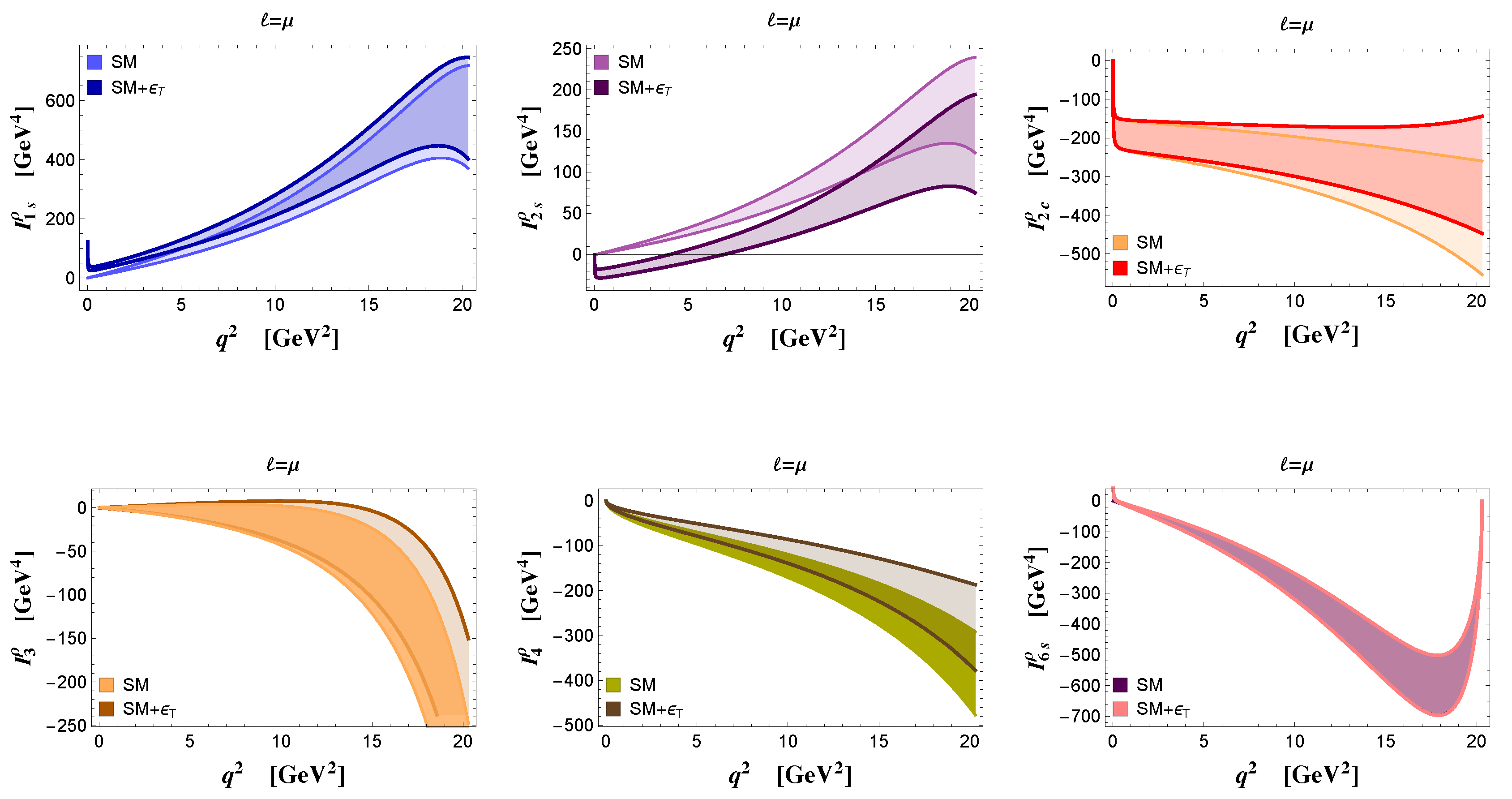
5. Observables in
6.
7. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Parametrization of the B→π form Factors
References
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Evidence for an excess of B → D(*)τ−ντ decays. Phys. Rev. Lett. 2012, 109, 101802. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Measurement of an Excess of B → D(*)τ−ντ Decays and Implications for Charged Higgs Bosons. Phys. Rev. 2013, D88, 072012. [Google Scholar]
- Huschle, M.; Kuhr, T.; Heck, M.; Goldenzweig, P.; Abdesselam, A.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Arinstein, K.; et al. Measurement of the branching ratio of B → D(*)τ−ντ relative to B → D(*)ℓ−ντ decays with hadronic tagging at Belle. Phys. Rev. 2015, D92, 072014. [Google Scholar]
- Sato, Y.; Iijima, T.; Adamczyk, K.; Aihara, H.; Asner, D.M.; Atmacan, H.; Aushev, T.; Ayad, R.; Aziz, T.; Babu, V.; et al. Measurement of the branching ratio of B0→D*+τ−ντ relative to B0→D*+ℓ−νℓ decays with a semileptonic tagging method. Phys. Rev. 2016, D94, 072007. [Google Scholar] [CrossRef]
- Hirose, S.; Iijima, T.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aulchenko, V.; Aushev, T.; et al. Measurement of the τ lepton polarization and R(D*) in the decay B → D*τ−ντ. Phys. Rev. Lett. 2017, 118, 211801. [Google Scholar] [CrossRef]
- Hirose, S.; Iijima, T.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aulchenko, V.; Aushev, T.; et al. Measurement of the τ lepton polarization and R(D*) in the decay B → D*τ−ντ with one-prong hadronic τ decays at Belle. Phys. Rev. 2018, D97, 012004. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of the ratio of branching fractions (B0→D*+τ−ντ)/(B0→D*+μ−ντ). Phys. Rev. Lett. 2015, 115, 111803. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Test of Lepton Flavor Universality by the measurement of the B0→D*−τ+ντ branching fraction using three-prong τ decays. Phys. Rev. 2018, D97, 072013. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Measurement of the ratio of the B0→D*−τ+ντ and B0→D*−μ+νμ branching fractions using three-prong τ-lepton decays. Phys. Rev. Lett. 2018, 120, 171802. [Google Scholar] [CrossRef]
- Amhis, Y.; Banerjee, S.; Ben-Haim, E.; Bernlochner, F.; Bozek, A.; Bozzi, C.; Chrząszcz, M.; Dingfelder, J.; Duell, S.; Gersabeck, M.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of summer 2016. Eur. Phys. J. 2017, C77, 895. [Google Scholar]
- Fajfer, S.; Kamenik, J.F.; Nisandzic, I. On the B → D*τντ Sensitivity to New Physics. Phys. Rev. 2012, D85, 094025. [Google Scholar]
- Biancofiore, P.; Colangelo, P.; De Fazio, F. On the anomalous enhancement observed in B → D(*)τντ decays. Phys. Rev. 2013, D87, 074010. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Measurement of the ratio of branching fractions (Bc+→J/ψτ+ντ)/(Bc+→J/ψμ+νμ). Phys. Rev. Lett. 2018, 120, 121801. [Google Scholar] [CrossRef] [PubMed]
- Dutta, R.; Bhol, A. Bc→(J/ψ,ηc)τν semileptonic decays within the standard model and beyond. Phys. Rev. 2017, D96, 076001. [Google Scholar]
- Watanabe, R. New Physics effect on Bc → J/ψτν in relation to the RD(*) anomaly. Phys. Lett. 2018, B776, 5. [Google Scholar] [CrossRef]
- Tran, C.T.; Ivanov, M.A.; Koerner, J.G.; Santorelli, P. Implications of new physics in the decays Bc→(J/ψ,ηc)τν. Phys. Rev. 2018, D97, 054014. [Google Scholar] [CrossRef]
- Leljak, D.; Melic, B.; Patra, M. On lepton flavour universality in semileptonic Bc → ηc, J/ψ decays. JHEP 2019, 5, 094. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Search for lepton-universality violation in B+→K+ℓ+ℓ− decays. Phys. Rev. Lett. 2019, 122, 191801. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Test of lepton universality with B0→K*0ℓ+ℓ− decays. JHEP 2017, 8, 055. [Google Scholar]
- Abdesselam, A.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Arinstein, K.; Arita, Y.; Asner, D.M.; Atmacan, H.; Ahn, J.K.; et al. Test of lepton flavor universality in B → K*ℓ+ℓ− decays at Belle. arXiv 2019, arXiv:hep-ex/1904.02440. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Test of lepton universality with Λb0→pK−ℓ+ℓ− decays. arXiv 2019, arXiv:hep-ex/1912.08139. [Google Scholar]
- Bifani, S.; Descotes-Genon, S.; Romero Vidal, A.; Schune, M.H. Review of Lepton Universality tests in B decays. J. Phys. 2019, G46, 023001. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. A test of heavy quark effective theory using a four-dimensional angular analysis of B → D*ℓ−νℓ. arXiv 2019, arXiv:hep-ex/1903.10002. [Google Scholar]
- Waheed, E.; Urquijo, P.; Ferlewicz, D.; Adachi, I.; Adamczyk, K.; Ahn, J.K.; Aihara, H.; Al Said, S.; Arinstein, K.; Arita, Y.; et al. Measurement of CKM Matrix Element |Vcb| from B → D*+ℓ−νℓ. arXiv 2018, arXiv:hep-ex/1809.03290. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Measurement of |Vcb| with Bs0→Ds(*)−μ+νμ decays. arXiv 2020, arXiv:hep-ex/2001.03225. [Google Scholar]
- Jaiswal, S.; Nandi, S.; Patra, S.K. Extraction of |Vcb| from B → D(*)ℓνℓ and the Standard Model predictions of R(D(*)). JHEP 2017, 12, 060. [Google Scholar] [CrossRef]
- Bigi, D.; Gambino, P.; Schacht, S. A fresh look at the determination of |Vcb| from B → D*ℓν. Phys. Lett. 2017, B769, 441. [Google Scholar] [CrossRef]
- Grinstein, B.; Kobach, A. Model-Independent Extraction of |Vcb| from B → D*ℓν. Phys. Lett. 2017, B771, 359. [Google Scholar] [CrossRef]
- Gambino, P.; Jung, M.; Schacht, S. The Vcb puzzle: An update. Phys. Lett. 2019, B795, 386–390. [Google Scholar] [CrossRef]
- Colangelo, P.; De Fazio, F. Tension in the inclusive versus exclusive determinations of |Vcb|: A possible role of new physics. Phys. Rev. 2017, D95, 011701. [Google Scholar] [CrossRef]
- Alonso, R.; Kobach, A.; Martin Camalich, J. New physics in the kinematic distributions of B → D(*)τ−(→ℓ−νℓντ)ντ. Phys. Rev. 2016, D94, 094021. [Google Scholar] [CrossRef]
- Ligeti, Z.; Papucci, M.; Robinson, D.J. New Physics in the Visible Final States of B → D(*)τν. JHEP 2017, 1, 083. [Google Scholar] [CrossRef]
- Alok, A.K.; Kumar, D.; Kumbhakar, S.; Sankar, S.U. D* polarization as a probe to discriminate new physics in B → D*τν. Phys. Rev. 2017, D95, 115038. [Google Scholar] [CrossRef]
- Colangelo, P.; De Fazio, F. Scrutinizing B → D*(Dπ)ℓ−νℓ and B → D*(Dγ)ℓ−νℓ in search of new physics footprints. JHEP 2018, 6, 082. [Google Scholar] [CrossRef]
- Becirevic, D.; Fedele, M.; Nisandzic, I.; Tayduganov, A. Lepton Flavor Universality tests through angular observables of B → D(*)ℓν decay modes. arXiv 2019, arXiv:hep-ph/1907.02257. [Google Scholar]
- Chen, C.H.; Nam, S.H. Left-right mixing on leptonic and semileptonic b → u decays. Phys. Lett. 2008, B666, 462–466. [Google Scholar] [CrossRef]
- Buras, A.J.; Gemmler, K.; Isidori, G. Quark flavour mixing with right-handed currents: An effective theory approach. Nucl. Phys. 2011, B843, 107. [Google Scholar] [CrossRef]
- Crivellin, A. Effects of right-handed charged currents on the determinations of |V(ub)| and |V(cb)|. Phys. Rev. 2010, D81, 031301. [Google Scholar]
- Crivellin, A.; Pokorski, S. Can the differences in the determinations of Vub and Vcb be explained by New Physics? Phys. Rev. Lett. 2015, 114, 011802. [Google Scholar] [CrossRef]
- Bernlochner, F.U.; Ligeti, Z.; Turczyk, S. New ways to search for right-handed current in B→ρℓν decay. Phys. Rev. 2014, D90, 094003. [Google Scholar] [CrossRef]
- Bernlochner, F.U. B → πτντ decay in the context of type II 2HDM. Phys. Rev. 2015, D92, 115019. [Google Scholar]
- Blanke, M.; Crivellin, A.; Kitahara, T.; Moscati, M.; Nierste, U.; Nisandzic, I. Addendum: “Impact of polarization observables and Bc → τν on new physics explanations of the b → cτν anomaly”. arXiv 2019, arXiv:hep-ph/1905.08253. [Google Scholar] [CrossRef]
- Banelli, G.; Fleischer, R.; Jaarsma, R.; Tetlalmatzi-Xolocotzi, G. Decoding (Pseudo)-Scalar Operators in Leptonic and Semileptonic B Decays. Eur. Phys. J. 2018, C78, 911. [Google Scholar] [CrossRef] [PubMed]
- Colangelo, P.; De Fazio, F.; Loparco, F. Probing New Physics with B → ρ(770)ℓ−νℓ and B → a1(1260)ℓ−νℓ. Phys. Rev. 2019, D100, 075037. [Google Scholar] [CrossRef]
- Buchmuller, W.; Wyler, D. Effective Lagrangian Analysis of New Interactions and Flavor Conservation. Nucl. Phys. 1986, B268, 621. [Google Scholar] [CrossRef]
- Cirigliano, V.; Jenkins, J.; Gonzalez-Alonso, M. Semileptonic decays of light quarks beyond the Standard Model. Nucl. Phys. 2010, B830, 95. [Google Scholar] [CrossRef]
- Jung, M.; Straub, D.M. Constraining new physics in b → cℓν transitions. JHEP 2019, 1, 009. [Google Scholar] [CrossRef]
- Celis, A.; Jung, M.; Li, X.Q.; Pich, A. Scalar contributions to b → c(u)τν transitions. Phys. Lett. 2017, B771, 168. [Google Scholar] [CrossRef]
- Leljak, D.; Melic, B. |Vub| determination and testing of lepton flavour universality in semileptonic Bc → D(*) decays. arXiv 2019, arXiv:hep-ph/1909.01213. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Determination of the quark coupling strength |Vub| using baryonic decays. Nat. Phys. 2015, 11, 743–747. [Google Scholar]
- Charles, J.; Le Yaouanc, A.; Oliver, L.; Pene, O.; Raynal, J.C. Heavy to light form-factors in the heavy mass to large energy limit of QCD. Phys. Rev. 1999, D60, 014001. [Google Scholar]
- Beneke, M.; Feldmann, T. Symmetry breaking corrections to heavy to light B meson form-factors at large recoil. Nucl. Phys. 2001, B592, 3. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C. Review of Particle Physics. Phys. Rev. 2018, D98, 030001. [Google Scholar] [CrossRef]
- Sibidanov, A.; Varvell, K.E.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Aushev, T.; Ayad, R.; Babu, V.; Badhrees, I.; et al. Search for B−→μ−νμ Decays at the Belle Experiment. Phys. Rev. Lett. 2018, 121, 031801. [Google Scholar] [CrossRef] [PubMed]
- Hamer, P.; Frey, A.; Abdesselam, A.; Adachi, I.; Aihara, H.; Al Said, S.; Arinstein, K.; Asner, D.M.; Aushev, T.; Ayad, R.; et al. Search for B0→π−τ+ντ with hadronic tagging at Belle. Phys. Rev. 2016, D93, 032007. [Google Scholar]
- Bharucha, A.; Straub, D.M.; Zwicky, R. B → Vℓ+ℓ− in the Standard Model from light-cone sum rules. JHEP 2016, 8, 098. [Google Scholar] [CrossRef]
- Ha, H.; Won, E.; Adachi, I.; Aihara, H.; Aziz, T.; Bakich, A.M.; Balagura, V.; Barberio, E.; Bay, A.; Belous, K.; et al. Measurement of the decay B0→π−ℓ+ν and determination of |Vub|. Phys. Rev. 2011, D83, 071101. [Google Scholar]
- Del Amo Sanchez, P.; Lees, J.P.; Poireau, V.; Prencipe, E.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Martinelli, M.; Milanes, D.A.; Palano, A.; et al. Measurement of the B0→πℓℓ+ν and B+→η(′)ℓ+ν Branching Fractions, the B0→π−ℓ+ν and B+→ηℓ+ν Form-Factor Shapes, and Determination of |Vub|. Phys. Rev. 2011, D83, 052011. [Google Scholar]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Branching fraction and form-factor shape measurements of exclusive charmless semileptonic B decays, and determination of |Vub|. Phys. Rev. 2012, D86, 092004. [Google Scholar]
- Li, R.H.; Lu, C.D.; Wang, W. Transition form factors of B decays into p-wave axial-vector mesons in the perturbative QCD approach. Phys. Rev. 2009, D79, 034014. [Google Scholar]
- Sentitemsu Imsong, I.; Khodjamirian, A.; Mannel, T.; van Dyk, D. Extrapolation and unitarity bounds for the B → π form factor. JHEP 2015, 2, 126. [Google Scholar] [CrossRef]
- Khodjamirian, A.; Rusov, A.V. Bs → Kℓνℓ and B(s)→π(K)ℓ+ℓ− decays at large recoil and CKM matrix elements. JHEP 2017, 8, 112. [Google Scholar] [CrossRef]
- Aoki, S.; Aoki, Y.; Becirevic, D.; Blum, T.; Colangelo, G.; Collins, S.; Morte, M.D.; Dimopoulos, P.; Dürr, S.; Fukaya, H.; et al. FLAG Review 2019. arXiv 2019, arXiv:hep-lat/1902.08191. [Google Scholar] [CrossRef]
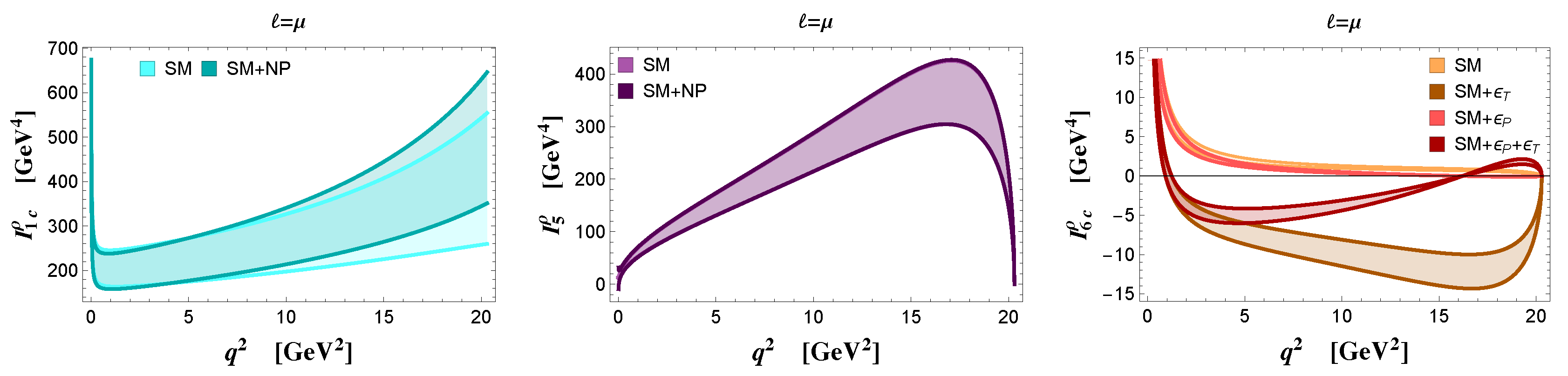
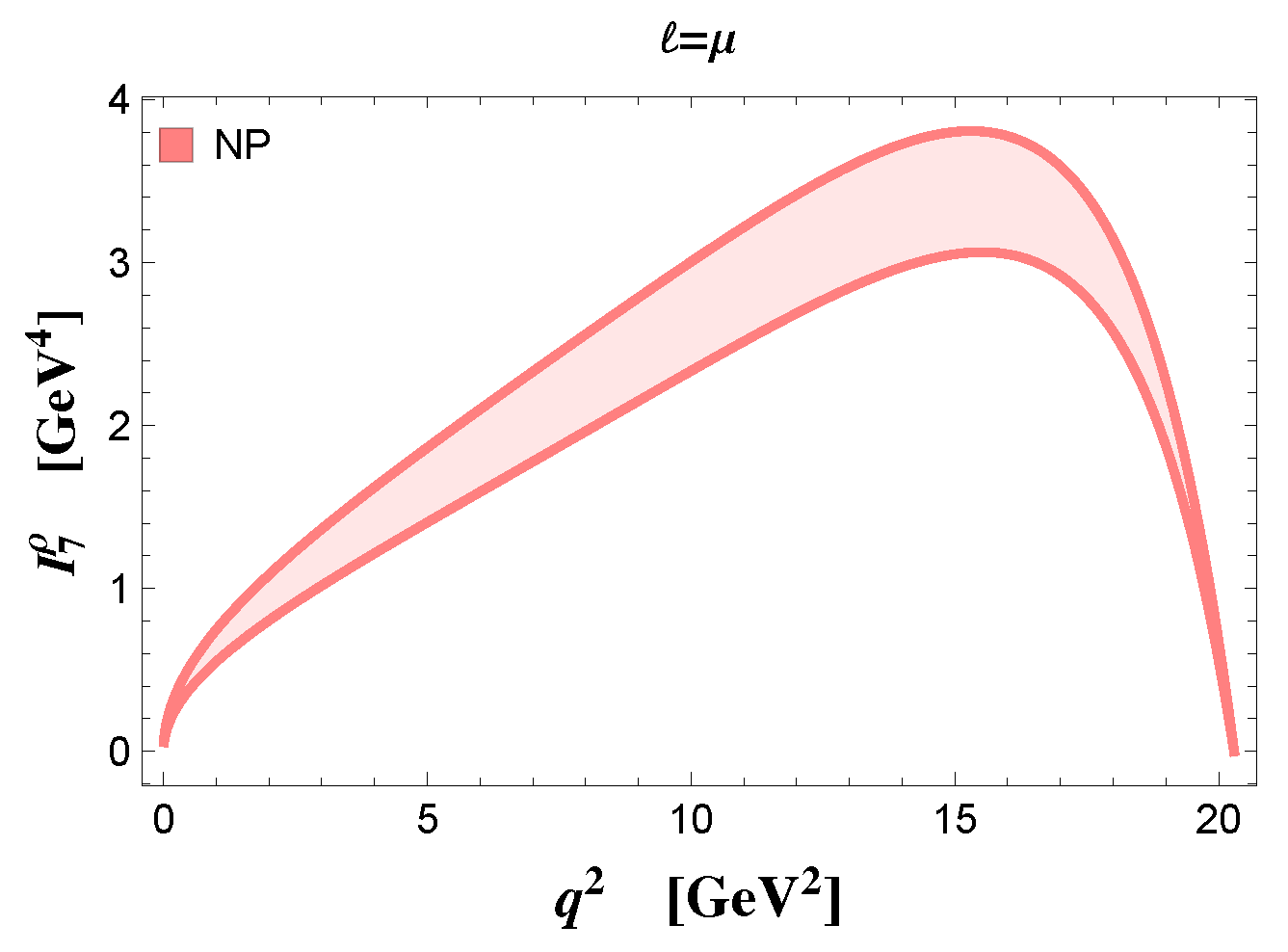
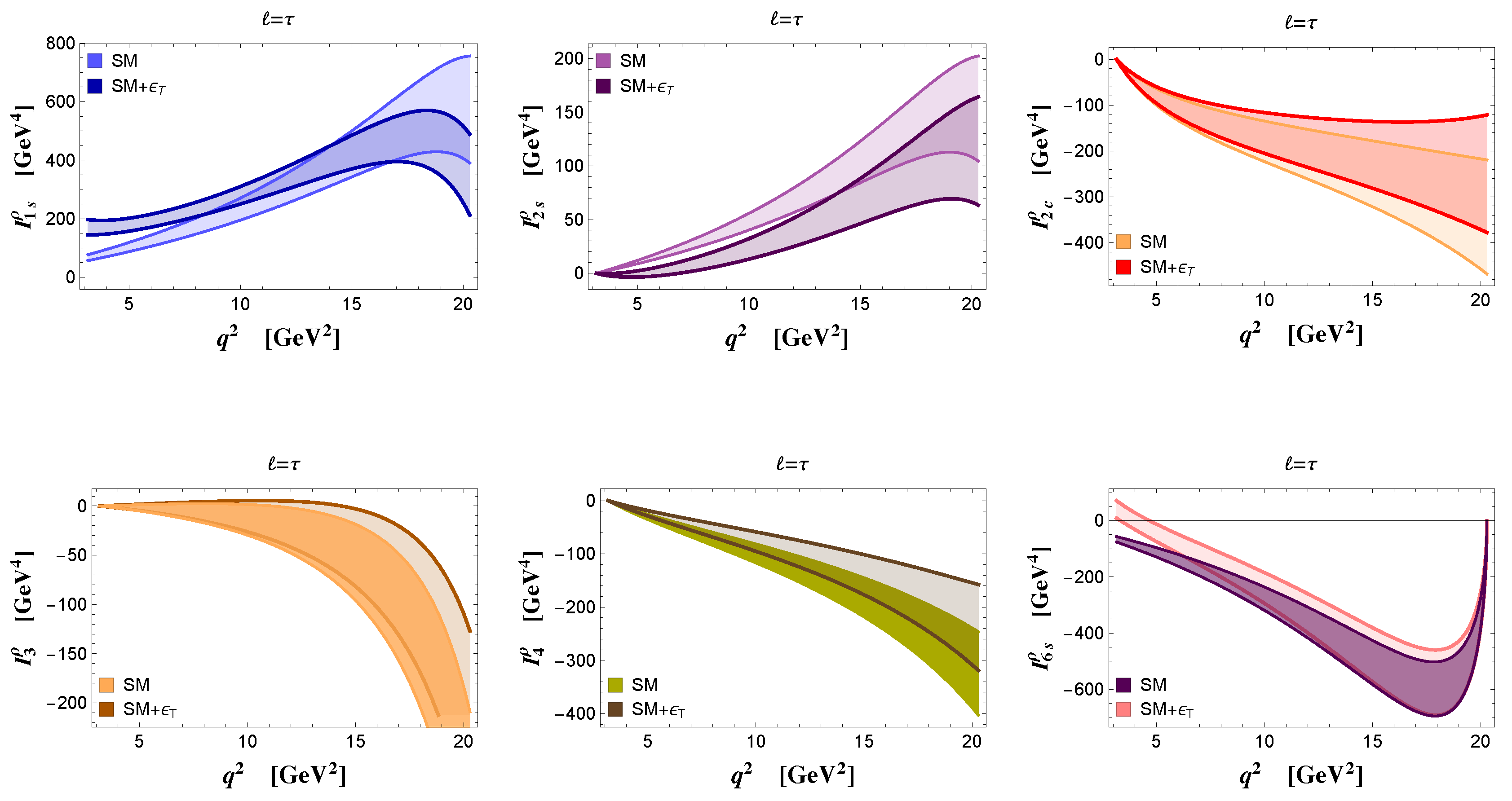
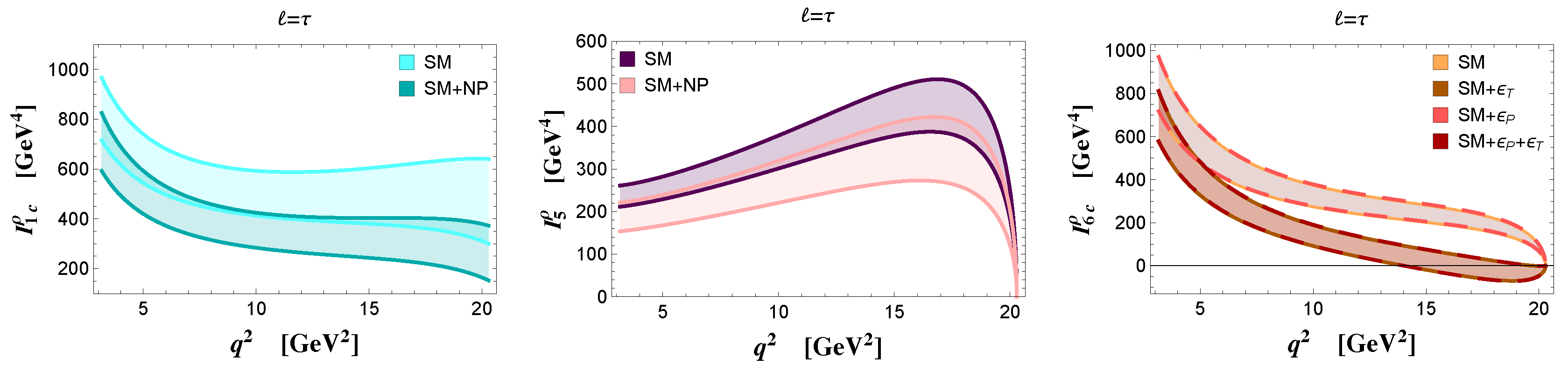

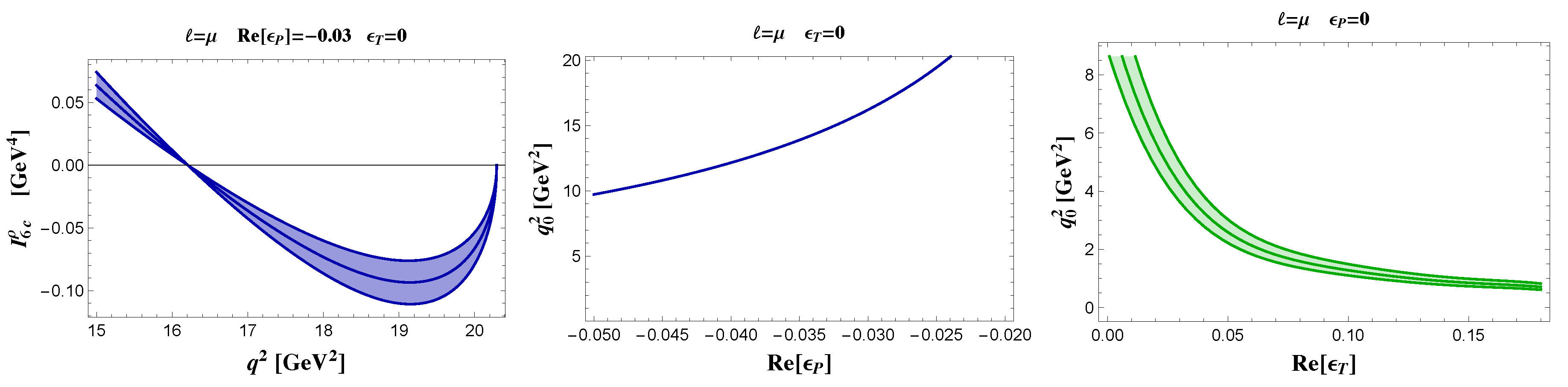

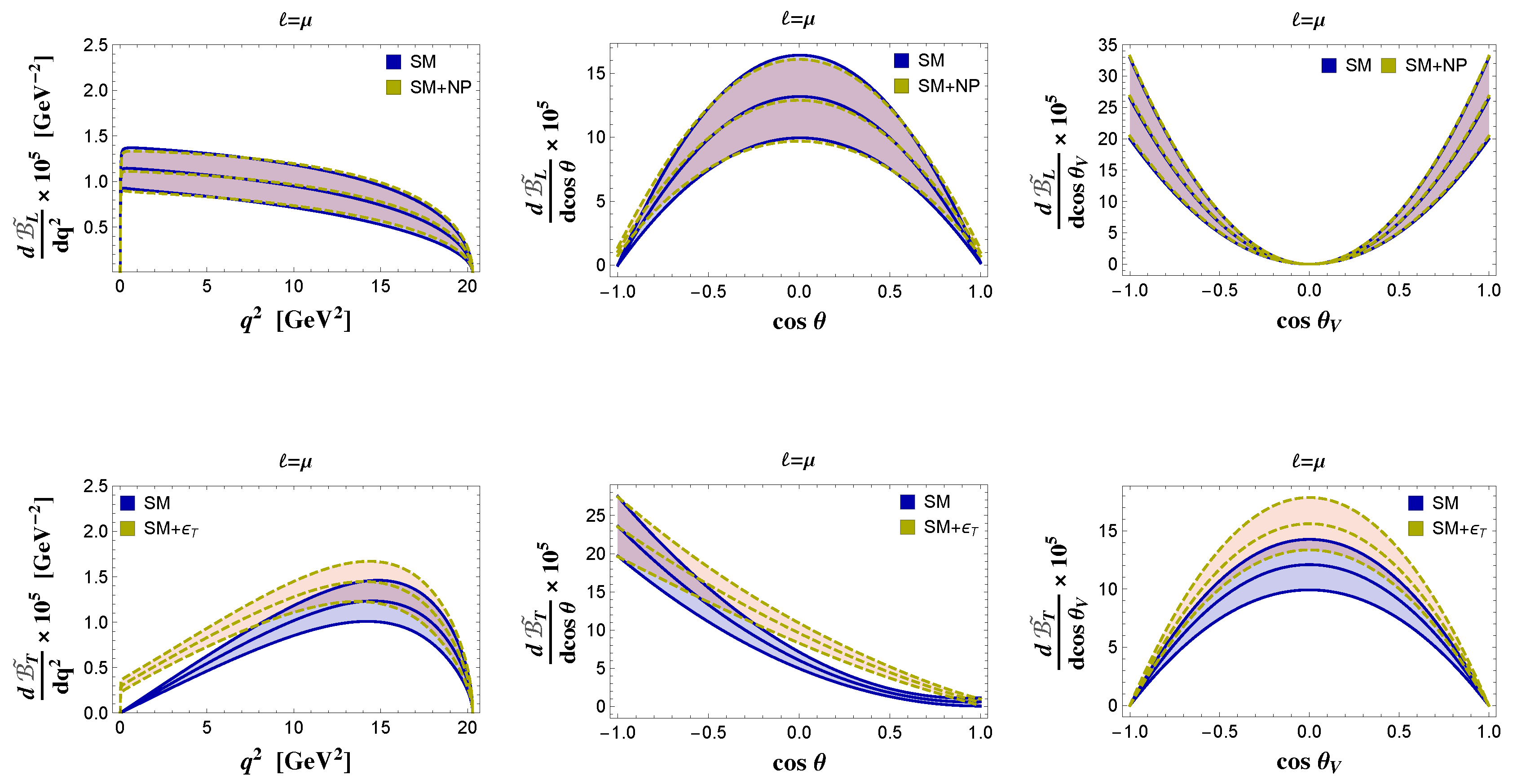
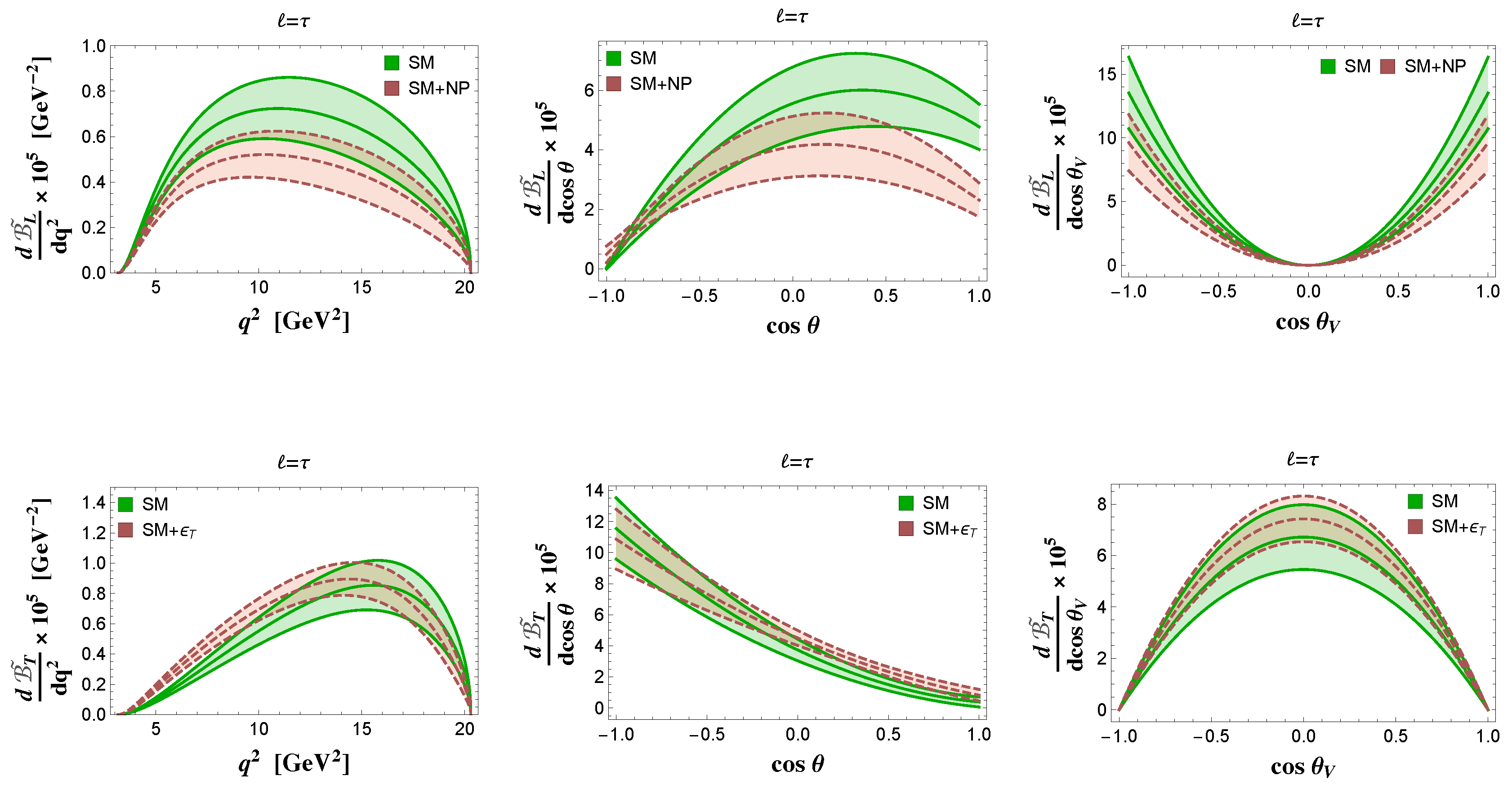


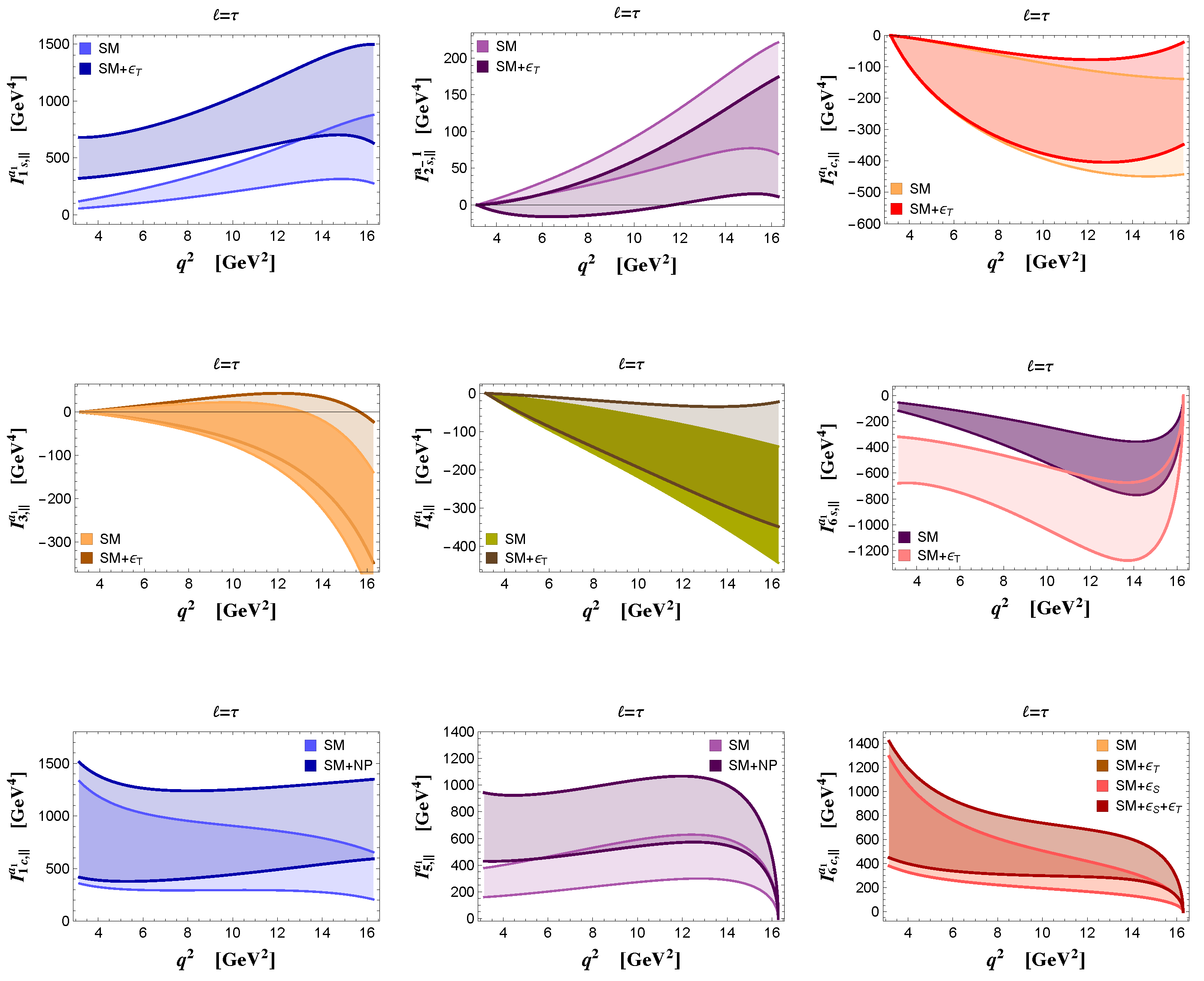
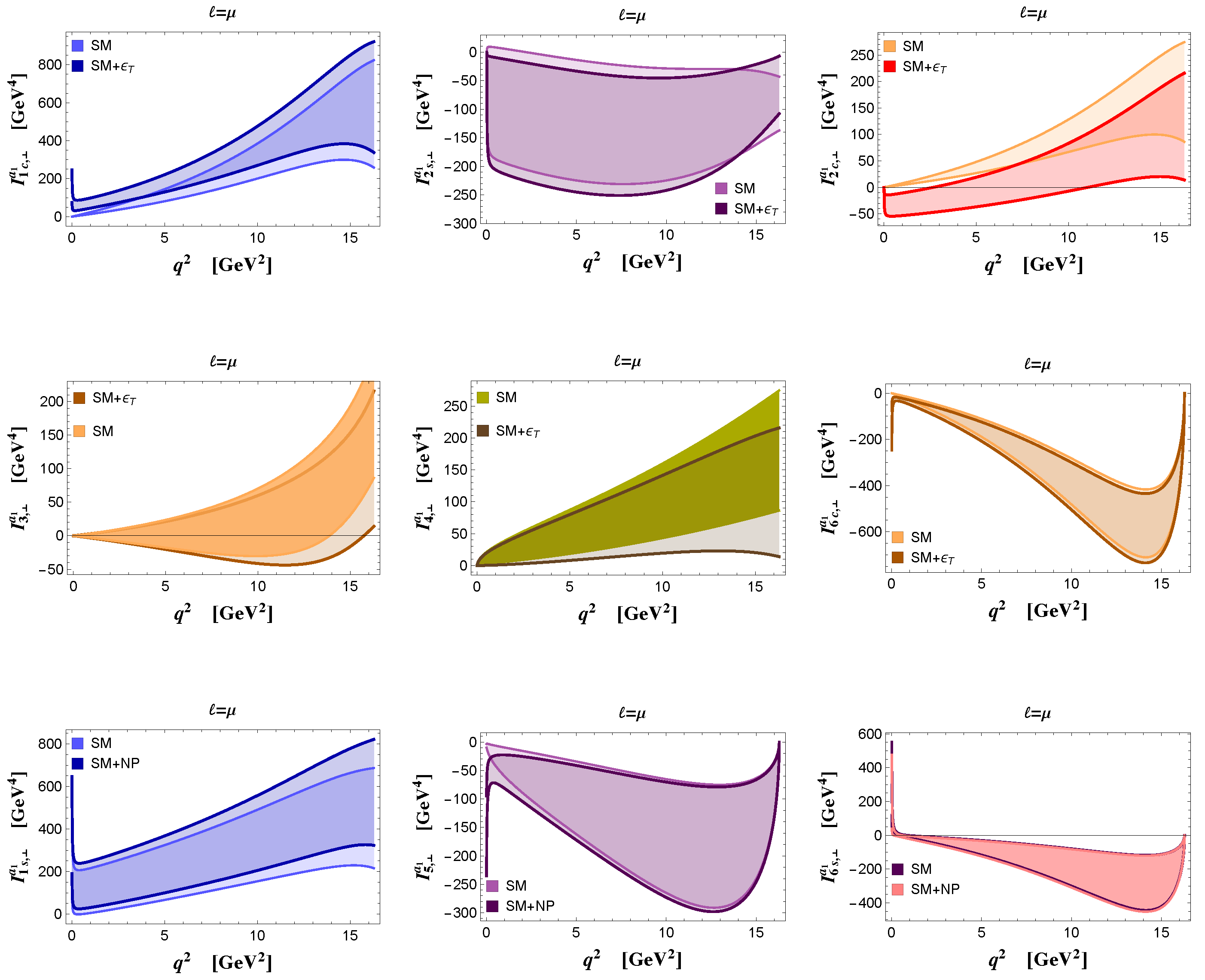
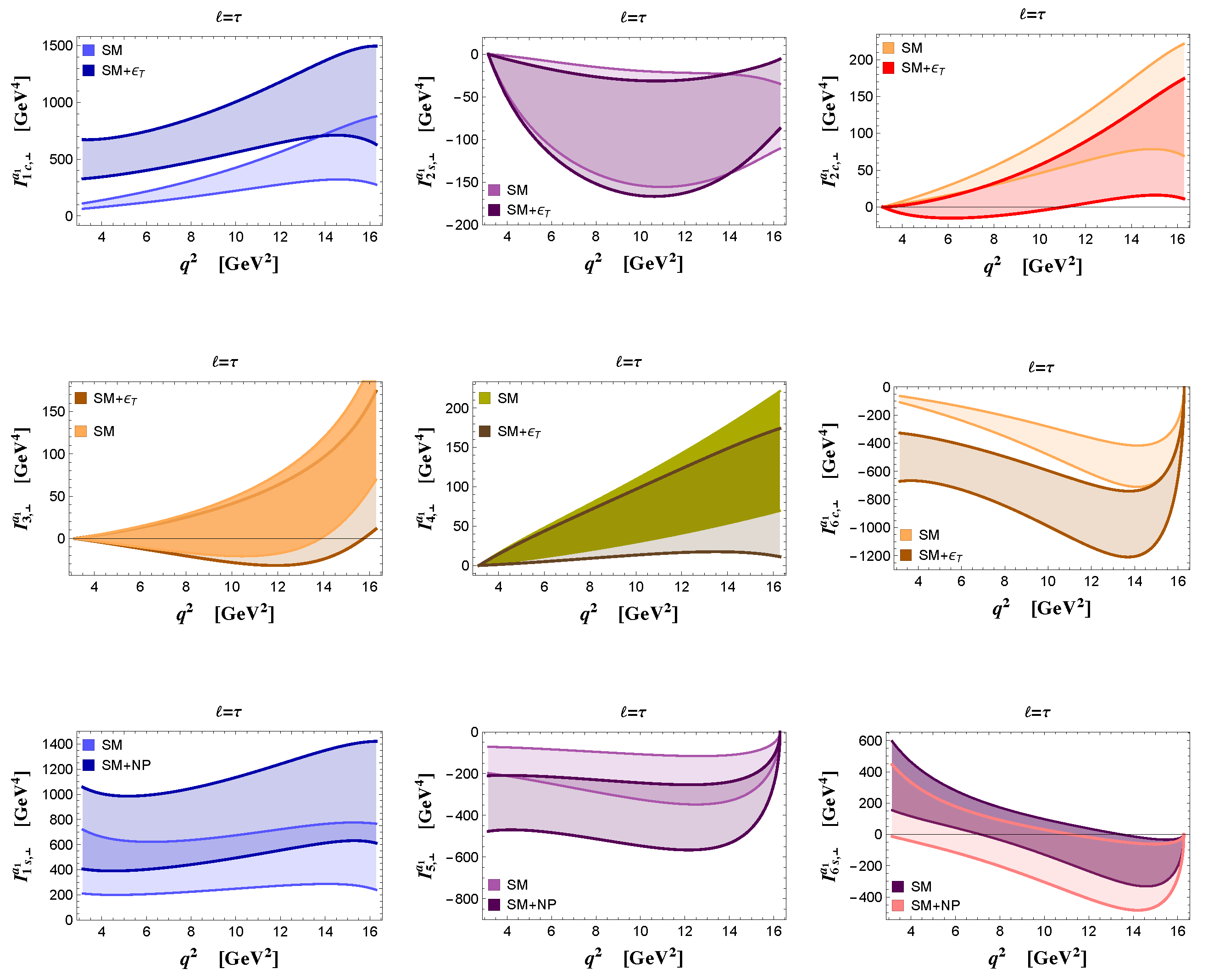
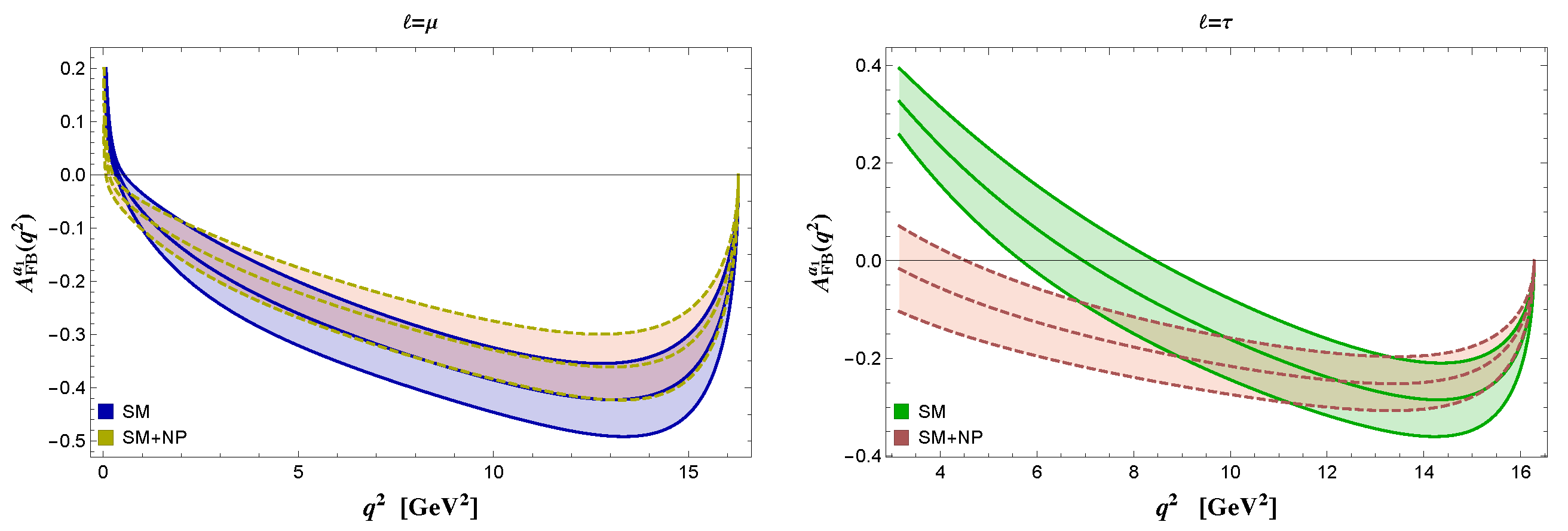
| SM | NP (Benchmark Point) | |
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colangelo, P.; De Fazio, F.; Loparco, F. Probes of Lepton Flavor Universality in b → u Transitions. Particles 2020, 3, 145-163. https://doi.org/10.3390/particles3010012
Colangelo P, De Fazio F, Loparco F. Probes of Lepton Flavor Universality in b → u Transitions. Particles. 2020; 3(1):145-163. https://doi.org/10.3390/particles3010012
Chicago/Turabian StyleColangelo, Pietro, Fulvia De Fazio, and Francesco Loparco. 2020. "Probes of Lepton Flavor Universality in b → u Transitions" Particles 3, no. 1: 145-163. https://doi.org/10.3390/particles3010012
APA StyleColangelo, P., De Fazio, F., & Loparco, F. (2020). Probes of Lepton Flavor Universality in b → u Transitions. Particles, 3(1), 145-163. https://doi.org/10.3390/particles3010012





