Abstract
In this lecture, we provide a basic introduction into the topic of charmed baryons and their nonleptonic two-body decays. Some features of the baryon weak decays on the quark level are discussed in detail in the framework of effective field theory. The calculation of the matrix elements of the four-quark operators arising in the effective theory proceeds by using the covariant constituent quark model. The model allows one to evaluate not only the factorizing tree-level diagrams but also more complicated diagrams with the internal W–exchange. The technique required for such calculation is discussed in some detail. Finally, the numerical results are presented, and comparison of the contributions coming from the W–exchange diagrams with those from the tree-level are carefully performed.
1. Introduction
In 1964, Gell–Mann proposed [1] the theory of quarks–fundamental particles that make up most ordinary matter. It was done by using the observation that the successful eightfold way of hadron classification would be naturally explained if hadrons were composed of a quark-antiquark pair or three quarks (or three antiquarks).
In the same year, George Zweig came to the same conclusion independently [2,3] by analyzing the suppressed strong decays of the -meson. He called three constituents by aces.
The existence of a fourth quark was discussed by a number of authors around 1964, for instance, by James Bjorken and Sheldon Glashow [4]. But there was little evidence for its existence. Its prediction is usually credited to Glashow–Iliopoulos–Maiani [5] for the so-called GIM mechanism, which forbids the flavor-changing neutral currents in the tree diagrams. It explains why weak interactions that change strangeness by a factor of 2 are suppressed. The first particle containing the charmed quark and antiquark was discovered in 1974 and named as the meson.
The masses of singly charmed baryons was predicted in one gluon exchange model developed in Reference [6]. The comprehensive review on heavy baryons, their spectroscopy, and semileptonic and nonleptonic decays may be found in Reference [7]. In Table 1 and Table 2, we display the names and quark contents of the low-lying multiplets of charmed baryons with spin 1/2 and 3/2, respectively. The values of masses with errors are taken from PDG [8], whereas without errors from Reference [7].

Table 1.
Charmed baryon states. Notation and for antisymmetric and symmetric flavor index combinations. The third column shows which SU(3) adjoint () or fundamental representation the quark state belongs to.

Table 2.
Charmed baryon states.
The lowest lying multiplet of charmed baryons with spin 1/2 can decay only weakly. Therefore, the study of the nonleptonic decays of charmed baryons is very important in the phenomenology of particle interactions. There are now more precise results on the branching ratios of the two-body decays of charmed baryons [9] and [10,11]. In 2005, a new era began in the studies of doubly charmed baryons when the SELEX Collaboration reported on the observation of a state with the quantum numbers of the spin 1/2 ground state baryon with a mass of MeV [12]. The SELEX (Segmented Large X baryon Spectrometer) is a fixed target experiment at Fermilab. This doubly charmed baryon state was conjectured to be an isospin- baryon with quark content and to have an isospin partner with the quark structure . However, other Collaborations (BABAR, Belle, LHCb [8]) found no evidence for the nor the states in the conjectured mass region of MeV. Recently, the LHCb Collaboration discovered the doubly charmed state [13,14,15] in the invariant mass spectrum of the final state particles . The LHCb is Large Hadron Collider beauty experiment at CERN. The extracted mass of the state was given as MeV and was MeV heavier than the mass of the original SELEX doubly charmed baryon state , which made it quite unlikely that the two states were isospin partners. On the other hand, the LHCb mass measurement was in agreement with theoretical mass value predictions for the doubly charmed baryon states. In particular, the central mass value of the LHCb result for the was very close the value 3610 MeV and 3620 MeV predicted in Reference [7,16] using the one gluon exchange model of de Rujula, Georgi, and Glashow [17] and a relativistic quark-diquark potential model [18], respectively. Fleck and Richard, using a variety of models, also predicted a mass value of [19], while Karliner et al. found MeV [20].
The new measurement of the LHCb Collaboration has stimulated much theoretical activity of the nonleptonic decays of doubly heavy baryons. The recent review can be found in Reference [21,22].
2. Light Baryons in SU(3)
In this section, let us recall the basic features of the -classification of light baryons. Baryons are classified into multiplets according to decomposition of reducible product of the fundamental quark representations:
The octet representation 8 is written as (see Reference [23]):
where a vector belonging to the representation can be written as
The matrix form of the octet representation looks like
The quark content of baryons are shown in Table 3.

Table 3.
Quark content of the baryon octet.
Up to now, we discussed only the flavor structure of quark fields. Generally speaking, they also depend on color, spin, and space coordinates. Therefore, one has to construct the relativistic three quark currents with quantum numbers corresponding to certain member of the baryon octet. One can start from construction of –currents, which are symmetric under permutation of all quarks in the case of exact -symmetry. This program has been realized in Reference [24]. The starting point is the relativistic three-quark current with quantum numbers of a baryon octet . The general form of this current can be written as
where ; are the color, spinor, and flavor indices. By using the Fierz transformations for both Dirac matrices and -matrices, one finds that there exist two independent currents for a baryon octet with quantum numbers . They may be written in the form:
where = (vector current) or (tensor current). is the usual charge conjugation matrix:
One can check that the diquark with identical flavors exists for and only:
Finally, the isotopic components for three-quark currents are written as in Table 4. The obtained expressions are coincided with those from Reference [25,26].

Table 4.
Three-quark currents of the baryon octet (tensor Levi-Civita skipped).
2.1. Fierz Transformations for Dirac Matrices
The basis of sixteen Dirac matrices is shown in Table 5.

Table 5.
Basis of Dirac matrices.
The matrices from the basis satisfy to the normalization condition given by Equation (7) in general form and conditions given by Equation (8) for each matrix from the basis.
Any product of Dirac matrices can be decomposed into 16 independent matrices:
One can derive from Equation (9) the useful property of the Dirac matrices called the Fierz transformation. One has
The last equality holds if and only if the following property is valid:
By using following, Equation (11), one can arrive at the Fierz transformation
Then, we introduce the short notation.
There are a plenty of useful identities which relate the product of two Dirac matrices with tilde to product of two Dirac matrices without tilde. Here, are some of them:
We will use the above identities to simplify the string of Dirac matrices involving two weak matrices with Left/Right chirality . One can prove that
By using these properties of the weak matrices, one can get the following simplifications:
2.2. SU(n)-Matrices
Here, let us recall some properties of the unitary matrices from the -group. For -group, there are generators , where are the Gell–Mann traceless matrices (). They satisfy the following relations:
For completeness, one has to add the unit matrix . Then, any matrix can be decomposed into basis matrices:
From Equation (18), it is easy to derive the completeness condition:
Some corollaries follow from Equation (19):
They allow to simplify the calculation of traces:
3. Charmed Baryons
The existence of a fourth quark had been discussed by a number of authors around 1964, for instance, by James Bjorken and Sheldon Glashow [4]. The addition of the charmed quark to the triplet extends the to . The irreducible representations are formed according to decomposition
But, in that time, there was little evidence for existence of the charmed quark and related hadrons. Its prediction is usually credited to Glashow–Iliopoulos–Maiani [5] for the so-called GIM mechanism, which forbids the flavor-changing neutral currents in the tree diagrams.
GIM Mechanism
The attempt to construct the weak interactions with three quarks led to existence of the flavor-changing neutral current (FCNC) at tree level. The left weak duplet is written as
where is the Cabbibo angle. It gives the following contribution to the weak Lagrangian
The charm quark allows one to construct an extra duplet:
It will give the additional contribution the the weak Lagrangian, where the FCNC contribute with the opposite sign:
As the result, the FCNC vanish from the weak Lagrangian and occur only at the level of loop diagrams:
For instance, the weak decay goes via sum of one-loop diagrams with u-quark and c-quark, as shown in Figure 1.
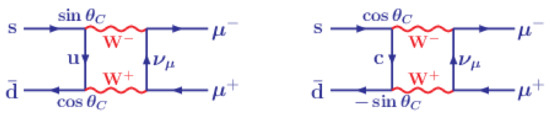
Figure 1.
Diagrams describing the decay . The left diagram describes the exchange by u-quark whereas the right by c-quark.
The matrix element is proportional to
The experimental data can be reproduced if the value of the charm quark mass is of order ⟶ GeV. It was the first solid confirmation of the charm in particle physics.
4. Nonleptonic Two-Body Weak Decays of Baryons
Ground states of baryons with can decay only weakly via the internal W-exchange. Two-body decays of baryons have five different quark topologies shown in Figure 2.
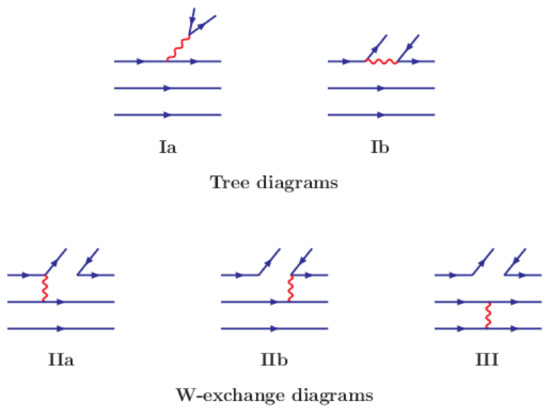
Figure 2.
Quark diagrams with five different topologies. The set of diagrams divides in two groups: (1) The reducible tree-diagrams called external (Ia) and internal W-emission (IIb) diagrams. (2) The irreducible W-exchange diagrams with the labeling introduced in [7,16]. In [27] the W–exchange diagrams are denoted as the Exchange (IIa), color-commensurate (IIb) and Bow tie (III) diagram.
The weak interactions of quarks at energy significantly less than the W-mass, the scale of charm quark mass in the given decays, are described in the framework of an effective low-energy theory. The formal framework is using the Wilson operator product expansion (OPE). As an example, let us consider the tree-level W–exchange amplitude for transition. One has
where is the weak Dirac matrix with left chirality, and are the CKM-matrix elements, and is the coupling of gauge group. Since the momentum transfer is less than the W-mass, i.e., , the terms of order may be neglected. It is easy to see that the leading term of the expansion can be obtained from an effective Hamiltonian
Then, one needs to take into account the one-loop QCD corrections both in full theory and in the theory with effective Hamiltonian. The corresponding tree and one-loop diagrams in full and effective theory are shown in Figure 3.
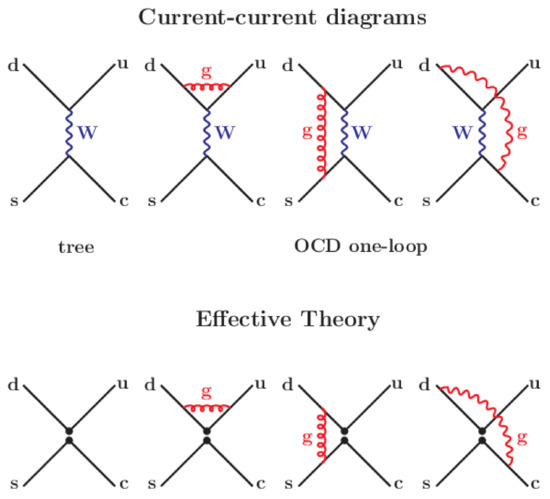
Figure 3.
Tree and one-loop diagrams in full and effective theory. In the full theory the tree diagram is described by exchange of the W-boson, whereas in the effective theory the tree diagram is generated by four-quark operator from an effective Hamiltonian. In both theories the next-to-leading corrections are described by gluon (g) exchanges between color quarks.
Including QCD corrections, the effective Hamiltonian is generalized to
where the Wilson coefficients are determined from the matching full and effective theories. The leading order in the strong QCD coupling looks as follows:
Obviously, this expansion will be reliable if the scale is of order of W-mass, i.e., . In this case, the value of is small due to asymptotic freedom, and the value of the logarithm is small, as well. Then, the Wilson coefficients are evaluated from down to the low-energy scale . The last step is to calculate the hadronic matrix elements of the operators that requires the nonperturbative methods.
5. Covariant Constituent Quark Model
The Covariant Constituent Quark Model (CCQM) is based on a phenomenological, nonlocal, relativistic Lagrangian describing the coupling of a hadron H to its constituents:
where is the quark current corresponding to a hadron H. For mesons, baryons, and tetraquarks, the corresponding quark currents may be written as
where and are color and flavor indices. The vertex functions should satisfy to translational invariance
The simple and obvious choice is written down as
where so that , and is an adjustable size parameter. The quark propagators are chosen in the local Dirac form
The quark confinement is realized by implementation of the so-called infrared confinement. We discuss how it works in the next sections.
5.1. Heavy Quark Limit in Transition
It is instructive to explore the heavy quark limit (HQL) in the heavy-to-heavy transition . The diagram describing the semileptonic decay is shown in Figure 4.
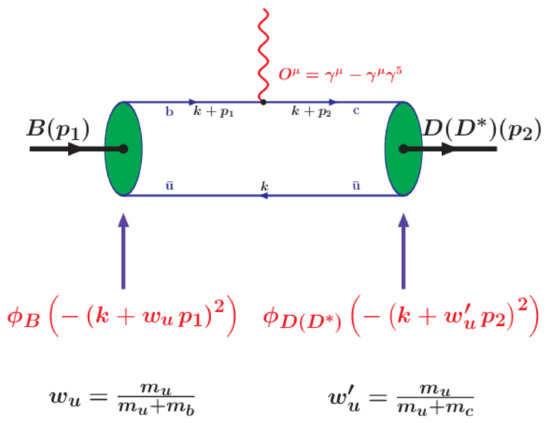
Figure 4.
Diagrams describing the semileptonic decay .
In the HQL, one takes the limit and in the expressions for the coupling constants and form factors. In this limit, the heavy quark propagators are reduced to the static form:
where and () are the momenta and the four-velocities of the initial and final states. Moreover, we have to keep the size parameters of heavy hadrons equal to each other in order to provide the correct normalization of the Isgur-Wise function at zero recoil. By using technique developed in our previous papers [28,29], one can arrive at the following expressions for the semileptonic heavy-to-heavy transitions:
Here, , and the Isgur-Wise function is equal to
where , , and . By using the definition of the form factors given in Reference [28,29], one can easily obtain the expressions of the form factors in the HQL. One finds
where . We use the physical masses of the heavy hadrons in the numerical calculations. For the size parameter, we adopt the average value GeV. The parameter E characterizes the difference in mass between the heavy hadron and the corresponding heavy quark. We use its minimal value GeV in order to avoid the complication with confinement. In Figure 5, we display the heavy-to-heavy transition form factors calculated in the HQL and compare them with the results of exact calculations [30]. One can see that the two results obtained with and without use of the HQL behave very similar to each other, which demonstrates the fidelity of HQET.
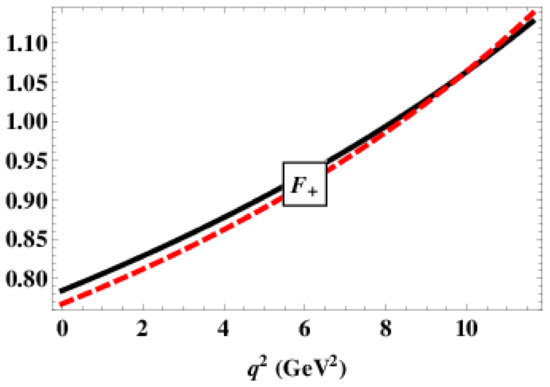
Figure 5.
Comparison of the exact calculation of the form factor (solid line) with those obtained in heavy quark limit (dashed line).
5.2. Infrared Confinement
We have shown in Reference [31] how the confinement of quarks can be effectively incorporated in the covariant quark model. In a first step, we introduced an additional scale integration in the space of Fock-Schwinger’s –parameters with an integration range from zero to infinity. In a second step, the scale integration was cut off at the upper limit which corresponds to the introduction of an infrared (IR) cutoff. In this manner, all possible thresholds present in the initial quark diagram were removed. The cutoff parameter was taken to be the same for all physical processes. Other model parameters, such as the constituent quark masses and size parameters, were determined from a fit to experimental data.
Let us describe the basic features of how IR confinement is implemented in our model. All physical matrix elements are described by Feynman diagrams written in terms of a convolution of free quark propagators and the vertex functions. In computation of Feynman diagrams, we use, in the momentum space, the Fock-Schwinger representation of the quark propagator:
The general form of a resulting Feynman diagrams is
where represents a linear combination of loop momenta, stands for a linear combination of external momenta, and refers to the numerator product of propagators and vertex functions. The integrand in Equation (42) has a Gaussian form with the exponential factor
where is a 4-vector of the “i”-loop integration, a is a matrix depending on the parameters and size parameters , is a 4- vector composed from the external momenta , and R is a quadratic form of the masses and external momenta. Tensor loop integrals are calculated with the help of the differential representation
which, in general, may be written in the form
where the polynomial operator means . After doing the loop integration, the differential operators will give cause to outer momenta tensors. It may be done in effective way by using the identity
The calculation of the polynomial can be automized by using the commutator We have written a FORM [32] program that achieves the necessary commutations of the differential operators in a very efficient way.
The last point which remains to be discussed is the infrared cut-off we impose on the integration over the Fock-Schwinger parameters. This integration is multidimensional with the limits from 0 to . In order to arrive to a single cut-off parameter, we first transform the integral over an infinite space into an integral over a simplex convoluted with only one-dimensional improper integral. For that purpose, we use the -function form of the identity
from which follows
where W represents the integrand of Schwinger parameters. The cut-off is then introduced in a natural way:
Such a cut-off makes the integral to be an analytic function without any singularities. In this way, all potential thresholds in the quark loop diagrams are removed together with corresponding branch points [31]. Within the covariant quark model, the cut-off parameter is universal for all processes, and its value, as obtained from a fit to data, is
The numerical evaluations have been done by a numerical program written in the fortran code.
As an example, let us consider a scalar one-loop two-point function:
where the numerator factor comes from the product of nonlocal vertex form factors of Gaussian form. are Euclidean momenta (). Doing the loop integration, one obtains
The function has a branch point at , which occurs at . By introducing a cut-off in the t–integration, one obtains
where the one-loop two-point function no longer has a branch point at . The confinement scenario also allows us to include all possible, both two-quark and multi-quark, resonance states in our calculations.
6. Some Nonleptonic Decays of Doubly Charmed Baryons
We will consider the decays that belong to the same topology class:
Their quantum numbers and interpolating currents are shown in Table 6.

Table 6.
Interpolating currents.
The W–exchange contributions to the above decays fall into two classes:
- The decays with a -baryon containing a symmetric diquark described by the interpolating current . The W–exchange contribution is strongly suppressed due to the Körner-Pati-Woo (KPW) theorem [33,34], which states that the contraction of the flavor antisymmetric current-current operator with a flavor symmetric final state configuration is zero in the limit.
- The decays with a -baryon containing a antisymmetric diquark described by the interpolating current . In this case, the W–exchange contribution is not a priori suppressed.
In our approach, the tree and W–exchange contributions are described by the Feynman diagrams shown in Figure 6.
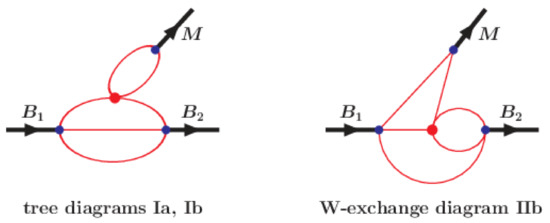
Figure 6.
Diagrams describing the nonleptonic decay .
The matrix element is written down as
where the combinations of the Wilson coefficients are given by
The factor of is set to zero in the numerical calculations. The contribution from the tree diagram factorizes into two pieces:
where
The is related to the leptonic decay constants:
The semileptonic and nonleptonic two-body decays of the doubly charmed baryons and have been studied in Reference [35] by considering those nonleptonic decay channels in which the decay proceeds solely via the factorizing contributions.
The W–exchange contribution has no factorization and is written as genuine three-loop diagram:
Here, for , and for . To verify the KPW theorem in the case of , we use the identity
Then, by shifting , one gets the same expression with opposite sign and interchange. Thus, if , then . It directly confirms the KPW–theorem.
7. Numerical Results
The transition amplitudes in terms of invariant amplitudes are written down as
The invariant amplitudes can be expressed in terms of helicity amplitudes as
Here, , and . The parity relations have taken place: . Finally, the decay widths are written as
where . All model parameters have been fixed in our previous studies, except for the size parameter of the doubly charmed baryons. As a first approximation, we equate the size parameter of doubly charmed baryons with that of singly charmed baryons, i.e., we take GeV, where we adopt the value of from Reference [36] obtained by fitting the magnetic moment of to its experimental value.
Numerical results for the helicity amplitudes and decay widths are displayed in the Table 7, Table 8, Table 9 and Table 10.

Table 7.
Decays .

Table 8.
Decays .

Table 9.
Decays .

Table 10.
Decays .
Our results highlight the importance of the KPW theorem for the nonleptonic decays when the final state involves a baryon containing a symmetric diquark. Table 7, Table 8, Table 9 and Table 10 show that the relevant W–exchange contributions are nonzero but are strongly suppressed. Nonzero values result from breaking effects, which are accounted for in our approach. Take, for example, the decay . When compared to the tree contribution, the breaking effects amount to . While the consequences of the KPW theorem for the W–exchange contribution are also incorporated in the pole model approach of Reference [37] (see Figure 7), they are not included in the final-state interaction approach of Reference [38].
Figure 7.
Schematic image of the pole model.
In Table 11, we compare our rate results with the results of some other approaches [37,38,39,40,41,42]. All calculations approximately agree on the rate of the decay , which is predicted to have a large branching ratio of . In our calculation, this mode is predicted to have by far the largest branching ratio of the decays analyzed in this paper. As concerns the decay discovered by the LHCb Collaboration [15], we find a branching ratio of using the central value of the life time measurement in Reference [14]. The small value of the branching ratio results from a substantial cancellation of the tree and W–exchange contributions. The branching ratio is somewhat smaller than the branching ratio calculated in Reference [43]. We think that the latter mode is more dominant in comparison with . We predict a branching ratio considerably smaller than the range of branching fractions calculated in Reference [37]. In our opinion, the calculations done in Reference [37] involve generous approximations for the errors, which are hard to quantify.

Table 11.
Comparison with other approaches. Abbreviation: M = NRQM, T = HQET.
The only free parameter in our approach is the size parameter of the double heavy baryons, for which we have chosen GeV in Table 7, Table 8, Table 9 and Table 10. In order to estimate the uncertainty caused by the choice of the size parameter, we allow the size parameter to vary from 0.6 to 1.135 GeV. We evaluate the mean and the mean square deviation . The results for are shown in Table 12. The rate errors amount to 6–15%. Since the dependence of the rates on is nonlinear, the central values of the rates in Table 12 do not agree with the rate values in Table 7, Table 8, Table 9 and Table 10.

Table 12.
Estimating uncertainties in the decay widths.
8. Outlook
The discovery of the doubly charmed baryon by the LHCb Collaboration [13,14] and the first observation of its two-body nonleptonic decay [15] provided strong encouragement for further theoretical analysis of the weak decays of doubly charmed baryons. As well known, such decays are described by the quark diagrams, which have several different topologies. One class of the diagrams having the so-called factorizing topology is easy to evaluate in almost model independent way, whereas another class with the internal W–exchange is extremely difficult to handle theoretically. In this lecture, we gave a basic introduction to the methods of how to calculate the relevant diagrams with any topologies in self-consistent way on the same basis. The theoretical background used for this purpose is the covariant constituent model previously developed in our papers. As the first step, we concentrated on the description of Cabibbo-favored nonleptonic two-body decays of the doubly charmed ground state baryons and where we have limited our analysis to the decay channels. It would be straightforward to also include the nonleptonic decays in the future. In addition, the study could be extended to the description of singly and doubly suppressed Cabibbo decays, not only for doubly charmed baryon decays but also for singly charmed baryon decays.
Funding
This research was partly supported by the PRISMA+Cluster of Excellence (Mainz Uni.).
Acknowledgments
I would like to thank Thomas Gutsche, Jürgen Körner, Valery Lyubovitskij, Pietro Santorelli and Zhomart Tyulemissov for their collaboration in which the results discussed in this lecture have been obtained.
Conflicts of Interest
The author declares no conflict of interest.
References
- Gell–Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214–215. [Google Scholar] [CrossRef]
- Zweig, G. An SU(3) Model for Strong Interaction Symmetry and Its Breaking; Version 1; PREPRINT CERN-TH-401; 1964; pp. 1–26. Available online: inspirehep.net/record/11881/files/CM-P00042883.pdf (accessed on 6 January 2020).
- Zweig, G. An SU(3) Model for Strong Interaction Symmetry and Its Breaking; Version 2; PREPRINT CERN-TH-412; 1964; pp. 1–68. Available online: https://cds.cern.ch/record/570209/files/CERN-TH-412.pdf (accessed on 6 January 2020).
- Bjorken, J.D.; Glashow, S.L. Elementary Particles and SU(4). Phys. Lett. 1964, 11, 255–257. [Google Scholar] [CrossRef]
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak Interactions with Lepton-Hadron Symmetry. Phys. Rev. D 1970, 2, 1285–1292. [Google Scholar] [CrossRef]
- De Rujula, A.; Georgi, H.; Glashow, S.L. Hadron Masses in a Gauge Theory. Phys. Rev. D 1975, 12, 147–162. [Google Scholar] [CrossRef]
- Körner, J.G.; Kramer, M.; Pirjol, D. Heavy baryons. Prog. Part. Nucl. Phys. 1994, 33, 787–868. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ai, X.C.; Albayrak, O.; Albrecht, M.; Ambrose, D.J.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; et al. Measurements of absolute hadronic branching fractions of Λc+ baryon. Phys. Rev. Lett. 2016, 116, 052001. [Google Scholar] [CrossRef]
- Li, Y.B.; Shen, C.P.; Yuan, C.Z.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Aushev, T.; Ayad, R.; Badhrees, I.; et al. First, measurements of absolute branching fractions of the Ξc0 baryon at Belle. Phys. Rev. Lett. 2019, 122, 082001. [Google Scholar] [CrossRef]
- Li, Y.B.; Shen, C.P.; Adachi, I.; Ahn, J.K.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aushev, T.; Ayad, R.; et al. First measurements of absolute branching fractions of the Ξc+ baryon at Belle. Phys. Rev. D 2019, 100, 031101. [Google Scholar] [CrossRef]
- Ocherashvili, A.; Moinester, M.A.; Russ, J.; Engelfried, J.; Torres, I.; Akgun, U.; Alkhazov, G.; Amaro-Reyes, J.; Atamantchouk, A.G.; Ayan, A.S.; et al. Confirmation of the double charm baryon Ξcc+(3520) via its decay pD+K-. Phys. Lett. B 2005, 628, 18. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Albero, A.A.; Ali, S.; et al. Observation of the doubly charmed baryon Ξcc++. Phys. Rev. Lett. 2017, 119, 112001. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. Measurement of the lifetime of the doubly charmed baryon Ξcc++. Phys. Rev. Lett. 2018, 121, 052002. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; Alexander, M.; et al. First, observation of the doubly charmed baryon decay Ξcc++→Ξc+π+. Phys. Rev. Lett. 2018, 121, 162002. [Google Scholar] [CrossRef] [PubMed]
- Körner, J.G.; Krämer, M. Exclusive nonleptonic charm baryon decays. Z. Phys. C 1992, 55, 659. [Google Scholar] [CrossRef]
- De Rujula, A.; Georgi, H.; Glashow, S.L. Vector Model of the Weak Interactions. Phys. Rev. D 1975, 12, 3589. [Google Scholar] [CrossRef]
- Ebert, D.; Faustov, R.N.; Galkin, V.O.; Martynenko, A.P. Mass spectra of doubly heavy baryons in the relativistic quark model. Phys. Rev. D 2002, 66, 014008. [Google Scholar] [CrossRef]
- Fleck, S.; Richard, J.M. Baryons with double charm. Prog. Theor. Phys. 1989, 82, 760. [Google Scholar] [CrossRef]
- Karliner, M.; Rosner, J.L. Baryons with two heavy quarks: Masses, production, decays, and detection. Phys. Rev. D 2014, 90, 094007. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E. Novel ideas in nonleptonic decays of double heavy baryons. Particles 2019, 2, 339–356. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Tyulemissov, Z. Ab initio three-loop calculation of the W-exchange contribution to nonleptonic decays of double charm baryons. Phys. Rev. D 2019, 99, 056013. [Google Scholar] [CrossRef]
- Fayyazuddin and Riazuddin. A Modern Introduction to Particle Physics; World Scientific: Singapore, 1994; 656p. [Google Scholar]
- Efimov, G.V.; Ivanov, M.A.; Lyubovitskij, V.E. Quark - diquark approximation of the three quark structure of baryons in the quark confinement model. Z. Phys. C 1990, 47, 583–594. [Google Scholar] [CrossRef]
- Ioffe, B.L. On The Choice Of Quark Currents In The Qcd Sum Rules For Baryon Masses. Z. Phys. C 1983, 18, 67. [Google Scholar] [CrossRef]
- Reinders, L.J.; Rubinstein, H.; Yazaki, S. Hadron Properties from QCD Sum Rules. Phys. Rept. 1985, 127, 1. [Google Scholar] [CrossRef]
- Leibovich, A.K.; Ligeti, Z.; Stewart, I.W.; Wise, M.B. Predictions for nonleptonic Lambda(b) and Theta(b) decays. Phys. Lett. B 2004, 586, 337. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Khomutenko, O.E.; Mizutani, T. Form-factors of semileptonic decays of heavy mesons in the quark confinement model. Phys. Rev. D 1992, 46, 3817. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Kalinovsky, Y.L.; Roberts, C.D. Survey of heavy meson observables. Phys. Rev. D 1999, 60, 034018. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Tran, C.T. Exclusive decays B→ℓ-ν¯ and B→D(*)ℓ-ν¯ in the covariant quark model. Phys. Rev. D 2015, 92, 114022. [Google Scholar] [CrossRef]
- Branz, T.; Faessler, A.; Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E. Relativistic constituent quark model with infrared confinement. Phys. Rev. D 2010, 81, 034010. [Google Scholar] [CrossRef]
- Vermaseren, J.A.M. The FORM project. Nucl. Phys. Proc. Suppl. 2008, 183, 19. [Google Scholar] [CrossRef]
- Körner, J.G. Octet behaviour of single-particle matrix elements <B′|H(W)|B> and <M′|H(W)|M> using a weak current current quark Hamiltonian. Nucl. Phys. B 1971, 25, 282. [Google Scholar]
- Pati, J.C.; Woo, C.H. Delta I=1/2 rule with fermion quarks. Phys. Rev. D 1971, 3, 2920. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G. Lyubovitskij, V.E.; Tyulemissov, Z. Analysis of the semileptonic and nonleptonic two-body decays of the double heavy charm baryon states Ξcc++,Ξcc++ and Ωcc+. Phys. Rev. D 2019, 100, 114037. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P. Semileptonic decays Λc+→Λℓ+νℓ(ℓ=e,μ) in the covariant quark model and comparison with the new absolute branching fraction measurements of Belle and BESIII. Phys. Rev. D 2016, 93, 034008. [Google Scholar] [CrossRef]
- Sharma, N.; Dhir, R. Estimates of W–exchange contributions to Ξcc decays. Phys. Rev. D 2017, 96, 113006. [Google Scholar] [CrossRef]
- Jiang, L.J.; He, B.; Li, R.H. Weak Decays of Doubly Heavy Baryons: Bcc→BcV. Eur. Phys. J. C 2018, 78, 961. [Google Scholar] [CrossRef]
- Dhir, R.; Sharma, N. Weak decays of doubly heavy charm Ωcc+ baryon. Eur. Phys. J. C 2018, 78, 743. [Google Scholar] [CrossRef]
- Wang, W.; Yu, F.S.; Zhao, Z.X. Weak decays of doubly heavy baryons: The 1/2→1/2 case. Eur. Phys. J. C 2017, 77, 781. [Google Scholar] [CrossRef]
- Yu, F.S.; Jiang, H.Y.; Li, R.H.; Lü, C.D.; Wang, W.; Zhao, Z.X. Discovery Potentials of Doubly Charmed Baryons. Chin. Phys. C 2018, 42, 051001. [Google Scholar] [CrossRef]
- Kiselev, V.V.; Likhoded, A.K. Baryons with two heavy quarks. Phys. Usp. 2002, 45, 455. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E. Decay chain information on the newly discovered double charm baryon state Ξcc++. Phys. Rev. D 2017, 96, 054013. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).