Meson Condensation
Abstract
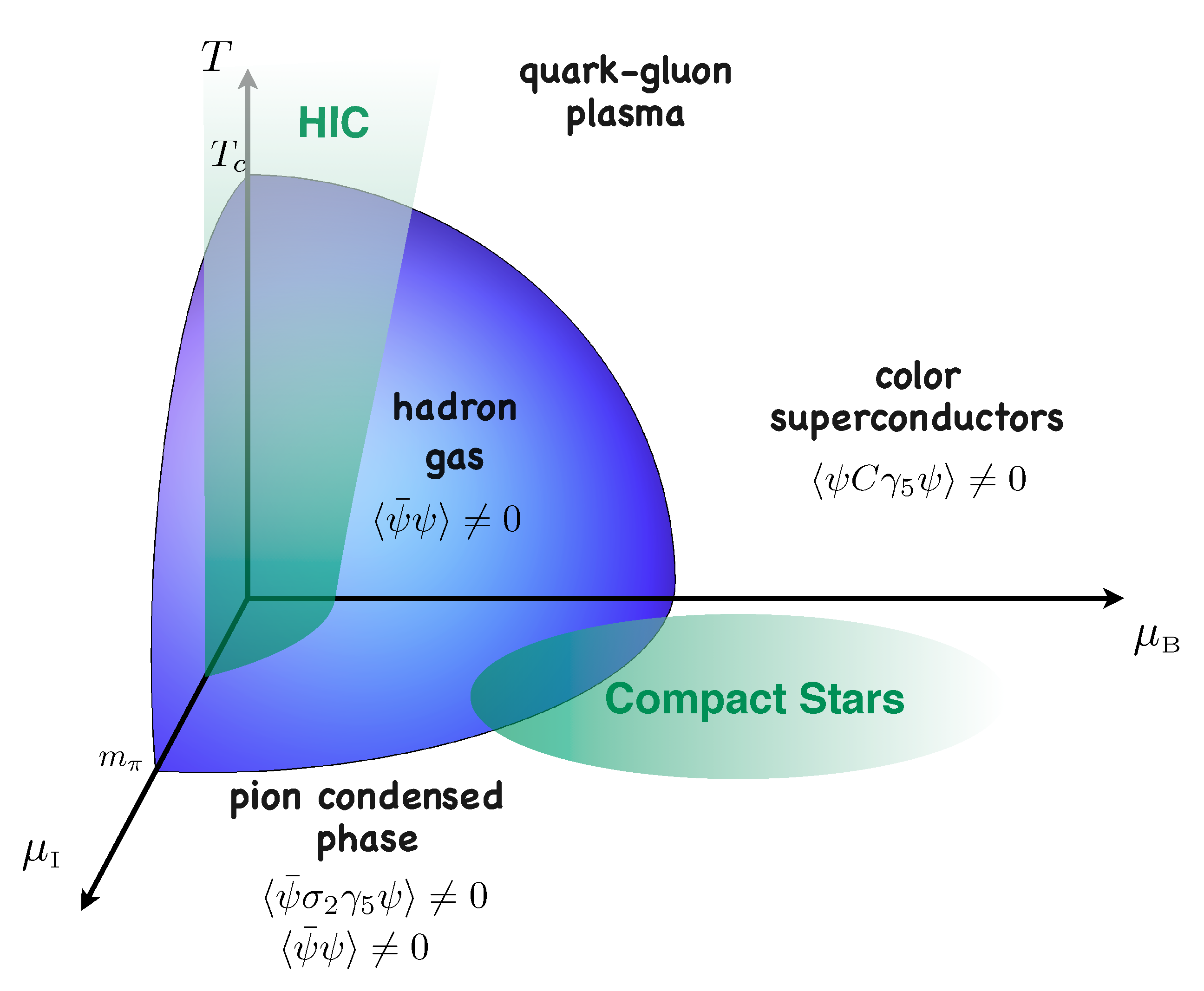
1. Introduction
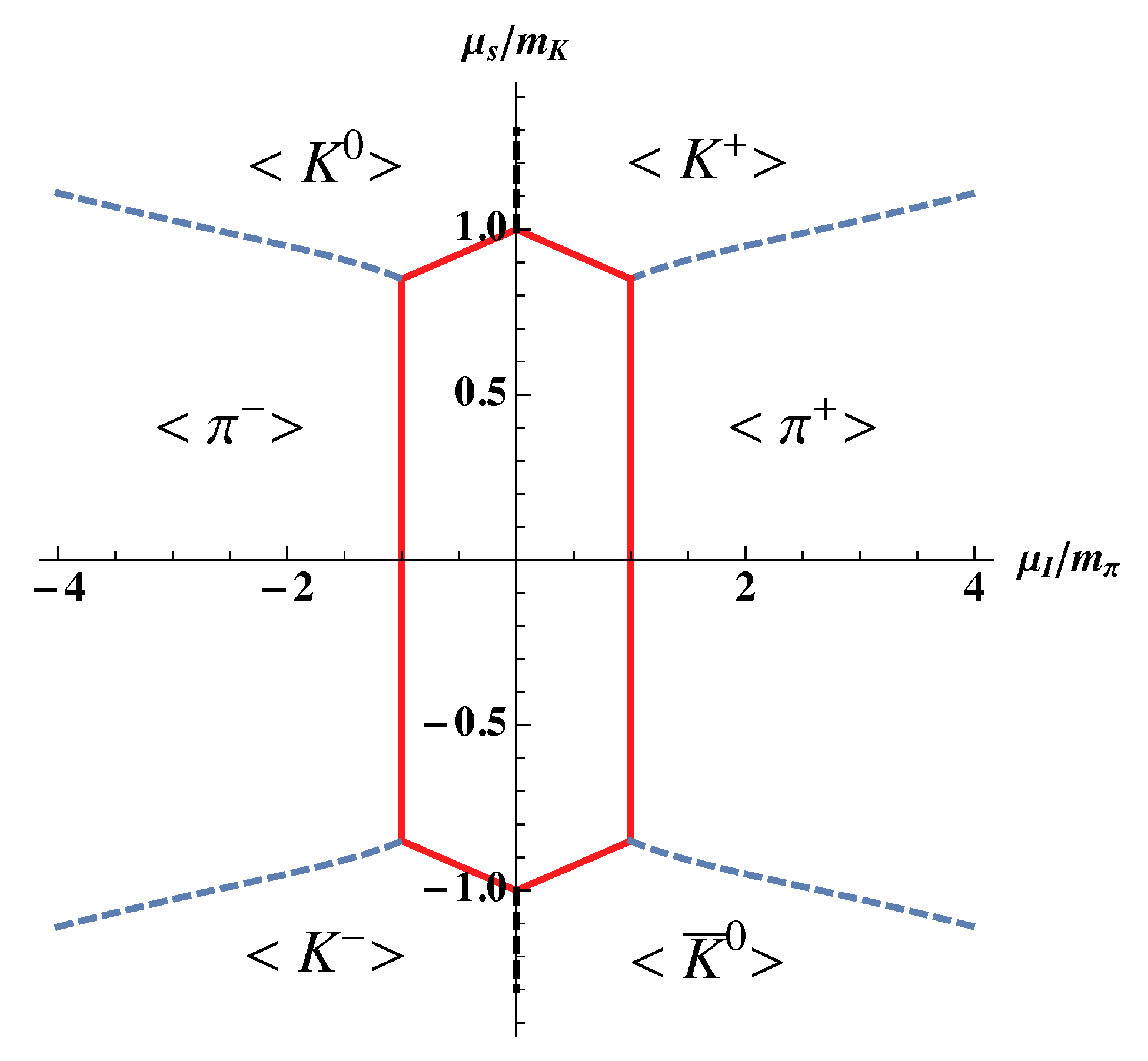
Outside the Beta-Equilibrated Sheet
2. The Early Works and Models
2.1. The Equilibrium Configuration
- The particles must be bosons, as He atoms, or boson-like, as Cooper pairs in the BCS theory
- The system has to be sufficiently cold: the particle condensation can be disrupted by the thermal disorder
- The particles must be stable.
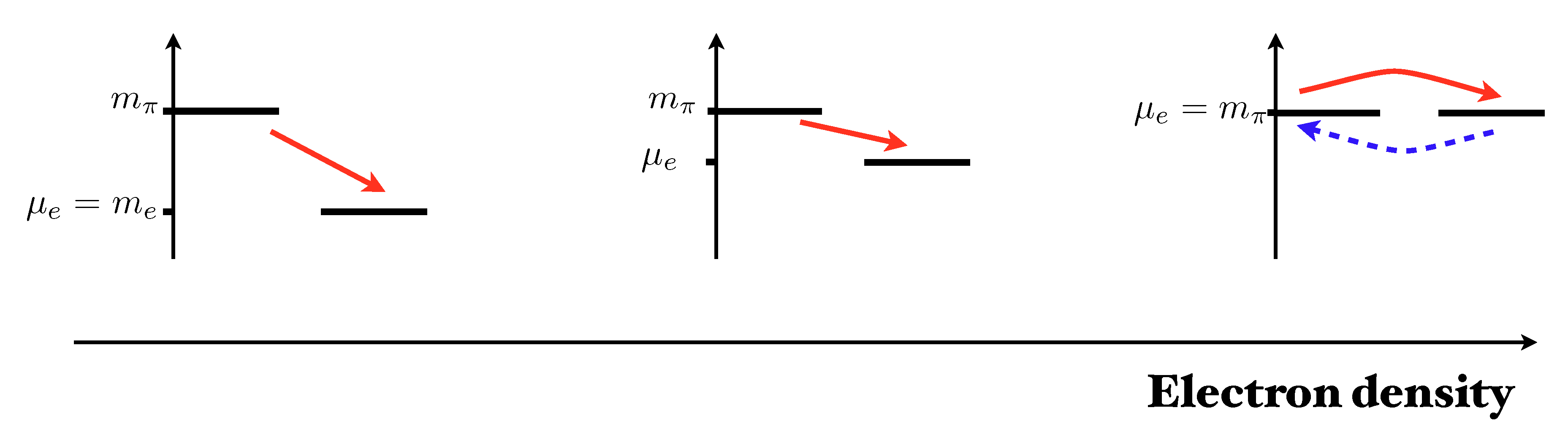
2.2. Including in-Medium Effects
3. Group Theory Analysis
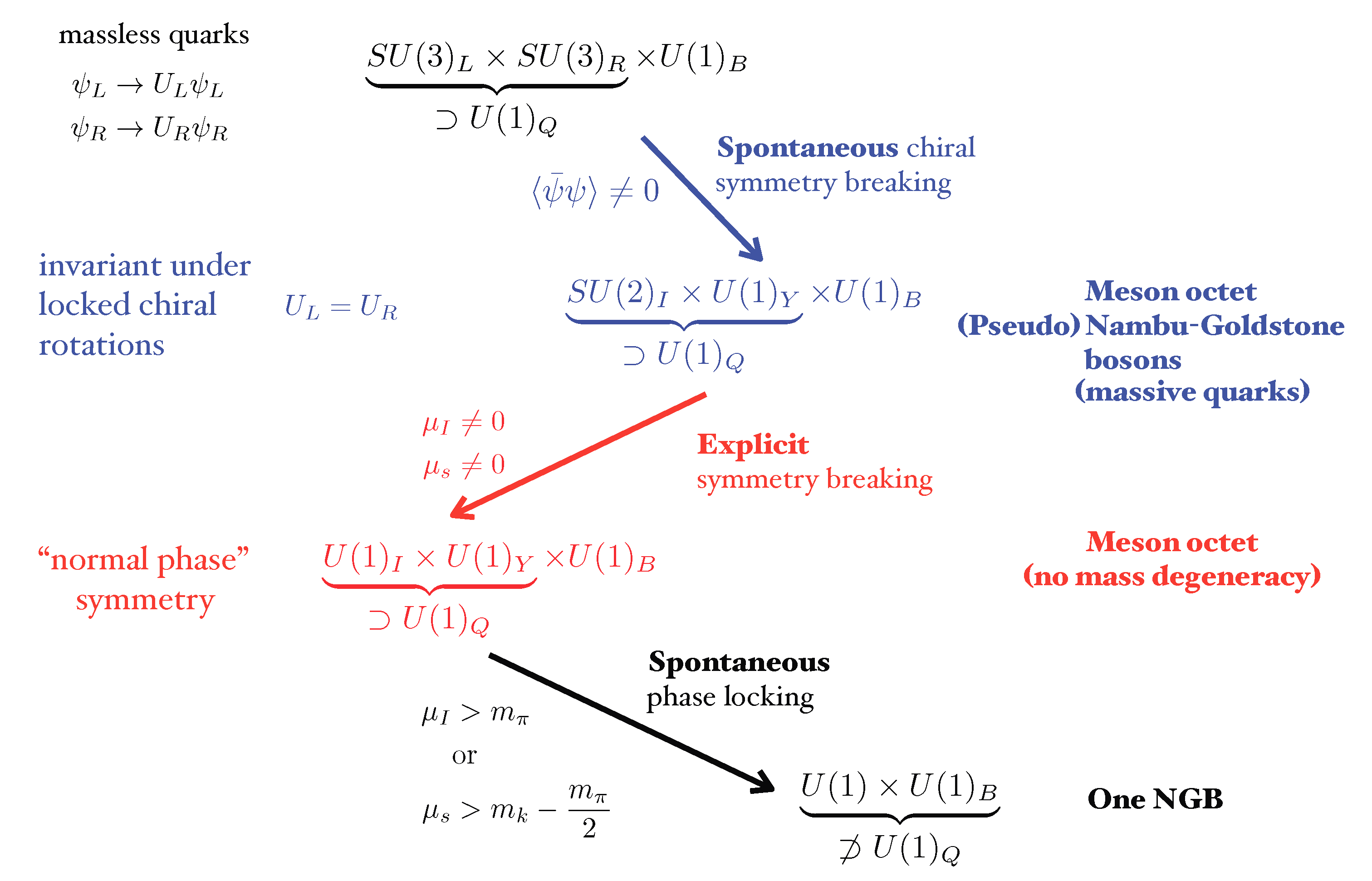
3.1. Global Symmetries of QCD
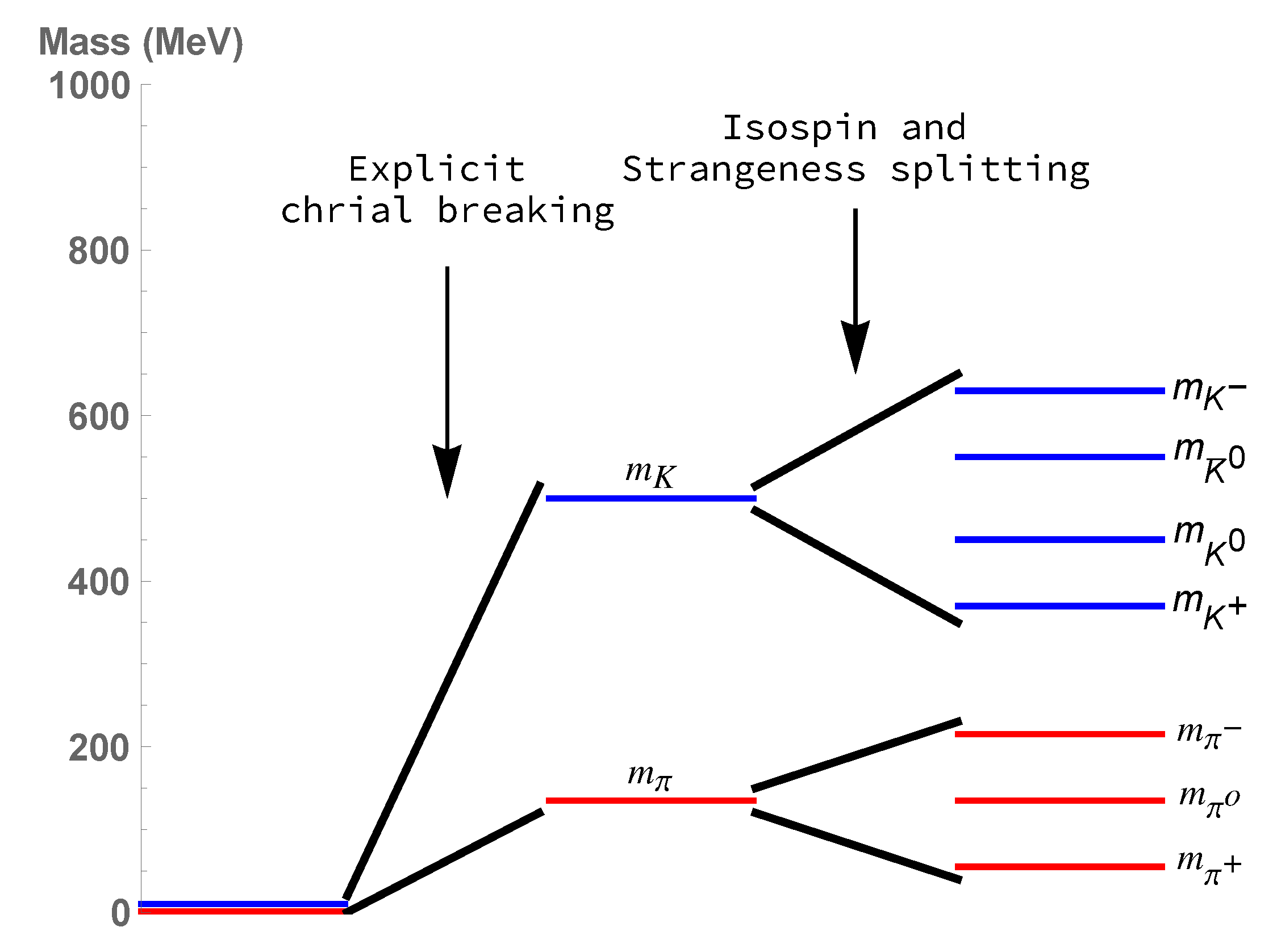
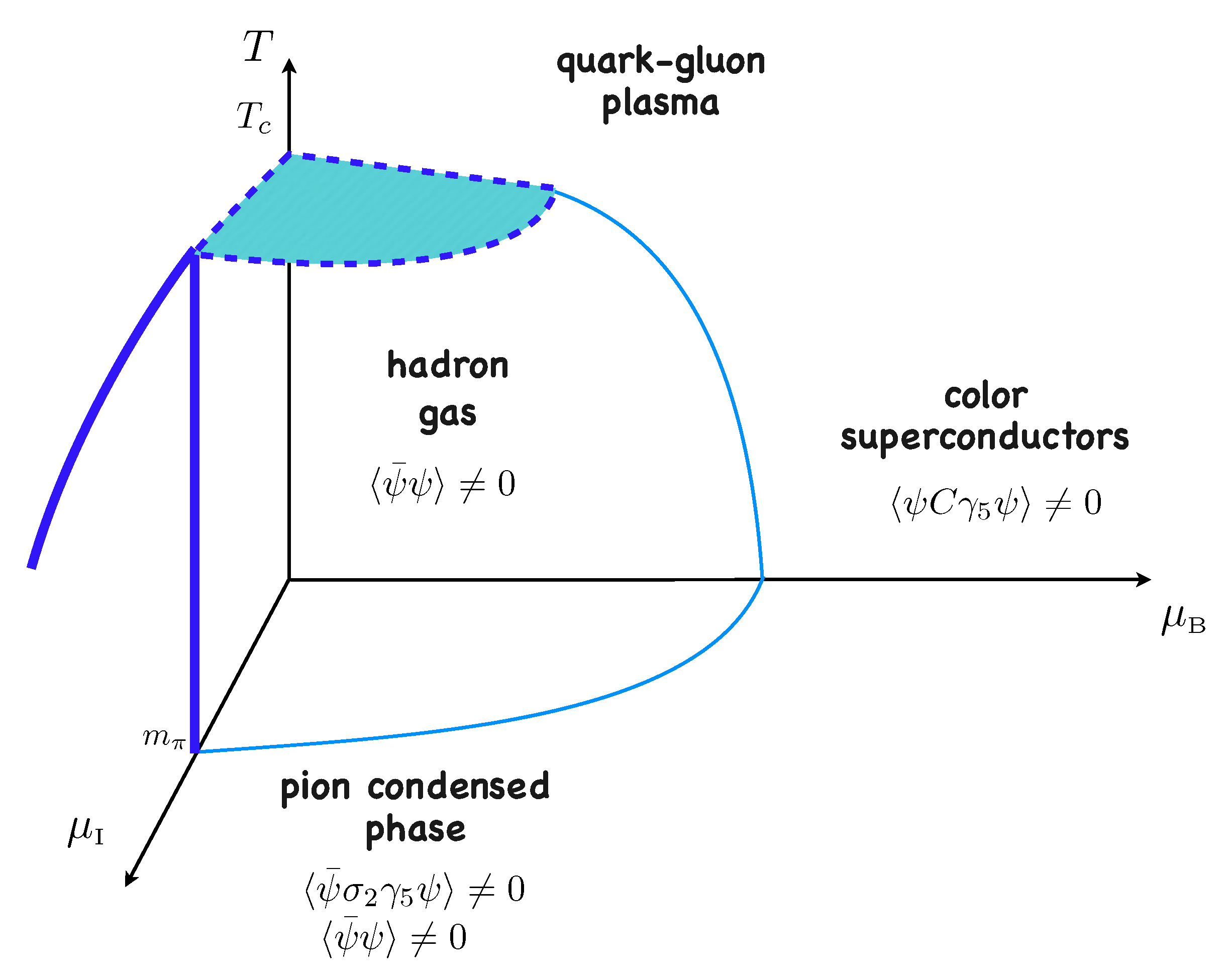
3.2. Phases of Condensed Mesons
4. Modern Approaches
4.1. Chiral Perturbation Theory
4.1.1. Ground State
- The normal phase is favored forwith the trivial vev . The nonvanishing condensates are the three chiral condensates, see Equation (7),where the subscript indicates the quark flavor and is the value of the chiral condensate in vacuum. In the normal phase the values of the chiral condensates are not affected by the chemical potentials. The pressure is given byand thus the isospin and strangeness number densities vanish, that is
- The condensed phase is favored forresulting in the vacuum in Equation (59) withdetermined by maximizing the static Lagrangian in Equation (58). The condensates are given byand the pressure produced by the condensation of pions is given by [10,11]where the normal phase pressure has been subtracted. This expression is valid for both and ; it is of course insensitive to the kaon mass and the strange quark chemical potential. The number densities areand the equation of state [27] is
- The condensed phase is favored forresulting in the vacuum in Equation (60) withwhere is the relevant combination of chemical potentials, because has isospin and strangeness 1. The condensates are given byand the normalized pressure bywhich consents to obtain the number densitiesThe EoS is
4.1.2. Low-Energy Excitations
4.2. The Nambu-Jona Lasinio Model
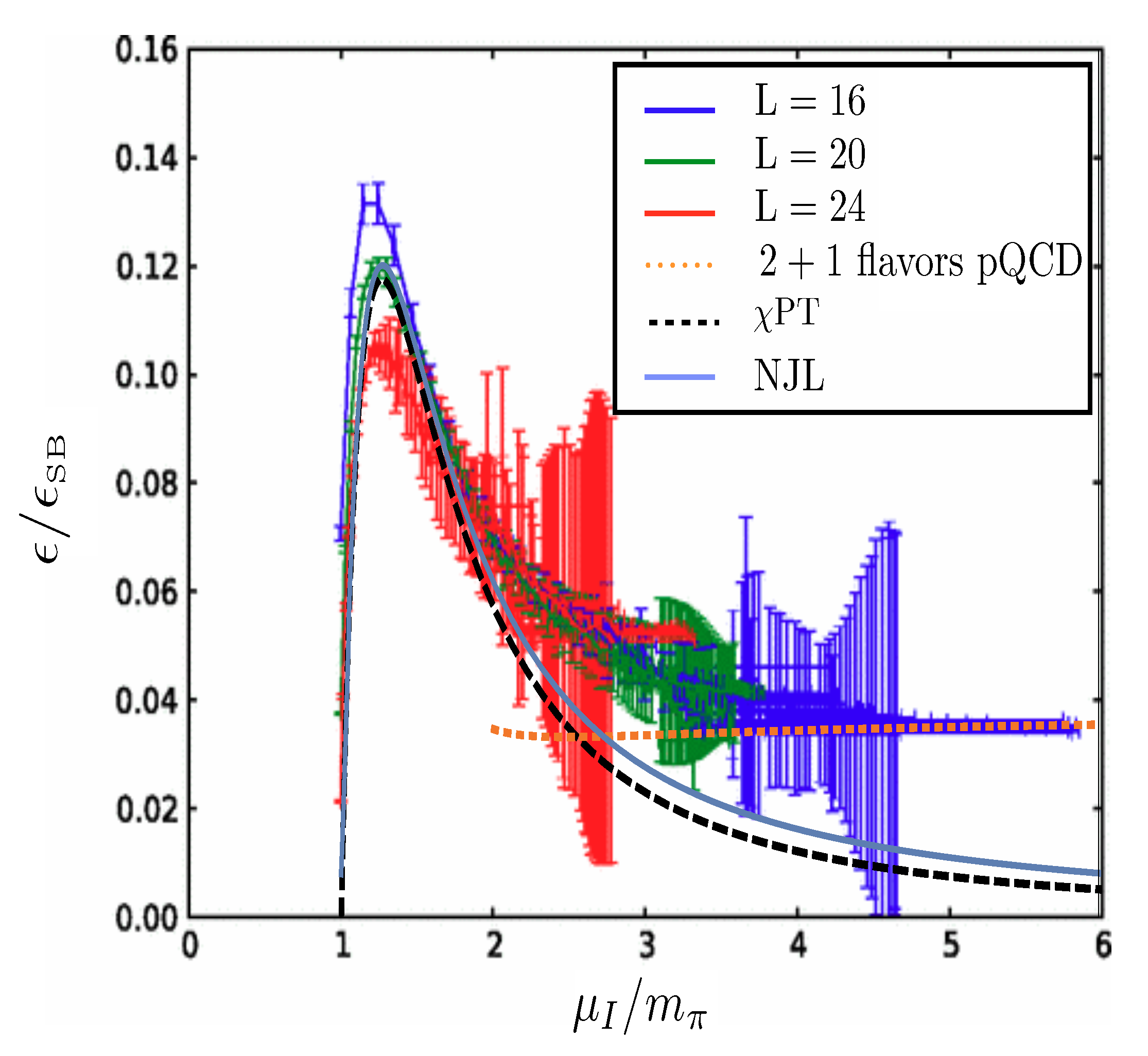
4.3. Comparison with Lattice QCD
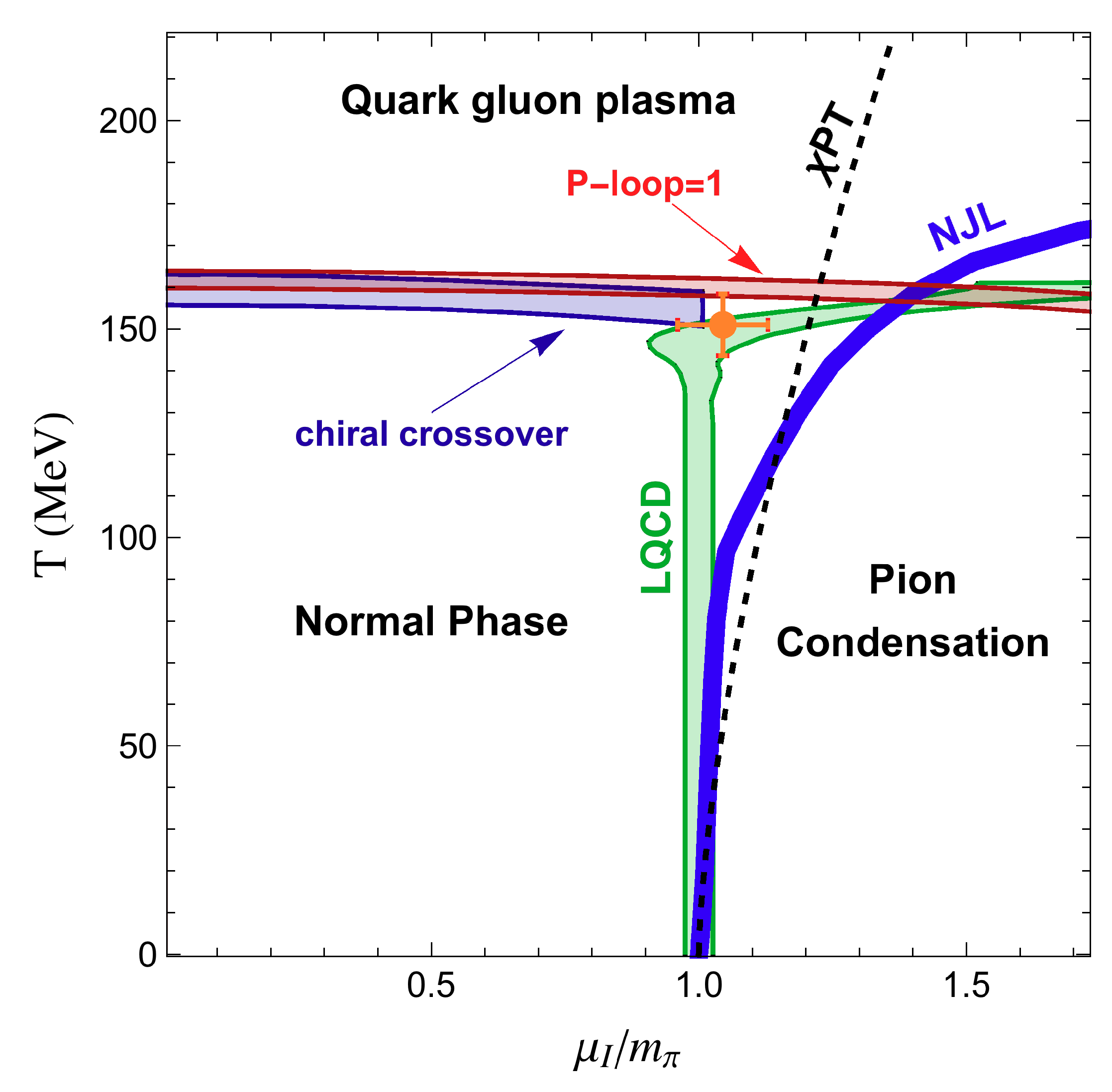
Nonvanishing Temperature
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Cabibbo, N.; Parisi, G. Exponential Hadronic Spectrum and Quark Liberation. Phys. Lett. B 1975, 59, 67–69. [Google Scholar] [CrossRef]
- Gyulassy, M. The QGP Discovered at RHIC. In Structure and Dynamics of Elementary Matter, Proceedings of the NATO Advanced Study Institute, Camyuva-Kemer, Turkey, 22 September–2 October 2003; Springer: Berlin/Heidelberg, Germany, 2004; pp. 159–182. [Google Scholar]
- Shuryak, E. Physics of Strongly coupled Quark-Gluon Plasma. Prog. Part. Nucl. Phys. 2009, 62, 48–101. [Google Scholar] [CrossRef]
- Satz, H. Extreme states of matter in strong interaction physics: An introduction. Lect. Notes Phys. 2012, 841, 1–239. [Google Scholar] [CrossRef]
- Rajagopal, K.; Wilczek, F. The Condensed matter physics of QCD. Front. Part. Phys. 2001, 3, 2061–2151. [Google Scholar]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schafer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Anglani, R.; Casalbuoni, R.; Ciminale, M.; Ippolito, N.; Gatto, R.; Mannarelli, M.; Ruggieri, M. Crystalline color superconductors. Rev. Mod. Phys. 2014, 86, 509–561. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Is there still any Tc mystery in lattice QCD? Results with physical masses in the continuum limit III. JHEP 2010, 09, 073. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Laermann, E.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Son, D.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef]
- Kogut, J.; Toublan, D. QCD at small nonzero quark chemical potentials. Phys. Rev. D 2001, 64, 034007. [Google Scholar] [CrossRef]
- Migdal, A.B. Stability of vacuum and limiting fields. Zh. Eksp. Teor. Fiz. 1971, 61, 2209–2224. [Google Scholar] [CrossRef]
- Migdal, A.B. Vacuum Stability and Limiting Fields. Soviet Phys. Uspekhi 1972, 14, 813. [Google Scholar] [CrossRef]
- Sawyer, R.F. Condensed pi- phase in neutron star matter. Phys. Rev. Lett. 1972, 29, 382–385. [Google Scholar] [CrossRef]
- Scalapino, D.J. Pi-condensate in dense nuclear matter. Phys. Rev. Lett. 1972, 29, 386–388. [Google Scholar] [CrossRef]
- Kogut, J.; Manassah, J.T. π−condensation and neutron star cooling. Phys. Lett. A 1972, 41, 129–131. [Google Scholar] [CrossRef]
- Migdal, A.B. Pi condensation in nuclear matter. Phys. Rev. Lett. 1973, 31, 257–260. [Google Scholar] [CrossRef]
- Baym, G.; Campbell, D.K. Chiral Symmetry and Pion Condensation. In Mesons in Nuclei; Rho, M., Wilkinson, D., Eds.; North Holland Pub. Co.: Amsterdam, The Netherlands, 1978; p. 1031. [Google Scholar]
- Kaplan, D.B.; Nelson, A.E. Strange Goings on in Dense Nucleonic Matter. Phys. Lett. B 1986, 175, 57–63. [Google Scholar] [CrossRef]
- Dominguez, C.; Loewe, M.; Rojas, J. Pion and nucleon thermal widths in the linear sigma model. Phys. Lett. B 1994, 320, 377–380. [Google Scholar] [CrossRef]
- Birse, M.C.; Cohen, T.D.; McGovern, J.A. Phases of QCD with nonvanishing isospin density. Phys. Lett. B 2001, 516, 27–32. [Google Scholar] [CrossRef]
- Splittorff, K.; Toublan, D.; Verbaarschot, J.J.M. Thermodynamics of chiral symmetry at low densities. Nucl. Phys. B 2002, 639, 524–548. [Google Scholar] [CrossRef]
- Loewe, M.; Villavicencio, C. Thermal pions at finite isospin chemical potential. Phys. Rev. D 2003, 67, 074034. [Google Scholar] [CrossRef]
- Loewe, M.; Villavicencio, C. Thermal pion masses in the second phase: |mu(I)|>m(pi). Phys. Rev. D 2004, 70, 074005. [Google Scholar] [CrossRef]
- Loewe, M.; Villavicencio, C. Pion stability in a hot dense media. arXiv 2011, arXiv:1107.3859. [Google Scholar]
- Mammarella, A.; Mannarelli, M. Intriguing aspects of meson condensation. Phys. Rev. D 2015, 92, 085025. [Google Scholar] [CrossRef]
- Carignano, S.; Mammarella, A.; Mannarelli, M. Equation of state of imbalanced cold matter from chiral perturbation theory. Phys. Rev. D 2016, 93, 051503. [Google Scholar] [CrossRef]
- Loewe, M.; Raya, A.; Villavicencio, C. Metastable Pions in Dense Media. Phys. Rev. D 2016, 95, 096013. [Google Scholar] [CrossRef]
- Carignano, S.; Lepori, L.; Mammarella, A.; Mannarelli, M.; Pagliaroli, G. Scrutinizing the pion condensed phase. Eur. Phys. J. A 2017, 53, 35. [Google Scholar] [CrossRef]
- Lepori, L.; Mannarelli, M. Multicomponent meson superfluids in chiral perturbation theory. Phys. Rev. D 2019, 99, 096011. [Google Scholar] [CrossRef]
- Adhikari, P.; Andersen, J.O.; Kneschke, P. QCD at finite isospin density: chiral perturbation theory confronts lattice data. arXiv 2019, arXiv:1909.01131. [Google Scholar]
- Tawfik, A.N.; Diab, A.M.; Ghoneim, M.T.; Anwer, H. SU(3) Polyakov Linear-Sigma Model With Finite Isospin Asymmetry: QCD Phase Diagram. arXiv 2019, arXiv:1904.09890. [Google Scholar]
- Mishustin, I.N.; Anchishkin, D.V.; Satarov, L.M.; Stashko, O.S.; Stoecker, H. Condensation of interacting scalar bosons at finite temperatures. Phys. Rev. C 2019, 100, 022201. [Google Scholar] [CrossRef]
- Barducci, A.; Casalbuoni, R.; De Curtis, S.; Gatto, R.; Pettini, G. Pion Decay Constant at Finite Temperature and Density. Phys. Rev. D 1990, 42, 1757–1763. [Google Scholar] [CrossRef] [PubMed]
- Toublan, D.; Kogut, J.B. Isospin chemical potential and the QCD phase diagram at nonzero temperature and baryon chemical potential. Phys. Lett. B 2003, 564, 212–216. [Google Scholar] [CrossRef][Green Version]
- Barducci, A.; Casalbuoni, R.; Pettini, G.; Ravagli, L. A Calculation of the QCD phase diagram at finite temperature, and baryon and isospin chemical potentials. Phys. Rev. D 2004, 69, 096004. [Google Scholar] [CrossRef]
- Barducci, A.; Casalbuoni, R.; Pettini, G.; Ravagli, L. Pion and kaon condensation in a 3-flavor NJL model. Phys. Rev. D 2005, 71, 016011. [Google Scholar] [CrossRef]
- He, L.Y.; Jin, M.; Zhuang, P.F. Pion superfluidity and meson properties at finite isospin density. Phys. Rev. D 2005, 71, 116001. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Gapless pion condensation in quark matter with finite baryon density. J. Phys. G 2006, 32, 599–608. [Google Scholar] [CrossRef][Green Version]
- Ebert, D.; Klimenko, K.G. Pion condensation in electrically neutral cold matter with finite baryon density. Eur. Phys. J. C 2006, 46, 771–776. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, S.; Mustafa, M.G.; Ray, R. Thermodynamics of the PNJL model with nonzero baryon and isospin chemical potentials. Phys. Rev. D 2007, 75, 094015. [Google Scholar] [CrossRef]
- He, L.; Zhuang, P. Phase structure of Nambu-Jona-Lasinio model at finite isospin density. Phys. Lett. B 2005, 615, 93–101. [Google Scholar] [CrossRef]
- He, L.; Jin, M.; Zhuang, P. Pion Condensation in Baryonic Matter: from Sarma Phase to Larkin-Ovchinnikov- Fudde-Ferrell Phase. Phys. Rev. D 2006, 74, 036005. [Google Scholar] [CrossRef]
- Sun, G.F.; He, L.; Zhuang, P. BEC-BCS crossover in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2007, 75, 096004. [Google Scholar] [CrossRef]
- Andersen, J.O.; Kyllingstad, L. Pion Condensation in a two-flavor NJL model: the role of charge neutrality. J. Phys. G 2009, 37, 015003. [Google Scholar] [CrossRef]
- Abuki, H.; Ciminale, M.; Gatto, R.; Ippolito, N.D.; Nardulli, G.; Ruggieri, M. Electrical neutrality and pion modes in the two flavor PNJL model. Phys. Rev. D 2008, 78, 014002. [Google Scholar] [CrossRef]
- Abuki, H.; Anglani, R.; Gatto, R.; Pellicoro, M.; Ruggieri, M. The Fate of pion condensation in quark matter: From the chiral to the real world. Phys. Rev. D 2009, 79, 034032. [Google Scholar] [CrossRef]
- Mu, C.f.; He, L.y.; Liu, Y.x. Evaluating the phase diagram at finite isospin and baryon chemical potentials in the Nambu-Jona-Lasinio model. Phys. Rev. D 2010, 82, 056006. [Google Scholar] [CrossRef]
- Xia, T.; He, L.; Zhuang, P. Three-flavor Nambu–Jona-Lasinio model at finite isospin chemical potential. Phys. Rev. D 2013, 88, 056013. [Google Scholar] [CrossRef]
- Xia, T.; Zhuang, P. Quark-antiquark Scattering Phase Shift and Meson Spectral Function in Pion Superfluid. Chin. Phys. D 2014, 43, 054103. [Google Scholar] [CrossRef]
- Chao, J.; Huang, M.; Radzhabov, A. Charged pion condensation under parallel electromagnetic fields. arXiv 2018, arXiv:1805.00614. [Google Scholar]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Chiral imbalanced hot and dense quark matter: NJL analysis at the physical point and comparison with lattice QCD. Eur. Phys. J. C 2019, 79, 151. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Dualities and inhomogeneous phases in dense quark matter with chiral and isospin imbalances in the framework of effective model. JHEP 2019, 06, 006. [Google Scholar] [CrossRef]
- Khunjua, T.; Klimenko, K.; Zhokhov, R. Charged Pion Condensation in Dense Quark Matter: Nambu–Jona-Lasinio Model Study. Symmetry 2019, 11, 778. [Google Scholar] [CrossRef]
- Avancini, S.S.; Bandyopadhyay, A.; Duarte, D.C.; Farias, R.L.S. Cold QCD at finite isospin density: confronting effective models with recent lattice data. arXiv 2019, arXiv:1907.09880. [Google Scholar]
- Lu, Z.Y.; Xia, C.J.; Ruggieri, M. Thermodynamics and susceptibilities of isospin imbalanced QCD matter. arXiv 2019, arXiv:1907.11497. [Google Scholar]
- Klevansky, S.P. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Andersen, J.O.; Naylor, W.R.; Tranberg, A. Phase diagram of QCD in a magnetic field: A review. Rev. Mod. Phys. 2016, 88, 025001. [Google Scholar] [CrossRef]
- Adhikari, P.; Andersen, J.O.; Kneschke, P. On-shell parameter fixing in the quark-meson model. Phys. Rev. D 2017, 95, 036017. [Google Scholar] [CrossRef]
- Adhikari, P.; Andersen, J.O.; Kneschke, P. Pion condensation and phase diagram in the Polyakov-loop quark-meson model. Phys. Rev. D 2018, 98, 074016. [Google Scholar] [CrossRef]
- Andersen, J.O.; Kneschke, P. Chiral density wave versus pion condensation at finite density and zero temperature. Phys. Rev. D 2018, 97, 076005. [Google Scholar] [CrossRef]
- Andersen, J.O.; Adhikari, P.; Kneschke, P. Pion Condensation and QCD Phase Diagram at Finite Isospin Density. In Proceedings of the 13th Conference on Quark Confinement and the Hadron Spectrum (Confinement XIII), Maynooth, Ireland, 31 July–6 August 2018. [Google Scholar]
- Klein, B.; Toublan, D.; Verbaarschot, J.J.M. The QCD phase diagram at nonzero temperature, baryon and isospin chemical potentials in random matrix theory. Phys. Rev. D 2003, 68, 014009. [Google Scholar] [CrossRef]
- Klein, B.; Toublan, D.; Verbaarschot, J. Diquark and pion condensation in random matrix models for two color QCD. Phys. Rev. D 2005, 72, 015007. [Google Scholar] [CrossRef]
- Lv, M.; Li, D.; He, S. Pion condensation in a soft-wall AdS/QCD model. arXiv 2018, arXiv:1811.03828. [Google Scholar]
- Graf, T.; Schaffner-Bielich, J.; Fraga, E.S. Perturbative thermodynamics at nonzero isospin density for cold QCD. arXiv 2015, arXiv:1511.09457. [Google Scholar]
- Andersen, J.O.; Haque, N.; Mustafa, M.G.; Strickland, M. Three-loop HTLpt thermodynamics at finite temperature and isospin chemical potential. arXiv 2015, arXiv:1511.04660. [Google Scholar]
- Alford, M.G.; Kapustin, A.; Wilczek, F. Imaginary chemical potential and finite fermion density on the lattice. Phys. Rev. D 1999, 59, 054502. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. Quenched lattice QCD at finite isospin density and related theories. Phys. Rev. D 2002, 66, 014508. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. Lattice QCD at finite isospin density at zero and finite temperature. Phys. Rev. D 2002, 66, 034505. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. The Finite temperature transition for 2-flavor lattice QCD at finite isospin density. Phys. Rev. D 2004, 70, 094501. [Google Scholar] [CrossRef]
- Beane, S.R.; Detmold, W.; Luu, T.C.; Orginos, K.; Savage, M.J.; Torok, A. Multi-Pion Systems in Lattice QCD and the Three-Pion Interaction. Phys. Rev. Lett. 2008, 100, 082004. [Google Scholar] [CrossRef]
- Detmold, W.; Savage, M.J.; Torok, A.; Beane, S.R.; Luu, T.C.; Orginos, K.; Parreno, A. Multi-Pion States in Lattice QCD and the Charged-Pion Condensate. Phys. Rev. D 2008, 78, 014507. [Google Scholar] [CrossRef]
- Detmold, W.; Orginos, K.; Savage, M.J.; Walker-Loud, A. Kaon Condensation with Lattice QCD. Phys. Rev. D 2008, 78, 054514. [Google Scholar] [CrossRef]
- Detmold, W.; Smigielski, B. Lattice QCD study of mixed systems of pions and kaons. Phys. Rev. D 2011, 84, 014508. [Google Scholar] [CrossRef]
- Detmold, W.; Orginos, K.; Shi, Z. Lattice QCD at non-zero isospin chemical potential. Phys. Rev. D 2012, 86, 054507. [Google Scholar] [CrossRef]
- Endrödi, G. Magnetic structure of isospin-asymmetric QCD matter in neutron stars. Phys. Rev. D 2014, 90, 094501. [Google Scholar] [CrossRef]
- Janssen, O.; Kieburg, M.; Splittorff, K.; Verbaarschot, J.J.M.; Zafeiropoulos, S. Phase Diagram of Dynamical Twisted Mass Wilson Fermions at Finite Isospin Chemical Potential. Phys. Rev. D 2016, 93, 094502. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G. QCD phase diagram with isospin chemical potential. arXiv 2016, arXiv:1611.06758. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G. Reliability of Taylor expansions in QCD. Phys. Rev. D 2019, 99, 014518. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD at finite isospin chemical potential. EPJ Web Conf. 2018, 175, 07020. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD at nonzero isospin asymmetry. arXiv 2018, arXiv:1811.06004. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; WILEY-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 1983. [Google Scholar]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: New York, NY, USA, 1997. [Google Scholar]
- Migdal, A.B.; Saperstein, E.; Troitsky, M.; Voskresensky, D. Pion degrees of freedom in nuclear matter. Phys. Rept. 1990, 192, 179–437. [Google Scholar] [CrossRef]
- Cameron, A.G. Neutron Star Models. Astrophys. J. 1959, 130, 884. [Google Scholar] [CrossRef]
- Ambartsumyan, V.A.; Saakyan, G.S. The Degenerate Superdense Gas of Elementary Particles. Sov. Astron. 1960, 4, 187. [Google Scholar]
- Salpeter, E.E. Matter at high densities. Ann. Phys. 1960, 11, 393–413. [Google Scholar] [CrossRef]
- Ambartsumyan, V.A.; Saakyan, G.S. Internal Structure of Hyperon Configurations of Stellar Masses. Sov. Astron. 1962, 5, 779. [Google Scholar]
- Bahcall, J.N.; Wolf, R.A. Neutron Stars. 1. Properties at Absolute Zero Temperature. Phys. Rev. 1965, 140, B1445–B1451. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1274. [Google Scholar] [CrossRef]
- Alford, M.G.; Harris, S.P. Beta equilibrium in neutron star mergers. Phys. Rev. C 2018, 98, 065806. [Google Scholar] [CrossRef]
- Sadzikowski, M. Coexistence of pion condensation and color superconductivity in two flavor quark matter. Phys. Lett. B 2003, 553, 45–50. [Google Scholar] [CrossRef][Green Version]
- Buballa, M.; Carignano, S. Inhomogeneous chiral condensates. Prog. Part. Nucl. Phys. 2015, 81, 39–96. [Google Scholar] [CrossRef]
- Carignano, S.; Mannarelli, M.; Anzuini, F.; Benhar, O. Crystalline phases by an improved gradient expansion technique. Phys. Rev. D 2018, 97, 036009. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica 1979, 96, 327. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142. [Google Scholar] [CrossRef]
- Georgi, H. Weak Interactions and Modern Particle Theory; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Leutwyler, H. On the foundations of chiral perturbation theory. Ann. Phys. 1994, 235, 165–203. [Google Scholar] [CrossRef]
- Ecker, G. Chiral perturbation theory. Prog. Part. Nucl. Phys. 1995, 35, 1–80. [Google Scholar] [CrossRef]
- Leutwyler, H. Phonons as goldstone bosons. Helv. Phys. Acta 1997, 70, 275–286. [Google Scholar]
- Pich, A. Effective Field Theory: Course. In Probing the Standard Model of Particle Interactions, Proceedings of the Summer School in Theoretical Physics, NATO Advanced Study Institute, 68th session, Les Houches, France, 28 July–5 September 1997; North Holland: Amsterdam, The Netherlands, 1998; pp. 949–1049. [Google Scholar]
- Scherer, S. Introduction to chiral perturbation theory. Adv. Nucl. Phys. 2003, 27, 277. [Google Scholar]
- Scherer, S.; Schindler, M.R. A Chiral perturbation theory primer. arXiv 2005, arXiv:hep-ph/0505265. [Google Scholar]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D. On two color QCD with baryon chemical potential. Phys. Lett. B 1999, 464, 183–191. [Google Scholar] [CrossRef]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M.; Zhitnitsky, A. QCD—Like theories at finite baryon density. Nucl. Phys. B 2000, 582, 477–513. [Google Scholar] [CrossRef]
- Hands, S.; Montvay, I.; Morrison, S.; Oevers, M.; Scorzato, L.; Skullerud, J. Numerical study of dense adjoint matter in two color QCD. Eur. Phys. J. C 2000, 17, 285–302. [Google Scholar] [CrossRef][Green Version]
- Kogut, J.B.; Sinclair, D.K.; Hands, S.J.; Morrison, S.E. Two color QCD at nonzero quark number density. Phys. Rev. D 2001, 64, 094505. [Google Scholar] [CrossRef]
- Brauner, T. On the chiral perturbation theory for two-flavor two-color QCD at finite chemical potential. Mod. Phys. Lett. A 2006, 21, 559–570. [Google Scholar] [CrossRef]
- Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Yu.; Molochkov, A.V.; Nikolaev, A.A. Study of the phase diagram of dense two-color QCD within lattice simulation. Phys. Rev. D 2016, 94, 114510. [Google Scholar] [CrossRef]
- Adhikari, P.; Beleznay, S.B.; Mannarelli, M. Finite Density Two Color Chiral Perturbation Theory Revisited. Eur. Phys. J. C 2018, 78, 441. [Google Scholar] [CrossRef]
- Le Bellac, M. Thermal Field Theory. In Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Nambu, Y. Axial vector current conservation in weak interactions. Phys. Rev. Lett. 1960, 4, 380–382. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on An Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Ebert, D.; Volkov, M.K. Composite Meson Model with Vector Dominance Based on U(2) Invariant Four Quark Interactions. Z. Phys. C 1983, 16, 205. [Google Scholar] [CrossRef]
- Ebert, D.; Reinhardt, H. Effective Chiral Hadron Lagrangian with Anomalies and Skyrme Terms from Quark Flavor Dynamics. Nucl. Phys. B 1986, 271, 188–226. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Alford, M.G.; Rajagopal, K.; Wilczek, F. Color flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef]
- Asakawa, M.; Yazaki, K. Chiral Restoration at Finite Density and Temperature. Nucl. Phys. A 1989, 504, 668–684. [Google Scholar] [CrossRef]
- Bernard, V.; Jaffe, R.L.; Meissner, U.G. Strangeness Mixing and Quenching in the Nambu-Jona-Lasinio Model. Nucl. Phys. B 1988, 308, 753–790. [Google Scholar] [CrossRef]
- Smit, J. Introduction to quantum fields on a lattice: A robust mate. Camb. Lect. Notes Phys. 2002, 15, 1–271. [Google Scholar]
- Gattringer, C.; Lang, C.B. Quantum chromodynamics on the lattice. Lect. Notes Phys. 2010, 788, 1–343. [Google Scholar] [CrossRef]
- Muroya, S.; Nakamura, A.; Nonaka, C.; Takaishi, T. Lattice QCD at finite density: An Introductory review. Prog. Theor. Phys. 2003, 110, 615–668. [Google Scholar] [CrossRef]
- Schmidt, C. Lattice QCD at finite density. PoS 2006, LAT2006, 021. [Google Scholar] [CrossRef]
- De Forcrand, P. Simulating QCD at finite density. PoS 2009, LAT2009, 010. [Google Scholar] [CrossRef]
- Philipsen, O. The QCD equation of state from the lattice. Prog. Part. Nucl. Phys. 2013, 70, 55–107. [Google Scholar] [CrossRef]
- Aarts, G. Introductory lectures on lattice QCD at nonzero baryon number. J. Phys. Conf. Ser. 2016, 706, 022004. [Google Scholar] [CrossRef]
- Lombardo, M.P. Finite density (might well be easier) at finite temperature. Nucl. Phys. Proc. Suppl. 2000, 83, 375–377. [Google Scholar] [CrossRef]
- Cea, P.; Cosmai, L.; D’Elia, M.; Papa, A.; Sanfilippo, F. The critical line of two-flavor QCD at finite isospin or baryon densities from imaginary chemical potentials. Phys. Rev. D 2012, 85, 094512. [Google Scholar] [CrossRef]
- Nishida, Y. Phase structures of strong coupling lattice QCD with finite baryon and isospin density. Phys. Rev. D 2004, 69, 094501. [Google Scholar] [CrossRef]
- Detmold, W. Nuclear Physics from Lattice QCD. Lect. Notes Phys. 2015, 889, 153–194. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD phase diagram for nonzero isospin-asymmetry. Phys. Rev. D 2018, 97, 054514. [Google Scholar] [CrossRef]
- Cheng, T.; Li, L. Gauge Theory of Elementary Particle Physics; Oxford science publications, Clarendon Press: Oxford, UK, 1984. [Google Scholar]
- Brandt, B.B.; Endrődi, G.; Fraga, E.S.; Hippert, M.; Schaffner-Bielich, J.; Schmalzbauer, S. New class of compact stars: Pion stars. Phys. Rev. D 2018, 98, 094510. [Google Scholar] [CrossRef]
- Andersen, J.O.; Kneschke, P. Bose-Einstein condensation and pion stars. arXiv 2018, arXiv:hep-ph/1807.08951. [Google Scholar]
- Barducci, A.; Pettini, G.; Ravagli, L.; Casalbuoni, R. Ladder QCD at finite isospin chemical potential. Phys. Lett. B 2003, 564, 217–224. [Google Scholar] [CrossRef]
- Toublan, D.; Kogut, J.B. The QCD phase diagram at nonzero baryon, isospin and strangeness chemical potentials: Results from a hadron resonance gas model. Phys. Lett. B 2005, 605, 129–136. [Google Scholar] [CrossRef]
- Schafer, T.; Wilczek, F. Continuity of quark and hadron matter. Phys. Rev. Lett. 1999, 82, 3956–3959. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannarelli, M. Meson Condensation. Particles 2019, 2, 411-443. https://doi.org/10.3390/particles2030025
Mannarelli M. Meson Condensation. Particles. 2019; 2(3):411-443. https://doi.org/10.3390/particles2030025
Chicago/Turabian StyleMannarelli, Massimo. 2019. "Meson Condensation" Particles 2, no. 3: 411-443. https://doi.org/10.3390/particles2030025
APA StyleMannarelli, M. (2019). Meson Condensation. Particles, 2(3), 411-443. https://doi.org/10.3390/particles2030025



