A Review on Vibration Sensor: Key Parameters, Fundamental Principles, and Recent Progress on Industrial Monitoring Applications
Abstract
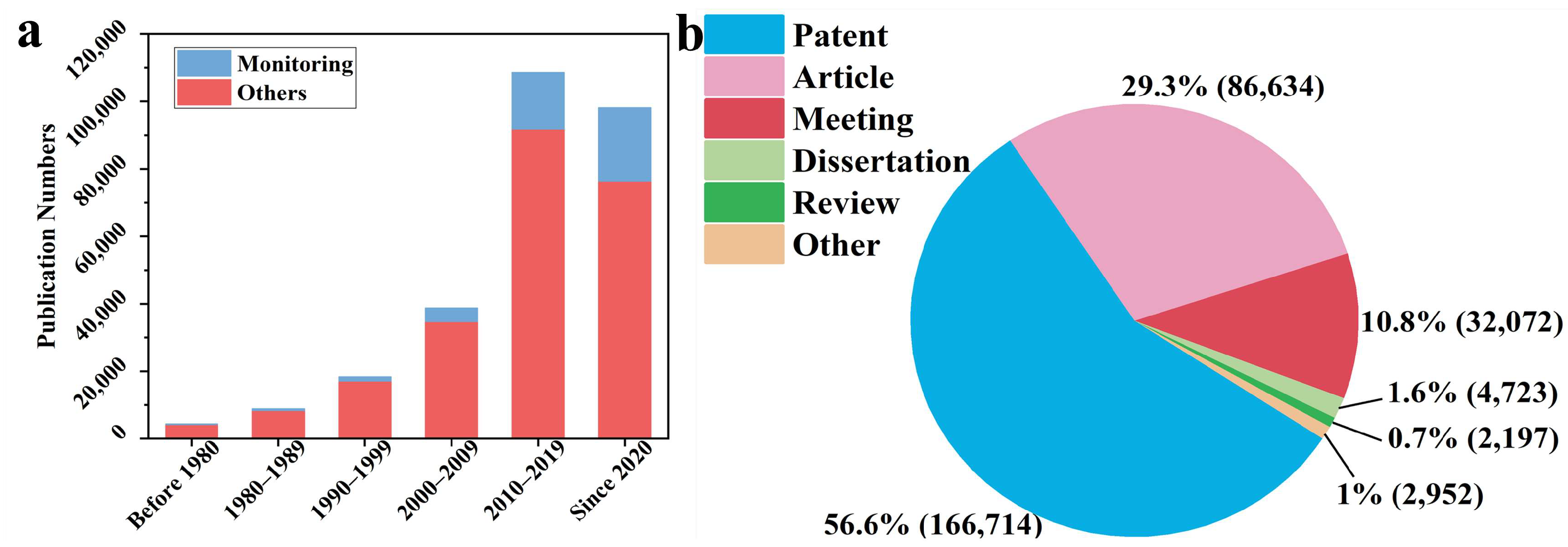
1. Introduction
2. Key Measurement Parameters for Vibration Sensing
2.1. Displacement and Amplitude
2.2. Frequency
2.3. Velocity
2.4. Acceleration
3. Principle and Recent Advancements of Vibration Sensors
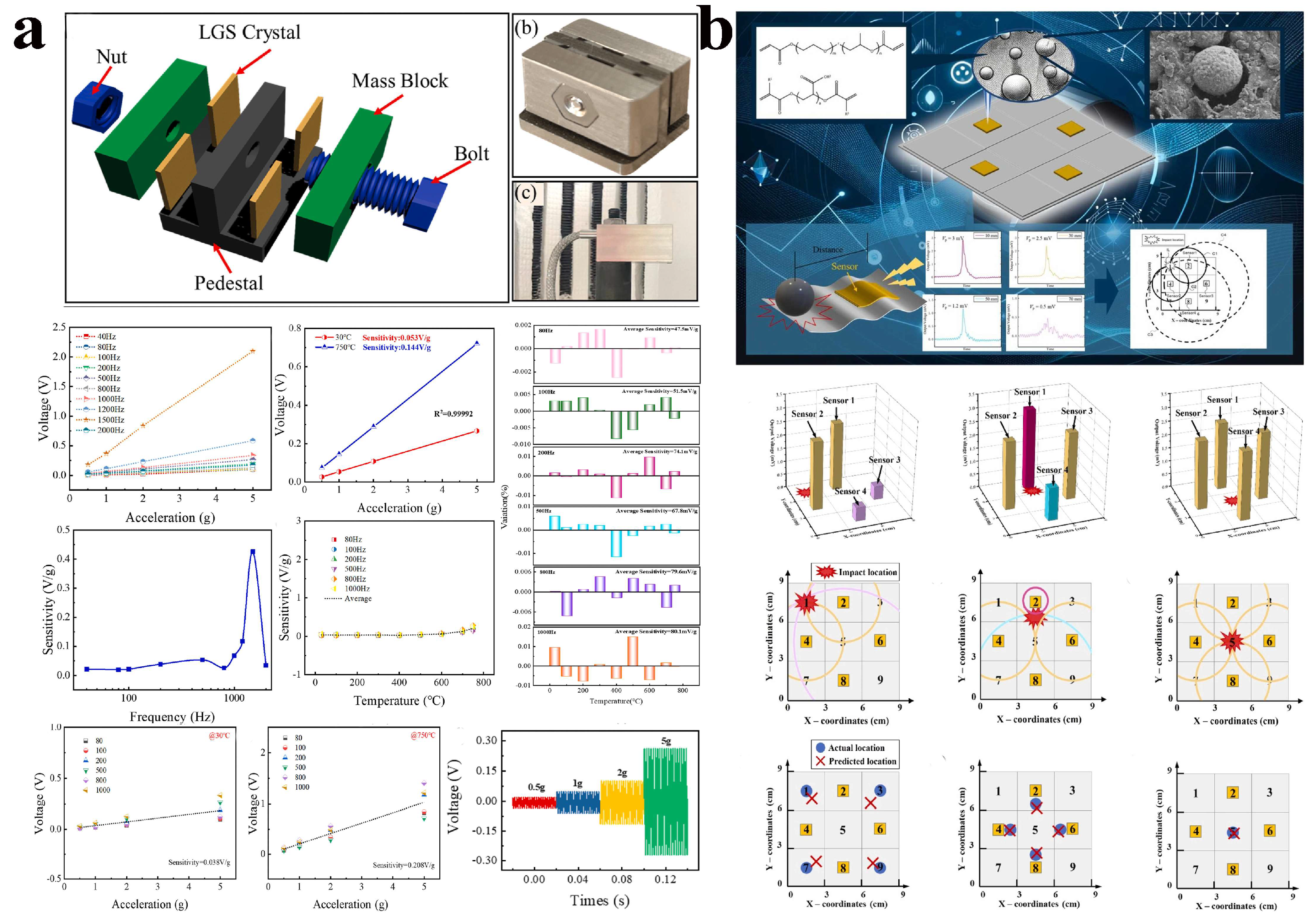
3.1. Piezoelectric
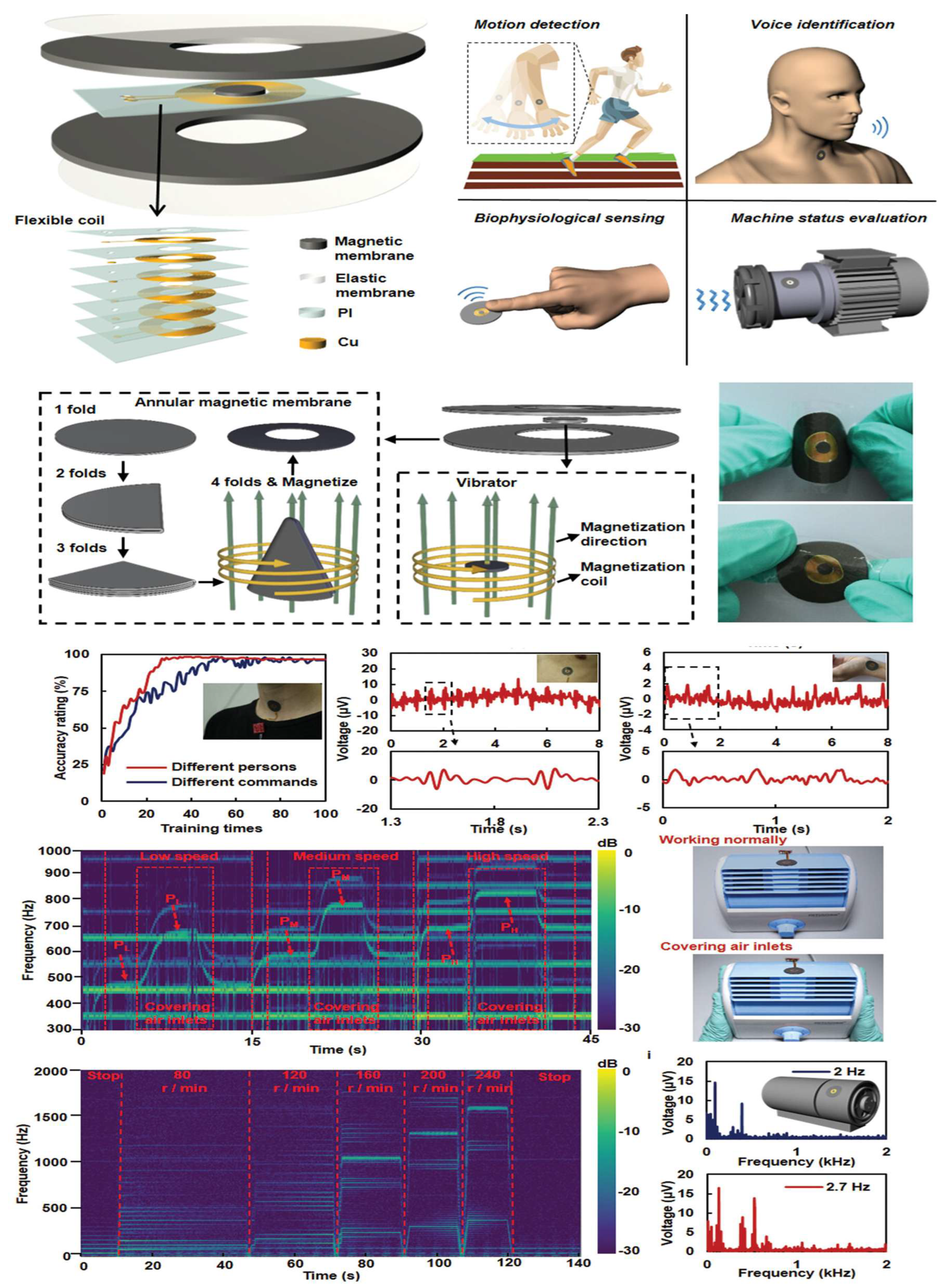
3.2. Electromagnetic
3.3. Photonic
3.4. Capacitive
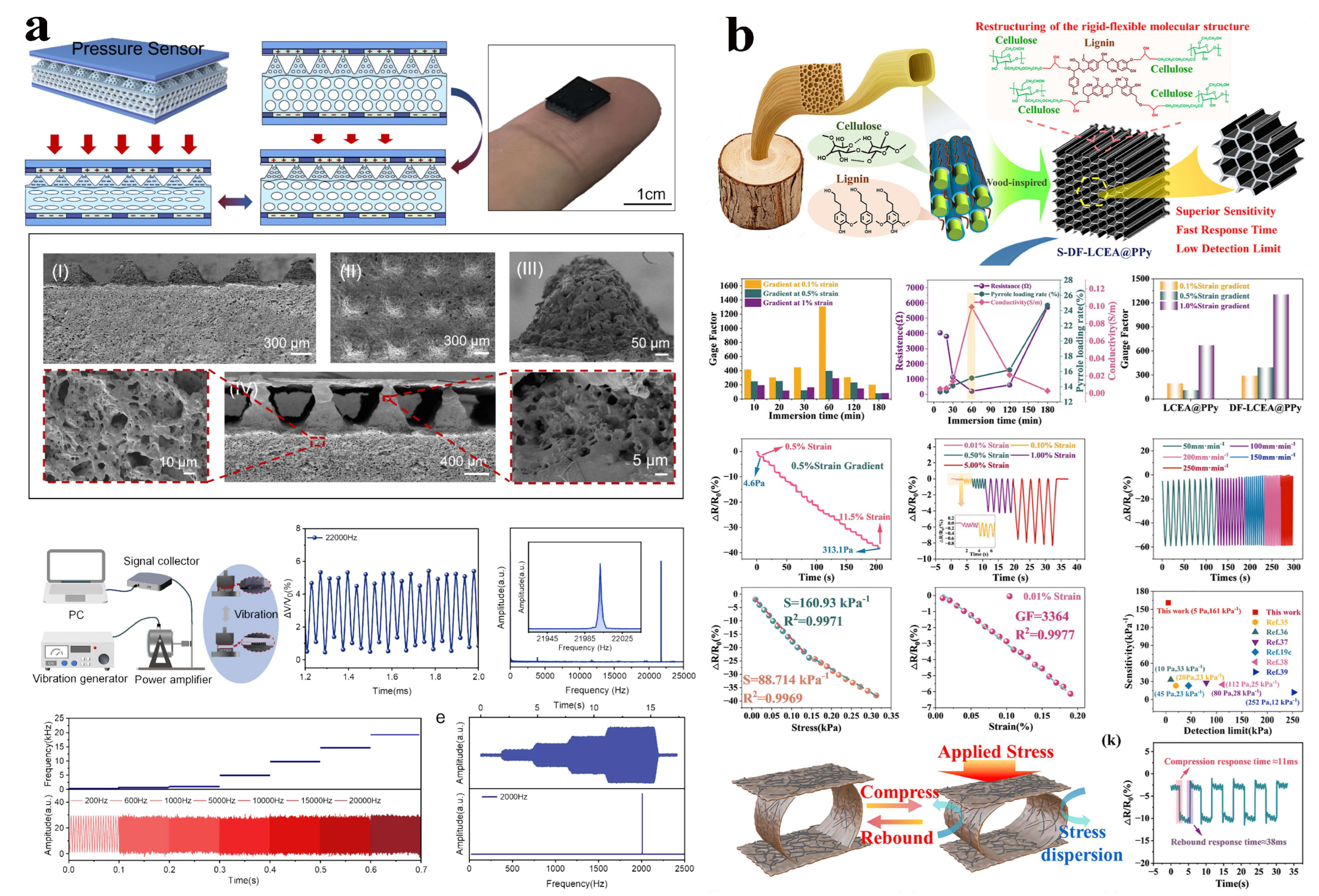
3.5. Piezoresistive
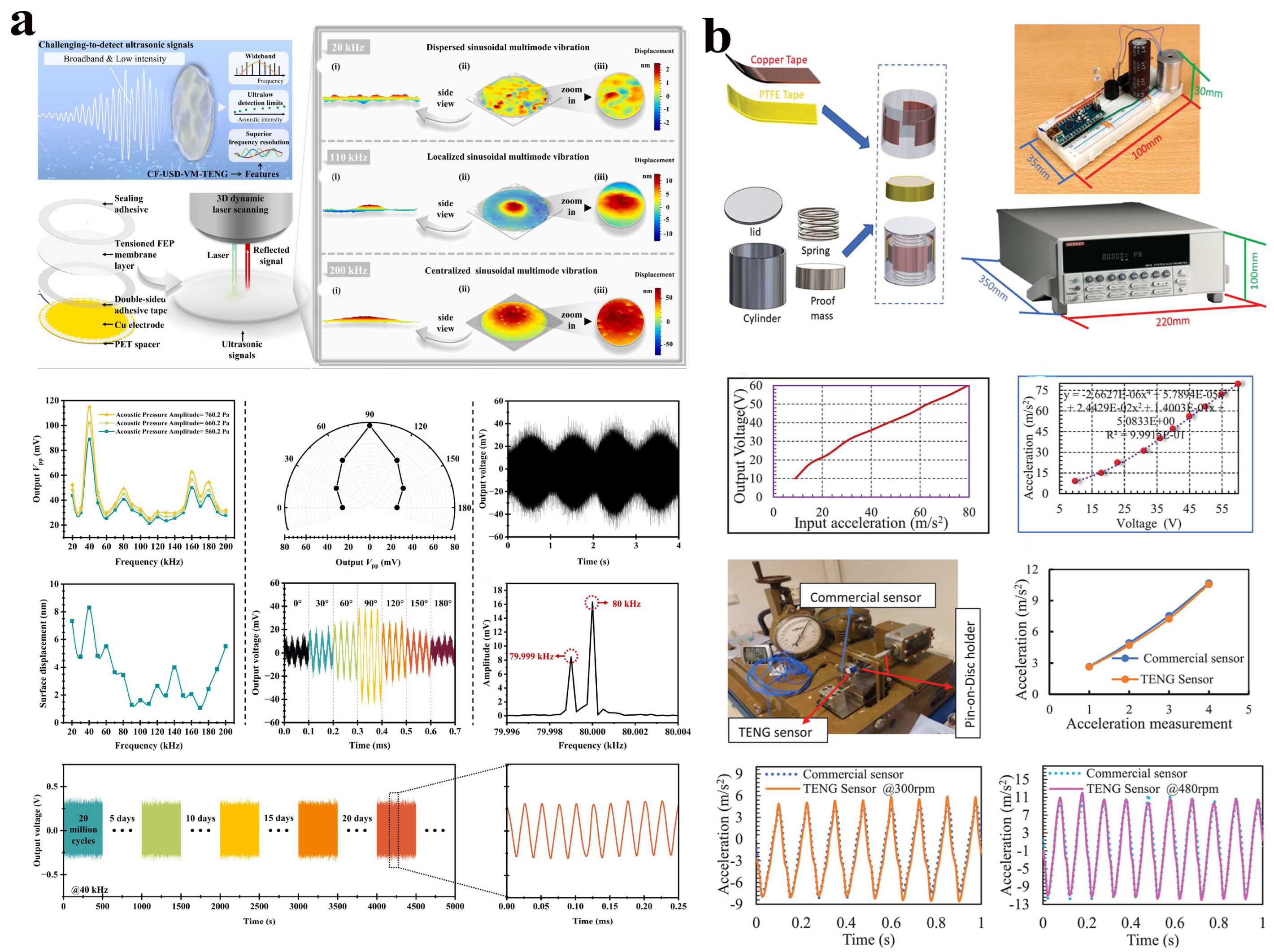
3.6. Triboelectric
3.7. Hybrid

4. Application of Vibration Sensors on Industrial Monitoring
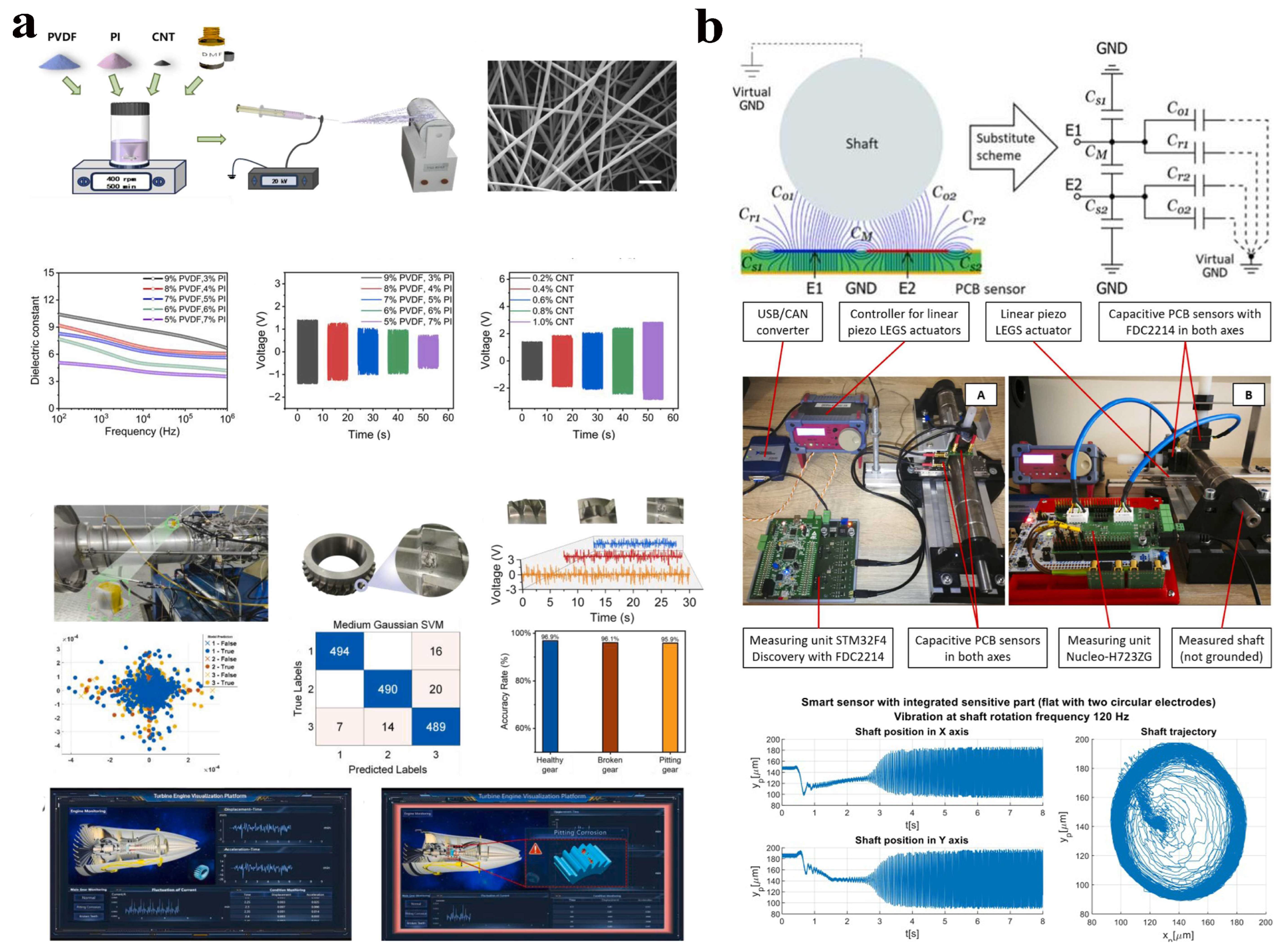
4.1. Fault Diagnosis
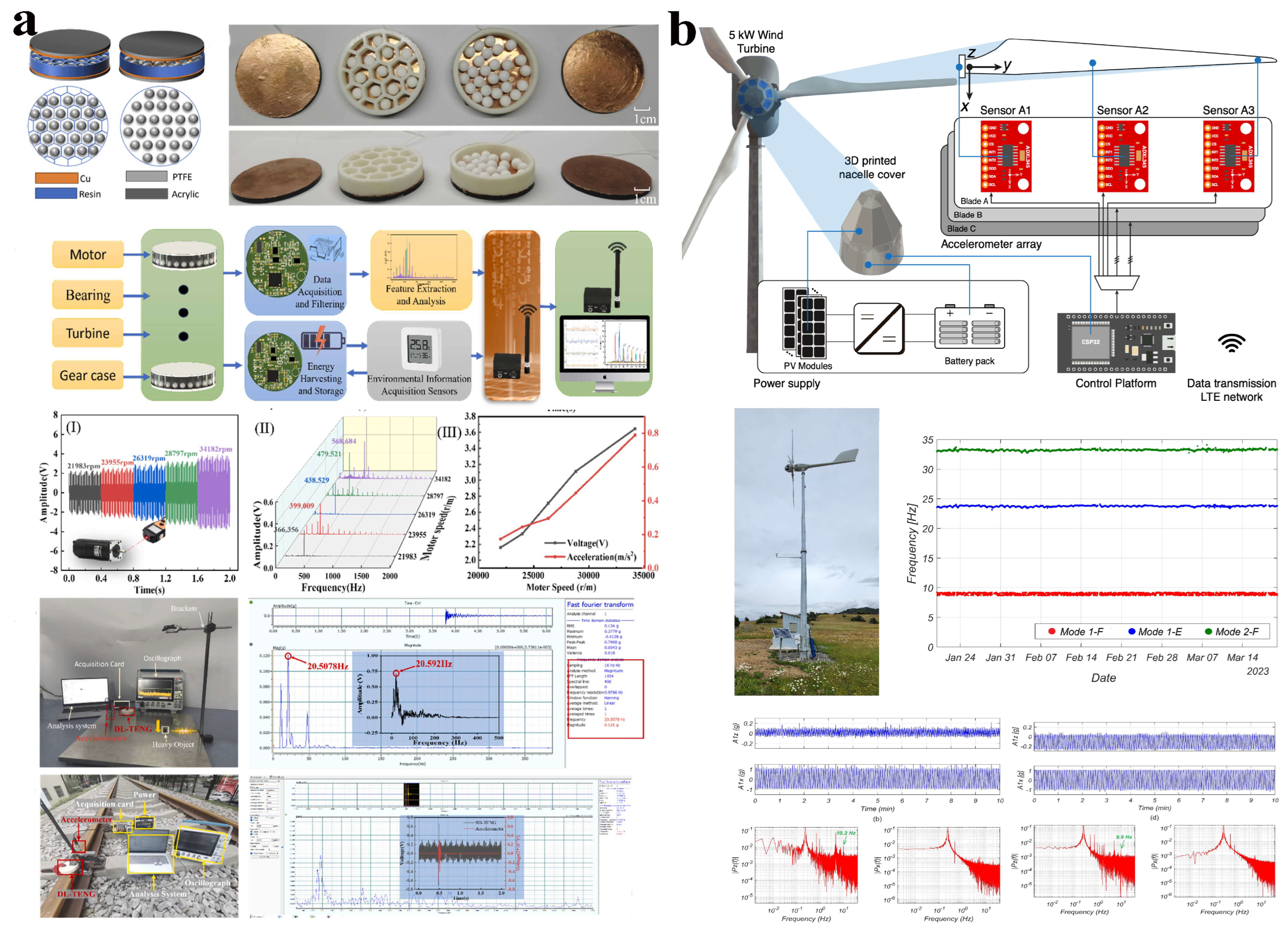
4.2. Structural Health Monitoring
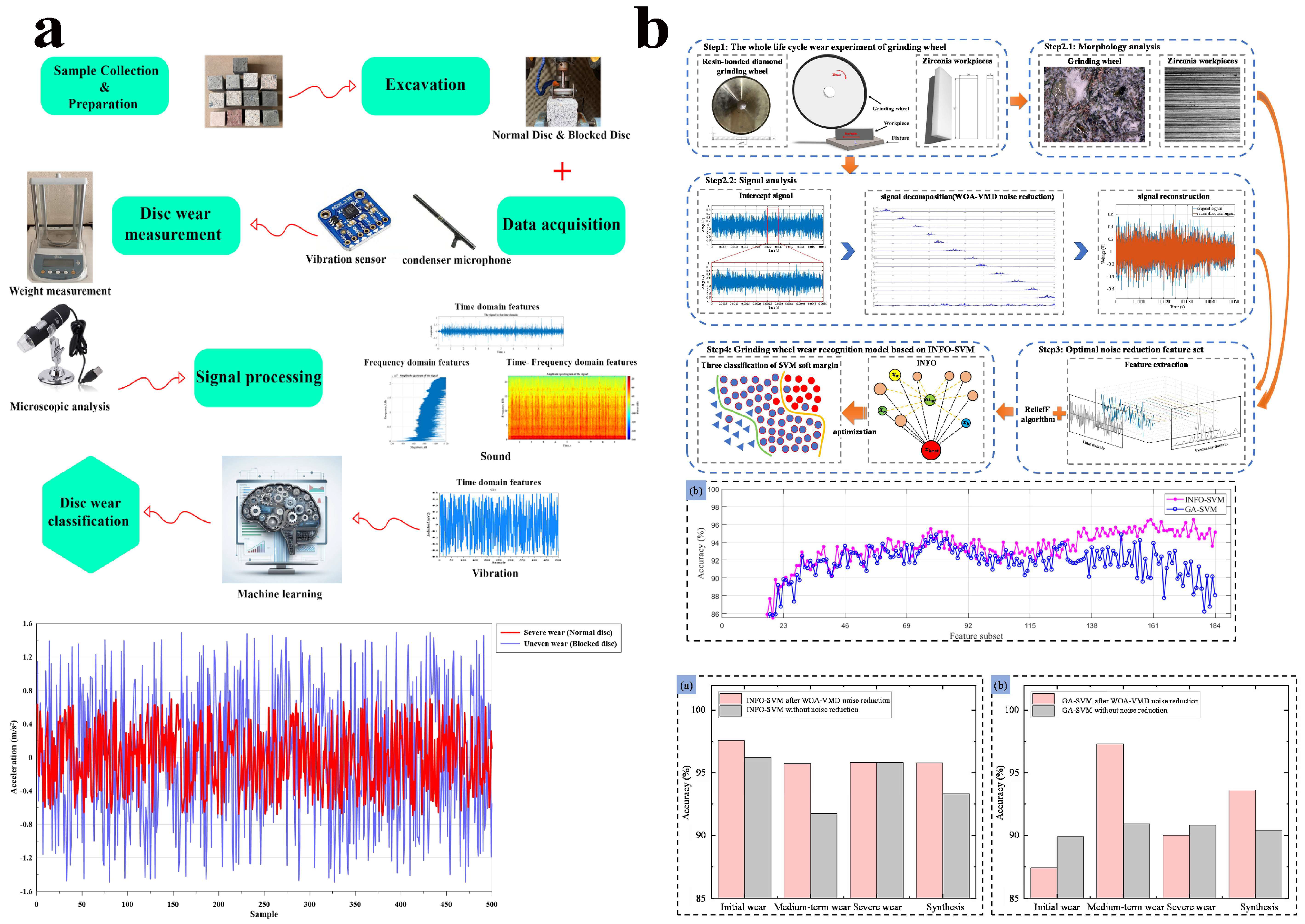
4.3. Tribological Status Analysis
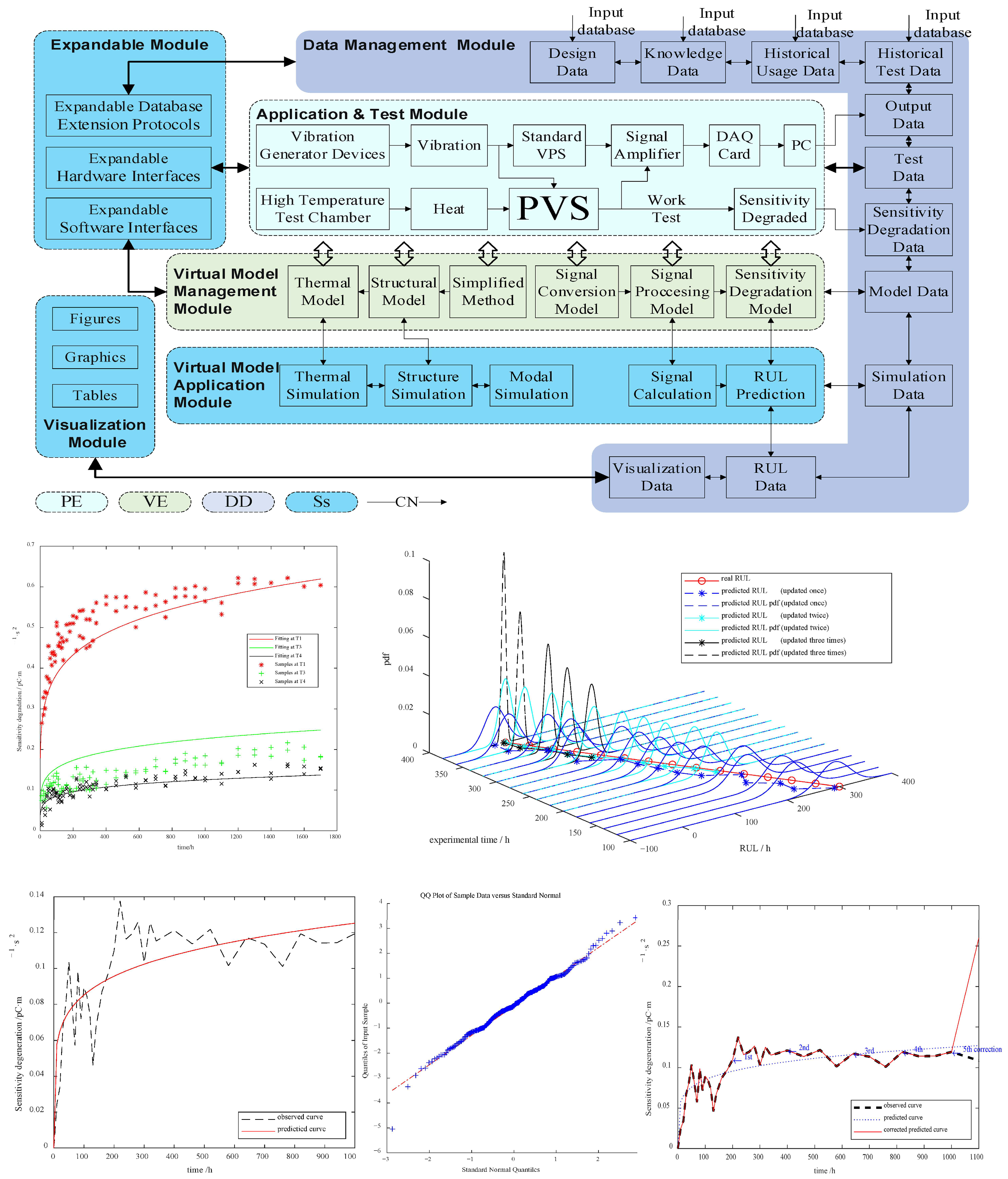
4.4. Early Warning and Service Life Prediction
5. Conclusions and Future Prospects
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SNR | signal-to-noise ratios |
| E | total energy |
| A | amplitude |
| k | elastic coefficient of the system |
| NF | natural frequency |
| m | mass of the block |
| Ek | kinetic energy |
| Ep | potential energy |
| RMS | root mean square |
| x | displacement of the mass block |
| amax | acceleration amplitude |
| ω | angular frequency |
| MAPE | mean absolute percentage error |
| R2 | coefficient of determination |
| PZT | lead zirconate titanate |
| BTO | barium titanate |
| PVDF | polyvinylidene fluoride |
| Tc | Curie temperature |
| MEMS | Micro-Electro-Mechanical Systems |
| GO | graphene oxide |
| PI | polyimide |
| PVA | polyvinyl alcohol |
| NWs | nanowires |
| PDMS | polydimethylsiloxane |
| TENG | triboelectric nanogenerator |
| PTFE | polytetrafluoroethylene |
| CNF | carbon nano fiber |
| DC | direct current |
| SHM | structural health monitoring |
| RUL | remaining useful life |
References
- Harms, J.; Ambrosino, F.; Angelini, L.; Braito, V.; Branchesi, M.; Brocato, E.; Cappellaro, E.; Coccia, E.; Coughlin, M.; Ceca, R.D.; et al. Lunar gravitational-wave antenna. Astrophys. J. 2021, 910, 1. [Google Scholar] [CrossRef]
- Maresca, R.; Guerriero, L.; Ruzza, G.; Mascellaro, N.; Guadagno, F.M.; Revellino, P. Monitoring ambient vibrations in an active landslide: Insights into seasonal material consolidation and resonance directivity. J. Appl. Geophys. 2022, 203, 104705. [Google Scholar] [CrossRef]
- Velez, S.T.; Seibold, K.; Kipfer, N.; Anderson, M.D.; Sudhir, V.; Galland, C. Preparation and decay of a single quantum of vibration at ambient conditions. Phys. Rev. X 2019, 9, 041007. [Google Scholar] [CrossRef]
- Mayyas, M. Modeling and analysis of vibratory feeder system based on robust stick–slip motion. J. Vib. Control 2022, 28, 2301–2309. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, L.; Yin, Z.; Wu, Y. Effects of ultrasonic vibration-assisted machining methods on the surface polishing of silicon carbide. J. Mater. Sci. 2024, 59, 7700–7715. [Google Scholar] [CrossRef]
- Duan, C.; Yuan, J.; Pan, M.; Huang, T.; Jiang, H.; Zhao, Y.; Qiao, J.; Wang, W.; Yu, S.; Lu, J. Variable elliptical vibrating screen: Particles kinematics and industrial application. Int. J. Min. Sci. Technol. 2021, 31, 1013–1022. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, Z.; Zhang, D.; Wang, J. Vibration properties of dual-rotor systems under base excitation, mass unbalance and gravity. Appl. Sci. 2022, 12, 960. [Google Scholar] [CrossRef]
- Wang, L.; Hu, L.; Zhang, J.; Liao, J. Vibration characteristics of a high-speed turbocharger rotor with mass unbalance based on simulation and experiment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 1607–1623. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Liu, J.; Zhang, Y.; Liu, J.; Pan, G.; Shi, Z. Vibration analysis of the propulsion shaft system considering dynamic misalignment in the outer ring. J. Sound Vib. 2024, 589, 118612. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Luo, Z.; Wen, C.; Zhu, Z.; Jin, L.; Li, B. Numerical and experimental investigations on dynamic behaviors of a bolted joint rotor system with pedestal looseness. J. Sound Vib. 2024, 571, 118036. [Google Scholar] [CrossRef]
- Hazwan, M.; Ghazali, M.; Rahiman, W. Vibration analysis for machine monitoring and diagnosis: A systematic review. Shock Vib. 2021, 2021, 9469318. [Google Scholar]
- Walter, P.L. Review: Fifty years plus of accelerometer history for shock and vibration (1940–1996). Shock Vib. 1999, 6, 281718. [Google Scholar] [CrossRef]
- Mason, W.P. Piezoelectricity, its history and applications. J. Acoust. Soc. Am. 1981, 70, 1561–1566. [Google Scholar] [CrossRef]
- Hassan, I.U.; Panduru, K.; Walsh, J. An in-depth study of vibration sensors for condition monitoring. Sensors 2024, 24, 740. [Google Scholar] [CrossRef]
- Hassan, I.; Panduru, K.; Walsh, P.J. Non-destructive testing methods for condition monitoring: A review of techniques and tools. Procedia Comput. Sci. 2025, 257, 420–427. [Google Scholar] [CrossRef]
- Babatain, W.; Bhattacharjee, S.; Hussain, A.M.; Hussain, M.M. Acceleration sensors: Sensing mechanisms, emerging fabrication strategies, materials, and applications. ACS Appl. Electron. Mater. 2021, 3, 504–531. [Google Scholar] [CrossRef]
- Haroun, A.; Tarek, M.; Mosleh, M.; Ismail, F. Recent progress on triboelectric nanogenerators for vibration energy harvesting and vibration sensing. Nanomaterials 2022, 12, 2960. [Google Scholar] [CrossRef] [PubMed]
- Burdzik, R.; Khan, D. An overview of the current state of knowledge and technology on techniques and procedures for signal processing, analysis, and accurate inference for transportation noise and vibration. Measurement 2025, 252, 117314. [Google Scholar] [CrossRef]
- Hassan, I.; Panduru, K.; Walsh, J. Predictive maintenance in industry 4.0: A review of data processing methods. Procedia Comput. Sci. 2025, 257, 896–903. [Google Scholar] [CrossRef]
- Soomro, A.A.; Muhammad, M.B.; Mokhtar, A.A.; Md Saad, M.H.; Lashari, N.; Hussain, M.; Sarwar, U.; Palli, A.S. Insights into modern machine learning approaches for bearing fault classification: A systematic literature review. Results Eng. 2024, 23, 102700. [Google Scholar] [CrossRef]
- Xu, S.; Xing, F.; Wang, R.; Li, W.; Wang, Y.; Wang, X. Vibration sensor for the health monitoring of the large rotating machinery: Review and outlook. Sens. Rev. 2018, 38, 44–64. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Wang, J. Forced vibration analysis of multi-degree-of-freedom nonlinear systems with the extended Galerkin method. Mech. Adv. Mater. Struct. 2023, 30, 794–802. [Google Scholar] [CrossRef]
- ISO 10816; Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts. International Organization for Standardization: Geneva, Switzerland, 1995.
- ISO 20816; Mechanical Vibration—Measurement and Evaluation of Machine Vibration. International Organization for Standardization: Geneva, Switzerland, 2016.
- ISO 13373; Condition Monitoring and Diagnostics of Machines—Vibration Condition Monitoring. International Organization for Standardization: Geneva, Switzerland, 2002.
- Peng, H.; Zhang, H.; Fan, Y.; Shangguan, L.; Yang, Y. A review of research on wind turbine bearings’ failure analysis and fault diagnosis. Lubricants 2023, 11, 14. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, S.; Ji, J.; Zhang, X.; Tong, V.-C.; Yin, S.; Feng, K.; Dong, H.; Xu, L. A review of fatigue failure and structural design of main bearings in tunnel boring machines based on engineering practical examples. Eng. Fail. Anal. 2024, 163, 108611. [Google Scholar] [CrossRef]
- Zhuang, H.; Ding, J.; Chen, P.; Chang, Y.; Zeng, X.; Yang, H.; Liu, X.; Wei, W. Numerical study on static and dynamic performances of a double-pad annular inherently compensated aerostatic thrust bearing. J. Tribol. 2019, 141, 051701. [Google Scholar] [CrossRef]
- Yang, J.; Rajasekar, S.; Sanjuán, M.A.F. Vibrational resonance: A review. Phys. Rep. 2024, 1067, 1–62. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; Guo, W.W. Analysis of resonance mechanism and conditions of train–bridge system. J. Sound Vib. 2006, 297, 810–822. [Google Scholar] [CrossRef]
- Burda, E.A.; Zusman, G.V.; Kudryavtseva, I.S.; Naumenko, A.P. An overview of vibration analysis techniques for the fault diagnostics of rolling bearings in machinery. Shock Vib. 2022, 2022, 6136231. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Z.; Liang, M. Analytical vibration signal model and signature analysis in resonance region for planetary gearbox fault diagnosis. J. Sound Vib. 2021, 498, 115962. [Google Scholar] [CrossRef]
- Chu, T.; Nguyen, T.; Yoo, H.; Wang, J. A review of vibration analysis and its applications. Heliyon 2024, 10, e26282. [Google Scholar] [CrossRef]
- Li, W.; Zhu, C. Noncontact rotor vibration velocity sensor and its application to vibration control of a flexible rotor on active magnetic bearings. IEEE Sens. J. 2024, 24, 34151–34161. [Google Scholar] [CrossRef]
- Khan, S.A.; Kim, J.M. Automated bearing fault diagnosis using 2D analysis of vibration acceleration signals under variable speed conditions. Shock Vib. 2016, 2016, 8729572. [Google Scholar] [CrossRef]
- Hashad, A. Additional stresses on buildings induced by vibration effects. Water Sci. 2015, 29, 134–145. [Google Scholar] [CrossRef][Green Version]
- Dong, X.; Miao, Z.; Li, Y.; Zhou, H.; Li, W. One data-driven vibration acceleration prediction method for offshore wind turbine structures based on extreme gradient boosting. Ocean Eng. 2024, 307, 118176. [Google Scholar] [CrossRef]
- Tressler, J.F. Piezoelectric sensors and sensor materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Habib, M.; Lantgios, I.; Hornbostel, K. A review of ceramic, polymer and composite piezoelectric materials. J. Phys. D: Appl. Phys. 2022, 55, 423002. [Google Scholar] [CrossRef]
- Promsawat, M.; Marungsri, B.; Promsawat, N.; Janphuang, P.; Luo, Z.; Pojprapai, S. Effects of temperature on aging degradation of soft and hard lead zirconate titanate ceramics. Ceram. Int. 2017, 43, 9709–9714. [Google Scholar] [CrossRef]
- Hao, J.; Li, W.; Zhai, J.; Chen, H. Progress in high-strain perovskite piezoelectric ceramics. Mater. Sci. Eng. R Rep. 2019, 135, 1–57. [Google Scholar] [CrossRef]
- Wang, Q.; Liang, E.-M.; Wang, C.-M. High-performance bismuth titanate-ferrite (Bi5Ti3FeO15) for high-temperature piezoelectric applications. J. Am. Ceram. Soc. 2024, 107, 4811–4823. [Google Scholar] [CrossRef]
- Sivagnanapalani, P.; Sahoo, B.; Panda, P.K. Calcium niobate based piezo-resistive materials for high temperature sensor application. Ceram. Int. 2018, 44, 20348–20353. [Google Scholar] [CrossRef]
- Zhang, L.S.; Liu, Y.B.; Pan, C.L.; Feng, Z.H. Leakage current characterization and compensation for piezoelectric actuator with charge drive. Sens. Actuators A Phys. 2013, 199, 116–122. [Google Scholar] [CrossRef]
- Ramany, K.; Shankararajan, R.; Savarimuthu, K.; Elumalai, P.; Rajamanickam, G.; Narendhiran, S.; Perumalsamy, R. Experimental study of different vanadium dopant concentrations in ZnO nanorods for a low frequency piezoelectric accelerometer. J. Electron. Mater. 2019, 48, 5310–5322. [Google Scholar] [CrossRef]
- Ramanathan, A.K.; Headings, L.M.; Dapino, M.J. Near static strain measurement with piezoelectric films. Sens. Actuators A Phys. 2020, 301, 111654. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y.; Liu, W.; Pan, Y.; Yang, P.; Meng, D.; Zheng, T.; Wu, J. Shear-structured piezoelectric accelerometers based on KNN lead-free ceramics for vibration monitoring. J. Mater. Chem. C 2024, 12, 18639–18650. [Google Scholar] [CrossRef]
- Deng, J.; Chuai, S.; Cai, Q.; An, D.; Yunbo, S.; Shen, C. Design and preparation of triaxial piezoelectric cryogenic vibration sensor based on PZT-7A. IEEE Sens. J. 2025, 25, 2301–2309. [Google Scholar] [CrossRef]
- Liang, X.; Cheng, W.; Li, S.; Hu, D.; Tan, Q. High-temperature shear-type vibration sensor based on langasite piezoelectric crystal. Heliyon 2024, 10, e38417. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Z.; He, L.; Yokota, H.; Okada, Y.; Narita, F. Local impact sensing via flexible piezoelectric composite film based on highly elastic resin. Sens. Actuators A Phys. 2024, 368, 115089. [Google Scholar] [CrossRef]
- Kinsler, P. Faraday’s Law and magnetic induction: Cause and effect, experiment and theory. Physics 2020, 2, 150–163. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Tudor, M.J.; Beeby, S.P.; White, N.M. An electromagnetic, vibration-powered generator for intelligent sensor systems. Sens. Actuators A Phys. 2004, 110, 344–349. [Google Scholar] [CrossRef]
- Xue, X.; Dong, Y.; Wu, X. Motion induced eddy current sensor for non-intrusive vibration measurement. IEEE Sens. J. 2020, 20, 735–744. [Google Scholar] [CrossRef]
- Ausanio, G.; Barone, A.C.; Hison, C.; Iannotti, V.; Luponio, C.; Lanotte, L. Mechanical vibration sensor based on elastomagnetic composite. Sens. Actuators A Phys. 2006, 129, 25–28. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, Y.; Jin, M.; Li, C.; Meng, Q. High sensitivity and wide range soft magnetic tactile sensor based on electromagnetic induction. IEEE Sens. J. 2021, 21, 2757–2766. [Google Scholar] [CrossRef]
- Gurusamy, V.; Capolino, G.A.; Akin, B.; Henao, H.; Romary, R.; Pusca, R. Recent trends in magnetic sensors and flux-based condition monitoring of electromagnetic devices. IEEE Trans. Ind. Appl. 2022, 58, 4668–4684. [Google Scholar] [CrossRef]
- Shen, W.; Zhu, S.; Xu, Y. An experimental study on self-powered vibration control and monitoring system using electromagnetic TMD and wireless sensors. Sens. Actuators A Phys. 2012, 180, 166–176. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, S.; Zhang, X.; Huo, W.; Xu, H.; Chen, C.; Li, J.; Xu, K.; Huang, X. Fully flexible electromagnetic vibration sensors with annular field confinement origami magnetic membranes. Adv. Funct. Mater. 2020, 30, 2001553. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N.; Voronkov, G.S.; Grakhova, E.P.; Kutluyarov, R.V. A review on photonic sensing technologies: Status and outlook. Biosensors 2023, 13, 568. [Google Scholar] [CrossRef]
- Wampler, L.; Xia, F.; Yeung, S.Y.F.; Hirano, T.; Alshehri, A.H.; Furokawa, M.; Youcef-Toumi, K. A foppler tadar eith a dweeping lock-in demodulator for machine vibration sensing. IEEE Sens. J. 2023, 23, 28833–28844. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Meng, D.; Shi, J.; Miao, C. Optical fiber vibration sensor for bearing fault detection based on Sagnac interferometer. Laser Phys. 2023, 33, 065101. [Google Scholar] [CrossRef]
- Dejdar, P.; Mokry, O.; Cizek, M.; Rajmic, P.; Munster, P.; Schimmel, J.; Pravdova, L.; Horvath, T.; Cip, O. Characterization of sensitivity of optical fiber cables to acoustic vibrations. Sci. Rep. 2023, 13, 7068. [Google Scholar] [CrossRef]
- Huang, Z.; Nie, Z.; Xu, H.; Zhao, S.; Chen, G.; Hu, X.; Li, C.; Wang, G.; Li, D. A multilongitudinal mode quadrature laser self-mixing vibration sensor for fault diagnosis of bearing. IEEE Sens. J. 2024, 24, 4407–4417. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Xiao, L.; Bai, Q.; Liu, X.; Gao, Y.; Zhang, H.; Jin, B. Phase demodulation methods for optical fiber vibration sensing system: A review. IEEE Sens. J. 2022, 22, 1842–1866. [Google Scholar] [CrossRef]
- Liu, K.; Jin, X.; Jiang, J.; Xu, T.; Ding, Z.; Huang, Y.; Sun, Z.; Xue, K.; Li, S.; Liu, T. Interferometer-based distributed optical fiber sensors in long-distance vibration detection: A review. IEEE Sens. J. 2022, 22, 21428–21444. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Progress toward sapphire optical fiber sensors for high-temperature applications. IEEE Trans. Instrum. Meas. 2020, 69, 8639–8655. [Google Scholar] [CrossRef]
- An, R.; Wang, Y.; Ping, X.; Wen, K.; Yuan, Y.; Wang, S.; Yang, J.; Wang, Y.; Qin, Y. Temperature compensation method for polarization-multiplexed fiber-optic vibration sensing unit. IEEE Sens. J. 2025, 25, 2658–2666. [Google Scholar] [CrossRef]
- Li, C.; Yang, W.; Wang, M.; Yu, X.; Fan, J.; Xiong, Y.; Yang, Y.; Li, L. A review of coating materials used to improve the performance of optical fiber sensors. Sensors 2020, 20, 4215. [Google Scholar] [CrossRef] [PubMed]
- Günther, P.; Pfister, T.; Büttner, L.; Czarske, J. Laser Doppler distance sensor using phase evaluation. Opt. Express 2009, 17, 2611–2622. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Zhu, W.D. Investigation of three-dimensional vibration measurement by a single scanning laser Doppler vibrometer. J. Sound Vibrat. 2017, 387, 36–52. [Google Scholar] [CrossRef]
- ISO 16063; Methods for the Calibration of Vibration and Shock Transducers. International Organization for Standardization (ISO): Geneva, Switzerland, 1998.
- Abbas, S.H.; Jang, J.-K.; Kim, D.-H.; Lee, J.-R. Underwater vibration analysis method for rotating propeller blades using laser Doppler vibrometer. Opt. Lasers Eng. 2020, 132, 106133. [Google Scholar] [CrossRef]
- Costanzo, A.; Falcone, S.; La Piana, C.; Lapenta, V.; Musacchio, M.; Sgamellotti, A.; Buongiorno, M.F. Laser scanning investigation and geophysical monitoring to characterise cultural heritage current state and threat by traffic-induce vibrations: The Villa Farnesina in Rome. Remote Sens. 2022, 14, 5818. [Google Scholar] [CrossRef]
- Wu, X.; Xia, W.; Wang, X.; Song, H.; Huang, C. Effect of surface reflectivity on photonic Doppler velocimetry measurement. Meas. Sci. Technol. 2014, 25, 055207. [Google Scholar] [CrossRef]
- Ho, J.; Jow, T.R.; Boggs, S. Historical introduction to capacitor technology. IEEE Electr. Insul. Mag. 2010, 26, 20–25. [Google Scholar] [CrossRef]
- Biswas, K.; Sen, S.; Dutta, P.K. MEMS capacitive accelerometers. Sens. Lett. 2007, 5, 471–484. [Google Scholar] [CrossRef]
- Bakhoum, E.G.; Cheng, M.H.M. Ultrahigh-sensitivity pressure and vibration sensor. IEEE Sens. J. 2011, 11, 3288–3294. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ngo, M.Q.; Nguyen, D.D.; Phan, N.T.; Le, T.T. Investigation of parasitic capacitance models for planar transformers: Accuracy and impedance prediction. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024. [Google Scholar]
- Zhao, F.; Lei, B.; Jiang, W.; Jiang, W.; Lu, H.; Li, T.; Shi, Y.; Yin, L.; Chen, B.; Liu, H. The intrinsic mechanism of the sensitivity improvement for capacitive strain sensors and its trade-off with sensing range. IEEE Sens. J. 2024, 24, 4565–4573. [Google Scholar] [CrossRef]
- Li, X.; Liang, Q.; Liu, H.; Zhao, L.; Sun, C.; Hou, C. High-sensitivity MXene/MWCNTs/PDMS flexible capacitive sensor for wearable health monitoring. Adv. Mater. Technol. 2025, 10, e00677. [Google Scholar] [CrossRef]
- Zhong, Y.; Liu, K.; Wu, L.; Ji, W.; Cheng, G.; Ding, J. Flexible tactile sensors with gradient conformal dome structures. ACS Appl. Mater. Interfaces 2024, 16, 52966–52976. [Google Scholar] [CrossRef] [PubMed]
- Ghanam, M.; Goldschmidtboeing, F.; Bilger, T.; Bucherer, A.; Woias, P. MEMS shielded capacitive pressure and force sensors with excellent thermal stability and high operating temperature. Sensors 2023, 23, 4248. [Google Scholar] [CrossRef]
- Qin, J.; Yin, L.; Hao, Y.-N.; Zhong, S.; Zhang, D.; Bi, K.; Zhang, Y.; Zhao, Y.; Dang, Z. Flexible and stretchable capacitive sensors with different microstructures. Adv. Mater. 2021, 33, 2008267. [Google Scholar] [CrossRef]
- Ghemari, Z.; Belkhiri, S.; Saad, S. A capacitive sensor with high measurement accuracy and low electrical energy consumption. Appl. Phys. A 2023, 129, 362. [Google Scholar] [CrossRef]
- Gomathi, K.; Balaji, A.; Mrunalini, T. Design and optimization of differential capacitive micro accelerometer for vibration measurement. J. Mech. Behav. Mater. 2021, 30, 19–27. [Google Scholar] [CrossRef]
- Do, C.; Seshia, A.A. Active temperature compensation for MEMS capacitive sensor. IEEE Sens. J. 2021, 21, 18588–18592. [Google Scholar] [CrossRef]
- Li, C.; Sun, B.; Jia, P.; Xue, Y.; Jia, M.; Xiong, J. Capacitive pressure sensor with integrated signal-conversion circuit for high-temperature applications. IEEE Access 2020, 8, 212787–212793. [Google Scholar] [CrossRef]
- Sui, Y.; Yu, T.; Wang, L.; Wang, Z.; Xue, K.; Chen, Y.; Liu, X.; Chen, Y. Analysis of a capacitive sensing circuit and sensitive structure based on a low-temperature-drift planar transformer. Sensors 2022, 22, 9284. [Google Scholar] [CrossRef] [PubMed]
- Augutis, V.; Balčiūnas, G.; Kuzas, P.; Gailius, D.; Raudienė, E. Smart capacitive transducer for high-frequency vibration measurement. Sensors 2025, 25, 1639. [Google Scholar] [CrossRef]
- Cheng, M.; Yuan, Y.; Li, Q.; Chen, C.; Chen, J.; Tian, K.; Zhang, M.; Fu, Q.; Deng, H. Polyimide aerogel-based capacitive pressure sensor with enhanced sensitivity and temperature resistance. J. Mater. Sci. Technol. 2025, 217, 60–69. [Google Scholar] [CrossRef]
- Su, D.; Shen, G.; Ma, K.; Li, J.; Qin, B.; Wang, S.; Yang, W.; He, X. Enhanced sensitivity and linear-response in iontronic pressure sensors for non-contact, high-frequency vibration recognition. J. Colloid Interface Sci. 2024, 659, 1042–1051. [Google Scholar] [CrossRef]
- Reverter, F. A tutorial on mechanical sensors in the 70th anniversary of the piezoresistive effect. Sensors 2024, 24, 3690. [Google Scholar] [CrossRef]
- Barlian, A.A.; Park, W.T.; Mallon, J.R.; Rastegar, A.J.; Pruitt, B.L. Review: Semiconductor piezoresistance for microsystems. Proc. IEEE 2009, 97, 513–552. [Google Scholar] [CrossRef]
- Chung, D.D.L. A critical review of piezoresistivity and its application in electrical-resistance-based strain sensing. J. Mater. Sci. 2020, 55, 15367–15396. [Google Scholar] [CrossRef]
- Irani, F.S.; Shafaghi, A.H.; Tasdelen, M.C.; Delipinar, T.; Kaya, C.E.; Yapici, G.G.; Yapici, M.K. Graphene as a piezoresistive material in strain sensing applications. Micromachines 2022, 13, 119. [Google Scholar] [CrossRef]
- Zhang, D.; Xie, J.; Meng, X.; Pang, H.; Sun, R.; Fan, H.; Nan, X.; Zhou, Z. Development of piezoresistive flexible sensor with dual-height cylindrical microstructure surfaces to achieve vehicle vibration monitoring. J. Micromech. Microeng. 2024, 34, 075005. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, C.; Deng, C. Research on vibration effect of piezoresistive pressure sensor. Instrum. Exp. Techol. 2022, 65, 653–667. [Google Scholar]
- Tian, K.; Sui, G.; Yang, P.; Deng, H.; Fu, Q. Ultrasensitive thin-film pressure sensors with a broad dynamic response range and excellent versatility toward pressure, vibration, bending, and temperature. ACS Appl. Mater. Interfaces 2020, 12, 20998–21008. [Google Scholar] [CrossRef]
- Han, S.; Wu, Q.; Zhu, J.; Zhang, J.; Chen, A.; Chen, Y.; Yang, X.; Huang, J.; Guan, L. Multifunctional, superelastic, and environmentally stable sodium alginate/mxene/polydimethylsiloxane aerogels for piezoresistive sensor. Chem. Eng. J. 2023, 471, 144551. [Google Scholar] [CrossRef]
- Yan, Y.; Zheng, J.; Zhang, Q.; Li, Y.; Li, G.; Zhang, Z.; Wang, P.; Wu, W.; Zhai, J.; Xu, Y. Ultrafast piezoresistive flexible pressure sensor for vibration and sound detection with a bandwidth over 20 kHz. Chem. Eng. J. 2025, 517, 164221. [Google Scholar] [CrossRef]
- Tan, Z.; Hu, Q.-a.; Yang, B.; Liu, W.; Zhang, Z.; Shu, L.; Qiu, X. Superelastic and highly sensitive biomass-derived piezoresistive aerogels for deep-learning-assisted sensing. Adv. Funct. Mater. 2025, e11831. [Google Scholar] [CrossRef]
- Wang, S.; Lin, L.; Wang, Z.L. Triboelectric nanogenerators as self-powered active sensors. Nano Energy 2015, 11, 436–462. [Google Scholar] [CrossRef]
- Niu, S.; Wang, Z.L. Theoretical systems of triboelectric nanogenerators. Nano Energy 2015, 14, 161–192. [Google Scholar] [CrossRef]
- Zhang, R.; Olin, H. Material choices for triboelectric nanogenerators: A critical review. EcoMat 2020, 2, e12062. [Google Scholar] [CrossRef]
- Wang, W.; Yin, N.; Wu, Z.; Zhang, Z. Omnidirectional energy harvesting with 3D-TENG for vibration diagnosis. Chem. Eng. J. 2025, 509, 161022. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.; Ma, X.; Li, X.; Guo, Y. A non-contact triboelectric vibration sensor with a spiral floating electrode structure for low-frequency vibration monitoring. Nano Energy 2025, 133, 110437. [Google Scholar] [CrossRef]
- Nguyen, V.; Yang, R. Effect of humidity and pressure on the triboelectric nanogenerator. Nano Energy 2013, 2, 604–608. [Google Scholar] [CrossRef]
- Zhang, J.; Boyer, C.; Zhang, Y.X. Enhancing the humidity resistance of triboelectric nanogenerators: A review. Small 2024, 20, 2401846. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, M.; Alzgool, M.; Davaji, B.; Towfighian, S. Event-driven MEMS vibration sensor: Integration of triboelectric nanogenerator and low-frequency switch. Mech. Syst. Signal Process. 2023, 187, 109921. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, H.; Xiao, Z.; Qin, M.; Mulvihill, D.M.; Zhang, Y.; Wang, Y.; Wen, J.; Jing, Q.; Cheng, Y. Self-powered wideband ultrasonic sensor based on capacitive triboelectric technology with ultralow detection limits and superior frequency resolution. Nano Energy 2025, 141, 111130. [Google Scholar] [CrossRef]
- Mehamud, I.; Björling, M.; Marklund, P.; Shi, Y. Small size and low-cost TENG-based self-powered vibration measuring and alerting system. Adv. Electron. Mater. 2023, 9, 2300111. [Google Scholar] [CrossRef]
- Feng, P.; Yuan, Y.; Zhong, M.; Shao, J.; Liu, X.; Xu, J.; Zhang, J.; Li, K.; Zhao, W. Integrated resistive-capacitive strain sensors based on polymer–nanoparticle composites. ACS Appl. Nano Mater. 2020, 3, 4357–4366. [Google Scholar] [CrossRef]
- Shen, J.; Yang, Y.; Yang, Z.; Li, B.; Ji, L.; Cheng, J. A multilayer triboelectric-electromagnetic hybrid nanogenerator for vibration energy harvesting and frequency monitoring. Nano Energy 2023, 116, 108818. [Google Scholar] [CrossRef]
- Wu, H.; Wang, Z.; Zhu, B.; Wang, H.; Lu, C.; Kang, M.; Kang, S.; Ding, W.; Yang, L.; Liao, R.; et al. All-in-One sensing system for online vibration monitoring via IR wireless communication as driven by high-power TENG. Adv. Energy Mater. 2023, 13, 2300051. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, R.; Zhao, Q.; He, H.; Huang, H.; Yang, L.; Xu, Y. High-linearity flexible sensor for real-time pressure monitoring across wide frequency range by integrating piezoelectric and piezoresistive effects. Chem. Eng. J. 2025, 506, 159919. [Google Scholar] [CrossRef]
- Wang, L.; Fei, Z.; Duan, C.; Han, X.; Li, M.; Gao, W.; Xia, Y.; Jia, C.; Lin, Q.; Zhao, Y.; et al. Self-sustained and self-wakeup wireless vibration sensors by electromagnetic-piezoelectric-triboelectric hybrid energy harvesting. Appl. Energy 2024, 355, 122207. [Google Scholar] [CrossRef]
- Wang, A.; Gao, Z.; Wu, S.; Wei, Y.; Lu, B.; Shi, J.; Shen, L.; Liu, Y.; Sun, X.; Wen, Z. Superelastic and ultra-soft MXene/CNF Aerogel@PDMS-based dual-modal pressure sensor for complex stimuli monitoring. Adv. Sci. 2025, 12, 2502797. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Qin, L.; Zhu, Q.; Wang, P.; Zhang, F.; Chu, F. An ultrasensitive self-powered smart bearing pedestal with fault locating capability. Mech. Syst. Signal Process. 2025, 235, 112924. [Google Scholar] [CrossRef]
- Gao, S.; Sha, Z.; Chen, Y.; Li, G.; He, S.; Wu, S.; Ladouceur, F.; Peng, S.; Wang, C.H. Self-powered optical-triboelectric sensor for remote vibration monitoring. Nano Energy 2025, 140, 111006. [Google Scholar] [CrossRef]
- Malla, C.; Panigrahi, I. Review of condition monitoring of rolling element bearing using vibration analysis and other techniques. J. Vib. Eng. Technol. 2019, 7, 407–414. [Google Scholar] [CrossRef]
- Kibrete, F.; Engida Woldemichael, D.; Shimels Gebremedhen, H. Multi-sensor data fusion in intelligent fault diagnosis of rotating machines: A comprehensive review. Measurement 2024, 232, 114658. [Google Scholar] [CrossRef]
- Zaitsev, I.; Bereznychenko, V.; Bajaj, M.; Taha, I.B.M.; Belkhier, Y.; Titko, V.; Kamel, S. Calculation of capacitive-based sensors of rotating shaft vibration for fault diagnostic systems of powerful generators. Sensors 2022, 22, 1634. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, R.; Wang, H.; Zhao, R.; Ning, R.; Huang, Z.; Chu, Z.; Peng, Y.; Zhang, Y.; Zhang, H. Gear-fault monitoring and digital twin demonstration of aircraft engine based on piezoelectric vibration sensor for engine health management. Nano Energy 2025, 133, 110448. [Google Scholar] [CrossRef]
- Pawlenka, T.; Škuta, J.; Tůma, J.; Juránek, M. Development of capacitive sensors for measuring vibrations and small displacements of a high-speed rotating machines for use in active vibration control systems. Sens. Actuators A Phys. 2024, 365, 114902. [Google Scholar] [CrossRef]
- Papathanasopoulos, D.A.; Giannousakis, K.N.; Dermatas, E.S.; Mitronikas, E.D. Vibration monitoring for position sensor fault diagnosis in brushless DC motor drives. Energies 2021, 14, 2248. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B.S. The vibration monitoring methods and signal processing techniques for structural health monitoring: A review. Arch. Comput. Methods Eng. 2016, 23, 585–594. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Lieven, N.A.J.; Ewins, D.J.; Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration–based structural damage identification. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar]
- Xiao, Y.; Song, D.; Wu, N. Development of compact smart bearing and novel hybrid feature assessment for weak defect identification. Nondestr. Test. Eval. 2025, 40, 1–27. [Google Scholar] [CrossRef]
- Lin, Z.; Sun, C.; Liu, W.; Fan, E.; Zhang, G.; Tan, X.; Shen, Z.; Qiu, J.; Yang, J. A self-powered and high-frequency vibration sensor with layer-powder-layer structure for structural health monitoring. Nano Energy 2021, 90, 106366. [Google Scholar] [CrossRef]
- Mustapha, S.; Lu, Y.; Ng, C.-T.; Malinowski, P. Sensor networks for structures health monitoring: Placement, implementations, and challenges—A review. Vibration 2021, 4, 551–585. [Google Scholar] [CrossRef]
- Li, X.Y.; Guan, Y.H.; Law, S.S.; Zhao, W. Monitoring abnormal vibration and structural health conditions of an in-service structure from its SHM data. J. Sound Vibrat. 2022, 537, 117185. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, T.; Zhu, R.; Zong, Y.; Liu, Z.; Xu, W. Damage identification of seismic-isolated structure based on CAE network using vibration monitoring data. Eng. Struct. 2023, 283, 115873. [Google Scholar] [CrossRef]
- Cui, J.; Li, X.; Wang, K.; Yan, X.; Zheng, Y.; Xue, C. A wide-frequency triboelectric vibration sensor for self-powered machinery health monitoring. Nano Energy 2025, 133, 110481. [Google Scholar] [CrossRef]
- Muxica, D.; Rivera, S.; Orchard, M.E.; Ahumada, C.; Jaramillo, F.; Bravo, F.; Gutiérrez, J.M.; Astroza, R. Autonomous sensor system for low-capacity wind turbine blade vibration measurement. Sensors 2024, 24, 1733. [Google Scholar] [CrossRef]
- Xiong, Q.; Tang, J.; Ding, T.; Wang, A.; Yu, X.; Zhang, W. Dynamic modeling and vibration response analysis of rolling bearings with composite faults considering the influence of elastohydrodynamic lubrication. Shock Vibrat. 2024, 2024, 1057592. [Google Scholar] [CrossRef]
- Chen, Q.; Cen, J.; Chen, K.; Zhang, X.; Feng, C.; Zhang, D.; Ge, S. Evolution behavior on friction-induced vibration and lubrication state identification. Tribol. Int. 2025, 210, 110817. [Google Scholar] [CrossRef]
- Cao, L.; Li, X.; Wang, Q.; Zhang, D. Vibration analysis and numerical simulation of rolling interface during cold rolling with unsteady lubrication. Tribol. Int. 2021, 153, 106604. [Google Scholar] [CrossRef]
- Hou, G.; Zhang, L. In-situ detection of lubrication status of bearings with acoustic emission monitoring. Wear 2025, 571, 205839. [Google Scholar] [CrossRef]
- Long, R.; Sun, Y.; Zhang, Y.; Shang, Q.; Ramteke, S.M.; Marian, M. Influence of micro-texture radial depth variations on the tribological and vibration characteristics of rolling bearings under starved lubrication. Tribol. Int. 2024, 194, 109545. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, W.; Li, R.; Jin, Y.; He, T. Experimental research on lubrication and vibration characteristics of water-lubricated stern bearing for underwater vehicles under extreme working conditions. Wear 2023, 523, 204778. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Li, X.; Xiao, S.; Gu, F.; Shi, Z. Effects of wear on lubrication performance and vibration signatures of rotor system supported by hydrodynamic bearings. Lubricants 2023, 11, 107. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, X.; Bai, X.; Wang, Z.; Zou, D.; Sun, J. Effect of the lubrication parameters on the ceramic ball bearing vibration in starved conditions. Appl. Sci. 2020, 10, 1237. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Luo, D.; Du, Z.; Yao, L.; Zhang, Y. Study on the tribological and tribo-vibration characteristics of laser textured tapered roller bearings under full oil lubrication. Ind. Lubr. Tribol. 2024, 77, 281–290. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, J.; Zhang, X.; Zhou, P.; Meng, W.; Bai, X.; Lu, H. Vibration properties of full ceramic bearing under elastohydrodynamic fluid lubrication based on the energy approach. Case Stud. Therm. Eng. 2024, 64, 105459. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lee, C.H. Vibration signals analysis by explainable artificial intelligence (XAI) approach: Application on bearing faults diagnosis. IEEE Access 2020, 8, 134246–134256. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, D.; Lu, Y.; Ma, Z.; Wang, X.; Song, X. Cutting tool wear monitoring based on a smart toolholder with embedded force and vibration sensors and an improved residual network. Measurement 2022, 199, 111520. [Google Scholar] [CrossRef]
- Akhlaghi, M.A.; Bagherpour, R.; Hoseinie, S.H. Real-time monitoring of disc cutter wear in tunnel boring machines: A sound and vibration sensor-based approach with machine learning technique. J. Rock Mech. Geotechol. Eng. 2025, 17, 1700–1722. [Google Scholar] [CrossRef]
- Wan, L.; Chen, Z.; Zhang, X.; Wen, D.; Ran, X. A multi-sensor monitoring methodology for grinding wheel wear evaluation based on INFO-SVM. Mech. Syst. Signal Process. 2024, 208, 111003. [Google Scholar] [CrossRef]
- Sayyad, S.; Kumar, S.; Bongale, A.; Kamat, P.; Patil, S.; Kotecha, K. Data-driven remaining useful life estimation for milling process: Sensors, algorithms, datasets, and future directions. IEEE Access 2021, 9, 110255–110286. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, L.; Gao, Y.; Li, S. Vibration signal extraction based on FFT and Least Square Method. IEEE Access 2020, 8, 224092–224107. [Google Scholar] [CrossRef]
- Brusa, E.; Bruzzone, F.; Delprete, C.; Di Maggio, L.G.; Rosso, C. Health indicators construction for damage level assessment in bearing diagnostics: A proposal of an energetic approach based on envelope analysis. Appl. Sci. 2020, 10, 8131. [Google Scholar] [CrossRef]
- Thoppil, N.M.; Vasu, V.; Rao, C.S.P. Health indicator construction and remaining useful life estimation for mechanical systems using vibration signal prognostics. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 1001–1010. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Addepalli, S. Remaining useful life prediction using deep learning approaches: A review. Procedia Manuf. 2020, 49, 81–88. [Google Scholar] [CrossRef]
- Ferreira, C.; Gonçalves, G. Remaining Useful Life prediction and challenges: A literature review on the use of Machine Learning Methods. J. Manuf. Syst. 2022, 63, 550–562. [Google Scholar] [CrossRef]
- Guo, J.; Wan, J.-L.; Yang, Y.; Dai, L.; Tang, A.; Huang, B.; Zhang, F.; Li, H. A deep feature learning method for remaining useful life prediction of drilling pumps. Energy 2023, 282, 128442. [Google Scholar] [CrossRef]
- Fu, C.; Gao, C.; Zhang, W. A digital-twin framework for predicting the remaining useful life of piezoelectric vibration sensors with sensitivity degradation modeling. Sensors 2023, 23, 8173. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Qiao, Z.; Xing, S.; Wu, Y.; Ji, H. A novel structural vibration sensing approach based on a miniaturized inertial measurement unit. Sensors 2025, 25, 3958. [Google Scholar] [CrossRef] [PubMed]
- Hong, L.; Wu, X.; Gao, Q.; Pei, C.; Liu, K. A study on double-cantilever miniaturized FBG acceleration sensors for low-frequency vibration monitoring. J. Opt. 2024, 53, 1282–1292. [Google Scholar] [CrossRef]
- Li, P.; Feng, Y.; Ding, C.; Zhong, R.; Yan, W.; Song, J.; Hong, Z.; Hu, B.; Tan, J.; Sun, J.; et al. Magnetointeractive Cr2Te3-coated liquid metal droplets for flexible memory arrays and wearable sensors. Adv. Mater. 2025, 37, 2414519. [Google Scholar] [CrossRef]
- Bhatta, T.; Faruk, O.; Islam, M.R.; Kim, H.S.; Rana, S.M.S.; Pradhan, G.B.; Deo, A.; Kwon, D.-S.; Yoo, I.; Park, J.Y. Polymeric multilayered planar spring-based hybrid nanogenerator integrated with a self-powered vibration sensor for automotive vehicles IoT applications. Nano Energy 2024, 127, 109793. [Google Scholar] [CrossRef]
- Tang, M.; Fang, Z.; Fan, C.; Zhang, Z.; Kong, L.; Chen, H.; Zeng, Z.; Yang, Y.; Qi, L. An AI-driven electromagnetic-triboelectric self-powered and vibration-sensing system for smart transportation. Eng. Struct. 2025, 323, 119275. [Google Scholar] [CrossRef]
- Lin, H.; Liu, D.; Zhou, Y.; Liu, M.; Huang, C.; Fu, Q.; Deng, K.; Huang, Y.; Huang, X.; Zhang, P.; et al. A flexible PTI-CNT strain sensor with high stretchable and sensitive for human movement and vocal cord vibration monitoring. Polymer 2024, 299, 126887. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, W.; Xiao, Z.; Yao, Q.; Xia, X.; Mei, J.; Zhang, D.; Chen, P.; Li, S.; Wang, Y.; et al. A high-temperature accelerometer with excellent performance based on the improved graphene aerogel. ACS Appl. Mater. Interfaces 2023, 15, 19337–19348. [Google Scholar] [CrossRef]
- Li, A.; Xu, J.; Xu, D.; Zhang, Z.; Cao, D.; Li, J.; Zhang, W.; Zhang, F. High-performance, breathable, and degradable fully cellulose-based sensor for multifunctional human activity monitoring. Chem. Eng. J. 2025, 505, 159564. [Google Scholar] [CrossRef]
- Philibert, M.; Yousry, Y.M.; Wong, V.K.; Yao, K. Ultrasonic surface wave transducers made of piezoelectric polylactic acid for structural health monitoring. IEEE Sens. J. 2024, 24, 29770–29777. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, S.; Jiang, H.; He, Y.; Chen, Z.; Zhang, B.; Zhang, Q.; Zhang, H. A robust biomass superhydrophobic sensor for re-healing and underwater vibration detection. Carbon 2024, 218, 118770. [Google Scholar] [CrossRef]
- Chai, B.; Shi, K.; Wang, Y.; Liu, Y.; Liu, F.; Zhu, L.; Huang, X. Integrated piezoelectric/pyroelectric sensing from organic–inorganic perovskite nanocomposites. ACS Nano 2024, 18, 25216–25225. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Qian, G.; Yu, Y.; Chen, C.; Li, H.; Li, D. High-performance flexible reduced graphene oxide/polyimide nanocomposite aerogels fabricated by double crosslinking strategy for piezoresistive sensor application. Chem. Eng. J. 2024, 480, 148203. [Google Scholar] [CrossRef]
- Wu, G.; Li, X.; Bao, R.; Pan, C. Innovations in tactile sensing: Microstructural designs for superior flexible sensor performance. Adv. Funct. Mater. 2024, 34, 2405722. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Liu, J.; Liu, X.; Zhang, C. 3D printing of anisotropic piezoresistive pressure sensors for directional force perception. Adv. Sci. 2024, 11, 2309607. [Google Scholar] [CrossRef]
- Zhang, L.; Bian, Y.; Wei, W.; Liao, Z.; Cang, M.; Yang, A.; Zhi, H.; Zhang, W.; Chen, M.; Cui, H.; et al. Dendrite-inspired and 3D printed multidirectional sensing piezoresistive metamaterials. Adv. Funct. Mater. 2025, 2508987. [Google Scholar] [CrossRef]
- Qin, L.; Zhang, L.; Feng, J.; Zhang, F.; Han, Q.; Qin, Z.; Chu, F. A hybrid triboelectric-piezoelectric smart squirrel cage with self-sensing and self-powering capabilities. Nano Energy 2024, 124, 109506. [Google Scholar] [CrossRef]
- Su, C.; Jia, P.; Zhao, A.; Tu, J.; Liu, J.; Ren, Q.; Xiong, J. Temperature-decoupled single-crystal MgO fiber-optic fabry–perot vibration sensor based on MEMS technology for harsh environments. Micromachines 2024, 15, 616. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Chen, P.H.; Chen, T.Y.; Lin, S.Y.; Wang, C.J.; Yeh, C.; Lin, T.J.; Chang, P.Z.; Li, W.C. Performance evaluation of MEMS vibration sensors for throat microphones. In Proceedings of the 2024 IEEE SENSORS, Kobe, Japan, 20–23 October 2024. [Google Scholar]
- Signore, M.A.; De Pascali, C.; Quaranta, F.; Velardi, L.; Valerini, D.; Farella, I.; Di Gloria, P.; De Giorgi, M.G.; Ficarella, A.; Francioso, L. Fabrication and characterization of a piezo-MEMS uniaxial accelerometer as a tool for the monitoring of combustion instability in gas turbine engines. Measurement 2025, 256, 118166. [Google Scholar] [CrossRef]
- Zhang, M.; Xing, X.; Wang, W. Smart sensor-based monitoring technology for machinery fault detection. Sensors 2024, 24, 2470. [Google Scholar] [CrossRef]
- Zhang, Z.; Lombardo, L.; Shi, T.; Han, X.; Parvis, M.; Li, J. A Smart combined wireless sensor for vibration and AE signals measurement. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 20–23 May 2024. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Li, Z.; Yang, S.; Wang, J. A Review on Vibration Sensor: Key Parameters, Fundamental Principles, and Recent Progress on Industrial Monitoring Applications. Vibration 2025, 8, 56. https://doi.org/10.3390/vibration8040056
Ma L, Li Z, Yang S, Wang J. A Review on Vibration Sensor: Key Parameters, Fundamental Principles, and Recent Progress on Industrial Monitoring Applications. Vibration. 2025; 8(4):56. https://doi.org/10.3390/vibration8040056
Chicago/Turabian StyleMa, Limin, Zhangpeng Li, Shengrong Yang, and Jinqing Wang. 2025. "A Review on Vibration Sensor: Key Parameters, Fundamental Principles, and Recent Progress on Industrial Monitoring Applications" Vibration 8, no. 4: 56. https://doi.org/10.3390/vibration8040056
APA StyleMa, L., Li, Z., Yang, S., & Wang, J. (2025). A Review on Vibration Sensor: Key Parameters, Fundamental Principles, and Recent Progress on Industrial Monitoring Applications. Vibration, 8(4), 56. https://doi.org/10.3390/vibration8040056