1. Introduction
To motivate the present study, we consider a conservative nonlinear oscillator:
where
is an odd function satisfying
. We cite the following result [
1,
2,
3]:
where
T is the period of the oscillator to satisfy
and
.
Equation (
2) is an integral formula in the spatial domain of
x, which can be derived by multiplying Equation (
1) by
,
integrating it at the first quadrant of the periodic orbit yields
Then, Equation (
2) follows readily.
Equation (
2) is a well-known formula to exactly compute the period and frequency
, which is, however, limited to the conservative nonlinear oscillator. Equation (
4) is the first integral of Equation (
1). The integrand in Equation (
2) is singular at
. To compute
T, it needs to perform two integrals and is, in general, an implicit function of
A.
We consider a general second-order nonlinear oscillator:
where
is the amplitude of an oscillation of the oscillator.
Let
; Equation (
5) can be expressed via a system of two first-order ODEs:
According to the Bendixson–Dulac Theorem [
3], a necessary condition for the existence of a periodic solution in a simply connected region
is that
must change its sign inside
. If
, there exists no periodic solution in
. He and Garcia [
4] proved that Equation (
5) possesses a periodic solution if and only if there exists a function
, such that
Using the Lipschitz condition for the right-hand side, the existence of
is guaranteed. As Equation (
4) for Equation (
1),
is the first integral of Equation (
5), if it allows a periodic solution.
Like
for Equation (
1),
is required for Equation (
5). The main problem we are concerned with is the derivation of a simple integral form of vibrational frequency under the assumption of
, so that the periodic solution of Equation (
5) is assumed to be existent.
Applying a similar operation in Equation (
3) for Equation (
5), we cannot simply obtain the relation between
and
x as that in Equation (
4) for the conservative oscillator. For a non-conservative nonlinear oscillator, if the first integral
exists, we can derive a similar exact formula:
which is like Equation (
2) for the conservative nonlinear oscillator in Equation (
1).
He and Garcia [
4] made a breakthrough for the following separable non-conservative oscillator:
In Corollary 1 of [
4], He and Garcia obtained an exact integral formula:
For Equation (
1), we have
and
; inserting them into Equation (
10) yields the same formula for
T in Equation (
2).
Rather than Equations (
2) and (
10), a direct relationship between the frequency and amplitude is more useful for a quick estimation of the frequency. For this purpose, a trial solution is often used to replace the exact solution by
which satisfies the initial conditions in Equation (
5), but with
an unknown function of
A. The corresponding trial ODE for Equation (
11) is
He [
5] rewrote Equation (
1) as
upon comparing Equations (
12) and (
13), He [
5] suggested a very simple frequency–amplitude formula:
where
for non-singular oscillator [
6], and
for singular oscillator [
7].
In [
8], Equation (
13) was augmented to
Integrating both the nominator and the denominator in the nonlinear stiffness term
, a formula was suggested as follows [
8,
9]:
which is an integral formula in the time domain of
t. This formula was established by El-Dib [
10] as an efficient formula. However, the theoretical foundation of Equation (
16) needs a further certification, to which the present paper is concerned with.
Antola [
11] introduced a weighted functional to determine the frequency:
By minimizing
one can arrive to the following formula:
Equation (
18) is a formal integral approach to the frequency formula in the spatial domain.
He’s frequency–amplitude formula [
12] to estimate the frequency of a nonlinear oscillator is simple and yet accurate. It, without needing a lot of computational costs, can provide a reasonable approximation that establishes a relationship between the vibration frequency and amplitude. He’s formula has demonstrated its effectiveness across a broad spectrum of challenges in many fields, particularly valuable in obtaining the closed-form analytical solutions for oscillators of the Duffing type [
4,
13]. The relationship between the frequency and amplitude is a mainly concerned property of the nonlinear oscillators. For improving the precision of the relationship, there were many modifications of He’s frequency formula [
14,
15,
16,
17]. Other modifications of He’s frequency–amplitude formulation were summarized in [
18,
19]. Recently, many discussions of the frequency–amplitude formulas, including those of He’s, were clarified in [
20].
Equation (
10) motivates us to develop the integral-type frequency formula for a general non-conservative nonlinear oscillator.
So far, different types of frequency formulas have been created one by one; there are still some challenging problems to set up a theoretical foundation of these formulas and derive a general type frequency–amplitude relationship in terms of the integrals of simple functions. Based on Equations (
5) and (
11), and other more complex trial solutions, we are going to theoretically derive some integral-type frequency–amplitude relationships for non-conservative nonlinear oscillators. Meanwhile, based on Equations (
1) and (
12), and other more complex trial ODEs, some general integral-type frequency–amplitude relationships for conservative nonlinear oscillators are to be derived. The idea of trial ODE is extended in the paper, and some weight functions are introduced to generalize the integral formulas. In many analytic methods with some trial functions as the bases to express the periodic solution of a nonlinear oscillator, there exist certain parameters in the approximation methods. A satisfactory choice of those parameters is of utmost important, because they intimately relate to the accuracy of the proposed analytic methods. By minimizing the error of periodicity conditions, the optimal value of the parameter in the proposed frequency–amplitude formula can be determined. The paper supplements the theoretical foundations for the existent or non-existent integral-type frequency–amplitude formulations in the literature, which are set up to lay out these methods. We are going to enlarge Equations (
16) and (
18) into a broad spectrum to involve the non-conservative nonlinear oscillator; meanwhile, we make a depth study of different integral-type frequency–amplitude formulations from the theoretical aspects.
The mentioned first integral for a non-conservative nonlinear oscillator can be treated as the energy integral. In addition, the so-called energy balance method appears in a vast literature. To name a few, Hill et al. [
21] introduced an energy-based interpretation of backbone curves in a two-degree-of-freedom nonlinear oscillator, demonstrating how undamped, unforced modal backbones correspond to resonant peaks in the forced, damped system and thus providing critical insight into nonlinear resonance phenomena. Building on this framework, Hill et al. [
22] developed an analytical method to detect isolated periodic solution branches (“isolas”) in weakly nonlinear structures, showing that the symmetry breaking gives rise to discrete backbone segments and simplifies numerical continuation strategies for uncovering these solution families. Sun et al. [
23] extended the energy balance method to systems with non-conservative nonlinearities by incorporating damped nonlinear normal modes (dNNMs), comparing complex nonlinear modes and extended periodic motion concepts to enhance the resonance prediction accuracy in practical engineering applications. Hill et al. [
24] examined the role of phase-locking in internal resonance from an NNM perspective, proving that phase-locked coupling is a necessary condition for internal resonance and elucidating how backbone curves reflect the stiffness-modulation effects of non-phase-locked interactions. Together, these contributions deepen our theoretical understanding of backbone curves, isolas, dNNMs, and phase-locking effects, and they lay the groundwork for advanced analytical and numerical tools in nonlinear forced-response analysis. The energy-preserving principle was adopted by Liu et al. [
25] for developing energy-preserving/group-preserving schemes to depict the nonlinear vibration behaviors of multi-coupled Duffing oscillators.
In the present paper, we do not attempt to develop the method for obtaining a highly accurate periodic solution in terms of harmonics for a non-conservative nonlinear oscillator. Instead of the present paper aims to the developments of highly accurate integral-type frequency–amplitude formulas to quickly estimate the frequency for a non-conservative nonlinear oscillator; unlike Equations (
16) and (
18), which are merely for conservative nonlinear oscillators.
Our results obtained are not applicable to the systems of Equation (
5) of a general form, when the existence of a periodic solution is not guaranteed. For the general system (
5), what conditions guarantee the existence of periodic solutions and how many periodic solutions exist is still an open problem. The present paper is strictly restricted to the systems with periodic solutions, which satisfy Equation (
5) and
.
The present paper also excludes the non-conservative nonlinear oscillator which exhibits a limit cycle, because this sort nonlinear oscillator does not satisfy the condition
. For example, the van der Pol equation is given by
where
. Obviously
not necessarily satisfies
. It is a self-sustained nonlinear oscillator with a unique limit cycle. However, it would be an interesting issue by extending Equation (
7) to this sort of nonlinear oscillator in the near future.
We highlight the innovation points of the present paper as follows:
A supplementary variable is introduced, which helps derive an integral-type frequency formula for a non-conservative nonlinear oscillator in the dimensionless time domain.
A novel integral-type frequency formula is derived for a non-conservative nonlinear oscillator in the time domain. Through a few lines of computations, the approximate value of the true frequency can be well estimated.
A novel integral-type frequency formula involving a weight function and parameter for a non-conservative nonlinear oscillator is derived. To meet the periodicity conditions by a parameter very accurate frequency can be obtained.
A generalized conservation law for a non-conservative nonlinear oscillator is derived in terms of a weight function. The resulting integral-type frequency formulas in the dimensionless time domain and time domain can be used to find accurate frequency.
For a conservative nonlinear oscillator, we derive three types of integral formulas in the dimensionless time domain, time domain, and spatial domain to quickly obtain the frequency with high accuracy.
For a non-conservative nonlinear oscillator, the integral formula in the spatial domain does not exist; unless the first integral exists.
2. Exact Formulations of Frequency–Amplitude Relationships for Nonlinear Oscillators
In this section, we derive the formulas depicting the frequency–amplitude relationship for Equation (
5) in a dimensionless time domain and then in the time domain. The technique in the dimensionless time domain was first developed by Liu and Chang [
26] as a numerical method to find the period and periodic solution of an
n-dimensional nonlinear system of ordinary differential equations. It has not yet been applied to the second-order nonlinear oscillator in Equation (
5) to compute the frequency using the derived formulations.
Letting
be a dimensionless time, considering
where the prime denotes the differential with respect to
, and by means of Equation (
6), we come to
Theorem 1. We assume that the periodic solution of Equation (5) exists inside a simply connected region wherein changes its sign. satisfiesThe frequency for Equation (5) reads as follows:whereis a supplementary variable satisfying . Furthermore, by means of Equations (22), (25) and (26),can be derived. Proof. We introduce a supplementary variable
given by Equation (
26), which satisfies
where
is an initial value of
.
The following identity is easily verified:
Multiplying Equation (
23) by
generates
which using Equations (
28) and (
29) yields
The periodicity conditions for a periodic motion in the
-domain are
The integration of Equation (
31) from
to
is
By means of
in Equation (
32), one has
; hence, the period
T can be derived from Equation (
33) as follows:
In terms of
, we can prove Equation (
25).
It can be seen that because the initial condition for
y is
,
is immaterial; hence, in Equation (
28), the initial value of
can be an arbitrary constant. Later, we will take
. If
, we can prove
to simplify the formula; it is implied by the periodicity of
y, such that
is also a periodic function of
with
. As shown by Equation (
34),
only influences the period but not the system of ODEs in Equation (
6).
Comparing Equation (
28) to Equation (
22), one has
if
is taken as the initial condition of the ODE in Equation (
28). Inserting Equation (
35) for
and
into Equation (
34) yields
which can be arranged to Equation (
27) using
. According to the assumption (
24),
,
in Equation (
36) is well-defined. The proof is complete. □
The assumption
in Equation (
24) is similar to
for Equation (
1).
Now we go back to the time domain formulation of the frequency with the help of Equations (
21) and (
36), which can generate a simple integral formula to compute the frequency in the
t-domain. Correspondingly, Equation (
27) is a frequency formula in the
-domain.
Theorem 2. Under the same assumptions in Theorem 1, the frequency for Equation (5) can be determined bywhere , which signifies that the kinetic energy and work are balanced within one period of the motion of the oscillator. Proof. Using
derived from Equation (
20) and inserting Equation (
21) for
into Equation (
36), we have
Dividing both sides by
produces
Then, using
, Equation (
37) follows readily. □
For an extension of Theorem 1, we consider a generalization of
given by Equation (
28) to the following result.
Theorem 3. A general frequency formula for Equation (5) is given bywhere satisfies, and is an integrable function of y satisfying . Proof. Inserting Equation (
41) for
into the identity (
29), we have
which being combined into Equation (
30) generates
Integrating Equation (
43) from
to
and using
renders
In terms of
, we can prove Equation (
40). □
When the double-integral Formula (
2) is applicable to the conservative system (
1) to compute the frequency, after rigorous proofs carried out for Theorems 1–3, we have the single-integral Formulas (
27), (
37) and (
40) to compute the frequency for a non-conservative system (
5), of which suitable conditions for the existence of these integral formulas were given. These results are undoubtedly correct.
Remark 1. In this section, we have derived three integral-type Formulas (27), (37), and (40) to compute the frequency. The key points are the introduction of a supplementary variable z in Equations (28) and (41) and the identity in Equation (29). These integral equations are all exact formulas, providing the exact value of the frequency if an exact solution is inserted into these formulas. As explained in Theorem 2, Equation (37) is a conservation law in the time domain for the balance of kinetic energy and work. Correspondingly, Equation (27) is a conservation law in the dimensionless time domain, and Equation (40) can be viewed as a generalized conservation law in the dimensionless time domain. Equation (
16) is a special case of Equation (
37) in Theorem 2. For the trial ODE (
12), kinetic energy is equal to potential energy, which leads to
inserting it into the left-hand side of Equation (
37) generates Equation (
16) with
for conservative nonlinear oscillator.
Remark 2. To demonstrate the exactness of Equation (37) in Theorem 2, we derive an exact solution of a nonlinear ODE in Appendix A. We prove that the following ODE:has an exact solution . By applying Equation (37) to determine the frequency of Equation (46), we suppose that the exact solution isand we can prove that is the frequency of Equation (46). Inserting Equation (47) into the left-hand side of Equation (37) yieldsInserting Equations (46) and (47) with into the right-hand side of Equation (37) yieldsComparing Equations (48) and (49) it is obvious that when , Equation (37) is satisfied. Equation (37) holds for the exact solution. Indeed, Equation (37) is an exact integral formula to determine the exact value of frequency, if the exact solution is given and inserted into the formula. However, in general, we do not have an exact solution for a given nonlinear oscillator; in practice, Equation (37) is in turn used as a convenient tool to find an approximate frequency by inserting a trial solution. 3. Applications of the Integral-Type Formulas to Compute Frequency
Notice that when
x and
y can be obtained exactly, Equations (
27) and (
37) provide the exact value of
; however, the latter one is an implicit form of the frequency equation. In general, the exact solution of a nonlinear oscillator is not available. To be an approximation of
, we assume that Equation (
11) is a suitable approximation of the real solution
x for the oscillatory system satisfying
and
.
In terms of
, using
and by Equation (
11), we have
Inserting them into Equation (
27) in Theorem 1 yields
which is a neater formula to compute
for a given function
to depict the nonlinear oscillator.
Directly inserting Equation (
11) into Equation (
37) in Theorem 2, we have
It is the counterpart of Equation (
51) in the time domain. Equation (
52) is not an exact formula, because it is obtained from Equation (
37) by inserting a trial solution in Equation (
11); however, it is a good approximation of the true frequency.
When we apply the above formulas to compute the frequency for a conservative nonlinear oscillator, we replace by .
We must emphasize that the accuracy of Equations (
51) and (
52) is merely of the first order, owing to the use of a first-order trial solution in Equation (
11). When the degree of nonlinearity of a nonlinear oscillator is increased, or the oscillation amplitude is increased, higher-order trial solutions must be considered to enhance the accuracy of
. For most examples to be shown below, we will adopt second-order and third-order harmonic functions as the trial solutions.
3.1. Duffing Oscillator
3.1.1. Initial Conditions and
We assess the integral formula in Equation (
52) derived from Theorem 2 for the Duffing oscillator:
Here, the restoring force is a cubic odd function:
which after inserting Equation (
11) for
leads to
Inserting Equation (
55) into Equation (
52) yields
where the last term in the first row gives no contribution to
, owing to the orthogonality between
and
:
It follows from Equation (
56) that
This is a well-known formula for the Duffing oscillator (
53).
In
Table 1 the exact value of
is compared to that computed by Equation (
57), whose accuracy is dropped down to one order for large amplitude
A.
3.1.2. Improving the Accuracy of
As shown in
Table 1 for the Duffing oscillator with the trial solution
to derive the frequency formula in Equation (
57), its accuracy is only of the first order. For a large amplitude of oscillation, we can consider a more complex elliptic function, as shown below for the trial solution. A more complicated trial solution can obtain a better value of frequency; however, the computational cost to derive the frequency formula is also increased. To overcome this drawback, we will introduce the parameter in the weight function to derive the frequency formula, and then seek the accurate value of frequency by adjusting the parameter to meet the periodicity conditions.
Below, we improve the accuracy of
by adopting the integral-type frequency Formula (
40) in Theorem 3. To enhance the accuracy of
, we consider the following
in Theorem 3:
where
is a parameter to be given, and
is indeed a requirement in Theorem 3. When
, the integral-type frequency formula was already derived in Equation (
51), whose accuracy of
is of first-order.
Using
and
, where
, and Equations (
41), (
55) and (
59), we can derive
Inserting them into Equation (
40) yields
where
If
, Equation (
63) recovers to Equation (
57).
If
, the frequency is given by
where the optimal value of
is determined by
is the absolute error of the periodicity condition
.
is computed by applying the fourth-order Runge–Kutta method to integrate Equation (
53) with a finer time increment
, where
is taken. The accuracy of Equation (
65) is still with five orders even with large amplitudes of
and
. The improvement of the frequency obtained by Equation (
65) over Equation (
57) is about three to five orders as tabulated in
Table 1.
Although a simple trial solution
in Equation (
11) was inserted into Equation (
40) in Theorem 3, the resulting formula (
65) is still very accurate. The key point lies in a free parameter
being appeared in Equation (
65), which is determined by matching the periodicity condition, such that highly accurate frequency can be achieved. The term
in Equation (
59) plays a role to correct Equation (
57), such that the resultant frequency formula in Equation (
65) is more accurate than Equation (
57) for large amplitude vibration.
3.1.3. Check the Accuracy of Equation (37) in Theorem 2
Remark 2 has explained the exactness of Equation (
37) in Theorem 2 by examining an exact solution in Equation (
46). Continuing this line, we can check the accuracy of Equation (
37) for the Duffing oscillator in Equation (
53). According to [
27], the exact solution of the Duffing oscillator is given by
where
is the Jacobian elliptic function. Up to the third-order approximation of Equation (
67), we consider
where
and
is the first kind complete elliptic integral.
Inserting Equation (
68) into Equation (
37), and after some operations we can derive
where
In
Table 2, the exact value obtained from Equation (
58) is compared to that computed by Equation (
75). It proves that the accuracy of Equation (
37) for evaluating the frequency is very good.
As shown in
Table 2 for the Duffing oscillator with the third-order trial solution in Equation (
68) to derive the frequency formula in Equation (
75), the accuracy of the frequency is enhanced upon comparing to that in
Table 1. The computational cost to derive the frequency formula (
75) is increased upon comparing to that in the derivation of Equation (
57).
3.1.4. Initial Conditions and
Next, we derive a simple formula for the Duffing oscillator by giving the general initial conditions:
Notice that
cannot have a constant term, say
; otherwise,
with a term
, which is not a periodic function of
. Because
is a periodic function of
and does not have a constant term,
defined in Equation (
26) is a periodic function. Even for
, the results in Theorems 1–3 are still applicable, since in Equation (
33) the constant term is zero, i.e.,
because
defined in Equation (
26) is indeed a periodic function satisfying
.
We begin with
where for satisfying the initial condition
in Equation (
77),
We insert the following terms into Equation (
37) in Theorem 2:
which leads to the following frequency equation:
and recovers to Equation (
57) if
. Then, a simple formula is given as follows:
The exact period is given by [
26]:
where
is the maximal displacement.
Table 3 compares
computed by Equations (
82) and (
83). For Equation (
82), the accuracy of frequency is good when a weak nonlinearity of the oscillator with the values of
is considered.
3.2. A Singular Oscillator
We consider a singular oscillator [
28,
29]:
where the restoring force
is singular at
. Recently, Kontomaris and Malamou [
30] explained the singular oscillator from physical considerations and mechanical analogies.
Inspired by the work in [
28], we take the following second-order trial solution:
Inserting it and
into Equation (
37) in Theorem 2 yields the formula for
:
which is a new formula for the singular oscillator.
Like
determined by Equation (
66), a suitable criterion to determine the optimal value of
is
The new method offers an easy way to raise the precision of
by inserting the above optimal value of
into the formula (
87) derived from Theorem 2 for the singular oscillator.
For the singular oscillator, the exact value is [
29]
According to Equation (
88), we take
, which is inserted into Equation (
87), and the resultant value is quite close to the exact one in Equation (
89); the relative error is very small:
Given
, in
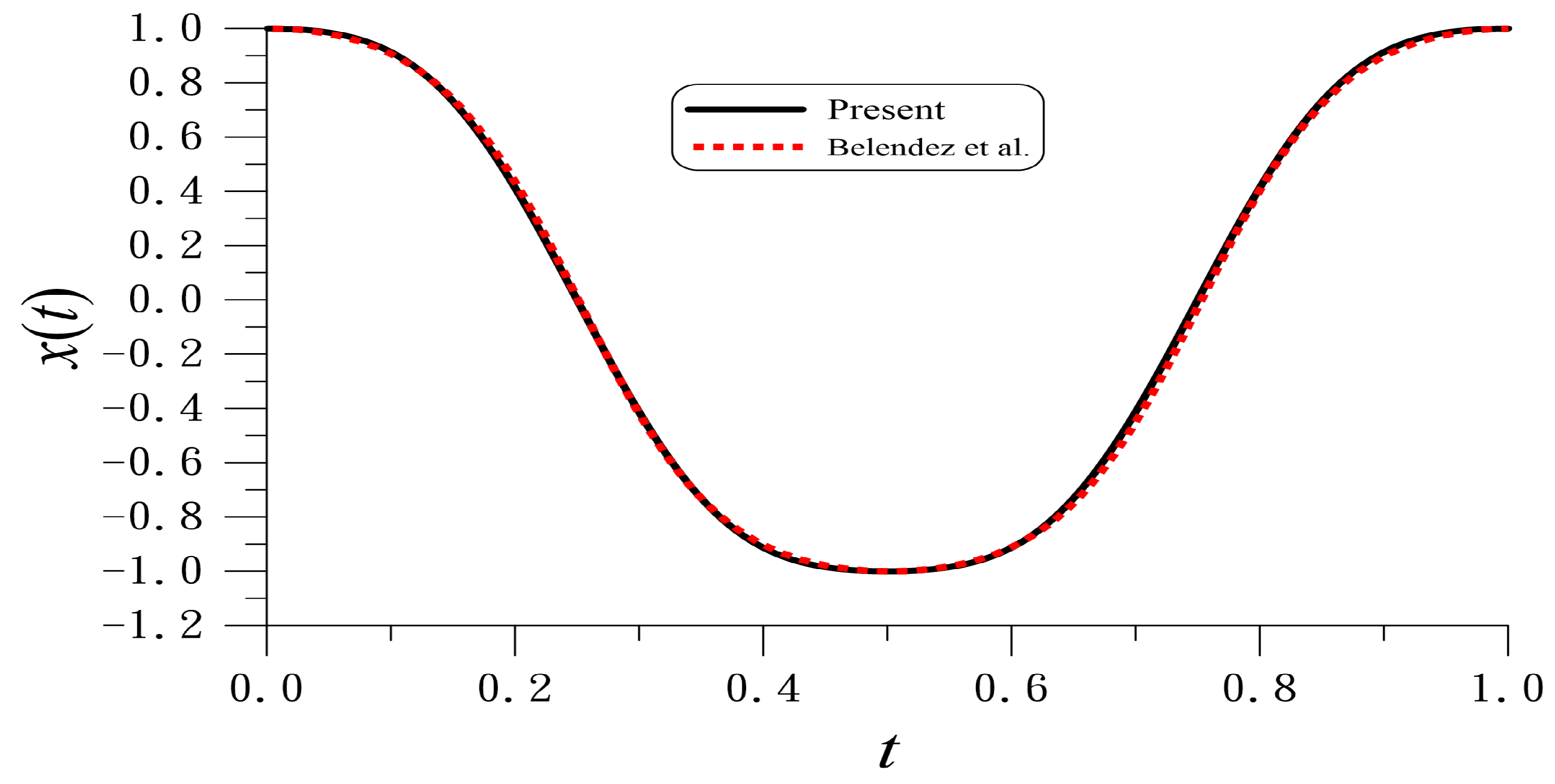
Figure 1 the periodic solution (
86) is compared to the following second-order one [
29]:
They are quite close with the maximal difference being
.
3.3. Mickens’ Oscillator
We consider the Mickens’ oscillator [
31]:
The assumption
in Equation (
24) is satisfied by Equation (
92), due to
.
Suppose that a second-order trial periodic solution is given by
where
is an integer, and like
,
is determined by Equation (
66).
Inserting Equation (
93) and
into Equation (
37) in Theorem 2 yields the following formula for
:
where
Given
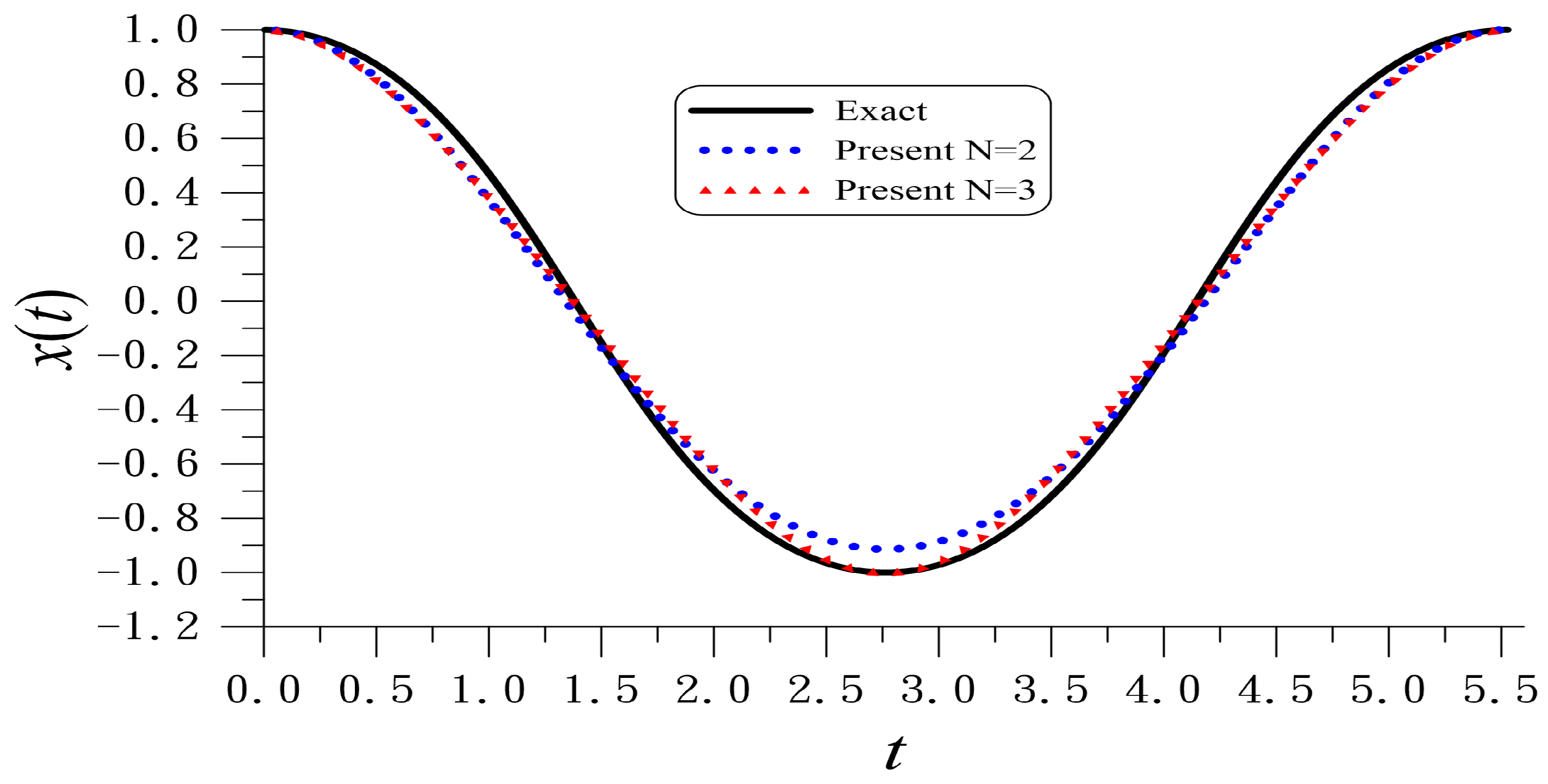
, in
Figure 2 the periodic solutions (
93) with
and
are compared to the exact one. For
, the optimal value is
, which leads to
. For
, the optimal value is
, which leads to
.
is better than
.
The major difference between the Mickens curves obtained by and is the portion between and , where the curve for is closer to the exact solution than the curve for .
Table 4 compares
computed by different values of
N. It can be seen that
N has little influence on the value of
.
In [
31], the following integral formula was derived:
When
,
is obtained, which is close to the above
with
, and
with
.
Mickens’ oscillator possesses the following first integral:
It is easy to check the following equation:
which is just Equation (
92). From Equation (
98) the period given by Equation (
97) follows immediately form Equation (
10) by inserting
in Equation (
98).
For comparison we derive an approximation of
using the first-order harmonic balance method [
31,
32]:
whose frequency is
When
, we obtain
. Upon comparing to the exact value
, the accuracy of Equation (
101) is not good.
To raise the accuracy of
using the harmonic balance method, we can consider a second-order trial solution:
where
B and
are unknown constants. After inserting Equation (
102), and
into Equation (
92), balancing the terms
and
, and through a lengthy manipulation, we can derive two coupled nonlinear algebraic equations:
However they are fifth-order nonlinear equations to hinder a closed-form formula for
, unlike the formula (
94) obtained from Theorem 2.
For the classical methods like the harmonic balance method and the perturbation method, the higher-order value of the frequency is hard to achieve, which requires performing a lot of algebraic operations. In general, the closed-form formula for is not available. In contrast, the advantage of the proposed integral formula is easy to derive the formula in closed form, and we can quickly compute quite accurate frequencies merely through a few lines of computations.
In Equation (
93) if we replace the second term by
,
it would be a failure to satisfy the initial conditions, and Equation (
92) cannot be satisfied by balancing the harmonic terms.
3.4. Quintic Duffing Oscillator
We consider a quintic Duffing oscillator [
33]:
Beléndez et al. [
33] using the technique of cubication through the Chebyshev polynomials to derive an approximation of Equation (
106):
where
and
For Equation (
107) the exact solution is given by
Up to third-order approximation, we consider
where
Inserting Equation (
110) into Equation (
37) in Theorem 2 with
, and through some operations we can derive
where
In
Table 5, the exact value of the frequency obtained from
is compared to that computed by Equation (
116).
6. A Weighted Integral Formula for Conservative Nonlinear Oscillators
The formulations of frequency in the -domain and t-domain are also applicable to the conservative nonlinear oscillator, if is replaced by . In this section, and the next two sections, we are going to derive simpler formulas in the spatial domain, namely the x-domain, to compute the frequency for a conservative nonlinear oscillator. The new formulations are based on the idea of a trial ODE to replace the acceleration term in the formulation. A more general result than Theorem 7 can be deduced by introducing a weight function.
Theorem 8. For the conservative nonlinear oscillator in Equation (1), an integral-type frequency–amplitude formula is given bywhere is a weight function satisfying and in the range of . Proof. Taking the product of
to Equation (
1) yields
which by inserting the trial ODE
for
, becomes
Integrating both sides from
to
, and considering its amplitude
, we can derive Equation (
157). □
It is not an easy issue to determine the optimal weight function
in its general form used in Equation (
157) for a general conservative nonlinear oscillator. In general, we take
to be a power function for an easier manner to compute the integrals
and
in Equation (
157).
If we take
, a suitable criterion to determine
p is
for the singular oscillator, or the periodicity condition
for the non-singular oscillator. Equation (
160) is an original criterion for the singular oscillator.
As an application of Equation (
157), we take
:
which was introduced by He and Liu [
36] for a modified frequency–amplitude formulation of the fractal vibration systems.
We take
in Equation (
157) derived from Theorem 8, such that Equation (
162) is the same as that proposed by He and Liu [
36]. For other system we take
and determine
p by Equation (
161).
In addition the conditions
,
and
, the principle for choosing
is that the integral terms
and
can be integrated explicitly, without resorting on the numerical integrations. In this manner, we can derive the explicit formula for
by means of Equation (
157).
6.1. Quintic Duffing Oscillator
We apply Equation (
157) in Theorem 8 to the quintic Duffing oscillator (
106). Inserting
and
into Equation (
157) generates
This formula is much simpler than that given in Equation (
116).
The frequency is a quantity to measure the periodicity of the solution for a periodic system. Therefore
must abide the rule of
, that is
. When Equation (
163) is used to compute
, the best value of
p is selected such that the condition
can be satisfied. Usually, the condition
cannot be solved exactly, because
is a highly nonlinear and implicit function of
T. Hence, we turn it to be a minimization problem in Equation (
161), which is easily implemented into a computer program to determine the optimal value of
p.
In view of
Table 6, we can observe that Equation (
163) with
is more accurate than Equation (
116) when
.
6.2. Singular Oscillators
We consider two singular oscillators with
and
in Equation (
138). Inserting
into Equation (
157), it immediately leads to
According to Equation (
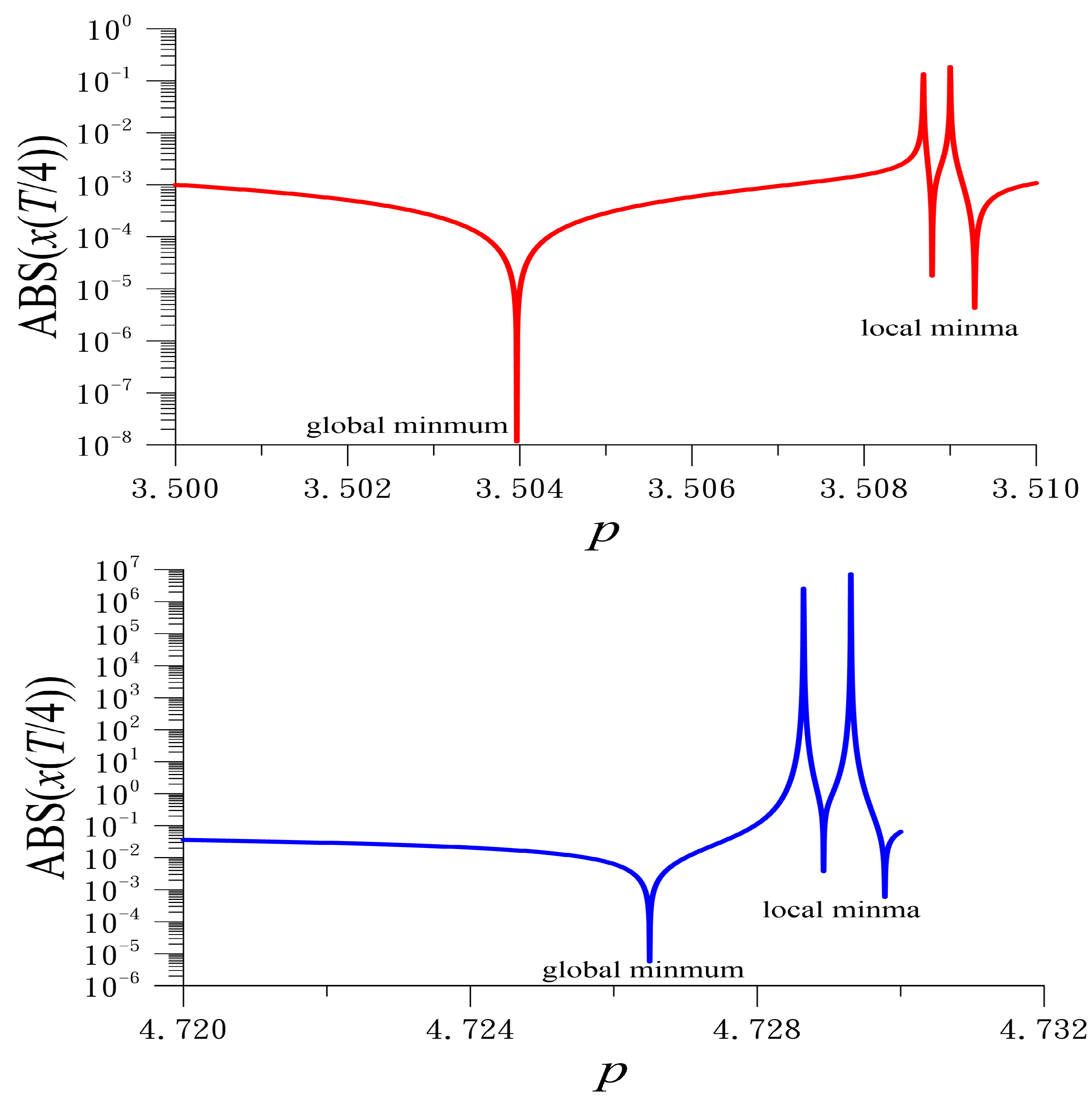
160), we plot the values of
in a finer interval
for
, and
for
in
Figure 3. Because the curves are obtained by the integration of the singular ODE (
138), which is infinite at
, they are irregular in some range of
p. In
Figure 3, one global minimum and two local minima are remarked. To satisfy the requirement in Equation (
160), we take the optimal value of
p at the global minimum point.
For
, the minimal point is
, rendering
, which is close to the exact one with the relative error
. This result is slightly better than that obtained by Equation (
87). For
, the minimal point is
, rendering
, which is close to the exact one with the relative error
.
For the singular oscillator with
, upon setting
into Equation (
18), the same formula can be derived in Equation (
165).
Now we check the theoretical foundation for Equation (
18) derived by Antola [
11]. Letting
and from Equation (
1), we have the following system of first-order ODEs:
where
is computed from Equation (
18) by inserting
, and
. We can integrate this system using the fourth-order Runge–Kutta method.
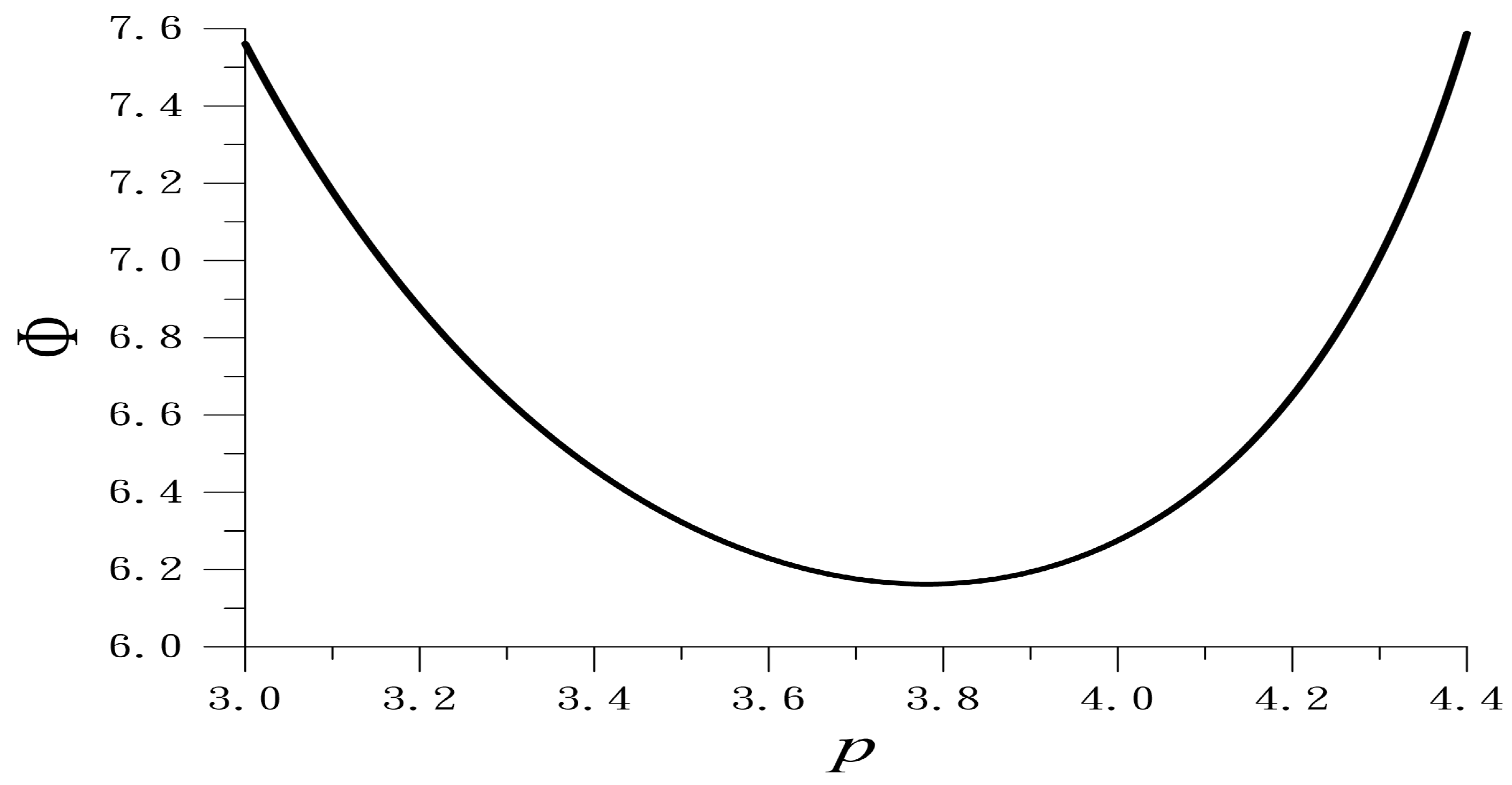
We plot the values of
vs.
p in an interval
in
Figure 4. The minimal point is
, and the corresponding
is
, which compared to the exact value
is with the relative error
. We can conclude that the weighted functional method, as advocated by Antola [
11], is less accurate than the method derived in Theorem 8.
7. A More Complex Trial ODE
Rather than
(or the trial solution
) used in the derivation of Theorem 8, we consider a more complex trial solution given in Equation (
86). If
for Equation (
86), we can prove that the corresponding ODE is
whose proof is relegated to
Appendix A.
It is interesting that
is the unique solution of Equation (
168) by subjecting to initial conditions
and
.
It follows from Equation (
169) that
By means of Equations (
169) and (
170) the initial conditions
and
are satisfied obviously. Using Equations (
169) and (
171), we can derive
It is Equation (
168). We proved that Equation (
169) is a unique solution of Equation (
168), subjecting to initial conditions
and
.
Theorem 9. For the conservative nonlinear oscillator in Equation (1), if the trial ODE is Equation (168), then an integral-type formula for ω is given bywhere is a weight function satisfying and in the range of . Proof. Inserting Equation (
168) for
into Equation (
158), we have
Integrating both sides from
to
, and considering its amplitude
, we can derive Equation (
173). □
Now, we apply Theorem 9 to the soft oscillator [
35,
37]:
whose exact frequency is given by
Integrating from
to
for the following first-order ODE derived from Equation (
175):
the error is
. Equation (
177) is the first integral of Equation (
175).
Inserting
and
into Equation (
173) generates a simple formula:
To meet the requirement in Equation (
160) the optimal value
is obtained, of which
is obtained, and
The error
is smaller than
obtained by the exact value of
. It is interesting that
in Equation (
178) with the optimal value
for A = 1 is more accurate than the exact one
in Equation (
176). Using Equation (
176) to compute
, a singular integral
is encountered when
s nears 1, which may cause a less accurate value of
.
The nonlinear oscillator (
168) and its solution (
169) has infinite frequency. To define, we insert
into
Inserting
into Equations (
168) and (
169), we compare the exact solution to that obtained by the fourth-order Runge–Kutta method in
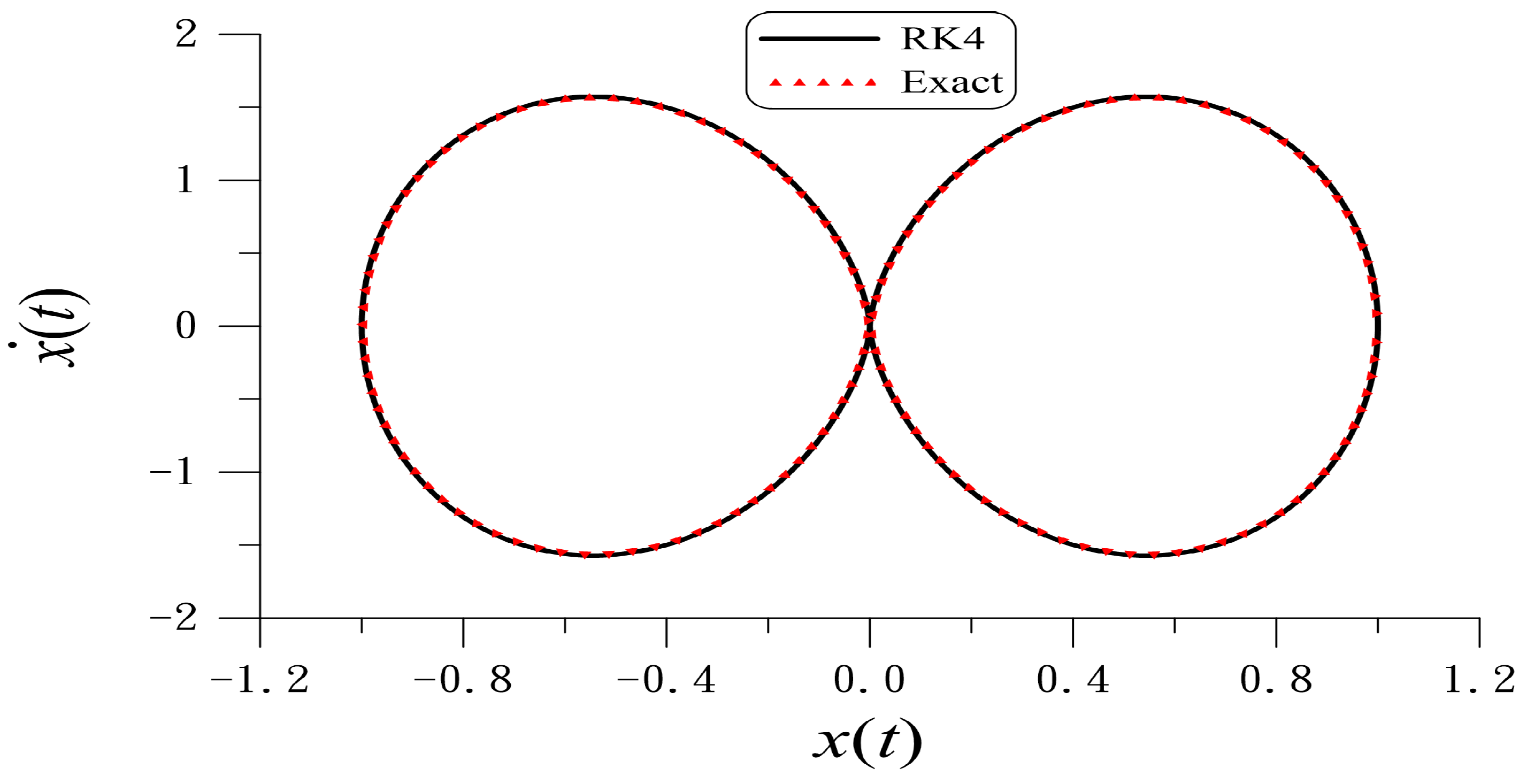
Figure 5; they are almost coincident. The closed orbit is not smooth near the cusp point
. The trajectory does not cross the cusp point, which immediately returns before reaching the cusp points on
and
.
Remark 4. We mention a counterexample for of Garcia’s conjecture. For Equation (147), the conjecture of Garcia [35] was proposed that an optimal integer value N to approximate the true amplitude-period relationship is . We consider the nonlinear oscillator (168) with a parameter :where signifies the linear spring constant, while is a soft spring constant. Inserting with and into Equation (147) as derived in [35] yieldswhich is quite different from the value in Equation (180). Hence, the optimal integer is not as conjectured by Garcia [35]. 8. A Generalized Trial ODE for Conservative Nonlinear Oscillators
For a given, more complex trial solution, the corresponding trial ODE may not be obtained easily. To generalize the frequency formula, we can relax this constraint by introducing a trial function in the trial ODE.
Theorem 10. Letbe a trial ODE, where . For the conservative nonlinear oscillator in Equation (1) an integral formula for ω is given bywhere is a weight function satisfying and in the range of . Proof. Taking the product of
to Equation (
1) yields
which by inserting Equation (
183) for
becomes
Integrating both sides from
to
, and considering its amplitude
, we can derive Equation (
184). □
For the Duffing oscillator in
Section 3.1, we take
and
where the factor
is employed to balance the power of
A when
is taken. Then, by inserting
,
and Equation (
187) into Equation (
184), we can derive
If
, we recover to the frequency formula given in Equation (
57). However,
is not the optimal value. As in Equation (
66) for
, we can obtain the optimal value of
. Formula (
188) is simpler than the one in Equation (
65) derived from Theorem 3 for the Duffing oscillator.
In
Table 7 the exact value of
given in Equation (
58) is compared to that computed by Equation (
188). Upon comparing to
Table 1, the improvement of accuracy of
is apparent.
When we consider the following initial conditions:
Equation (
188) is still applicable but with the following maximal displacement
A:
The formula (
188) for this case is much simpler than Equation (
82) derived from Theorem 2 for the Duffing oscillator.
Table 8 compares
to the exact ones with the values of
. Comparing
Table 8 to
Table 3, the improvement of the accuracy of
is significant.
Then, we raise the values of
and
to
and
.
Table 9 compares
to the exact ones with different values of
for Equation (
190). The accuracy of the frequency can be appreciated when large values of
are considered.
9. Conclusions
The theoretical foundations of integral-type formulations were incorporated into the frequency–amplitude formulas to estimate the frequency for both conservative and non-conservative nonlinear oscillators. For a newly received model of a nonlinear oscillator, if there exists no simple method to accurately estimate the vibration frequency, the proposed integral-type methods can quickly produce a good approximation of the vibration frequency with a few lines of computation. The frequency–amplitude formulas were developed as the integral-type equations in the -domain and t-domain for the non-conservative nonlinear oscillators. Because they are derived mathematically from an identity and the governing equations without adopting any approximation, the frequency obtained is exact if one inserts the exact solution into the formulas. Suitable conditions for these formulas were given, and the results are correct because they are derived through a rigorous mathematical procedure.
In general, the exact solution is not available; hence, we inserted a simple trial solution into the formulas to obtain the approximate value of the true frequency of the nonlinear oscillator. The basic requirement of the trial solution is that it must satisfy the given initial conditions.
For two examples in
Section 3.1.1 and
Section 5.1, we took the simplest trial solution
to derive the frequencies in order to compare them to the results obtained by other methods. A more complicated trial solution or trial ODE can obtain a better value of frequency; however, the computational cost to derive the frequency formula is also increased. To overcome this drawback, we have introduced a parameter in the weight function to derive the frequency formula, and then sought an accurate value of the frequency by adjusting the parameter to meet the periodicity conditions. For most examples, we have employed more complex trial solutions to obtain more accurate frequencies.
The frequency–amplitude formulas were also developed as the integral type in the x-domain for conservative nonlinear oscillators. The idea of trial ODE is introduced, which, being inserted into the integration of the governing equation, can generate very simple yet effective formulas to compute the frequency. After introducing the weight functions, these formulas are generalized to more powerful ones, which involve some parameters. When the parameter in the formulas is obtained by minimizing the absolute error of the periodicity condition, the accuracy of the frequency obtained from the new frequency–amplitude formulas can be significantly increased by several orders. A more complex trial ODE is introduced. It enlarged the application range of the integral-type frequency–amplitude formulas. Many examples of both conservative and non-conservative nonlinear oscillators were examined to confirm the efficiency and accuracy of the proposed theoretical integral methods.
Consequently, for the conservative nonlinear oscillators, we have three integral-type formulations of the frequency in the -domain, t-domain, and x-domain. For the first two types, the integral formulations are exact. When some simple trial solutions are inserted into the formulas, we can obtain the approximate values of the frequency. The x-domain formulations are not the exact ones, because the acceleration term was replaced by the trial ODE. However, its advantage is that we do not need to use the trial solution to compute the frequency, and its form is simpler than that in the -domain and t-domain. For the non-conservative nonlinear oscillator, the x-domain formulation does not exist, because the integral term cannot be expressed as a function of A.
The method based on the balance of kinetic energy and work during the oscillation period is conceptual simple. It allowed us to quickly obtain the integral-type formulas for determining the oscillator oscillation frequency. Even with complex trial functions up to three orders, the algebraic manipulations to derive the explicit formula of frequency are quite saving.
Main points for the novel contributions of the present paper are summarized as follows.
The theoretical contributions were substantial, with a comprehensive study on deriving and validating the integral-type formulas for estimating the vibrational frequencies of both conservative and non-conservative nonlinear oscillators.
Significant contributions were made to the field of nonlinear oscillations by providing theoretically sound and practically useful integral-type frequency–amplitude formulas.
Three integral-type integral formulas for conservative nonlinear oscillator were constructed, respectively, in the dimensionless time domain, time domain, and spatial domain.
Novel integral-type frequency formulas were derived for a non-conservative nonlinear oscillator in the dimensionless time domain and time domain. Through a few lines of computations, the approximate value of frequency can be well estimated by these formulas.