Weibull Reliability Based on Random Vibration Performance for Fiber Optic Connectors
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Foundations of Weibull Reliability Analysis
2.2. Random Vibration Analysis
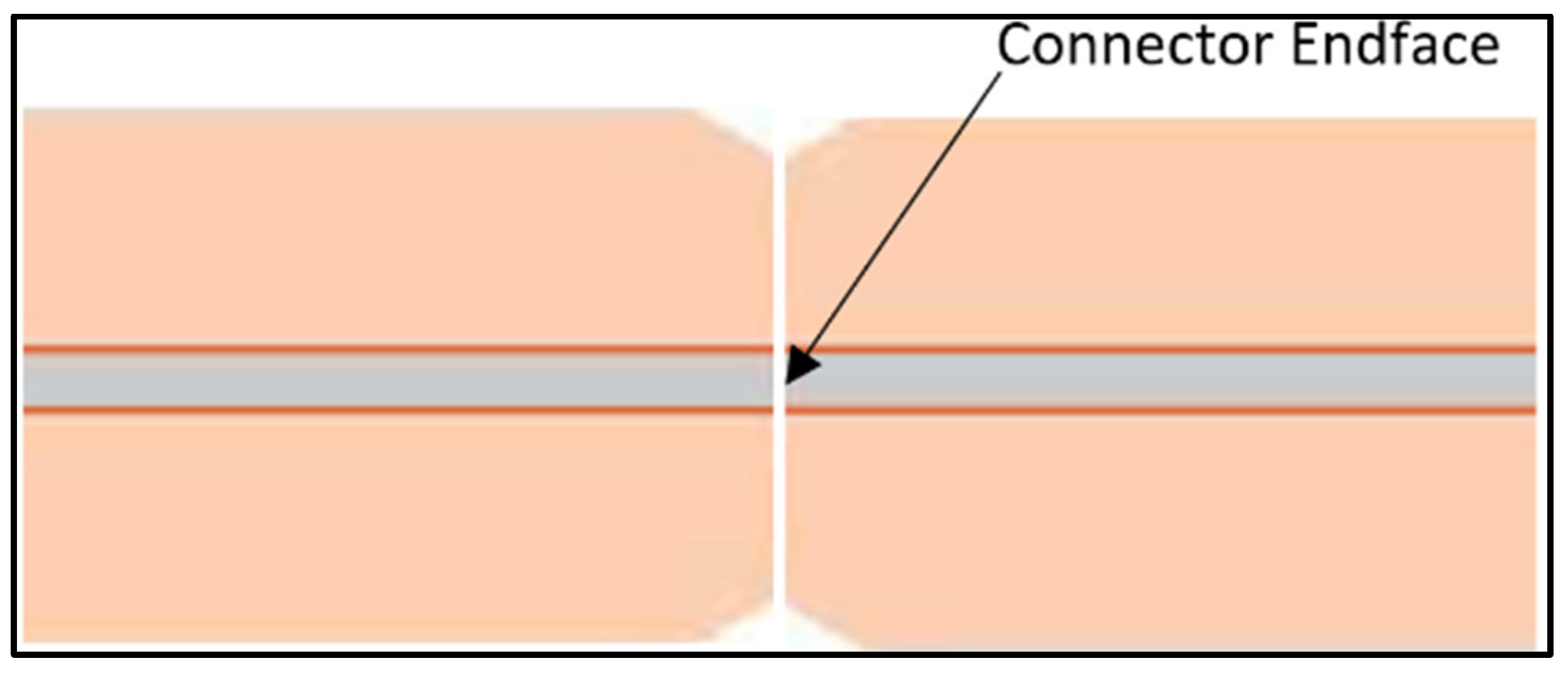
2.3. Fiber Optic Connectors
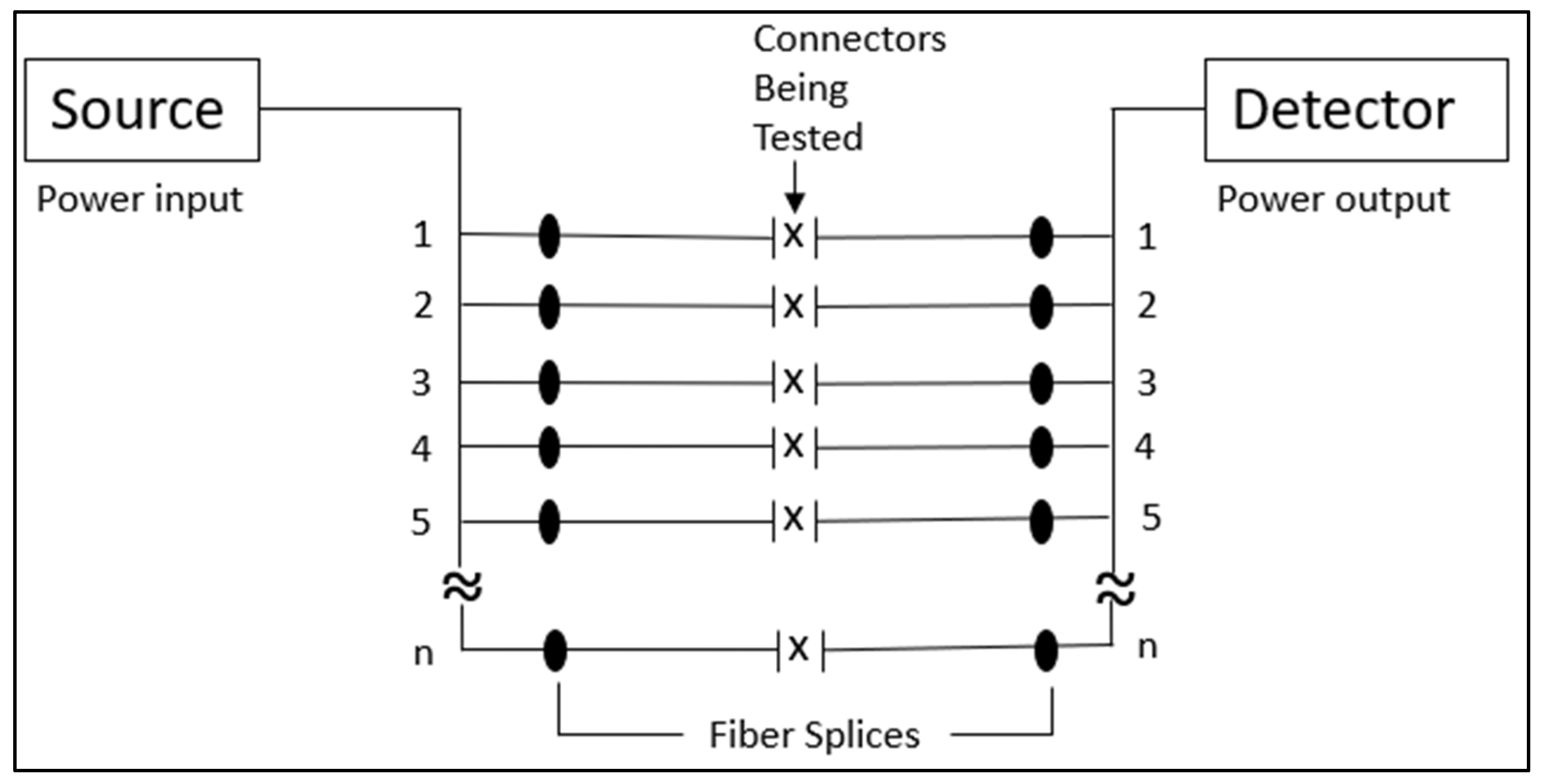
3. Methodology and Experimental Design
4. Results
5. Discussion
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IL | Insertion loss |
| dB | Decibels |
| PC | Physical contact |
References
- Fenta, M.C.; Potter, D.K.; Szanyi, J. Fibre Optic Methods of Prospecting: A Comprehensive and Modern Branch of Geophysics. Surv. Geophys. 2021, 42, 551–584. [Google Scholar] [CrossRef]
- Butt, M.A.; Voronkov, G.S.; Grakhova, E.P.; Kutluyarov, R.V.; Kazanskiy, N.L.; Khonina, S.N. Environmental Monitoring: A Comprehensive Review on Optical Waveguide and Fiber-Based Sensors. Biosensors 2022, 12, 1038. [Google Scholar] [CrossRef]
- Pandiaraj, S.; Krishnamoorthy, R.; Ushasukhanya, S.; Ramesh, J.V.N.; Alsowail, A.; Selvarajan, A. Optimization of IoT circuit for flexible optical network system with high speed utilization. Opt. Quantum Electron. 2023, 55, 1206. [Google Scholar] [CrossRef]
- Liu, X. Optical Communications in the 5G Era; Elsevier: London, UK, 2022; pp. 16–63. [Google Scholar]
- Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Hernández-Ramos, M.M.; Monclova-Quintana, O.; Ramos-Lozano, S. Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors. Appl. Sci. 2024, 14, 6198. [Google Scholar] [CrossRef]
- Wang, R.; Xu, L.; Zhou, Y.; Li, Y. A Systematic Approach for the Reliability Evaluation of Electric Connector. J. Electr. Comput. Eng. 2021, 1, 1742. [Google Scholar] [CrossRef]
- Glaesemann, G.S. Optical Fiber Failure Probability Predictions from Long-Length Strength Distributions. In Proceedings of the 40th International Wire and Cable Symposium, St. Louis, MO, USA, 18 November 1991. [Google Scholar]
- Annovazzi-Ledi, V.; Donati, S.; Merlo, S.; Zapelloni, G. Statistical analysis of fiber failures under bending-stress fatigue. J. Light. Technol. 1997, 15, 288–293. [Google Scholar] [CrossRef]
- Zeng, Z.; Barros, A.; Coit, D. Dependent failure behavior modeling for risk and reliability: A systematic and critical literature review. Reliab. Eng. Syst. Saf. 2023, 239, 109515. [Google Scholar] [CrossRef]
- Shahriari, M.; Shahrasbi, H. Reliability analysis of lifetime systems based on Weibull distribution. Int. J Nonlinear Anal. Appl. 2024, 15, 321–329. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Gallardo, D.I.; Marchant, C.; Sánchez, L.; Bourguignon, M. An In-Depth Review of the Weibull Model with a Focus on Various Parameterizations. Mathematics 2023, 12, 56. [Google Scholar] [CrossRef]
- Bhandari, K.B.; Shrestha, B.; Shrestha, S. Quantifying Optical Link Loss of Fiber-to-the-Home Infrastructure. Int. J. Adv. Smart Converg. 2024, 13, 48–58. [Google Scholar] [CrossRef]
- Khodayari, M. Vibration Analysis for Predictive Maintenance of Optical Fiber Cable Production Line. Master’s Thesis, Aalto University, Espoo, Finland, 2024. [Google Scholar]
- Wang, L.; Pan, Y.; Li, K.; He, L.; Wang, Q.; Wang, W. Modeling and Reliability Analysis of MEMS Gyroscope Rotor Parameters under Vibrational Stress. Micromachines 2024, 15, 648. [Google Scholar] [CrossRef]
- Bagri, I.; Tahiry, K.; Hraiba, A.; Touil, A.; Mousrij, A. Vibration Signal Analysis for Intelligent Rotating Machinery Diagnosis and Prognosis: A Comprehensive Systematic Literature Review. Vibration 2024, 7, 1013–1062. [Google Scholar] [CrossRef]
- Guo, P.; Xiong, Z.; Dong, Z.; Zhang, S. Spindle vibration induced optical performance deterioration and its trans-scale characterization for diamond turned large-aperture optics. Appl. Opt. 2024, 63, 8380–8388. [Google Scholar] [CrossRef]
- Papapavlou, C.; Paximadis, K.; Uzunidis, D.; Tomkos, I. Toward SDM-Based Submarine Optical Networks: A Review of Their Evolution and Upcoming Trends. Telecom 2022, 3, 234–280. [Google Scholar] [CrossRef]
- McKenzie, I.; Ibrahim, S.; Haddad, E.; Abad, S.; Hurni, A.; Cheng, L.K. Fiber Optic Sensing in Spacecraft Engineering: An Historical Perspective from the European Space Agency. Front. Phys. 2021, 9, 719441. [Google Scholar] [CrossRef]
- Indmeskine, F.; Saintis, L.; Kobi, A. Review on accelerated life testing plan to develop predictive reliability models for electronic components based on design-of-experiments. Qual. Reliab. Eng. Int. 2023, 39, 2594–2607. [Google Scholar] [CrossRef]
- Edson, L. The GMW3172 Users Guide; The Electrical Validation Engineers Handbook Series; Electrical Component Testing; General Motors Co.: Detroit, MI, USA, 2015. [Google Scholar]
- Woo, S. Introduction to the Necessity of Design Methodology. In Design of Mechanical Systems; Springer Series in Reliability Engineering; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–49. [Google Scholar]
- Ghazali, M.H.M.; Rahiman, W. Vibration Analysis for Machine Monitoring and Diagnosis: A Systematic Review. Shock. Vib. 2021, 1, 3148. [Google Scholar] [CrossRef]
- Rauber, T.W.; da Silva Loca, A.L.; Boldt, F.D.A.; Rodrigues, A.L.; Varejão, F.M. An experimental methodology to evaluate machine learning methods for fault diagnosis based on vibration signals. Expert Syst. Appl. 2021, 167, 114022. [Google Scholar] [CrossRef]
- Uzunidis, D.; Logothetis, M.; Stavdas, A.; Hillerkuss, D.; Tomkos, I. Fifty years of fixed optical networks evolution: A survey of architectural and technological developments in a layered approach. Telecom 2022, 3, 619–674. [Google Scholar] [CrossRef]
- Xu, M.; Mao, H. q-Weibull Distributions: Perspectives and Applications in Reliability Engineering. IEEE Trans. Reliab. 2024. Early Access. [Google Scholar] [CrossRef]
- Yadav, A.K.; Malik, H.; Yadav, V.; Alotaibi, M.A.; Márquez, F.G.; Afthanorhana, A. Comparative analysis of Weibull parameters estimation for wind power potential assessments. Results Eng. 2024, 23, 102300. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens Litografiska Anstalts Forlag: Stockholm, Sweden, 1939. [Google Scholar]
- Piña-Monarrez, M.R. Weibull stress distribution for static mechanical stress and its stress/strength analysis. Qual. Reliab. Eng. Int. 2018, 34, 229–244. [Google Scholar] [CrossRef]
- Tran, M.Q.; Sousa, H.S.; Ngo, T.V.; Nguyen, B.D.; Nguyen, Q.T.; Nguyen, H.X.; Baron, E.; Matos, J.; Dang, S.N. Structural Assessment Based on Vibration Measurement Test Combined with an Artificial Neural Network for the Steel Truss Bridge. Appl. Sci. 2023, 13, 7484. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Wang, P.; Bai, Q.; Gao, Y.; Zhang, H.; Jin, B. Pattern Recognition for Distributed Optical Fiber Vibration Sensing: A Review. IEEE Sensors J. 2021, 21, 11983–11998. [Google Scholar] [CrossRef]
- Telcordia. Generic Requirements for Singlemode Optical Connectors and Jumper Assemblies GR-326, 4th ed.; Telcordia: Piscataway, NJ, USA, 2010; pp. 4–17. [Google Scholar]
- Park, B.-C.; Seo, S. Development of a Handheld Optical Fusion Splicer with a Wing Sleeve Optical Connector. Electronics 2023, 12, 4629. [Google Scholar] [CrossRef]
- Psaila, N.; Nekkanty, S.; Shia, D.; Tadayon, P. Detachable Optical Chiplet Connector for Co-Packaged Photonics. J. Light. Technol. 2023, 41, 6315–6323. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, X.; Ma, L.; Immonen, M.; Zhu, L.; He, Z. Optical printed circuit boards with multimode polymer waveguides and pluggable connectors for high-speed optical interconnects. Opt. Express 2023, 31, 27776–27789. [Google Scholar] [CrossRef]
- Brückner, V. Fiber Optic Connections and Couplers; Elements of Optical Networking; Springer: Berlin/Heidelberg, Germany, 2024; pp. 67–80. [Google Scholar]
- Unión Internacional de Telecomunicaciones. Empalmes de Fibra Óptica; Recomendación UIT-T L.12; UIT-T: Geneva, Switzerland, 2001; pp. 14–19. [Google Scholar]
- Piña-Monarrez, M.R.; Ramos-López, M.L.; Alvarado-Iniesta, A.; Molina-Arredondo, R.D. Robust sample size for Weibull demonstration test plan. DYNA 2016, 83, 52–57. [Google Scholar] [CrossRef]
- Piña-Monarrez, M.R. Weibull analysis for normal/accelerated and fatigue random vibration test. Qual. Reliab. Eng. Int. 2019, 35, 2408–2428. [Google Scholar] [CrossRef]
- Kamimura, K.; Fujimaki, Y.; Matsuda, K.; Nagase, R. Ferrule Endface Dimension Optimization for Standard Outer Diameter 4-Core Fiber Connector. IEICE Trans. Electron. 2023, E106, 781–788. [Google Scholar] [CrossRef]
- Fathi, E.; Belyadi, F.; Adenan, M.F.; Pacheco, C. Application of Fiber Optics for Completion Design Optimization: A Methodological Approach and Key Findings. Fuels 2024, 5, 33–52. [Google Scholar] [CrossRef]

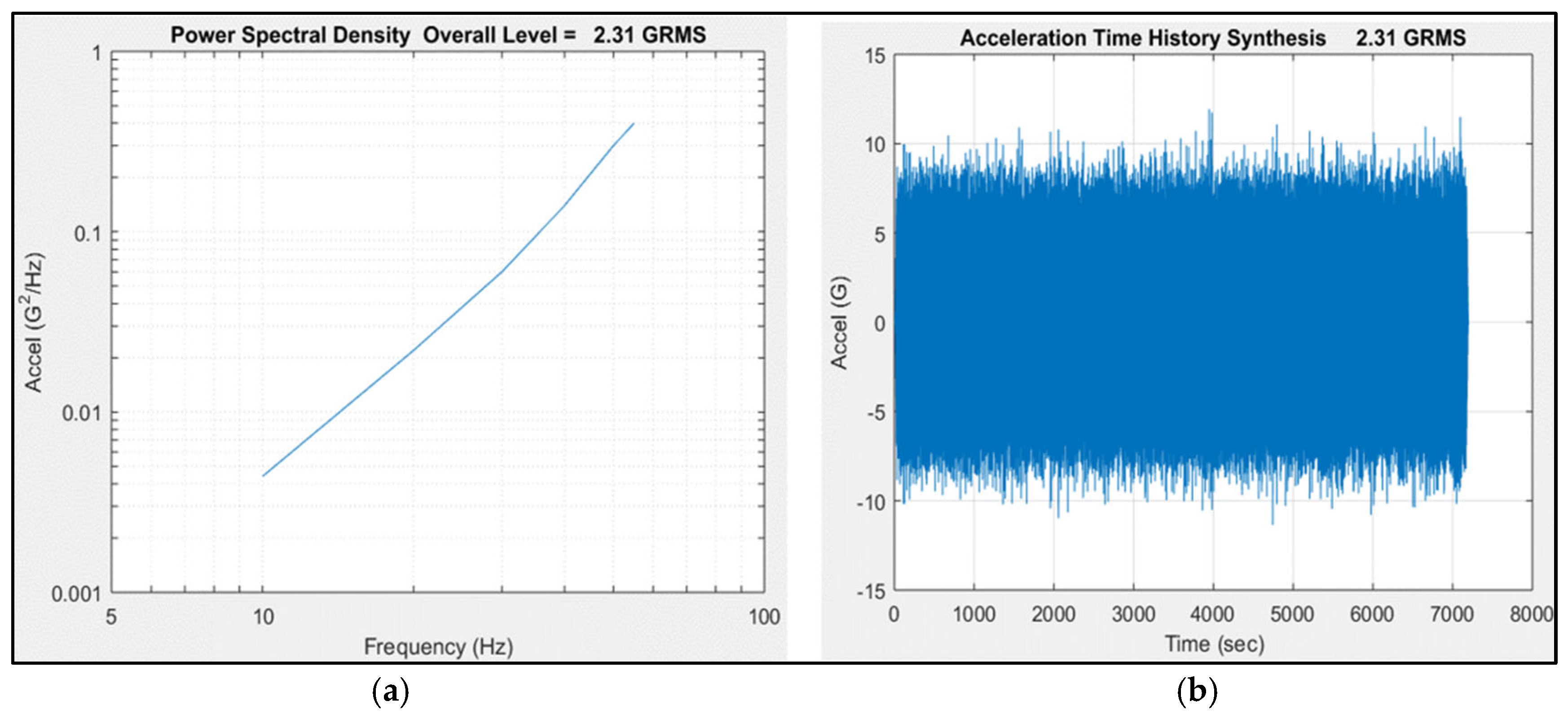

| fi (Hz) | PSDi (G2/Hz) | dB Equation (12) | Oct Equation (13) | m Equation (11) | Ai Equation (10) | Grms Equation (14) |
|---|---|---|---|---|---|---|
| 10 | 0.0040 | 0.0000 | 0.0000 | 0.0000 | 0.0400 | |
| 20 | 0.0200 | 6.990 | 1.0000 | 6.9900 | 0.1080 | |
| 30 | 0.0600 | 4.771 | 0.5850 | 8.1560 | 0.3770 | |
| 40 | 0.1400 | 3.680 | 0.4150 | 8.8660 | 0.9630 | |
| 50 | 0.3000 | 3.310 | 0.3220 | 10.2820 | 2.1290 | |
| 55 | 0.4000 | 1.249 | 0.1380 | 9.0860 | 1.7420 | |
| 5.3200 | 2.3060 |
| Category | Condition |
|---|---|
| Testing | GR-326 I4 |
| Mechanical vibration 2.3060 Grms | |
| with 2 h per axis | |
| Optical Monitoring | IL—During test at 1310 nm and 1550 nm |
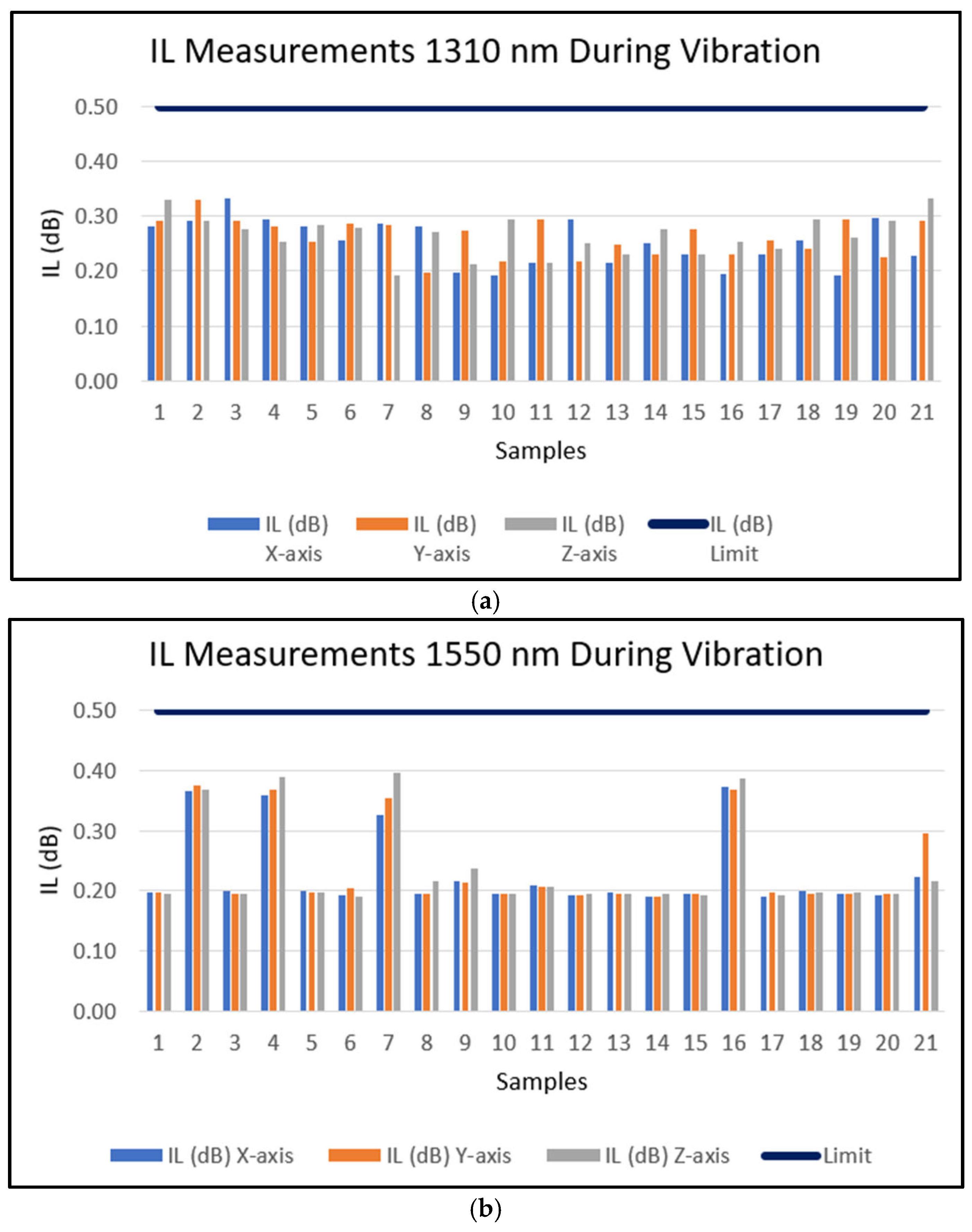
| Sample ID | IL (dB) X-Axis | IL (dB) Y-Axis | IL (dB) Z-Axis | |||
|---|---|---|---|---|---|---|
| 1310 nm | 1550 nm | 1310 nm | 1550 nm | 1310 nm | 1550 nm | |
| 1 | 0.2810 | 0.1980 | 0.2910 | 0.1980 | 0.3300 | 0.1940 |
| 2 | 0.2920 | 0.3650 | 0.3300 | 0.3750 | 0.2910 | 0.3680 |
| 3 | 0.3330 | 0.1990 | 0.2920 | 0.1940 | 0.2750 | 0.1960 |
| 4 | 0.2940 | 0.3590 | 0.2810 | 0.3670 | 0.2520 | 0.3890 |
| 5 | 0.2820 | 0.1990 | 0.2530 | 0.1970 | 0.2840 | 0.1970 |
| 6 | 0.2560 | 0.1930 | 0.2860 | 0.2040 | 0.2790 | 0.1910 |
| 7 | 0.2860 | 0.3250 | 0.2830 | 0.3540 | 0.1930 | 0.3960 |
| 8 | 0.2810 | 0.1950 | 0.1960 | 0.1960 | 0.2710 | 0.2150 |
| 9 | 0.1980 | 0.2150 | 0.2730 | 0.2130 | 0.2130 | 0.2380 |
| 10 | 0.1920 | 0.1950 | 0.2170 | 0.1950 | 0.2930 | 0.1960 |
| 11 | 0.2150 | 0.2090 | 0.2950 | 0.2060 | 0.2150 | 0.2060 |
| 12 | 0.2950 | 0.1930 | 0.2170 | 0.1930 | 0.2500 | 0.1950 |
| 13 | 0.2160 | 0.1980 | 0.2490 | 0.1950 | 0.2290 | 0.1950 |
| 14 | 0.2500 | 0.1910 | 0.2290 | 0.1910 | 0.2750 | 0.1960 |
| 15 | 0.2310 | 0.1960 | 0.2750 | 0.1940 | 0.2290 | 0.1930 |
| 16 | 0.1940 | 0.3720 | 0.2300 | 0.3680 | 0.2540 | 0.3870 |
| 17 | 0.2310 | 0.1910 | 0.2550 | 0.1980 | 0.2400 | 0.1930 |
| 18 | 0.2560 | 0.1990 | 0.2410 | 0.1940 | 0.2950 | 0.1980 |
| 19 | 0.1930 | 0.1960 | 0.2950 | 0.1940 | 0.2600 | 0.1980 |
| 20 | 0.2970 | 0.1920 | 0.2250 | 0.1940 | 0.2910 | 0.1950 |
| 21 | 0.2280 | 0.2240 | 0.2910 | 0.2960 | 0.3310 | 0.2170 |
| Max IL | 0.3330 | 0.3720 | 0.3300 | 0.3750 | 0.3310 | 0.3960 |
| Min IL | 0.1920 | 0.1910 | 0.1960 | 0.1910 | 0.1930 | 0.1910 |
| ni | Yi Equation (21) | µy Equation (7) | toi Equation (17) | R(toi) Equation (22) | σ2i Equation (19) | σ1i Equation (18) |
|---|---|---|---|---|---|---|
| 1 | −3.4035 | −0.1702 | 0.3226 | 0.9673 | 0.0887 | 0.8525 |
| −3.0446 | −0.1450 | 0.3635 | 0.9535 | 0.1000 | 0.7567 | |
| 2 | −2.4917 | −0.1246 | 0.4368 | 0.9206 | 0.1201 | 0.6296 |
| 3 | −2.0035 | −0.1002 | 0.5138 | 0.8738 | 0.1413 | 0.5353 |
| −1.7982 | −0.5978 | 0.5500 | 0.8474 | 0.1513 | 0.5000 | |
| 4 | −1.6616 | −0.0831 | 0.5756 | 0.8271 | 0.1583 | 0.4778 |
| 5 | −1.3944 | −0.0697 | 0.6291 | 0.7804 | 0.1730 | 0.4372 |
| 6 | −1.1721 | −0.0586 | 0.6773 | 0.7336 | 0.1863 | 0.4060 |
| −1.0967 | −0.3646 | 0.6945 | 0.7161 | 0.1910 | 0.3960 | |
| 7 | −0.9794 | −0.0490 | 0.7221 | 0.6869 | 0.1986 | 0.3808 |
| 8 | −0.8074 | −0.0404 | 0.7646 | 0.6402 | 0.2103 | 0.3597 |
| 9 | −0.6505 | −0.0325 | 0.8055 | 0.5935 | 0.2215 | 0.3414 |
| 10 | −0.5045 | −0.0252 | 0.8456 | 0.5467 | 0.2326 | 0.3252 |
| 11 | −0.3665 | −0.0183 | 0.8853 | 0.5000 | 0.2435 | 0.3107 |
| 12 | −0.2341 | −0.0117 | 0.9251 | 0.4533 | 0.2544 | 0.2973 |
| 13 | −0.1053 | −0.0053 | 0.9656 | 0.4065 | 0.2656 | 0.2848 |
| 14 | 0.0219 | 0.0011 | 1.0073 | 0.3598 | 0.2770 | 0.2730 |
| 15 | 0.1495 | 0.0075 | 1.0510 | 0.3131 | 0.2890 | 0.2617 |
| 16 | 0.2798 | 0.0140 | 1.0975 | 0.2664 | 0.3018 | 0.2506 |
| 17 | 0.4160 | 0.0208 | 1.1483 | 0.2196 | 0.3158 | 0.2395 |
| 18 | 0.5625 | 0.0281 | 1.2056 | 0.1729 | 0.3316 | 0.2281 |
| 19 | 0.7276 | 0.0364 | 1.2736 | 0.1262 | 0.3503 | 0.2159 |
| 20 | 0.9293 | 0.0465 | 1.3619 | 0.0794 | 0.3746 | 0.2019 |
| 21 | 1.2297 | 0.0615 | 1.5049 | 0.0327 | 0.4139 | 0.1827 |
| β = 3.0000 ƞ = 0.2570 µy = −0.6344 σ1 = 0.3960 σ2 = 0.1910 | ||||||
| Weibull | Mechanical Vibration Testing |
|---|---|
| Shape parameter | 3.0000 |
| Scale parameter | 0.2570 |
| Mean | −0.5456 |
| Log-mean | −1.2909 |
| Reliability [] | 0.8474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barraza-Contreras, J.M.; Piña-Monárrez, M.R.; Hernández-Ramos, M.M.; Ramos-Lozano, S. Weibull Reliability Based on Random Vibration Performance for Fiber Optic Connectors. Vibration 2025, 8, 46. https://doi.org/10.3390/vibration8030046
Barraza-Contreras JM, Piña-Monárrez MR, Hernández-Ramos MM, Ramos-Lozano S. Weibull Reliability Based on Random Vibration Performance for Fiber Optic Connectors. Vibration. 2025; 8(3):46. https://doi.org/10.3390/vibration8030046
Chicago/Turabian StyleBarraza-Contreras, Jesús M., Manuel R. Piña-Monárrez, María M. Hernández-Ramos, and Secundino Ramos-Lozano. 2025. "Weibull Reliability Based on Random Vibration Performance for Fiber Optic Connectors" Vibration 8, no. 3: 46. https://doi.org/10.3390/vibration8030046
APA StyleBarraza-Contreras, J. M., Piña-Monárrez, M. R., Hernández-Ramos, M. M., & Ramos-Lozano, S. (2025). Weibull Reliability Based on Random Vibration Performance for Fiber Optic Connectors. Vibration, 8(3), 46. https://doi.org/10.3390/vibration8030046






