Machine Learning Approach to Nonlinear Fluid-Induced Vibration of Pronged Nanotubes in a Thermal–Magnetic Environment
Abstract
1. Introduction
2. Model Formulation
2.1. Model Formulation for Velocity of Flow of Nanotube
2.2. Model Formulation for Influence of Nanomagnetic Fluid at Nanotube Junction
2.3. Model Formulation for Vibration of Carbon-Nanotube
2.4. Galerkin Decomposition Method
3. Analytical Solutions to the Developed Models
3.1. After Treatment Techniques
3.1.1. Cosine-After Treatment Technique (CAT Technique)
3.1.2. Sine-After Treatment Technique (SAT Technique)
3.2. SAT and CAT Combinations
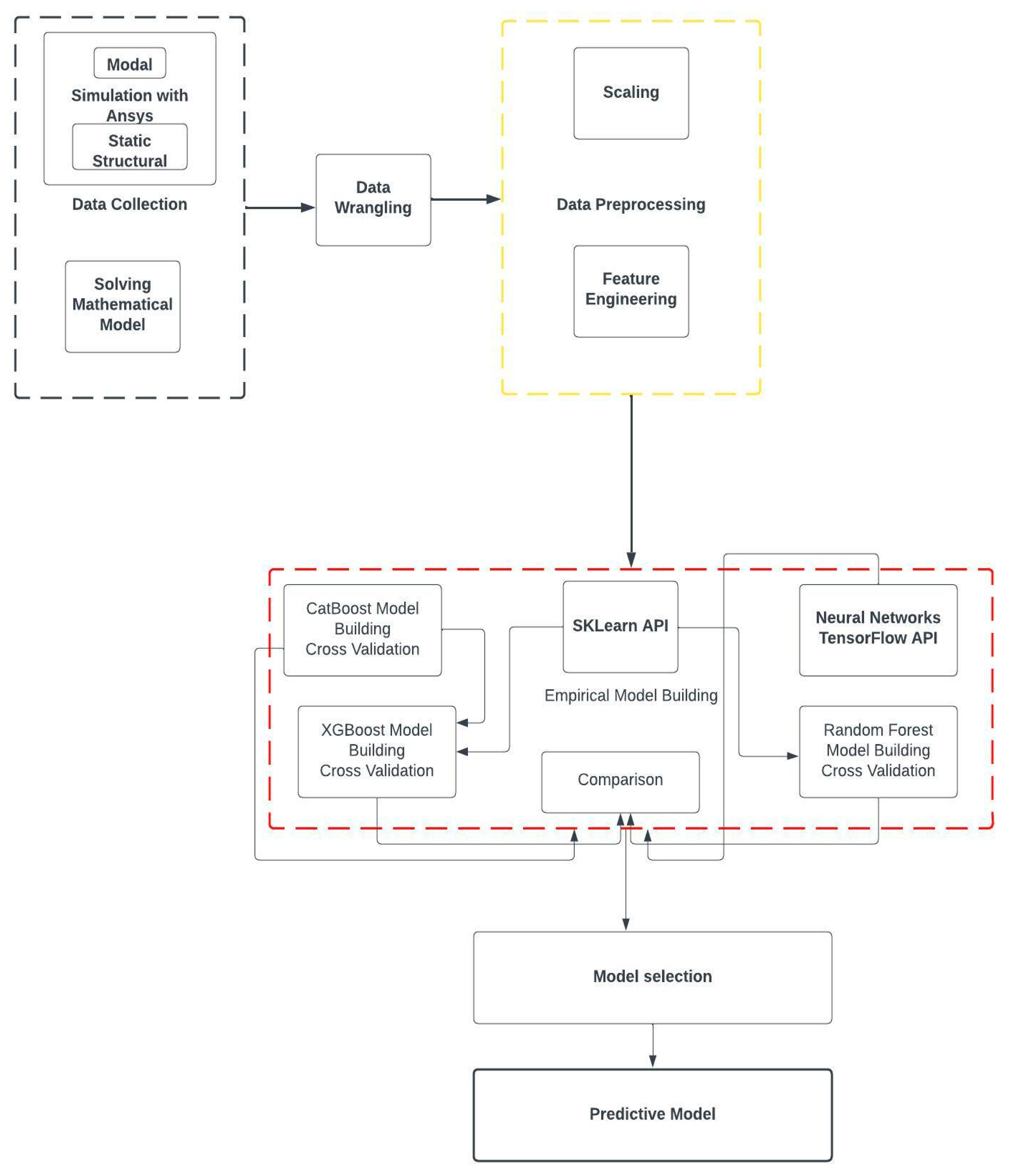
3.3. Simulation and Data Collection
- Modeling;
- Engineering data;
- Meshing;
- Magnetostatic analysis;
- Static structural analysis;
- Modal analysis;
- Transient structural analysis;
- Data collection.
3.3.1. Modeling
3.3.2. Engineering Data
3.3.3. Meshing
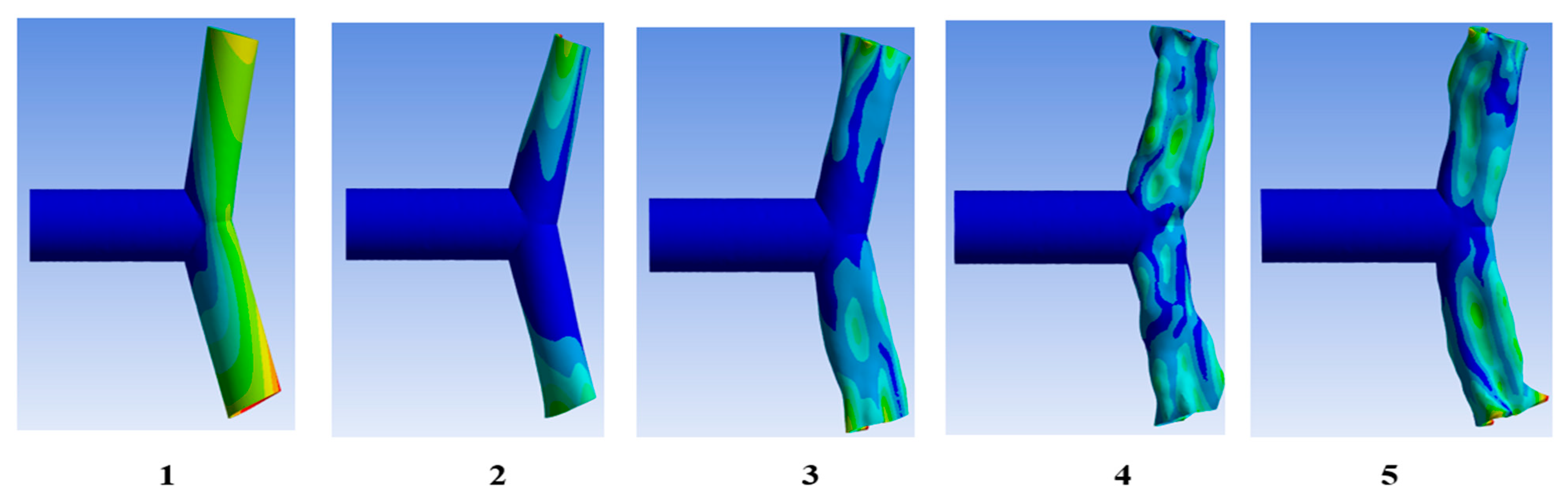
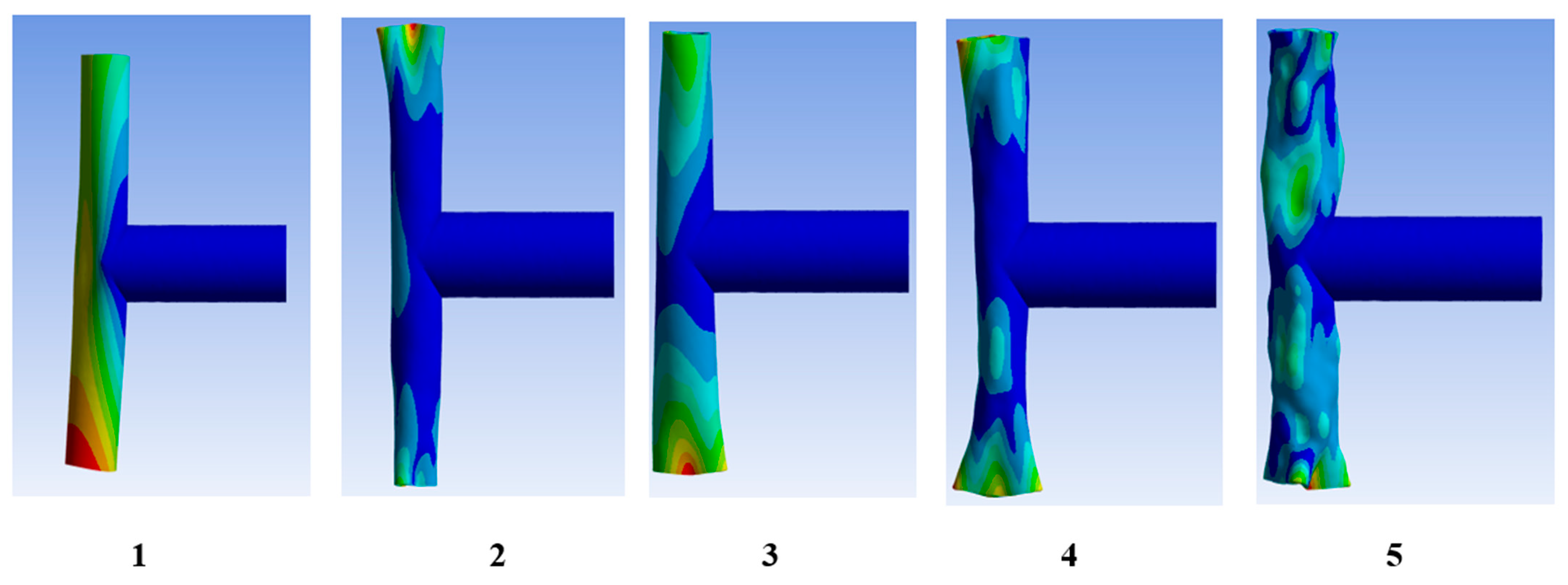
3.3.4. Mode and Mode Shape Analysis
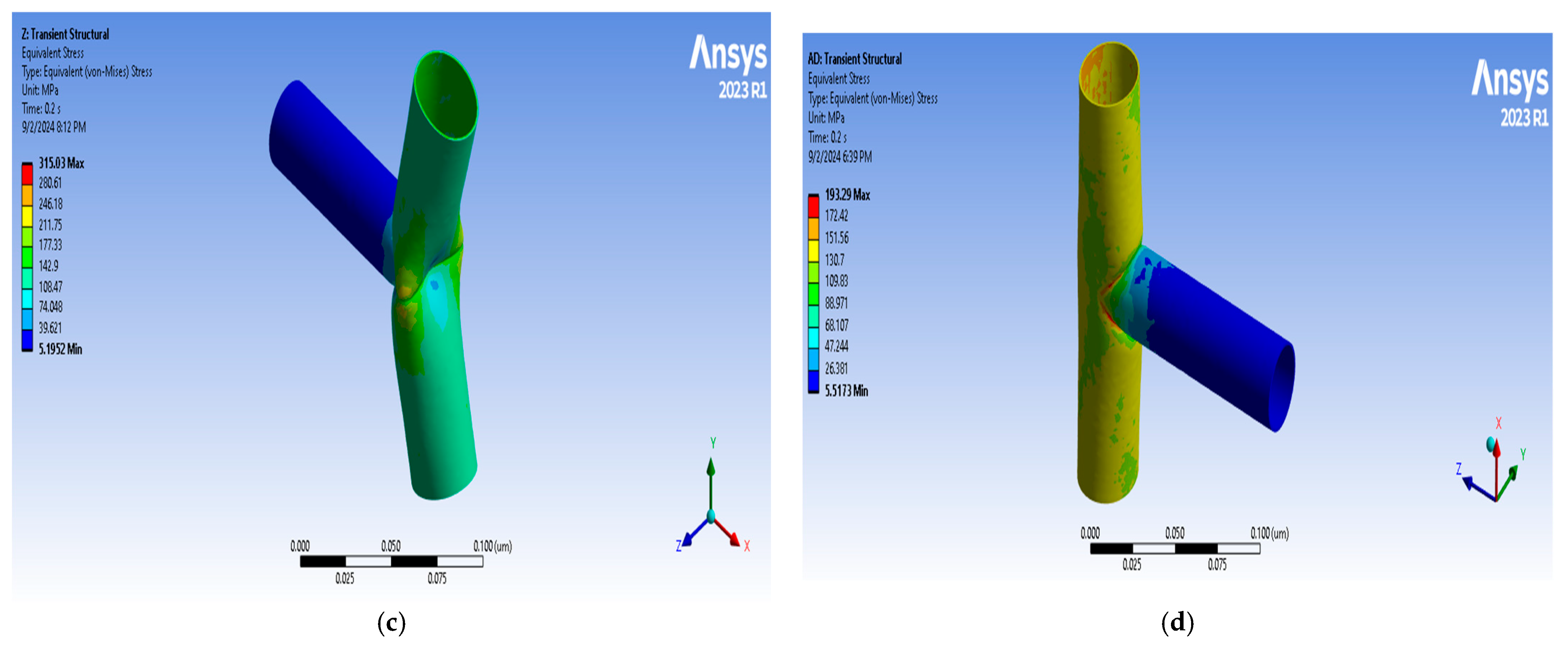
3.3.5. Transient Structural Analysis
3.3.6. Grid Independence Test
3.3.7. Data Collection
3.3.8. Data Preparation
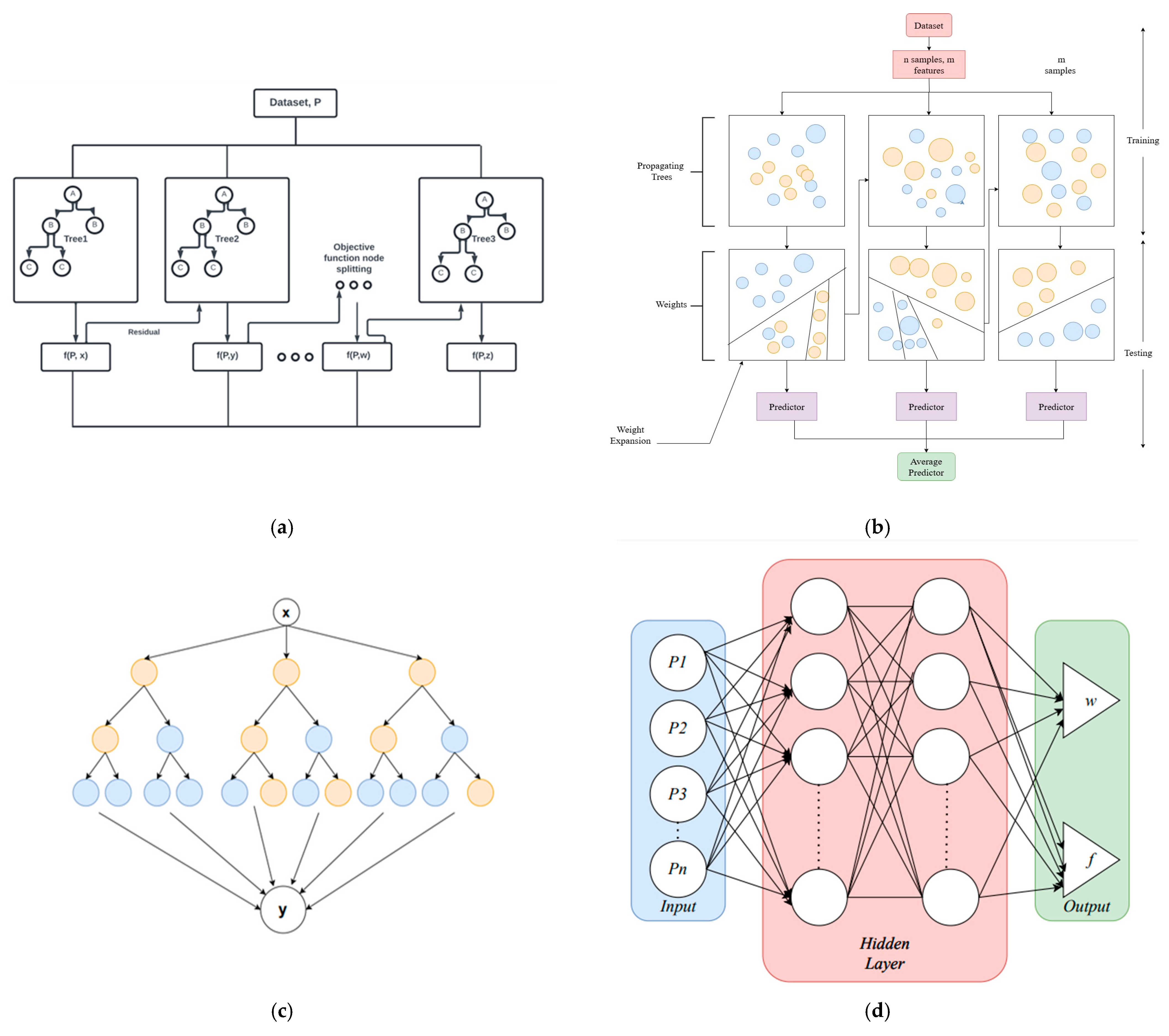
3.4. Model Building
4. Results and Discussion
4.1. Results from Mathematical Modeling
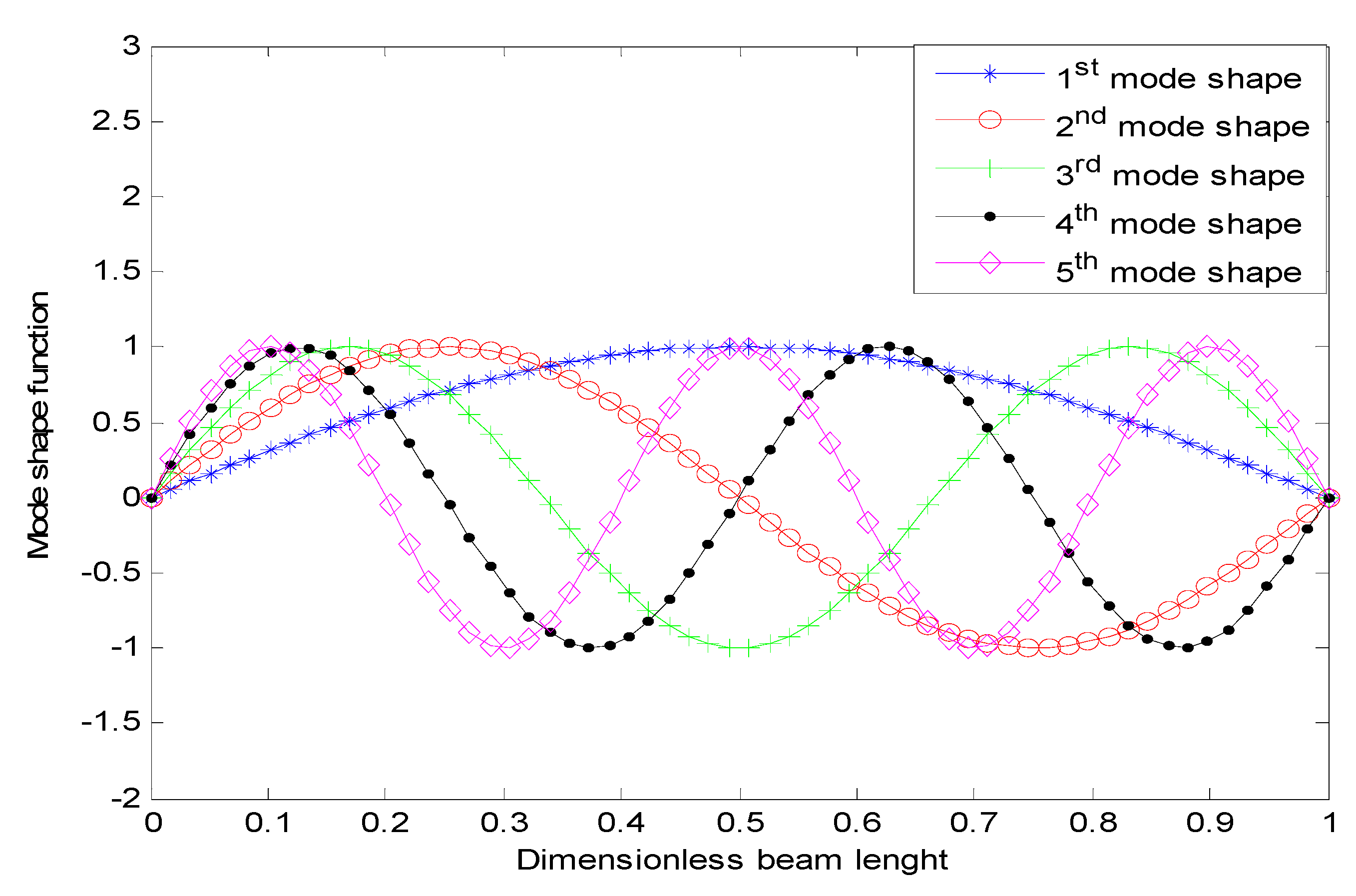
4.1.1. Modal Numbers’ Impact on Nanotube’s Mode Shapes
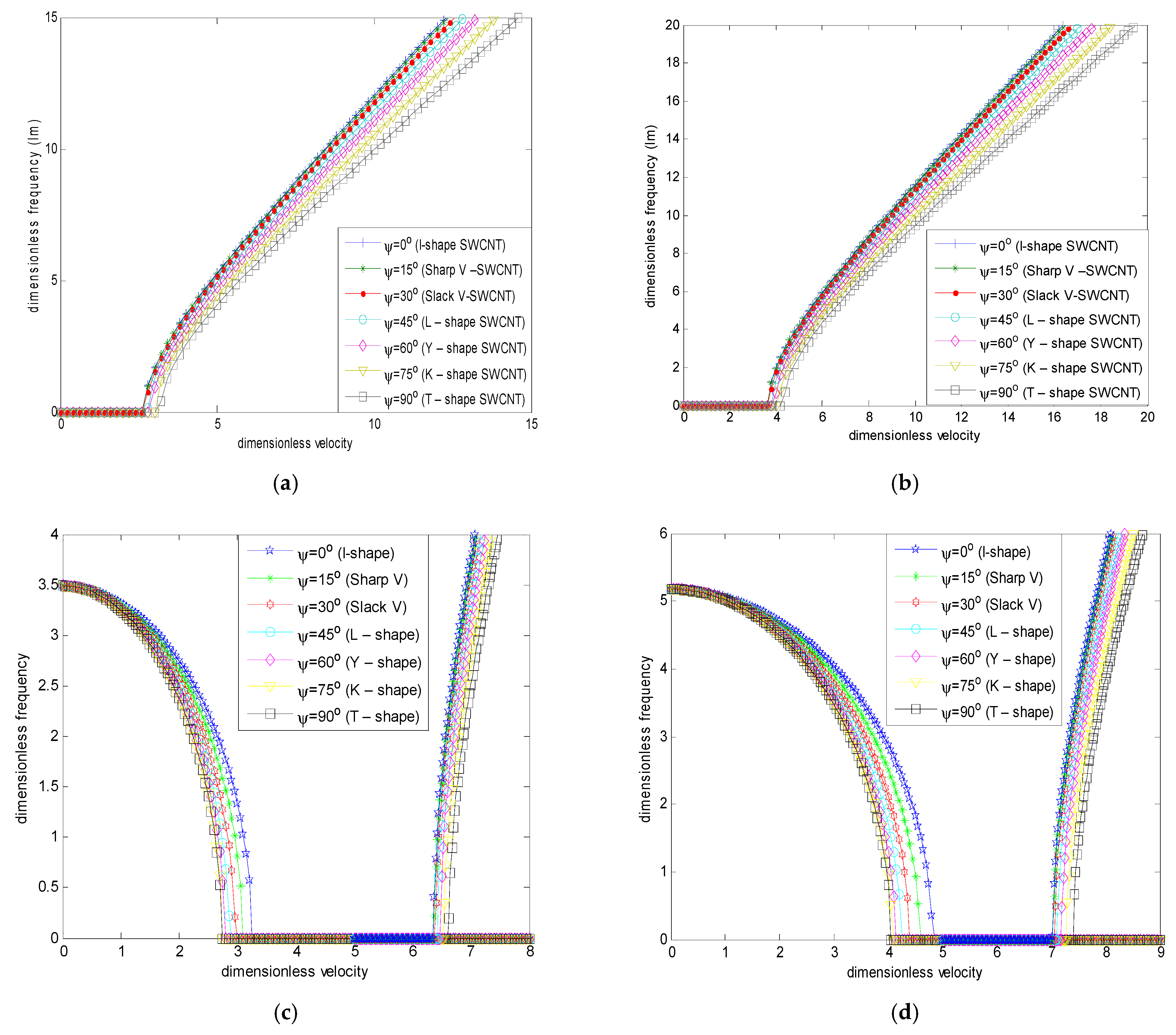
4.1.2. Branch Angles’ Impacts on Stability
4.1.3. Winkler’s Foundations Effects on Stability of SWCNT
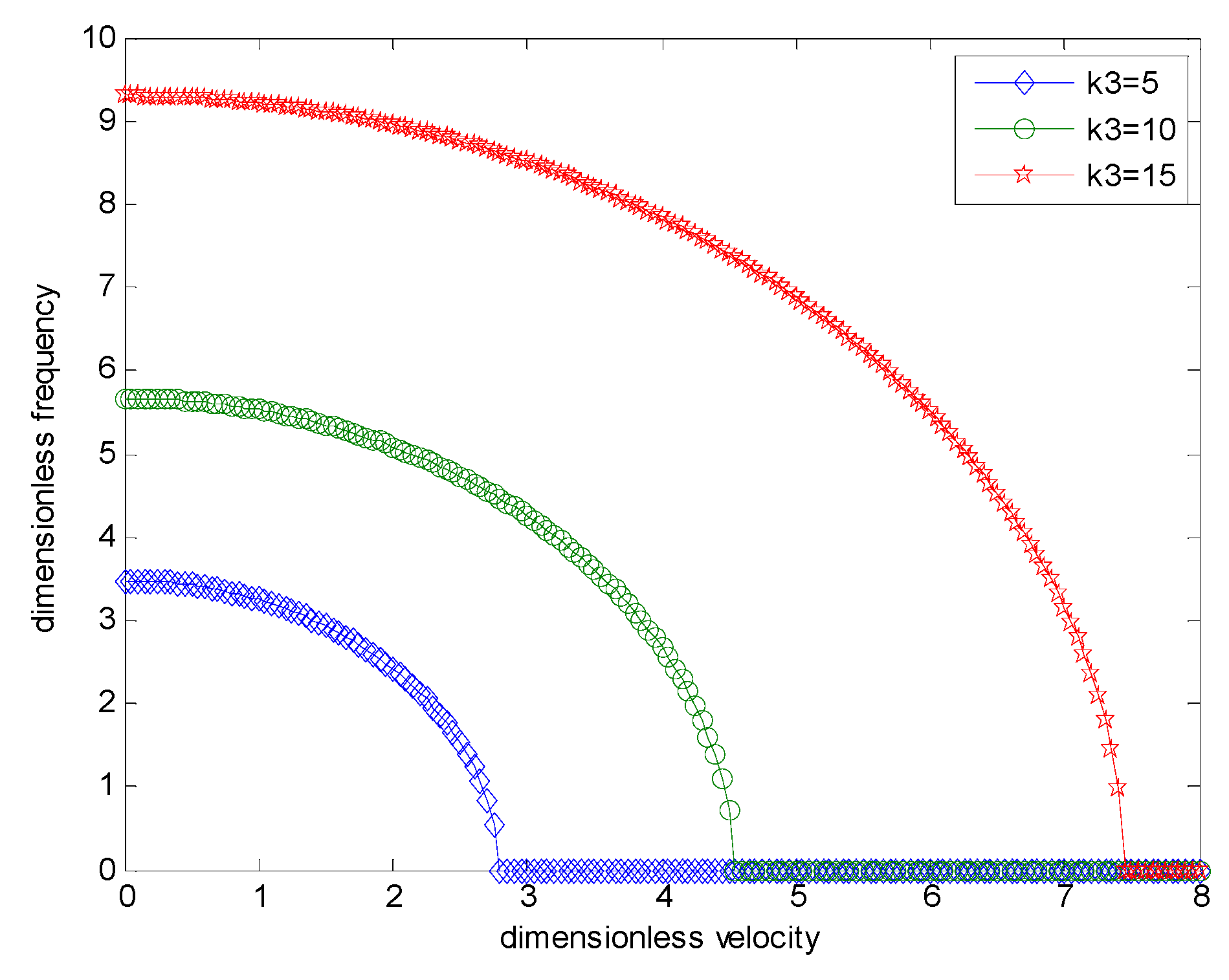
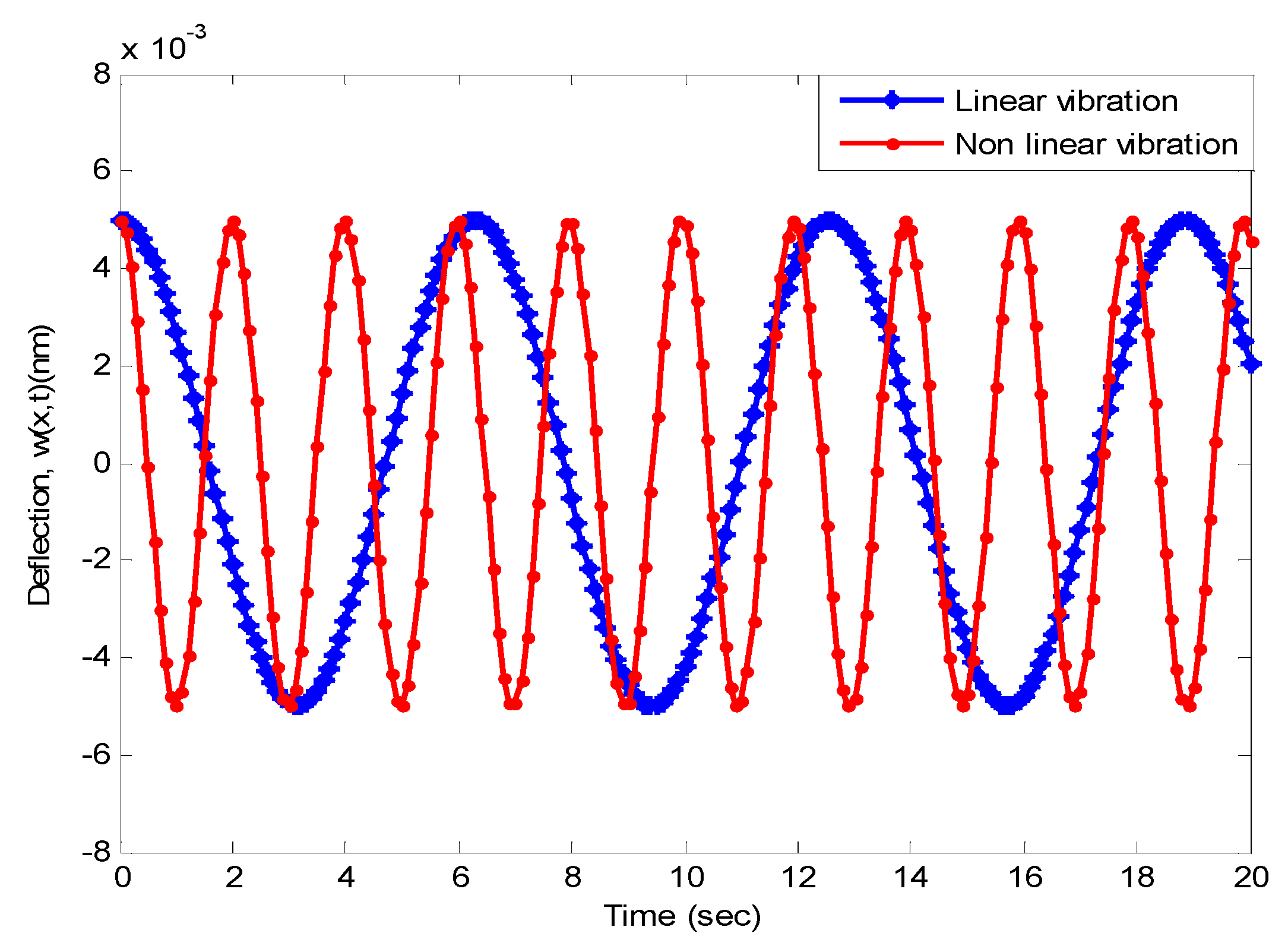
4.1.4. Vibrational Dynamic Responses of the SWCNT
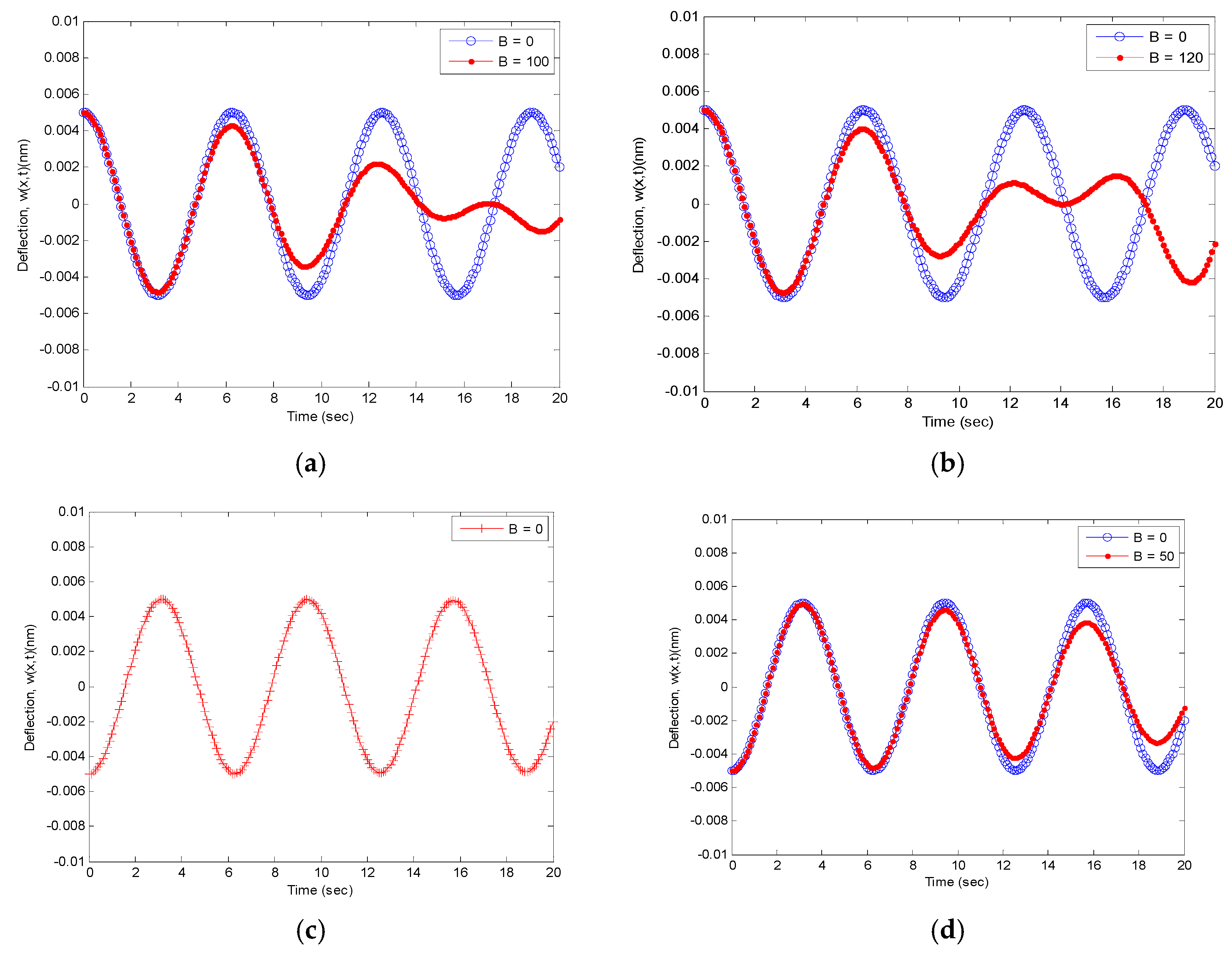
4.1.5. Magnetic Term’s Influence on SWCNT Response
4.2. Simulation Results
4.2.1. Magnetostatic Analysis
4.2.2. Modal Analysis
4.2.3. Transient Structural Analysis
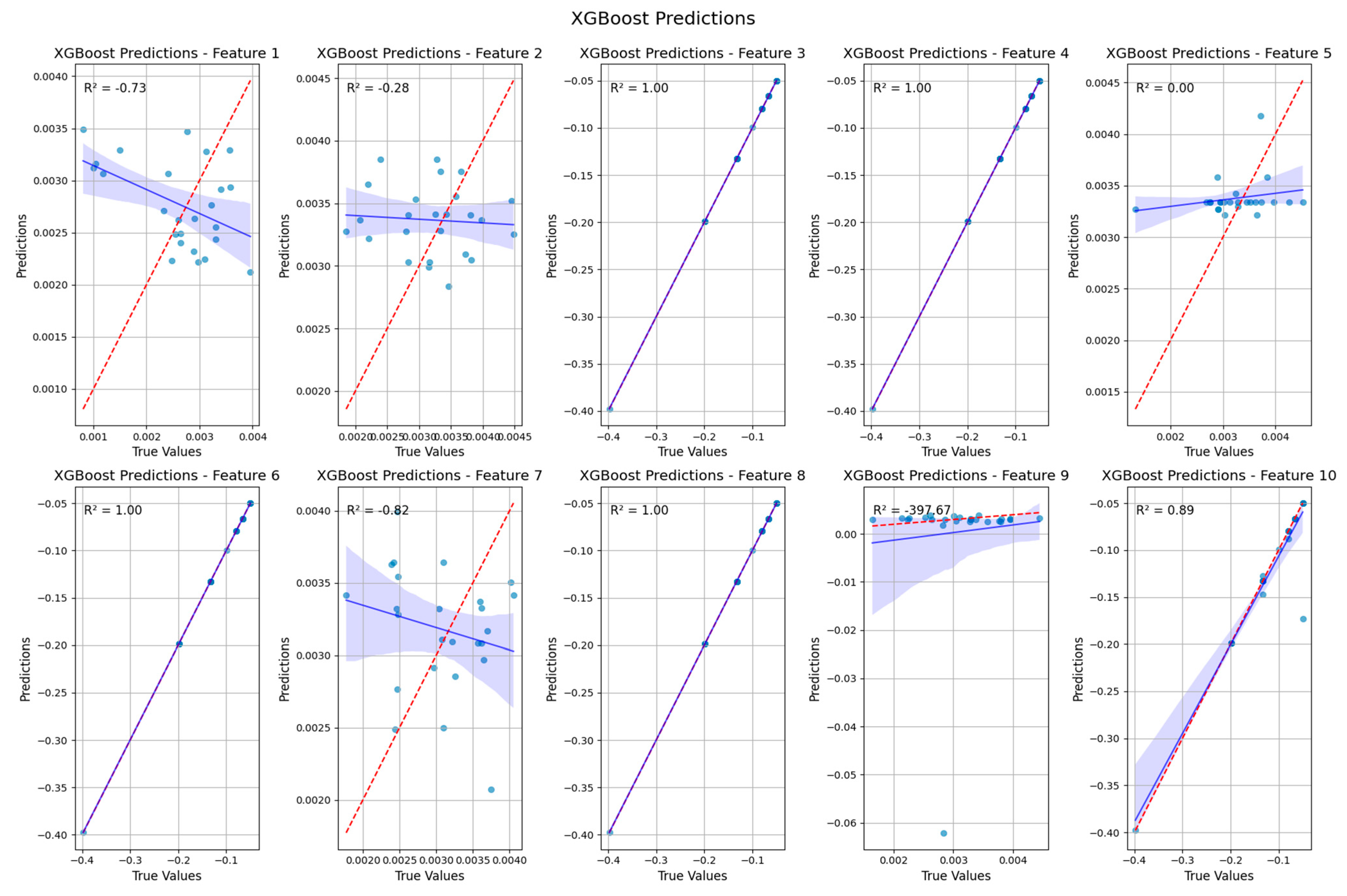
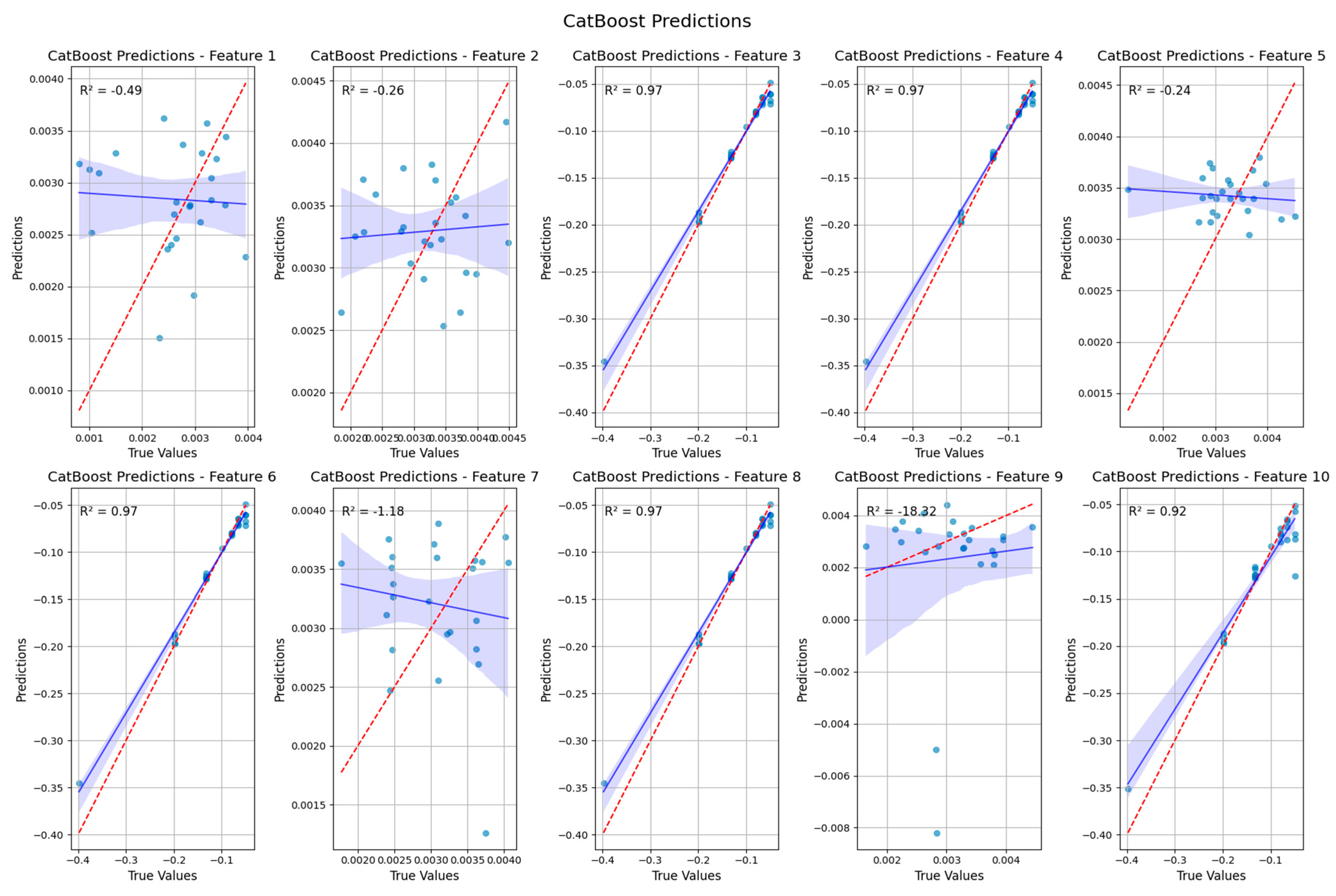
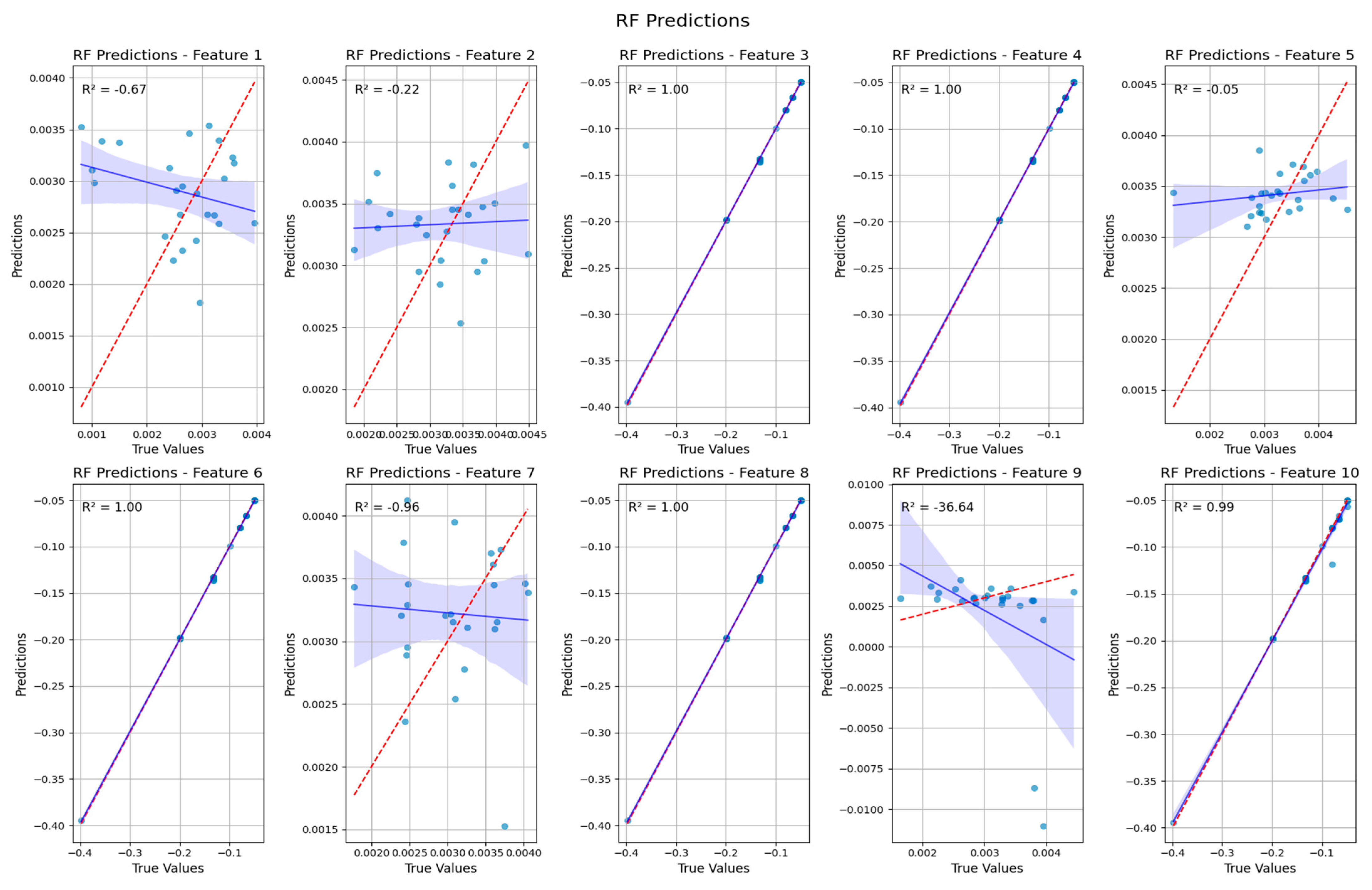
4.3. Machine Learning Results
4.4. Comparison of Machine Learning Models for Carbon Nanotube Vibration Prediction
5. Conclusions
- The angle at which the nanotube branches significantly affects its stability. A larger angle has been demonstrated to reduce stability.
- The dynamic behavior of the SWCNT is dampened by the existing magnetic field introduced to the environment.
- The nonlocal term has a major impact on flow velocity and frequency. Furthermore, raising the foundation parameters and shear moduli increases the fundamental frequency of the nanotube.
- The fluid–structure mass ratio becomes particularly important in post-bifurcation regions, where frequencies and velocities increase with rising temperatures.
- The difference between linear and nonlinear vibration frequencies becomes more pronounced as flow velocity and amplitude rise.
- Increasing axial pre-tension on the nanotube reduces its stability, especially as it deviates further from linear behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| L | Length |
| ρ | Mass Density of Beam |
| I | Moment of Inertia |
| (e0a) | Nonlocal Parameter |
| K | Spring Stiffness |
| A | Area of Cross-Section |
| I0, I1 | Bessel Terms |
| t | Time |
| t* | Dimensionless Time |
| P | Pressure |
| w | Lateral Displacement of Beam |
| k1, k2 | Winkler-Like Elastic Foundation Coefficient |
| T | Number of Trees in the Ensemble |
| B | 2D Magnetic Field |
| G | Shear Modulus |
| Ri | Radius of CNT |
| t | Elastic Stiffness Matrix of Classical Isotropic Elasticity |
| MFI | Magnetic Field Intensity |
| MFD | Magnetic Field Density |
| ρf | Fluid Density |
| Tb(x) | Prediction of the b-th Tree at an Instance x |
| wij | The Weight of the j-th Leaf in the i-th Tree |
| λj | The L2 Regularization Parameter |
| ΩCAT | The regularization Term for CATBoost |
| E | Youngs Modulus |
| U(r) | Fluid Velocity Distribution |
| mf | Mass of Nanofluid |
| tb | Thickness |
| σx x | Nonlocal Stress Tensor |
| Is | Surface Moment of Inertia |
| yi | True Label of the i-th Instance |
| Predicted Label for the i-th Instance | |
| Kn | Knusden Number |
| ∅ | Downstream Angle |
| d | The Number of Leaves in Each Tree |
| γL | The L1-Regularisation Parameter |
| La | The Loss Function |
| ni | The Number of Trees in the Forest |
References
- Chen, X.; Zhao, J.; She, G.-L.; Luo, J. Nonlinear free vibration analysis of functionally graded carbon nanotube reinforced fluid-conveying pipe in thermal environment. Steel Compos. Struct. 2022, 35, 641–652. [Google Scholar] [CrossRef]
- Saifuddin, N.; Raziah, A.Z.; Junizah, A.R. Carbon Nanotubes: A Review on Structure and Their Interaction with Proteins. J. Chem. 2013, 2013, 676815. [Google Scholar] [CrossRef]
- Rust, C.; Shapturenka, P.; Spari, M.; Jin, Q.; Li, H.; Bacher, A.; Guttmann, M.; Zheng, M.; Adel, T.; Hight Walker, A.R.; et al. The Impact of Carbon Nanotube Length and Diameter on their Global Alignment by Dead-End Filtration. Small 2023, 19, 2206774. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Pereira, G.A.F.; Antunes, J.M.; Fernandes, J.V. Mechanical Characterization of Multiwalled Carbon Nanotubes: Numerical Simulation Study. Materials 2020, 13, 4283. [Google Scholar] [CrossRef]
- Xu, L.; Jiao, X.; Shi, C.; Wu, A.-P.; Hou, P.-X.; Liu, C.; Cheng, H.-M. Single-Walled Carbon Nanotube/Copper Core–Shell Fibers with a High Specific Electrical Conductivity. ACS Nano 2023, 17, 9245–9254. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Cui, K.; Chuang, J.; Feo, L.; Chow, C.; Lau, D. Developments and Applications of Carbon Nanotube Reinforced Cement-Based Composites as Functional Building Materials. Front. Mater. 2022, 9, 861646. [Google Scholar] [CrossRef]
- Yinusa, A.; Sobamowo, M.; Adelaja, A. Nonlinear vibration analysis of an embedded branched nanofluid-conveying carbon nanotube: Influence of downstream angle, temperature change and two-dimensional external magnetic fields. Nano Mater. Sci. 2020, 2, 323–332. [Google Scholar] [CrossRef]
- Mahmure, A.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials 2021, 11, 2090. [Google Scholar] [CrossRef]
- Huang, K.; Yao, J. Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes. Nanomaterials 2021, 11, 923. [Google Scholar] [CrossRef]
- Shaba, A.I.; Jiya, M.; Aiyesimi, Y.M.; Mohammed, A.A. Vibration of Single–Walled Carbon Nanotube (SWCNT) on a Winkler Foundation with Magnetic Field Effect. Sci. World J. 2021, 16, 402–406. [Google Scholar]
- Yinusa, A.; Sobamowo, M. Mechanics of nonlinear internal flow-induced vibration and stability analysis of a pre-tensioned single-walled carbon nanotube using classical differential transform method with CAT and SAT after-treatment techniques. Forces Mech. 2022, 7, 100083. [Google Scholar] [CrossRef]
- Yan, Y.; Li, J.; Ma, X.; Wang, W. Application and dynamical behaviour of CNTs as fluidic nanosensors based on the nonlocal strain gradient theory. Sens. Actuators A Phys. 2021, 330, 112836. [Google Scholar] [CrossRef]
- Chen, Y.; Lyu, M.; Zhang, Z.; Yang, F.; Li, Y. Controlled Preparation of Single-Walled Carbon Nanotubes as Materials for Electronics. ACS Cent. Sci. 2022, 8, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Miyashiro, D.; Taira, H.; Hamano, R.; Reserva, R.L.; Umemura, K. Mechanical vibration of single-walled carbon nanotubes at different lengths and carbon nanobelts by modal analysis method. Compos. Part C Open Access 2020, 2, 100028. [Google Scholar] [CrossRef]
- Dat, N.D.; Quan, T.Q.; Mahesh, V.; Duc, N.D. Analytical solutions for nonlinear magneto-electro-elastic vibration of the smart sandwich plate with carbon nanotube reinforced nanocomposite core in hygrothermal environment. Int. J. Mech. Sci. 2020, 186, 105906. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Lippiello, M.; Babilio, E.; Ceraldi, C. Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass. Materials 2021, 14, 3445. [Google Scholar] [CrossRef]
- Oveissi, S.; Eftekhari, S.A.; Toghraie, D. Longitudinal vibration and instabilities of carbon nanotubes conveying fluid considering size effects of nanoflow and nanostructure. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 83, 164–173. [Google Scholar] [CrossRef]
- Chang, X.; Hong, X.; Qu, C.; Li, Y. Stability and nonlinear vibration of carbon nanotubes-reinforced composite pipes conveying fluid. Ocean. Eng. 2023, 281, 114960. [Google Scholar] [CrossRef]
- Sabahi, M.A.; Saidi, A.R.; Khodabakhsh, R. An analytical solution for nonlinear vibration of functionally graded porous micropipes conveying fluid in damping medium. Ocean. Eng. 2022, 245, 110482. [Google Scholar] [CrossRef]
- Moborukoje, K.I.; Oladosu, S.; Kuku, R.; Sobamowo, G. Exploring the Significances of Surface Energy, Initial Stress and Nonlocality Effects on Vibration of Carbon Nanotubes Conveying Fluid Resting on Elastic Foundations in a Magneto-Thermal Environment. World Sci. News 2022, 179, 112–134. [Google Scholar]
- Ghadirian, H.; Mohebpour, S.; Malekzadeh, P.; Daneshmand, F. Nonlinear free vibrations and stability analysis of FG-CNTRC pipes conveying fluid based on Timoshenko model. Compos. Struct. 2022, 292, 115637. [Google Scholar] [CrossRef]
- Heidary, Z.; Ramezani, S.R.; Mojra, A. Exploring the benefits of functionally graded carbon nanotubes (FG-CNTs) as a platform for targeted drug delivery systems. Comput. Methods Programs Biomed. 2023, 238, 107603. [Google Scholar] [CrossRef] [PubMed]
- Oveissi, S.; Ghassemi, A.; Salehi, M.; Eftekhari, S.A.; Ziaei-Rad, S. Hydro–Hygro–Thermo–Magneto–Electro elastic wave propagation of axially moving nano-cylindrical shells conveying various magnetic-nano-fluids resting on the electromagnetic-visco-Pasternak medium. Thin-Walled Struct. 2022, 173, 108926. [Google Scholar] [CrossRef]
- Oveissi, S.; Salehi, M.; Ghassemi, A.; Ali Eftekhari, S.; Ziaei-Rad, S. Energy harvesting of nanofluid-conveying axially moving cylindrical composite nanoshells of integrated CNT and piezoelectric layers with magnetorheological elastomer core under external fluid vortex-induced vibration. J. Magn. Magn. Mater. 2023, 572, 170551. [Google Scholar] [CrossRef]
- Yinusa, A.; Sobamowo, M.; Adelaja, A.; Ojolo, S.; Waheed, M.; Usman, M.; Siqueira, A.M.D.O.; Campos, J.C.C.; Ola-Gbadamosi, R. Numerical investigation on the thermal-nanofluidic flow induced transverse and longitudinal vibrations of single and multi-walled branched nanotubes resting on nonlinear elastic foundations in a magnetic environment. Partial Differ. Equ. Appl. Math. 2024, 9, 100602. [Google Scholar] [CrossRef]
- Vivanco-Benavides, L.E.; Martínez-González, C.L.; Mercado-Zúñiga, C.; Torres-Torres, C. Machine learning and materials informatics approaches in the analysis of physical properties of carbon nanotubes: A review. Comput. Mater. Sci. 2021, 201, 110939. [Google Scholar] [CrossRef]
- Pollayi, H.; Rao, P. Stealth Carbon Nano-tubes (S-CNTs): AI/ML Based Modelling of Nano-structured Composites for Attenuation and Shielding in Aircraft. In Proceedings of the International Symposium on Lightweight and Sustainable Polymeric Materials (LSPM23), Bangkok, Thailand, 17 February 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Čanađija, M. Deep learning framework for carbon nanotubes: Mechanical properties and modelling strategies. Carbon 2021, 184, 891–901. [Google Scholar] [CrossRef]
- Yang, J.; Ni, Z.; Fan, Y.; Hang, Z.; Liu, H.; Feng, C. Machine learning aided uncertainty analysis on nonlinear vibration of cracked FG-GNPRC dielectric beam. Structures 2023, 58, 105456. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Akbarzadeh, K.; Ramezanzadeh, M.; Naderi, R.; Mahdavian, M.; Olivier, M. Corrosion resistance enhancement of a sol-gel coating by incorporation of modified carbon nanotubes: Artificial neural network (ANN) modelling and experimental explorations. Prog. Org. Coat. 2022, 174, 107296. [Google Scholar] [CrossRef]
- Khanam, P.N.; AlMaadeed, M.A.; AlMaadeed, S.; Kunhoth, S.; Ouederni, M.; Sun, D.; Hamilton, A.; Harkin Jones, E.; Mayoral, B. Optimization and Prediction of Mechanical and Thermal Properties of Graphene/LLDPE Nanocomposites by Using Artificial Neural Networks. Int. J. Polym. Sci. 2016, 2016, 5340252. [Google Scholar] [CrossRef]
- Hajilounezhad, T.; Bao, R.; Palaniappan, K.; Bunyak, F.; Calyam, P.; Maschmann, M.R. Predicting carbon nanotube forest attributes and mechanical properties using simulated images and deep learning. NPJ Comput. Mater. 2021, 7, 134. [Google Scholar] [CrossRef]
- Kekez, S.; Kubica, J. Application of Artificial Neural Networks for Prediction of Mechanical Properties of CNT/CNF Reinforced Concrete. Materials 2021, 14, 5637. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Sunday, G.J.; Oladosu, S.A.; Kuku, R.O.; Sobamowo, G.M.; Yinusa, A.A. Explorations of the combined effects of surface energy, initial stress and nonlocality on the dynamic behaviour of carbon nanotubes conveying fluid resting on elastic foundations in a thermo-magnetic environment. J. Nanosci. Technol. 2023, 1, 102. [Google Scholar]
- Abubakar, E.H.; Sobamowo, M.G.; Sadiq, M.O.; Yinusa, A.A. Vibration of Single-walled Carbon Nanotubes Resting on Elastic Medium with Magnetic and Thermal Effects under the Influence of Electrostatic Force. World Sci. News 2024, 188, 93–118. [Google Scholar]
- Selim, M.M.; Musa, A. Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model. Nanomaterials 2020, 10, 974. [Google Scholar] [CrossRef]
- Strozzi, M.; Elishakoff, I.E.; Bochicchio, M.; Cocconcelli, M.; Rubini, R.; Radi, E. A Comparison of Shell Theories for Vibration Analysis of Single-Walled Carbon Nanotubes Based on an Anisotropic Elastic Shell Model. Nanomaterials 2023, 13, 1390. [Google Scholar] [CrossRef]
- Olaleye, T.I.; Oladosu, S.A.; Kuku, R.O.; Sobamowo, G.M. Variation iteration method to the investigations of surface energy, initial stress and nonlocality on vibration of carbon nanotubes conveying fluid resting on elastic foundations in a thermo-magnetic environment. J. Mater. Environ. Sci. 2023, 14, 520–538. [Google Scholar]
- Brociek, R.; Pleszczyński, M. Differential Transform Method and Neural Network for Solving Variational Calculus Problems. Mathematics 2023, 12, 2182. [Google Scholar] [CrossRef]








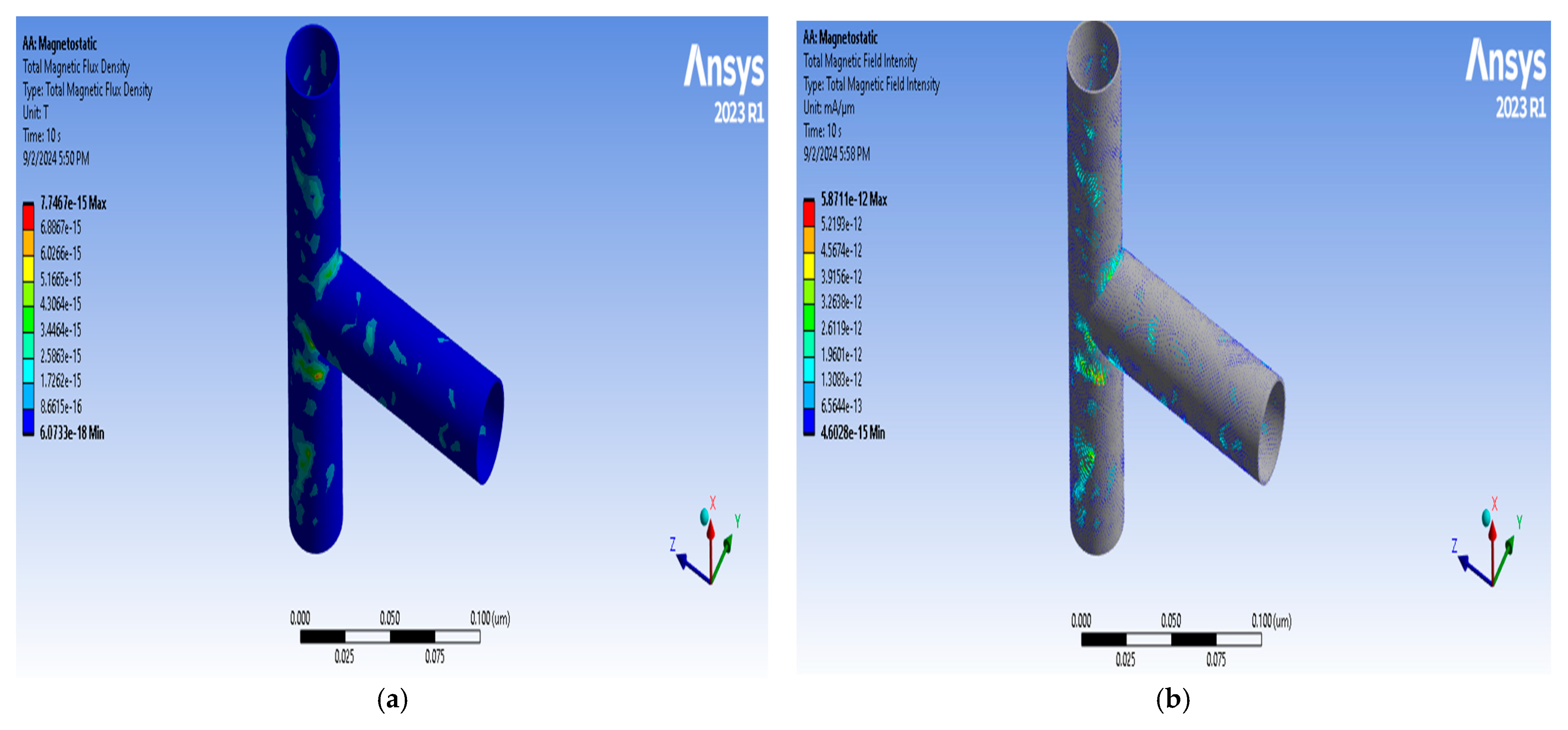



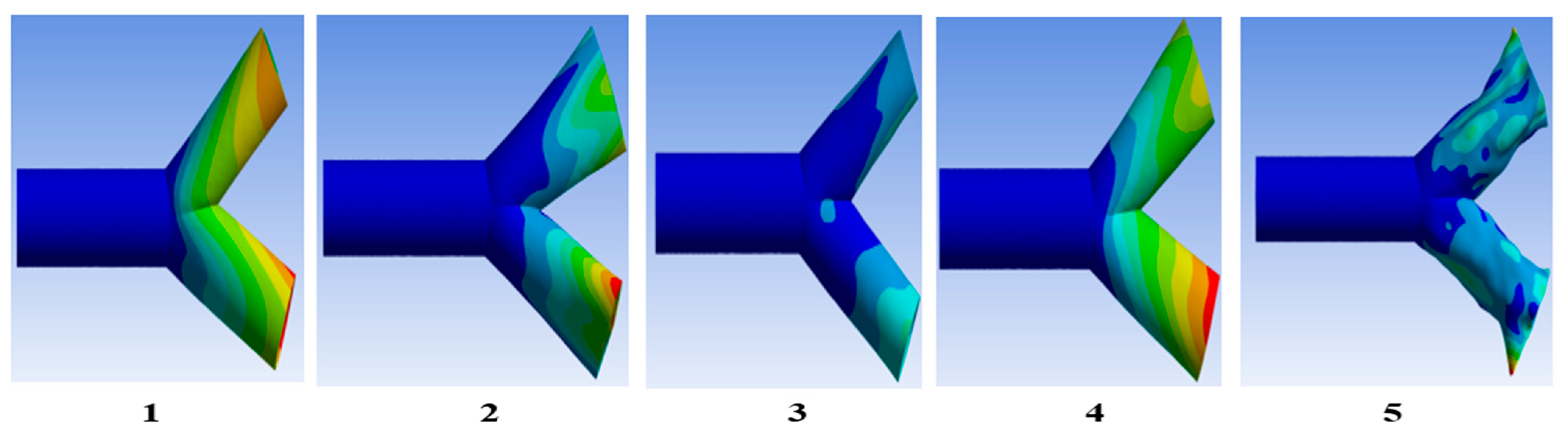
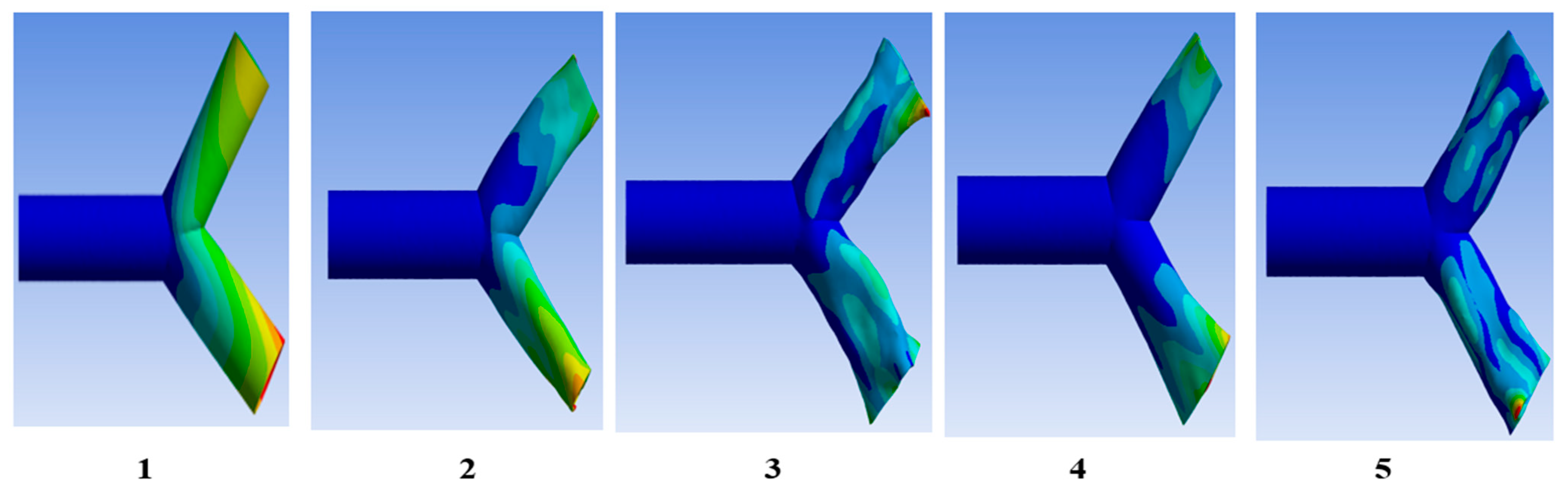
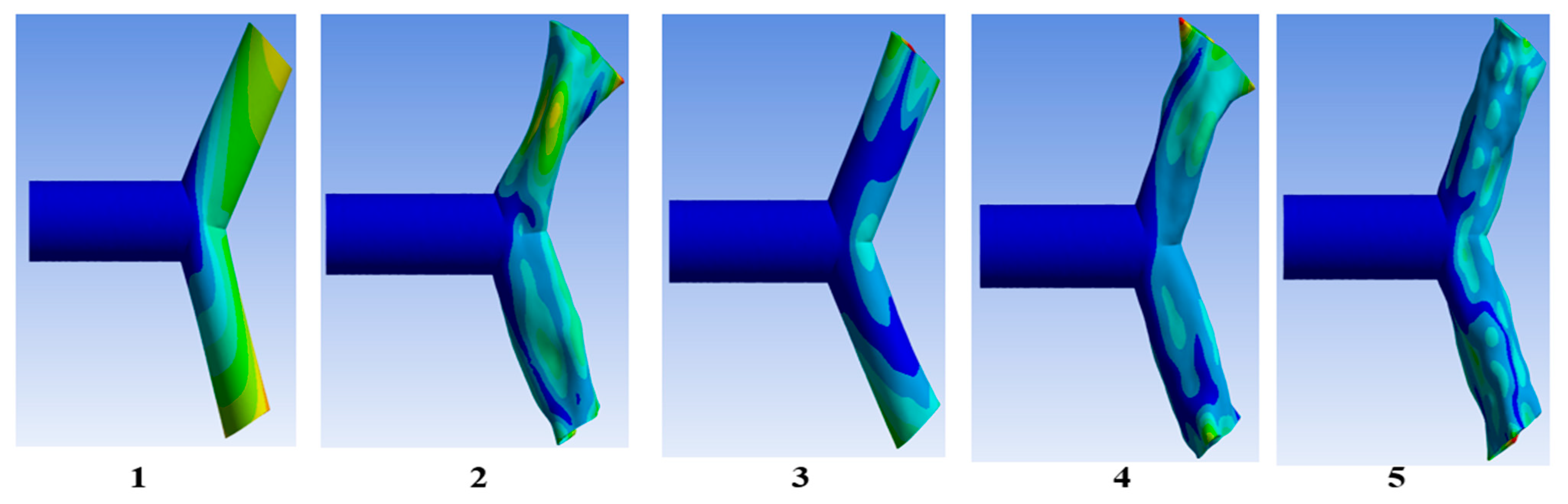



| S/N | Downstream Angle (ϕ deg) | Horizontal Length [nm] | Slant Length [nm] | Area [nm2] |
|---|---|---|---|---|
| 1 | 0 | 200 | - | 18,849.5559 |
| 2 | 15 | 100 | 83.43 | 21,467.0328 |
| 3 | 30 | 100 | 80.00 | 22,463.1906 |
| 4 | 45 | 100 | 70.71 | 21,107.2913 |
| 5 | 60 | 100 | 80.00 | 22,945.5640 |
| 6 | 75 | 100 | 80.00 | 22,882.0359 |
| 7 | 90 | 100 | 80.00 | 24,023.8767 |
| S/N | Property | Values |
|---|---|---|
| 1 | Density | 1330 kg/m3 |
| 2 | Isotropic Secant Coefficient of Expansion | −1.5 C−1 |
| 3 | Melting Temperature | 3550 C |
| 4 | Young’s Moduli | 3.6 TPa |
| 5 | Poisson’s Ratio | 0.273 |
| 6 | Bulk’s moduli | 2.6432 TPa |
| 7 | Shear’s Moduli | 1.414 TPa |
| 8 | Strength Coefficient | 63 GPa |
| 9 | Strength Exponent | −0.18 |
| 10 | Ductility Coefficient | 0.05 |
| 11 | Ductility Exponent | −0.5 |
| 12 | Cyclic Strength Coefficient | 63 GPa |
| 13 | Cyclic Strength Hardening Exponent | 0.15 |
| 14 | Tensile Yield Strength | 630 GPa |
| 15 | Compressive Yield Strength | 150 GPa |
| 16 | Tensile Ultimate Strength | 93 GPa |
| 17 | Compressive Ultimate Strength | 112 GPa |
| 18 | Isotropic Relative Permeability | 1.05 |
| 19 | Isotropic Resistivity | 3 × 10−7 Ωm |
| S/N | Property | Value |
|---|---|---|
| 1 | Mesh Type | Adaptive Sizing |
| 2 | Element Quality | 0.95 |
| 3 | Element Order | Quadratic |
| 4 | Transition Ratio | 0.272 |
| 5 | Growth Rate | 1.2 |
| 6 | Number of Element | 8905 |
| 7 | Number of Nodes | 60,595 |
| 8 | Bounding Box Diagonal | 2.0445 × 10−4 mm |
| 9 | Average Surface Area | 9.1458 × 10−9 mm2 |
| 10 | Minimum Edge Length | 8.7965 × 10−5 mm |
| Parameter | Symbol | Value Range | Units |
|---|---|---|---|
| Magnetic Field Strength | B | 50–150 | mT |
| Axial Flow Velocity | U | 0–300 | m/s |
| Nanotube Diameter | D | 30 | nm |
| Nanotube Wall Thickness | t | 1 | nm |
| Young’s Modulus | E | 3.6 | TPa |
| Density of Nanotube Material | Ρ | 1330 | kg/m3 |
| Magnetic Permeability | Μ | 1.05 | - |
| Winkler Foundation Stiffness | kw | 3 × 10−7 | N/mm2 |
| Branching Angle | Φ | 0–90° | Degrees |
| Thermal Environment Temperature | T | 300–400 | K |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 0 | 0 | 0 | 0 | 0 | 0 |
| 2. | 5.1727 × 10−4 | 6.9473 × 10−2 | 2.9487 × 10−2 | 4.1163 × 10−5 | 5.5285 × 10−3 | 2.3465 × 10−3 |
| 3. | 5.8193 × 10−4 | 7.8157 × 10−2 | 3.3173 × 10−2 | 4.6309 × 10−5 | 6.2195 × 10−3 | 2.6398 × 10−3 |
| 4. | 6.4659 × 10−4 | 8.6841 × 10−2 | 3.6858 × 10−2 | 5.1454 × 10−5 | 6.9106 × 10−3 | 2.9331 × 10−3 |
| 5. | 7.1125 × 10−4 | 9.5525 × 10−2 | 4.0544 × 10−2 | 5.66 × 10−5 | 7.6016 × 10−3 | 3.2264 × 10−3 |
| 6. | 7.7591 × 10−4 | 0.10421 | 4.423 × 10−2 | 6.1745 × 10−5 | 8.2927 × 10−3 | 3.5197 × 10−3 |
| 7. | 9.0523 × 10−4 | 0.12158 | 5.1602 × 10−2 | 7.2036 × 10−5 | 9.6748 × 10−3 | 4.1063 × 10−3 |
| 8. | 9.9144 × 10−4 | 0.13316 | 5.6516 × 10−2 | 7.8896 × 10−5 | 1.0596 × 10−2 | 4.4974 × 10−3 |
| 9. | 1.0777 × 10−3 | 0.14473 | 6.1431 × 10−2 | 8.5757 × 10−5 | 1.1518 × 10−2 | 4.8885 × 10−3 |
| 10. | 1.1639 × 10−3 | 0.15631 | 6.6345 × 10−2 | 9.2618 × 10−5 | 1.2439 × 10−2 | 5.2796 × 10−3 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 4.414 × 10−12 | 1.0579 × 10−8 | 4.922 × 10−10 | 3.5126 × 10−13 | 8.4186 × 10−10 | 3.9168 × 10−11 |
| 2. | 1.1035 × 10−11 | 2.6448 × 10−8 | 1.2305 × 10−9 | 8.7814 × 10−13 | 2.1047 × 10−9 | 9.792 × 10−11 |
| 3. | 1.7215 × 10−11 | 4.1259 × 10−8 | 1.9196 × 10−9 | 1.3699 × 10−12 | 3.2833 × 10−9 | 1.5275 × 10−10 |
| 4. | 1.7656 × 10−11 | 4.2317 × 10−8 | 1.9688 × 10−9 | 1.405 × 10−12 | 3.3675 × 10−9 | 1.5667 × 10−10 |
| 5. | 2.4277 × 10−11 | 5.8185 × 10−8 | 2.7071 × 10−9 | 1.9319 × 10−12 | 4.6303 × 10−9 | 2.1542 × 10−10 |
| 6. | 2.8691 × 10−11 | 6.8765 × 10−8 | 3.1993 × 10−9 | 2.2832 × 10−12 | 5.4721 × 10−9 | 2.5459 × 10−10 |
| 7. | 3.0898 × 10−11 | 7.4054 × 10−8 | 3.4454 × 10−9 | 2.4588 × 10−12 | 5.893 × 10−9 | 2.7417 × 10−10 |
| 8. | 3.5312 × 10−11 | 8.4633 × 10−8 | 3.9376 × 10−9 | 2.81 × 10−12 | 6.7349 × 10−9 | 3.1334 × 10−10 |
| 9. | 3.9726 × 10−11 | 9.5213 × 10−8 | 4.4298 × 10−9 | 3.1613 × 10−12 | 7.5768 × 10−9 | 3.5251 × 10−10 |
| 10. | 4.414 × 10−11 | 1.0579 × 10−7 | 4.922 × 10−9 | 3.5126 × 10−12 | 8.4186 × 10−9 | 3.9168 × 10−10 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 9.4821 × 10−13 | 3.5836 × 10−9 | 2.3093 × 10−10 | 7.5456 × 10−14 | 2.8517 × 10−10 | 1.8377 × 10−11 |
| 2. | 2.95 × 10−12 | 1.1149 × 10−8 | 7.1844 × 10−10 | 2.3475 × 10−13 | 8.8721 × 10−10 | 5.7172 × 10−11 |
| 3. | 4.9518 × 10−12 | 1.8714 × 10−8 | 1.206 × 10−9 | 3.9405 × 10−13 | 1.4892 × 10−9 | 9.5967 × 10−11 |
| 4. | 6.9535 × 10−12 | 2.628 × 10−8 | 1.6935 × 10−9 | 5.5334 × 10−13 | 2.0913 × 10−9 | 1.3476 × 10−10 |
| 5. | 8.9553 × 10−12 | 3.3845 × 10−8 | 2.181 × 10−9 | 7.1264 × 10−13 | 2.6933 × 10−9 | 1.7356 × 10−10 |
| 6. | 1.0957 × 10−11 | 4.1411 × 10−8 | 2.6685 × 10−9 | 8.7194 × 10−13 | 3.2954 × 10−9 | 2.1235 × 10−10 |
| 7. | 1.2959 × 10−11 | 4.8976 × 10−8 | 3.156 × 10−9 | 1.0312 × 10−12 | 3.8974 × 10−9 | 2.5115 × 10−10 |
| 8. | 1.4961 × 10−11 | 5.6541 × 10−8 | 3.6435 × 10−9 | 1.1905 × 10−12 | 4.4994 × 10−9 | 2.8994 × 10−10 |
| 9. | 1.6962 × 10−11 | 6.4107 × 10−8 | 4.131 × 10−9 | 1.3498 × 10−12 | 5.1015 × 10−9 | 3.2874 × 10−10 |
| 10. | 1.8964 × 10−11 | 7.1672 × 10−8 | 4.6185 × 10−9 | 1.5091 × 10−12 | 5.7035 × 10−9 | 3.6753 × 10−10 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 3.3458 × 10−10 | 1.0181 × 10−6 | 4.7945 × 10−8 | 2.6625 × 10−11 | 8.1019 × 10−8 | 3.8153 × 10−9 |
| 2. | 7.1046 × 10−10 | 2.1619 × 10−6 | 1.0181 × 10−7 | 5.6537 × 10−11 | 1.7204 × 10−7 | 8.1017 × 10−9 |
| 3. | 1.0863 × 10−9 | 3.3057 × 10−6 | 1.5567 × 10−7 | 8.6449 × 10−11 | 2.6306 × 10−7 | 1.2388 × 10−8 |
| 4. | 1.4622 × 10−9 | 4.4496 × 10−6 | 2.0954 × 10−7 | 1.1636 × 10−10 | 3.5408 × 10−7 | 1.6674 × 10−8 |
| 5. | 1.8381 × 10−9 | 5.5934 × 10−6 | 2.634 × 10−7 | 1.4627 × 10−10 | 4.4511 × 10−7 | 2.0961 × 10−8 |
| 6. | 2.214 × 10−9 | 6.7372 × 10−6 | 3.1727 × 10−7 | 1.7618 × 10−10 | 5.3613 × 10−7 | 2.5247 × 10−8 |
| 7. | 2.5899 × 10−9 | 7.881 × 10−6 | 3.7113 × 10−7 | 2.061 × 10−10 | 6.2715 × 10−7 | 2.9534 × 10−8 |
| 8. | 2.9658 × 10−9 | 9.0248 × 10−6 | 4.2499 × 10−7 | 2.3601 × 10−10 | 7.1817 × 10−7 | 3.382 × 10−8 |
| 9. | 3.3417 × 10−9 | 1.0169 × 10−5 | 4.7886 × 10−7 | 2.6592 × 10−10 | 8.0919 × 10−7 | 3.8106 × 10−8 |
| 10. | 3.7175 × 10−9 | 1.1312 × 10−5 | 5.3272 × 10−7 | 2.9583 × 10−10 | 9.0021 × 10−7 | 4.2393 × 10−8 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 3.3317 × 10−19 | 9.7811 × 10−16 | 4.5868 × 10−17 | 2.525 × 10−16 | 7.4129 × 10−13 | 3.4763 × 10−14 |
| 2. | 6.6633 × 10−19 | 1.9562 × 10−15 | 9.1737 × 10−17 | 5.05 × 10−16 | 1.4826 × 10−12 | 6.9525 × 10−14 |
| 3. | 9.995 × 10−19 | 2.9343 × 10−15 | 1.376 × 10−16 | 7.575 × 10−16 | 2.2239 × 10−12 | 1.0429 × 10−13 |
| 4. | 1.3327 × 10−18 | 3.9125 × 10−15 | 1.8347 × 10−16 | 1.01 × 10−15 | 2.9652 × 10−12 | 1.3905 × 10−13 |
| 5. | 1.6658 × 10−18 | 4.8906 × 10−15 | 2.2934 × 10−16 | 1.2625 × 10−15 | 3.7065 × 10−12 | 1.7381 × 10−13 |
| 6. | 1.999 × 10−18 | 5.8687 × 10−15 | 2.7521 × 10−16 | 1.515 × 10−15 | 4.4478 × 10−12 | 2.0858 × 10−13 |
| 7. | 2.3322 × 10−18 | 6.8468 × 10−15 | 3.2108 × 10−16 | 1.7675 × 10−15 | 5.1891 × 10−12 | 2.4334 × 10−13 |
| 8. | 2.6653 × 10−18 | 7.8249 × 10−15 | 3.6695 × 10−16 | 2.02 × 10−15 | 5.9304 × 10−12 | 2.781 × 10−13 |
| 9. | 2.9985 × 10−18 | 8.803 × 10−15 | 4.1281 × 10−16 | 2.2725 × 10−15 | 6.6716 × 10−12 | 3.1286 × 10−13 |
| 10. | 3.3317 × 10−18 | 9.7811 × 10−15 | 4.5868 × 10−16 | 2.525 × 10−15 | 7.4129 × 10−12 | 3.4763 × 10−13 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 4.0206 × 10−19 | 1.1934 × 10−15 | 3.3235 × 10−17 | 3.0472 × 10−16 | 9.0442 × 10−13 | 2.5188 × 10−14 |
| 2. | 8.0412 × 10−19 | 2.3867 × 10−15 | 6.647 × 10−17 | 6.0943 × 10−16 | 1.8088 × 10−12 | 5.0376 × 10−14 |
| 3. | 1.2062 × 10−18 | 3.5801 × 10−15 | 9.9705 × 10−17 | 9.1415 × 10−16 | 2.7133 × 10−12 | 7.5565 × 10−14 |
| 4. | 1.6082 × 10−18 | 4.7734 × 10−15 | 1.3294 × 10−16 | 1.2189 × 10−15 | 3.6177 × 10−12 | 1.0075 × 10−13 |
| 5. | 2.0103 × 10−18 | 5.9668 × 10−15 | 1.6618 × 10−16 | 1.5236 × 10−15 | 4.5221 × 10−12 | 1.2594 × 10−13 |
| 6. | 2.4124 × 10−18 | 7.1601 × 10−15 | 1.9941 × 10−16 | 1.8283 × 10−15 | 5.4265 × 10−12 | 1.5113 × 10−13 |
| 7. | 2.8144 × 10−18 | 8.3535 × 10−15 | 2.3265 × 10−16 | 2.133 × 10−15 | 6.331 × 10−12 | 1.7632 × 10−13 |
| 8. | 3.2165 × 10−18 | 9.5469 × 10−15 | 2.6588 × 10−16 | 2.4377 × 10−15 | 7.2354 × 10−12 | 2.0151 × 10−13 |
| 9. | 3.6186 × 10−18 | 1.074 × 10−14 | 2.9912 × 10−16 | 2.7424 × 10−15 | 8.1398 × 10−12 | 2.2669 × 10−13 |
| 10. | 4.0206 × 10−18 | 1.1934 × 10−14 | 3.3235 × 10−16 | 3.0472 × 10−15 | 9.0442 × 10−12 | 2.5188 × 10−13 |
| Time Steps | MiMFD (mT) | MaMFD (mT) | AvMFD (mT) | MiMFI (mA/mm) | MaMFI (mA/mm) | AvMFI (mA/mm) |
|---|---|---|---|---|---|---|
| 1. | 6.0733 × 10−19 | 7.7467 × 10−16 | 4.8008 × 10−17 | 4.6028 × 10−16 | 5.8711 × 10−13 | 3.6384 × 10−14 |
| 2. | 1.2147 × 10−18 | 1.5493 × 10−15 | 9.6016 × 10−17 | 9.2056 × 10−16 | 1.1742 × 10−12 | 7.2768 × 10−14 |
| 3. | 1.822 × 10−18 | 2.324 × 10−15 | 1.4402 × 10−16 | 1.3808 × 10−15 | 1.7613 × 10−12 | 1.0915 × 10−13 |
| 4. | 2.4293 × 10−18 | 3.0987 × 10−15 | 1.9203 × 10−16 | 1.8411 × 10−15 | 2.3484 × 10−12 | 1.4554 × 10−13 |
| 5. | 3.0366 × 10−18 | 3.8734 × 10−15 | 2.4004 × 10−16 | 2.3014 × 10−15 | 2.9355 × 10−12 | 1.8192 × 10−13 |
| 6. | 3.644 × 10−18 | 4.648 × 10−15 | 2.8805 × 10−16 | 2.7617 × 10−15 | 3.5227 × 10−12 | 2.1831 × 10−13 |
| 7. | 4.2513 × 10−18 | 5.4227 × 10−15 | 3.3606 × 10−16 | 3.222 × 10−15 | 4.1098 × 10−12 | 2.5469 × 10−13 |
| 8. | 4.8586 × 10−18 | 6.1974 × 10−15 | 3.8406 × 10−16 | 3.6823 × 10−15 | 4.6969 × 10−12 | 2.9107 × 10−13 |
| 9. | 5.466 × 10−18 | 6.9721 × 10−15 | 4.3207 × 10−16 | 4.1425 × 10−15 | 5.284 × 10−12 | 3.2746 × 10−13 |
| 10. | 6.0733 × 10−18 | 7.7467 × 10−15 | 4.8008 × 10−16 | 4.6028 × 10−15 | 5.8711 × 10−12 | 3.6384 × 10−13 |
| Frequency (MHz) | |||||||
|---|---|---|---|---|---|---|---|
| Modes | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
| 1 | 2.353 × 10−11 | 2.08 × 10−12 | 9.08 × 10−6 | 2.56 × 10−13 | −2.0479 × 10−13 | 2.0312 × 10−13 | 4.0616 × 10−13 |
| 2 | 1.5417 × 10−11 | 3.32 × 10−7 | 3.33 × 10−6 | 3.90 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 3 | 1.2398 × 10−10 | 4.02 × 10−7 | 3.13 × 10−5 | 1.47 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 4 | 2.058 × 10−10 | 3.43 × 10−7 | 3.19 × 10−5 | 5.67 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 5 | 2.7809 × 10−10 | 9.83 × 10−7 | 4.75 × 10−5 | 4.52 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 6 | 3.9117 × 10−10 | 3.70 × 10−7 | 6.89 × 10−5 | 7.40 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 7 | 3.9954 × 10−10 | 1.38 × 10−6 | 5.18 × 10−5 | 5.21 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 8 | 4.0446 × 10−10 | 5.30 × 10−7 | 6.97 × 10−5 | 9.04 × 10−7 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 9 | 4.0489 × 10−10 | 1.82 × 10−6 | 7.64 × 10−5 | 1.13 × 10−6 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| 10 | 4.0499 × 10−10 | 6.90 × 10−7 | 1.52 × 10−4 | 1.26 × 10−6 | −1.061 × 10−9 | 1.061 × 10−9 | 1.061 × 10−9 |
| Deformation (Ⴏm) | |||||||
|---|---|---|---|---|---|---|---|
| Modes | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
| 1 | 31.998 | 0.00018869 | 5.72 × 10−5 | 3.39 × 10−5 | 9.604 × 10−3 | 9.2143 × 10−3 | 8.2562 × 10−3 |
| 2 | 347.69 | 1.732 | 2.512 | 1.6242 | 1.7744 | 1.8811 | 2.2076 |
| 3 | 430.27 | 1.7666 | 2.3358 | 2.1649 | 1.9492 | 2.4072 | 1.8218 |
| 4 | 567.02 | 1.6772 | 2.1682 | 1.9493 | 2.6251 | 2.2065 | 1.8914 |
| 5 | 614.73 | 1.7843 | 2.3358 | 2.3673 | 2.4339 | 2.2916 | 2.2211 |
| 6 | 561.82 | 1.684 | 2.1682 | 2.6993 | 2.6043 | 2.1477 | 1.7175 |
| 7 | 571.76 | 2.3413 | 2.3115 | 1.9122 | 2.5140 | 2.4863 | 1.7255 |
| 8 | 502.72 | 1.9917 | 2.2874 | 2.15218 | 1.6629 | 1.8826 | 1.9705 |
| 9 | 518.4 | 1.7508 | 2.1793 | 2.2192 | 2.9362 | 2.1940 | 1.9857 |
| 10 | 489.92 | 1.4758 | 2.2088 | 1.6817 | 2.0070 | 1.1628 | 1.9993 |
| Model | Overall Performance | Strengths | Weaknesses |
|---|---|---|---|
| Random Forest | Moderate | Good performance on features 1, 4, 6, and 9 | Poor performance on other features |
| XGBoost | Good | Excellent performance on features 3, 4, 6, and 8; good performance on others 1, 7, and 10 | Fair performance on feature 2, poor performance on feature 5, very poor performance on feature 9 |
| CATBoost | Good | Excellent performance on several features (3, 4, 6, and 8); good performance on feature 10 | Fair performance on features 1 and 5, poor performance on feature 2, very poor performance on features 7 and 9 |
| ANN | Very Poor | None | Poor performance on all features |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yinusa, A.; Amokun, R.; Eke, J.; Sobamowo, G.; Oguntala, G.; Ehinmowo, A.; Salami, F.; Osigwe, O.; Adelaja, A.; Ojolo, S.; et al. Machine Learning Approach to Nonlinear Fluid-Induced Vibration of Pronged Nanotubes in a Thermal–Magnetic Environment. Vibration 2025, 8, 35. https://doi.org/10.3390/vibration8030035
Yinusa A, Amokun R, Eke J, Sobamowo G, Oguntala G, Ehinmowo A, Salami F, Osigwe O, Adelaja A, Ojolo S, et al. Machine Learning Approach to Nonlinear Fluid-Induced Vibration of Pronged Nanotubes in a Thermal–Magnetic Environment. Vibration. 2025; 8(3):35. https://doi.org/10.3390/vibration8030035
Chicago/Turabian StyleYinusa, Ahmed, Ridwan Amokun, John Eke, Gbeminiyi Sobamowo, George Oguntala, Adegboyega Ehinmowo, Faruq Salami, Oluwatosin Osigwe, Adekunle Adelaja, Sunday Ojolo, and et al. 2025. "Machine Learning Approach to Nonlinear Fluid-Induced Vibration of Pronged Nanotubes in a Thermal–Magnetic Environment" Vibration 8, no. 3: 35. https://doi.org/10.3390/vibration8030035
APA StyleYinusa, A., Amokun, R., Eke, J., Sobamowo, G., Oguntala, G., Ehinmowo, A., Salami, F., Osigwe, O., Adelaja, A., Ojolo, S., & Usman, M. (2025). Machine Learning Approach to Nonlinear Fluid-Induced Vibration of Pronged Nanotubes in a Thermal–Magnetic Environment. Vibration, 8(3), 35. https://doi.org/10.3390/vibration8030035










