Studying the Behavior of a Paperboard Box: Experiment and Finite Element Model
Abstract
1. Introduction
2. Theory
2.1. Random Vibrations
- -
- Probability Density Function (PDF)
- -
- Autocorrelation function
- -
- Power Spectral Density—PSD:
- -
- Amplitude:
- -
- Phase: Represents the phase change of the output signal relative to the input signal. The phase part shows the time shift between the input signal and the output at a given frequency. Power spectrum density (PSD) is used in random vibration analysis. The output power density spectrum is calculated as:
- -
- Random Vibration Table: Programmed to replicate PSD spectra.
- -
- Data Recorder: Used to measure the responses of the cardboard box.
- -
- Control and Sensor System: Includes accelerometers, pressure sensors, or motion sensors.
- -
- ASTM (American Society for Testing and Materials): Standards for random vibration testing of transportation packaging.
2.2. Material Model
3. Experiment
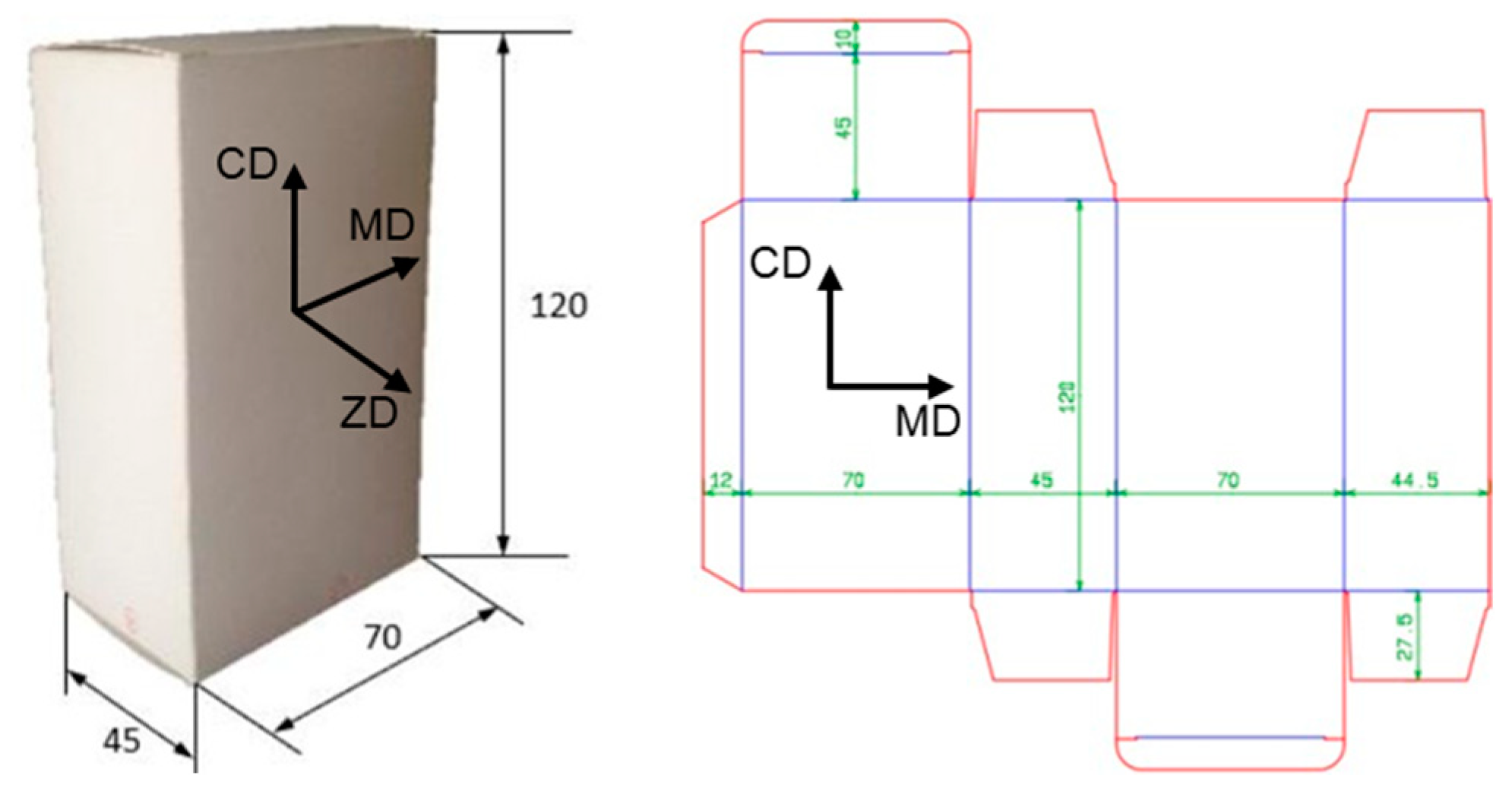
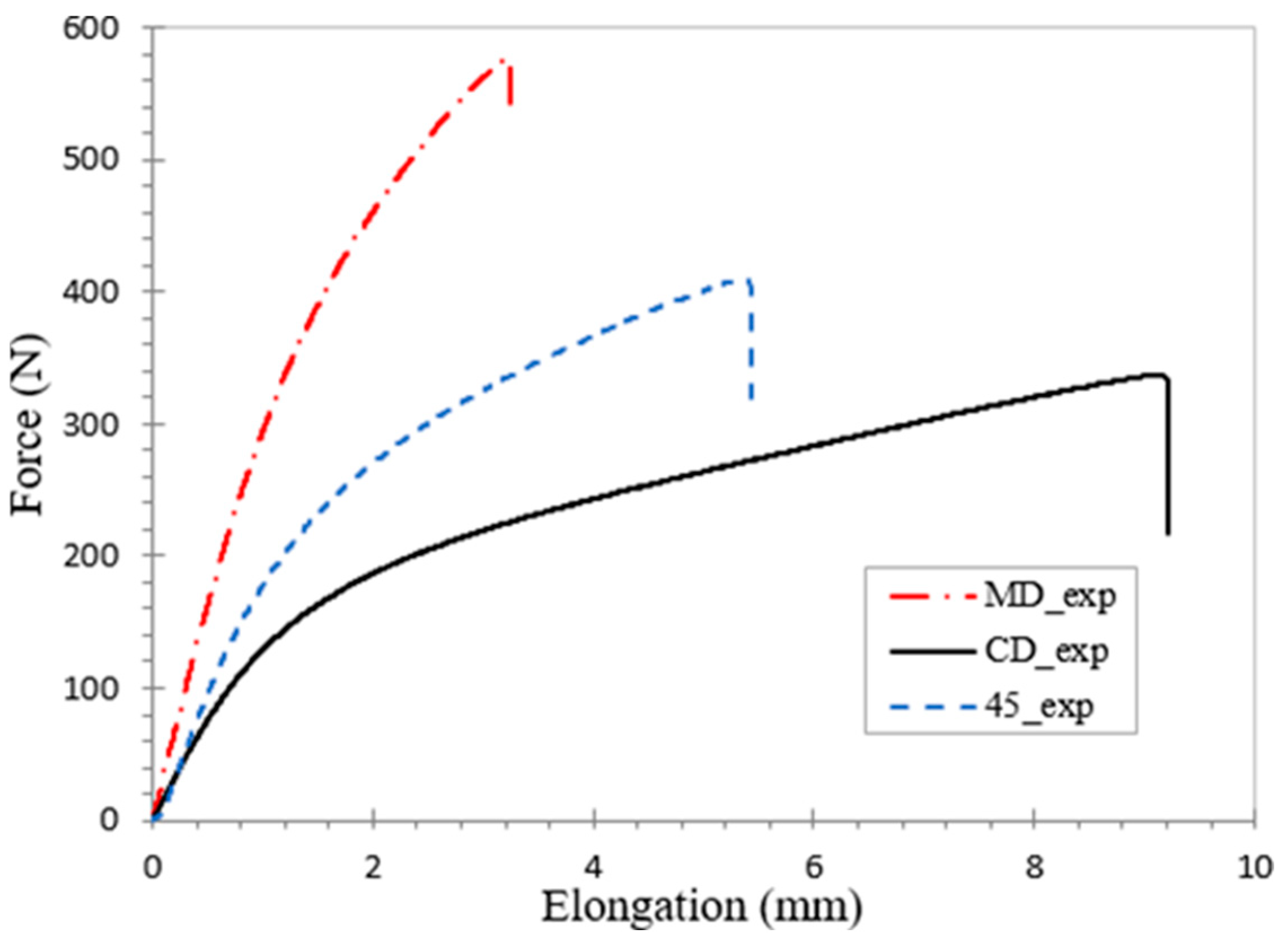
3.1. Studied Material
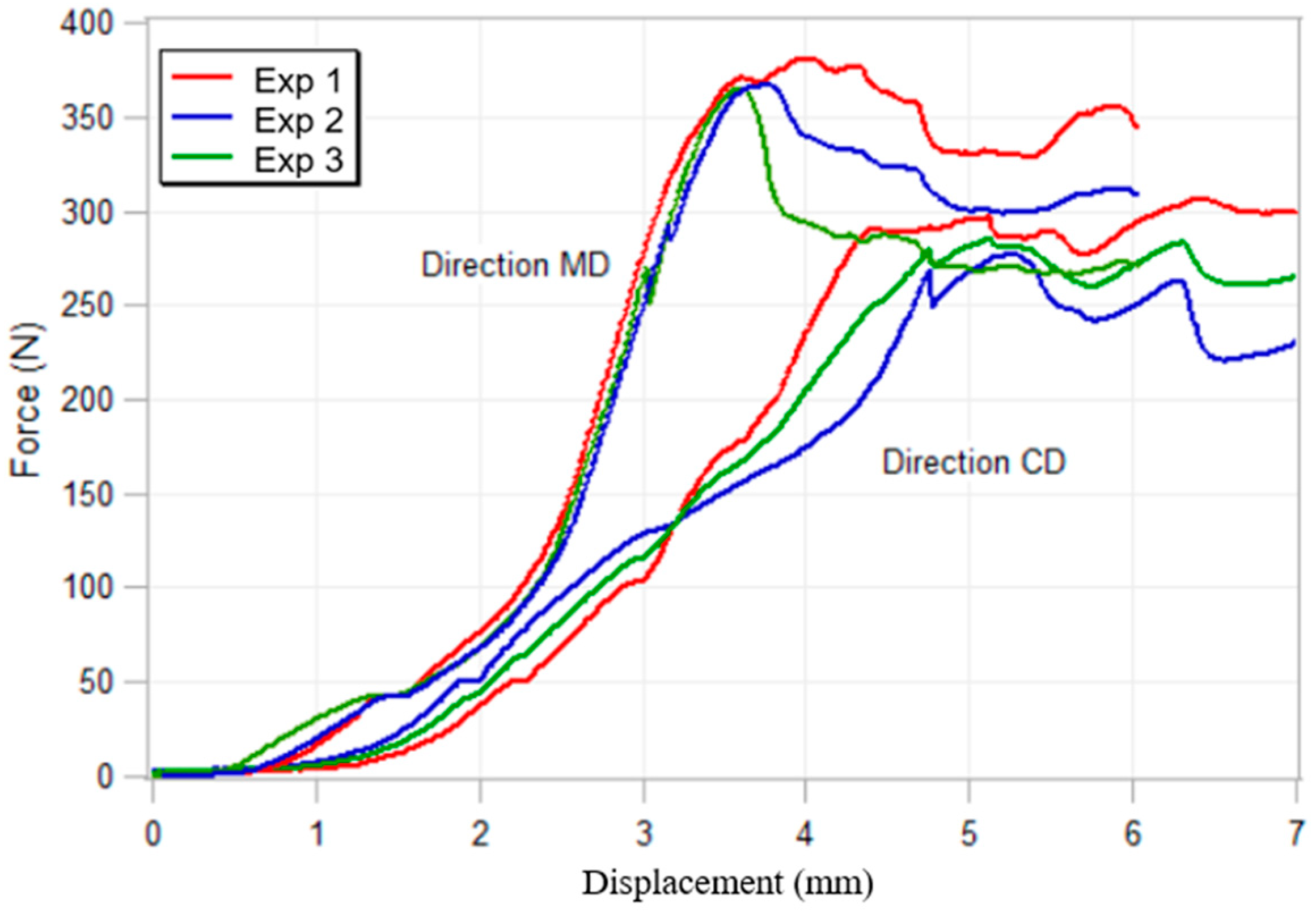
3.2. Static Compression Test
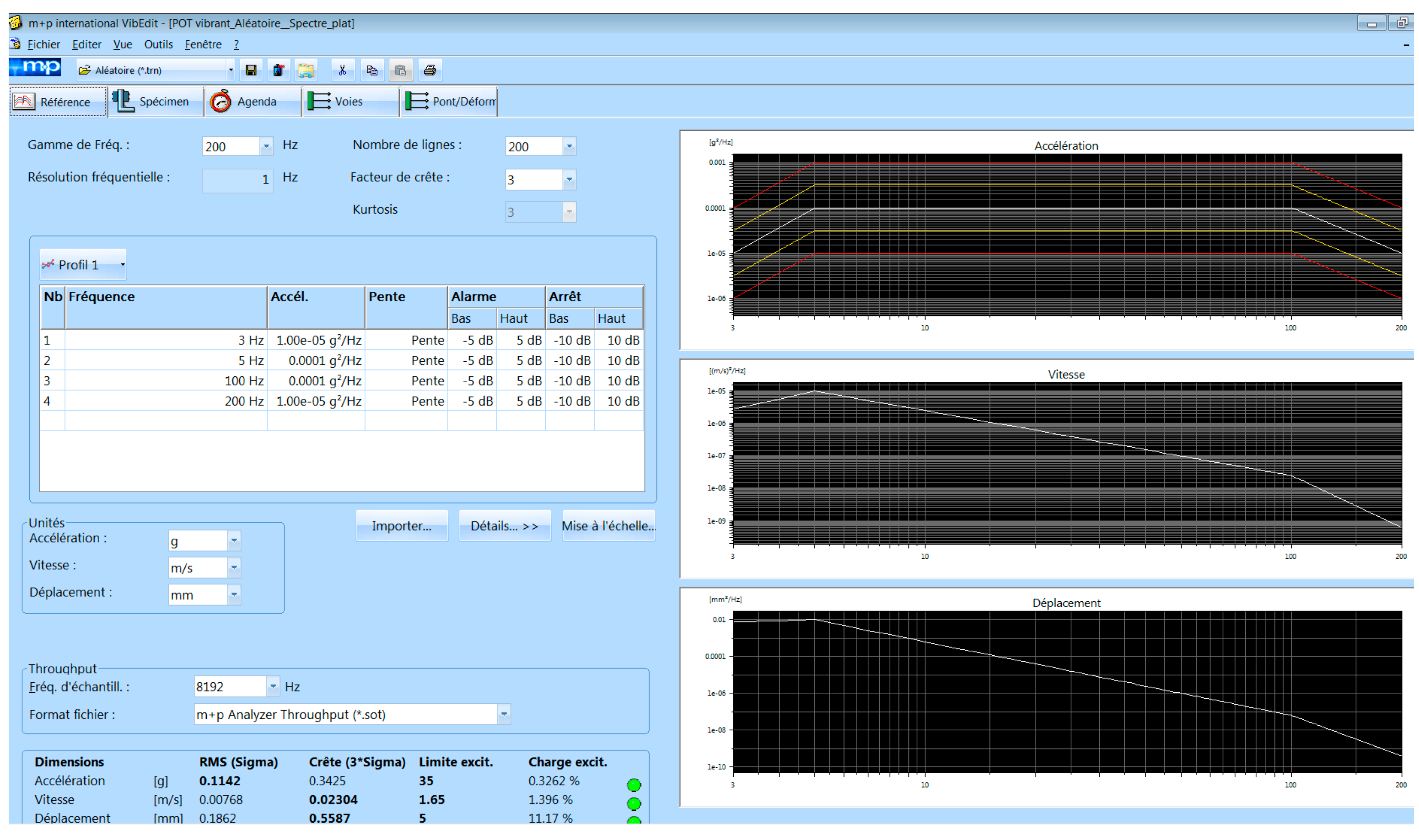
3.3. Vibration Test
4. Simulation
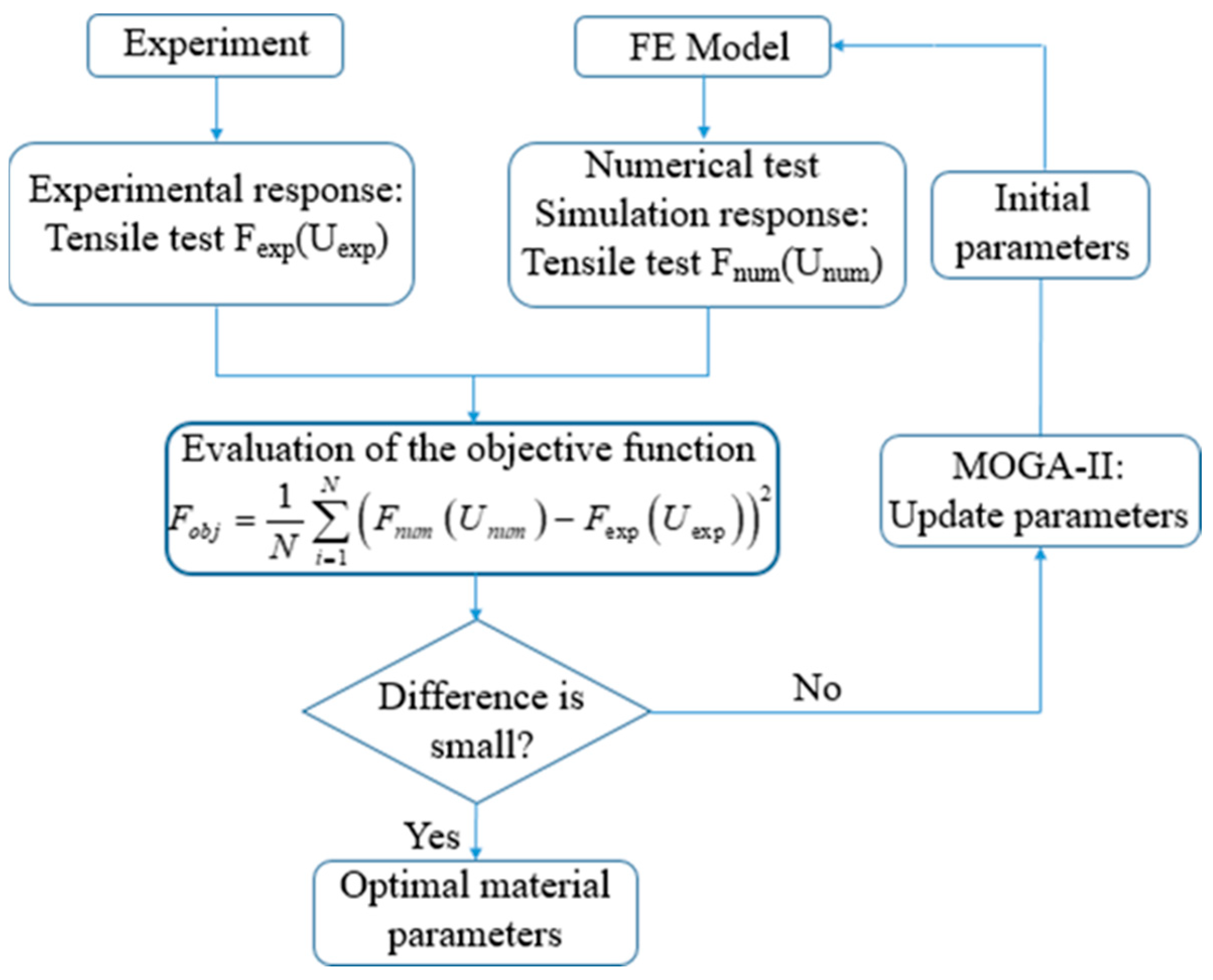
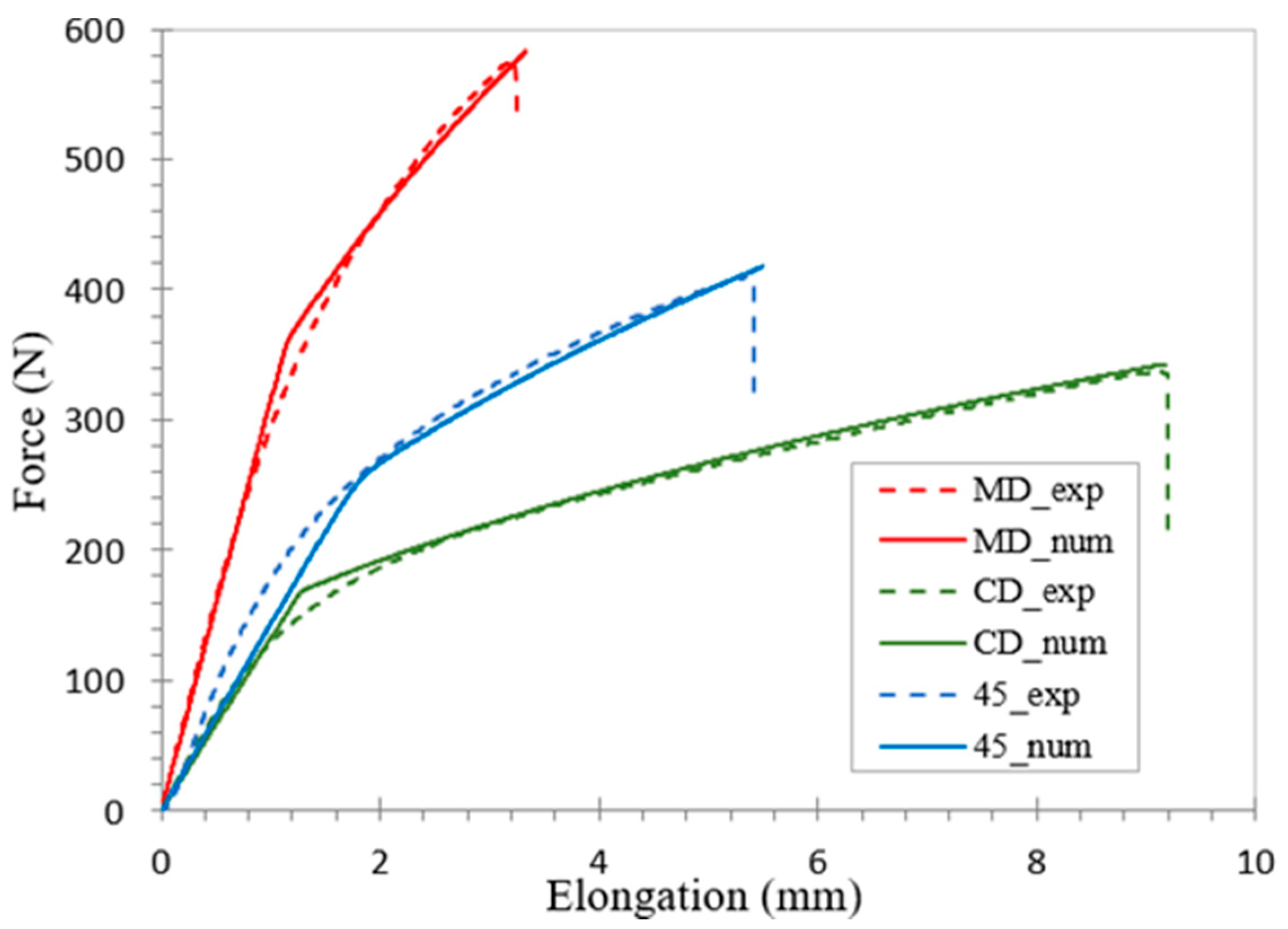
4.1. Material Parameter Identification
4.2. Simulation Experimental Compression
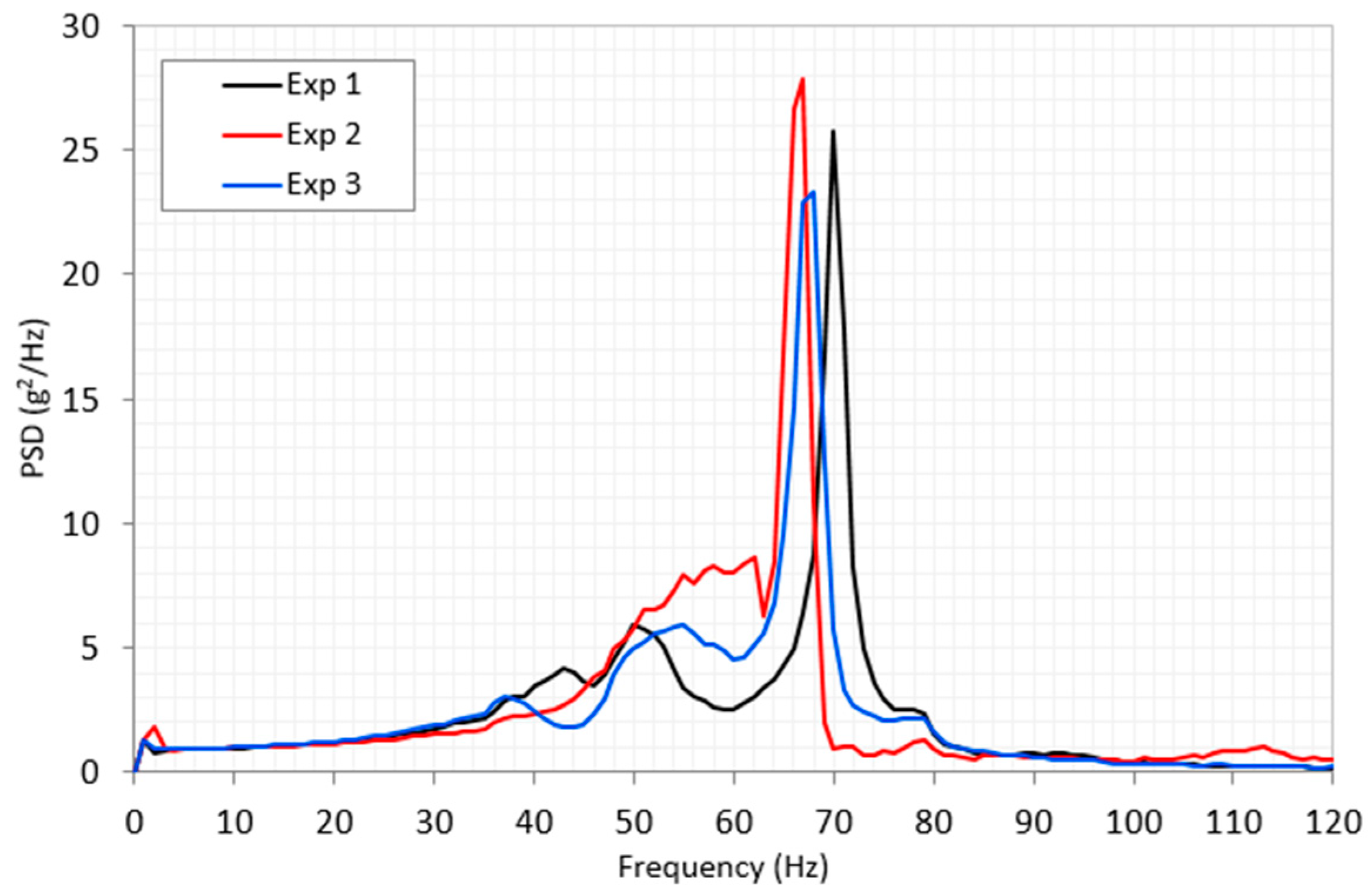
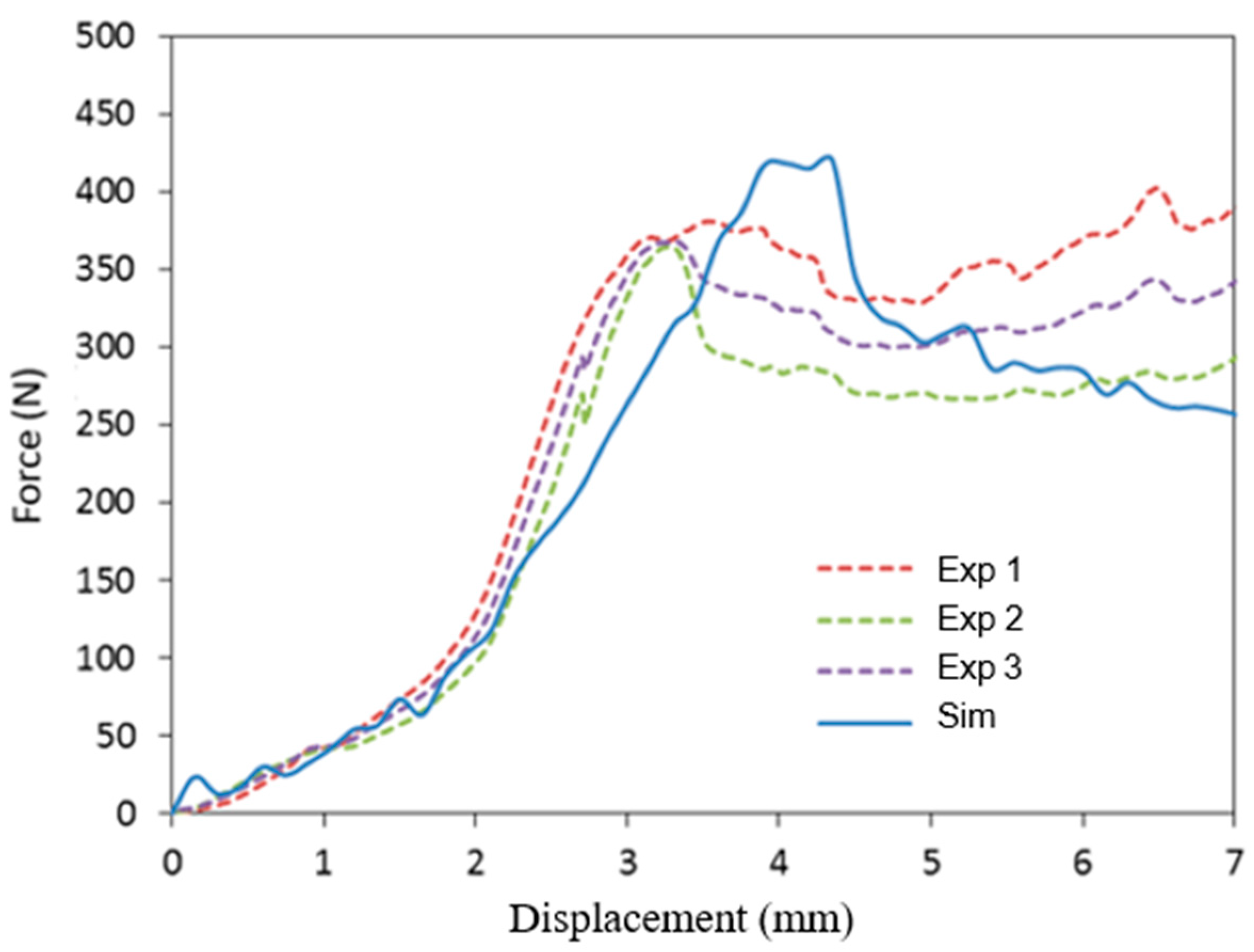
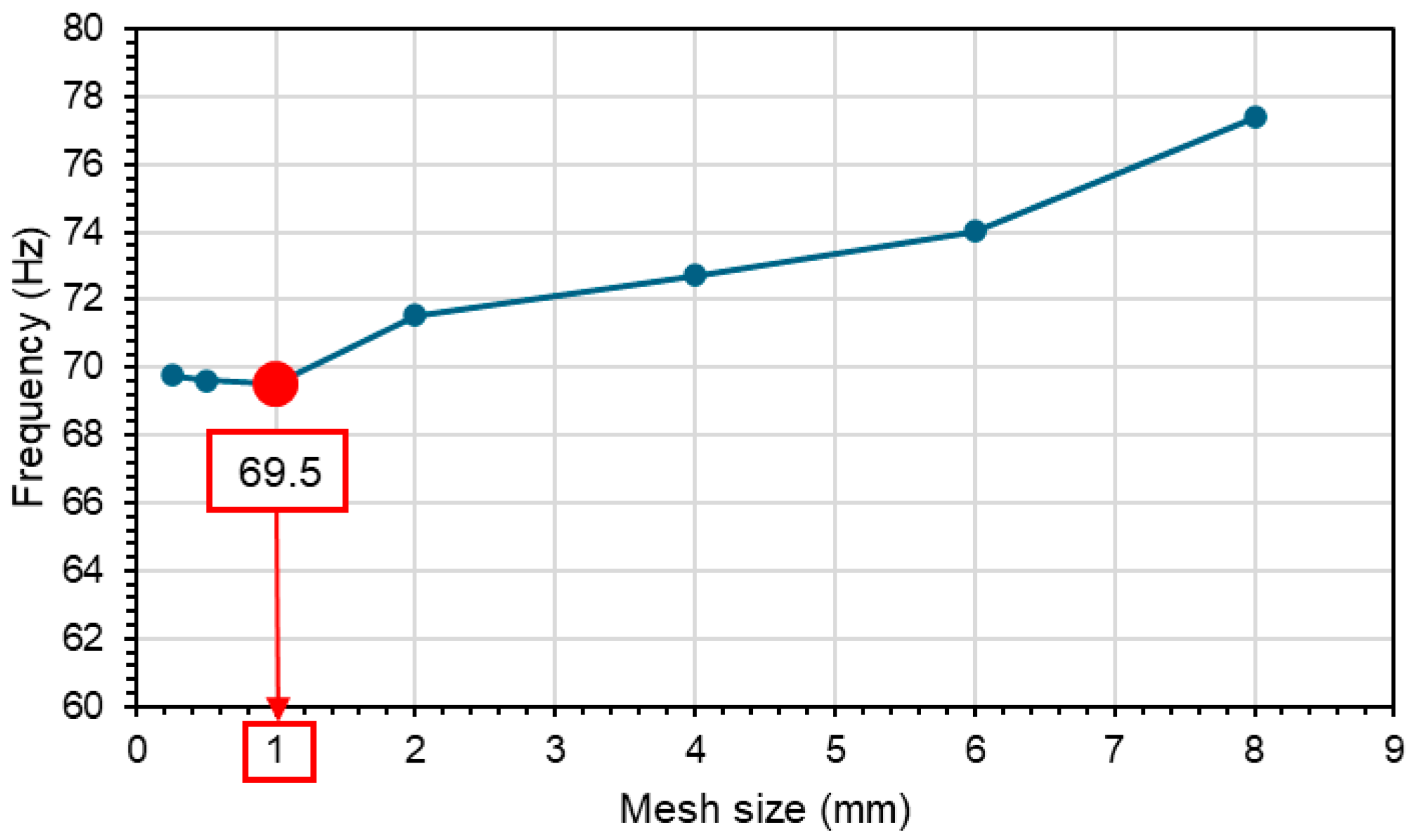
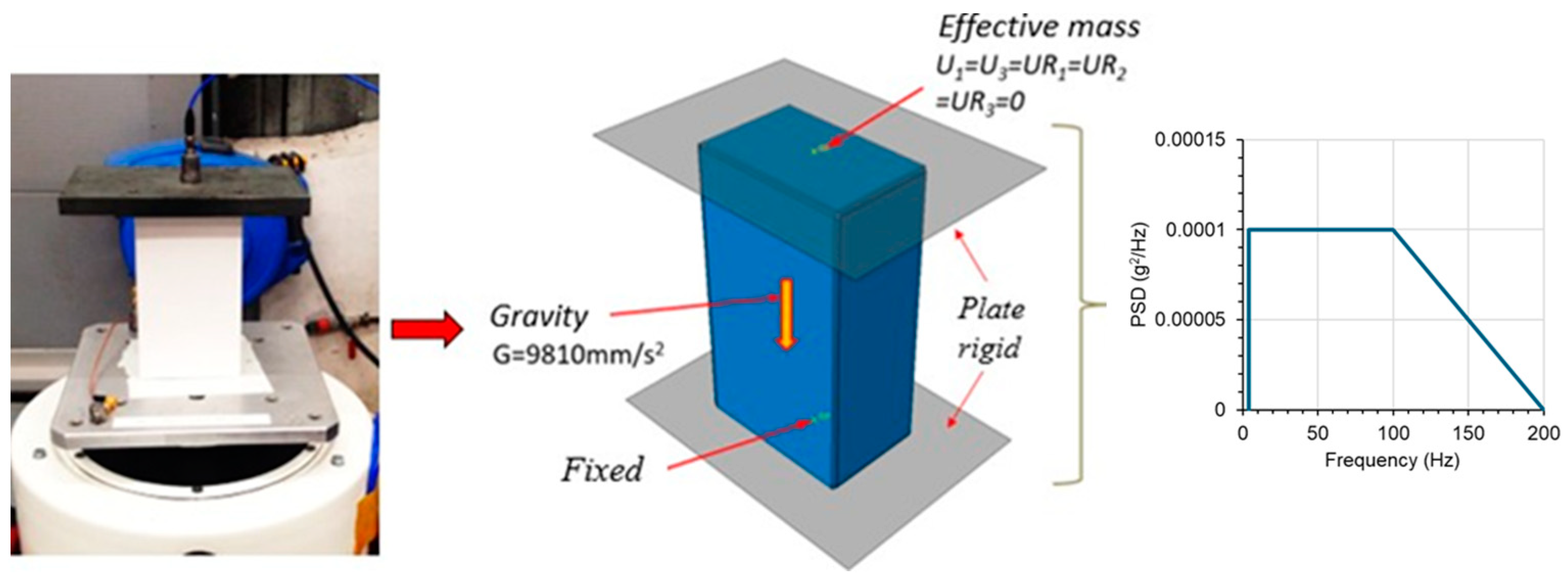
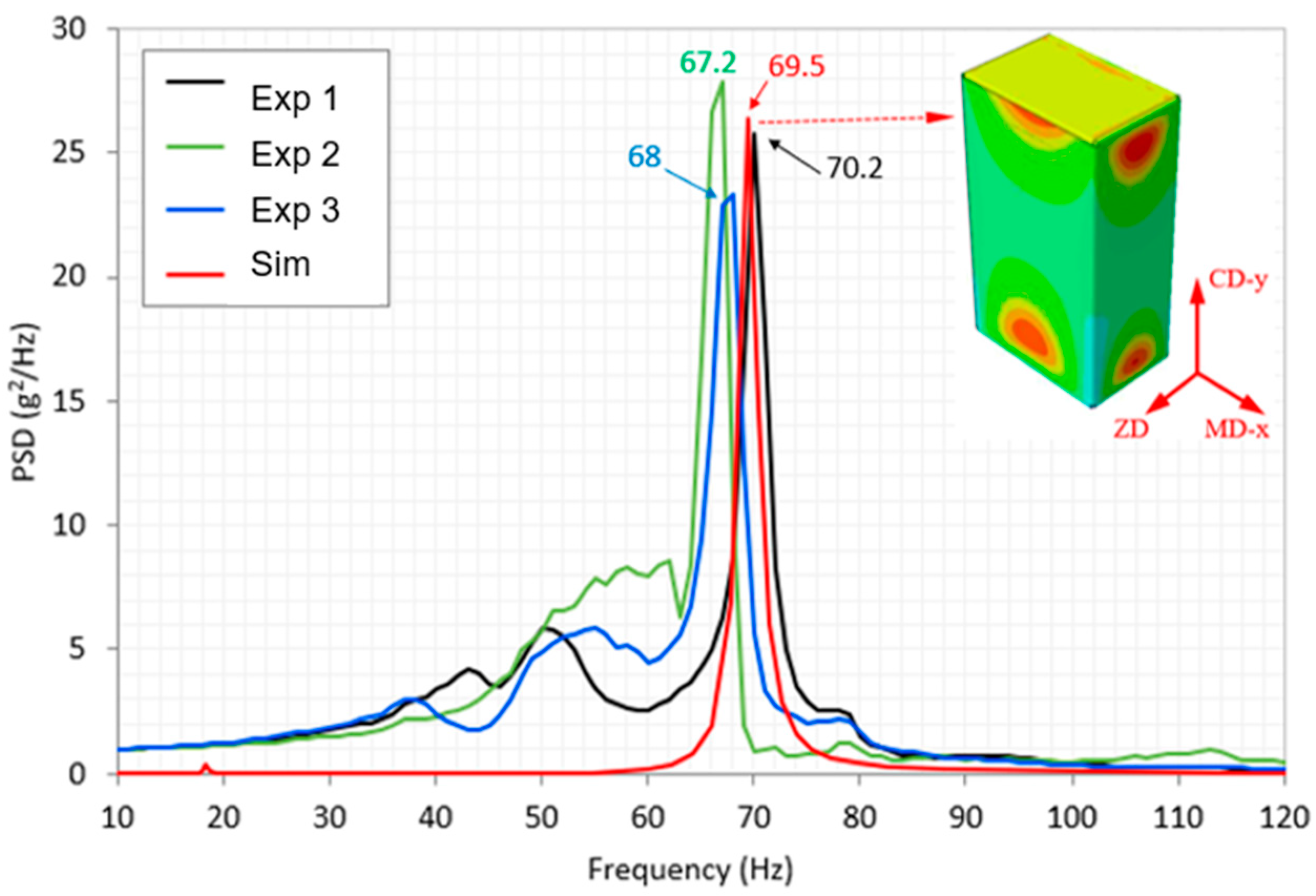
4.3. Vibration Test Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carlsson, L.; De Ruvo, A.; Fellers, C. Bending properties of creased zones of paperboard related to interlaminar defects. J. Mater. Sci. 1983, 18, 1365–1373. [Google Scholar] [CrossRef]
- Carlsson, L.; Fellers, C.; De Ruvo, A. The mechanism of failure in bending of paperboard. J. Mater. Sci. 1980, 15, 2636–2642. [Google Scholar] [CrossRef]
- Cavlin, S. The unique convertibility of paperboard. Packag. Technol. Sci. 1988, 1, 77–92. [Google Scholar] [CrossRef]
- Edholm, B. Bending stiffness loss of paperboard at conversion—Predicting the bending ability of paperboard. Packag. Technol. Sci. Int. J. 1998, 11, 131–140. [Google Scholar] [CrossRef]
- Giampieri, A.; Perego, U.; Borsari, R. A constitutive model for the mechanical response of the folding of creased paperboard. Int. J. Solids Struct. 2011, 48, 2275–2287. [Google Scholar] [CrossRef]
- Cavlin, S.; Dunder, I.; Edholm, B. Creasability testing by inclined rules—A base for standardized specification of paperboard. Packag. Technol. Sci. Int. J. 1997, 10, 191–207. [Google Scholar] [CrossRef]
- Nygårds, M.; Just, M.; Tryding, J. Experimental and numerical studies of creasing of paperboard. Int. J. Solids Struct. 2009, 46, 2493–2505. [Google Scholar] [CrossRef]
- Beex, L.; Peerlings, R. An experimental and computational study of laminated paperboard creasing and folding. Int. J. Solids Struct. 2009, 46, 4192–4207. [Google Scholar] [CrossRef]
- Amigo, J.C. Stiffness Design of Paperboard Packages Using the Finite Element Method. Master‘s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.; Desloges, I. Mauret. Some experimental aspects of the compression behaviour of boxes made up of g-flute corrugated boards. Packag. Technol. Sci. Int. J. 2010, 23, 69–89. [Google Scholar] [CrossRef]
- Haidar, M. Modelling of Failure Mechanisms for Corrugated Board. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2015. [Google Scholar]
- Rodrigues, D.F.; Pereira, J.C. Experimental tests and numerical simulations for failure investigation on corrugated boxes used on house- hold appliance packaging. J. Appl. Packag. Res. 2018, 10, 6. [Google Scholar]
- Biancolini, M.; Brutti, C. Numerical and experimental investigation of the strength of corrugated board packages. Packag. Technol. Sci. Int. J. 2003, 16, 47–60. [Google Scholar] [CrossRef]
- Kwak, W. Analysis of Compression Strength of Corrugated Shipping Containers with Different Designed Hand Holes. Master’s Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2010. [Google Scholar]
- Lamb, M.J.; Rouillard, V. Static and dynamic strength of paperboard containers subjected to variations in climatic conditions. Packag. Technol. Sci. 2017, 30, 103–114. [Google Scholar] [CrossRef]
- Thorpe, J.L.; Choi, D. Corrugated container failure. II: Strain measurements in laboratory compression tests. Tappi J. 1992, 75, 155–161. [Google Scholar]
- Viguié, J.; Dumont, P.J.; Vacher, P.; Org, L.; Desloges, I.; Mauret, E. Analysis of the strain and stress fields of cardboard box during compression by 3D digital image correlation. Appl. Mech. Mater. 2010, 24, 103–108. [Google Scholar] [CrossRef]
- Jarimopas, B.; Singh, S.P.; Saengnil, W. Measurement and analysis of truck transport vibration levels and damage to packaged tangerines during transit. Packag. Technol. Sci. Int. J. 2005, 18, 179–188. [Google Scholar] [CrossRef]
- Singh, S.P.; Sandhu, A.; Singh, J.; Joneson, E. Measurement and analysis of truck and rail shipping environment in India. Packag. Technol. Sci. Int. J. 2007, 20, 381–392. [Google Scholar] [CrossRef]
- Rissi, G.O.; Singh, S.P.; Burgess, G.; Singh, J. Measurement and analysis of truck transport environment in Brazil. Packag. Technol. Sci. Int. J. 2008, 21, 231–246. [Google Scholar] [CrossRef]
- Garcia-Romeu-Martinez, M.-A.; Singh, S.P.; Cloquell-Ballester, V.-A. Measurement and analysis of vibration levels for truck transport in Spain as a function of payload, suspension and speed. Packag. Technol. Sci. Int. J. 2008, 21, 439–451. [Google Scholar] [CrossRef]
- Böröcz, P.; Singh, S.P. Measurement and analysis of vibration levels in rail transport in central Europe. Packag. Technol. Sci. 2017, 30, 361–371. [Google Scholar] [CrossRef]
- Paternoster, A.; Vanlanduit, S.; Springael, J.; Braet, J. Vibration and shock analysis of specific events during truck and train transport of food products. Food Packag. Shelf Life 2018, 15, 95–104. [Google Scholar] [CrossRef]
- Paternoster, A.; Vanlanduit, S.; Springael, J.; Braet, J. Measurement and analysis of vibration and shock levels for truck transport in Belgium with respect to packaged beer during transit. Food Packag. Shelf Life 2018, 15, 134–143. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.; Chen, L.; Chukwu, O.; Opara, U.L. Susceptibility of apples to bruising inside ventilated corrugated paperboard packages during simulated transport damage. Postharvest Biol. Technol. 2016, 118, 111–119. [Google Scholar] [CrossRef]
- Fernando, I.; Fei, J.; Stanley, R.; Rouillard, V. Evaluating packaging performance for bananas under simulated vibration. Food Packag. Shelf Life 2020, 23, 100428. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, W.; Fu, Y.; Zhang, W. Comparison studies on dynamic packaging properties of corrugated paperboard pads. Engineering 2010, 2, 378. [Google Scholar] [CrossRef]
- Zhang, Q.; Saito, K.; Nagaoka, K. Damping package design using structural corrugated board. J. Appl. Packag. Res. 2017, 9, 19–33. [Google Scholar]
- Marcondes, J.; Batt, G. Update on dynamic compression measurement and testing. In Proceedings of Dimensions 2003 Conference (pp. 1–10). International Safe Transit Association (ISTA) and Institute of Packaging Professionals (IoPP). Available online: https://paperzz.com/doc/7932764 (accessed on 29 April 2025).
- Roberts, J.B.; Spanos, P.D. Random Vibration and Statistical Linearization; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
- Beranek, L.; Mellow, T. Acoustics: Sound Fields, Transducers and Vibration; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Materazzi, A.L.; Breccolotti, M. Stochastic Analysis of Nonlinear Systems. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I., Patelli, E., Au, I.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Norouzi, M. Random vibration Monte Carlo simulation using multiple harmonic function schemes. Int. J. Veh. Noise Vib. 2014, 10, 214–225. [Google Scholar] [CrossRef]
- Chang, T.P.; Chang, H.C.; Liu, M.F. A finite element analysis on random vibration of nonlinear shell structures. J. Sound Vib. 2006, 291, 240–257. [Google Scholar] [CrossRef]
- Kamiński, M. Uncertainty analysis in solid mechanics with uniform and triangular distributions using stochastic perturbation-based Finite Element Method. Finite Elem. Anal. Des. 2022, 200, 103648. [Google Scholar] [CrossRef]
- Do, N.T.; Tran, T.T. Random vibration analysis of FGM plates subjected to moving load using a refined stochastic finite element method. Def. Technol. 2024, 34, 42–56. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. A simplified dynamic strength analysis of cardboard packaging subjected to transport loads. Materials 2023, 16, 5131. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Liu, Y.; Chen, X.; Wu, H.; Yin, F.; Gao, R.; Li, Y.; Zhao, T. Experimental and numerical investigations of the vibration and acoustic properties of corrugated sandwich composite panels. Appl. Sci. 2022, 12, 8553. [Google Scholar] [CrossRef]
- Wang, L.J.; Lai, Y.Z.; Wang, Z.W. Fatigue failure and Grms–N curve of corrugated paperboard box. J. Vib. Control. 2020, 26, 793–803. [Google Scholar] [CrossRef]
- Wang, L.J.; Wang, Z.W. FEM verification of accelerated vibration test method based on Grms–N curve. J. Mech. Sci. Technol. 2022, 36, 1703–1712. [Google Scholar] [CrossRef]
- Broch, J.T.; Courrech, J. Mechanical Vibration and Shock Measurements; Bruël & Kjaer: Nærum, Denmark, 1980. [Google Scholar]
- Mäkelä, P.; Östlund, S. Orthotropic elastic–plastic material model for paper materials. Int. J. Solids Struct. 2003, 40, 5599–5620. [Google Scholar] [CrossRef]
- Karafillis, A.; Boyce, M. A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 1993, 41, 1859–1886. [Google Scholar] [CrossRef]
- Frank, B. Corrugated box compression—A literature survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Gudavicius, D. Finite Element Analysis of E-Commerce Corrugated Board Cushioning. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Marin, G.; Srinivasa, P.; Nygårds, M.; Östlund, S. Experimental and finite element simulated box compression tests on paperboard packages at different moisture levels. Packag. Technol. Sci. 2021, 34, 229–243. [Google Scholar] [CrossRef]
- ABAQUS 2019; ABAQUS Documentation; Dassault Systèmes: Providence, RI, USA, 2019.
- Luong, V.D.; Abbès, B.; Abbès, F.; Nolot, J.B.; Erre, D. Experimental Characterisation and Finite Element Modelling of Paperboard for the Design of Paperboard Packaging. IOP Conf. Ser. Mater. Sci. Eng. 2019, 540, 012014. [Google Scholar] [CrossRef]
- Laulusa, A.; Bauchau, O.A.; Choi, J.Y.; Tan, V.B.C.; Li, L. Evaluation of some shear deformable shell elements. Int. J. Solids Struct. 2006, 43, 5033–5054. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhang, Q.; Song, H.; Wang, Z.W. Mechanical damage of ‘Huangguan’ pear using different packaging under random vibration. Postharvest Biol. Technol. 2022, 187, 111847. [Google Scholar] [CrossRef]







| Box | Direction MD | Direction CD |
|---|---|---|
| BCT Strength (N) | 371.9 ± 7.6 | 289.6 ± 15.5 |
| Ex (MPa) | Ey (MPa) | νxy | Gxy (MPa) |
|---|---|---|---|
| 3710 | 1559 | 0.36 | 1200 |
| n | a | b | c | d | ε0 | E0 |
|---|---|---|---|---|---|---|
| 2.31 | 1.0 | 2.04 | 2.48 | 1.08 | 0.0046 | 301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbès, B.; Abbès, F.; Dao, L.T.; Duong, P.T.M.; Luong, V.D. Studying the Behavior of a Paperboard Box: Experiment and Finite Element Model. Vibration 2025, 8, 23. https://doi.org/10.3390/vibration8020023
Abbès B, Abbès F, Dao LT, Duong PTM, Luong VD. Studying the Behavior of a Paperboard Box: Experiment and Finite Element Model. Vibration. 2025; 8(2):23. https://doi.org/10.3390/vibration8020023
Chicago/Turabian StyleAbbès, Boussad, Fazilay Abbès, Lien Tien Dao, Pham Tuong Minh Duong, and Viet Dung Luong. 2025. "Studying the Behavior of a Paperboard Box: Experiment and Finite Element Model" Vibration 8, no. 2: 23. https://doi.org/10.3390/vibration8020023
APA StyleAbbès, B., Abbès, F., Dao, L. T., Duong, P. T. M., & Luong, V. D. (2025). Studying the Behavior of a Paperboard Box: Experiment and Finite Element Model. Vibration, 8(2), 23. https://doi.org/10.3390/vibration8020023







