Comparative Study of Different Linear Analysis for Seismic Resistance of Buildings According to Eurocode 8
Abstract
1. Introduction
2. Methodology
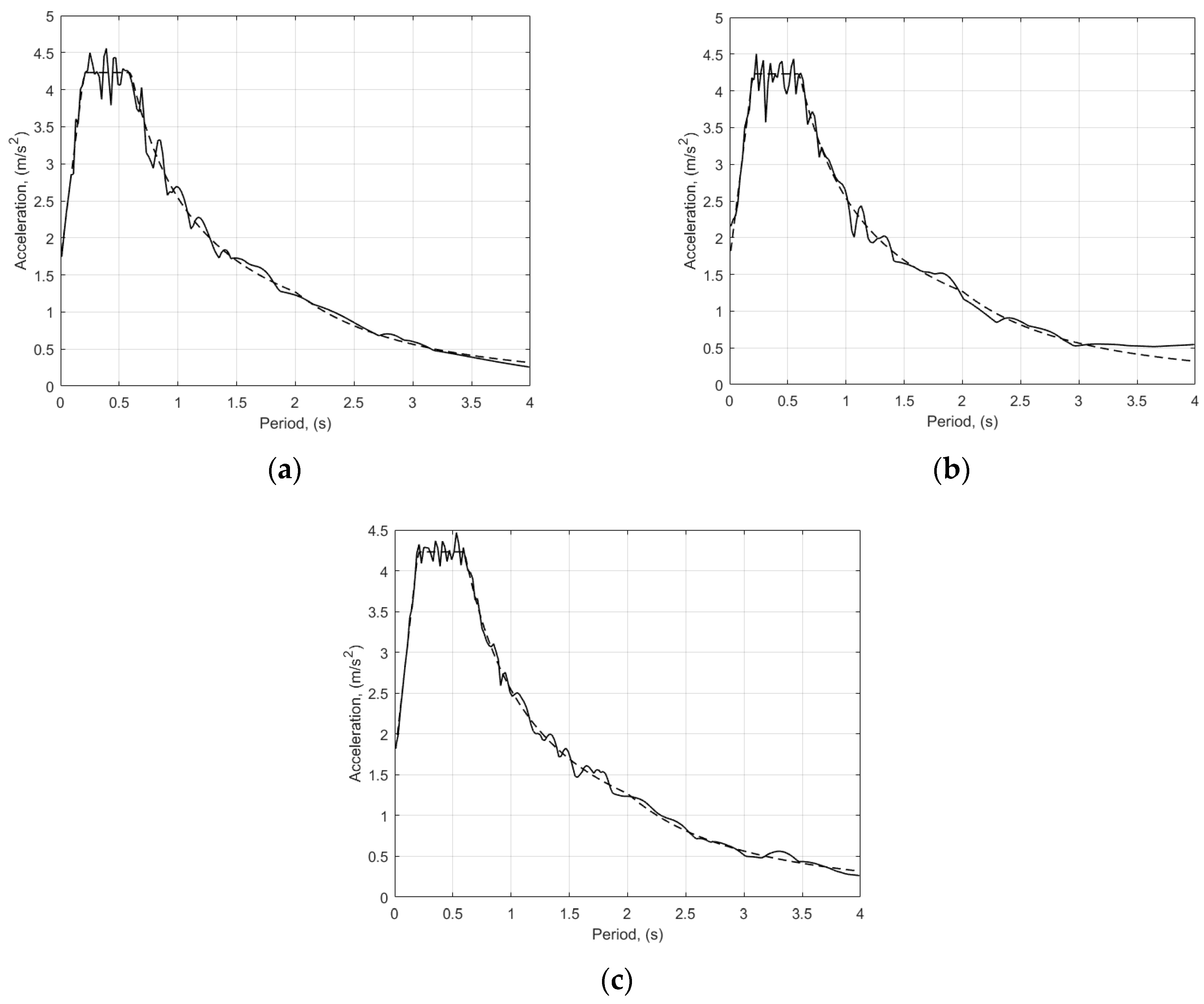
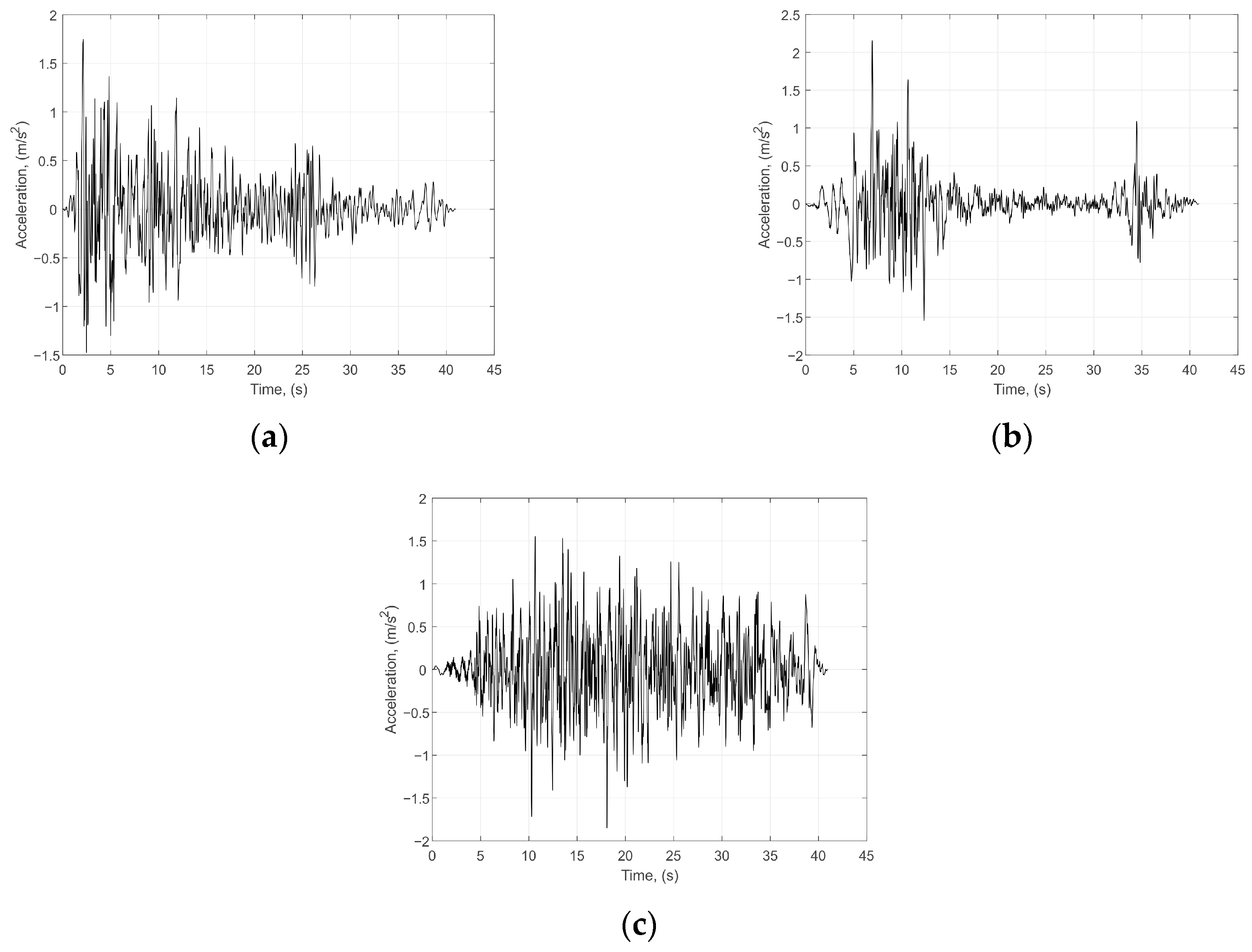
2.1. Artificial Accelerograms
- ElCentro Earthquake (1940);
- Gebze Earthquake (1999);
- Mexico City Earthquake (1985).
2.2. Time History Analysis
2.2.1. Implicit Time Integration Method
2.2.2. Explicit Time Integration Method
2.2.3. Modal Transient Dynamics
2.3. Response Spectrum Analysis
2.3.1. Lateral Force Method for Static Loading
2.3.2. Modal Response Spectrum Analysis
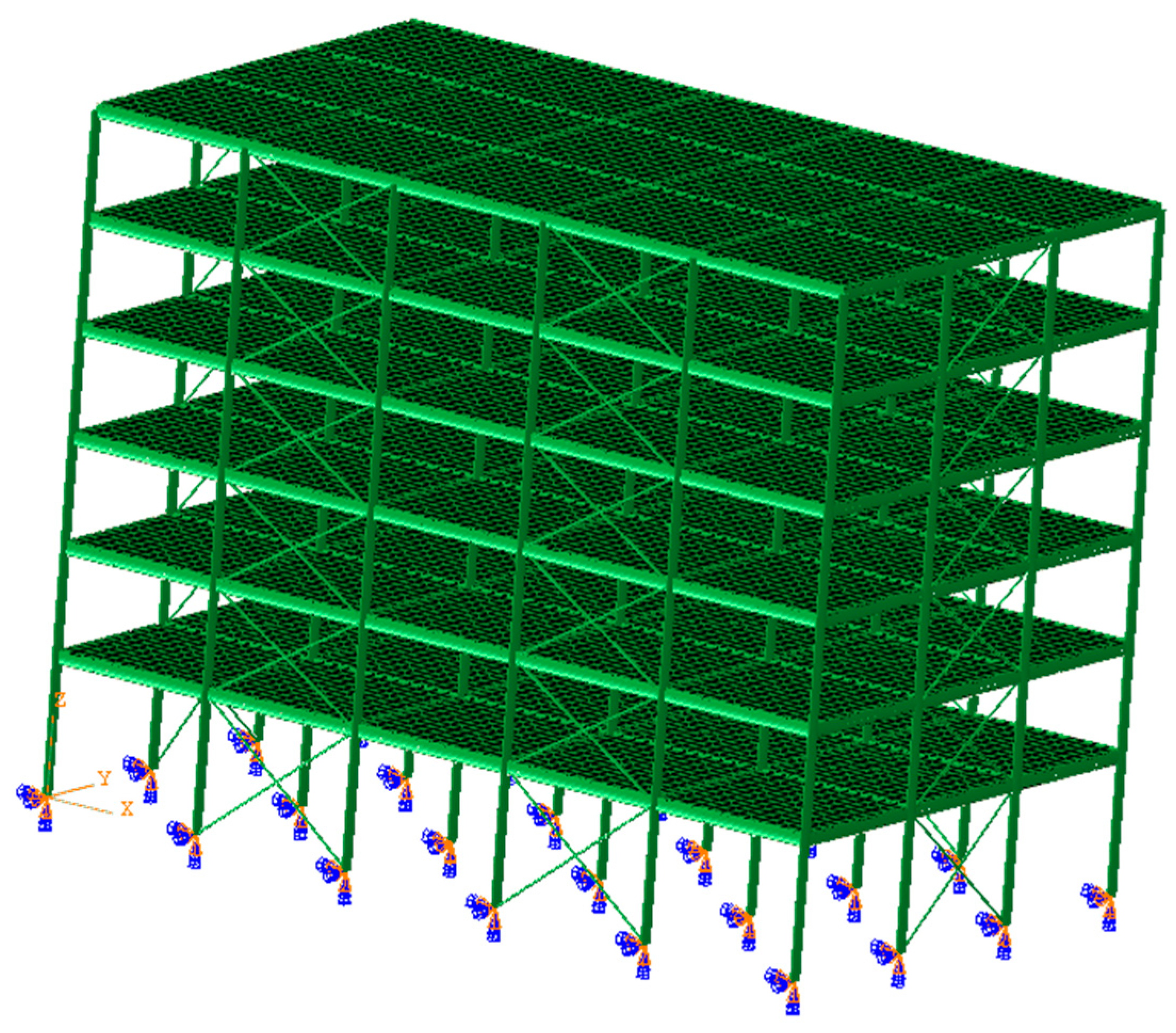
3. Structural Model
4. Results and Discussion
5. Conclusions
- The artificial accelerograms, although having very similar spectra, have a great diversity in the dynamic response of structures and in the effects of loadings. Looking for the maximum response and effects, it is necessary to try more than the minimum requirement of three accelerograms in one direction.
- All methods for time history analysis have similar results, and the fastest and cheapest method is the modal transient dynamic method, which, however, is the only linear method of analysis. The method could reveal torsional effects and structural response with higher stresses.
- When nonlinear simulations with accelerograms are needed, the explicit time integration method is superior and it is not so expensive, because the building frame structure model have relatively few DOF and a high critical time step, so it can be easily calculated even with a double precision, while the implicit nonlinear method could have low convergence and slower calculation.
- The response spectrum methods are very fast and easy for calculations. However, they are not so conservative. Compared with time history analysis methods, they can underestimate the effects of seismic loadings by approximately 10%, but use more diverse accelerograms, and the underestimation could be even greater.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EC8 | Eurocode 8, EN 1998-1 |
| SDOF | Single Degree of Freedom |
| MDOF | Multi Degree of Freedom |
| SRSS | Square Root of Sum of Squires |
| CQC | Complete Quadratic Combination |
| DOF | Degrees of Freedom |
References
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004; pp. 33–76.
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 4th ed.; Prentice-Hall of India: New Delhi, India, 2005. [Google Scholar]
- Gupta, A.K.; Hall, W.J. Response Spectrum Method: In Seismic Analysis and Design of Structures; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hadjian, A.H. Seismic response of structures by the response spectrum method. Nucl. Eng. Des. 1981, 66, 179–201. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chen, D.C. Comparison of modal combination methods. Nucl. Eng. Des. 1984, 78, 53–68. [Google Scholar] [CrossRef]
- Khatiwada, P.; Hu, Y.; Lumantarna, E.; Menegon, S.J. Dynamic Modal Analyses of Building Structures Employing Site-Specific Response Spectra Versus Code Response Spectrum Models. CivilEng 2023, 4, 134–150. [Google Scholar] [CrossRef]
- Dhileep, M.; Bose, P.R. A comparative study of “missing mass” correction methods for response spectrum method of seismic analysis. Comp. Struct. 2008, 86, 2087–2094. [Google Scholar] [CrossRef]
- Salmonte, A.J. Considerations on the residual contribution in modal analysis. Earthq. Eng. Struc. Dyn. 1982, 10, 295–304. [Google Scholar] [CrossRef]
- Fragiadakis, M.; Papadrakakis, M. Modeling, analysis and reliability of seismically excited structures: Computational issues. Int. J. Comput. Methods 2008, 5, 483–511. [Google Scholar] [CrossRef]
- Argyris, J.H.; Hilpert, O.; Malejannakis, G.A.; Scharpf, D.W. On the geometrical stiffness of a beam in space—A consistent v. w. approach. Comput. Meth. Appl. Mech. Eng. 1979, 20, 105–131. [Google Scholar] [CrossRef]
- Filippou, F.C.; Fenves, G.L. Ch. 6 Methods of analysis for earthquake-resistant structures. In Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; CRC Press: Boca Raton, FL, USA, 2004; eBook; ISBN 9780429204968. [Google Scholar]
- Fajfar, P.; Gaspersic, P. The N2 method for the seismic damage analysis of RC buildings. Earthq. Eng. Struct. Dyn. 1996, 25, 31–46. [Google Scholar] [CrossRef]
- Krawinkler, H.; Seneviratna, G.D.P.K. Pros and cons of a pushover analysis of seismic performance evaluation. Eng. Struct. 1998, 20, 452–464. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Aschheima, M.; Tjhinb, T.; Comartinc, C.; Hamburgerd, R.; Inele, M. The scaled nonlinear dynamic procedure. Eng. Struct. 2007, 29, 1422–1441. [Google Scholar] [CrossRef]
- Li, H.; Du, Y.; Han, J.; Li, F. Investigation on seismic behavior of a new beam-column joint for precast concrete structures under reversed cyclic loading. Structures 2024, 70, 107782. [Google Scholar] [CrossRef]
- Foti, F.; Lago, B.D.; Martinelli, L. On the coupled dynamics of vertical cladding panels and industrial frame structures subject to out-of-plane seismic loading. Eng. Struct. 2023, 296, 116909. [Google Scholar] [CrossRef]
- Jayaram, N.; Lin, T.; Baker, J.W. A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance. Earthq. Spectra 2011, 27, 797–815. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C. Spectral shape, epsilon and record selection. Earthq. Eng. Struct. Dyn. 2006, 35, 1077–1095. [Google Scholar] [CrossRef]
- Iervolino, I.; De Luca, F.; Cosenza, E. Spectral shape-based assessment of SDOF nonlinear response to real, adjusted and artificial accelerograms. Eng. Struct. 2010, 32, 2776–2792. [Google Scholar] [CrossRef]
- Baker, J.W. Conditional mean spectrum: Tool for ground-motion selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Hu, Y.; Lam, N.; Menegon, S.J.; Wilson, J. The Selection and Scaling of Ground Motion Accelerograms for Use in Stable Continental Regions. J. Earthq. Eng. 2022, 26, 6284–6303. [Google Scholar] [CrossRef]
- Lam, N.; Wilson, J.; Hutchinson, G. Generation of synthetic earthquake accelerograms using seismological modelling: A review. J. Earthq. Eng. 2000, 4, 321–354. [Google Scholar] [CrossRef]
- Suárez, L.E.; Montejo, L.A. Generation of artificial earthquakes via the wavelet transform. Int. J. Solids Struct. 2005, 42, 5905–5919. [Google Scholar] [CrossRef]
- Causse, M.; Laurendeau, A.; Perrault, M.; Douglas, J.; Bonilla, L.F.; Guéguen, P. Eurocode 8-compatible synthetic time-series as input to dynamic analysis. Bullet. Earthq. Eng. 2014, 12, 755–768. [Google Scholar] [CrossRef]
- Trovato, S.; D’Amore, E.; Yue, Q.; Spanos, P.D. An approach for synthesizing tri-component ground motions compatible with hazard-consistent target spectrum—Italian aseismic code application. Soil Dyn. Earthq. Eng. 2017, 93, 121–134. [Google Scholar] [CrossRef]
- Wu, S.R.; Gu, L. Introduction to the Explicit Finite Element Method for Nonlinear Transient Dynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements in for Continua and Structures; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Petyt, M. Introduction to Finite Element Vibration Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2010; pp. 367–412. [Google Scholar]
- Bommer, J.J.; Stafford, P.J. Seismic hazard and earthquake actions. In Seismic Design of Buildings to Eurocode 8, 2nd ed.; Elghazouli, A.Y., Ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2017; pp. 7–40. [Google Scholar]
- Bathe, K.J.; Cimento, A.P. Some practical procedures for the solution of nonlinear finite element equations. Comput. Meth. Appl. Mech. Eng. 1980, 22, 59–85. [Google Scholar] [CrossRef]
- Ferreira, F.; Moutinho, C.; Cunha, Á.; Caetano, E. An artificial accelerogram generator code written in Matlab. Eng. Rep. 2020, 2, e12129. [Google Scholar] [CrossRef]
- EN 10365; Hot rolled steel channels, I and H sections - Dimensions and masses. European Committee for Standardization: Brussels, Belgium, 2015.
| S | |||
|---|---|---|---|
| 1.15 | 0.2 | 0.6 | 2.0 |
| Profile | ||||
|---|---|---|---|---|
| HE 500A | 197.5 | 86,970 | 10,370 | 317.84 |
| IPE 450 | 98.8 | 33,740 | 1676 | 66.75 |
| UPN 120 | 17.0 | – | – | – |
| Mode No. | Frequency, (Hz) | Effec. Mass in X, (t) | Effec. Mass in Y, (t) |
|---|---|---|---|
| 1 | 1.2459 | 1576.8 | 0 |
| 2 | 1.3647 | 0 | 1547.6 |
| 3 | 1.875 | 0 | 0 1 |
| 4 | 3.7649 | 179.28 | 0 |
| 5 | 4.2729 | 0 | 182.51 |
| Accumulated mass | – | 96.77% | 95.34% |
| Residual modes in X and Y, respectively | 6.711; 8.1311 | 48.1 | 67.2 |
| Loading Direction | Residual Mode | Method | , (cm) | , (MPa) | , (MPa) | , (MPa) |
|---|---|---|---|---|---|---|
| X | No | CQC | 6.662 | 206.0 | 85.96 | 369.2 |
| Yes | CQC | 6.662 | 206.0 | 85.97 | 369.5 | |
| No | SRSS | 6.662 | 206.0 | 85.96 | 369.2 | |
| Yes | SRSS | 6.662 | 206.0 | 85.97 | 369.5 | |
| Y | No | CQC | 6.067 | 196.3 | 175.6 | 281.3 |
| Yes | CQC | 6.067 | 196.4 | 175.6 | 281.4 | |
| No | SRSS | 6.067 | 196.3 | 175.6 | 281.3 | |
| Yes | SRSS | 6.067 | 196.4 | 175.6 | 281.4 |
| Loading Direction | Distributions | , (kN) | , (cm) | , (MPa) | , (MPa) | , (MPa) |
|---|---|---|---|---|---|---|
| X | Height | 4878 | 6.730 | 203.0 | 84.73 | 357.1 |
| Mode 1 | 4878 | 6.528 | 200.8 | 83.74 | 357.2 | |
| Y | Height | 5343 | 6.180 | 196.5 | 174.3 | 278.5 |
| Mode 1 | 5343 | 6.057 | 195.2 | 174.2 | 278.7 |
| Direction | Accelerogram No | Explicit, (s) | Implicit, (s) | Modal, 5 m, (s) | Modal, 6 m, (s) |
|---|---|---|---|---|---|
| 1 | 6118 | 5307 | 1096 | 1137 | |
| X | 2 | 6146 | 5186 | 1075 | 1100 |
| 3 | 6326 | 5283 | 1087 | 1166 | |
| 1 | 6240 | 5148 | 1137 | 1120 | |
| Y | 2 | 6290 | 5259 | 1088 | 1082 |
| 3 | 6293 | 5242 | 1081 | 1076 |
| Loading Direction | Method | Accelerogram No | , (kN) | , (cm) | , (MPa) | , (MPa) | , (MPa) |
|---|---|---|---|---|---|---|---|
| X | 1 | 4821 | 6.374 | 195.3 | 82.12 | 353.5 | |
| Explicit | 2 | 5199 | 6.770 | 212.1 | 87.45 | 382.0 | |
| 3 | 4811 | 6.726 | 193.2 | 87.14 | 351.4 | ||
| 1 | 4830 | 6.381 | 197.3 | 82.49 | 354.5 | ||
| Implicit | 2 | 5212 | 6.783 | 210.7 | 87.82 | 383.1 | |
| 3 | 4814 | 6.735 | 192.3 | 87.17 | 352.1 | ||
| 1 | 4898 | 6.369 | 197.1 | 82.37 | 358.4 | ||
| Modal, 5 modes | 2 | 5254 | 6.766 | 209.1 | 87.36 | 384.5 | |
| 3 | 4762 | 6.748 | 191.4 | 85.39 | 348.5 | ||
| 1 | 5666 | 6.377 | 216.9 | 89.16 | 407.5 | ||
| Modal, 6 modes | 2 | 5 533 | 6.718 | 215.3 | 90.68 | 402.3 | |
| 3 | 5033 | 6.711 | 197.0 | 87.17 | 365.8 | ||
| Y | 1 | 5186 | 5.637 | 180.1 | 163.0 | 267.9 | |
| Explicit | 2 | 6095 | 6.523 | 215.7 | 193.8 | 314.3 | |
| 3 | 5762 | 6.323 | 202.3 | 182.5 | 298.3 | ||
| 1 | 5175 | 5.658 | 180.1 | 163.8 | 267.6 | ||
| Implicit | 2 | 6338 | 6.539 | 221.4 | 199.0 | 326.0 | |
| 3 | 5826 | 6.382 | 203.7 | 185.1 | 300.4 | ||
| 1 | 5199 | 5.657 | 183.3 | 165.1 | 268.8 | ||
| Modal, 5 modes | 2 | 6130 | 6.575 | 217.8 | 196.6 | 317.7 | |
| 3 | 5881 | 6.363 | 205.5 | 186.8 | 304.3 | ||
| 1 | 5284 | 5.650 | 182.2 | 165.1 | 271.6 | ||
| Modal, 6 modes | 2 | 6117 | 6.575 | 217.6 | 196.5 | 317.3 | |
| 3 | 5899 | 6.350 | 204.4 | 186.4 | 302.3 |
| Loading Direction | Accelerogram No. | , % | , % | , % | , % | , % |
|---|---|---|---|---|---|---|
| X | 1 | 7.27 | 5.85 | 7.92 | 6.09 | 7.46 |
| 3 | 7.46 | 0.65 | 8.91 | 0.35 | 8.01 | |
| Y | 1 | 14.91 | 13.58 | 16.50 | 15.89 | 14.76 |
| 3 | 5.46 | 3.07 | 6.21 | 5.83 | 5.09 |
| Loading Direction | Method | , % | , % | , % | , % | , % |
|---|---|---|---|---|---|---|
| Implicit | −0.25 | −0.19 | 0.66 | −0.42 | −0.29 | |
| X | Modal, 5 modes | −1.06 | 0.06 | 1.41 | 0.10 | −0.65 |
| Modal, 6 modes | −6.42 | 0.77 | −1.51 | −3.69 | −5.31 | |
| Implicit | −3.99 | −0.25 | −2.64 | −2.68 | −3.72 | |
| Y | Modal, 5 modes | −0.57 | −0.80 | −0.97 | −1.44 | −1.08 |
| Modal, 6 modes | −0.36 | −0.80 | −0.88 | −1.39 | −0.95 |
| Loading Direction | Method | , % | , % | , % | |
|---|---|---|---|---|---|
| Modal response spectrum | 1.60 | 2.88 | 1.70 | 3.35 | |
| X | Lateral force., height distr. | 0.59 | 4.29 | 3.11 | 6.52 |
| Lateral force., mode 1 distr. | 3.57 | 5.33 | 4.24 | 6.49 | |
| Modal response spectrum | 6.99 | 8.95 | 9.39 | 10.47 | |
| Y | Lateral force., height distr. | 5.26 | 8.90 | 10.06 | 11.39 |
| Lateral force., mode 1 distr. | 7.14 | 9.50 | 10.11 | 11.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, I.; Velchev, D. Comparative Study of Different Linear Analysis for Seismic Resistance of Buildings According to Eurocode 8. Vibration 2025, 8, 21. https://doi.org/10.3390/vibration8020021
Ivanov I, Velchev D. Comparative Study of Different Linear Analysis for Seismic Resistance of Buildings According to Eurocode 8. Vibration. 2025; 8(2):21. https://doi.org/10.3390/vibration8020021
Chicago/Turabian StyleIvanov, Ivelin, and Dimitar Velchev. 2025. "Comparative Study of Different Linear Analysis for Seismic Resistance of Buildings According to Eurocode 8" Vibration 8, no. 2: 21. https://doi.org/10.3390/vibration8020021
APA StyleIvanov, I., & Velchev, D. (2025). Comparative Study of Different Linear Analysis for Seismic Resistance of Buildings According to Eurocode 8. Vibration, 8(2), 21. https://doi.org/10.3390/vibration8020021






