Abstract
Flexure-based Stirling cryocooler compressors are a critical technology in providing cryogenic temperatures in various advanced engineering fields, such as aerospace, defense, and medical imaging. The most challenging problem in the design of this type of compressor is achieving a precise alignment that preserves small gaps between the components moving relative to each other and avoids severe friction and wear. This paper introduces a novel experimental procedure for designing Stirling cryocooler compressors, leveraging a recently developed nonlinear experimental modal analysis method known as response-controlled stepped-sine testing (RCT). The alignment in a compressor prototype was significantly improved in light of a series of RCT with base excitation. The enhanced compressor design was subsequently validated though a series of constant-current tests, which confirmed the elimination of the sticking/locking phenomenon observed in the initial design. Furthermore, an indirect harmonic force surface (HFS)-based approach proposed for weakly nonlinear systems was extended to identify the high and nonlinear damping (up to a 65% hysteretic modal damping ratio) observed in the enhanced compressor design due to excessive friction. As another contribution, it was shown that the extrapolation of the HFS gives accurate results in the prediction of the nonlinear modal parameters at response levels where no experimental data are available. In light of these findings, it was concluded that the enhanced design needs further design modifications to further decrease the friction and wear between the moving parts. Overall, this study provides valuable insights for designing cryocooler compressors, with implications for aerospace and medical applications.
1. Introduction
Stirling cryocoolers have emerged as a key technology for achieving the cryogenic temperatures required in advanced engineering applications such as aerospace, defense, and medical imaging. Their oil-free operation and high reliability under extreme environmental conditions make them especially suited for precision cooling in systems such as satellites, infrared detectors, and superconducting devices. Their split design further amplifies their advantages in sensitive applications requiring low-vibration and -noise characteristics, making them superior to conventional cooling systems [1,2]. Unlike conventional refrigeration systems, Stirling cryocoolers operate on a closed regenerative thermodynamic cycle, typically employing helium as a working fluid. This approach ensures both environmental safety and operational longevity, aligning with the stringent demands of critical applications [3].
Stirling cryocoolers can be classified based on different features. For example, one such classification can be made considering the arrangement of the compressor and cold finger: split and integral designs. Another classification can be made according to the moving parts: the moving iron, moving coil, and moving magnet. A third classification can be based on the compressor type: linear or rotary. This last classification creates opportunities to discuss the advantages of linear compressors which are at the center of this paperwork. Linear compressors, unlike rotary compressors, operate without a crankshaft mechanism, instead using a direct electromagnetic drive system that eliminates lateral forces and reduces the mechanical complexity. This design, supported by flexure springs, ensures precise alignment, minimizes friction, and allows oil-free operation. In contrast, rotary compressors rely on oil-based lubrication and complex mechanical linkages, which introduce higher energy losses, greater wear, and a shorter lifespan. Thus, linear compressors offer superior energy efficiency, reliability, and dynamic stability, addressing many limitations of rotary systems and proving especially advantageous in high-precision and reliability-critical applications like Stirling cryocoolers for aerospace and medical technologies [1,4,5]. This paper mainly focuses on the design and dynamical identification of split linear Stirling cryocoolers with moving magnets, as illustrated in Figure 1.
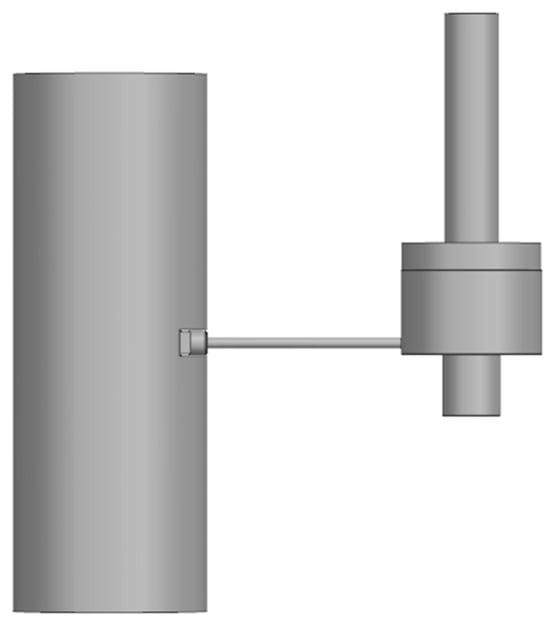
Figure 1.
Split linear Stirling cryocooler.
Flexure-based linear compressors form the cornerstone of modern Stirling cryocooler designs due to their efficiency and reliability. The flexure bearings illustrated in Figure 2 enable frictionless operation through elastic deformation, significantly reducing wear while enhancing system reliability [1,6]. Their ability to maintain high radial stiffness while permitting axial flexibility is crucial for ensuring precise piston alignment in linear compressors, thereby minimizing gas leakage and optimizing the performance [7].
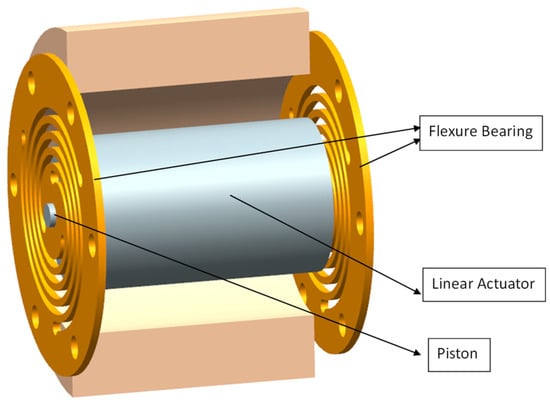
Figure 2.
Flexure bearings used in Stirling cryocooler compressors.
It is possible to find considerable studies about the design and implementations of flexure-based linear compressors in the literature. A remarkable one of these studies was recently published by Amoedo et al. [8]. In this work, a design method is proposed to select the geometrical parameters of a flexure bearing to be used in a Stirling cryocooler. The method conducts a parameter study that relates the geometrical parameters (e.g., the bearing thickness, spiral turn angle) to the structural parameters, such as the radial stiffness, the natural frequency, and the maximum stresses induced in the flexure bearing. This relation is used to determine the optimum bearing geometry that satisfies pre-determined structural design objectives and/or constraints. In another interesting work [9], Simcock shows that the stress distribution over flexure bearings at a given axial displacement obtained from finite element analysis (FEA) agrees well with the experimental stress distribution and concludes that FEA can replace time-consuming fatigue testing for design qualification if the stress levels are below the material endurance limit. In an earlier work [10], Ross et al. experimentally reveal that the mechanical efficiency of a cryocooler compressor is maximized if its operating frequency is tuned to the resonance frequency of the piston/flexure bearing/compressed gas assembly that acts as a single-degree-of-freedom (DOF) oscillator. In the same work, the force-level-dependent nature of the resonance frequency and modal damping of this oscillator is demonstrated by a series of constant-current sine sweep tests. In a follow-up study [11], Ross et al. also investigate the working fluid (gas) effects on the cryocooler resonance characteristics in detail. In another study [12], Yuan et al. show that although operating the cooler at its resonance frequency ensures the highest mechanical efficiency, it does not guarantee the best refrigeration performance. In the same study, it was demonstrated through simulations of an experimentally validated computer model (the Stirling refrigerator performance model) that for the best cooler performance, i.e., the maximum cooling performance with the minimum energy loss, the system has to be designed such that the natural frequency coincides with the optimal thermodynamic frequency.
Despite the rich literature addressing the design and optimization of flexure bearings, the prominent examples of which are shared above, to the best knowledge of the authors, no studies address the serious challenges posed by flexure-based Stirling cryocoolers, such as alignment sensitivities and nonlinear dynamic responses that can adversely affect the overall reliability and performance. In a typical cryocooler design, the piston/magnet assembly must be able to make sinusoidal motion maintaining very small gaps in three different regions, as illustrated in Figure 3. According to the authors’ experience, achieving a precise alignment that preserves these small gaps and avoids severe friction and wear is the most challenging problem in the design process of flexure-based Stirling cryocoolers. The most important contribution of this paper is the provision of a novel approach to investigate this challenging problem by making use of a state-of-the-art nonlinear experimental modal analysis method, namely, response-controlled stepped-sine testing (RCT) [13,14]. It is important to note that in all of the experimental applications throughout this study, the Stirling cryocoolers were not pressurized with working gas. The effect of the gas on cryocooler dynamics is out of the scope of this paper and will be studied in future work.
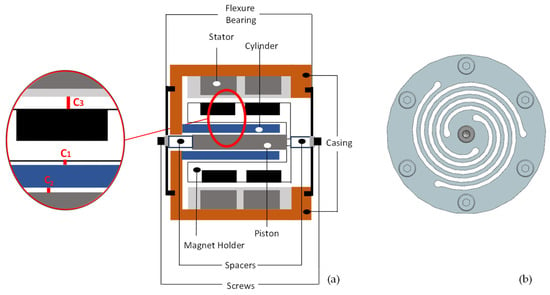
Figure 3.
(a) Small gaps in a typical flexure-based Stirling cryocooler; (b) flexure bearing.
This paper starts with the presentation of the sticking/locking problem that resulted from the severe friction observed during open-loop constant-amplitude harmonic current tests (shortly, constant-current tests) of a flexure-based Stirling cryocooler compressor prototype. It continues with a series of closed-loop RCT conducted on simplified versions of the prototype to understand the main cause of the friction problem. Since the simplified versions do not have a working actuator like the original prototype, RCT was implemented using an external excitation source. It is important to note that in almost all of its applications so far, the RCT method has been applied by using external modal shaker excitation [13,14,15,16]. Only in a recent study [17] was the applicability of the RCT in the case of base excitation tested for the first time, but a poor amplitude control performance around the resonance region was reported with the PI controller adopted. In the same study, the authors attempted to solve this control problem by combining phase control with amplitude control, which resulted in control instabilities in some cases. In this current study, RCT was applied using base excitation for two reasons: Firstly, a poor amplitude control performance and severe time variability in the nonlinear dynamics were observed due to the mechanical connection attaching the modal shaker to the compressor in the case of stinger-based excitation. Secondly, it was suspected that because this mechanical connection does not exist in reality and the assembly procedure, which is very effective on the alignment, is different from that of the original system, the nonlinear dynamics of the original system may significantly change. In this current study, the RCT method with base excitation was conducted with commercial hardware and software (Simcenter SCADAS Mobile and Simcenter TestLab), which gave very satisfactory results. Therefore, this study can be regarded as the first successful application of the RCT method in the case of base excitation, which is thought to be an important contribution.
Another important contribution of this current paper is the use of an indirect approach to experimentally extract quasi-linear constant-response frequency response functions (FRFs) as an alternative to direct measurement with conventional RCT. In this alternative approach, the key concept is the harmonic force surface (HFS) measured from open-loop constant-current sine tests. Quasi-linear FRFs are experimentally extracted by cutting the HFS with constant-response amplitude planes and are then processed by standard linear modal analysis techniques to extract the response-level-dependent modal parameters, i.e., the modal constant, natural frequency, and modal damping ratio. So far, the applicability of this approach has been demonstrated on weakly nonlinear systems: a stack-type piezo-actuator [18] and a benchmark beam with a bolted lap joint [19]. This paper goes a step further and shows the applicability of the method to an electromechanical system with very high and nonlinear damping, as discussed below. Furthermore, it is shown that the extrapolation of the HFS gives accurate results in the prediction of the nonlinear modal parameters at response levels where no experimental data are available.
In this study, the applicability of the HFS-based indirect approach mentioned above was demonstrated on the enhanced design of the Stirling cryocooler compressor prototype. The enhanced design was obtained by improving the fastener configuration as well as by increasing the radial stiffness of the flexure bearings in light of the response-controlled tests conducted on the simplified versions of the preliminary prototype mentioned above. Constant-current tests conducted on the enhanced design showed that the sticking/locking problem was solved; yet, unacceptably strong friction resulting in very high and nonlinear damping still exists. In the literature, the identification of high and nonlinear damping is still a challenging and active research field. Recently, three state-of-the-art techniques achieved significant success in this field: PLL, velocity feedback, and RCT. The PLL and velocity feedback approaches were successfully applied on a cantilever beam that exhibits very high and nonlinear hysteretic modal damping [20,21]. Similarly, the RCT method was recently extended in [14] to non-conservative systems with friction-induced strong nonlinear damping and was experimentally validated on the control fin actuation mechanism of a real missile. Coincidentally, in all three of these applications, hysteretic modal damping ratios of up to 30% could be identified, which was the highest value achieved so far in the literature, to the best knowledge of the authors. In this paper, the indirect approach based on the HFS concept and proposed as an alternative to the conventional RCT method raised the bar further and a nonlinear hysteretic modal damping ratio that goes up to 65% could be identified for the enhanced Stirling cryocooler design, which can be considered another important contribution.
Concluding this section, it is important to note that although the identification of high and nonlinear damping is very interesting and valuable, this level of damping is not acceptable for a reasonable cooler performance, and the enhanced design studied herein needs further design modifications to further decrease the friction and wear between the moving parts.
2. Methodology
2.1. Experiment-Based Design Procedure for Flexure-Based Stirling Cryocooler Compressors
As briefly discussed in the previous section, the design of Stirling cryocooler compressors requires preserving very small gaps in different regions, as shown in Figure 3, while avoiding contact, friction, and wear. According to the experience of the authors, this is a very challenging design objective that led to the development of an experiment-based design procedure supported by a state-of-the-art nonlinear experimental modal analysis method, namely, response-controlled testing (RCT) [13,14].
The flow chart of the design procedure is given in Figure 4. As seen from the figure, the procedure started with constant-amplitude harmonic current experiments conducted on the preliminary compressor prototype. As explained in the next section, a sticking/locking problem due to severe friction was observed at this stage. This problem essentially points out a friction-induced, strong mechanical nonlinearity. The characterization and identification of this type of nonlinearity is still a hot research topic in the structural dynamics community, and state-of-the-art techniques that can handle this issue are quite rare [14,20,21], as discussed in the Introduction. One of these techniques is RCT, invented by one of the authors of this paper, which became very popular in a very short period of time. Accordingly, RCT has become a key component of the design process described in Figure 4.
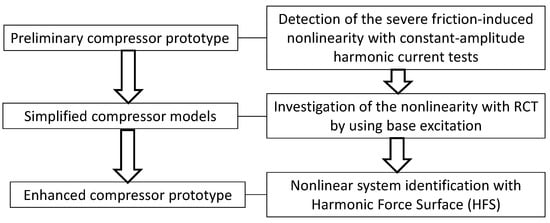
Figure 4.
Experiment-based design procedure for flexure-based Stirling cryocooler compressors.
According to Figure 4, in the second step of the design procedure, to better understand the root cause of the excessive friction and locking phenomena, a series of response-controlled tests at various constant-stoke (displacement) levels were conducted on 4 different simplified models (see Figure 8) of the compressor by using base excitation. Experimental results of these simplified models and conclusions drawn from them are discussed in detail in the Experiments Section (Section 3).
In light of the results and conclusions obtained from the simplified compressor models, the design of the preliminary compressor prototype was modified, which gave rise to the enhanced compressor design. The design modifications consist of increasing the radial stiffness of the flexure bearings and changing the fastener configuration of the flexure bearings to improve the alignment (see Section 3.3).
In the last step of the design procedure, constant-current sine tests conducted on the preliminary design were repeated with the enhanced compressor design by driving its linear actuator with constant-amplitude harmonic currents. In conclusion, the locking problem encountered in the preliminary design was eliminated. However, it was observed that the compressor still exhibited strong friction that caused very high and nonlinear damping. At this point, an indirect approach based on the harmonic force surface (HFS) concept was implemented as an alternative to the conventional RCT method for the nonlinear modal identification of the enhanced compressor design. Results indicated an excessive hysteretic modal damping ratio. It should be noted that this finding indicates that the enhanced design exhibits very high damping, which is still not acceptable for a reasonable cooler design, and a second design iteration is needed.
2.2. Implementation of the RCT Method with Base Excitation
Response-controlled stepped-sine testing (RCT) [13] is a novel nonlinear experimental modal analysis method proposed by Karaağaçlı and Özgüven in 2021. The method is based on the single nonlinear mode (SNM) theory [22], which postulates that the nonlinear modal parameters of an isolated mode depend on a single independent variable, the modal amplitude. Therefore, if the modal amplitude is kept constant throughout the stepped-sine testing around a resonance region of a nonlinear system, near-resonant constant-response FRFs come out in the quasi-linear form. The RCT method has shown, through many experiments [13,14,15,16], that the modal amplitude can be kept constant by keeping the displacement amplitude of a single reference point (usually the excitation point) constant in single-input stepped-sine testing with closed-loop control. A detailed explanation of the theoretical background and implementation of the RCT framework can be found in [13,14].
The most important contribution of the RCT method to the literature is to empirically validate the single independent variable hypothesis of the SNM theory by showing that nonlinear systems generally exhibit quasi-linear behavior when the modal amplitude is kept constant. In a very short period, the RCT method successfully accomplished the nonlinear modal identification of various mechanical systems by applying standard linear modal analysis techniques to measured quasi-linear constant-response FRFs: a T-beam with local cubic stiffness [13], a metal strip with continuously distributed (geometrical) nonlinearity [16], a cantilever beam with magnets [23], a bolted beam [24], a real missile [13], and a control fin actuation mechanism [14].
In all the above applications of the RCT method, systems were excited by using a stringer connected to an electrodynamic modal shaker. However, in some applications, excitation with a modal shaker may not be suitable. Accordingly, in a very recent study [17], RCT with base excitation was implemented on the so-called TRC benchmark system: a double-clamped thin metal plate with bolted connections. However, with the PI controller adopted, a reasonable amplitude control performance > 1 Hz away from resonance could not be achieved, which impeded the identification of the modal parameters from the measured FRF segments. In the same study, to solve the issue, it was proposed to conduct RCT for a fixed phase range around the resonance instead of a fixed frequency range. Besides solving the amplitude control problem, this elegant approach brings an important benefit: avoiding high excitation levels that are typically required far away from resonance and that may lead to the damage of the test structure, the shaker–structure interaction, and/or excessive heat generation causing the severe time variability in the nonlinear dynamics. However, these benefits came with a compromise: the simultaneous use of the phase and amplitude controllers led to instability problems for the test rig in some cases [17].
In this current study, response-controlled testing conducted on the simplified models of the cooler compressor (see Section 3.2) could not be achieved by using the compressor’s electrodynamic actuator because the simplified models included a mass equivalent version of the real actuator. Therefore, the integration of an external excitation source was necessary. Accordingly, preliminary response-controlled tests were conducted on the simplified models of the cooler compressor by mechanically attaching the stringer/force transducer assembly of a modal shaker to the flexure bearing/piston assembly. However, this approach was found to be inappropriate for two reasons: Firstly, a poor amplitude control performance and severe time variability in the nonlinear dynamics were observed in some cases due to the loosening of the mechanical connection attaching the piston/flexure bearing assembly to the shaker’s stinger/force transducer assembly. Secondly, it was assessed that because this mechanical connection does not exist in reality and the assembly procedure is different from that of the original system, the nonlinear dynamics of the original system may significantly change. Consequently, RCT with base excitation was necessarily implemented on the simplified models of the flexure-based cooler compressor instead of the conventional RCT with modal shaker excitation. Unlike the PI controller used in [17], in this study, the response amplitude control with base excitation was achieved by using commercial hardware and software (Simcenter SCADAS Mobile and Simcenter TestLab). The commercial controller showed a very satisfactory amplitude control performance far away from the resonance region, which made it possible to successfully identify the nonlinear model parameters of the simplified compressor models, draw conclusions, and improve the compressor design. Considering the poor amplitude control performance and control instabilities due to the dual amplitude/phase control strategy reported in [17], the compressor case studied herein can be considered the first successful implementation of the RCT method with base excitation, which is thought to be an important contribution. However, this should not lead the reader to the wrong conclusion that the controller used in this study is superior to the one used in [17], or vice versa, because both controllers were implemented on completely different systems.
2.3. Experimental Extraction of Quasi-Linear Constant-Response FRFs by Using the Harmonic Force Surface (HFS) Concept
In the conventional RCT-HFS framework [13,14,16,24], quasi-linear constant-response FRFs are directly measured by keeping the displacement amplitude of a reference point (usually the excitation point) constant in a closed-loop control. These constant-response FRFs measured at different response levels are then processed with standard linear modal analysis techniques (e.g., peak picking) to identify the response-level-dependent nonlinear modal parameters. Meanwhile, the HFS can be constructed by combining V-shaped harmonic force spectra measured by RCT at different constant-displacement amplitude levels. Constant-force FRFs (possibly including unstable branches) can then be extracted by cutting the HFS with constant-force planes. These FRFs can then be compared with the ones synthesized from the identified nonlinear modal parameters for assessing the accuracy of the RCT methodology.
It is important to note that the implementation of the HFS concept is not restricted to the standard RCT-HFS framework described above. Instead of combining V-shaped harmonic force spectra, the HFS can alternatively be constructed by using constant-force (or constant-voltage) frequency responses. Quasi-linear constant-response FRFs can then be extracted indirectly by cutting the HFS with constant-displacement amplitude planes instead of direct measurement. It should be noted that this alternative approach has an important limitation: it is restricted to nonlinear systems that do not exhibit unstable branches because constant-force testing cannot capture unstable regions due to the jump phenomenon. Recently, the applicability of this approach has been demonstrated on two different systems: a stack-type piezo-actuator [18] and a benchmark beam with a bolted lap joint [19].
In Ref. [18], an HFS was constructed by using open-loop constant-amplitude harmonic voltage tests. Quasi-linear FRFs between the input voltage (proportional to the excitation force) and the output response of the actuator were then obtained by cutting the HFS with constant-response planes. Finally, these quasi-linear FRFs were processed to identify the response-level-dependent nonlinear modal parameters. Similarly, in Ref. [19], the HFS was obtained by conducting constant-force sine tests with a feedback (closed-loop) control.
The common point of the systems studied in Refs. [18,19] is that they exhibit weak stiffness and damping nonlinearities. An important contribution of this current paper is that the applicability of the HFS-based indirect approach to extract quasi-linear FRFs is demonstrated on a flexure-based Stirling cryocooler compressor that exhibits very strong nonlinear damping due to friction. In Section 3.3, we describe a series of open-loop constant-current tests that were conducted by driving the electrodynamic actuator of the compressor with a constant-amplitude harmonic current. Frequency responses corresponding to different constant-current levels were then merged to construct the HFS. It should be noted that although the constructed surface is essentially a harmonic current surface, in this paper, the surface is still referred to as an HFS for convenience. This is reasonable because in Stirling cryocooler actuators, the input current is nearly proportional to the excitation force. Finally, processing of the quasi-linear FRFs extracted from the HFS revealed a severe hysteretic modal damping ratio. Concluding this section, it is important to note that the limitation that restricts the indirect method to nonlinear systems not exhibiting unstable branches still applies. Fortunately, despite the strong nonlinear damping, constant-current frequency responses of the cooler compressor do not exhibit unstable regions.
3. Experiments
3.1. Constant-Current Sine Tests on Preliminary Compressor Prototype
The experimental design procedure proposed in this paper for flexure-based Stirling cryocooler compressors starts with a series of open-loop constant-amplitude harmonic current tests conducted on a preliminary compressor design. The schematic view of the preliminary design is shown in Figure 3. The piston/magnet holder assembly is supported by flexure bearings. The axial harmonic motion of this assembly is achieved by the stator that drives the magnets in the magnet holder. This type of design is called a Stirling cryocooler with moving magnets. The stator and the cylinder component (shown in blue in Figure 3) are fixed to the chassis of the compressor; i.e., they do not move. As can be seen from the figure, there exist very small gaps in three different regions: between the cylinder and the piston (C1), between the magnet holder and the cylinder (C2), and between the stator and the magnet holder (C3). These gaps should be kept small in order to minimize the working gas leakage to the backside of the piston, which reduces pressure fluctuations and improves the cooling performance.
The constant-current sine test setup is shown in Figure 5. The harmonic current driving the actuator was generated by a Brushless PWM Servo Amplifier (Camarillo, CA, USA). The response of the piston was measured by an Eltrotec Inc. Series LDS 70/10 laser displacement sensor (Padasjoki, Finland)at a sampling rate of 1000 Hz.
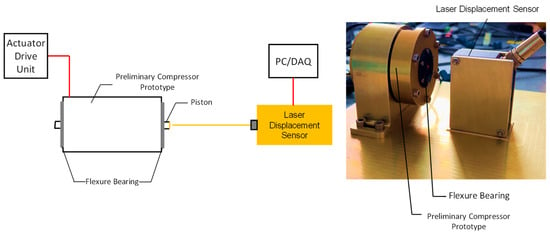
Figure 5.
Experimental setup for preliminary compressor prototype.
Constant-current tests conducted on the preliminary compressor prototype revealed a severe instability issue: the piston/magnet holder assembly, which was expected to oscillate, steadily stopped all of a sudden during the tests though the current was not cut off. This issue is illustrated at the excitation amplitude level of 1 A at 40 and 50 Hz in Figure 6, where the harmonic displacement response of the piston suddenly drops to zero. The problem seems to be caused by the piston/magnet holder assembly being pulled into the cylinder/stator assembly and sticking. The pulling effect probably stems from the nonzero net radial magnetic force caused by the non-uniformity of the small gaps (i.e., misalignment) described above. The net magnetic force should be ideally balanced by the radial stiffness of the flexure bearings, which does not seem to be the case in this study.
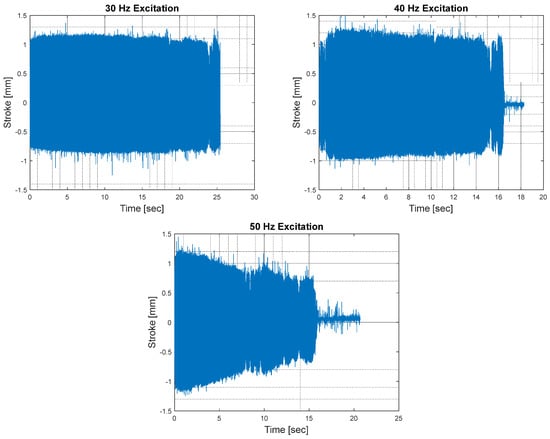
Figure 6.
Harmonic responses of the piston measured during constant-current sine tests of the preliminary compressor prototype conducted at 1 A amplitude level and different excitation frequencies.
Considering Figure 6, it is interesting to note that although the instability issue discussed above does not exist at 30 Hz, it becomes a serious problem at higher frequencies (i.e., 40 and 50 Hz). This is reasonable because the radial stiffness of a flexure bearing, shown in Figure 3b, is typically very sensitive to its vibration amplitude, as shown in [25], and there is an inverse correlation between the vibration amplitude and the radial stiffness. In this context, as the excitation frequency nears the resonance frequency of the single-DOF oscillator, which is around 59 Hz, the piston’s displacement amplitude gradually increases. This significantly reduces the radial stiffness of the bearing. Consequently, it cannot balance the net radial magnetic force caused by misalignment anymore and leads to the sticking/locking phenomenon, as discussed above.
Another interesting observation relevant to the preliminary compressor prototype is the considerable friction-induced wear at the inner face of the magnet holder observed after the disassembly of the prototype, as shown in Figure 7. This finding points out the occurrence of severe friction between the magnet holder and the cylinder (see Figure 3) during the motion of the piston/magnet holder assembly before the sticking/locking phenomenon.

Figure 7.
Considerable wear at the inner face of the magnet holder due to friction between the magnet holder and the cylinder.
3.2. Response-Controlled Tests with Base Excitation on Simplified Compressor Models
In order to find the root cause of the instability and excessive wear discussed in the previous section, a series of constant-response tests were conducted on four different simplified models of the preliminary compressor design illustrated in Figure 8. As can be seen from the figure, the simplified models range from System A to System D with gradually increasing complexity.
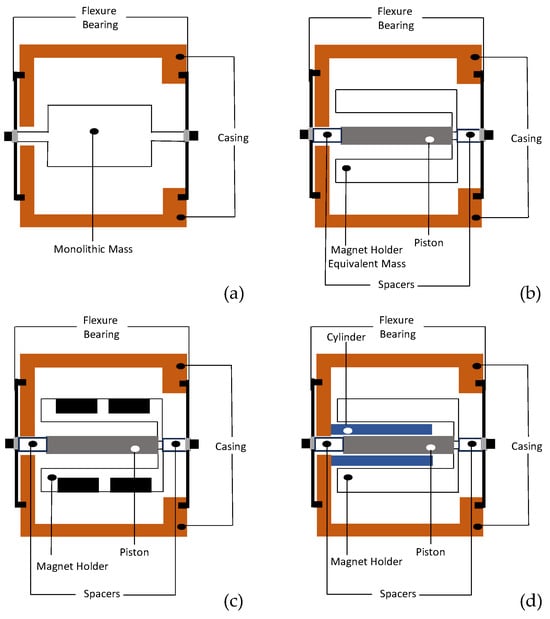
Figure 8.
Simplified models of the preliminary compressor prototype: (a) System A; (b) System B; (c) System C; (d) System D.
System A consists of a monolithic mass whose inertia is equivalent to that of the magnet holder and piston assembly. The purpose of this simplified model is to study the degree of nonlinearities exhibited by the stiffness of the flexure bearing and the screw connections. System B includes the original piston, the spacers, and the mass equivalent of the magnet holder/magnet assembly. This system is dedicated to determining the effect of holding multiple parts together mechanically on the nonlinear dynamics. On the other side, System C contains real magnets, which aims to study the effect of magnetic forces on the system dynamics. Finally, System D includes the original cylinder, the original piston, and the mass equivalent version of the magnet holder to study purely the effects of the misalignment on the system dynamics, excluding the contribution of magnetic effects.
As seen in Figure 8, the simplified models do not possess an active actuator. Therefore, RCT was necessarily implemented with an external excitation source. Furthermore, since an electrodynamic modal shaker attachment was found to be inappropriate, as explained in detail in Section 2.2, tests were conducted with base excitation, as illustrated in Figure 9. As seen from the figure, closed-loop amplitude control was achieved by using Simcenter SADAS Mobile and Simcenter TestLab. (Munich, Germany) A DynaLabs Inc. shaker (DYN-PM-400) (Ankara, Turkey) was used for base excitation.
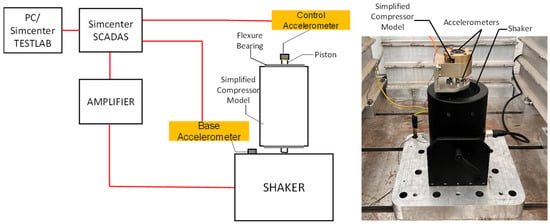
Figure 9.
Response-controlled testing with base excitation.
It is also important to note that since the vertical positioning of the laser displacement sensor was difficult, a miniature accelerometer (PCB 352A73) attached to the piston was used as the control sensor. The slight shift in the resonance frequency due to the additional mass of this accelerometer was tolerable because it did not affect the main purpose of this study. In this configuration, the displacement amplitude is kept constant indirectly by defining an appropriate reference acceleration profile for the controller. The reference accelerometer (PCB 352A73) corresponding to the base DOF is attached to the fixture connecting the compressor to the shaker, as shown in Figure 9.
The response-controlled stepped-sine tests were conducted with a fixed frequency range (58.5–61 Hz) and a frequency step size of 0.125 Hz. The quasi-linear FRFs measured at different amplitude levels ranging from 0.5 mm to 3.75 mm for the simplified models, A, B, and C, are shown in Figure 10. These quasi-linear FRFs were then processed by using a standard linear experimental modal analysis technique, namely, the peak-picking method [13], to extract the natural frequencies and modal damping ratios.
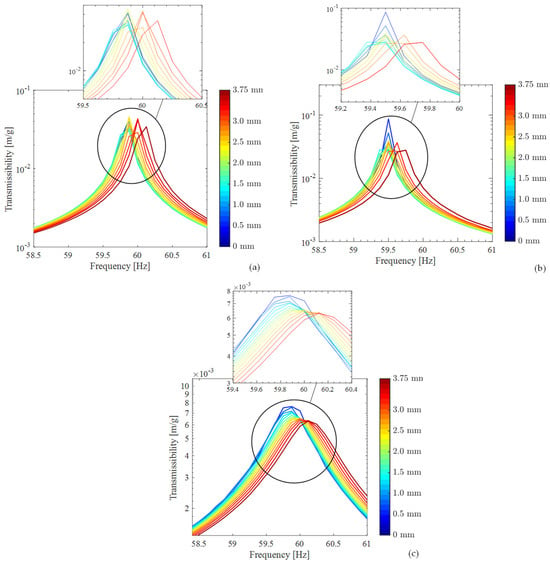
Figure 10.
Quasi-linear FRFs measured by response-controlled testing with base excitation: (a) System A; (b) System B; (c) System C.
The response-level-dependent nonlinear modal parameters identified by using the peak-picking method for Systems A, B, and C are given in Figure 11, with the 95% confidence intervals obtained by repeating the tests three times. The first important conclusion that can be drawn from the figure is that the repeatability is good, and the simplified models exhibit weak stiffness and damping nonlinearities in general. The slight increase in the natural frequencies with the increasing response amplitude results from the weak, stiffening nonlinearity of the flexure bearings in the axial direction. In contrast, the modal damping ratio curves of Systems A and B are almost constant. In other words, these systems exhibit insignificant damping nonlinearities. The slightly lower natural frequency of System B stems from the slightly higher inertia values due to the exceeded manufacturing tolerances.
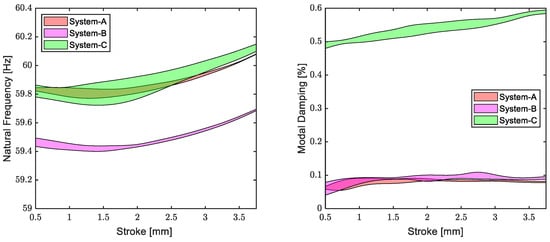
Figure 11.
Natural frequencies and viscous modal damping ratios identified from measured quasi-linear FRFs of simplified compressor models.
Although the mechanical connections of System C are identical to those of System A and B, its modal damping ratio significantly deviates from those of Systems A and B both in the magnitude and degree of nonlinearity. This can be attributed to the magnetic field generated by the magnets included in System C. It can be concluded that the magnetic field significantly increases both the magnitude and the nonlinearity of the modal damping ratio.
Finally, in order to study the effects of the misalignment on the system dynamics, excluding the contribution of magnetic effects, RCT with base excitation was conducted on System D shown in Figure 8d. However, a very poor amplitude control performance was observed due to the excessive friction between the components, and the quasi-linear FRFs could not be measured reliably. This finding is a clear indication of poor alignment.
In light of the results discussed above, the design of the flexure bearings was modified as illustrated in Figure 12 and Figure 14b. In this enhanced design, instead of directly attaching the flexure bearings to the piston with a single-screw connection, they are attached to the magnet holder with three screws.
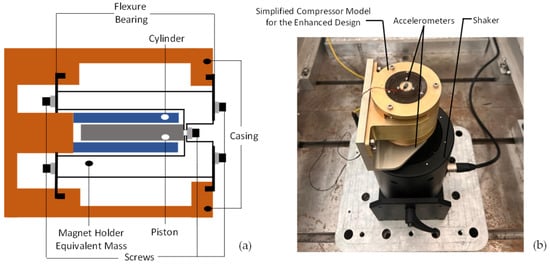
Figure 12.
A simplified model corresponding to the enhanced compressor design: (a) schematic view; (b) response-controlled test configuration.
Fortunately, response-controlled tests with base excitation conducted on the enhanced design shown in Figure 12 gave very satisfactory results. Precise amplitude control could be achieved. The modal parameters identified for the enhanced design are given in Figure 13. The results are very similar to those obtained for Systems A and B. The modal damping ratio is very low, and the system exhibits very weak stiffness and damping nonlinearity, which is the ideal case that maximizes the mechanical efficiency and minimizes the energy loss for an acceptable cryocooler performance. It can be concluded that the design modifications provided precise alignment and eliminated contact and friction between the magnet holder, cylinder, and piston, despite the small gaps shown in Figure 12.
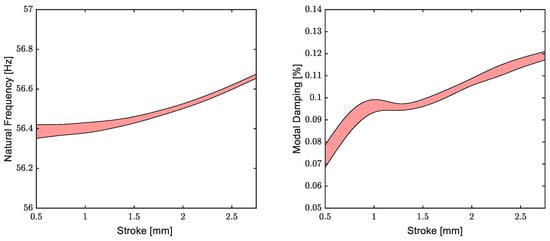
Figure 13.
Natural frequency and viscous modal damping ratio obtained from quasi-linear FRFs of simplified model corresponding to the enhanced compressor design.
3.3. Nonlinear Experimental Modal Analysis of the Enhanced Compressor Design with the Harmonic Force Surface (HFS) Concept
As demonstrated in the previous section, the new flexure-bearing design shown in Figure 14b significantly improved the alignment of the components in the absence of electromagnetic forces. In order to test the performance of this new design in the actual compressor, an enhanced compressor prototype, whose schematic is shown in Figure 14a, was manufactured. In this new prototype, apart from the modification of the fastener configuration, the second important modification is the increase in the radial stiffness of the flexure bearings by increasing their thicknesses. As discussed in Section 3.1, radial stiffness plays a key role in balancing the net magnetic forces caused by the misalignment of the components. Therefore, this second modification aims to avoid the pulling and sticking of the piston/magnet holder assembly to the cylinder/stator assembly, contrary to the preliminary compressor design (see Section 3.1).
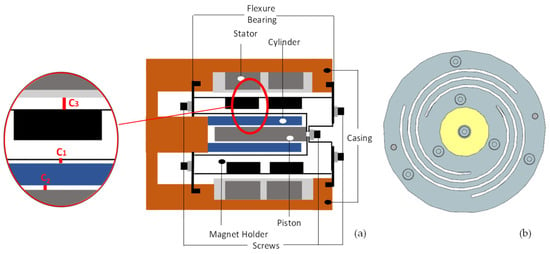
Figure 14.
(a) Schematic view of the enhanced compressor design; (b) enhanced flexure bearing design.
In order to test the performance of the enhanced design, an experimental setup, which is very similar to that of the preliminary compressor prototype (Figure 5), was constructed, as shown in Figure 15. Then, a series of open-loop constant-current tests were conducted at harmonic current amplitude levels ranging from 0.3 A to 2.5 A within a frequency range of 10–80 Hz. Frequency response curves measured from these tests are shown in Figure 16a. In this application, the sticking/locking phenomenon was not observed, contrary to the preliminary design. At this stage, it can be concluded that the design modifications mentioned above proved to be quite effective. However, there is still one critical question: Are the mechanical losses at an acceptable level for a reasonable compressor performance? The answer to this question requires the identification of the system’s dynamical properties, especially its damping.

Figure 15.
Experimental setup for the enhanced compressor design.
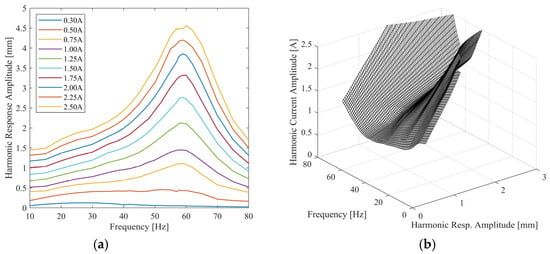
Figure 16.
(a) Frequency response curves measured from constant-current tests; (b) HFS constructed from measured frequency response curves.
Post-processing of the frequency responses given in Figure 16a indicated that linear analytical models do not accurately represent the system dynamics, especially at low current levels. In this context, response-controlled testing looks suitable for the modal analysis of the enhanced compressor prototype. As explained in Section 2.3, in the conventional RCT framework, quasi-linear constant-response FRFs are directly measured by keeping the displacement amplitude of a reference point constant in a closed-loop control. These FRFs can then be processed by using standard linear modal analysis techniques to identify the response-level-dependent nonlinear modal parameters. In such a framework, the driving current spectrum takes the form of a V-shape curve that makes a dip at the resonance frequency. In other words, the actuator draws the minimum current (and therefore power) at resonance, which makes sense.
In this application, the conventional RCT method was not preferred for several reasons. Firstly, closed-loop control may be invasive in some cases; i.e., it may affect the actual system dynamics. However, open-loop testing is non-invasive by nature because the system response is not forced to match a reference profile. Secondly, RCT may require excessive current to keep the displacement amplitude constant at frequencies far away from resonance, especially if the system exhibits excessive friction-induced damping. This may lead to the damage of the actuator and/or excessive heat generation causing the severe time variability in the nonlinear dynamics [17]. Finally, the frequency responses shown in Figure 16a do not exhibit the jump phenomenon, which makes them very suitable for extracting quasi-linear FRFs by using the HFS-based indirect approach explained in Section 2.3.
In light of the above discussion, first of all, the constant-current frequency response curves shown in Figure 16a were combined to construct the HFS, as shown in Figure 16b. Cutting the HFS with different constant-displacement amplitude planes gave V-shaped harmonic current spectra. Finally, by dividing each constant-displacement amplitude value with the corresponding V-shaped harmonic current spectrum, quasi-linear constant-response FRFs were obtained, as illustrated in Figure 17.
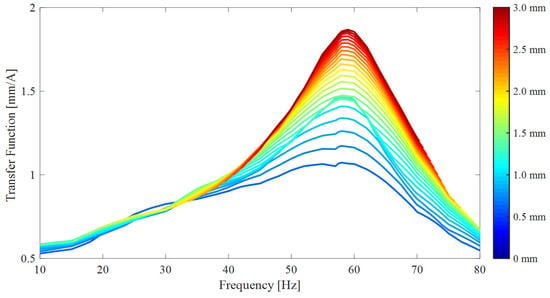
Figure 17.
Constant-response FRFs extracted by cutting the HFS with constant-displacement amplitude planes.
According to the single nonlinear mode theory [13], near-resonant FRFs between the driving current amplitude and the displacement amplitude of the control DOF of the enhanced compressor prototype can be represented analytically as follows:
where , , and are the modal constant, natural frequency, and hysteretic modal damping ratio of the th nonlinear mode, respectively. indicates the response coordinate, is the displacement amplitude of the response coordinate (control DOF), and represents the excitation frequency.
Equation (1) indicates that all modal parameters are functions of a single independent variable: the displacement amplitude. Therefore, if the displacement amplitude is kept constant throughout the frequency sweep, FRFs come out in the quasi-linear form. In this context, the nonlinear modal identification of the enhanced compressor design is achieved by fitting the analytical model given in Equation (1) to the quasi-linear FRFs shown in Figure 17. In this study, at each constant-response level, nonlinear modal parameters are identified by using the simple peak-picking method [13]. The identified modal parameters are illustrated in Figure 18 and Figure 19.
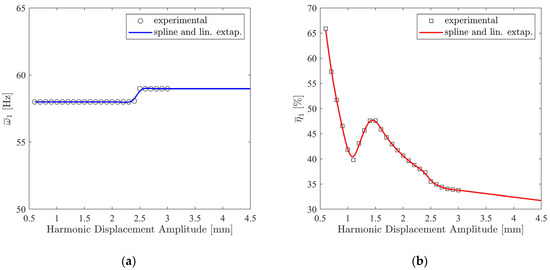
Figure 18.
Variation in the nonlinear modal parameters of the enhanced compressor prototype with respect to the response level: (a) natural frequency; (b) modal damping ratio.
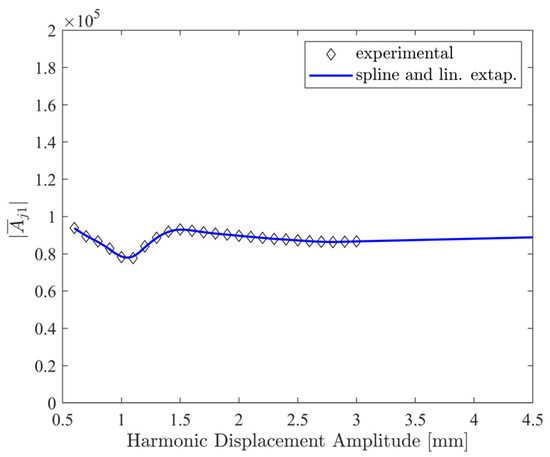
Figure 19.
Variation in the modal constant of the enhanced compressor prototype with respect to the response level.
The most important conclusion that can be drawn from Figure 18 is that the enhanced compressor prototype exhibits extremely high and nonlinear damping that goes up to 65%. However, the system exhibits very weak stiffness nonlinearity.
In order to validate the accuracy of the identified nonlinear modal parameters, constant-current FRFs were synthesized by iteratively solving Equation (1) with the Newton–Raphson method and the arc-length continuation algorithm. Then, the synthesized FRFs were compared with the directly measured FRFs in Figure 20.
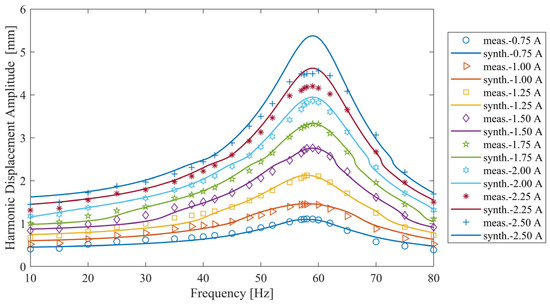
Figure 20.
Comparison of the constant-current frequency response curves synthesized by using the identified nonlinear modal parameters with the ones directly measured by constant-current sine tests.
Figure 20 shows that the match between the synthesized and measured frequency response curves is very satisfactory up to and including the 1.75 A level. At the current level of 2 A and above, the match is not good, especially near the resonance peaks. A careful investigation of Figure 17 and Figure 18 makes the reason behind this discrepancy clear. In Figure 17, the constant-response FRFs are plotted only up to the 3 mm response level because cutting the HFS at higher levels captures only a small portion of the FRFs, which does not include half-power points and impedes the modal analysis. Accordingly, the nonlinear modal parameters could only be identified up to the 3 mm level, as illustrated in Figure 18 and Figure 19. However, Figure 20 indicates that the constant-current frequency response curves at and above the 2 A current level go above 3 mm near resonance, and therefore their synthesis requires extrapolation, as shown in Figure 18 and Figure 19. In this first attempt, the synthesis was based on the linear extrapolation of the nonlinear modal parameters, which did not give satisfactory results.
In order to increase the accuracy of the nonlinear modal model, another approach is proposed herein. In this approach, the first step is the linear extrapolation of the HFS itself, as shown in Figure 21, instead of the direct extrapolation of the identified nonlinear modal parameters. The extrapolated part is shown in the red color in Figure 21. This makes it possible to extract quasi-linear FRFs at higher response levels up to 4.5 mm, including half-power points, which are the highest response levels reached in Figure 20. Variations in the nonlinear modal parameters identified from the extrapolated HFS are shown in Figure 22 and Figure 23. In these figures, modal parameters identified from the extrapolated HFS and corresponding to response amplitude levels above 3 mm are indicated with the red star markers. A comparison of Figure 22 with Figure 18 indicates that the modal damping ratios predicted by the proposed approach for amplitude levels above 3 mm considerably deviate from those predicted by the direct linear extrapolation. As seen in Figure 18, the direct linear extrapolation predicted a damping ratio monotonically decreasing from 34% to 32%. However, according to Figure 22, the damping ratio remains constant around 34% up to the 4 mm amplitude level, and it slightly increases up to 37% around the 4.5 mm amplitude level.
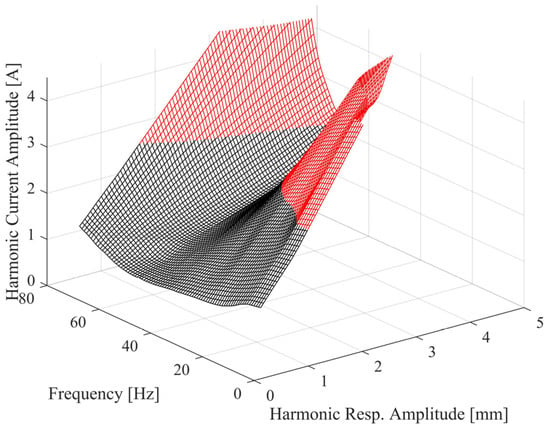
Figure 21.
Extrapolated HFS.
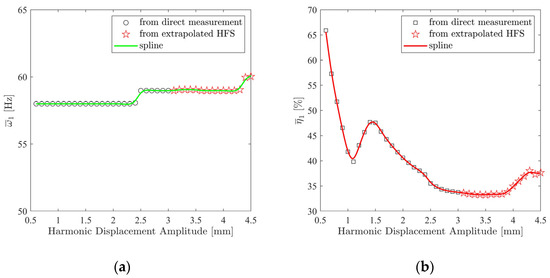
Figure 22.
Variation in the nonlinear modal parameters obtained from the extrapolated HFS: (a) natural frequency; (b) modal damping ratio.
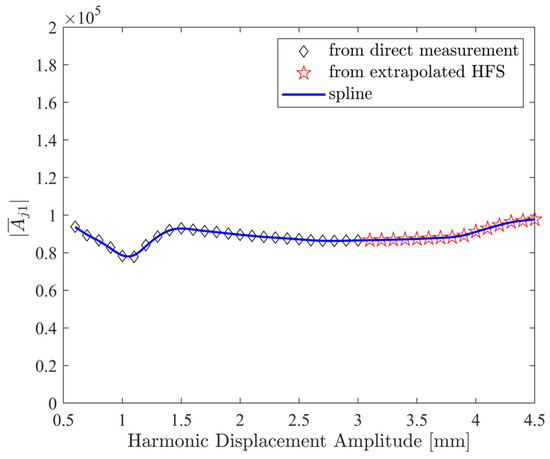
Figure 23.
Variation in the modal constant obtained from the extrapolated HFS.
Finally, the accuracy of the extrapolated-HFS approach was validated by comparing the synthesized FRFs with the directly measured FRFs in Figure 24. The synthesized FRFs in the figure were obtained by inserting the identified nonlinear modal parameters shown in Figure 22 and Figure 23 into Equation (1) and iteratively solving it with the Newton–Raphson scheme and arc-length continuation algorithm at different constant-amplitude current levels. Surprisingly, an excellent match was achieved between the synthesized and measured FRFs at all the current levels. Comparing Figure 20 and Figure 24, it can be concluded that the nonlinear modal parameters (Figure 22 and Figure 23) identified from the extrapolated-HFS approach predicted constant-current frequency response functions much more accurately than the nonlinear modal parameters (Figure 18 and Figure 19) estimated by the direct linear extrapolation at ampere levels of 2.0 A and above, where the response amplitude exceeded the 3 mm amplitude level. Consequently, the proposed extrapolation scheme can be regarded as a valuable contribution to the literature.
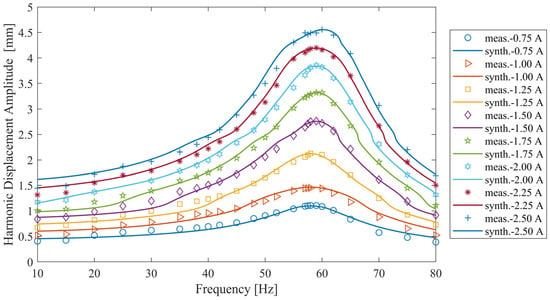
Figure 24.
Comparison of the constant-current frequency response curves synthesized by using the nonlinear modal parameters identified from the extrapolated HFS with the ones directly measured by constant-current sine tests.
4. Conclusions
Stirling cryocoolers play a key role in achieving the cryogenic temperatures required in aerospace, defense, and medical applications. Flexure-based linear compressors form the cornerstone of modern Stirling cryocooler designs due to their efficiency and reliability. Flexure bearings enable frictionless operation through elastic deformation, significantly reducing wear while enhancing system reliability.
Despite the rich literature addressing the design and optimization of flexure bearings, no studies address the serious challenges posed by flexure-based Stirling cryocoolers, such as alignment sensitivities and nonlinear dynamic responses that can adversely affect the overall reliability and performance. According to the authors’ experience, achieving a precise alignment that preserves small gaps between the components and avoids severe friction and wear is the most challenging problem in the design process of flexure-based Stirling cryocoolers.
The main contribution of this paper is the proposal of an experiment-based Stirling cryocooler compressor design procedure based on a recently developed nonlinear experimental modal analysis method, namely, response-controlled stepped-sine testing (RCT). This procedure gives valuable insights for designing cryocooler compressors, with implications for aerospace, defense, and medical applications. The alignment in a compressor prototype has been significantly improved in light of a series of response-controlled tests with base excitation. The applicability of RCT with base excitation was tested for the first time in a recent study, but a poor amplitude control performance was reported. This current study is seemingly the first successful implementation of RCT with base excitation, which can be regarded as a humble contribution that broadens the applicability of the RCT approach to nonlinear mechanical systems wherein excitation with a modal shaker may not be practically suitable, for example, due to shaker–structure interaction or geometrical constraints.
The performance of the design improved in light of RCT with base excitation was tested with a series of constant-current tests. These tests showed that the sticking/locking phenomenon observed in the preliminary design was eliminated. However, this outcome was not sufficient to finalize the design. An acceptable design requires the minimization of mechanical losses for a reasonable compressor performance. In order to assess this feature, an indirect harmonic force surface (HFS)-based approach proposed for weakly nonlinear systems was extended to identify the high and nonlinear damping (up to a 65% hysteretic modal damping ratio) due to the friction of the enhanced compressor design. Furthermore, it was shown that the extrapolation of the HFS gives accurate results in the prediction of nonlinear modal parameters at response levels where no experimental data are available.
As previously discussed in this paper, the identification of high and nonlinear damping is still a challenging and active research field, and most of the state-of-the-art nonlinear system identification techniques lack this capability. In this context, the extension of the indirect HFS-based approach for the modal identification of mechanical systems with friction-induced high and nonlinear damping, as mentioned above, can be regarded as an important contribution to the field of nonlinear system identification.
Although the identification of high and nonlinear damping is very interesting and valuable, this level of damping is not acceptable for a reasonable cooler performance, and it was concluded that the enhanced design studied herein needs further design modifications to further decrease the friction and wear between the moving parts. An acceptable modal damping of the compressor (without working gas) would be on the order of magnitude shown in Figure 11 and Figure 13 (i.e., less than 1%). This level of damping can only be achieved by completely avoiding contact and friction between the components of the compressor moving against each other and strictly preserving small gaps. Design modifications such as increasing the radial stiffness of the flexure bearings by simply increasing their thicknesses and/or optimizing the size of small gaps among the components can be further investigated to achieve the target level of damping.
Author Contributions
Conceptualization, S.G.Ç. and T.K.; methodology, S.G.Ç. and T.K.; software, S.G.Ç. and T.K.; validation, S.G.Ç. and T.K.; formal analysis, S.G.Ç. and T.K.; investigation, S.G.Ç.; resources, S.G.Ç.; data curation, S.G.Ç.; writing—original draft preparation, S.G.Ç. and T.K.; writing—review and editing, T.K.; visualization, S.G.Ç. and T.K.; supervision, A.H.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is unavailable due to confidentiality issues.
Acknowledgments
The provision of TÜBİTAK SAGE for modal testing and analysis capabilities is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Marquardt, E.; Radebaugh, R. Design Equations and Scaling Laws for Linear Compressors with Flexure Springs. Cryogenics 1992, 32, 783–804. [Google Scholar]
- Radebaugh, R. Cryocoolers: The state of the art and recent developments. J. Phys. Condens. Matter 2009, 21, 164219. [Google Scholar] [CrossRef]
- Walker, G. Cryocoolers: Part 1: Fundamentals; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Veprik, A.; Zechtzer, S.; Pundak, N. Split Stirling linear cryogenic cooler for a new generation of high-temperature infrared imagers. In Infrared Technology and Applications XXXVI; SPIE: Bellingham, WA, USA, 2010; pp. 810–822. [Google Scholar]
- Liang, K.; Dadd, M.; Bailey, P. Clearance seal compressors with linear motor drives. Part 1: Background and system analysis. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 242–251. [Google Scholar] [CrossRef]
- Meijers, M.; Benschop, A.A.J.; Mulli, P.C. Flexure Bearing Cryocoolers at Thales Cryogenics. AIP Conf. Proc. 2002, 613, 699–706. [Google Scholar]
- Benschop, T.; Mullié, J.; Bruins, P.; Martin, J.Y. Development of a 6W High-Reliability Cryogenic Cooler at Thales Crypgenics. In Infrared Technology and Applications XXVIII; SPIE: Bellingham, WA, USA, 2003; Volume 4850, pp. 144–154. [Google Scholar]
- Amoedo, S.; Thebaud, E.; Gschwendtner, M.; White, D. Novel parameter-based flexure bearing design method. Cryogenics 2016, 76, 1–9. [Google Scholar] [CrossRef]
- Simcock, C.J. Investigation of Materials for Long-Life, High-Reliability Flexure Bearing Springs for Stirling Cryocooler Applications. Cryocoolers 2007, 47, 335–343. [Google Scholar]
- Ross Jr, R.G.; Johnson, D.L.; Mon, G.R.; Smedley, G. Cryocooler resonance characterization. Cryogenics 1994, 34, 435–442. [Google Scholar] [CrossRef]
- Heun, M.K.; Collins, S.A.; Johnson, D.L.; Ross, R.G., Jr. Investigation of gas effects on cryocooler resonance characteristics. In Cryocoolers 9; Springer: Boston, MA, USA, 1997; pp. 421–430. [Google Scholar]
- Yuan, S.W.K.; Naes, L.G.; Nast, T.C. Prediction of natural frequency of the NASA 80 K cooler by the Stirling refrigerator performance model. Cryogenics 1994, 34, 383–388. [Google Scholar] [CrossRef]
- Karaağaçlı, T.; Özgüven, H.N. Experimental modal analysis of nonlinear systems by using response-controlled stepped sine testing. Mech. Syst. Signal Process. 2021, 146, 107023. [Google Scholar] [CrossRef]
- Karaağaçlı, T.; Çelik, F.K. Modal analysis of non-conservative systems with friction-induced strong nonlinear damping by using response-controlled testing. Mech. Syst. Signal Process. 2024, 221, 111718. [Google Scholar] [CrossRef]
- Karaağaçlı, T.; Özgüven, H.N. Experimental modal analysis of structures with high nonlinear damping by using response-controlled stepped-sine testing. In Proceedings of the 41st International Modal Analysis Conference (IMAC), Austin, TX, USA, 13–16 February 2023. [Google Scholar]
- Karaağaçlı, T.; Özgüven, H.N. Experimental quantification and validation of modal properties of geometrically nonlinear structures by using response-controlled stepped-sine testing. Exp. Mech. 2022, 62, 199–211. [Google Scholar] [CrossRef]
- Bhattu, A.; Hermann, S.; Jamia, N.; Müller, F.; Scheel, M.; Schwingshackl, C.; Özgüven, H.N.; Krack, M. Experimental analysis of the TRC benchmark system. J. Struct. Dyn. 2024, 26–45, Special issue on Tribomechadynamics. [Google Scholar] [CrossRef]
- Koyuncu, A.; Karaağaçlı, T.; Şahin, M.; Özgüven, H.N. Experimental modal analysis of nonlinear amplified piezoelectric actuators by using response-controlled stepped-sine testing. Exp. Mech. 2022, 62, 1579–1594. [Google Scholar] [CrossRef]
- Gürbüz, M.F.; Karaağaçlı, T.; Özer, M.B.; Özgüven, H.N. Bypassing the repeatability issue in nonlinear experimental modal analysis of jointed structures by using the RCT-HFS framework. In Proceedings of the 41st International Modal Analysis Conference (IMAC), Austin, TX, USA, 13–16 February 2023. [Google Scholar]
- Scheele, M.; Weigele, T.; Krack, M. Challenging an experimental nonlinear modal analysis method with a new strongly friction-damped structure. J. Sound Vib. 2020, 485, 115580. [Google Scholar] [CrossRef]
- Scheel, M. Nonlinear modal testing of damped structures: Velocity feedback vs. phase resonance. Mech. Syst. Signal Process. 2022, 165, 108305. [Google Scholar] [CrossRef]
- Szemplinska-Stupnicka, W. The modified single mode method in the investigations of the resonant vibrations of nonlinear systems. J. Sound Vib. 1979, 63, 475–489. [Google Scholar] [CrossRef]
- Bahari, A.R.; Yunus, M.A.; Abdul Rani, M.N.; Yahya, Z.; Rahim, M.A. Reliability of response-controlled stepped sine testing for experimental detection of nonlinear structure. Int. J. Automot. Mech. Eng. 2023, 20, 1618–1625. [Google Scholar]
- Khairul, K.A.; Bahari, A.R.; Abdul Rani, M.N.; Konstaeos, R.; Andreas, K. Identification of nonlinearity in bolted beam using response-controlled testing and force-controlled testing. J. Mech. Eng. 2024, 13, 177–197. [Google Scholar]
- Gaunekar, A.S.; Göddenhenrich, T.; Heiden, C. Finite element analysis and testing of flexure bearing element. Cryogenics 1996, 36, 359–364. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).