Railway Bridge Runability Safety Analysis in a Vessel Collision Event
Abstract
1. Introduction
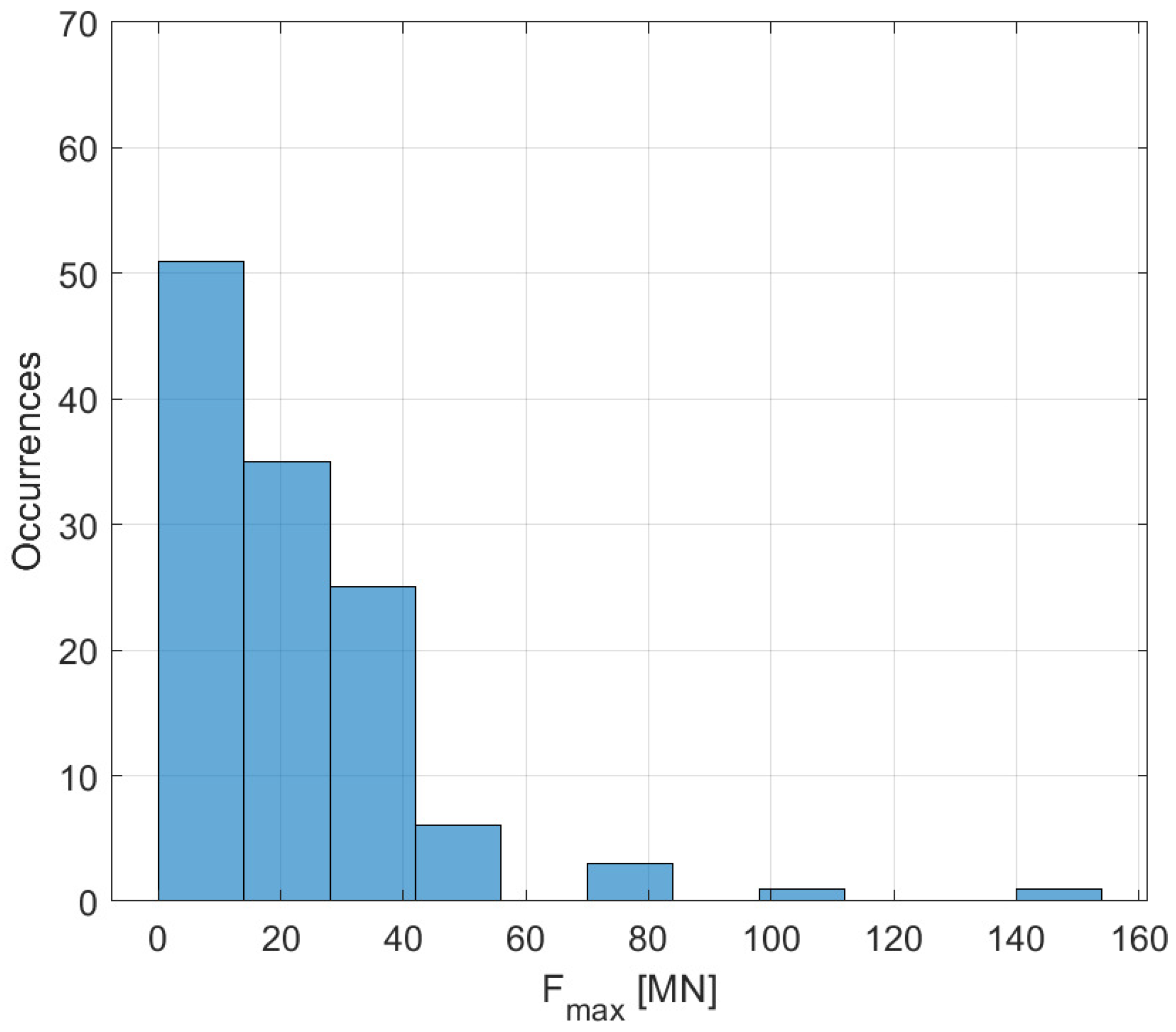
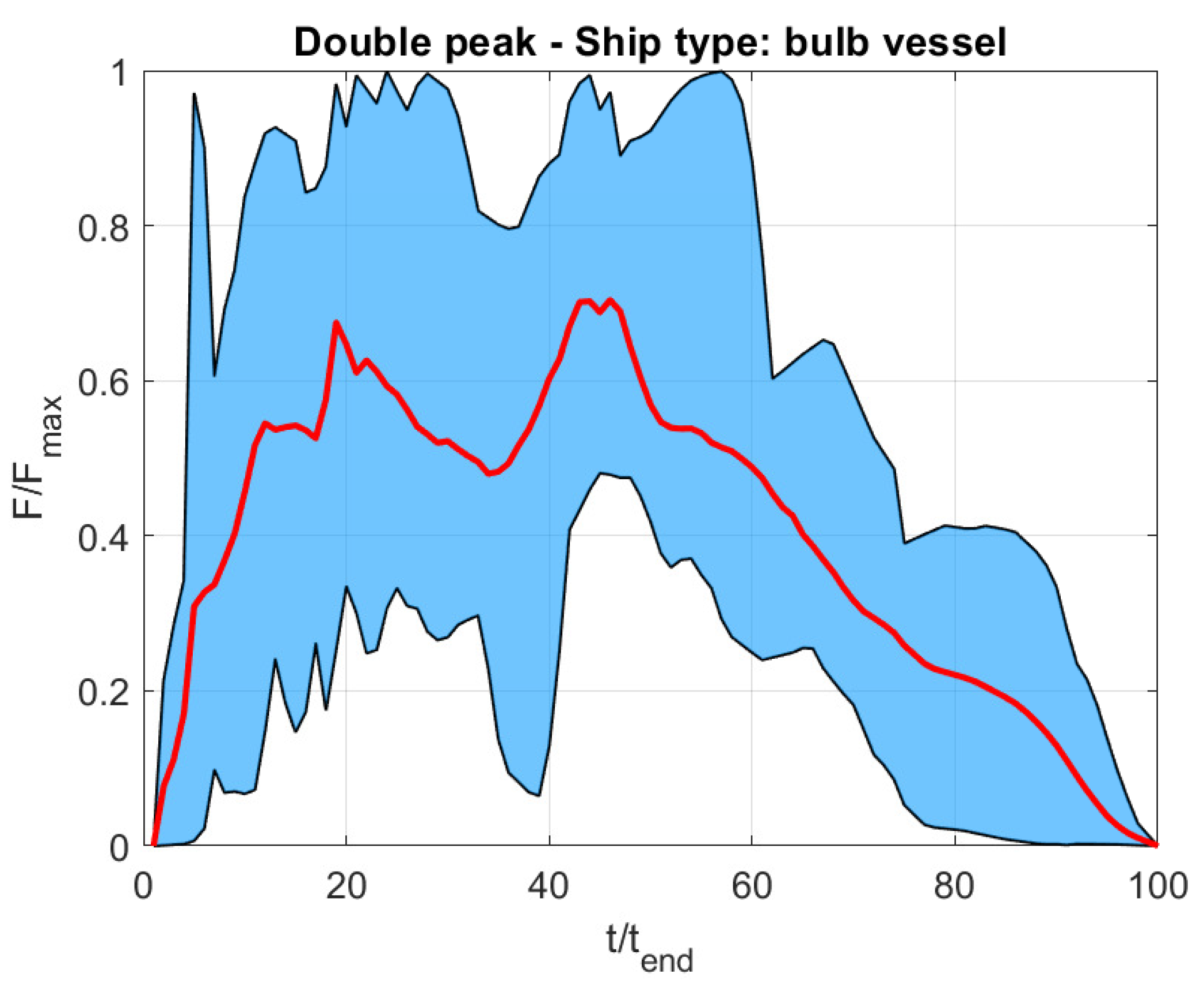
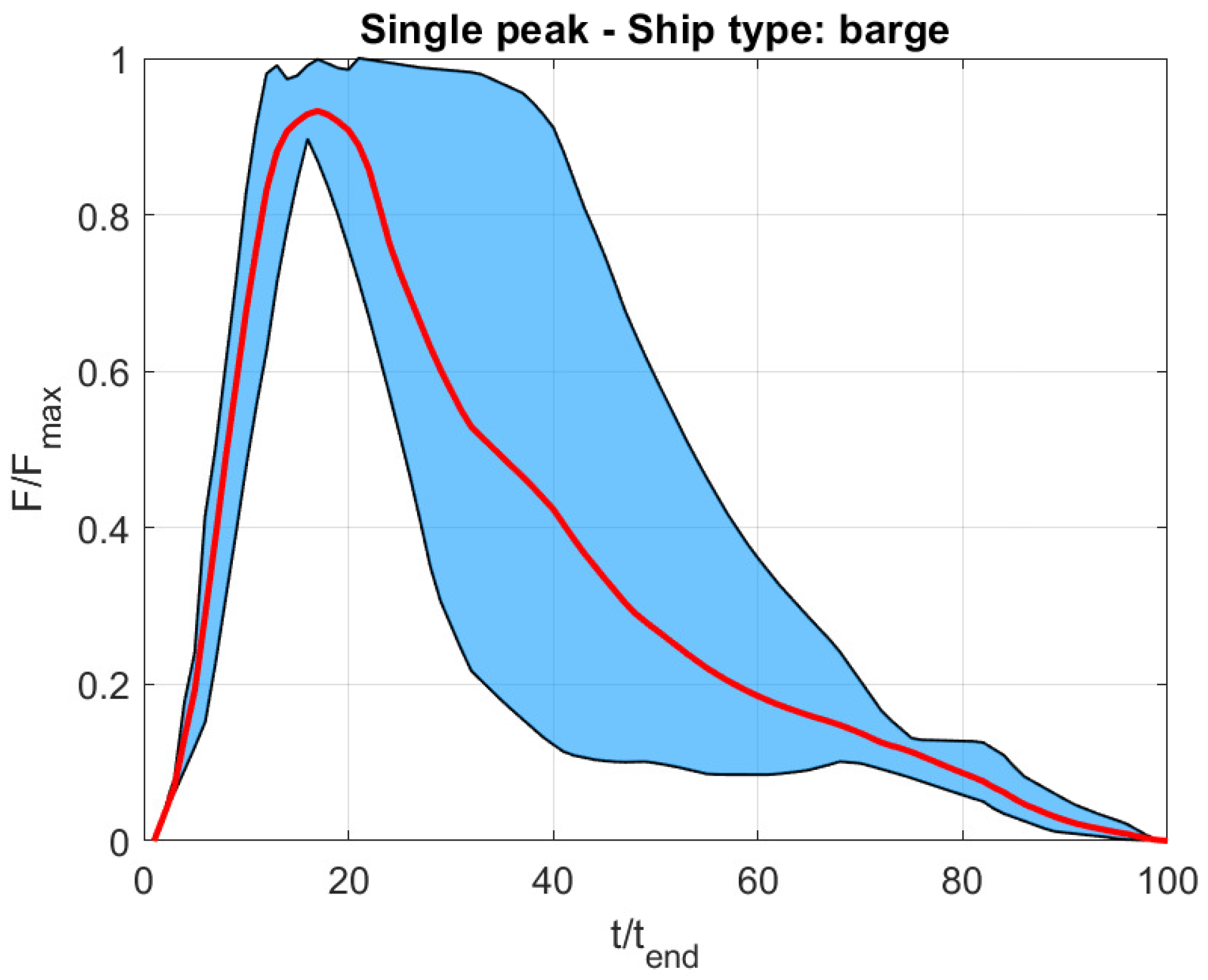
2. Clustering Ship Impact Events
- The bridge impact region.
- The peak impact force.
- The type of involved vessel.
3. Models and Scenarios
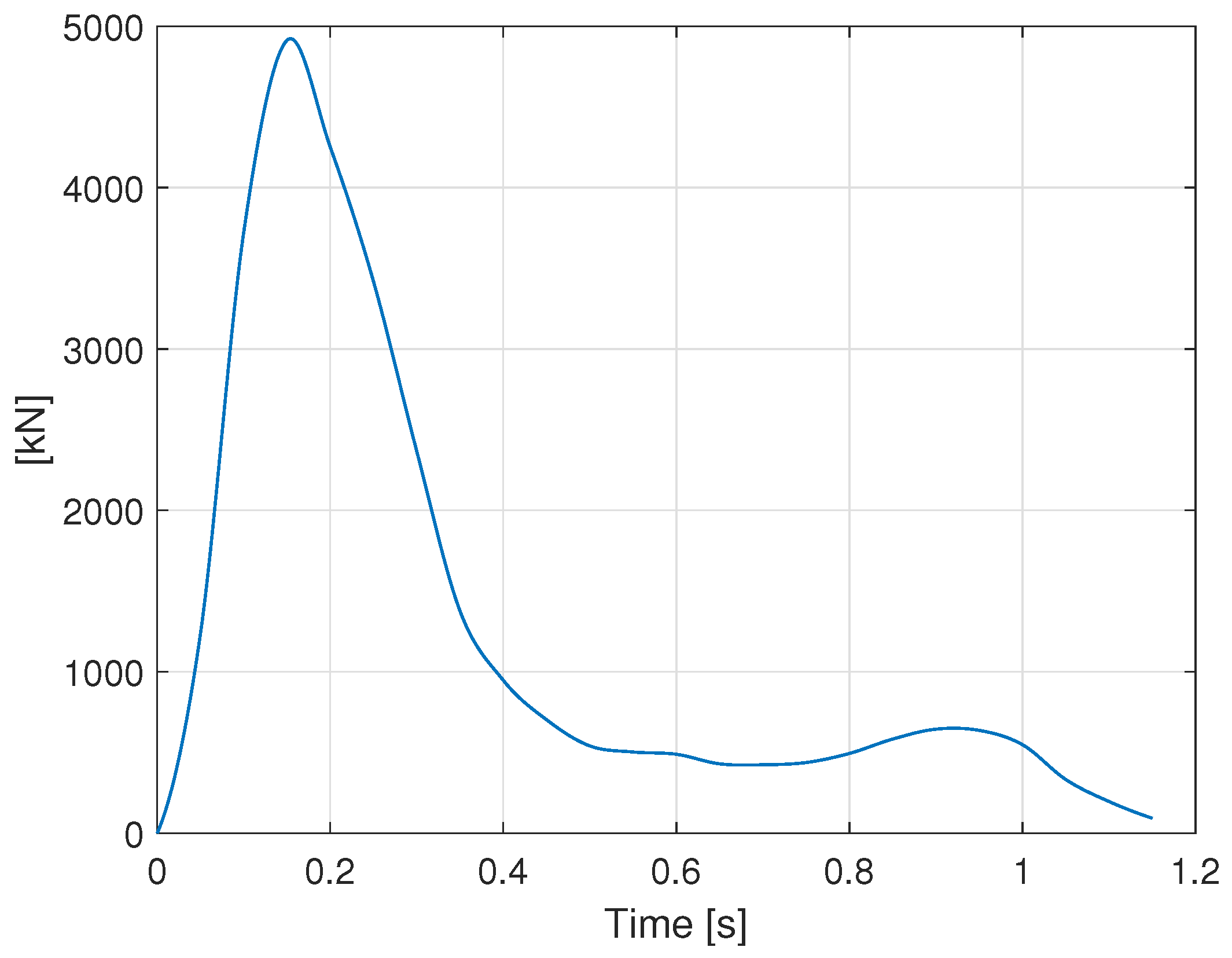
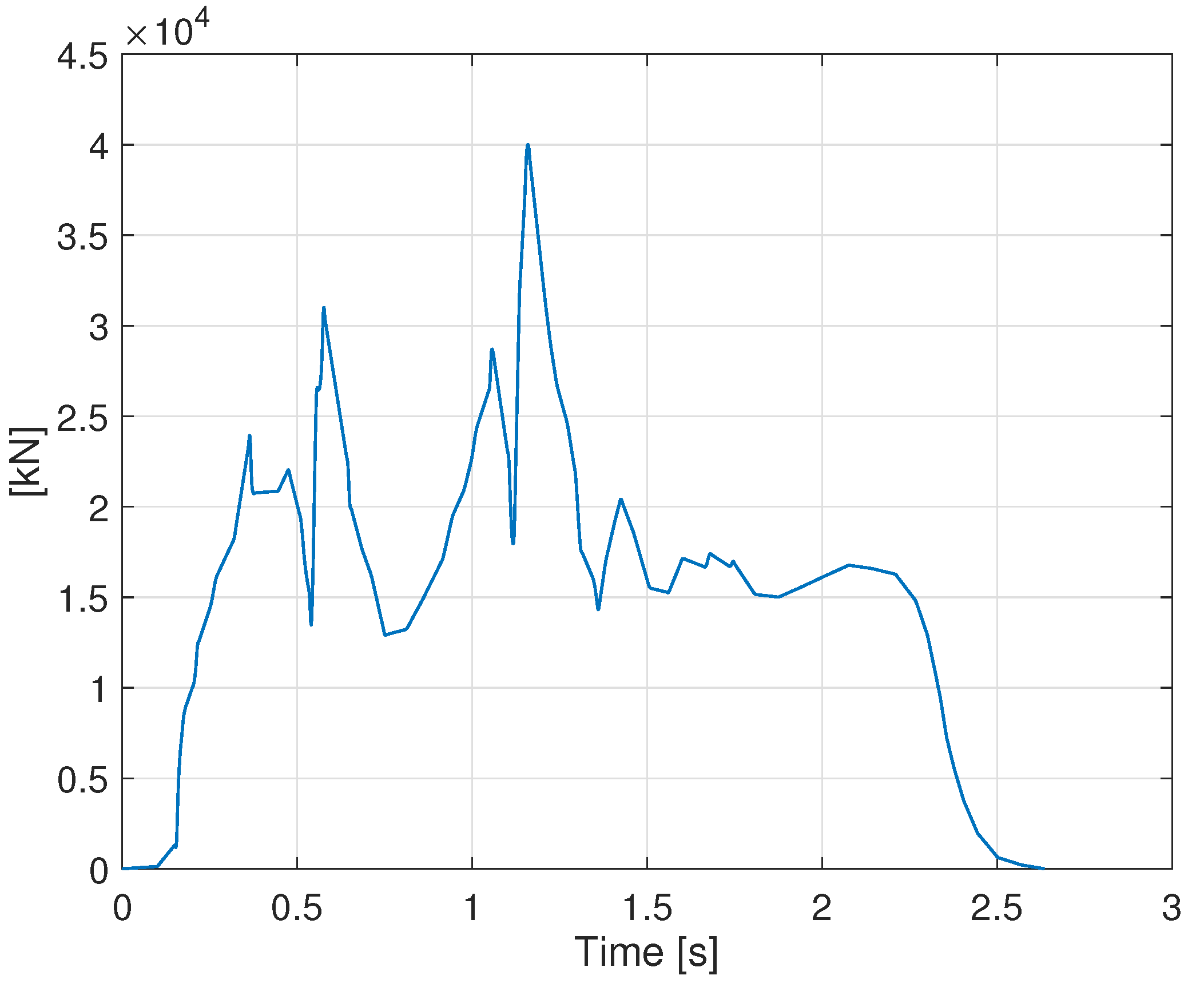
3.1. Impact Forces
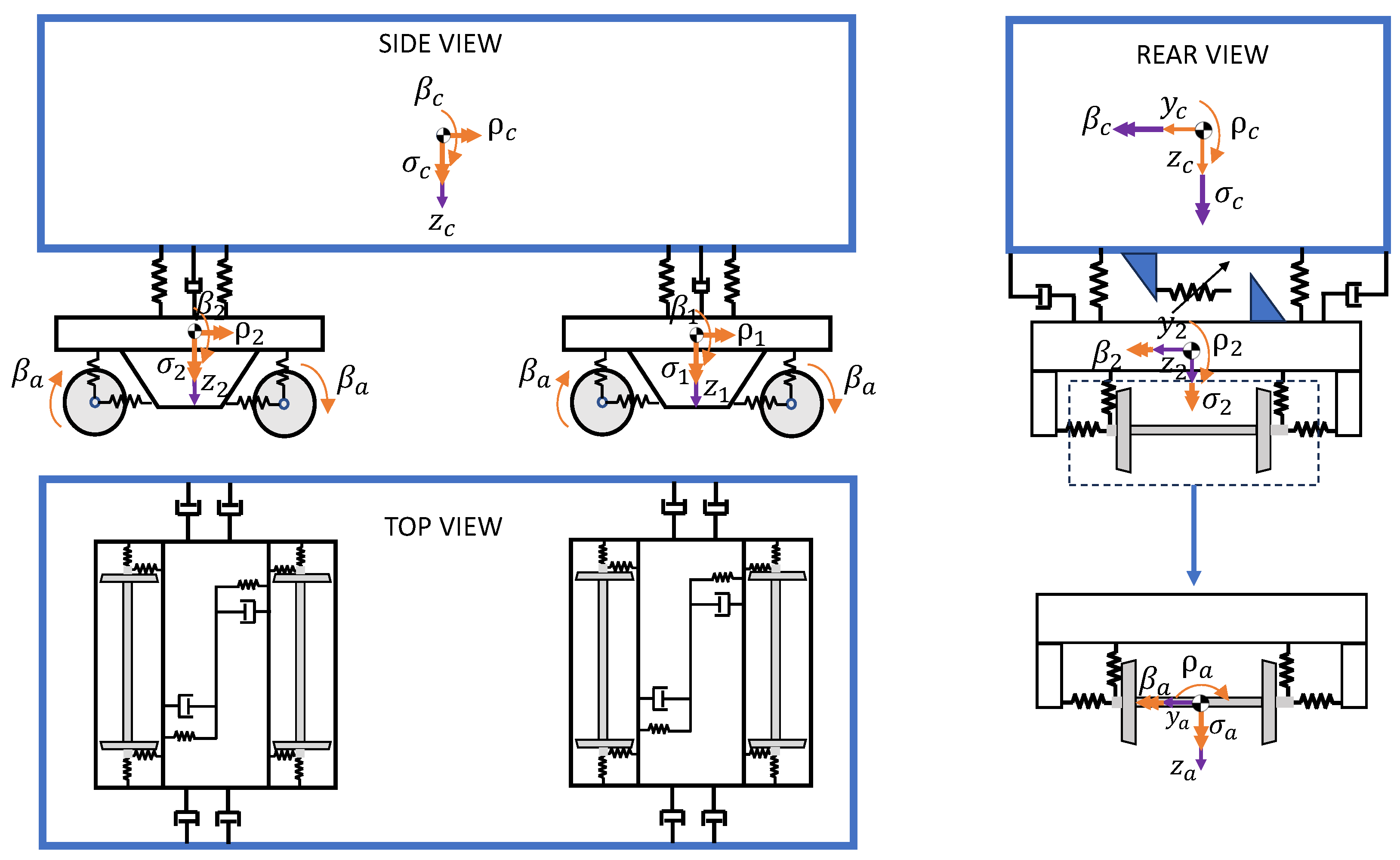
3.2. Bridge Model
3.3. Train Model
3.4. Safety Coefficients
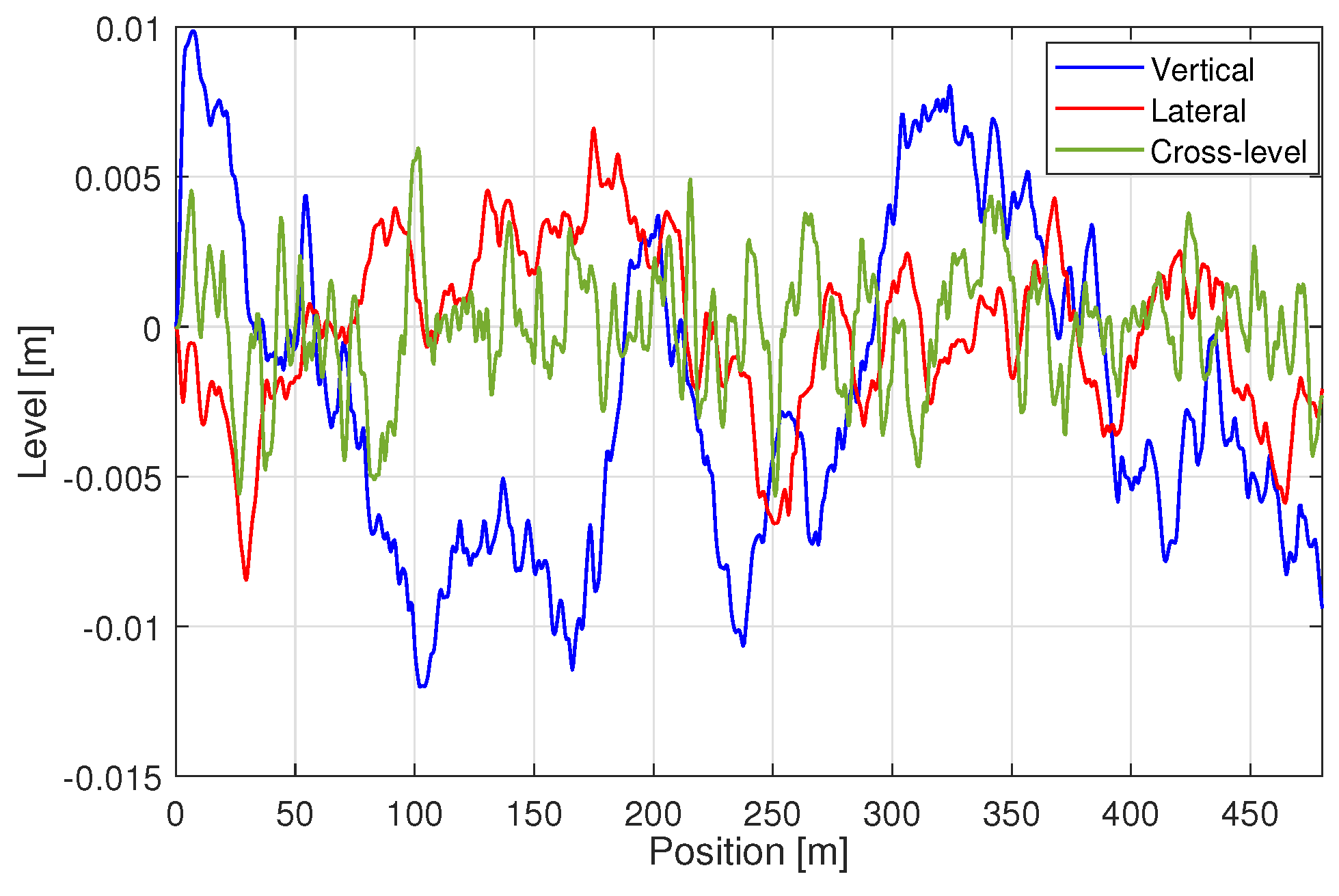
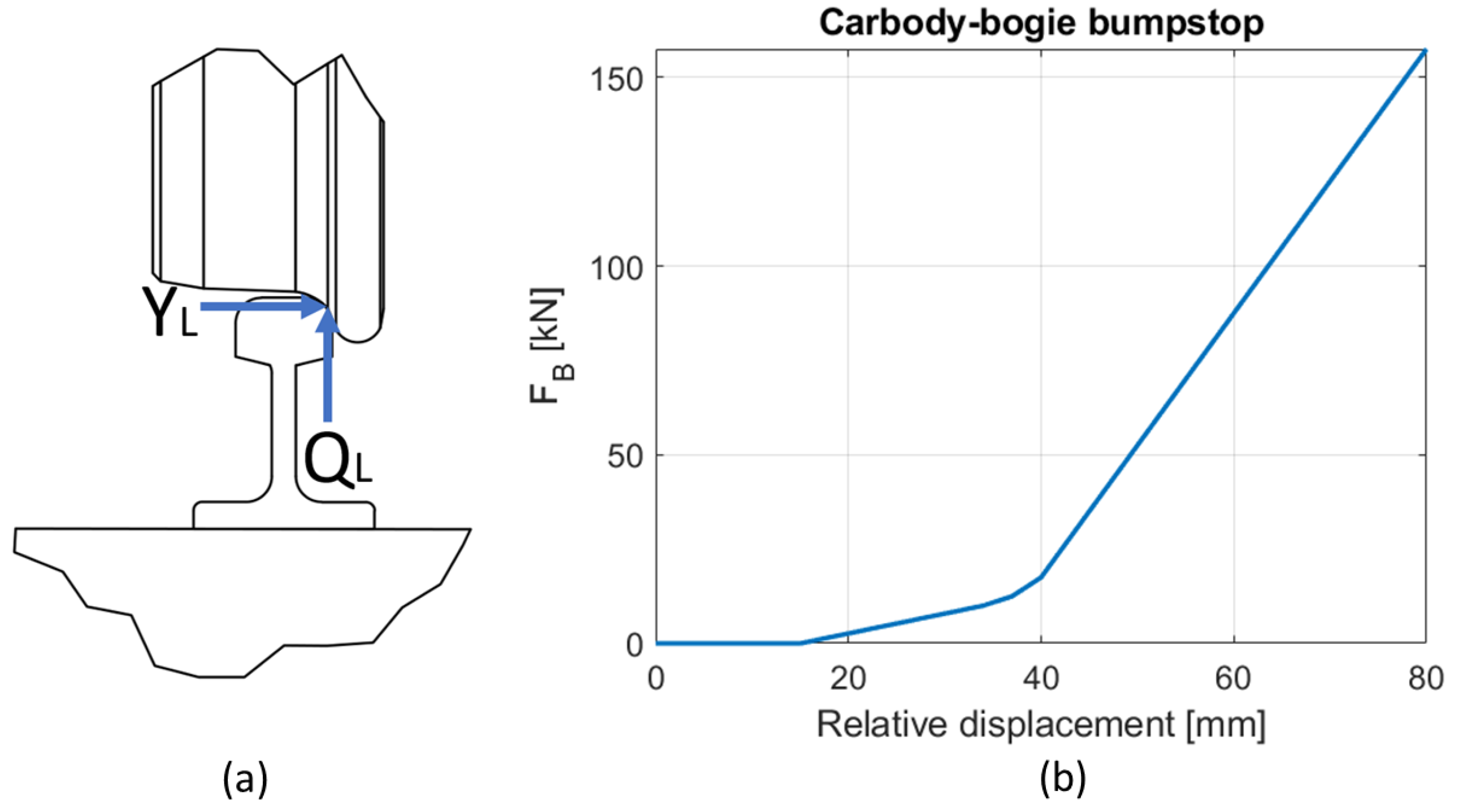
3.5. Wheel–Rail Contact Profiles
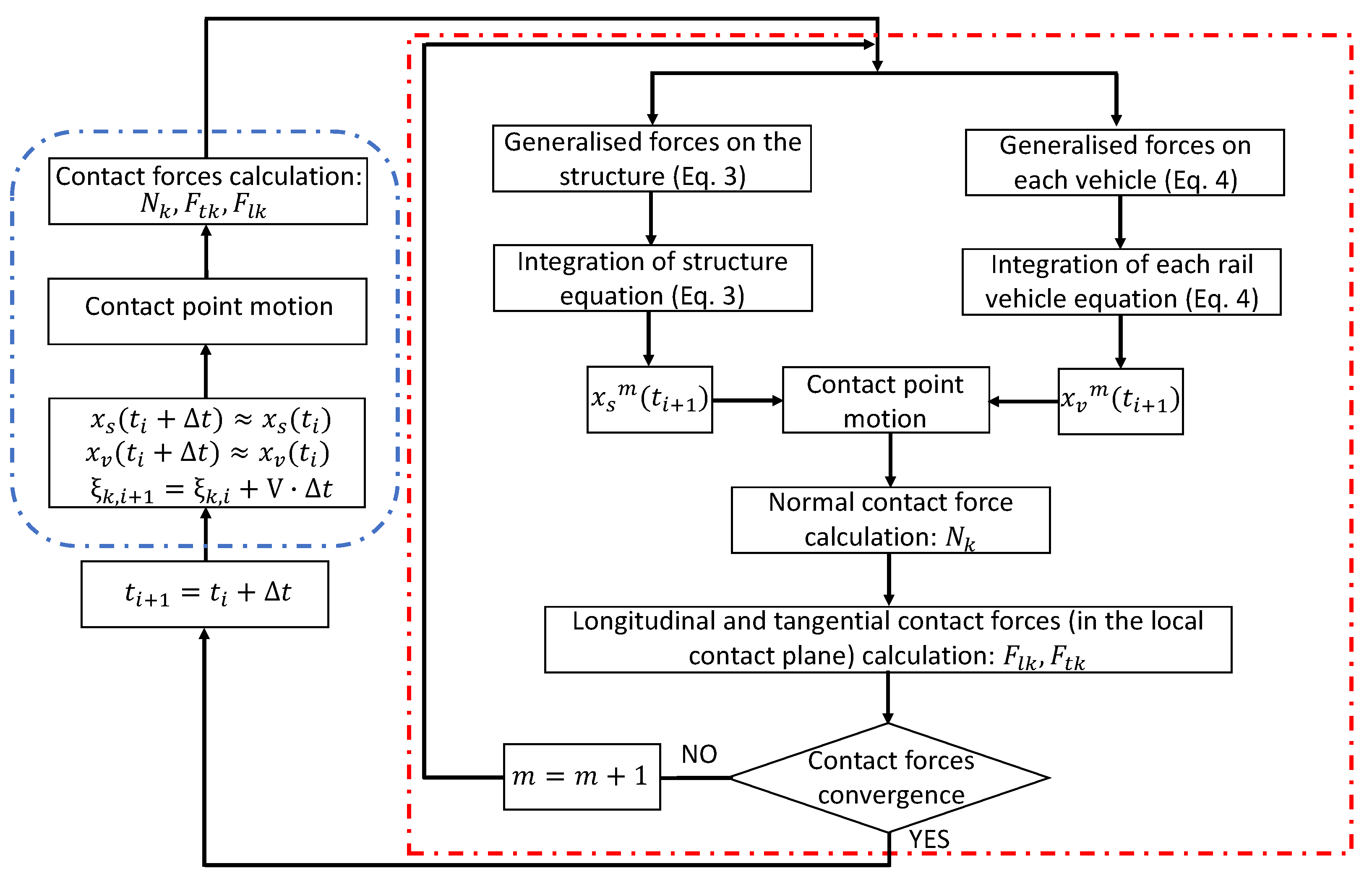
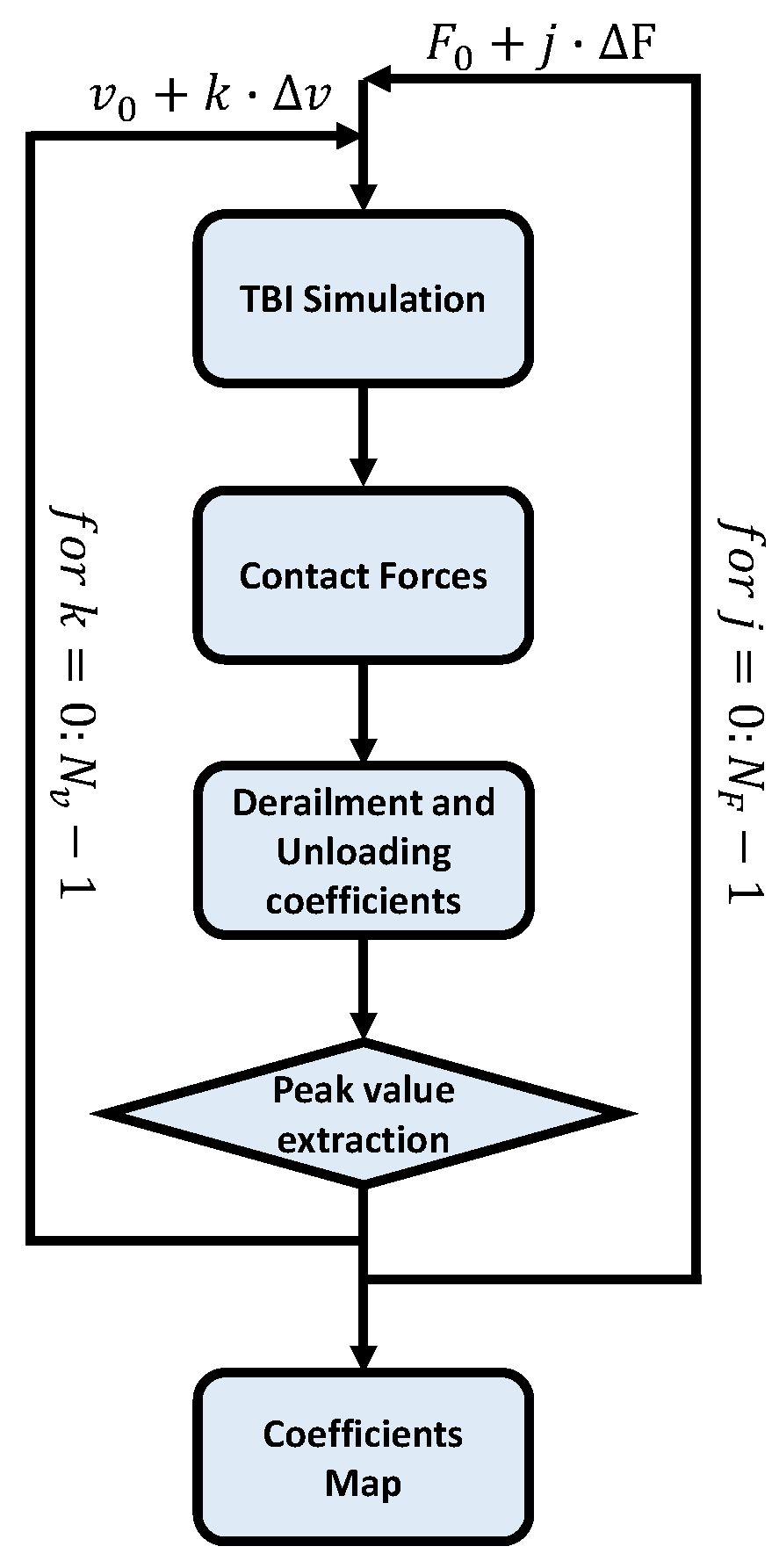
3.6. TBI Time Integration Procedure
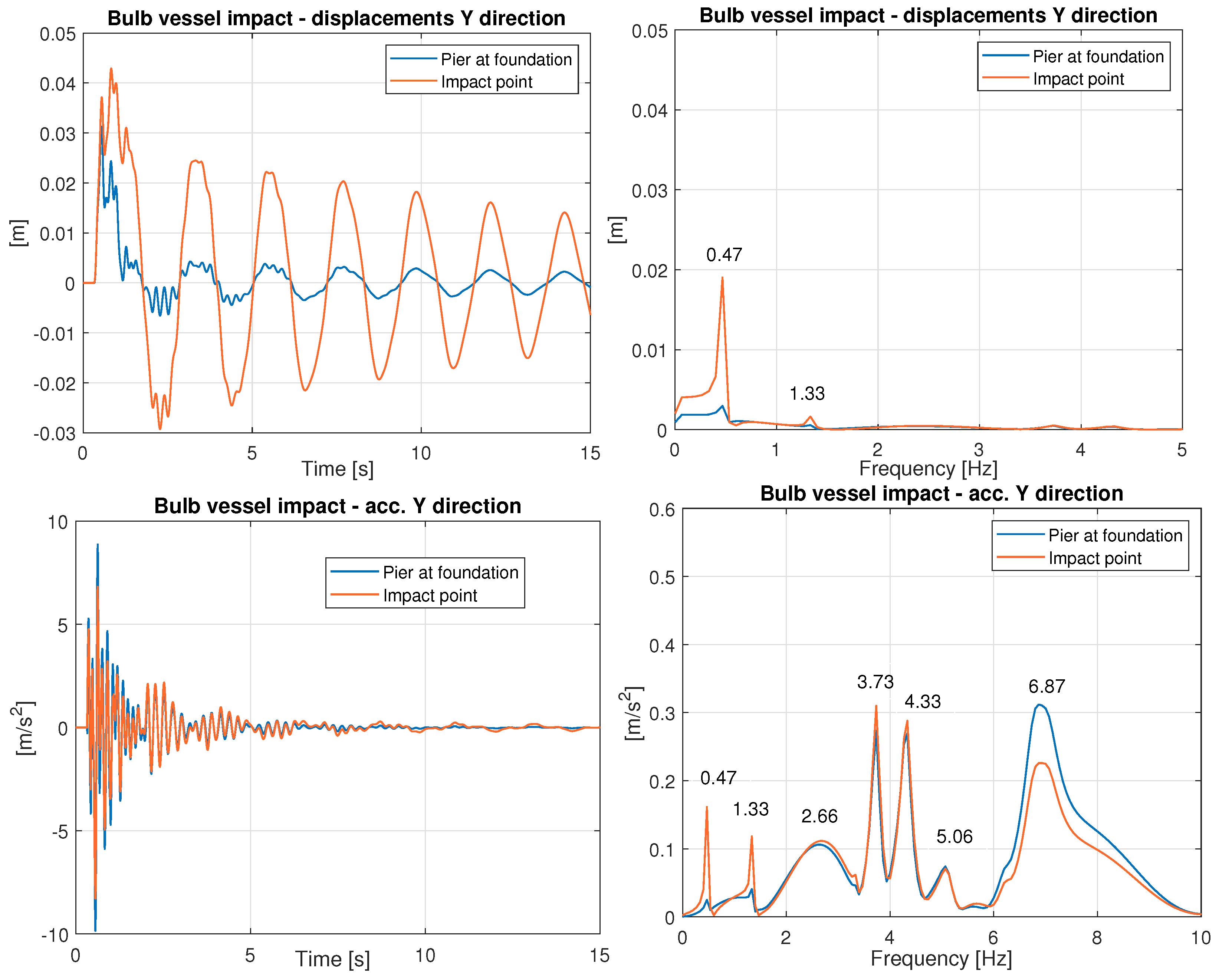
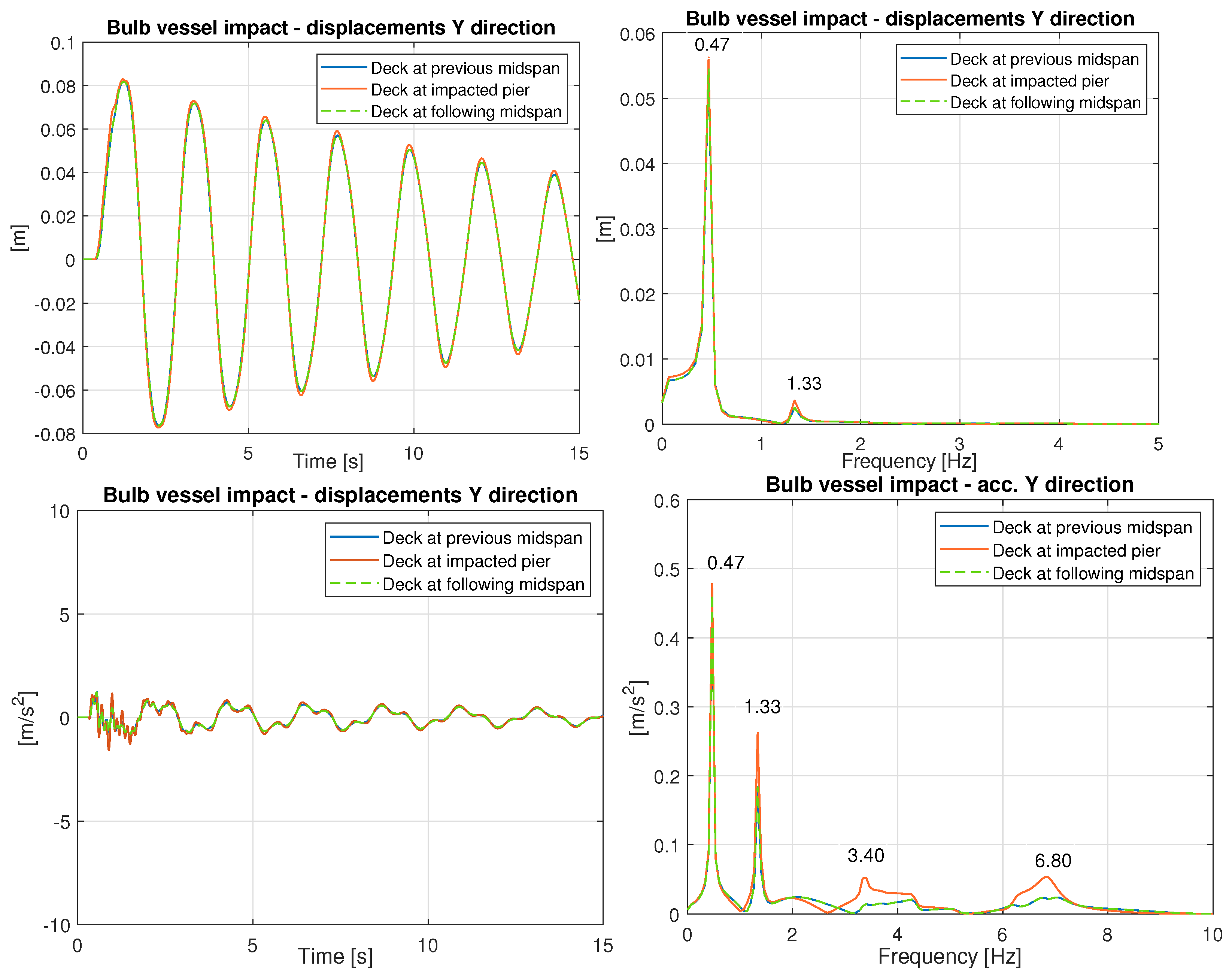
4. Structural Response to Ship Impact Events
- The effect of the travelling speed.
- The effect of the type of impact force due to barge and bulb vessel collisions. Their magnitude is scaled from 5 MN to 40 MN.
- The effect of the wheel–rail contact profile. An analysis is conducted considering new and moderately worn wheel–rail contact profiles.
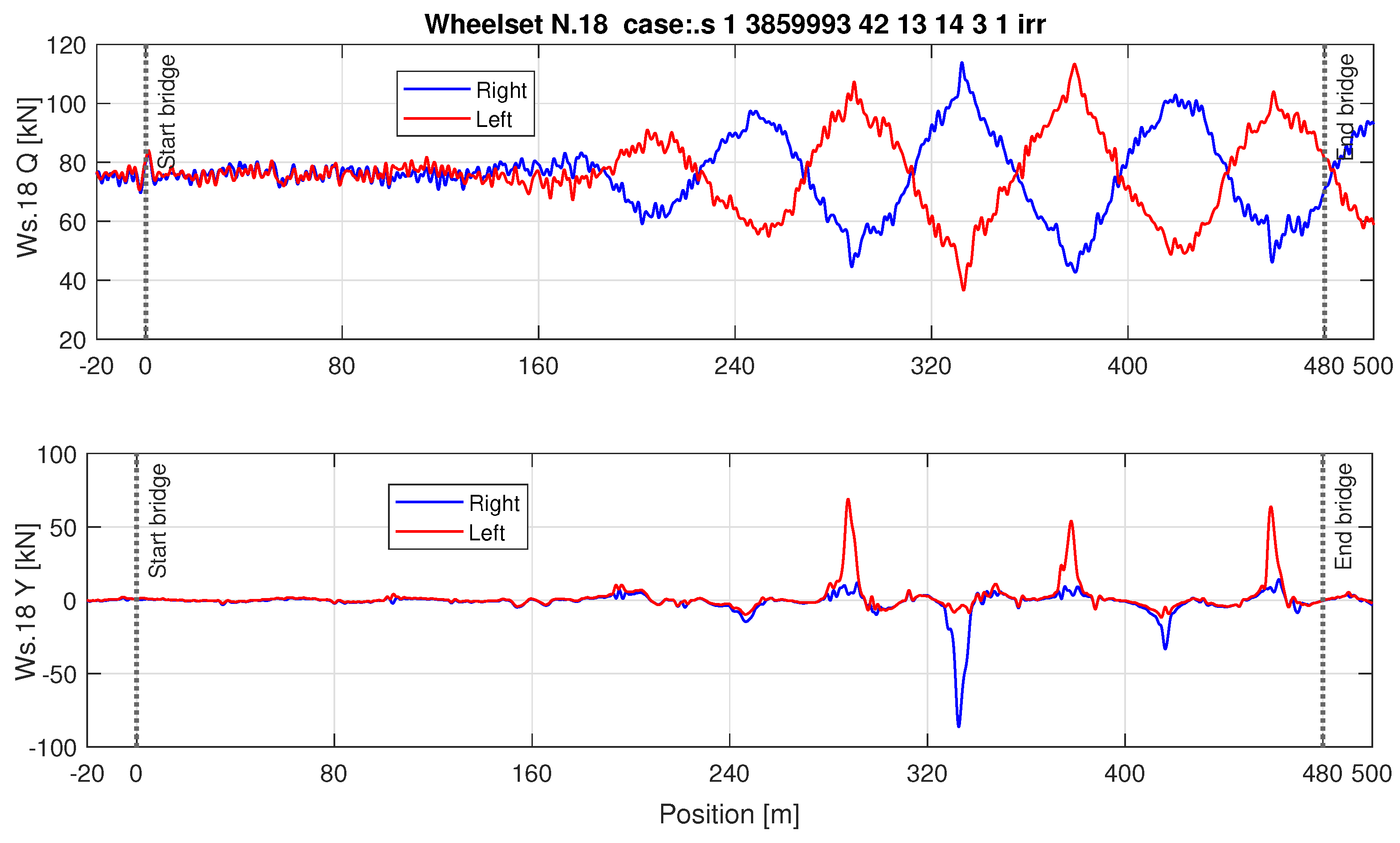
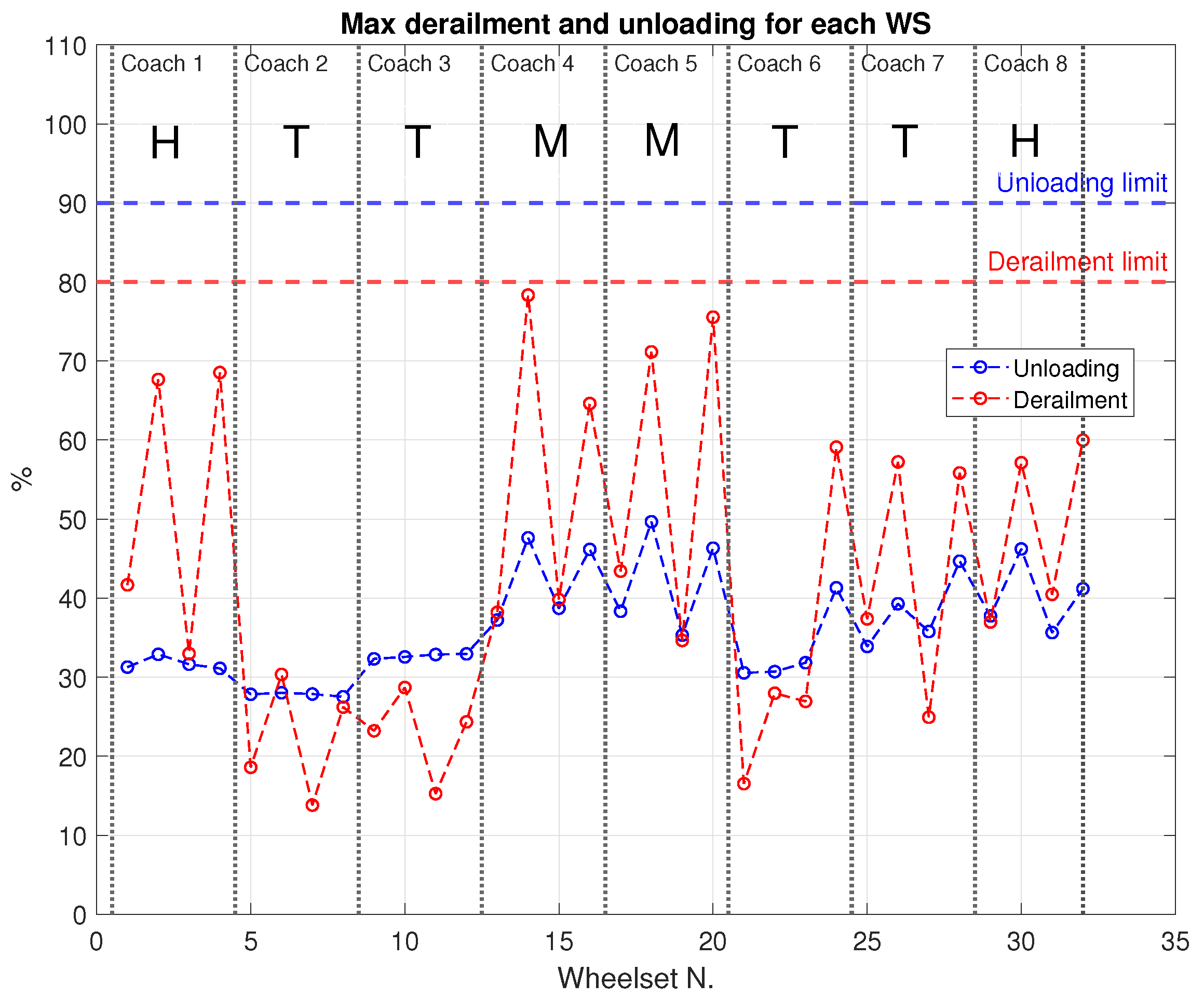
5. Train Running Safety Coefficients
6. Conclusions
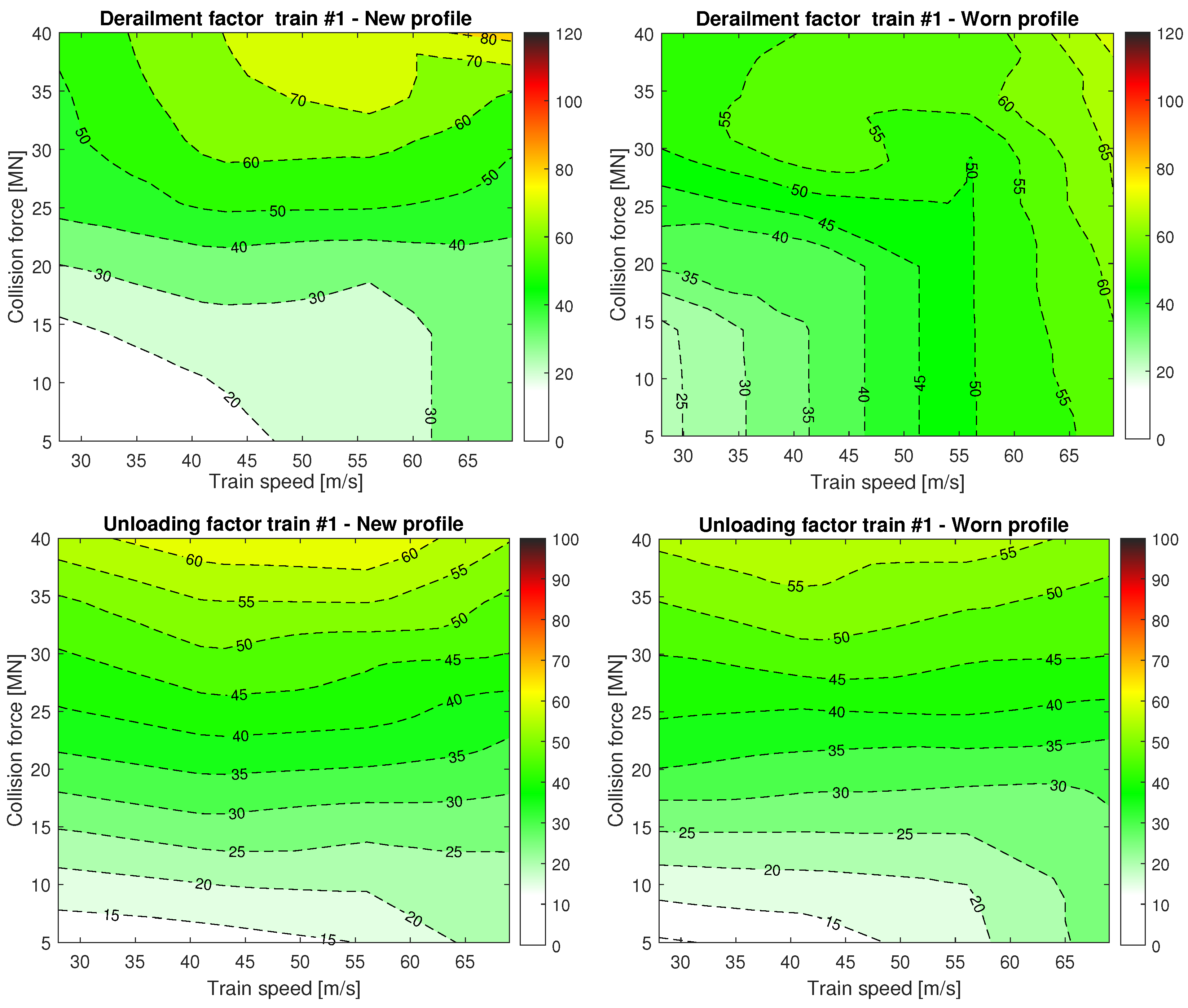
- Bulb vessel impacts were found to be a more critical scenario for both wheel–rail profiles (i.e., new and worn) in terms of train running safety. In fact, the resulting safety maps highlighted larger areas of higher values of derailment and unloading coefficients in the case of a bulb vessel collision with the central pier of a bridge than in the case of barge impact. This is caused by the difference in the impact force–time function of the two types of vessels (a barge and a bulb vessel).
- The derailment coefficient is more sensitive to train speed, especially in the extreme ranges of impact forces, considering that the highest safety coefficients are not necessarily found at the maximum train speed.
- The unloading coefficient is predominantly sensitive to the magnitude of the impact force and less dependent on the train speed.
- The wheel–rail contact geometry can significantly affect the train dynamic response and the running safety after a ship impact. Due to the increased conicity, moderately worn wheels (0.15 was examined) tend to limit the motion of the wheel set inside the track, also improving the running safety in the region of high impact forces. In this respect, simulations with new wheel and rail profiles are more demanding than those with a worn profile.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| H, M | T | u.m. | |
|---|---|---|---|
| Car body | |||
| Mass | 45,000 | 52,800 | kg |
| Yaw moment of inertia | 2.25 | 2.64 | kg·m2 |
| Pitch moment of inertia | 2.35 | 2.76 | kg·m2 |
| Roll moment of inertia | 1.40 | 1.64 | kg·m2 |
| Bogie | |||
| Mass | 4.50 | 4.20 | kg |
| Yaw moment of inertia | 7.25 | 6.77 | kg·m2 |
| Pitch moment of inertia | 8.55 | 7.98 | kg·m2 |
| Roll moment of inertia | 3.36 | 3.14 | kg·m2 |
| Primary vertical stiffness | 2.86 | 3.00 | N/m |
| Primary lateral stiffness | 2.00 | 2.00 | N/m |
| Primary vertical damping | 3.44 | 3.44 | N·s/m |
| Lateral axle-box damping | 6.70 | 6.70 | N·s/m |
| Secondary vertical stiffness | 1.01 | 1.01 | N/m |
| Secondary lateral stiffness | 3.20 | 3.70 | N/m |
| Torsion bar stiffness | 3.40 | 3.40 | N/rad |
| Secondary vertical damping | 3.15 | 3.70 | N·s/m |
| Secondary lateral damping | 1.70 | 2.42 | N·s/m |
| Yaw damping | 8.00 | 8.00 | N·s/rad |
| Wheel set | |||
| Mass | 2000 | 1500 | kg |
| Wheelbase | 2.3 | 2.5 | m |
References
- Bruni, S.; Collina, A.; Corradi, R.; Diana, G. Numerical simulation of train-track-bridge dynamic interaction. In Computational Mechanics, Proceedings; Tsinghua University Press: Beijing, China, 2004; pp. 237–242. [Google Scholar]
- Heleno, R.; Montenegro, P.; Carvalho, H.; Ribeiro, D.; Calcada, R.; Baker, C. Influence of the railway vehicle properties in the running safety against crosswinds. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104732. [Google Scholar] [CrossRef]
- He, X.; Kawatani, M.; Hayashikawa, T.; Matsumoto, T. Numerical analysis on seismic response of Shinkansen bridge-train interaction system under moderate earthquakes. Earthq. Eng. Eng. Vib. 2011, 10, 85–97. [Google Scholar] [CrossRef]
- Yang, X.; Wang, H.; Jin, X. Numerical Analysis of a Train-Bridge System Subjected to Earthquake and Running Safety Evaluation of Moving Train. Shock Vib. 2016, 2016, 9027054. [Google Scholar] [CrossRef]
- Jin, Z.; Pei, S.; Li, X.; Liu, H.; Qiang, S. Effect of vertical ground motion on earthquake-induced derailment of railway vehicles over simply-supported bridges. J. Sound Vib. 2016, 383, 277–294. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Derailment mechanism of trains running over bridges during strong earthquakes. Procedia Eng. 2017, 199, 2633–2638. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Vehicle–bridge interaction analysis modeling derailment during earthquakes. Nonlinear Dyn. 2018, 93, 2315–2337. [Google Scholar] [CrossRef]
- Wu, X.; Liang, S.; Chi, M. An investigation of rocking derailment of railway vehicles under the earthquake excitation. Eng. Fail. Anal. 2020, 117, 104913. [Google Scholar] [CrossRef]
- Goto, K.; Sogabe, M.; Tokunaga, M. Evaluation of vehicle running safety on railway Structures during earthquake. Int. J. Transp. Dev. Integr. 2020, 4, 113–128. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, W.; Pei, S. Probabilistic evaluation of railway vehicle’s safety on bridges under random earthquake and track irregularity excitations. Eng. Struct. 2022, 266, 114527. [Google Scholar] [CrossRef]
- Guo, J.; He, J. Dynamic response analysis of ship-bridge collisions experiment. J. Zhejiang Univ.-Sci. A 2020, 21, 525–534. [Google Scholar] [CrossRef]
- Fan, W.; Sun, Y.; Yang, C.; Sun, W.; He, Y. Assessing the response and fragility of concrete bridges under multi-hazard effect of vessel impact and corrosion. Eng. Struct. 2020, 225, 111279. [Google Scholar] [CrossRef]
- Wang, J.; Yan, H.; Qian, H. Comparisons of Ship Collision Design Formula for Bridges Based on FEM Simulations. J. Highw. Transp. Res. Dev. 2006, 1, 46–50. [Google Scholar] [CrossRef]
- Fan, W.; Liu, Y.; Liu, B.; Guo, W. Dynamic Ship-Impact Load on Bridge Structures Emphasizing Shock Spectrum Approximation. J. Bridge Eng. 2016, 21. [Google Scholar] [CrossRef]
- Wan, Y.; Zhu, L.; Fang, H.; Liu, W.; Mao, Y. Experimental testing and numerical simulations of ship impact on axially loaded reinforced concrete piers. Int. J. Impact Eng. 2019, 125, 246–262. [Google Scholar] [CrossRef]
- Consolazio, G.R.; Cowan, D.R. Numerically Efficient Dynamic Analysis of Barge Collisions with Bridge Piers. J. Struct. Eng. 2005, 131, 1256–1266. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, W.; Fang, H.; Chen, J.; Zhuang, Y.; Han, J. Design and simulation of innovative foam-filled Lattice Composite Bumper System for bridge protection in ship collisions. Compos. Part B Eng. 2019, 157, 24–35. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, C.; Chen, Z. Dynamic performance and damage evaluation of a scoured double-pylon cable-stayed bridge under ship impact. Eng. Struct. 2020, 216, 110772. [Google Scholar] [CrossRef]
- Tao, F.; Xiaoqian, R.; Kai, W. Vessel-Bridge Collision Reliability Assessment Based on Structural Dynamic Analysis. Adv. Civ. Eng. 2021, 2021, 5929019. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J. Development of the impact force time-history for determining the responses of bridges subjected to ship collisions. Ocean Eng. 2019, 187, 106182. [Google Scholar] [CrossRef]
- Sha, Y.; Amdahl, J.; Dørum, C. Numerical and analytical studies of ship deckhouse impact with steel and RC bridge girders. Eng. Struct. 2021, 234, 111868. [Google Scholar] [CrossRef]
- Sha, Y.; Amdahl, J.; Dørum, C. Dynamic responses of a floating bridge subjected to ship collision load on bridge girders. Procedia Eng. 2017, 199, 2506–2513. [Google Scholar] [CrossRef]
- Xia, C.; Xia, H.; De Roeck, G. Dynamic response of a train-bridge system under collision loads and running safety evaluation of high-speed trains. Comput. Struct. 2014, 140, 23–38. [Google Scholar] [CrossRef]
- Xia, C.; Lei, J.; Zhang, N.; Xia, H.; De Roeck, G. Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load. J. Sound Vib. 2012, 331, 2334–2347. [Google Scholar] [CrossRef]
- Li, P.; Li, Z.; Han, Z.; Zhu, S.; Zhai, W.; Lou, H. Running safety evaluation of high-speed train subject to the impact of floating ice collision on bridge piers. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 220–233. [Google Scholar] [CrossRef]
- Kalajahi, A.R.; Esmaeili, M.; Zakeri, J.A. Dynamic analysis of a coupled high-speed train and bridge system subjected to a sea wave hydrodynamic load. Lat. Am. J. Solids Struct. 2021, 18, e341. [Google Scholar] [CrossRef]
- Jensen, J.L.; Svensson, E.; Eiriksson, H.; Ennemark, F. Ship-induced derailment on a railway bridge. Struct. Eng. Int. 1996, 6, 107–112. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, N.; Xia, H.; Ma, Q.; Wu, X. A framework for carrying out train safety evaluation and vibration analysis of a trussed-arch bridge subjected to vessel collision. Struct. Eng. Mech. Int. J. 2016, 59, 683–701. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.; Wang, B.; Yu, C. Running Safety of Trains under Vessel-Bridge Collision. Shock Vib. 2015, 2015, 252574. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Zhu, Z.; Liu, D.; Li, X. Train-Track-Bridge coupling vibration and train running safety under vessel impact. J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Gong, K.; Liu, L.; Yu, C.; Wang, C. Train derailment process analysis on heavy haul railway bridge under Ship impact. Symmetry 2021, 13, 2122. [Google Scholar] [CrossRef]
- Xia, C.; Ma, J.; Xia, H. Dynamic analysis of a train-bridge system to vessel collision and running safety of high-speed trains. Vibroeng. Procedia 2015, 5, 509–514. [Google Scholar]
- AbuBakar, A.; Dow, R. The impact analysis characteristics of a ship’s bow during collisions. Eng. Fail. Anal. 2019, 100, 492–511. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, W.; Chen, B. Steel Fender Limitations and Improvements for Bridge Protection in Ship Collisions. J. Bridge Eng. 2015, 20. [Google Scholar] [CrossRef]
- Yang, L.; Liu, J. A study on ship impacting a flexible crashworthy device for protecting bridge pier. EPJ Web Conf. 2015, 94, 01059. [Google Scholar] [CrossRef]
- Chen, G.; Huang, H.; Xiang, Z. Experimental Investigation on the Anticollision Performance of Corrugated Steel-Reinforced Composites for Bridge Piers. Shock Vib. 2021, 2021, 5847559. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Effects of axial load on nonlinear response of RC columns subjected to lateral impact load: Ship-pier collision. Eng. Fail. Anal. 2018, 91, 397–418. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Nonlinear failure analysis of bridge pier subjected to vessel impact combined with blast loads. Ocean Eng. 2021, 234, 109209. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Nonlinear numerical analysis and progressive damage assessment of a cable-stayed bridge pier subjected to ship collision. Mar. Struct. 2020, 69, 102662. [Google Scholar] [CrossRef]
- Sha, Y.; Amdahl, J. Numerical investigations of a prestressed pontoon wall subjected to ship collision loads. Ocean Eng. 2019, 172, 234–244. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Analysis of girder bridge pier subjected to barge collision considering the superstructure interactions: The case study of a multiple-pier bridge system. Struct. Infrastruct. Eng. 2019, 15, 392–412. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, Z.; Huang, X.; Sun, W. A simplified method to efficiently design steel fenders subjected to vessel head-on collisions. Mar. Struct. 2020, 74, 102840. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, P.; Cao, H.; Wang, F. Research on New Flexible Bridge Pier Anti-collision Technology. IOP Conf. Ser. Earth Environ. Sci. 2020, 565, 1291. [Google Scholar] [CrossRef]
- McVay, M.C.; Wasman, S.J.; Consolazio, G.R.; Bullock, P.J.; Cowan, D.G.; Bollmann, H.T. Dynamic Soil-Structure Interaction of Bridge Substructure Subject to Vessel Impact. J. Bridge Eng. 2009, 14, 7–16. [Google Scholar] [CrossRef]
- Peng, K. Dynamic Ship-bridge Collision Risk Decision Method Based on Time-Dependent AASHTO Model. J. Inst. Eng. (India) Ser. A 2021, 102, 305–313. [Google Scholar] [CrossRef]
- Jilun, M.; Chuang, C.; Shengxie, X. Evaluation on Risk for Ship Collision with Archbridge and Crash Capability of Anti-Collision. Open Civ. Eng. J. 2014, 8, 351–359. [Google Scholar] [CrossRef][Green Version]
- Fan, W.; Yuan, W. Ship Bow Force-Deformation Curves for Ship-Impact Demand of Bridges considering Effect of Pile-Cap Depth. Shock Vib. 2014, 2014, 201425. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, W. A Simple Procedure for Determination of the Dynamic Ship-Impact Load on Bridge Structures; WIT Press: Billerica, MA, USA, 2014; Volume 141, pp. 73–85. [Google Scholar] [CrossRef]
- ORE B176; Bogies with Steered or Steering Wheelsets. Report No. 1: Specifications and Preliminary Studies, Vol. 2, Specification for a Bogie with Improved Curving Characteristics. ORE: Utrecht, The Netherlands, 1989.
- EN14363; Railway Applications—Testing and Simulation for the Acceptance of Running Characteristics of Railway Vehicles—Running Behaviour and Stationary Tests. CEN: Brussels, Belgium, 2016.
- EN14067-6; Railway Applications—Aerodynamics—Part 6: Requirements and Test Procedures for Cross Wind Assessment. CEN: Brussels, Belgium, 2010.
- Pascal, J.P.; Sany, J.R. Dynamics of an isolated railway wheelset with conformal wheel–rail interactions. Veh. Syst. Dyn. 2019, 57, 1947–1969. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Hedrick, J.K.; Elkins, J.A. A Comparison of Alternative Creep Force Models for Rail Vehicle Dynamic Analysis. Veh. Syst. Dyn. 1983, 12, 79–83. [Google Scholar] [CrossRef]
- Diana, G.; Cheli, F.; Bruni, S. Railway runnability and train-track interaction in long span cable supported bridges. Adv. Struct. Dyn. 2000, 1, 43–54. [Google Scholar]



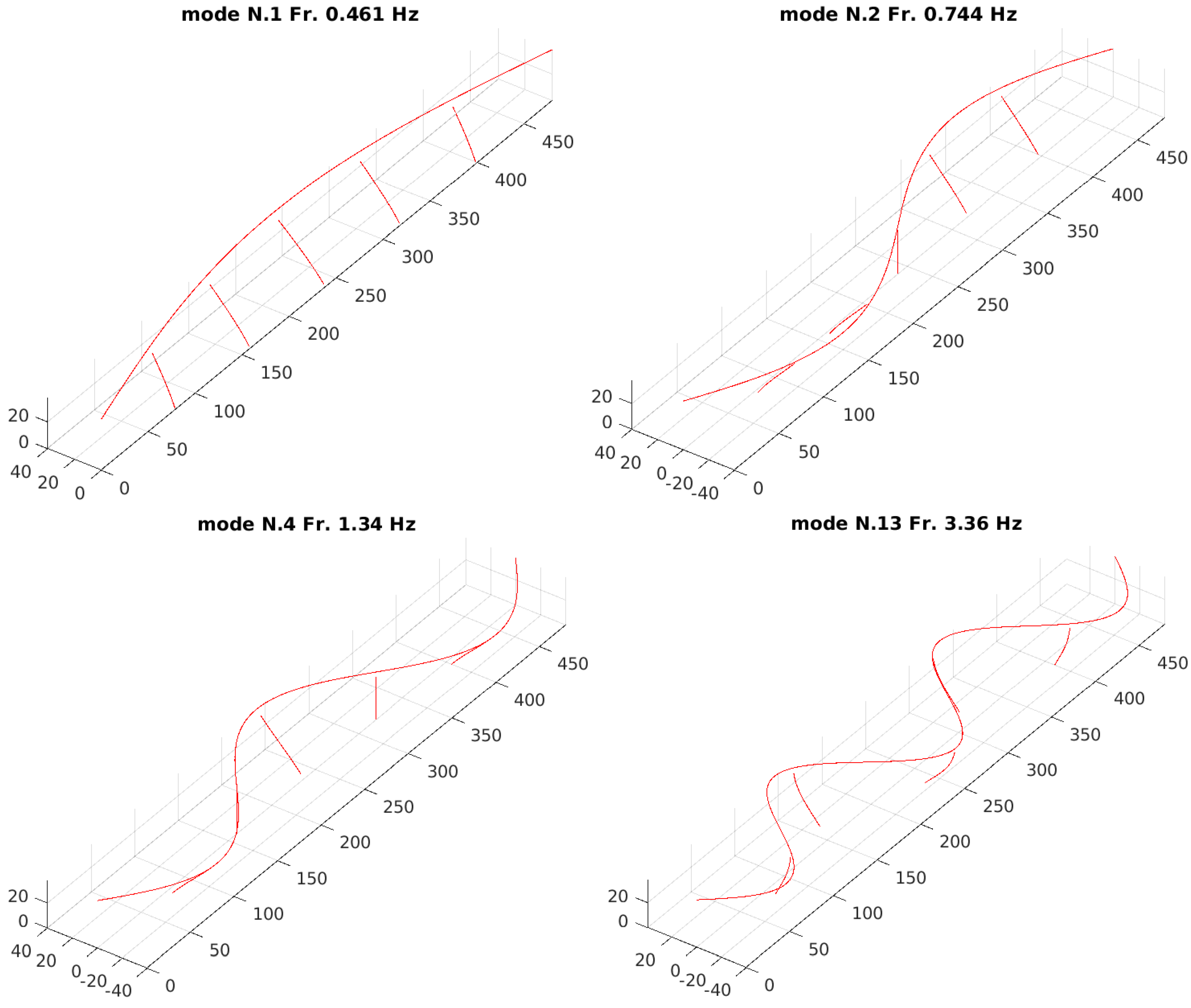







| A [m2] | [m4] | I2 [mm4] | I3 [mm4] | E [Gpa] | [kg/m3] | |
|---|---|---|---|---|---|---|
| Piers | 21.9 | 53.0 | 19.0 | 83.0 | 35.2 | 2460.0 |
| Deck | 25.8 | 173.0 | 879.0 | 69.0 | 35.2 | 2760.0 |
| Rayleigh Damping Coefficients | ||||||
| Piers | 0.1 | 0.001 | ||||
| Deck | 0.1 | 0.001 | ||||
| Span [m] | Width [m] | Height [m] | Mass per Meter [kg/m] | |||
| Deck | 6× | 80.0 | 25.0 | 4.5 | 71,208.0 | |
| Modes | L1 | L2 | L3 | L4 | ||
| Freq. [Hz] | 0.47 | 0.74 | 1.33 | 3.36 | ||
| Foundation | Deck Bearings | |
|---|---|---|
| [N/m] | 9.50 | 0.00 |
| [N/m] | 9.47 | 4.00 |
| [N/m] | 3.92 | 4.00 |
| [N·m/rad] | 8.47 | 3.92 |
| [N·m/rad] | 1.04 | 0.00 |
| [N·m/rad] | 9.95 | 0.00 |
| [N·s/m] | 9.50 | 0.00 |
| [N·s/m] | 1.89 | 4.00 |
| [N·s/m] | 3.92 | 4.00 |
| [N·m·s/rad] | 4.24 | 3.92 |
| [N·m·s/rad] | 5.20 | 0.00 |
| [N·m·s/rad] | 4.98 | 0.00 |
| Double-Deck Train | |||
|---|---|---|---|
| Configuration | H–T–T–M–M–T–T–H | ||
| Lat. [Hz] | Yaw [Hz] | Vert. [Hz] | |
| M, H | 0.46 | 0.76 | 0.9 |
| T | 0.45 | 0.83 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardini, L.; Collina, A.; Soldavini, G. Railway Bridge Runability Safety Analysis in a Vessel Collision Event. Vibration 2024, 7, 326-350. https://doi.org/10.3390/vibration7020016
Bernardini L, Collina A, Soldavini G. Railway Bridge Runability Safety Analysis in a Vessel Collision Event. Vibration. 2024; 7(2):326-350. https://doi.org/10.3390/vibration7020016
Chicago/Turabian StyleBernardini, Lorenzo, Andrea Collina, and Gianluca Soldavini. 2024. "Railway Bridge Runability Safety Analysis in a Vessel Collision Event" Vibration 7, no. 2: 326-350. https://doi.org/10.3390/vibration7020016
APA StyleBernardini, L., Collina, A., & Soldavini, G. (2024). Railway Bridge Runability Safety Analysis in a Vessel Collision Event. Vibration, 7(2), 326-350. https://doi.org/10.3390/vibration7020016








