Theoretical and Non-Dimensional Investigations into Vibration Control Using Viscoelastic and Endochronic Elements
Abstract
:1. Introduction
2. Modeling Lamped Systems with Viscoelastic and Elastoplastic Elements
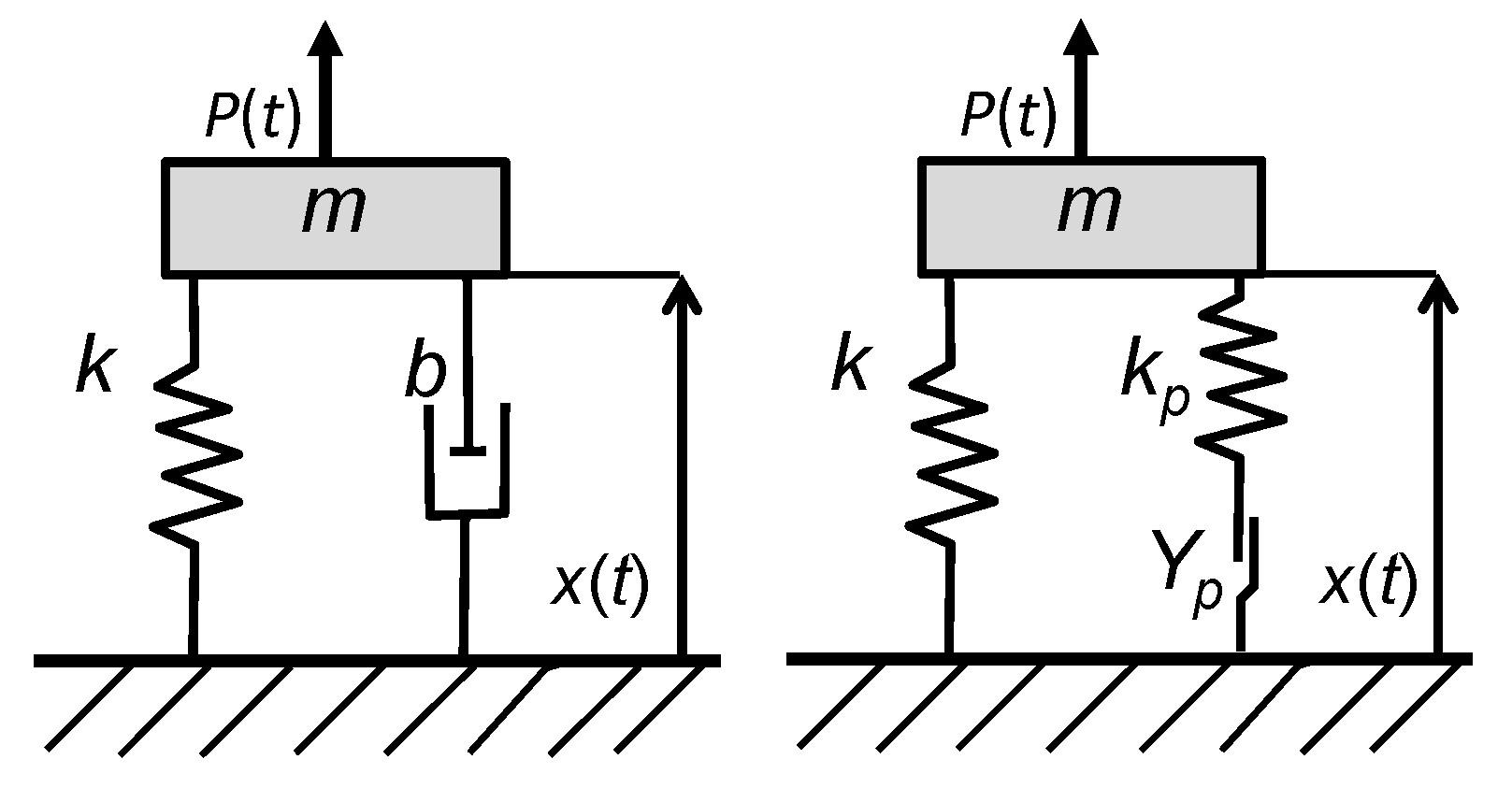
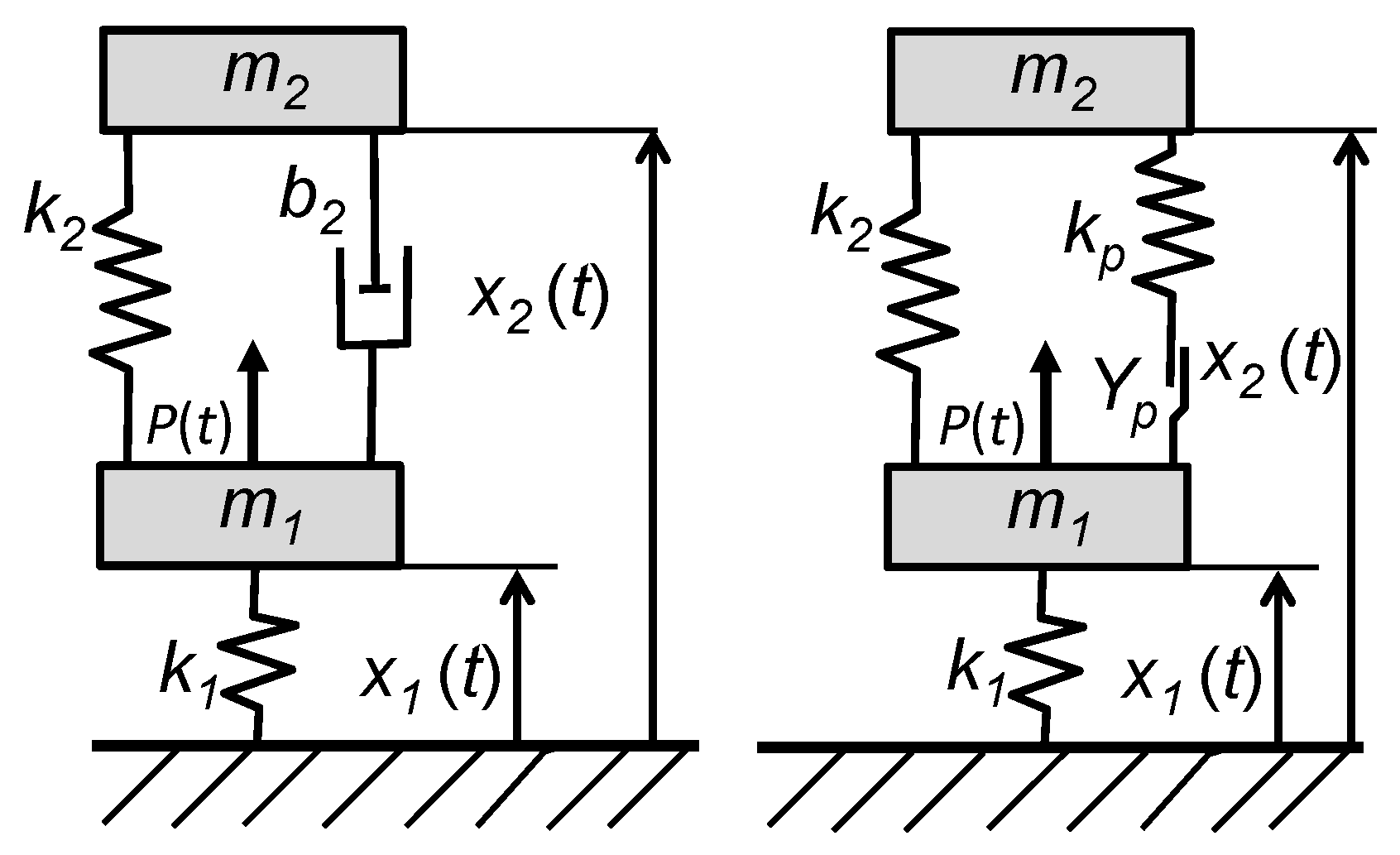
2.1. Modeling Energy Dissipation Considering Viscoelastic and Endochronic Material Behavior
2.2. Vibration Models for Dynamic Systems with One Degree of Fredom
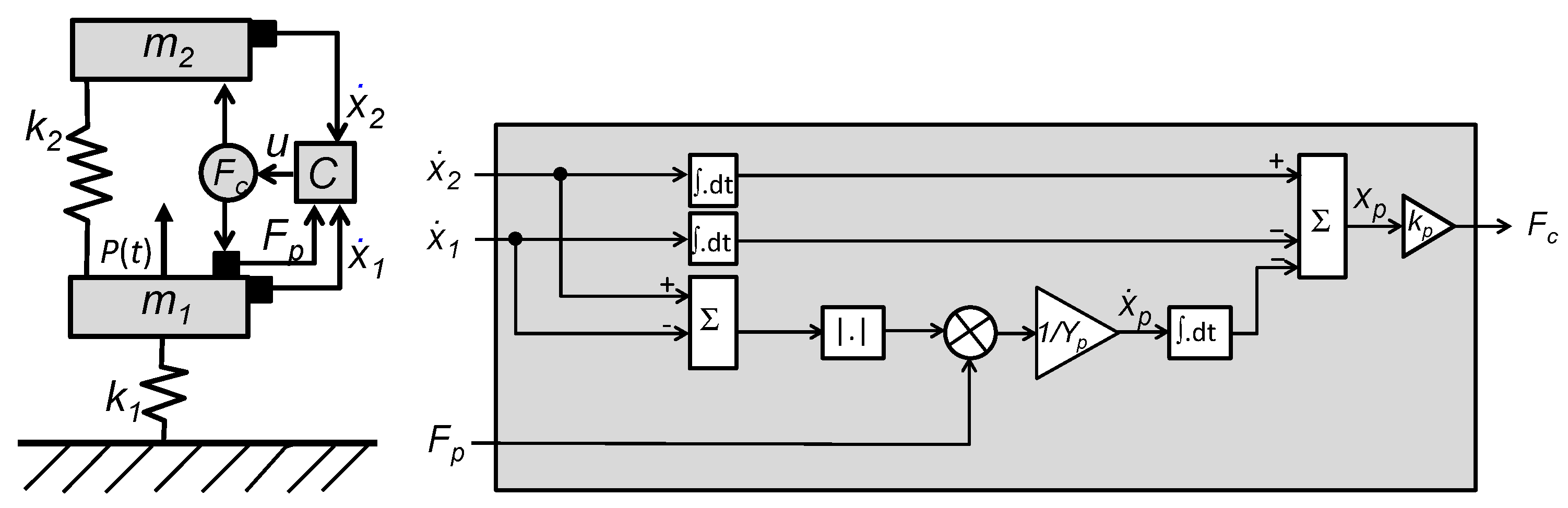
2.3. Vibration Models for Coupled Systems with Two Degrees of Freedom
3. Results of Numerical Investigations and Discussion of Noise-Control Potential
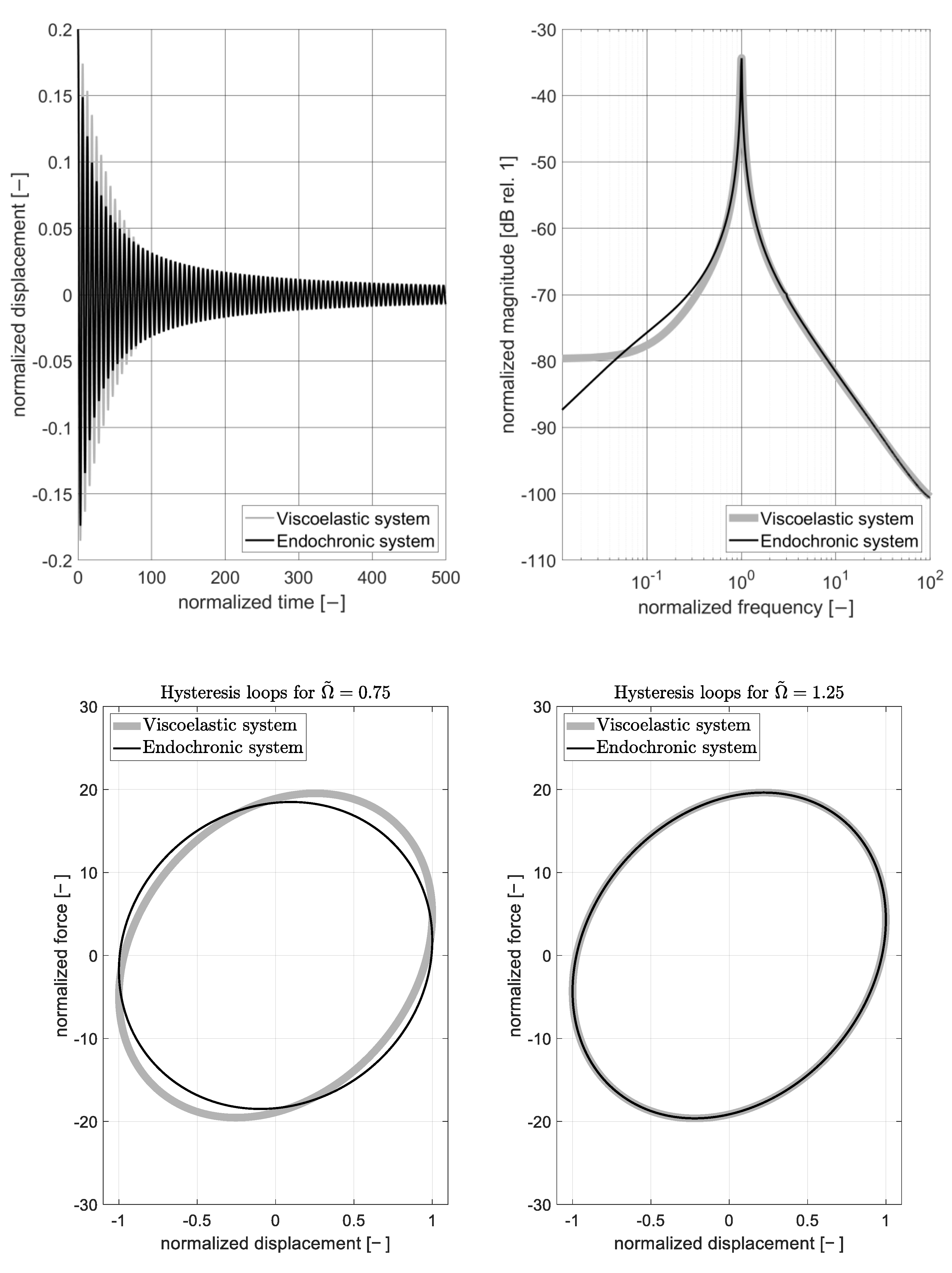
3.1. Energy Dissipation Described by Viscoelastic and Endochronic Rheological Models
3.2. Dynamic Behavior of Systems with One Degree of Freedom
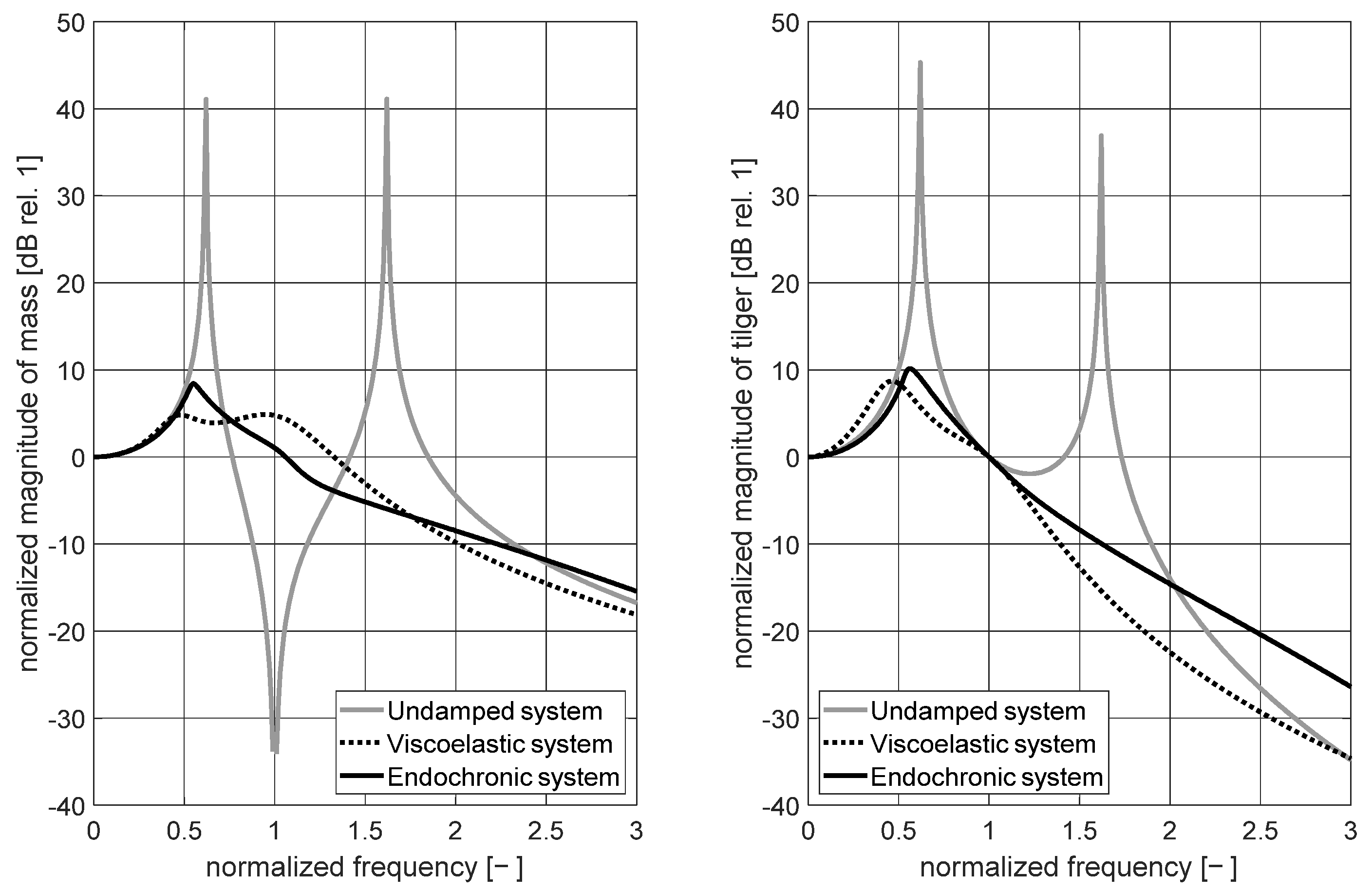
3.3. Discussion of Dynamic Behavior and Evaluation of Control Profit for Coupled Systems
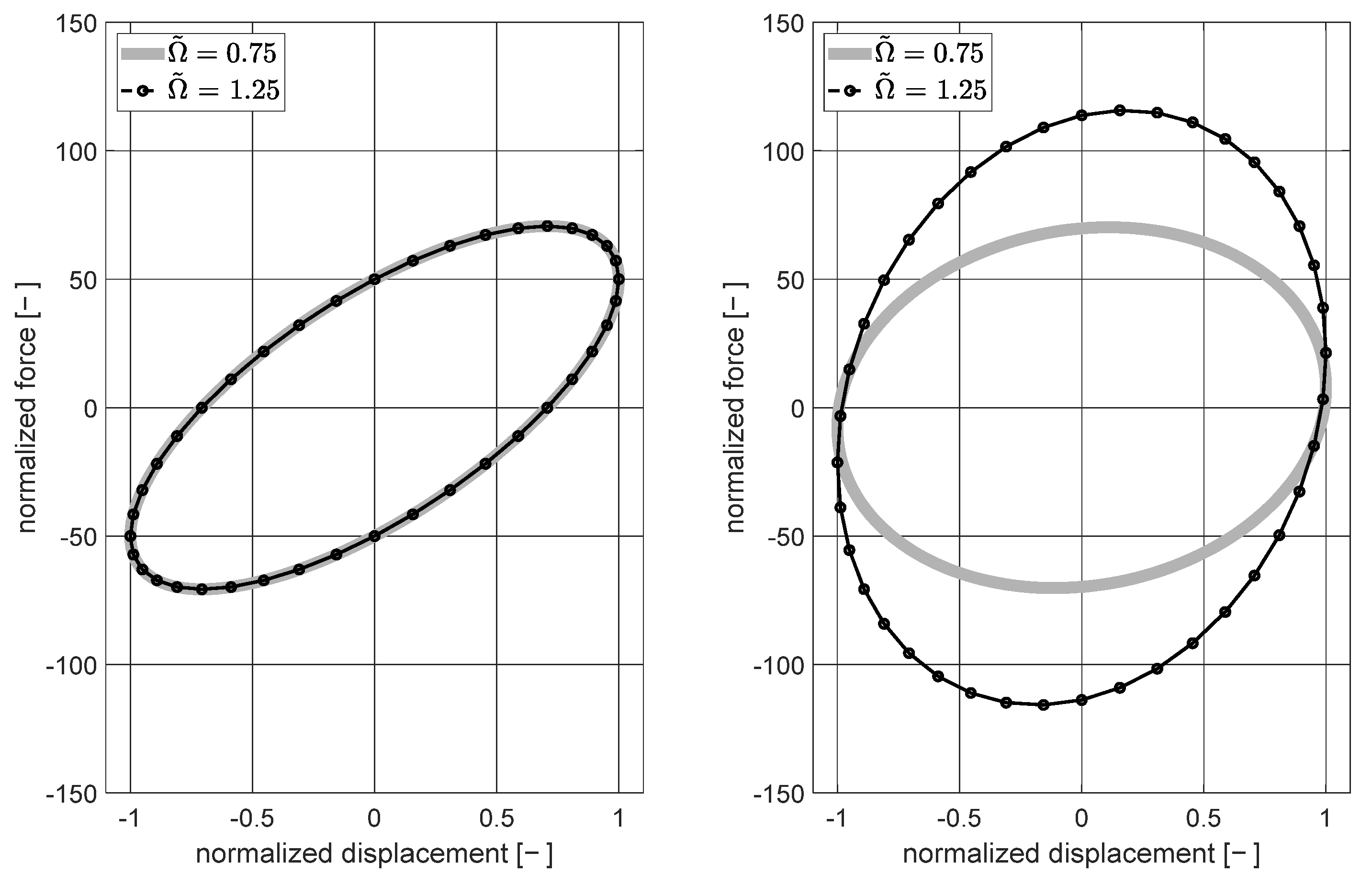
3.3.1. Time–Harmonic Analysis of Coupled Systems
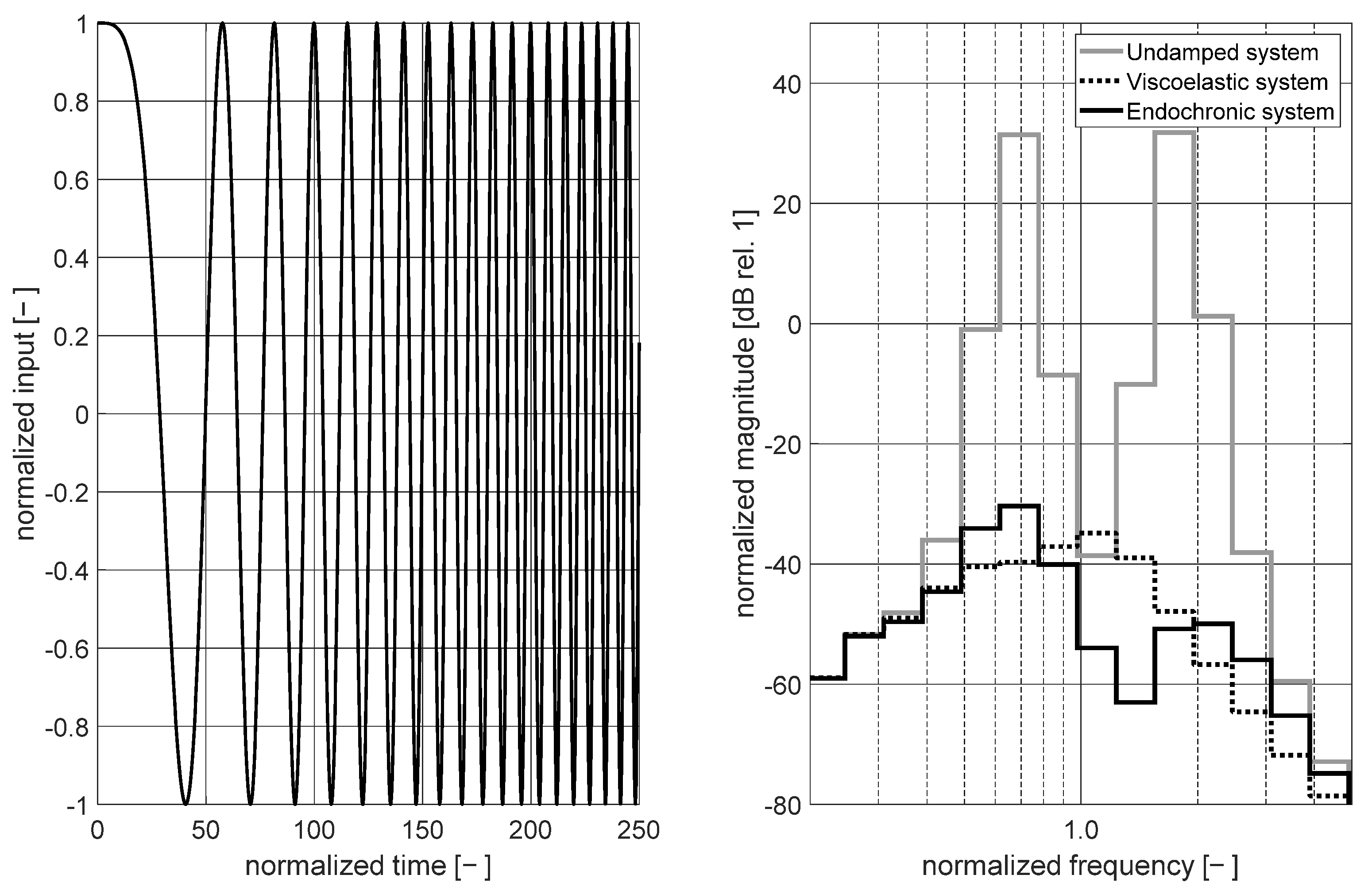
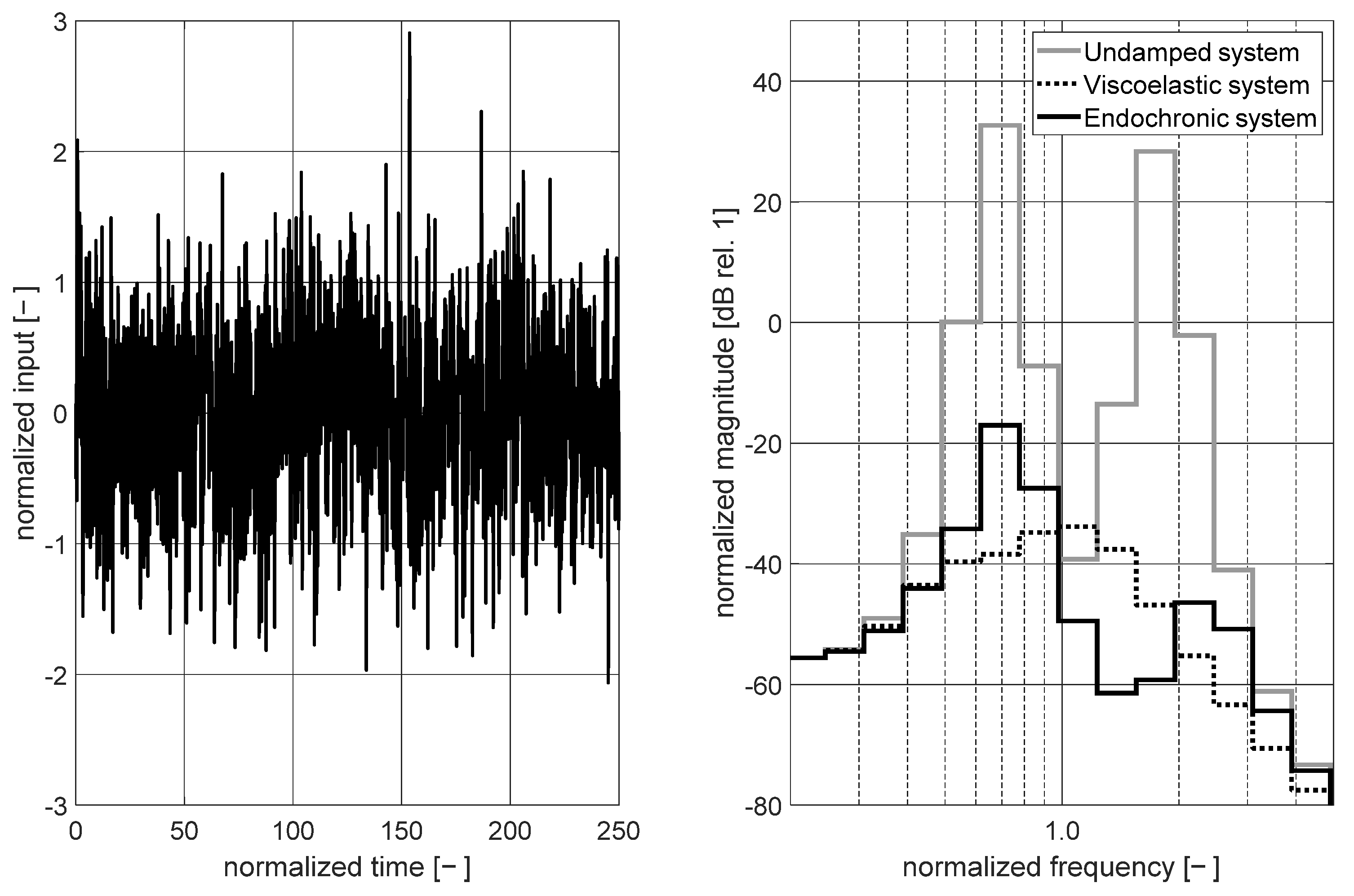
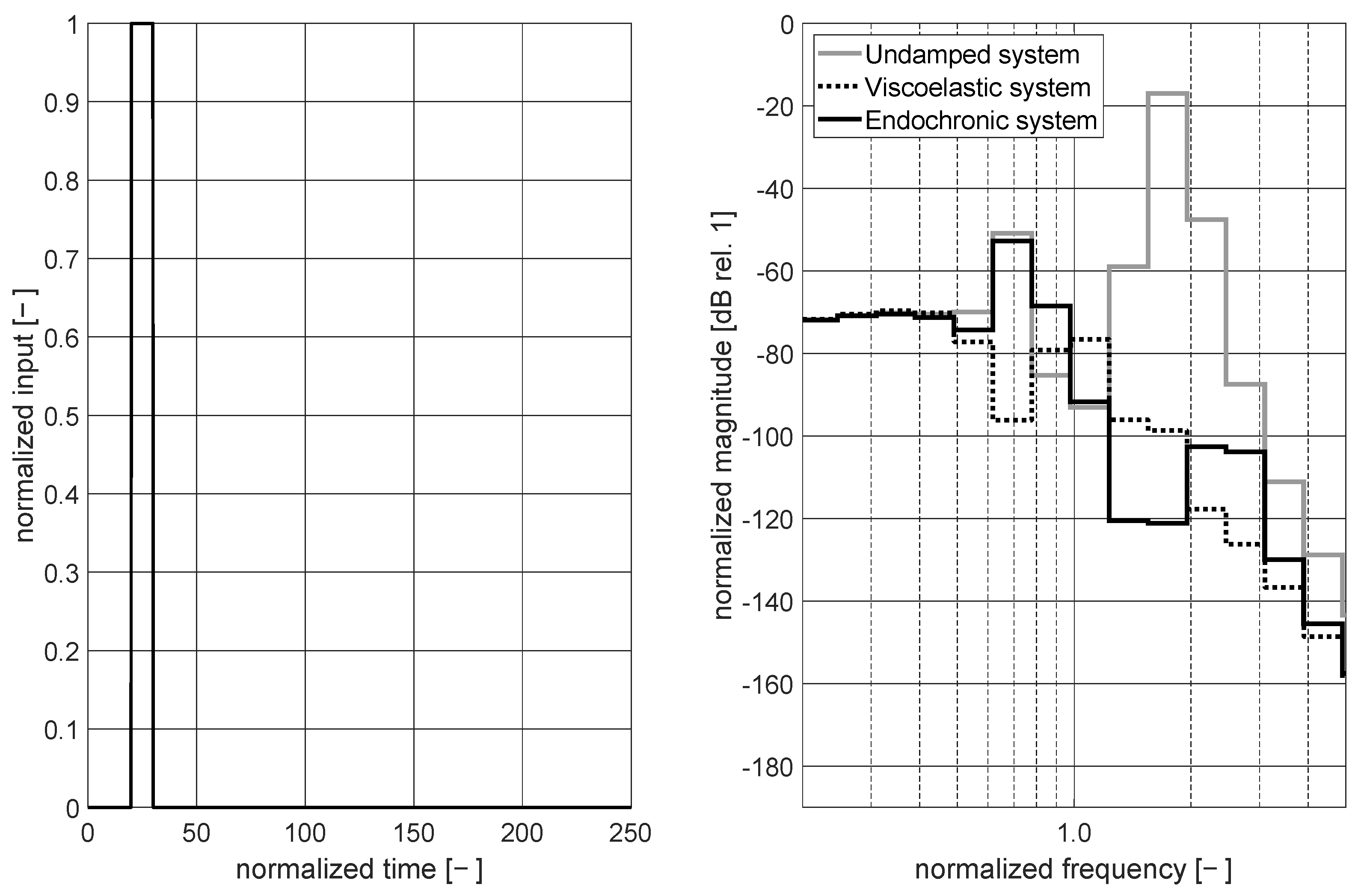
3.3.2. System Analysis Considering Broadband and Time-Varying Excitation Signals
3.3.3. Discussion of Noise-Control Potential
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Den Hartog, J.P. Mechanische Schwingungen, 1st ed.; Springer: Berlin, Germany, 1936. [Google Scholar]
- Stammers, C.W.; Sireteanu, T. Vibration control of machines by use of Semi-active dry friction damping. J. Sound Vib. 1998, 209, 671–684. [Google Scholar] [CrossRef]
- Gaul, L.W.; Nitsche, R. Friction control for vibration suppression. Mech. Syst. Signal Process 2000, 14, 139–150. [Google Scholar] [CrossRef]
- Valanis, K. A theory of viscoplasticity without a yield surface, Part I: General theory. Arch. Appl. Mech. 1971, 23, 517–533. [Google Scholar]
- Valanis, K. A theory of viscoplasticity without a yield surface, Part I: Application to mechanical behaviour of metals. Arch. Appl. Mech. 1971, 23, 535–551. [Google Scholar]
- Haupt, P. Viskoelastizität und Plastizität. In Thermodynamisch Konsistente Materialgleichungen, 1st ed.; Springer: Berlin, Germany, 1977. [Google Scholar]
- Krawietz, A. Materialtheorie. In Mathematische Beschreibung des Phänomenologischen Thermomechanischen Verhaltens, 1st ed.; Springer: Berlin, Germany, 1986. [Google Scholar]
- Kletschkowski, T.; Bertram, A.; Schomburg, U. Endochronic viscoplastic material models for filled PTFE. Mech. Mater. 2002, 34, 795–808. [Google Scholar] [CrossRef]
- Albrecht, F.; Kletschkowski, T. Simulation von Wellendichtringen mit einer Vielteilchenmethode. In Proceedings of the 19th ISC International Sealing Conference, Stuttgart, Germany, 12–13 October 2016. [Google Scholar]
- Crede, E.C. Vibration Isolation. In Handbook of Noise Control, 1st ed.; Harris, C.M., Ed.; McGraw-Hill: New York, NY, USA, 1957; Volume 1, pp. 13.1–13.42. [Google Scholar]
- Broch, J.T. Mechanical Vibration and Shock Measurements, 1st ed.; Brühl & Kjaer: Kopenhagen, Denmark, 1980. [Google Scholar]
- Fuller, C.R.; Elliott, S.J.; Nelson, P.A. Active Control of Vibration, 1st ed.; Academic Press: London, UK, 1996. [Google Scholar]
- Ciuncanu, M. The dynamic response of the elastomeric isolators modeled as Voigt-Kelvin to the action of the seismic motion. Appl. Mech. Mater. 2015, 801, 154–158. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F. Dynamic modeling and analysis of elastic isolation damping gears. J. Vibroeng. 2022, 24, 637–650. [Google Scholar] [CrossRef]
- Jurevicius, M.; Vekteris, V.; Turla, V.; Kilikevicius, A.; Viselga, G. Investigation of the dynamic efficiency of complex passive low-frequency vibration isolation systems. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 608–614. [Google Scholar] [CrossRef]
- Lin, C.Y.; Chen, Y.C.; Lin, C.H.; Chang, K.V. Constitutive equations for analyzing stress relaxation and creep of viscoelastic materials based on standard linear solid model derived with finite loading rate. Polymers 2022, 14, 2124. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y. Alternative form of standard linear solid model for characterizing stress relaxation and creep: Including a novel parameter for quantifying the ratio of fluids to solids of a viscoelastic solid. Front. Mater. (Sec. Mech. Mater.) 2020, 7, 7. [Google Scholar] [CrossRef]
- Menga, N.; Bottiglione, F.; Carbone, G. The nonlinear dynamic behavior of a Rubber-Layer Roller Bearing (RLRB) for vibration isolation. J. Sound Vib. 2019, 463, 114952. [Google Scholar] [CrossRef]
- Menga, N.; Bottiglione, F.; Carbone, G. Nonlinear viscoelastic isolation for seismic vibration mitigation. Mech. Syst. Signal Process 2021, 157, 107626. [Google Scholar] [CrossRef]
- Simo, J.C. A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: Part I. Continuum formulation. Comput. Methods Appl. Eng. 1988, 66, 199–219. [Google Scholar] [CrossRef]
- Vaiana, N.; Rosati, L. Analytical and differential reformulations of the Vaiana–Rosati model for complex rate-independent mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2023, 199, 110448. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Vestroni, F. Nonclassical response of oscillators with hysteresis. Nonlinear Dyn. 2023, 32, 235–258. [Google Scholar] [CrossRef]
- Formica, G.; Vaiana, N.; Rosati, L.; Lacarbonara, W. Pathfollowing of high-dimensional hysteretic systems under periodic forcing. Nonlinear Dyn. 2021, 103, 3515–3528. [Google Scholar] [CrossRef]
- Wang, Y.; Kletschkowski, T. Semi-active vibration control based on a smart exciter with an optimized electrical shunt circuit. Appl. Sci. 2021, 11, 9404. [Google Scholar] [CrossRef]
- ANSI S1.11-2004; Specification for Octave-Band and Fractional-Octave-Band Analog and Digital Filters. Acoustical Society of America: Melville, NY, USA, 2004.


| Type of Input Signal | Control Profit DA | Control Profit EA |
|---|---|---|
| sine | 19.7 dB | 20.9 dB |
| chirp | 65.0 dB | 62.9 dB |
| white Gaussian noise | 58.8 dB | 46.6 dB |
| shock | 46.9 dB | 35.4 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kletschkowski, T. Theoretical and Non-Dimensional Investigations into Vibration Control Using Viscoelastic and Endochronic Elements. Vibration 2023, 6, 1030-1047. https://doi.org/10.3390/vibration6040060
Kletschkowski T. Theoretical and Non-Dimensional Investigations into Vibration Control Using Viscoelastic and Endochronic Elements. Vibration. 2023; 6(4):1030-1047. https://doi.org/10.3390/vibration6040060
Chicago/Turabian StyleKletschkowski, Thomas. 2023. "Theoretical and Non-Dimensional Investigations into Vibration Control Using Viscoelastic and Endochronic Elements" Vibration 6, no. 4: 1030-1047. https://doi.org/10.3390/vibration6040060
APA StyleKletschkowski, T. (2023). Theoretical and Non-Dimensional Investigations into Vibration Control Using Viscoelastic and Endochronic Elements. Vibration, 6(4), 1030-1047. https://doi.org/10.3390/vibration6040060






