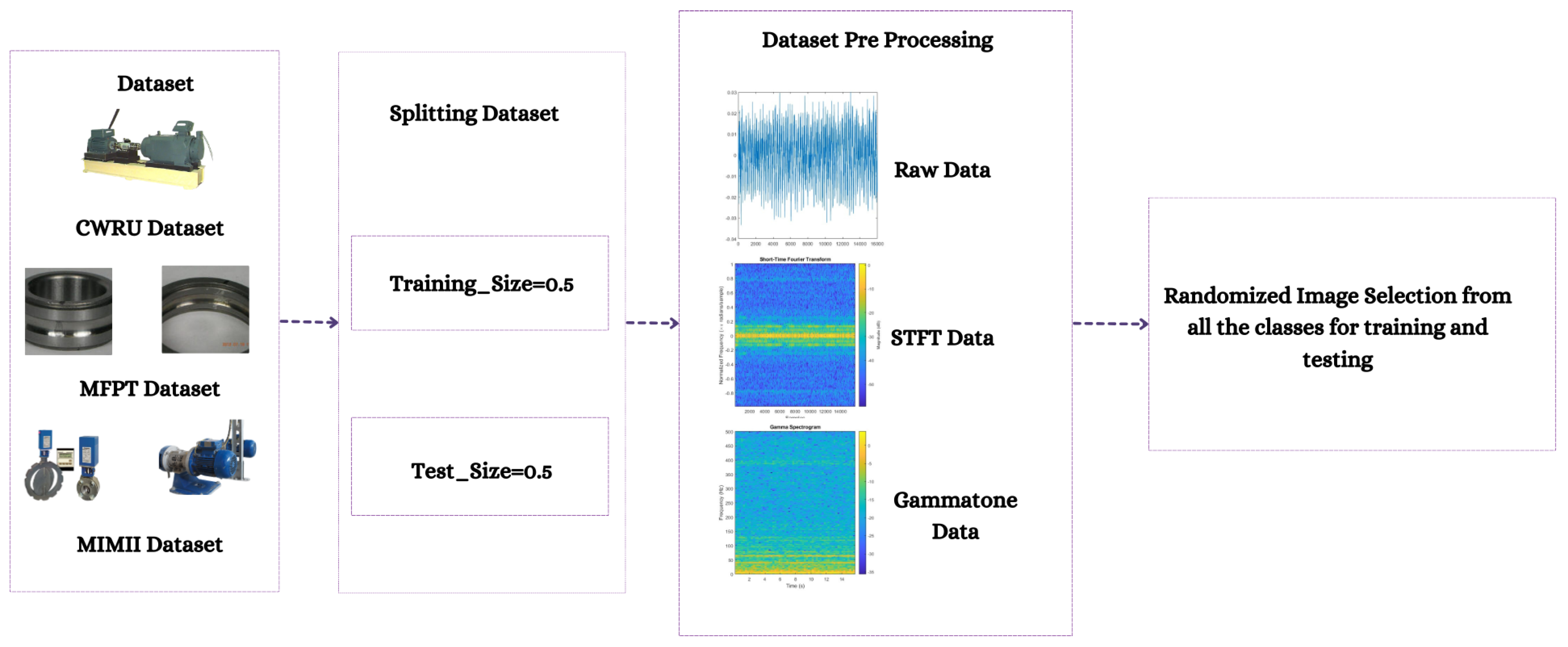
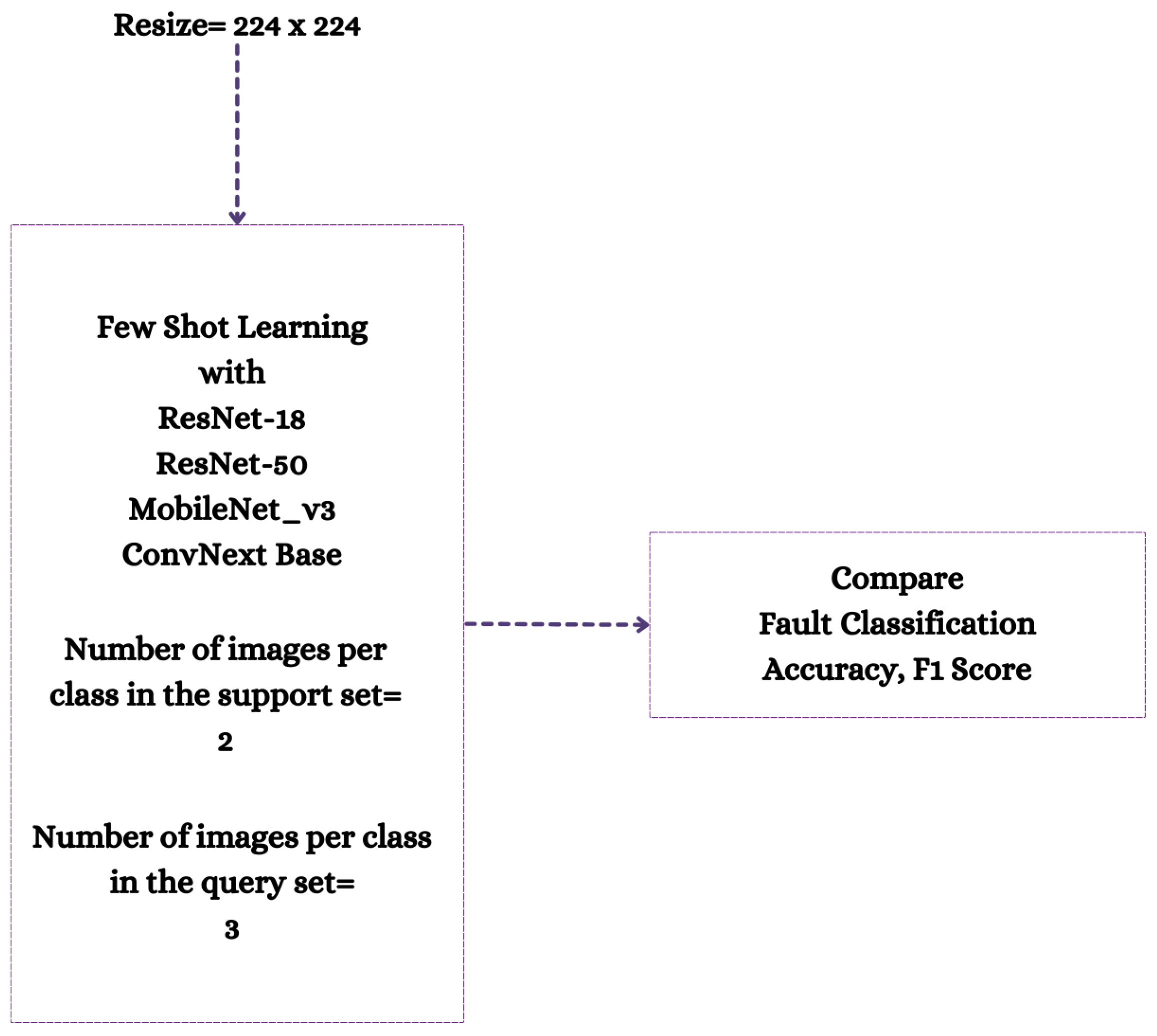
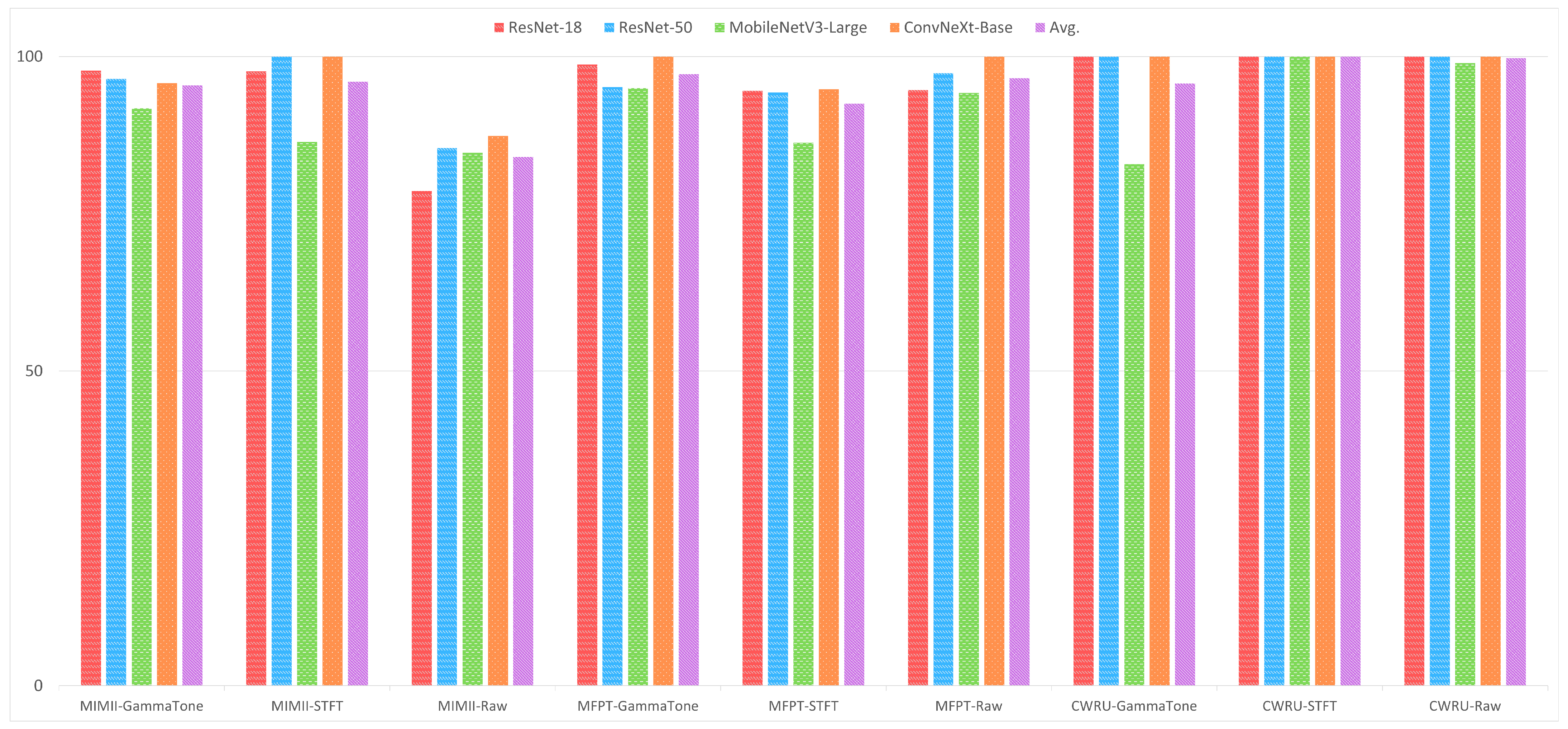
In emerging or nascent fields, as well as in professions where data collection is either difficult or costly, like industrial fault detection, tasks can be mastered using few-shot learning algorithms that generalize from limited data samples. To develop and advance few-shot learning models for machinery fault diagnosis, we followed a systematic research methodology. First, we acquired and curated a diverse repository of three datasets, including MFPT, MIMII, and CWRU. Next, we applied three data preprocessing techniques: 2D Raw Plotting, Short-Time Fourier Transform (STFT), and Gammatone Transformation. These techniques enhance feature extraction and representation, which are essential for building robust few-shot learning models. We then evaluated four architectures: ResNet-18, ResNet-50, ConvNext Base, and MobileNetV3-Large. We compared their performance under few-shot learning conditions, where labeled data is scarce. In
Figure 1 and
Figure 2, we have shown our approach in short.
We also conducted a detailed comparative analysis of the three data preprocessing methods to understand their impact on feature enhancement. Finally, we compared and contrasted the performance of the four architectures across the curated datasets. The analysis shed light on the intricacies of few-shot learning for machinery fault diagnosis, allowing us to pinpoint the best architecture to address the challenges posed by limited labeled data.
3.1. Datasets
Purohit et al. introduced the MIMII dataset, a benchmark dataset for sound-based machine fault diagnosis [
25]. The “MIMII Dataset” [
25] is an essential tool for industrial machine inquiry and inspection since it offers a vast array of audio recordings of three different kinds of industrial machines: fans, pumps, and sliders. Our understanding of malfunction detection and assessment in industrial settings has improved because of the use of this dataset. The diversity of recording conditions is a distinguishing feature of the dataset, enhancing its realism and practicality. While the slider’s sound was recorded in a hard −6 dB setting, the audio recordings of fans and pumps were made in a controlled 0 dB environment. The value of the dataset in developing reliable and adaptable fault detection systems is enhanced by the diverse recording settings that reflect real-world situations. Each audio file in the dataset maintains a consistent sample rate of 16,000 Hz, ensuring precise recording of machine noises.
The dataset has been divided into six classes (6-way). They are Fan Abnormal, Fan Normal, Pump Abnormal, Pump Normal, Slider Abnormal, and Slider Normal.
The MIMII dataset stands out for its collection of both typical and unusual machine sounds for each industrial category. This inclusion of unusual noises is important for training and assessing algorithms designed to detect errors in industrial machines. The dataset has been painstakingly divided into sub-levels to enable sophisticated analysis and feature extraction. Additionally, the dataset has been transformed using the Short-Time Fourier Transform (STFT), Gammatone treatment, and raw audio plot. These methods enable the extraction of relevant characteristics that could be crucial for differentiating between normal and pathological machine noises. The MIMII dataset offers a wide variety of real audio samples from different machines and environmental situations, making it a useful tool in the field of industrial machine study. The dataset offers a robust foundation for developing and validating innovative fault detection techniques. These methods could profoundly influence the realms of industrial maintenance and quality control due to their thorough organization, transformative analysis, and diverse sound profiles.
We went outside the bounds of a single dataset in our quest to improve diagnostic and prognostic algorithms for Condition-Based Maintenance (CBM), and we also made use of the “MFPT’s Dataset”. Stefaniak et al. introduced the MFPT dataset, a benchmark dataset for machine failure prediction [
26]. The MFPT dataset [
26] is a priceless tool created to aid in the testing and improvement of CBM systems. It was curated and compiled by Dr. Eric Bechhoefer, Chief Engineer of NRG Systems. The data that were collected from MFPT used the bearing shown in
Figure 4.
To hasten the development of CBM methods and systems, this dataset serves both researchers and CBM practitioners. The dataset has been divided into four classes (4-way). They are Baseline, Inner Race Fault Varied Load, Outer Race Fault, and Outer Race Fault Varied Load. The Condition-Based Maintenance Fault Database’s main goal is to provide a wide range of rigorously recorded datasets covering various bearing and gear problems. This dataset offers a thorough assessment of diagnostic and prognosis algorithms in diverse circumstances by including scenarios of known good and faulty states. Furthermore, The MFPT dataset has a sizable bearing analysis component. The dataset contains information from a customized bearing test rig to enable an in-depth investigation of bearing behavior. In addition to nominal bearing data, outer race faults under various loads, inner race faults under varied loads, and three actual faults, this test rig covers a wide range of situations. The test rig’s bearing complies with the following requirements: Roller diameter (rd): 0.235 Pitch diameter (PD): 1.245 Number of elements (ne): 8 Contact angle (ca): 0. The dataset is structured into distinct sets of conditions, as mentioned in
Table 2; each crucial for understanding different aspects of bearing behavior:
We carefully picked the dataset as well as further separated it into ten different samples to increase the depth of our study. Furthermore, we utilized the Short-Time Fourier Transform (STFT) and Gammatone Transformation, two essential signal processing methods. We were able to extract relevant characteristics from the audio data using these approaches, which may have shown patterns and differences between various circumstances that were otherwise obscured.
We also kept the raw signal so we could test our models. We wanted to examine the performance of our diagnostic and prognostic algorithms in their most raw form by including unprocessed data, ensuring resilience and accuracy across various settings.
In conclusion, our work involves a thorough investigation of the dataset from the MFPT, which is specially designed for developing CBM methods. We aimed to uncover insights and develop models capable of precisely diagnosing and predicting faults in industrial machinery through meticulous selection, transformative processing, and rigorous testing, ultimately assisting in the improvement and acceleration of Condition-Based Maintenance systems.
We included the priceless materials provided by the Case Western Reserve University (CWRU) Bearing Data Center [
27] in the last phase of our study inquiry. This archive is a veritable gold mine of ball-bearing test data, painstakingly recording both healthy and unhealthy bearing states. The information is crucial for the field of equipment condition monitoring and provides a rare look at how motor properties and bearing health interact. A Reliance Electric motor with a 2-horsepower capacity was used in the experimental configuration. The focus was placed on acceleration data, which was captured at locations near and far from the motor bearings. These online resources’ thorough documentation of test circumstances and bearing defect status for every experiment is one of their most notable qualities. The technique of electro-discharge machining (EDM) was used to introduce defects into the motor bearings. This resulted in the introduction of a variety of flaws at the inner raceway, rolling element (ball), and outside raceway, each with a diameter ranging from 0.007 inches to 0.040 inches. The test motor was subsequently rebuilt using these defective bearings, and vibration data were methodically gathered at various motor loads, from 0 to 3 horsepower, and corresponding motor speeds, from 1797 to 1720 RPM. The dataset includes several different situations, such as those using standard bearings as well as single-point drive end and fan end faults. High sampling rates—12,000 samples per second and 48,000 samples per second for drive end-bearing experiments—were used to carefully record the data. Data from the fan end bearings was consistently gathered at a rate of 12,000 samples per second.
The dataset has been divided into five classes (5-way). They are: 12 k RPM 0.007 Diameter 0 Load Baseline; 12 k RPM 0.007 Diameter 0 Load Inner Race; 48 k RPM 0.007 Diameter 0 Load Baseline; 48 k RPM 0.007 Diameter 0 Load Inner Race, Baseline.
Each dataset file encompasses critical information, such as fan and drive-end vibration data, in addition to the motor’s rotational speed. The variable naming conventions are designed to facilitate clarity and understanding. They are DE: drive-end accelerometer data, FE: fan-end accelerometer data, BA: base accelerometer data, Time: time series data, and RPM: rotations per minute during testing. Our plan for doing this research was properly thought out. We purposefully chose particular datasets, such as the 12 k drive end, 48 k drive end, and baseline datasets. We then selected a motor speed of around 1797 RPM and a motor load of 0 horsepower for each dataset. After this, we began the meticulous process of dividing each dataset into ten distinct subgroups. These subsets went through a thorough transformation procedure that included the Short-Time Fourier Transform (STFT), analysis of the Gammatone spectrograms, and the preservation of raw data. The complex preprocessing made it possible to train and evaluate our models.
In conclusion, our interaction with the CWRU Bearing Data Center’s resources constituted an important turning point in our study. We sought to identify patterns, trends, and fault-related differences that would aid in the creation of sophisticated fault detection and prognostic algorithms by utilizing meticulously documented ball-bearing test data. We aimed to increase machine health evaluation, predictive maintenance methods, and, eventually, the reliability of industrial machinery through meticulous division, transformation, and model assessment.
3.3. Few-Shot Learning
Researchers started looking into the idea of few-shot learning in the 1980s [
31], and it has since grown in significance as a means of addressing the problem of scarce data availability. With this method, we can successfully categorize data with a minimal number of instances. Let’s explore a few-shot learning’s core concepts after providing a thorough justification.
Consider teaching a model to distinguish between various items, such as cats and dogs. To aid the model’s learning, several instances of each would be required in conventional learning. However, with few-shot learning, we employ a more sophisticated strategy. This is how:
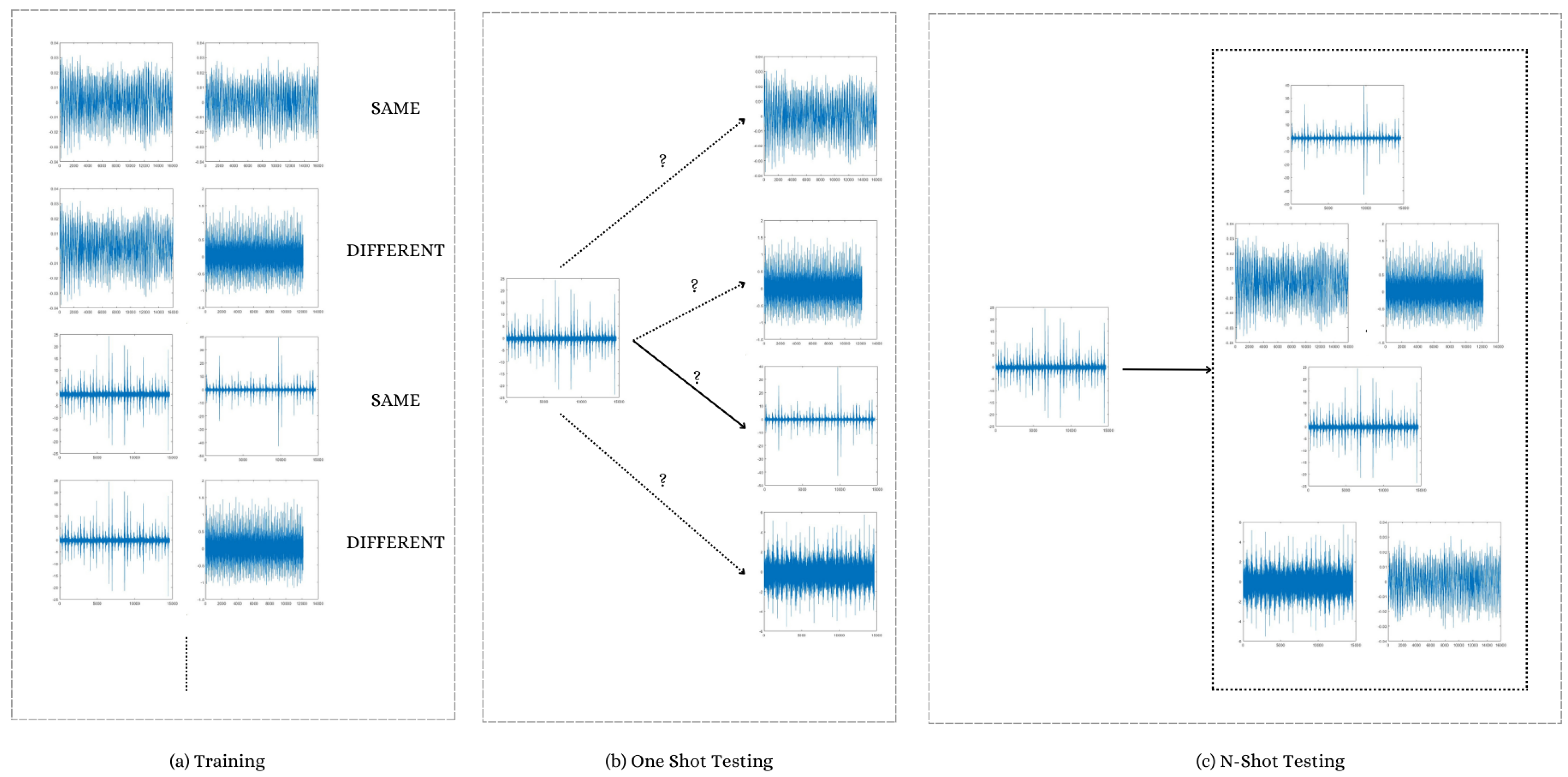
We first use pairs of data to train our model. These samples may be drawn from the same category (such as two distinct photographs of cats) or a different category (such as a cat image and a dog image). Whether the provided pairs of samples are similar or different must be taught to the model.
The model seeks to determine whether the two input samples, denoted mathematically as x and y, fall into the same category or distinct categories . The chance that x and y are comparable can be produced using a function called .
Later on, we separate our data into two sets for few-shot learning: the query set and the support set. Examples of various categories are included in the support set for the model to learn from. We utilize the query set’s many categories to assess the model’s effectiveness.
Finally, one-shot k-way and N-shot k-way are the two primary testing approaches. This is what they signify:
For the one-shot k-way, by using this technique, we assess the model’s capacity to categorize new categories using just a single sample for each category. The k indicates how many various categories we are testing. Mathematically, our goal is to categorize the query sets k categories using the knowledge we’ve gained from the support set.
Lastly, for N-shot k-way, like the one-shot strategy, the N-shot k-way method tests the model using N instances from each of the k categories.
The model must generate correct classifications based on this sparse data if we have N instances for each of the k categories in the query set.
Few-shot learning has two types of representations of the task. They are: Task
T, Support set
, and Query set
. The Embedding Function is:
Additionally, the Task-Specific Embedding functions are: Embedding of support set:
To find the Similarity, the mentioned equation is being used (known as Cosine similarity):
Attention weights for support set examples:
Weighted sum for classifying the query:
Lastly, the Cross-entropy loss:
In conclusion, the Few-shot learning approach shown in
Figure 9 is an effective method that lets us classify data even when there are very few instances. The model is trained with pairs of samples. The data is divided into query and support sets, and the model’s ability to classify new categories is assessed using a limited sample size.
3.4. Prototypical Network
Few-shot learning supports several networks for training the model. Researchers are always looking for new approaches to overcome the difficulties presented by situations with little available data and improve the effectiveness of few-shot learning models. Ravi and Larochelle provide a comprehensive survey of few-shot learning algorithms [
32]. Prototypical Networks, one of the significant techniques used, stands out because it creates category prototypes from support set samples and then uses prototype-query distance calculations to quickly and accurately classify query set samples. Similar to this, Relation Networks (RNs) excel at tasks requiring few trials by modeling relationships between pairs of inputs and emerging as potent tools for capturing complicated inter-instance correlations. Siamese Networks made up of weight-sharing twin networks, offer a convincing solution for one-shot or few-shot similarity tasks, complementing previous methods by using shared areas to learn about and quantify distances or similarities. This is especially useful in situations where learning is taking place remotely.
We have used a Prototypical Network for our research study. Prototypical networks are a simple yet effective few-shot learning algorithm [
33]. Among all the available architectures for few-shot learning, we used the prototype network in this study to tackle the challenge. In few-shot learning [
33,
34], prototype networks generalize to new classes using a metric-based methodology. According to [
1], prototypical networks outperformed other few-shot learning algorithms. To generate feature vectors and compute prototypes for recognized classes, they learn an embedding function. It is possible to estimate the similarity of classes accurately during classification by measuring the distance between query feature vectors and class prototypes. In few-shot learning, a support set of N-labeled samples
is supplied, where each
is the dimensional feature vector D and each
is the label of
.
stands for the support set’s classes. Prototype
is calculated using an embedding function
as follows:
The distance function d(.) is used to determine distance during classification; the likelihood that query point
X belongs to class
K may be represented as: