Abstract
The aim of this work is to perform an uncertainty propagation and global sensitivity analysis of a surface acoustic wave (SAW) gas sensor using finite elements and sparse polynomial chaos. The SAW gas sensor is modeled using finite elements (FEM) under COMSOL, and the sensitivity to DCM of its Sezawa mode is considered to be the quantity of interest. The importance of several geometrical (width and PIB thickness), material (PIB Young’s modulus and density), and ambient (pressure, temperature, and concentration) parameters on the sensor’s sensitivity is figured out by means of Sobol’ indices using sparse polynomial chaos expansions. It is shown that when the variability of the input parameters is low (inferior to 5%), the only impacting parameter is the cell width. However, when the variability of the input parameters reaches medium levels (around 10%), all the input parameters except the ambient temperature are impacting the sensor’s sensitivity. It is also reported that in the medium variability case, the sensor’s sensitivity experiences high variations that can lead to a degradation of its performances.
1. Introduction
Surface acoustic waves (SAW) were first described by Lord Rayleigh in his seminal paper [1] as acoustic waves propagating along the surface of an elastic material with an amplitude decaying exponentially with depth into the substrate. The resulting high energy density in the surface region of the substrate is the key feature that explains the high sensitivity of SAW-based sensors. In the past two decades, SAW have gained tremendous interest for sensor applications where the delay line device composed of a transmitting and a receiving interdigital transducer (IDT) on a piezoelectric substrate has become commonplace [2]. It must be pointed out that the piezoelectric substrate is connected only with the ease of producing SAW by IDTs [3]. In such a configuration, SAW propagation is characterized by an electric field resulting in an acousto-electric coupling. Different types of SAW can be distinguished: Rayleigh waves, Lamb waves, Love waves, and surface transverse waves—each of which has its advantages advantages and disadvantages with respect to sensitivity, stability, usability in liquids or gases, and fabrication complexity [4]. By placing the delay line in the feedback loop of an amplifier, an acoustic-wave oscillator is formed. SAW gas sensors have a sensitive layer, between the two IDTs transducers, that can absorb gas molecules from the surrounding atmosphere. This changes the propagation characteristics of the SAW because of the variations of the physical properties (density, conductivity, permittivity, etc.) of the sensing region. For gas sensors, two parallel delay lines, one without a sensitive layer serving as a reference and another with a sensitive layer are used. The response of the sensitive layer to the particular gas is detected as a difference between the two oscillators frequencies f and . A large variety of gas sensors have been conceived using such a configuration [5,6,7,8]. It is worth noting that other versatile gas sensors have been developed as well, including field effect transistor (FET) [9], bulk acoustic wave [10], resistance [11], quartz crystal microbalance [12], and self-powered [13]. Dichloromethane (or methylene dichloride, abbreviated herein as DCM) is a volatile organic compound that has received attention for its concentration reduction as it is known to be toxic to the central nervous system when the exposure level is high [14]. Recently, SAW have been used to identify the presence of VOCs in various applications [15,16] by covering the acoustic path with a thin layer of sensitive material. Due to its low density, low crystalline, good adhesion, and high permeability properties, PIB has demonstrated a higher sensitivity than other polymers to DCM [17]. This setup has been analyzed numerically by many authors in the literature [18,19,20,21]. Furthermore, over the years, many simulation techniques and methods have been developed and applied to surface wave acoustic modeling such as the coupling of modes method [22], Green’s function method [23], and finite element methods [24,25,26]. However, none of these approaches have proposed to treat the impact of uncertain parameters (geometry, materials properties, etc.) on the sensitivity of a SAW device. To the author’s best knowledge, there is no study in the literature that proposes a systematic way to propagate uncertainty of input parameters and to assess the impact of these parameters on the sensitivity of a SAW based gas sensor. In this work, uncertainty propagation and global sensitivity analyses based on finite elements and sparse polynomial chaos are proposed to assess in a systematic way the impact of various parameters on the sensitivity of SAW gas sensors. In Section 2, the finite element model of the SAW gas sensor is presented. Then in Section 3, uncertainty propagation is introduced, and in Section 4 global sensitivity analysis using Sobol’ indices is detailed. In Section 5, sparse polynomial chaos is introduced, and in Section 6 results and discussion are presented.
2. Simulation Model
A FEM simulation of the SAW gas sensor is performed using COMSOL.
2.1. Geometry
The sensor consists of an IDT etched onto a piezoelectric YZ-cut LiNbO (lithium niobate) substrate and covered with a thin polyisobutylene (PIB) film. IDTs used in SAW devices consist of hundreds of identical electrodes that can be each about 100 times longer than they are wide. The edge effects can therefore be neglected and the model geometry can be reduced to a periodic unit cell.
The width of the unit cell is equal to the acoustic wavelength that is fixed to 4 µm. The PIB layer thickness is 0.5 µm. Aluminum electrodes height is equal to and their width is while the space between them is . The height of the unit cell does not have to extend all the way to the bottom of the substrate but only a few wavelengths down, so that the SAW has almost died out at the lower boundary. The total height of the unit cell is chosen to be as shown in Figure 1.
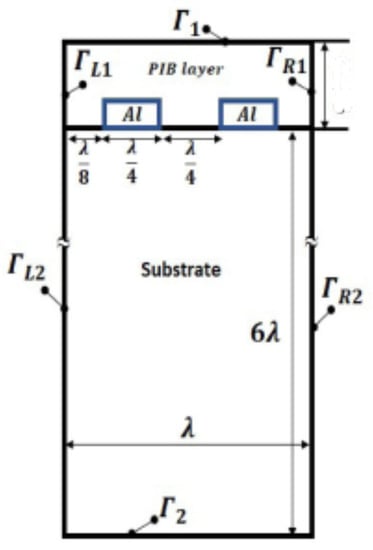
Figure 1.
Boundaries conditions.
2.2. Sensing Model
The mass of the PIB film increases as PIB selectively adsorbs DCM from the surrounding air. The adsorption of DCM gas is represented as a change in the density of the PIB film as follows:
with
where [27] is the air/PIB partition coefficient for DCM, M its molar mass and its concentration in parts per million, p the air pressure, T the ambient temperature, and R the gas constant. Any effects of the DCM adsorption on the material properties other than the density are neglected.
2.3. Material Properties
The material properties of the Al and LiNbO are implemented from the accessible built-in library of the COMSOL software. The density of PIB is 0.918 g/cm [27]. It is assumed that its Young’s modulus is 10 GPa, its Poisson’s ratio is 0.48, and its relative permittivity is 0.22.
2.4. Boundary Conditions
A 2D model with a plane strain (see Figure 1) hypothesis is adopted with periodic boundary conditions for displacement and electrical potential imposed at the left () and right () vertical boundaries. A zero displacement boundary condition is enforced at the bottom of the structure (). This does not contribute to any significant reflection from the lower boundary back into the bulk of the substrate as long as we are observing surface waves and in particular Rayleigh waves. As the electrodes have a much higher electrical conductivity compared to PIB and LiNbO, one can expect that each of them is iso-potential. The boundaries of the left electrode are set to electrical ground, and those of the right one are assigned to a floating potential with zero surface charge accumulation. This combination of electrical boundary conditions corresponds to an open circuit configuration, which is typically suitable for sensing applications. The boundary () is left mechanically free and with zero surface charge accumulation. All other boundaries are left to the default boundary conditions which are free for the solid mechanics interface and zero charge for the electrostatics interface, respectively.
2.5. Mesh
A structured quadrangular mesh is used for the whole geometry as shown in Figure 2.

Figure 2.
Mesh distribution for the top of the SAW unit cell. The length of one electrode is 1 µm.
For the PIB layer, a uniform distribution of 25 elements is used along the vertical edges (left and right) which results in a uniform distribution of more than 100 elements along the wavelength. It has been confirmed that the output did not change by increasing the number of elements along this edge. For the LiNbO region, 50 elements along the vertical edges with an arithmetic growing sequence are employed. It has been confirmed that the output did not vary by increasing the number of elements along this edge. The displacement and electrical potential discretized using quadratic serendipity elements.
2.6. Sensor Sensitivity
The SAW frequency should be an integer fraction of the width of the geometry. It can be determined by performing an eigenvalue analysis under COMSOL around a reference frequency. As the Rayleigh velocity in LiNbO is around 3488 m/s, the lowest SAW frequency , whose wavelength is equal to , should be around . Using as a reference frequency one can estimate the resonant frequencies of interest with the eigensolver ARPACK under COMSOL. As stated earlier, the adsorption of DCM on the PIB layer results in a change of density of the PIB layer which produces a frequency shift of the SAW sensor that is proportional to the DCM gas concentration. By conducting an eigenvalue analysis at (without DCM) and (with DCM), one can quantify this frequency shift . The sensitivity of the sensor is defined by:
3. Uncertainty Propagation (UP)
Uncertainty propagation aims at determining the output model response statistical characteristics (moments, probability density function, cumulative density function, etc.) knowing the probability distributions of the input parameters. A probabilistic framework is adopted with a complete probability space, where is a sample space, is a -algebra on the subsets of , a probability measure on , and M a strictly positive natural integer. Let a random parameter vector, whose joint probability density function is denoted by , which represents the input uncertain parameters. We suppose, the existence of a computational model whose entries are defined by . The real output Y of this model is defined by the mapping . In the last few years several methods for UP have been developed so far such as Monte Carlo simulation (MCS) [28] and polynomial chaos expansions (PCE) [29]. To mitigate the “curse of dimensionality” [30] alternatives approaches such as sparse polynomial chaos expansions [31,32], tensor decompositions [33], low-rank approximations [34], sparse grids [35,36], and their dimension adaptive [37] and spatially adaptive [38] variants have been established.
4. Global Sensitivity Analysis (GSA)
4.1. Generalities
Sensitivity analysis aims to describe how the variability of a model response is affected by the variability of each input. It is worth recalling that the variability of a parameter is quantified by its coefficient of variation which is equal to its standard deviation divided by its mean.
It is useful to spot unimportant variables and help reduce the dimension of the problem. It is generally performed in a black-box fashion, i.e., only based on the model response evaluations for a certain sample of inputs. Furthermore, it is often the case that each run of the model is expensive in terms of computer time and, therefore, sensitivity methods generally aim at reducing the number of model evaluations as much as possible. More specifically, global sensitivity analysis takes into account the whole input parameter domain and aims at decomposing the variance of the model output in terms of contributions of each single input parameter or combinations thereof. For an up-to-date review and classification of sensitivity analysis techniques one can see [39].
4.2. Sobol’ Indices
In this work, a variance based method is used for GSA. Sobol’ indices [40] are based on the idea of defining the expansion of the computational model into summands of increasing dimension. This decomposition only holds for independent input variables and is often referred to as ANOVA (ANalysis Of VAriance). The Sobol’s decomposition of a function of the random input parameter vector is defined as follows:
in such a way that
- The term is equal to the expected value of ;
- The expected value of the summands with respect to their own variables in (4) is equal to zero.
The expansion (4) is shown to be unique for integrable functions f and independent input vectors . The summands can be computed in a recursive manner as follows:
where the notation ∼ indicates that variables are excluded. The total variance can be computed by and the partial variances by
The latter equations have the property that they sum up to the total variance. A natural sensitivity measure can be defined by
which represents the contribution of the random variables to the total variance. is called first order Sobol’ index as it represents the effect of alone. The total Sobol’ index of variable is given by
Sobol’ indexes can be estimated using Monte-Carlo simulations [41,42], sparse PCE [43] or LRA [34]. In this work, sparse polynomial chaos expansions will be used to evaluate Sobol’ indices.
5. Sparse Polynomial Chaos Expansions
5.1. Polynomial Chaos Expansion
We recall the existence of a computational model whose entries are defined by the random parameter vector and its real output Y by the mapping . Hence as outlined in Section 4, Sobol’ indices can be computed for each entry of the random parameter vector . In the sequel, these entries are supposed to be independent. The polynomial chaos expansion of Y is defined as:
where are multivariate polynomials orthonormal with respect to and is a multi-index. The polynomials are built as product of one-dimensional orthonormal polynomials such as:
where is the order of the polynomial . Classical families of univariate orthonormal polynomials and the distributions to which they are orthonormal, also called Askey scheme orthonormal polynomials, are given in [29]. In practice the polynomial chaos expansion is truncated such as:
where is the set of multi-indices that corresponds to the total-degree truncation scheme. The total number of multivariate polynomial terms in this expansion is . The hyperbolic truncation scheme corresponds to a set defined by with q a real number. It is worth noticing that this set is less populated than the total degree truncation set that corresponds to . In practice, nor p or q are known and it is possible to infer them from the data with a basis adaptive approach that increases gradually p and/or q and takes the combination that decreases the leave-one-out error.
5.2. Sparse Least Squares Coefficients Computation
Once a set of multi-indices is chosen, the polynomials can be numbered from 0 to with such that . The truncated polynomial chaos expansion can also be re-written such as:
The first step is to evaluate the computational model at well chosen design points of the multi-variate parameter space. The model response at these locations are denoted by and the experimental design matrix is given by . Then the coefficients can be computed by ordinary least-squares [44] such as:
where is the vector of model responses. The vector of coefficients can also be computed by projection such as which needs the use of Gaussian or sparse quadrature schemes. To favor sparsity in high dimensions, a penalized or constrained least-squares problem can be solved, as proposed by the least angle regression (LAR) algorithm [32] or the orthogonal matching pursuit (OMP) algorithm [45]. These methods iteratively retrieve the polynomial basis elements that are most correlated with the current approximation residual and add them to the active set of regressors. The accuracy of the PCE for both algorithms through the iterations can be assessed by the computation of a posteriori error estimates such as leave-one-out error [31,46] as follows:
where is ith component of the vector and
5.3. Sobol’ Indices Computation
As the polynomials are orthonormal, it is easy to show that the mean and variance of polynomial chaos expansion are given by:
Let us define the as the set of tuples such that only the indices are nonzero. It has been shown in [43] that first order polynomial chaos based Sobol’ indices can be computed by
The total Sobol’ indices follow from (10) after replacing by .
5.4. Steps for Uncertainty Propagation and Global Sensitivity Analysis with Sparse Polynomial Chaos
The different steps involving the computation of Sobol’ indices are as follows:
- Form a DoCE by choosing appropriate design points of the multi-variate parameter space by a suitable sampling method (Monte Carlo, LHS, Sobol sequence, Halton sequence, etc.);
- Evaluate the computational model at these points and obtain the model responses ;
- Compute the polynomial chaos coefficients using sparse least squares (LAR or OMP algorithms);
- Use the polynomial chaos expansion to determine mean, variance, higher order moments and density of the output;
- Compute total Sobol’ indices for each variable using (19).
6. Results
6.1. Model Validation
To validate our finite element simulation model, we impose short circuit conditions by imposing a tension of 1 V on the right electrode while the left one is set to the ground. By performing a frequency analysis we can plot the logarithm of the admittance in seconds in function of the frequency in MHz as shown in Figure 3.
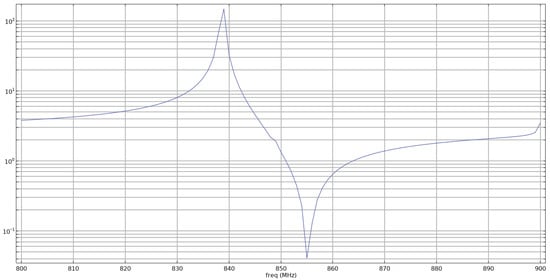
Figure 3.
Logarithm of the admittance (in seconds) versus the frequency in MHz.
One can see the existence of two peaks, the first corresponding to a resonant mode and the second to an anti-resonant mode whose respective frequencies and are 839 MHz and 855 MHz. The interval between these two frequencies can be used to determine the electro-mechanical coupling coefficient using [47]:
which results for the present model in a value of 0.0471. This implies a relative error less than 2% in comparison with the value of 0.048 documented in the literature [48]. Hence, we can conclude that the finite element model is reliable.
6.2. SAW Modes and Resonant Frequencies
The open circuit conditions are imposed again by specifying a floating potential with zero charge accumulation for the right electrode. The eigenvalue analysis allows to identify two SAW modes, the first at a frequency of 849 MHz (see Figure 4) that is a Rayleigh mode and the second at a frequency of 855 MHz (see Figure 5). The latter is called a Sezawa mode after the two seismologists Sezawa and Kanai that revealed it in 1935. The frequency of the second mode is confirmed by the work of [19].
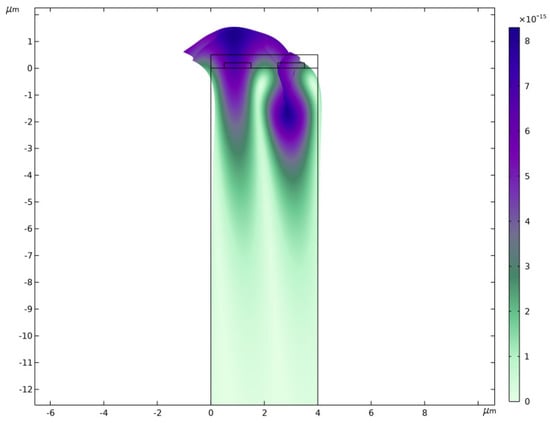
Figure 4.
Rayleigh mode (displacement).
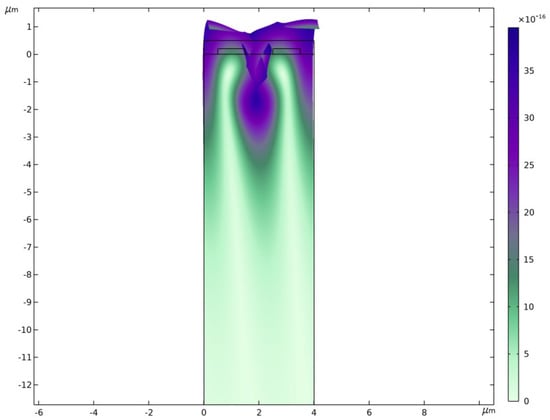
Figure 5.
Sezawa mode (displacement).
It can be visually seen in Figure 4 and Figure 5 that for the two modes the displacements fields are localized in the vicinity of the surface, acknowledging the denomination of surface acoustic waves. The Sesawa mode will be used in the sequel for frequency shift computation as it presents a higher phase velocity and electro-mechanical coupling coefficient than the Rayleigh mode [49].
6.3. Global Sensitivity Analysis
The COMSOL simulation model is converted into a MATLAB script that can be run using the COMSOL Livelink for MATLAB. It can then be used as a function with input parameters and outputs. The parameters whose impact on the sensor sensitivity is of interest are reported in Table 1 with their means or nominal values.

Table 1.
Parameters and nominal values.
It is worth noticing that the width of the electrodes is also changed since it depends on w. These parameters are supposed to be independent and follow log-normal laws with the same coefficient of variation % (the standard deviation being the mean times the coefficient of variation) that will be varied in the sequel. In the present work we have deliberately chosen to restrict our attention on the impact of ambient parameters such as temperature or pressure as well as PIB layer related parameters such as thickness, modulus, and density since the SAW velocity shift is induced by the interaction of VOC molecules with the PIB sensing layer. It is beyond the scope of this article to study the effect of the material and geometrical parameters relative to the LiBNO layer as it would have resulted in a tedious high dimensional global sensitivity analysis problem requiring many resources to be dealt with.
The sampling plan (DoCE) consists of a points Sobol sequence on which a sparse PCE is fitted thanks to the UqLab toolbox [50]. The sparse regression problem is solved using the OMP algorithm with a degree adaptive strategy (the maximal degree being varied from 1 to 17 and the sparse PCE with the lowest leave-one-out error is selected) along with the total degree truncation scheme. The number of points of the DoCE are varied and the convergence of Sobol’ indices monitored.
6.3.1. Low Input Variability
A scatter-plot matrix of a DoCE of 50 points is shown in Figure 6. It represents pairwise scatterplots of one parameter versus the other and on the diagonal the histogram of the sampled values for each parameter. One can notice that the parameter space is well covered in all its dimensions with such a sampling as there are no gaps appearing in the scatter-plots.
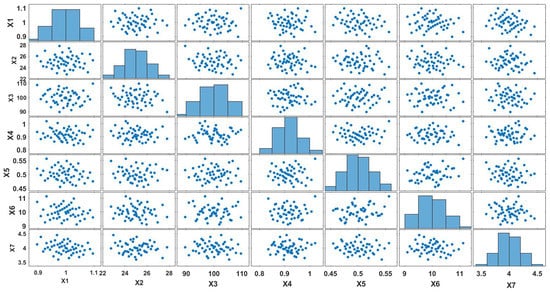
Figure 6.
Scatterplot of a sampling plan with 50 points using a Sobol sequence.
To check the convergence of Sobol’ indices, the number of points of the DoCE is varied. The leave-one-out error of the obtained sparse PCE is less than for each sampling plan. Table 2 shows the Sobol’ indices for and points. It is worth noticing that the Sobol’ indices do not vary much with increasing the number of points of the sampling plan, pointing out that convergence is almost reached.

Table 2.
Sobol’ indices for and .
For points, the sparse PCE has a maximal degree of 13, a leave-one-out error of , a sparse basis of 148 elements, a mean of 2.22, and a coefficient of variation of 12.5%. The corresponding Sobol’ indices are represented in Figure 7 where one can easily notice that only one parameter is of importance, the width of the unit cell (parameter ), all the other parameters having a minor effect on the sensor’s sensitivity. Moreover, the a coefficient of variation in the output, i.e., the sensor’s sensitivity , is of about 12.5% which is about 2.5 times as much as the input variability of 5%. So for low input variability, the situation remains quite controllable since there is only one parameter to control to ensure robust performances of the gas sensor. This can be well understood if a large number of SAW gas sensors for which the sensitivity could be measured are considered if within the design process small variations are tolerated in the PIB thickness, PIB modulus, PIB density, and cell width and that the ambient pressure, temperature and DCM concentration also experience small variations then one could expect moderate variations in SAW gas sensor’s sensitivity that could be attributed mainly to the variations in the cell width. In the linear regime, in the case of mass loading, sensor’s sensitivity is given by [51]:
where is the SAW velocity and a mass coefficient. This expression shows that the cell width is twice as impacting as the others parameters which explains the high sensitivity to sensor’s sensitivity to the cell width. Furthermore, by performing a Monte-Carlo simulation on the sparse PCE, it is also possible to obtain the density of the sensor’s sensitivity as can be seen in Figure 8. The output density is characteristic of a log normal distribution with moderate dispersion.
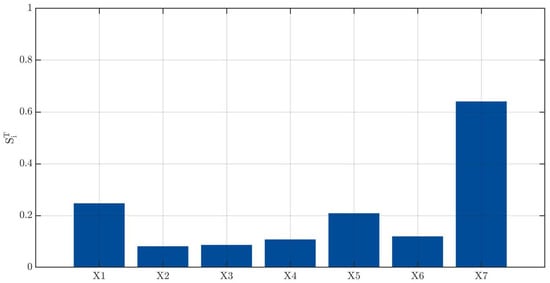
Figure 7.
Total Sobol’ indices of the parameters .
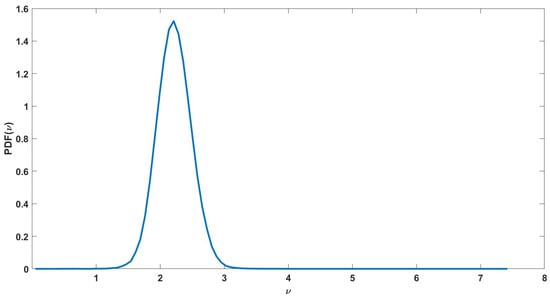
Figure 8.
Probability density of the sensor’s sensitivity using evaluations of the sparse PCE for low input variability.
6.3.2. Medium Input Variability
A scatterplot matrix of a DoCE of 50 points is shown in Figure 9. One can notice that the parameter space is well covered in all its dimensions with such a sampling as there are no gaps appearing in the scatter-plots.
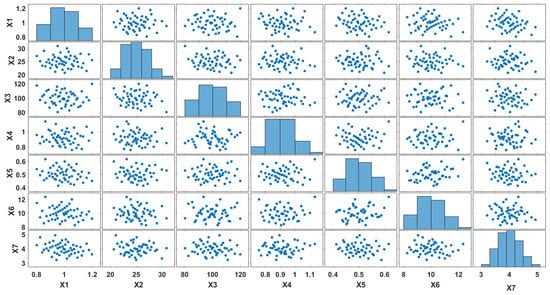
Figure 9.
Scatterplot of a sampling plan with 50 points using a Sobol sequence.
To check the convergence of Sobol’ indices, the number of points of the DoCE is varied. The leave-one-out error of the obtained sparse PCE is less than for each sampling plan. Figure 10 represents the Sobol’ indices for different values of . It is worth noticing that beginning from 250 points there is a stabilization of the Sobol’ indices and the indices obtained for are retained for analysis.
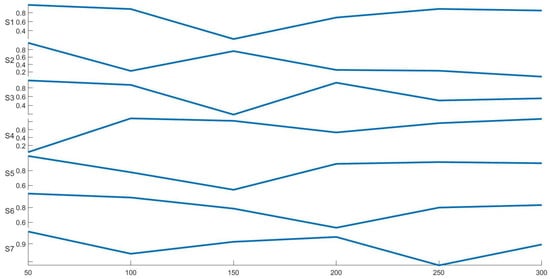
Figure 10.
Sobol’ indices for varying between 50 and 300.
For points, the sparse PCE has a maximal degree of 16, a leave-one-out error of , a sparse basis of 297 elements, a mean of 2.24, and a coefficient of variation of 95%. As can be seen in Figure 11, almost all the parameters impact the sensor sensitivity except the ambient temperature that seems to have little effect. One reason to that may be that the model does not take into account thermomechanical effects. Moreover, the coefficient of variation in the output, i.e., the sensor’s variability, is about 95% so about ten times the input variability highlighting strong variations of the sensor’s sensitivity. In this case, in order to guarantee robust performances of the gas sensor it is mandatory to control all the parameters except one. This can be well understood if a large number of SAW gas sensors for which the sensitivity could be measured are considered if within the design process moderate variations are tolerated in the PIB thickness, PIB modulus, PIB density, and cell width and that the ambient pressure, temperature, and DCM concentration also experience moderate variations then one could expect very high variations in SAW gas sensor’s sensitivity that could be attributed to all the previously cited parameters. By performing a Monte-Carlo simulation on the sparse PCE, it is also possible to obtain the density of the sensor’s sensitivity as can be seen in Figure 12. The output density flattens and its mode noting a characteristic behavior of log normal densities with high variance.
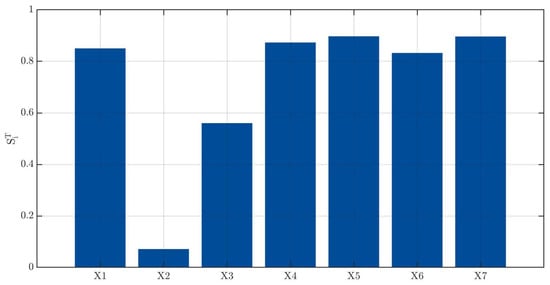
Figure 11.
Total Sobol’ indices of the parameters .
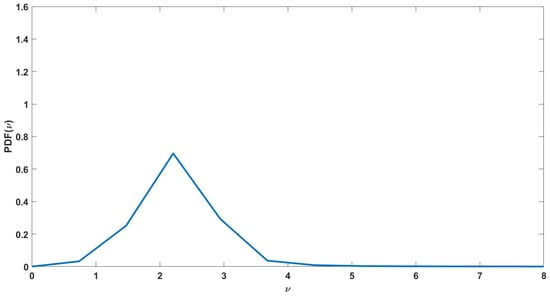
Figure 12.
Probability density of the sensor’s sensitivity using evaluations of the sparse PCE for medium input variability.
7. Conclusions
In this work, a COMSOL finite element model of a SAW gas sensor have been used to build a sparse PCE metamodel to estimate the impact of different parameters on the sensor’s sensitivity. A highly accurate sparse PCE metamodel is obtained by using a Sobol sequence sampling and a degree adaptive scheme along with the OMP algorithm for sparse regression. The Sobol’ indices computed from this metamodel show that if the cell width is the most impacting parameter when the variability of the input parameters is low, it is not the case for the medium variability case where all the parameters except one become important. It is also shown that the sensor’s sensitivity experiences high variations in the medium variability case that can degrade the performance of the sensor. In perspective, the methodology can be easily applied to layered SAW gas sensor structures that show promising results especially in the range of high sensitivities [2].
Funding
This research received no external funding.
Acknowledgments
The author performed this work will he was enjoying his stay between 2019 and 2022 at ENSIM, 1 Rue Aristote, 72000 Le Mans, France.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, s1-17, 4–11. [Google Scholar] [CrossRef]
- Jakubik, W.P. Surface acoustic wave-based gas sensors. Thin Solid Films 2011, 520, 986–993. [Google Scholar] [CrossRef]
- White, R.M.; Voltmer, F.W. Direct piezoelectric coupling to surface elastic waves. Appl. Phys. Lett. 1965, 7, 314–316. [Google Scholar] [CrossRef]
- Vellekoop, M. Acoustic wave sensors and their technology. Ultrasonics 1998, 36, 7–14. [Google Scholar] [CrossRef]
- Thompson, M.; Stone, D.C. Surface-Launched Acoustic Wave Sensors: Chemical Sensing and Thin-Film Characterization; Wiley-Interscience: Hoboken, NJ, USA, 1997; Volume 144. [Google Scholar]
- D’Amico, A.; Palma, A.; Verona, E. Hydrogen sensor using a palladium coated surface acoustic wave delay-line. In Proceedings of the 1982 Ultrasonics Symposium, San Diego, CA, USA, 27–29 October 1982; pp. 308–311. [Google Scholar] [CrossRef]
- Galipeau, J.; LeGore, L.; Snow, K.; Caron, J.; Vetelino, J.; Andle, J. The integration of a chemiresistive film overlay with a surface acoustic wave microsensor. Sens. Actuators B Chem. 1996, 35, 158–163. [Google Scholar] [CrossRef]
- Urbańczyk, M.; Jakubik, W.; Kochowski, S. Investigation of sensor properties of copper phthalocyanine with the use of surface acoustic waves. Sens. Actuators B Chem. 1994, 22, 133–137. [Google Scholar] [CrossRef]
- Yu, R.; Niu, S.; Pan, C.; Wang, Z. Piezotronic effect enhanced performance of Schottky-contacted optical, gas, chemical and biological nanosensors. Nano Energy 2015, 14, 312–339. [Google Scholar] [CrossRef]
- Seh, H.; Hyodo, T.; Tuller, H. Bulk acoustic wave resonator as a sensing platform for NOx at high temperatures. Sens. Actuators B Chem. 2005, 108, 547–552. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, M.; Luo, X.; Tai, H.; Jiang, Y.; Yang, M.; Xie, G.; Su, Y. Ni-Co-P hollow nanobricks enabled humidity sensor for respiratory analysis and human-machine interfacing. Sens. Actuators B Chem. 2022, 370, 132441. [Google Scholar] [CrossRef]
- Wang, S.; Xie, G.; Su, Y.; Su, L.; Zhang, Q.; Du, H.; Tai, H.; Jiang, Y. Reduced graphene oxide-polyethylene oxide composite films for humidity sensing via quartz crystal microbalance. Sens. Actuators B Chem. 2018, 255, 2203–2210. [Google Scholar] [CrossRef]
- Su, Y.; Chen, S.; Liu, B.; Lu, H.; Luo, X.; Chen, C.; Li, W.; Long, Y.; Tai, H.; Xie, G.; et al. Maxwell displacement current induced wireless self-powered gas sensor array. Mater. Today Phys. 2023, 30, 100951. [Google Scholar]
- Estill, C.F.; Spencer, A.B. Case study: Control of methylene chloride exposures during furniture stripping. Am. Ind. Hyg. Assoc. J. 1996, 57, 43–49. [Google Scholar] [CrossRef]
- Li, S.; Wan, Y.; Su, Y.; Fan, C.; Bhethanabotla, V.R. Gold nanoparticles amplified surface acoustic wave biosensors for immunodetection. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]
- He, S.-T.; Gao, Y.-B.; Shao, J.-Y.; Lu, Y.-Y. Application of saw gas chromatography in the early screening of lung cancer. In Proceedings of the 2015 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Jinan, China, 30 October–2 November 2015; pp. 22–25. [Google Scholar] [CrossRef]
- Joo, B.-S.; Lee, J.-H.; Lee, E.-W.; Song, K.-D.; Lee, D.-D. Polymer film saw sensors for chemical agent detection. In Proceedings of the Conference on Sensing Technology, Palmerston North, New Zealand, 21–23 November 2005; pp. 307–310. [Google Scholar]
- Abraham, N.; Krishnakumar, R.R.; Unni, C.; Philip, D. Simulation studies on the responses of ZnO-CuO/CNT nanocomposite based saw sensor to various volatile organic chemicals. J. Sci. Adv. Mater. Devices 2019, 4, 125–131. [Google Scholar] [CrossRef]
- Kumar, M.; Bhadu, D. Design Performance and Frequency Response Analysis of SAW-Based Sensor for Dichloromethane Gas Sensing Amidst the COVID-19. J. Vib. Eng. Technol. 2021, 9, 725–732. [Google Scholar] [CrossRef]
- Moustafa, M.; Alzoubi, T.; Elnaggar, M.; Laouini, G. Finite element analysis of multilayered ZnO/AIN/Si strucuture saw sensor for efficient VOCs gas detection. Rom. J. Phys. 2021, 66, 607. [Google Scholar]
- Ionescu, V. Design and analysis of a Rayleigh saw resonator for gas detecting applications. Rom. J. Phys. 2015, 60, 502–511. [Google Scholar]
- Hashimoto, K.Y.; Endoh, G.; Yamaguchi, M. Coupling-of-modes modelling for fast and precise simulation of leaky surface acoustic wave devices. In Proceedings of the 1995 IEEE Ultrasonics Symposium. Proceedings. An International Symposium, Seattle, WA, USA, 7–10 November 1995; Volume 1, pp. 251–256. [Google Scholar]
- Tewary, V. Green’s-function method for modeling surface acoustic wave dispersion in anisotropic material systems and determination of material parameters. Wave Motion 2004, 40, 399–412. [Google Scholar] [CrossRef]
- El Gowini, M.M.; Moussa, W.A. A finite element model of a mems-based surface acoustic wave hydrogen sensor. Sensors 2010, 10, 1232–1250. [Google Scholar] [CrossRef]
- Kabir, K.M.M.; Matthews, G.I.; Sabri, Y.M.; Russo, S.P.; Ippolito, S.J.; Bhargava, S.K. Development and experimental verification of a finite element method for accurate analysis of a surface acoustic wave device. Smart Mater. Struct. 2016, 25, 035040. [Google Scholar] [CrossRef]
- Xu, G. Direct finite-element analysis of the frequency response of a lithium niobate saw filter. Smart Mater. Struct. 2000, 9, 973–980. [Google Scholar] [CrossRef]
- Ho, C.K.; Lindgren, E.R.; Rawlinson, K.S.; McGrath, L.K.; Wright, J.L. Development of a surface acoustic wave sensor for in-situ monitoring of volatile organic compounds. Sensors 2003, 3, 236–247. [Google Scholar] [CrossRef]
- Gobet, E. Monte-Carlo Methods and Stochastic Processes: From Linear to Non-Linear; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The wiener–askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Bellman, R.; R Corporation. Adaptive Control Processes: A Guided Tour: R-350; Rand Corporation: Santa Monica, CA, USA, 1961. [Google Scholar]
- Blatman, G. Adaptive Sparse Polynomial Chaos Expansions for Uncertainty Propagation and Sensitivity Analysis. Ph.D. Thesis, Université Blaise Pascal, Clermont-Ferrand, France, 2009. [Google Scholar]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Konakli, K.; Sudret, B. Global sensitivity analysis using low-rank tensor approximations. Reliab. Eng. Syst. Saf. 2016, 156, 64–83. [Google Scholar] [CrossRef]
- Smoliak, S. Quadrature and interpolation formulae on tensor products of certain classes of functions. Dokl. Akad. Nauk SSSR 1963, 148, 1042–1045. [Google Scholar]
- Bungartz, H.-J.; Griebel, M. Sparse grids. Acta Numer. 2004, 13, 147–269. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Dimension–adaptive tensor–product quadrature. Computing 2003, 71, 65–87. [Google Scholar] [CrossRef]
- Rehme, M.F.; Franzelin, F.; Pflueger, D. B-splines on sparse grids for surrogates in uncertainty quantification. Reliab. Eng. Syst. Saf. 2021, 209, 107430. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A Review on Global Sensitivity Analysis Methods; Springer: Boston, MA, USA, 2015; pp. 101–122. [Google Scholar] [CrossRef]
- Sobol, I. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Janon, A.; Klein, T.; Lagnoux, A.; Nodet, M.; Prieur, C. Asymptotic normality and efficiency of two Sobol index estimators. ESAIM Probab. Stat. 2014, 18, 342–364. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Berveiller, M.; Sudret, B.; Lemaire, M. Stochastic finite element: A non intrusive approach by regression. Eur. J. Comput. Mech./Rev. Eur. Méc. Numér. 2006, 15, 81–92. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Blatman, G.; Sudret, B. Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2010, 95, 1216–1229. [Google Scholar] [CrossRef]
- Raghib, A.A.B.M.R.M.; Nordin, A.N. Analysis of electromechanical coupling coefficient of surface acoustic wave resonator in zno piezoelectric thin film structure. In Proceedings of the 2014 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), Cannes, France, 1–4 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids I: Free and Guided Propagation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Hadj-Larbi, F.; Serhane, R. Sezawa saw devices: Review of numerical-experimental studies and recent applications. Sens. Actuators A Phys. 2019, 292, 169–197. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in Matlab. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management, Proceedings of the Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty Modeling and Analysis (ISUMA), Liverpool, UK, 13–16 July 2014; ASCE Library: Reston, VA, USA, 2014; pp. 2554–2563. [Google Scholar] [CrossRef]
- Ricco, A.; Martin, S. Thin metal film characterization and chemical sensors: Monitoring electronic conductivity, mass loading and mechanical properties with surface acoustic wave devices. Thin Solid Films 1991, 206, 94–101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).