Assessing the Welfare of Technicians during Transits to Offshore Wind Farms
Abstract
1. Introduction
1.1. The Effect of Vessel Motions on Technician Welfare
1.2. International Standards
2. Materials and Methods
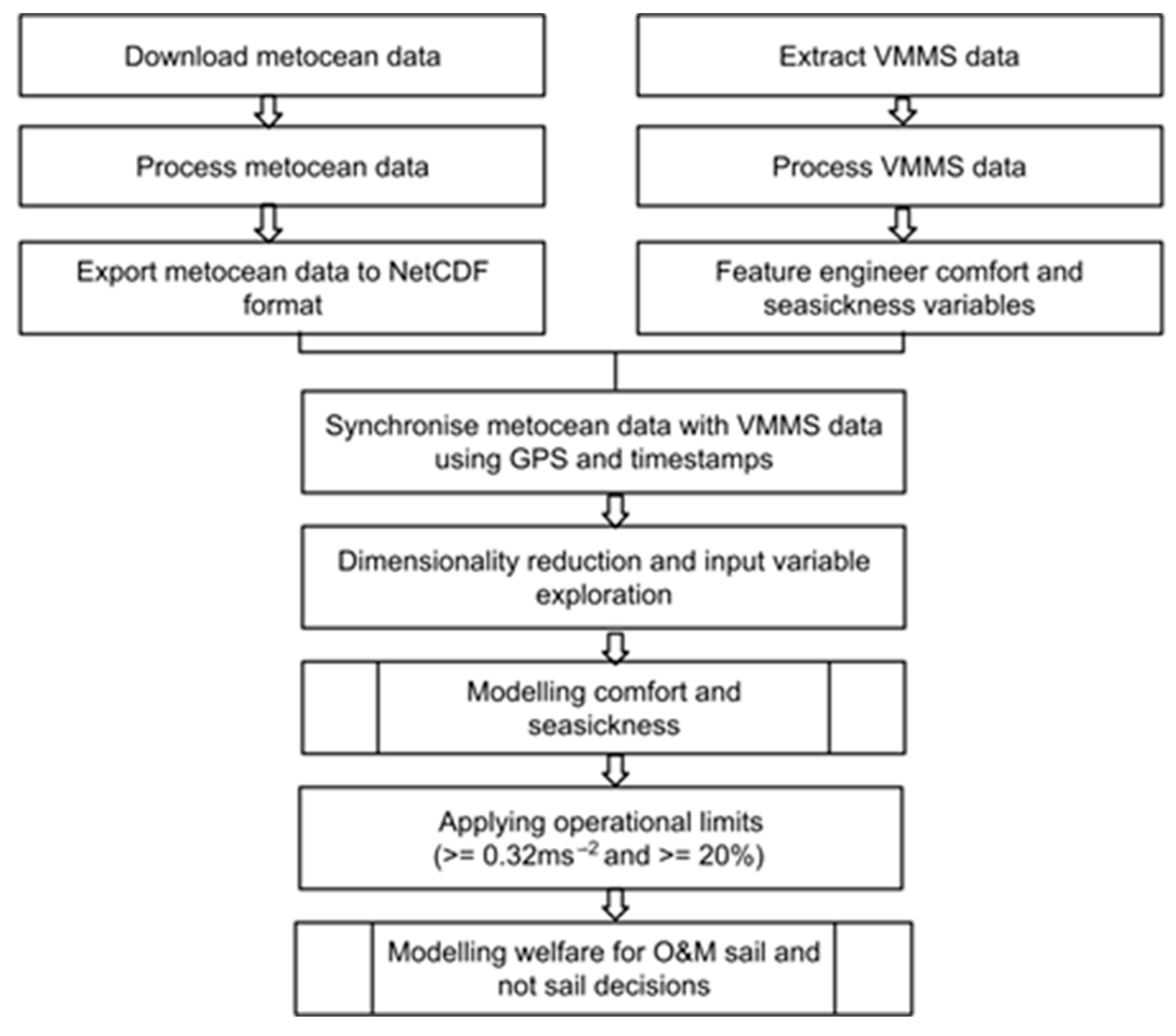
2.1. Scope
2.2. Data and Instrumentation
- I.
- Tri-hourly wave data through the Atlantic—European Northwest Shelf product (NWSHELF_REANALYSIS_WAV_004_015), resampled at a daily resolution and provided at approximately 1.5 km resolution from the WAVEWATCH III wave model [29]. The product outputs included wave parameters for the significant wave height, wave period, and directional characteristics.
- II.
- Daily sea surface height and current hindcast data through the Atlantic—European Northwest Shelf product (NORTHWESTSHELF_ANALYSIS_FORECAST_PHY_004_013), provided at 1.5 km resolution from the NEMO (Nucleus for European Modelling of the Ocean) ocean model [30]. The product provided outputs for current speed, current direction, and sea surface heights.
- III.
- Daily hindcast remotely sensed surface winds from the Global Ocean Wind Product (WIND_GLO_WIND_L4_REP_OBSERVATIONS_012_006). The product provided outputs from scatterometers and radiometers for directional wind velocities and stresses.
2.3. Study Area
2.4. Modelling the Welfare of Technicians
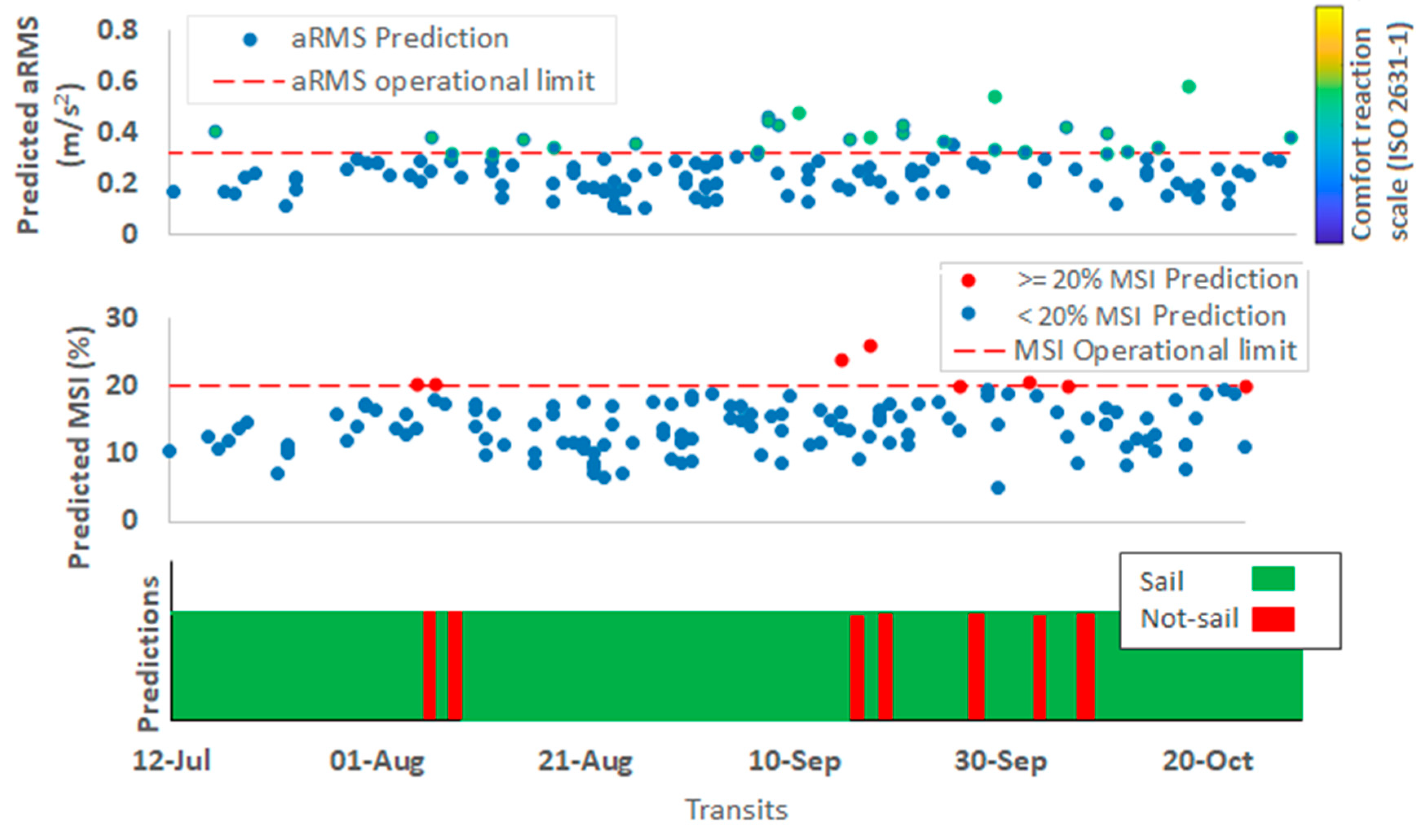
3. Results and Discussion
Welfare Modelling
4. Conclusions
4.1. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scheu, M.; Matha, D.; Hofmann, M.; Muskulus, M. Maintenance strategies for large offshore wind farms. Energy Procedia 2012, 24, 281–288. [Google Scholar] [CrossRef]
- Ding, F.; Tian, Z. Opportunistic maintenance for wind farms considering multi-level imperfect maintenance thresholds. Renew Energy 2012, 45, 175–182. [Google Scholar] [CrossRef]
- Shafiee, M. Maintenance logistics organization for offshore wind energy: Current progress and future perspectives. Renew Energy 2015, 77, 182–193. [Google Scholar] [CrossRef]
- Seyr, H.; Muskulus, M. Decision Support Models for Operations and Maintenance for Offshore Wind Farms: A Review. Appl. Sci. 2019, 9, 278. [Google Scholar] [CrossRef]
- Phillips, S.; Shin, I.; Armstrong, C. Crew Transfer Vessel Performance Evaluation. In Design and Operation of Wind Farm Support Vessels: RINA International Conference; Phillips, S., Shin, I., Armstrong, C., Eds.; Royal Institution of Naval Architects: London, UK, 2015; pp. 1–5. Available online: https://app.knovel.com/web/toc.v/cid:kpDOWFSVR5/viewerType:toc/ (accessed on 23 November 2020).
- Mansfield, N.J. Human Response to Vibration 1; CRC Press: New York, NY, USA, 2005; Volume 1. [Google Scholar]
- Scheu, M.; Matha, D.; Schwarzkopf, M.A.; Kolios, A. Human exposure to motion during maintenance on floating offshore wind turbines. Ocean Eng. 2018, 165, 293–306. [Google Scholar] [CrossRef]
- Stevens, S.C.; Parsons, M.G. Effects of Motion at Sea on Crew Performance: A Survey. Mar. Technol. SNAME News 2002, 39, 29–47. [Google Scholar] [CrossRef]
- Griffin, M.J. Handbook of Human Vibration, 1st ed.; Academic Press Limited: London, UK, 1990; Volume 1. [Google Scholar]
- Cardinale, M.; Pope, M.H. The effects of whole body vibration on humans: Dangerous or advantageous? Acta Physiol. Hung. 2003, 90, 195–206. [Google Scholar] [CrossRef]
- Coyte, J.L.; Stirling, D.; Du, H.; Ros, M. Seated Whole-Body Vibration Analysis, Technologies, and Modeling: A Survey. IEEE Trans. Syst. Man. Cybern. Syst. 2016, 46, 725–739. [Google Scholar] [CrossRef]
- Mette, J.; Garrido, M.V.; Harth, V.; Preisser, A.M.; Mache, S. Healthy offshore workforce? A qualitative study on offshore wind employees’ occupational strain, health, and coping. BMC Public Health 2018, 18, 172. [Google Scholar] [CrossRef]
- Reason, J.T.; Brand, J.J. Motion Sickness, 1st ed.; Academic Press Inc.: London, UK, 1975; Volume 1. [Google Scholar]
- O’Hanlon, J.F.; McCauley, M.E. Motion sickness incidence as a function of the frequency and acceleration of vertical sinusoidal motion. Aerosp. Med. 1974, 45, 366–369. [Google Scholar] [CrossRef]
- Donohew, B.E.; Griffin, M.J. Motion sickness: Effect of the frequency of lateral oscillation. Aviat. Space Environ. Med. 2004, 75, 649–656. [Google Scholar] [PubMed]
- Wertheim, A.H.; Bos, J.E.; Bles, W. Contributions of roll and pitch to sea sickness. Brain Res. Bull. 1998, 47, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Dobie, T.G. Motion Sickness: A Motion Adaptation Syndrome; Springer: New Orleans, LA, USA, 2019; Volume 6. [Google Scholar]
- Matsangas, P.; McCauley, M.E.; Becker, W. The effect of mild motion sickness and sopite syndrome on multitasking cognitive performance. Hum. Factors 2014, 56, 1124–1135. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.L.; Wang, J.Q.; Qi, R.R.; Pan, L.L.; Li, M.; Cai, Y.L. Motion Sickness: Current Knowledge and Recent Advance. CNS Neurosci. Ther. 2016, 22, 15–24. [Google Scholar] [CrossRef]
- Marjanen, Y.; Mansfield, N.J. Application of ISO 2631-1 (1997) for evaluating discomfort from whole-body vibration: Verification using field and laboratory studies. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE, Osaka, Japan, 4–7 September 2011; pp. 3475–3480. [Google Scholar]
- Newell, G.S.; Mansfield, N.J. Evaluation of reaction time performance and subjective workload during whole-body vibration exposure while seated in upright and twisted postures with and without armrests. Int. J. Ind. Ergon. 2008, 38, 499–508. [Google Scholar] [CrossRef]
- Olausson, K. On Evaluation and Modelling of Human Exposure to Vibration and Shock on Planing High-Speed Craft. Licentiate Thesis, KTH Royal Institute of Technology: Stockholm, Sweden, 2015. [Google Scholar]
- Leung, A.W.S.; Chan, C.C.H.; Ng, J.J.M.; Wong, P.C.C. Factors contributing to officers’ fatigue in high-speed maritime craft operations. Appl. Ergon. 2006, 37, 565–576. [Google Scholar] [CrossRef]
- ISO 2631-1; Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration. International Organization for Standardization: Geneva, Switzerland, 1997.
- Huston, D.R.; Zhao, X.; Johnson, C.C. Whole-body shock and vibration: Frequency and amplitude dependence of comfort. J. Sound Vib. 2000, 230, 964–970. [Google Scholar] [CrossRef]
- Shoenberger, R.W. Discomfort judgements of translational and angular whole-body vibrations. Aviat. Space Environ. Med. 1982, 53, 454–457. Available online: https://pubmed.ncbi.nlm.nih.gov/7092753/ (accessed on 14 June 2022).
- Offshore Energy. BMO Offshore Presents CTV Engine Monitoring—Offshore Energy. Offshore-energy.biz. 19 July 2016. Available online: https://www.offshore-energy.biz/bmo-offshore-presents-ctv-engine-monitoring/ (accessed on 3 November 2022).
- Earle, F.; Huddlestone, J.; Williams, T.; Stock-Williams, C.; van der Mijle-Meijer, H.; de Vries, L.; van Heemst, H.; Hoogerwerf, E.; Koomen, L.; de Ridder, E.-J.; et al. SPOWTT: Improving the safety and productivity of offshore wind technician transit. Wind Energy 2021, 25, 34–51. [Google Scholar] [CrossRef]
- Lewis, H.W.; Sanchez, J.M.C.; Siddorn, J.; King, R.R.; Tonani, M.; Saulter, A.; Sykes, P.; Pequignet, A.-C.; Weedon, G.P.; Palmer, T.; et al. Can wave coupling improve operational regional ocean forecasts for the north-west European Shelf? Ocean Sci. 2019, 15, 669–690. [Google Scholar] [CrossRef]
- Tonani, M.; Sykes, P.; King, R.R.; McConnell, N.; Péquignet, A.-C.; O’Dea, E.; Graham, J.A.; Polton, J.; Siddorn, J. The impact of a new high-resolution ocean model on the Met Office North-West European Shelf forecasting system. Ocean Sci. 2019, 15, 1133–1158. [Google Scholar] [CrossRef]
- Kumari, B.; Swarnkar, T. Filter versus Wrapper Feature Subset Selection in Large Dimensionality Micro array: A Review. Int. J. Comput. Sci. Inf. Technol. 2011, 2, 1048–1053. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Lal, T.N.; Chapelle, O.; Western, J.; Elisseeff, A. Embedded methods. In Feature Extraction. Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 137–165. [Google Scholar] [CrossRef]
- Cepowski, T. The prediction of the Motion Sickness Incidence index at the initial design stage. Zesz. Nauk. Akad. Morska W Szczec. 2012, 31, 45–48. [Google Scholar]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, U.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, C. Machine learning methods for wind turbine condition monitoring: A review. Renew Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Griffin, M.J.; Whitham, E.M. Time dependency of whole-body vibration discomfort. J. Acoust. Soc. Am. 1998, 68, 1523. [Google Scholar] [CrossRef]
- Maeda, S.; Morioka, M. Measurement of whole-body vibration exposure from garbage trucks. J. Sound Vib. 1998, 215, 959–964. Available online: https://www.academia.edu/8126588/MEASUREMENT_OF_WHOLE_BODY_VIBRATION_EXPOSURE_FROM_GARBAGE_TRUCKS (accessed on 9 January 2022). [CrossRef]
- Eger, T.; Contratto, M.; Dickey, J. Influence of Driving Speed, Terrain, Seat Performance and Ride Control on Predicted Health Risk Based on ISO 263I-I and EU Directive 2002/44/EC:. J. Low Freq. Noise Vib. Act. Control 2011, 30, 291–312. [Google Scholar] [CrossRef]
- Cepowski, T. On the modeling of car passenger ferryship design parameters with respect to selected sea-keeping qualities and additional resistance in waves. Pol. Marit. Res. 2009, 16, 3–10. [Google Scholar] [CrossRef]
- Rumawas, V.; Asbjørnslett, B.E.; Klöckner, C.A. Human Factors Evaluation in Ship Design and Operation: An Case Study in Norwegian Sea. In Maritime Safety International Conference (MASTIC 2018); CSP: Bali, Indonesia, 2018; pp. 66–78. [Google Scholar]
- Piscopo, V.; Scamardella, A. The overall motion sickness incidence applied to catamarans. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 655–669. [Google Scholar] [CrossRef]
- Jenkins, B.; Prothero, A.; Collu, M.; Carroll, J.; McMillan, D.; McDonald, A. Limiting Wave Conditions for the Safe Maintenance of Floating Wind Turbines. J. Phys. Conf. Ser. 2021, 2018, 012023. [Google Scholar] [CrossRef]
- Bos, J.E.; Diels, C.; Souman, J.L.; Rahmatalla, S.; Boileau, P.-É. Beyond Seasickness: A Motivated Call for a New Motion Sickness Standard across Motion Environments. Vibration 2022, 5, 755–769. [Google Scholar] [CrossRef]
- Medina-Lopez, E.; McMillan, D.; Lazic, J.; Hart, E.; Zen, S.; Angeloudis, A.; Bannon, E.; Browell, J.; Dorling, S.; Dorrell, R.; et al. Satellite data for the offshore renewable energy sector: Synergies and innovation opportunities. Remote Remote Sens. Environ. 2021, 264, 112–588. [Google Scholar] [CrossRef]
- UK Government. The Control of Vibration at Work Regulations 2005; UK Statutory Instruments: London, UK, 2005. Available online: https://legislation.gov.uk (accessed on 16 March 2022).
- UK Government. Health and Safety at Work etc Act; UK Statutory Instruments: London, UK, 1974; pp. 1–166. Available online: https://legislation.gov.uk (accessed on 16 March 2022).
| The Magnitude of Acceleration in ms−2 | Comfort Reaction |
|---|---|
| Less than 0.315 | Not uncomfortable |
| 0.315–0.63 | A little uncomfortable |
| 0.5–1 | Fairly uncomfortable |
| 0.8–1.6 | Uncomfortable |
| 1.25–2.5 | Very uncomfortable |
| Greater than 2 | Extremely uncomfortable |
| Category | R2 | RMSE | p-Value | Locations |
|---|---|---|---|---|
| Significant wave height | 0.89 | 0.20 | <0.05 | Project site 1 |
| Significant wave height | 0.84 | 0.25 | <0.05 | Project site 3 |
| Significant wave height | 0.86 | 0.15 | <0.05 | Project site 4 |
| Wind speed | 0.54 | 1.74 | <0.05 | Project site 1 |
| Wind speed | 0.847 | 0.213 | <0.05 | Project site 4 |
| Regression Model | R2 (aWRMS) | RMSE (aWRMS) | R2 (MSI) | RMSE (MSI) |
|---|---|---|---|---|
| Linear | 0.51 | 0.08 | 0.29 | 4.63 |
| Interactions linear | 0.52 | 0.08 | 0.27 | 4.68 |
| Robust linear | 0.50 | 0.09 | 0.28 | 4.64 |
| Stepwise linear | 0.53 | 0.08 | 0.27 | 4.69 |
| Fine tree | 0.40 | 0.09 | 0.25 | 4.77 |
| Medium tree | 0.43 | 0.09 | 0.30 | 4.62 |
| Coarse tree | 0.46 | 0.09 | 0.31 | 4.57 |
| Linear SVM | 0.50 | 0.09 | 0.27 | 4.68 |
| Quadratic SVM | 0.54 | 0.08 | 0.37 | 4.35 |
| Cubic SVM | 0.54 | 0.08 | 0.38 | 4.32 |
| Fine Gaussian SVM | 0.21 | 0.12 | 0.24 | 4.78 |
| Medium Gaussian SVM | 0.56 | 0.08 | 0.41 | 4.20 |
| Coarse Gaussian SVM | 0.51 | 0.08 | 0.33 | 4.47 |
| Boosted tree | 0.58 | 0.08 | 0.45 | 4.02 |
| Bagged trees | 0.56 | 0.08 | 0.45 | 4.02 |
| Squared exponential GPR | 0.61 | 0.08 | 0.43 | 4.02 |
| Matern 5/2 GPR | 0.59 | 0.08 | 0.42 | 4.02 |
| Exponential GPR | 0.60 | 0.08 | 0.43 | 4.02 |
| Rational quadratic GPR | 0.63 | 0.07 | 0.46 | 4.02 |
| RMSE | R2 | MSE | Speed (s) | Time (s) | Model | |
|---|---|---|---|---|---|---|
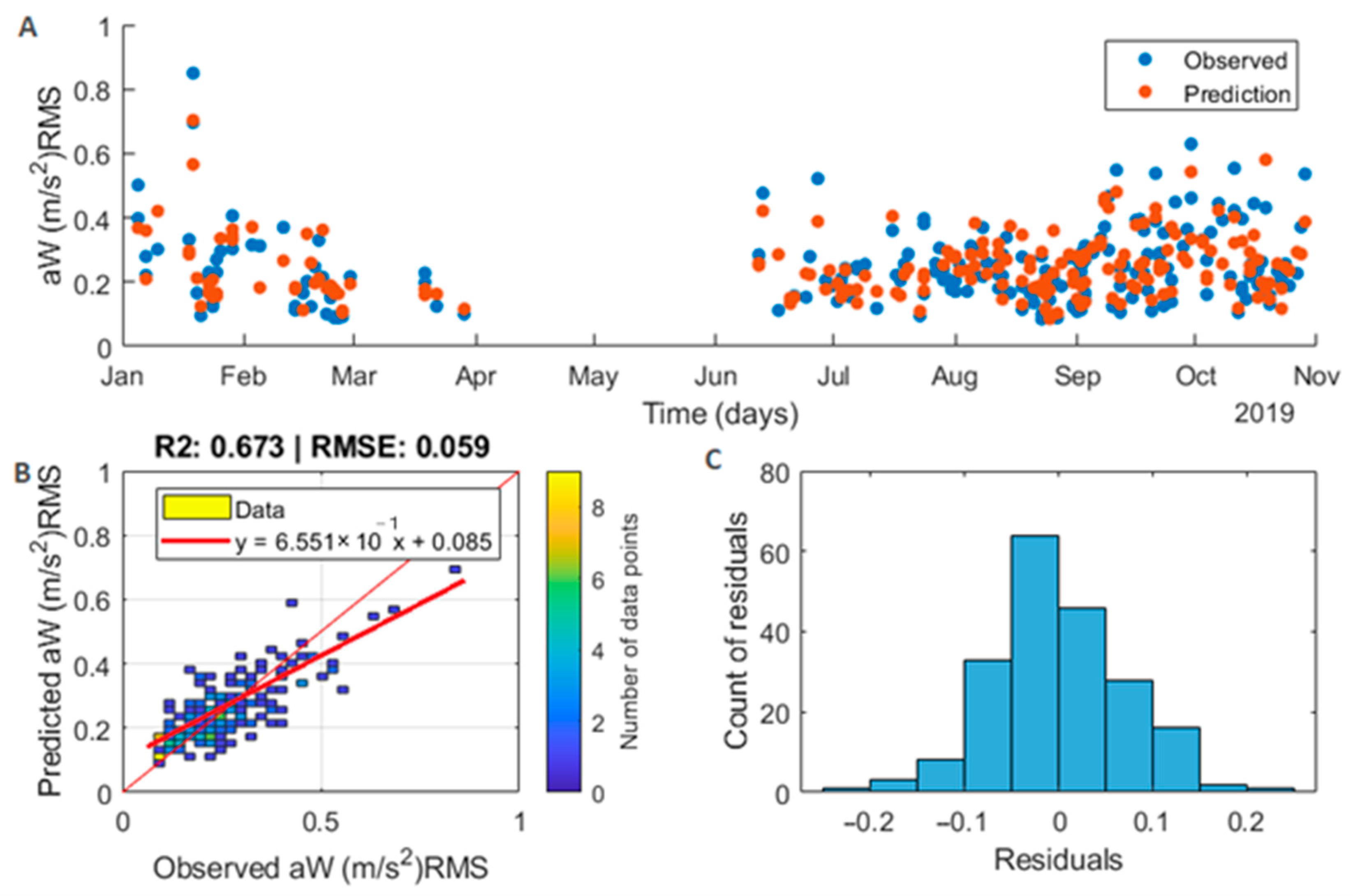
| Training set | 0.07 | 0.63 | 0.005 | 25,000 | 12.11 | aWRMS Rational quadratic GPR (ms−2) |
| Testing set | 0.06 | 0.67 | 0.004 | 8800 | 3.05 | |
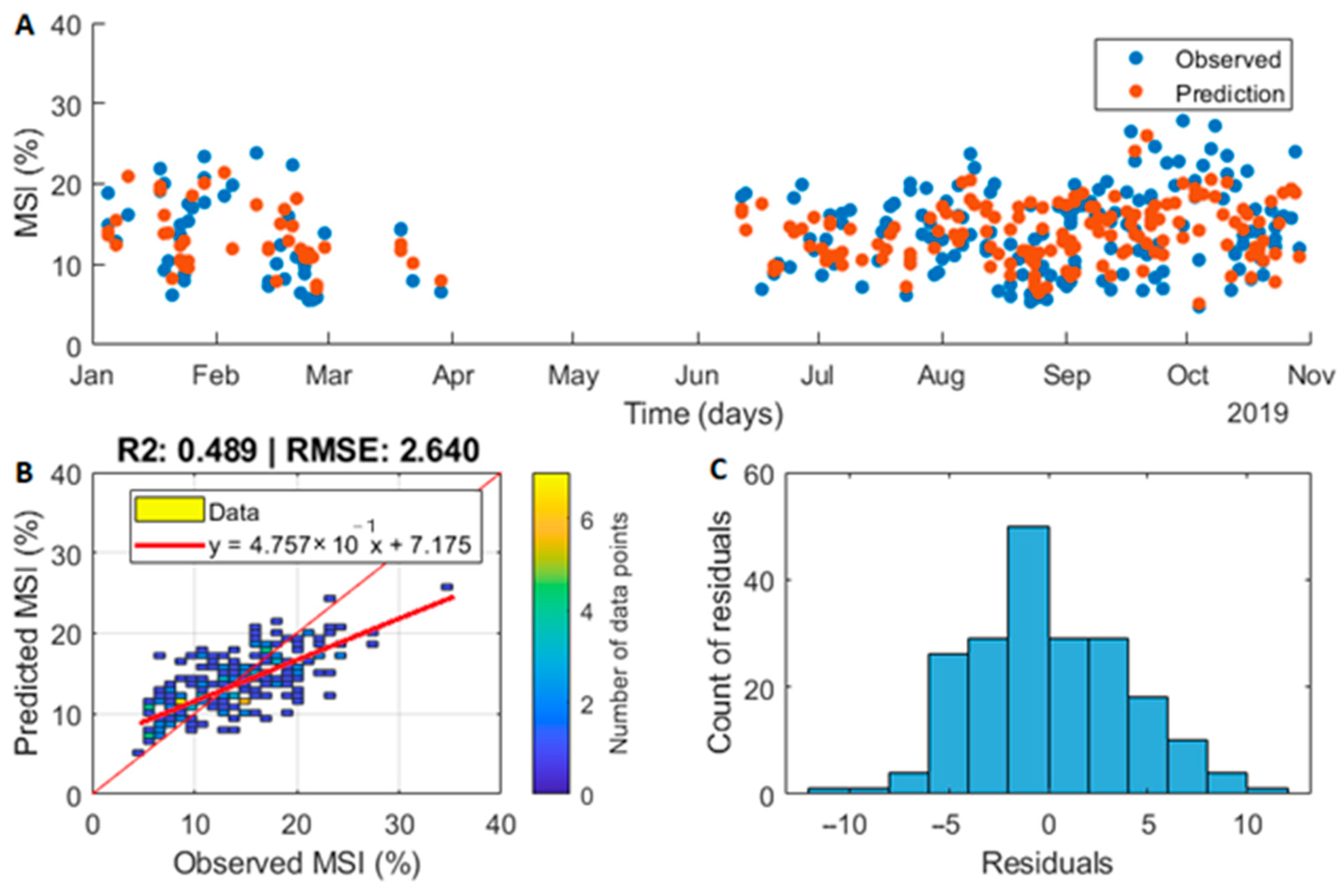
| Training set | 4.02 | 0.46 | 16.15 | 24,000 | 16.56 | MSI Rational quadratic GPR (%) |
| Testing set | 2.64 | 0.49 | 6.97 | 8800 | 12.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzuegbunam, T.D.; Forster, R.; Williams, T. Assessing the Welfare of Technicians during Transits to Offshore Wind Farms. Vibration 2023, 6, 434-448. https://doi.org/10.3390/vibration6020027
Uzuegbunam TD, Forster R, Williams T. Assessing the Welfare of Technicians during Transits to Offshore Wind Farms. Vibration. 2023; 6(2):434-448. https://doi.org/10.3390/vibration6020027
Chicago/Turabian StyleUzuegbunam, Tobenna D., Rodney Forster, and Terry Williams. 2023. "Assessing the Welfare of Technicians during Transits to Offshore Wind Farms" Vibration 6, no. 2: 434-448. https://doi.org/10.3390/vibration6020027
APA StyleUzuegbunam, T. D., Forster, R., & Williams, T. (2023). Assessing the Welfare of Technicians during Transits to Offshore Wind Farms. Vibration, 6(2), 434-448. https://doi.org/10.3390/vibration6020027







