Investigations into Nonlinear Effects of Normal Pressures on Dynamic Cyclic Responses of Novel 3D-Printed TPMS Bridge Bearings
Abstract
:1. Introduction
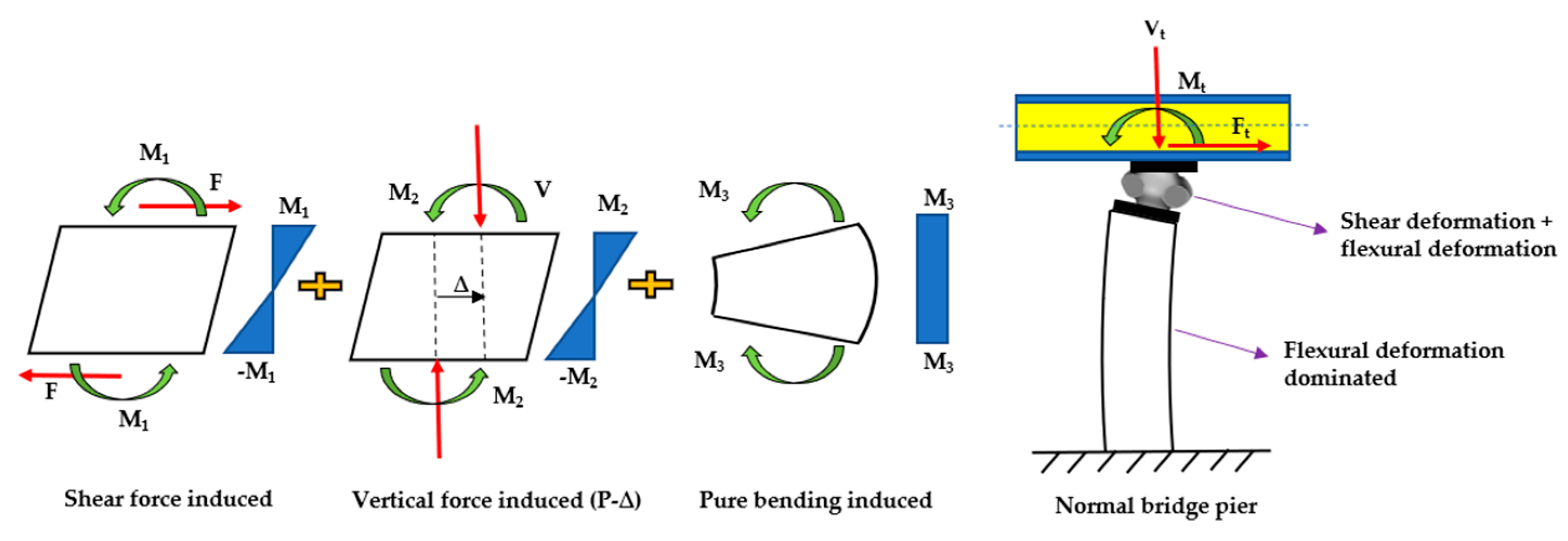
2. Theoretical Background for the Cyclic Response of a Novel TPMS Bridge Bearing (NTBB)
Fully Bonded Novel TPMS Bridge Bearing
3. A Proposed 3D-Printed TPMS Bridge Bearing (TPMSB)
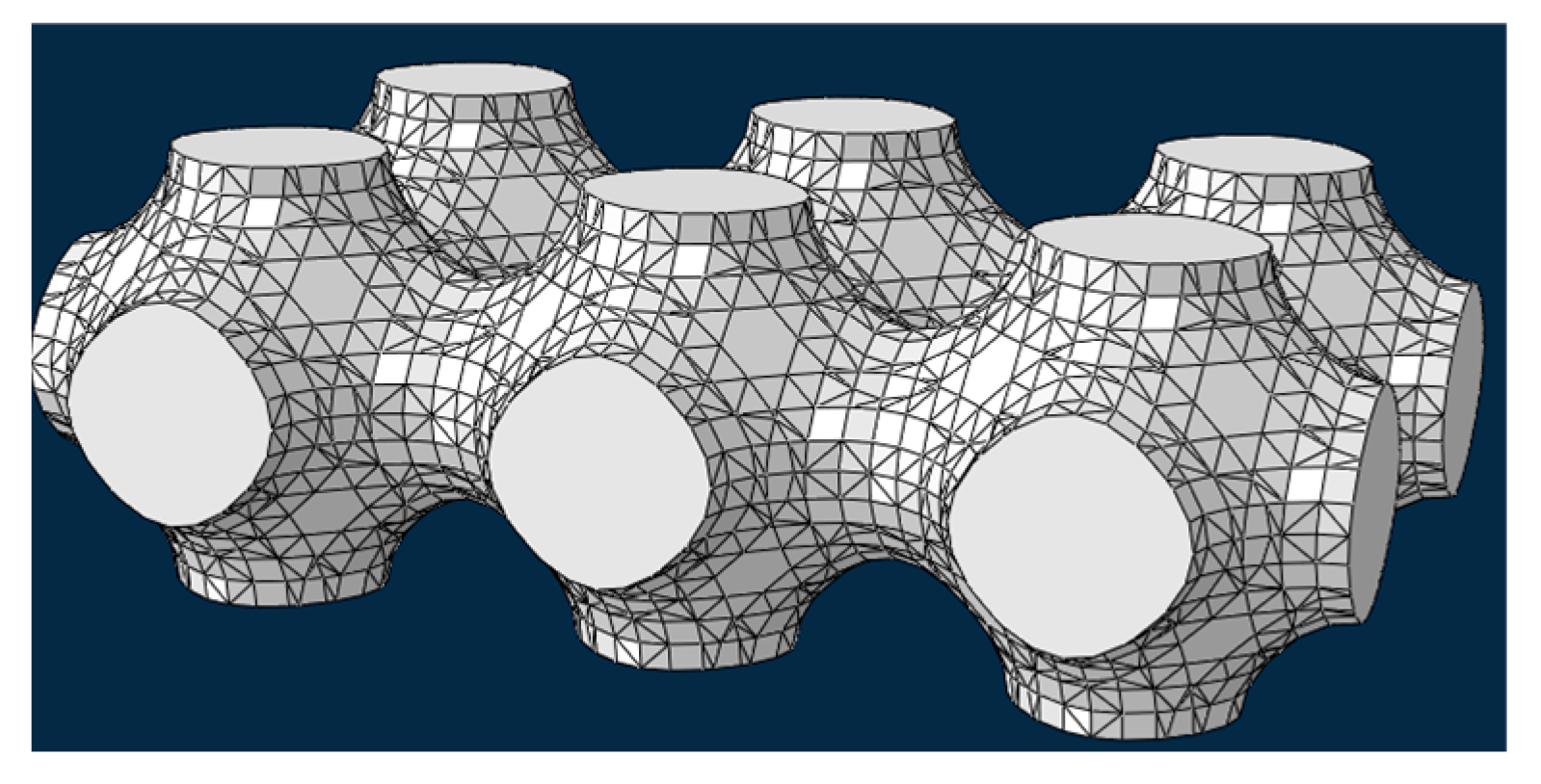
3.1. Proposed TPMS Bridge Bearing Specimens
3.2. A Proposed TPMS Bridge Bearing Model
3.3. Material Model
3.4. Methods
3.4.1. Simulation Program
3.4.2. Model Validation
4. Results
4.1. Observed Performance
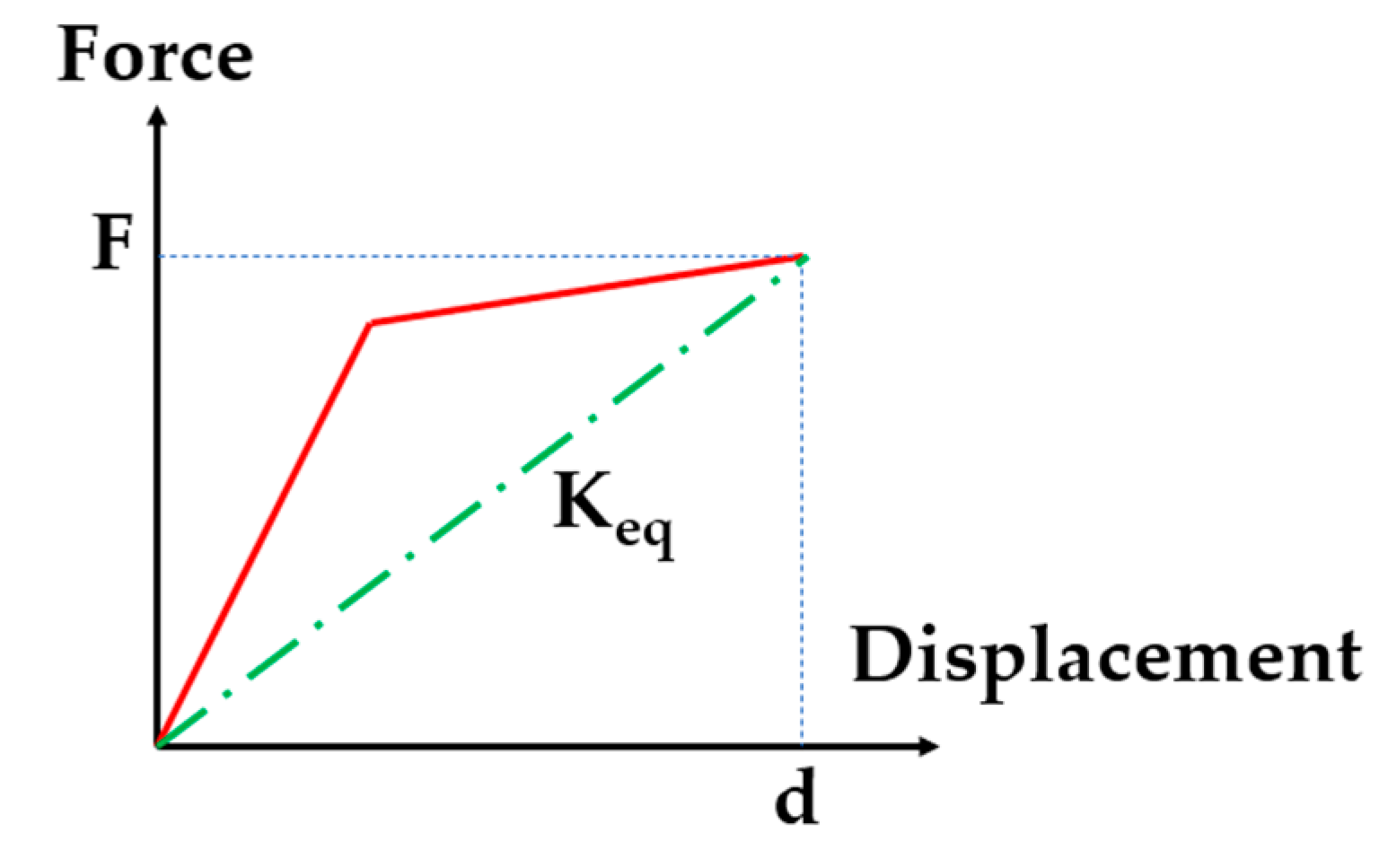
4.2. Force–Displacement Response
4.3. Bearing Shear Stiffness and Shear Deformation
5. Discussion
6. Conclusions
- (1)
- The proposed model is prone to mimic the cyclic behaviour of a typical bridge bearing for bridge bearing applications, as well as nearly offering an identical dissipated energy for bridge bearing applications, as seen in Figure 7 and Table 2, respectively. The model can act exactly as a cellular rubber block structure of a bridge bearing, transferring/facilitating horizontal forces/displacements between the superstructure and the substructure while supporting the weight of the superstructure.
- (2)
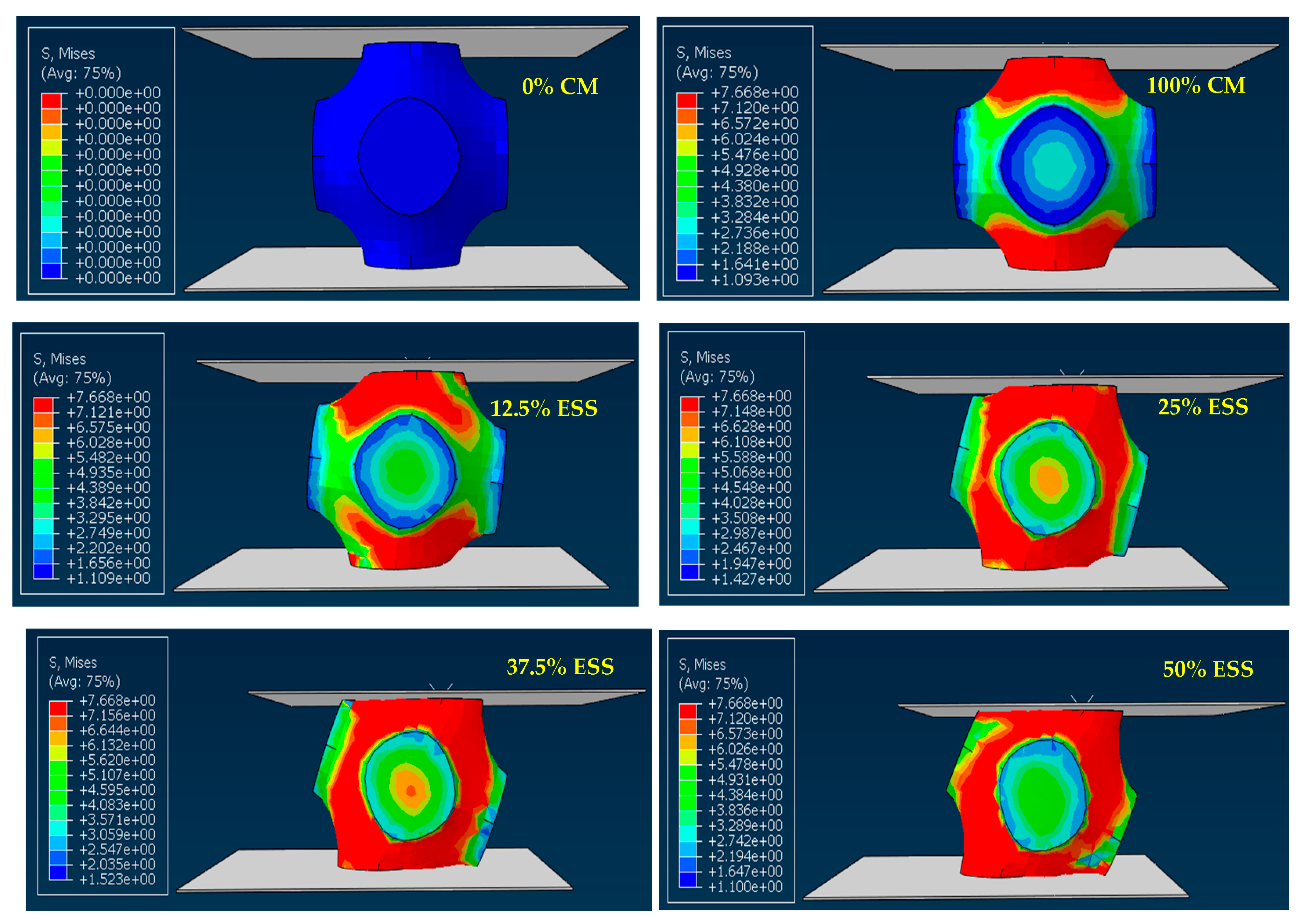
- The difference in the von Mises stress distribution of the proposed model between 1 and 3.5 MPa is observed and found to have an increasing trend with the increase in normal pressure (Figure 8 and Figure 9). The distribution pattern is the same at the initial state (12.5% ESS), and higher stress distributions are found over the whole model when the model’s applied horizontal displacement reaches the target shear strain (50% ESS).
- (3)
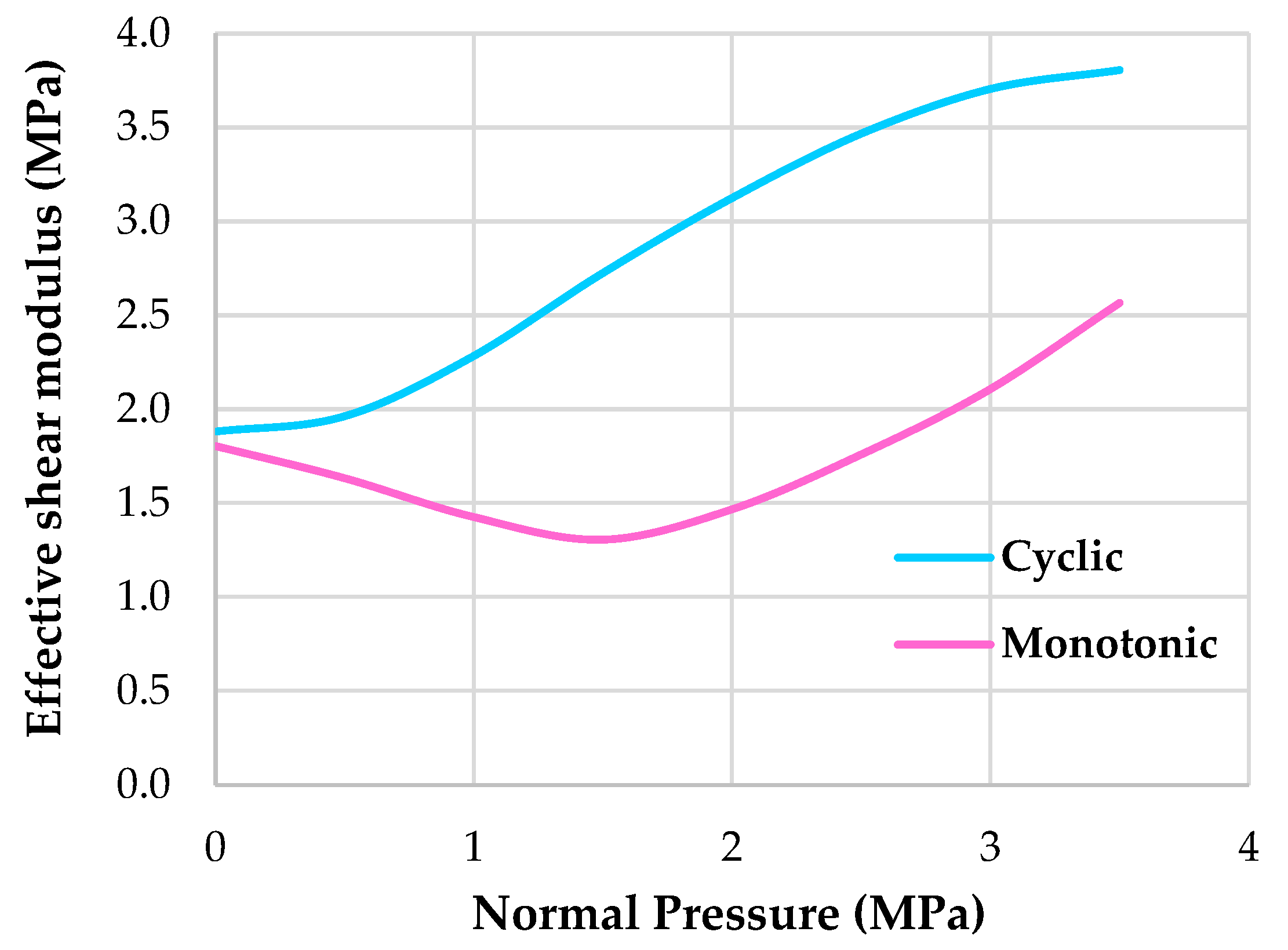
- In terms of the TPMS bearing’s characteristics, for dynamic cyclic analysis, the effective shear moduli of the proposed model are observed to have an increasing trend with the increase in normal pressures. Unlike monotonic analysis, its effective shear moduli are found to decrease in the initial phase until the normal pressure is more than 1.5 MPa. This is because the nonlinearity of the complex TPMS structure mainly changes the structure shape to be wider horizontally (a column into a block) in order to resist higher shear strains. The cause of the structure change into the rubber block-like structure (the well-known crashworthiness behaviour) is that the model initially experiences a higher yield stress while experiencing shear.
- (4)
- (5)
- The better performance of the proposed model is also found to offer strain hardening with the increasing number of cycles due to the material model being considered as an elastic–plastic behaviour, which differs from the Mullins phenomenon that occurs in common elastomeric bridge bearings. This leads to the increase in shear strength of the proposed model after unloading or reloading during repetitive cycles.
- (6)
- The effective dynamic shear moduli for cyclic loadings are 1.6 times higher than those for monotonic loadings, because the proposed model behaves immediately under dynamic cyclic loading conditions. For example, the dynamic shear force of 4 kN at a 3.5 MPa normal pressure is more than that of the static force of 2.5 kN (Figure 10 and Figure 14, respectively), resulting from the dynamic shear modulus, which is higher than the static one for monotonic loading conditions. Furthermore, the load patterns between both conditions make different initial responses with the increase in normal pressure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sengsri, P.; Kaewunruen, S. Additive manufacturing meta-functional composites for engineered bridge bearings: A review. Constr. Build. Mater. 2020, 262, 120535. [Google Scholar] [CrossRef]
- Naeim, F.; Kelly, J. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Lee, D.J. Bridge Bearings and Expansion Joints; E & FN Spon: London, UK, 1994. [Google Scholar]
- Al-Anany, Y.; Tait, M. Fiber-reinforced elastomeric isolators for the seismic isolation of bridges. Compos. Struct. 2016, 160, 300–311. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Seismic Isolation Design, 3rd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010. [Google Scholar]
- Constantinou, M.; Kalpakidis, I.; Filiatrault, A.; Ecker, L.R. LRFD-Based Analysis and Design Procedures for Bridge Bearings and Seismic Isolators; Report No.MCEER-11e0004; Multidisciplinary Center for Earthquake Engineering Research, University at Buffalo, State University of New York: Buffalo, NY, USA, 2011. [Google Scholar]
- Al-Anany, Y. Fiber Reinforced Elastomeric Isolators for Bridge Applications. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2016. [Google Scholar]
- Zhong, J.; Shi, L.; Yang, T.; Liu, X.; Wang, Y. Probabilistic seismic demand model of UBPRC columns conditioned on Pulse-Structure parameters. Eng. Struct. 2022, 270, 114829. [Google Scholar] [CrossRef]
- Zhong, J.; Ni, M.; Hu, H.; Yuan, W.; Yuan, H.; Pang, Y. Uncoupled multivariate power models for estimating performance-based seismic damage states of column curvature ductility. Structures 2022, 36, 752–764. [Google Scholar] [CrossRef]
- AASHTO. LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012. [Google Scholar]
- Caltrans. Bridge Memo to Designers. Section 7: Bridge Bearings; California Department of Transportation: Sacramento, CA, USA, 1994.
- Ramberger, G. Structural Bearings and Expansion Joints for Bridges; International Association for Bridges and Structural Engineering (IABSE): Zurich, Switzerland, 2002. [Google Scholar]
- Xiang, N.; Goto, Y.; Alam, M.S.; Li, J. Effect of bonding or unbonding on seismic behavior of bridge elastomeric bearings: Lessons learned from past earthquakes in China and Japan and inspirations for future design. Adv. Bridge Eng. 2021, 2, 14. [Google Scholar] [CrossRef]
- Sengsri, P.; Kaewunruen, S. Local failure modes and critical buckling loads of a meta-functional auxetic sandwich core for composite bridge bearing applications. Appl. Sci. 2021, 11, 10844. [Google Scholar] [CrossRef]
- Sengsri, P.; Fu, H.; Kaewunruen, S. Mechanical properties and energy-absorption capability of a 3D-printed TPMS sandwich lattice model for meta-functional composite bridge bearing applications. J. Compos. Sci. 2022, 6, 71. [Google Scholar] [CrossRef]
- Sengsri, P.; Marsico, R.M.; Kaewunruen, S. Modal analysis of free vibration of an extremely lightweight panel model for bridge bearing applications. IOP Conf. Ser. Mater. Sci. Eng. 2022, 603, 02206. [Google Scholar]
- Sengsri, P.; Baniotopoulos, C.; Kaewunruen, S. Engineered model for the numerical investigation into vibration characteristics of a novel bridge bearing under free-free and fixed boundary condition. In Proceedings of the EURODYN 2020 XI International Conference on Structural Dynamics: EURODYN 2020 European Association for Structural Dynamics, EURODYN 2020 XI International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar]
- Sengsri, P.; Kaewunruen, S. Dynamic Modal Parameters of an Extremely Lightweight Structure using a Gyroid Core for Bridge Bearings. In Proceedings of the Seventeenth East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-17), Singapore, 27–30 June 2022. [Google Scholar]
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti-6Al-4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Raymont, D. Advanced lightweight 316L stainless steel cellular lattice structures fabricated via selective laser melting. Mater. Des. 2014, 55, 533–541. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and failure behaviour of Ti-6Al-4V lattice structures manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar] [CrossRef]
- Xiang, N.; Li, J. Experimental and numerical study on seismic sliding mechanism of laminated-rubber bearings. Eng. Struct. 2017, 141, 159–174. [Google Scholar] [CrossRef]
- Kingston, J.G.R.; Muhr, A.H. Effect of scragging on parameters in viscoplastic model for filled rubber. Plast. Rubber Compos. 2011, 40, 161–168. [Google Scholar] [CrossRef]
- Steelman, J.S.; Fahnestock, L.A.; Filipov, E.T.; LaFave, J.M.; Hajjar, J.F.; Foutch, D.A. Shear and friction response of nonseismic laminated elastomeric bridge bearings subject to seismic demands. J. Bridge Eng. 2012, 18, 612–623. [Google Scholar] [CrossRef]
- Nagavinothini, R. A comparative study of phenomenological hysteretic models with application to recycled rubber-fibre reinforced bearings. J. Vibroeng. 2020, 22, 1798–1813. [Google Scholar] [CrossRef]
- Triply Periodic Level Surfaces, Archived. 2019. Available online: http://www.msri.org/publications/sgp/jim/geom/level/library/triper/index.html (accessed on 18 June 2022).
- Standard Drawings for Highway Design and Construction 2015 Revision, Thai Version. BP-102. 2015. Available online: http://www.doh.go.th/uploads/tinymce/service/bid/doc_bid/STANDARD%20DRAWING%202015%20EDTION_2018.pdf (accessed on 28 June 2022).
- Abaqus CAE User’s Guide; DS Simulia Abaqus: Providence, RI, USA, 2017.
- Losanno, D.; Sierra, I.E.M.; Spizzuoco, M.; Marulanda, J.; Thomson, P. Experimental assessment and analytical modeling of novel fiber-reinforced isolators in unbounded configuration. Compos. Struct. 2019, 212, 66–82. [Google Scholar] [CrossRef]
- Sengsri, P.; Ngamkhanong, C.; de Melo, A.L.O.; Kaewunruen, S. Experimental and Numerical Investigations into Dynamic Modal Parameters of Fiber-Reinforced Foamed Urethane Composite Beams in Railway Switches and Crossings. Vibration 2020, 3, 174–188. [Google Scholar] [CrossRef]
- Sengsri, P.; Ngamkhanong, C.; Melo, A.L.O.d.; Papaelias, M.; Kaewunruen, S. Damage Detection in Fiber-Reinforced Foamed Urethane Composite Railway Bearers Using Acoustic Emissions. Infrastructures 2020, 5, 50. [Google Scholar] [CrossRef]
- Kaewunruen, S.; AbdelHadi, M.; Kongpuang, M.; Pansuk, W.; Remennikov, A.M. Digital Twins for Managing Railway Bridge Maintenance, Resilience, and Climate Change Adaptation. Sensors 2023, 23, 252. [Google Scholar] [CrossRef] [PubMed]








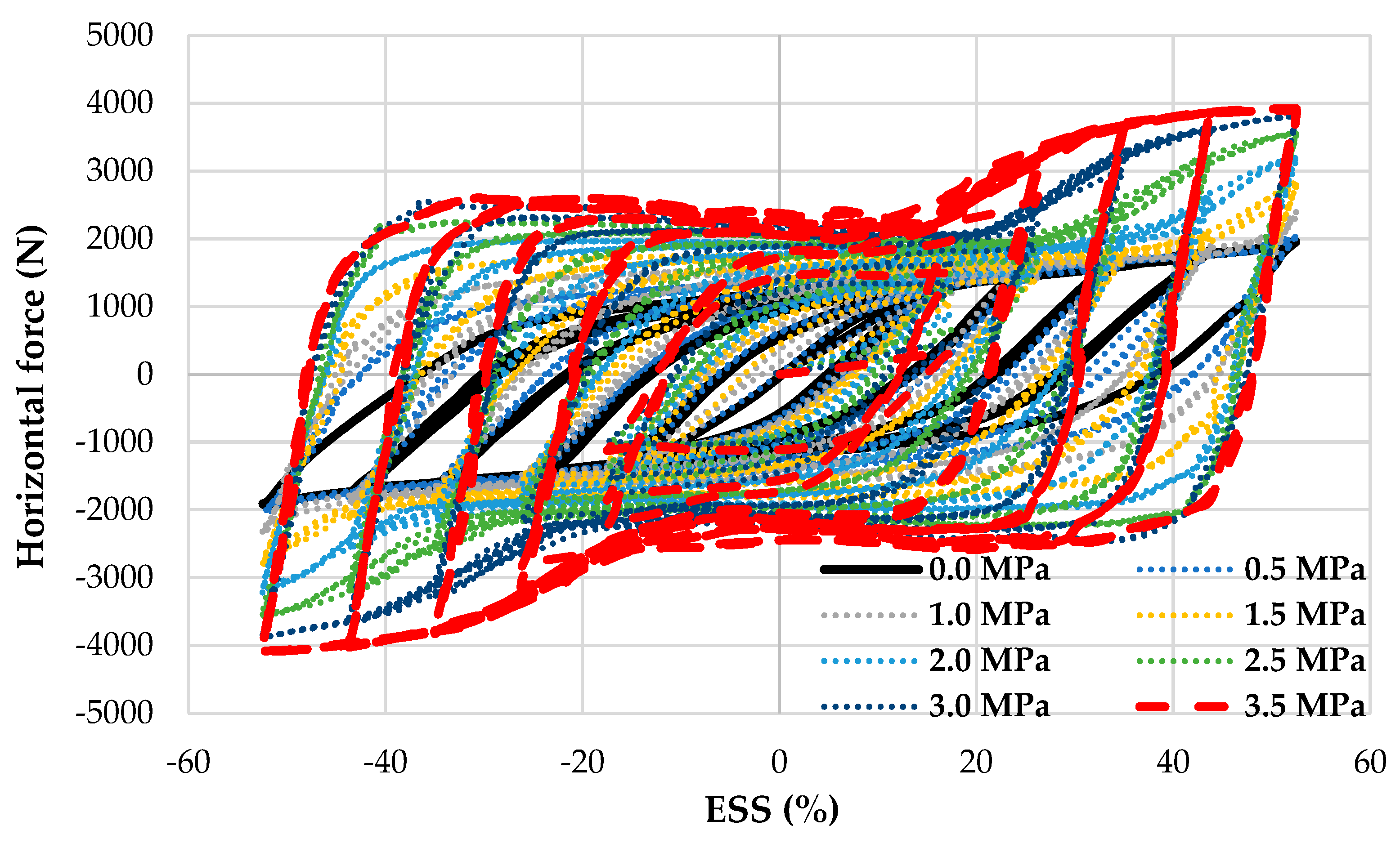
| Simulation Series | Program | Normal Pressure (MPa) | ESS (%) |
|---|---|---|---|
| 1-1 | Monotonic | 0.0 | 50 |
| 1-2 | Monotonic | 0.5 | 50 |
| 1-3 | Monotonic | 1.0 | 50 |
| 1-4 | Monotonic | 1.5 | 50 |
| 1-5 | Monotonic | 2.0 | 50 |
| 1-6 | Monotonic | 2.5 | 50 |
| 1-7 | Monotonic | 3.0 | 50 |
| 1-8 | Monotonic | 3.5 | 50 |
| 2-1 | Cyclic | 0.0 | 50 |
| 2-2 | Cyclic | 0.5 | 50 |
| 2-3 | Cyclic | 1.0 | 50 |
| 2-4 | Cyclic | 1.5 | 50 |
| 2-5 | Cyclic | 2.0 | 50 |
| 2-6 | Cyclic | 2.5 | 50 |
| 2-7 | Cyclic | 3.0 | 50 |
| 2-8 | Cyclic | 3.5 | 50 |
| Equivalent Stiffness, Keq (N/mm) | Dissipated Energy, Den (N·mm) | |
|---|---|---|
| Experimental | 123.08 | 61,175 |
| Numerical | 118.17 | 56,346 |
| Difference ratio (%) | 3.99 | 7.89 |
| Normal Pressure Variation (MPa) | Gem (MPa) | Gec (MPa) | ESS (%) |
|---|---|---|---|
| 0.0 | 1.80 | 1.88 | 50 |
| 0.5 | 1.63 | 1.96 | 50 |
| 1.0 | 1.43 | 2.28 | 50 |
| 1.5 | 1.31 | 2.73 | 50 |
| 2.0 | 1.47 | 3.13 | 50 |
| 2.5 | 1.76 | 3.47 | 50 |
| 3.0 | 2.11 | 3.70 | 50 |
| 3.5 | 2.57 | 3.81 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sengsri, P.; Kaewunruen, S. Investigations into Nonlinear Effects of Normal Pressures on Dynamic Cyclic Responses of Novel 3D-Printed TPMS Bridge Bearings. Vibration 2023, 6, 65-81. https://doi.org/10.3390/vibration6010006
Sengsri P, Kaewunruen S. Investigations into Nonlinear Effects of Normal Pressures on Dynamic Cyclic Responses of Novel 3D-Printed TPMS Bridge Bearings. Vibration. 2023; 6(1):65-81. https://doi.org/10.3390/vibration6010006
Chicago/Turabian StyleSengsri, Pasakorn, and Sakdirat Kaewunruen. 2023. "Investigations into Nonlinear Effects of Normal Pressures on Dynamic Cyclic Responses of Novel 3D-Printed TPMS Bridge Bearings" Vibration 6, no. 1: 65-81. https://doi.org/10.3390/vibration6010006
APA StyleSengsri, P., & Kaewunruen, S. (2023). Investigations into Nonlinear Effects of Normal Pressures on Dynamic Cyclic Responses of Novel 3D-Printed TPMS Bridge Bearings. Vibration, 6(1), 65-81. https://doi.org/10.3390/vibration6010006







