Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation
Abstract
1. Introduction
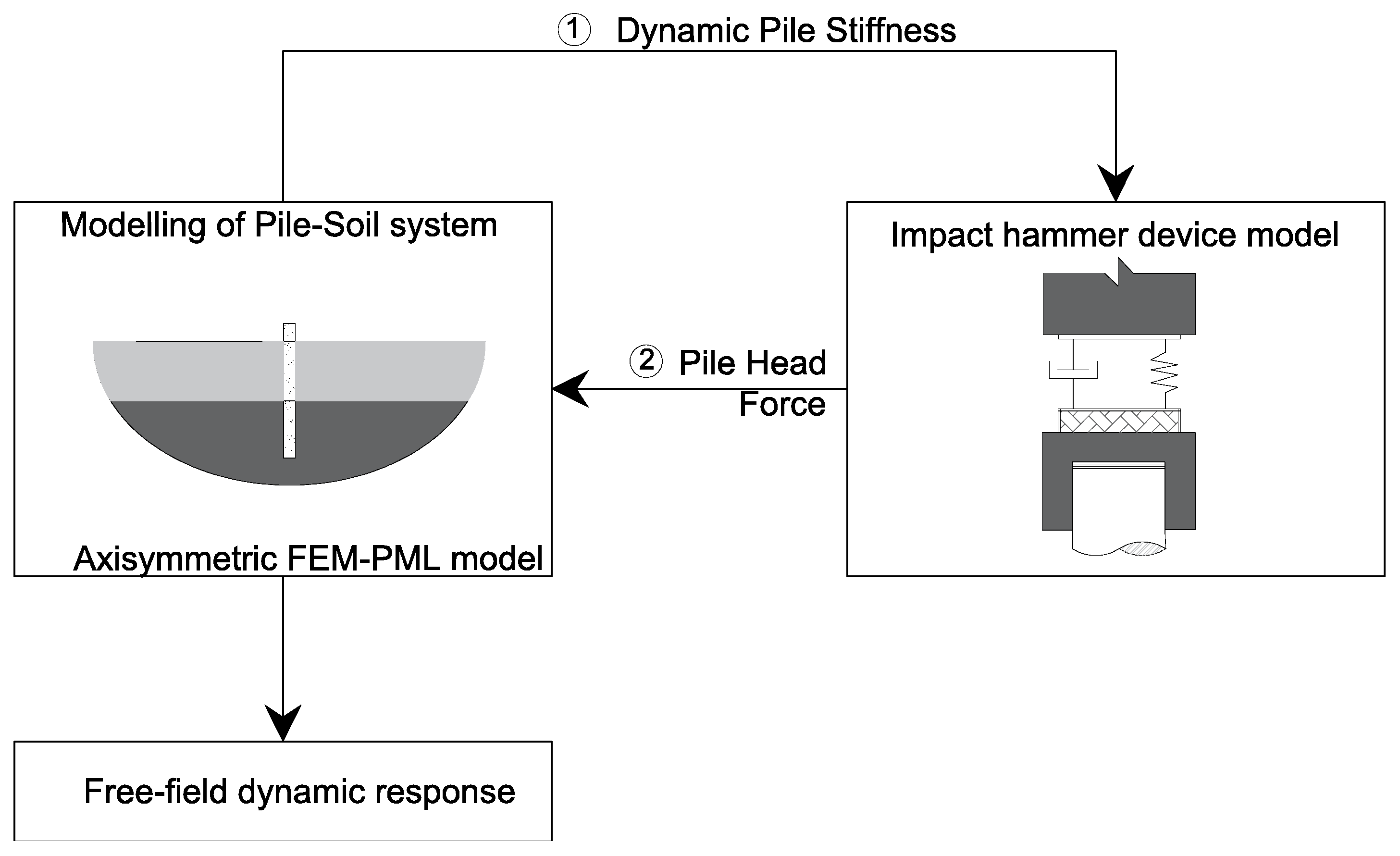
2. Modeling Approach
2.1. Generalities
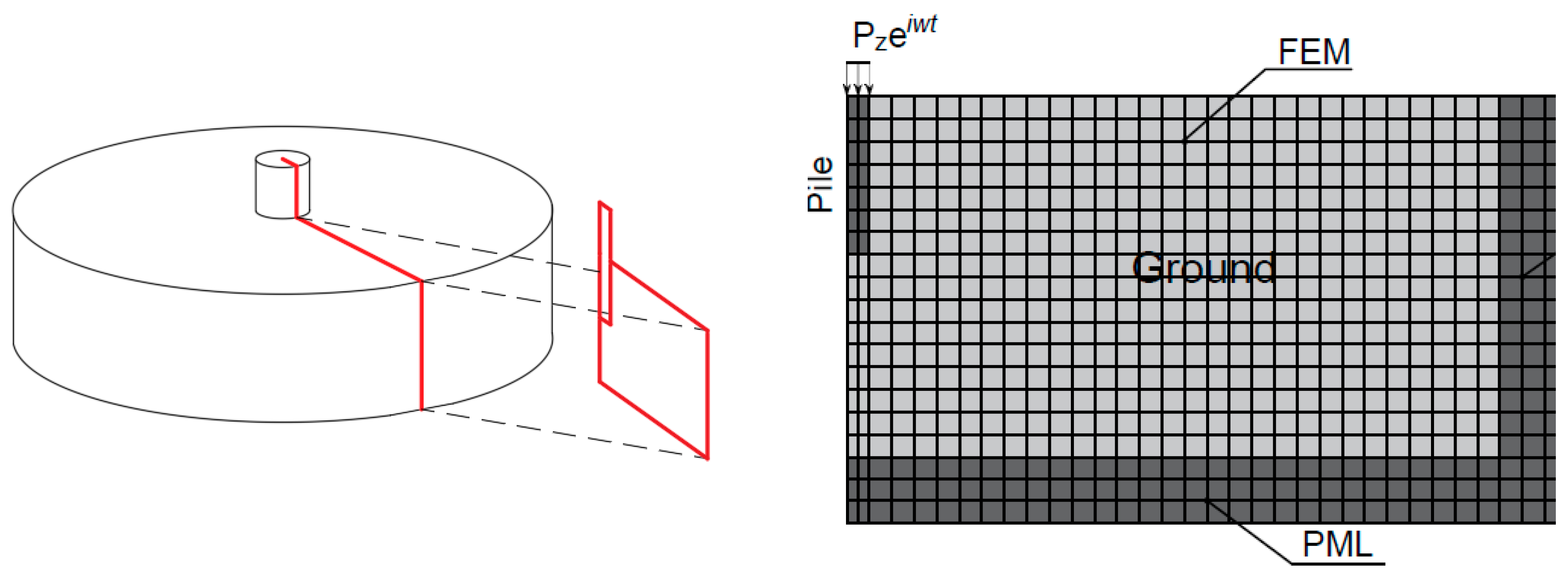
2.2. Axisymmetric FEM-PML Approach: Modeling of the Pile–Ground System
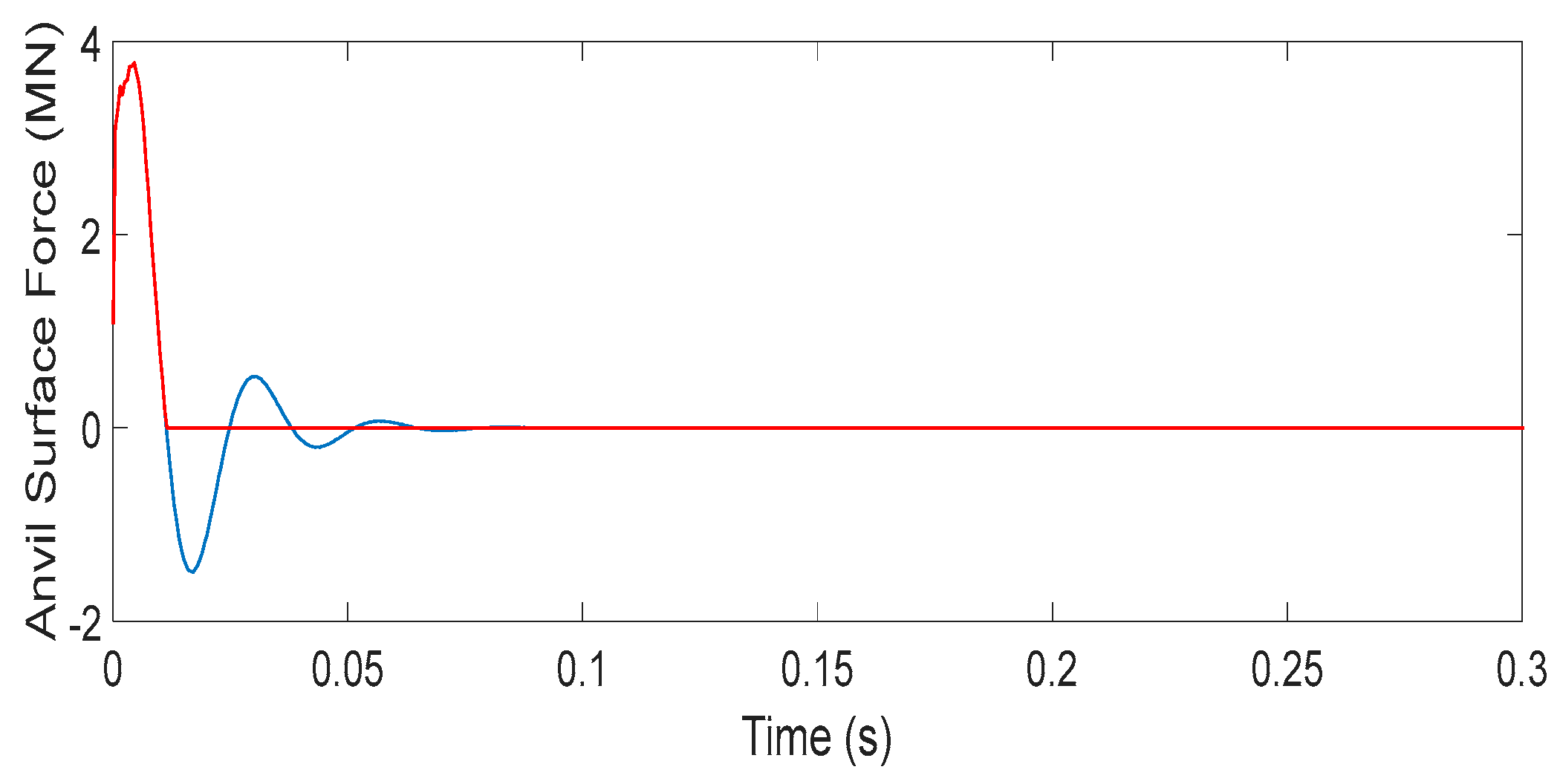
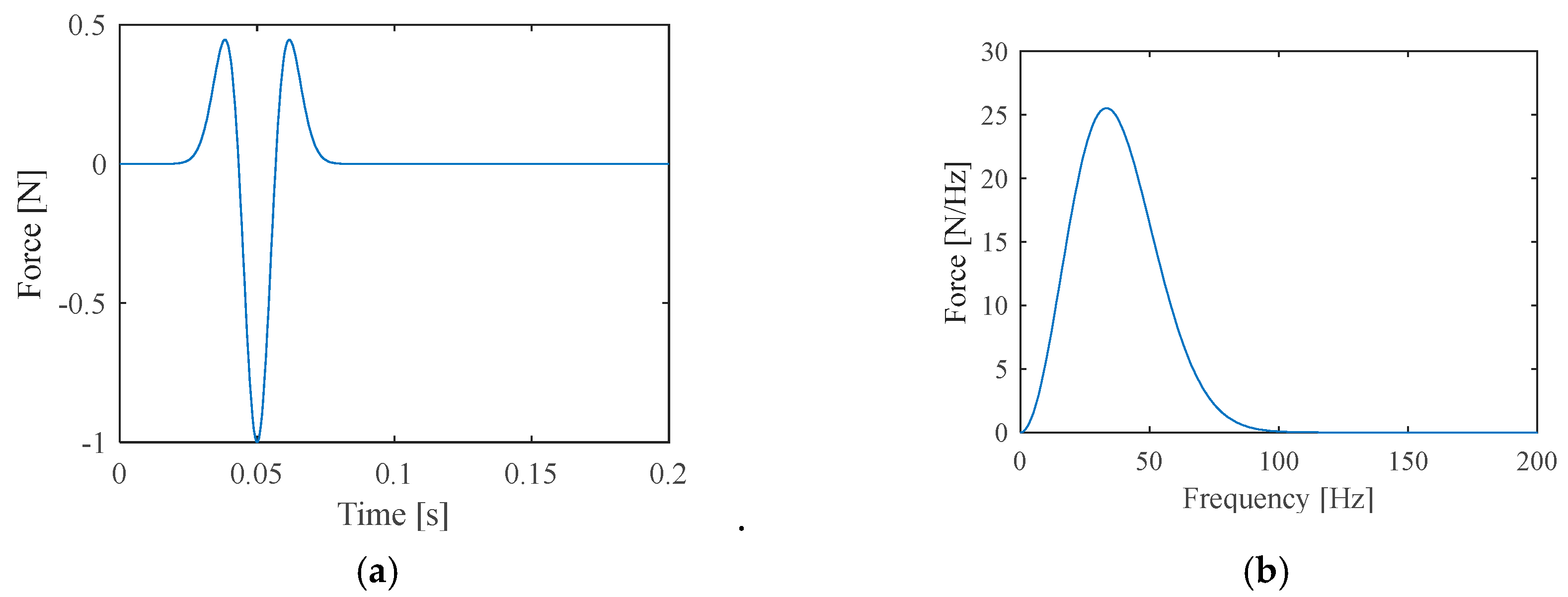
2.3. Impact Hammer Model and Hammer–Pile Interaction

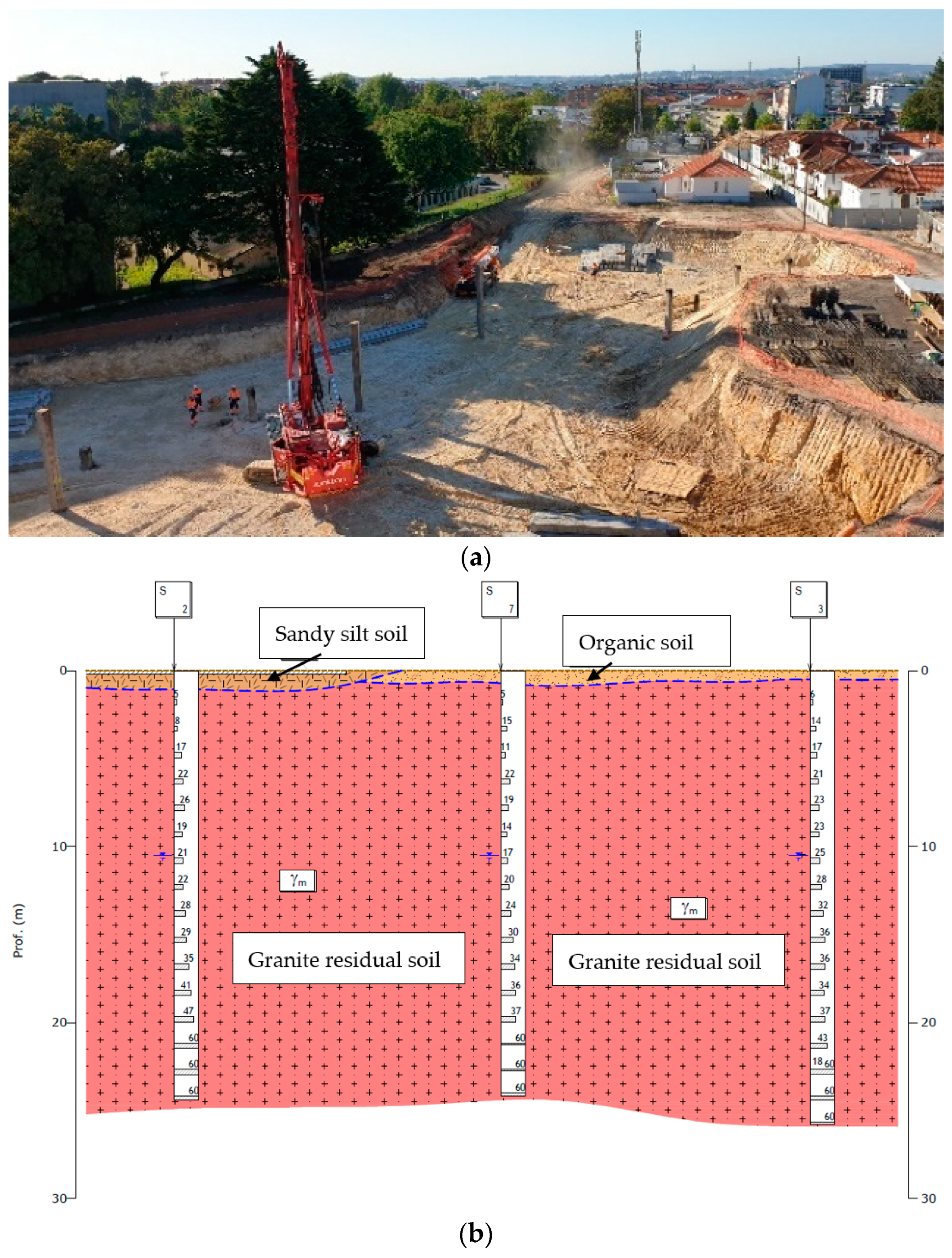
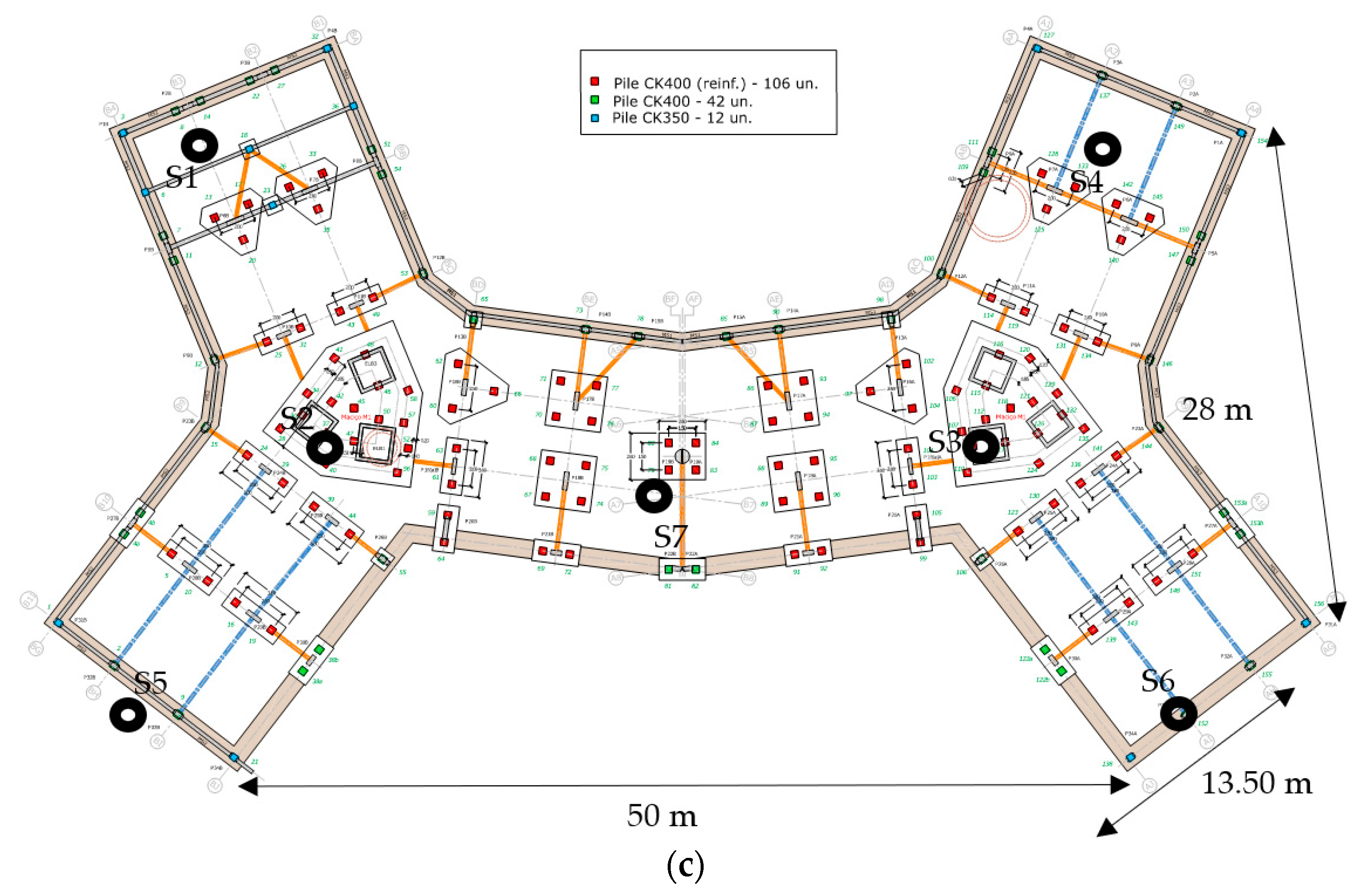
3. Characterization of the Construction Site
4. Experimental Validation of the Axisymmetric FEM-PML Approach in Low-Strain Conditions
4.1. Experimental Setup
4.2. Numerical Considerations
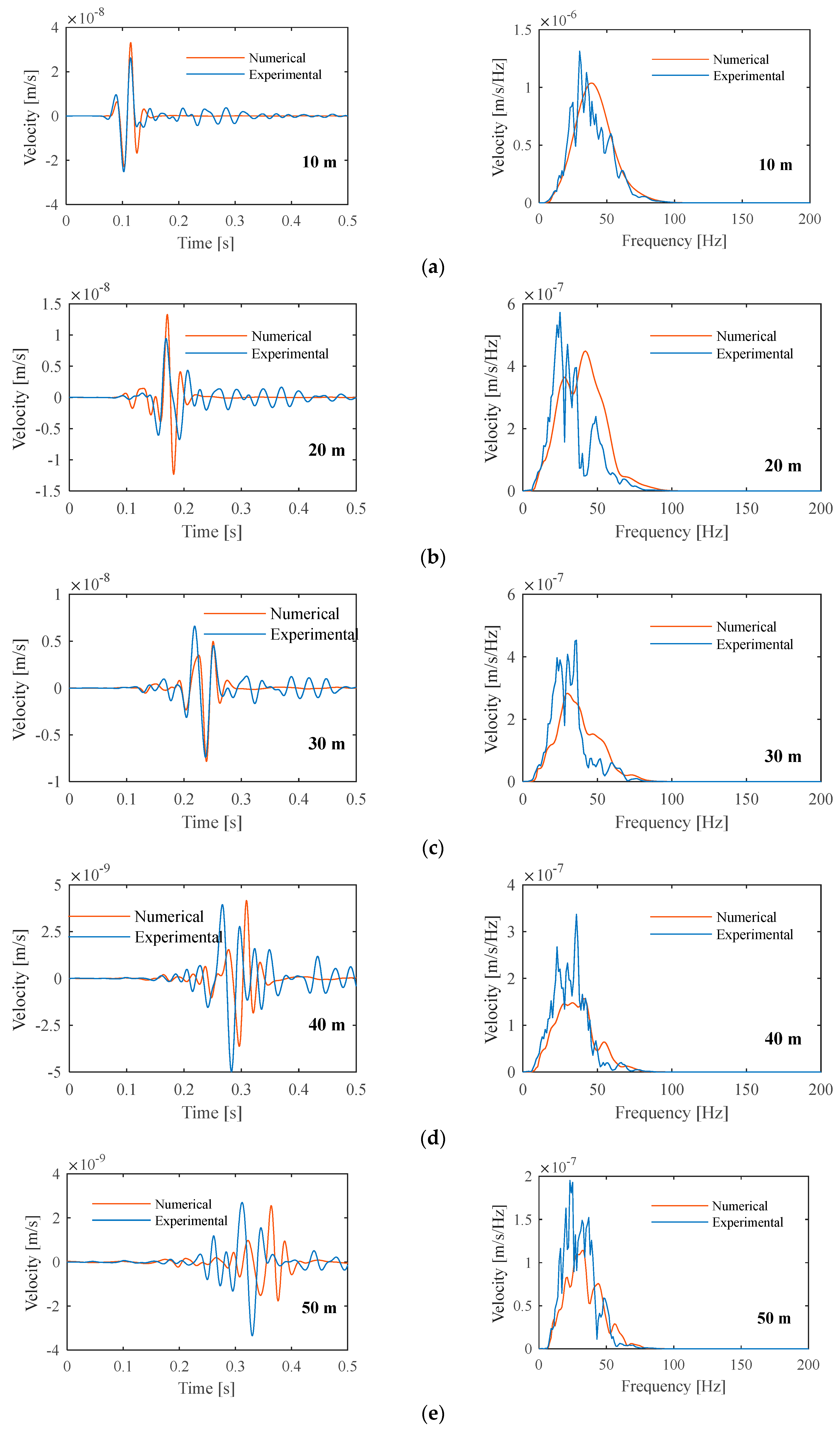
4.3. Comparison between Experimental and Numerical Results
5. Is Linear Modeling Reasonable for Predicting Vibrations Induced by Pile Driving?
6. Conclusions
- (i)
- Given the uncertainties regarding the material damping of the soil, a parametric study was performed, allowing to discuss the relevant influence of this parameter on the dynamic response of the ground and finding an optimized value that fits the experimental results;
- (ii)
- The comparison between the experimental and numerical results shows a very satisfactory agreement. This general comment is valid not only in terms of the maximum levels of vibration but also in the frequency range of the response;
- (iii)
- Given the results obtained, the proposed numerical model can be used in the prediction of ground-borne vibrations for situations where low-strain deformations are expected.
Author Contributions
Funding

Data Availability Statement
Conflicts of Interest
References
- Hindmarsh, J.J.; Smith, W.L. Quantifying construction vibration effects on daily radiotherapy treatments. J. Appl. Clin. Med. Phys. 2018, 19, 733–738. [Google Scholar] [CrossRef] [PubMed]
- Rahman, N.A.A.; Musir, A.A.; Dahalan, N.H.; Ghani, A.N.A.; Khalil, M.K.A. Review of vibration effect during piling installation to adjacent structure. AIP Conf. Proc. 2017, 1901, 110009. [Google Scholar]
- Athanasopoulos, G.A.; Pelekis, P.C. Ground vibrations from sheetpile driving in urban environment: Measurements, analysis and effects on buildings and occupants. Soil Dyn. Earthq. Eng. 2000, 19, 371–387. [Google Scholar] [CrossRef]
- Massarsch, K.R.; Fellenius, B.H. Ground vibrations from pile and sheet pile driving. Part 1 Building Damage. In Proceedings of the DFIEFFC International Conference on Piling and Deep Foundations, Stockholm, Sweden, 21–23 May 2014; pp. 131–138. [Google Scholar]
- Cleary, J.C.; Steward, E.J. Analysis of ground vibrations induced by pile driving and a comparison of vibration prediction methods. DFI J.—J. Deep Found. Inst. 2016, 10, 125–134. [Google Scholar] [CrossRef]
- Massarsch, K.R.; Fellenius, B.H. Ground vibrations induced by impact pile driving. In Proceedings of the 6th International Conference on Case Histories in Geotechnical Engineering, Arlington, VA, USA, 11–16 August 2008; pp. 1–38. [Google Scholar]
- Attewell, P.B.; Farmer, I.W. Attenuation of ground vibrations from pile driving. Ground Eng. 1973, 63, 26–29. [Google Scholar]
- Attewell, P.B.; Selby, A.R.; O’Donnell, L. Tables and graphs for the estimation of ground vibration from driven piling operations. Geotech. Geol. Eng. 1992, 10, 61–85. [Google Scholar] [CrossRef]
- Massarsch, K.R.; Fellenius, B.H. Engineering assessment of ground vibrations caused by impact pile driving. Geotech. Eng. 2015, 46, 54–63. [Google Scholar]
- Whyley, P.J.; Sarsby, R.W. Ground borne vibration from piling. Ground Eng. 1992, 25, 32–37. [Google Scholar]
- Grizi, A.; Athanasopoulos-Zekkos, A.; Woods, R.D. Pile Driving Vibration Attenuation Relationships: Overview and Calibration Using Field Measurements. In Geotechnical Earthquake Engineering and Soil Dynamics V: Numerical Modeling and Soil Structure Interaction; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 435–444. [Google Scholar]
- Ramshaw, C.L.; Selby, A.R.; Bettess, P. Ground Waves Generated by Pile Driving, and Structural Interaction. In Proceedings of the International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 26–31 March 2001. [Google Scholar]
- Khoubani, A.; Ahmadi, M.M. Numerical study of ground vibration due to impact pile driving. Proc. Inst. Civ. Eng. Geotech. Eng. 2014, 167, 28–39. [Google Scholar] [CrossRef]
- Homayoun Rooz, A.F.; Hamidi, A. A numerical model for continuous impact pile driving using ALE adaptive mesh method. Soil Dyn. Earthq. Eng. 2019, 118, 134–143. [Google Scholar] [CrossRef]
- Sofiste, T.; Godinho, L.; Alves Costa, P.; Soares Júnior, D. An effective time domain numerical model for the prediction of ground-borne vibrations induced by pile driving. In Proceedings of the Inter-Noise 2020, Seoul, Republic of Korea, 23–26 August 2020. [Google Scholar]
- Masoumi, H.R.; Degrande, G.; Lombaert, G. Prediction of free field vibrations due to pile driving using a dynamic soil-structure interaction formulation. Soil Dyn. Earthq. Eng. 2007, 27, 126–143. [Google Scholar] [CrossRef]
- Masoumi, H.R.; Degrande, G.; Holeyman, A. Pile response and free field vibrations due to low strain dynamic loading. Soil Dyn. Earthq. Eng. 2009, 29, 834–844. [Google Scholar] [CrossRef]
- Masoumi, H.R.; François, S.; Degrande, G. A non-linear coupled finite element-boundary element model for the prediction of vibrations due to vibratory and impact pile driving. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 245–274. [Google Scholar] [CrossRef]
- Grizi, A.; Athanasopoulos-Zekkos, A.; Woods, R.D. H-Pile Driving Induced Vibrations: Reduced-Scale Laboratory Testing and Numerical Analysis. In Proceedings of the IFCEE 2018 Conference, Orlando, FL, USA, 5–10 March 2018; pp. 165–175. [Google Scholar]
- Tsouvalas, A. Underwater Noise Emission Due to Offshore Pile Installation: A Review. Energies 2020, 13, 3037. [Google Scholar] [CrossRef]
- Fricke, M.B.; Rolfes, R. Towards a complete physically based forecast model for underwater noise related to impact pile driving. J. Acoust. Soc. Am. 2015, 137, 1564–1575. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage. J. Mar. Sci. Eng. 2016, 4, 44. [Google Scholar] [CrossRef]
- Peng, Y.; Tsouvalas, A.; Stampoultzoglou, T.; Metrikine, A. A fast computational model for near- and far-field noise prediction due to offshore pile driving. J. Acoust. Soc. Am. 2021, 149, 1772–1790. [Google Scholar] [CrossRef] [PubMed]
- Berenger, J. A perfectly matched layer for absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Johnson, S.G. Notes on Perfectly Matched Layers (PMLs). arXiv 2021, arXiv:2108.05348. [Google Scholar]
- Lopes, P.; Costa, P.A.; Ferraz, M.; Calçada, R.; Cardoso, A.S. Numerical modeling of vibrations induced by railway traffic in tunnels: From the source to the nearby buildings. Soil Dyn. Earthq. Eng. 2014, 61–62, 269–285. [Google Scholar] [CrossRef]
- Lopes, P.; Alves Costa, P.; Calçada, R.; Silva Cardoso, A. Numerical Modeling of Vibrations Induced in Tunnels: A 2.5D FEM-PML Approach. In Traffic Induced Environmental Vibrations and Controls: Theory and Application; Xia, H., Calçada, R., Eds.; Nova: Hauppauge, NY, USA, 2013; pp. 133–166. [Google Scholar]
- Masoumi, H.; Degrande, G. Numerical modeling of free field vibrations due to pile driving using a dynamic soil-structure interaction formulation. J. Comput. Appl. Math. 2008, 215, 503–511. [Google Scholar] [CrossRef]
- Deeks, A.; Randolph, M. Analytical Modeling of Hammer Impact for Pile Driving. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 279–302. [Google Scholar] [CrossRef]
- Degrande, G.; Badsar, S.A.; Lombaert, G.; Schevenels, M.; Teughels, A. Application of the coupled local minimizers method to the optimization problem in the spectral analysis of surface waves method. J. Geotech. Geoenviron. Eng. 2008, 134, 1541–1553. [Google Scholar] [CrossRef]
- Ricker, N. The form and laws of propagation of seismic wavelets. Geophysics 1953, 18, 10–40. [Google Scholar] [CrossRef]
- Zekkos, A.A.; Woods, R.D.; Grizi, A. Effect of Pile-Driving Induced Vibrations on Nearby Structures and Other Assets. Michigan Department of Transportation; Report: ORBP Number OR10-046; University of Michigan: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Szilvágyi, Z.; Ray, R. Measuring and Modeling the Dynamic Behavior of Danube Sands. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering: Challenging and Innovations in Geotechnics, Paris, France, 2–6 September 2013. [Google Scholar]

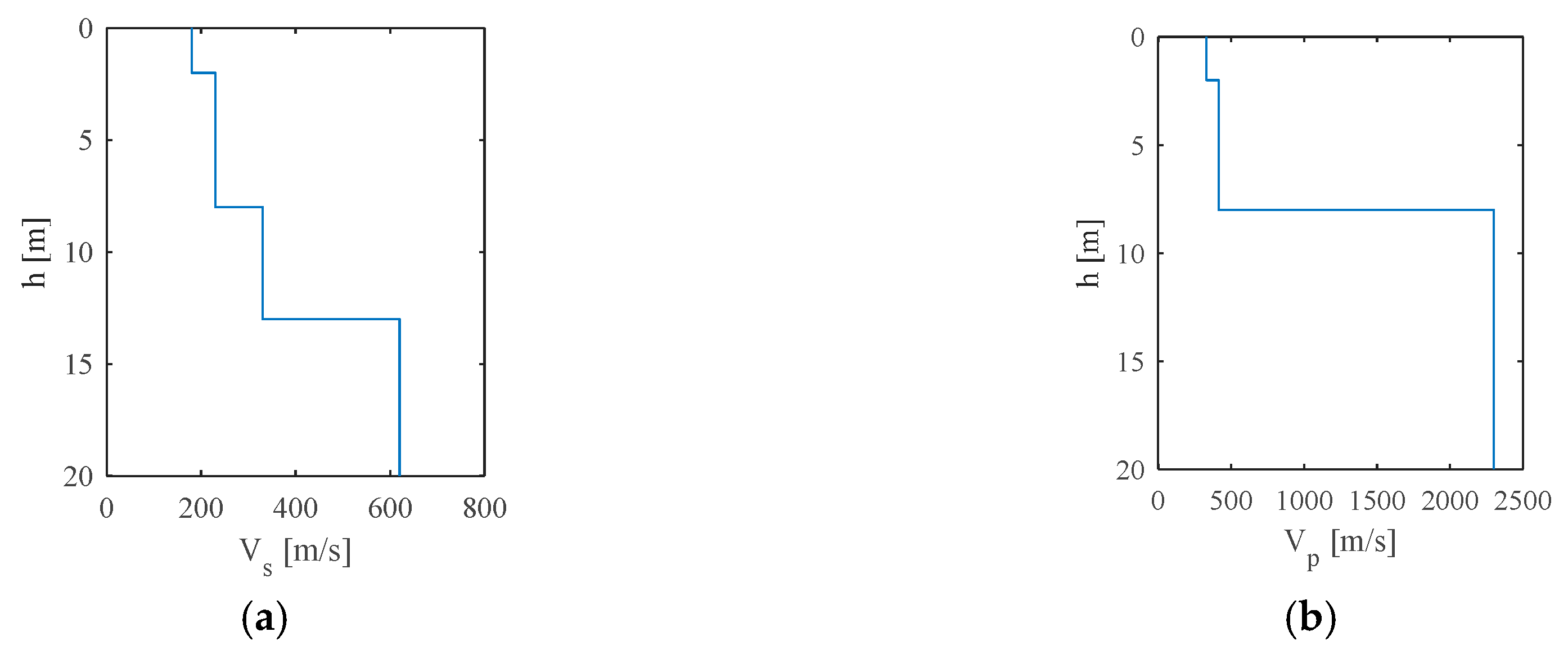






| Element | h (m) | E (MPa) | ν (-) | ρ (kg/m3) | ξ (%) |
|---|---|---|---|---|---|
| Soil | 2 | 154 | 0.25 | 1900 | 5 |
| 6 | 251 | 0.25 | 2.5 | ||
| 5 | 620 | 0.49 | |||
| inf | 2200 | 0.49 | |||
| Pile | L = 12 m | 30,000 | 0.20 | 2500 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colaço, A.; Costa, P.A.; Parente, C.; Abouelmaty, A.M. Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation. Vibration 2022, 5, 829-845. https://doi.org/10.3390/vibration5040049
Colaço A, Costa PA, Parente C, Abouelmaty AM. Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation. Vibration. 2022; 5(4):829-845. https://doi.org/10.3390/vibration5040049
Chicago/Turabian StyleColaço, Aires, Pedro Alves Costa, Cecília Parente, and Ahmed M. Abouelmaty. 2022. "Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation" Vibration 5, no. 4: 829-845. https://doi.org/10.3390/vibration5040049
APA StyleColaço, A., Costa, P. A., Parente, C., & Abouelmaty, A. M. (2022). Vibrations Induced by a Low Dynamic Loading on a Driven Pile: Numerical Prediction and Experimental Validation. Vibration, 5(4), 829-845. https://doi.org/10.3390/vibration5040049











