Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature
Abstract
1. Introduction
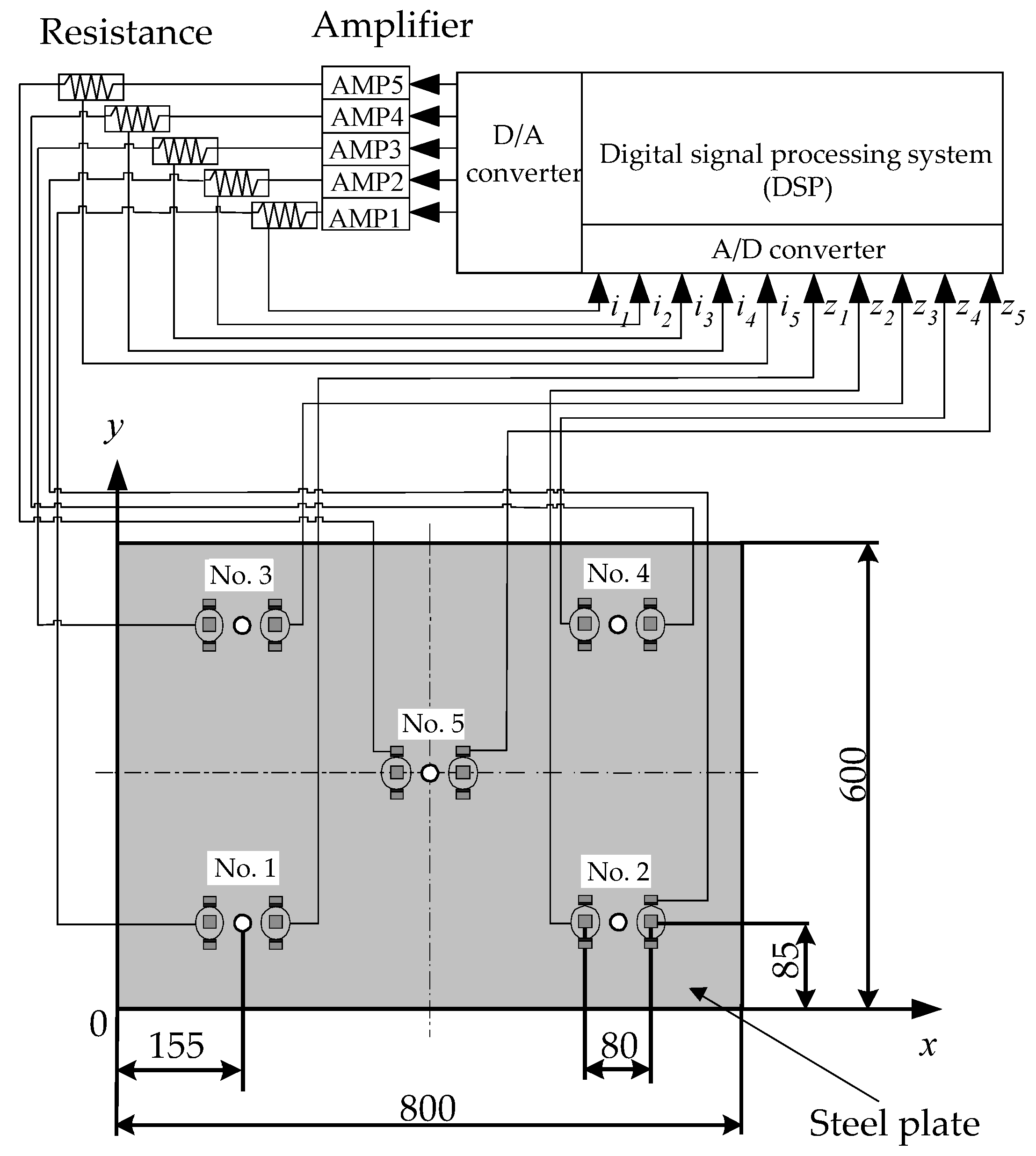
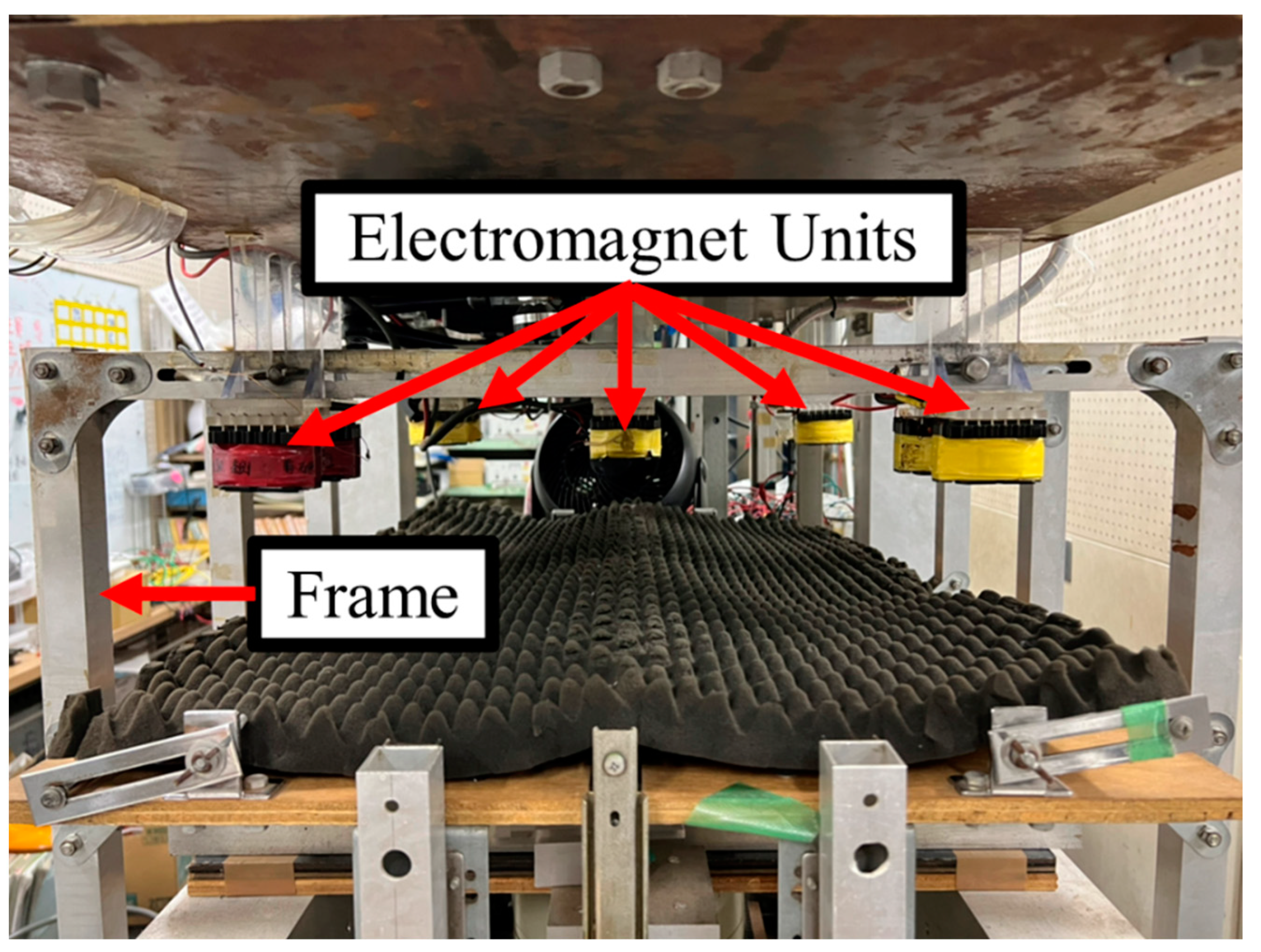
2. Bending Levitation System
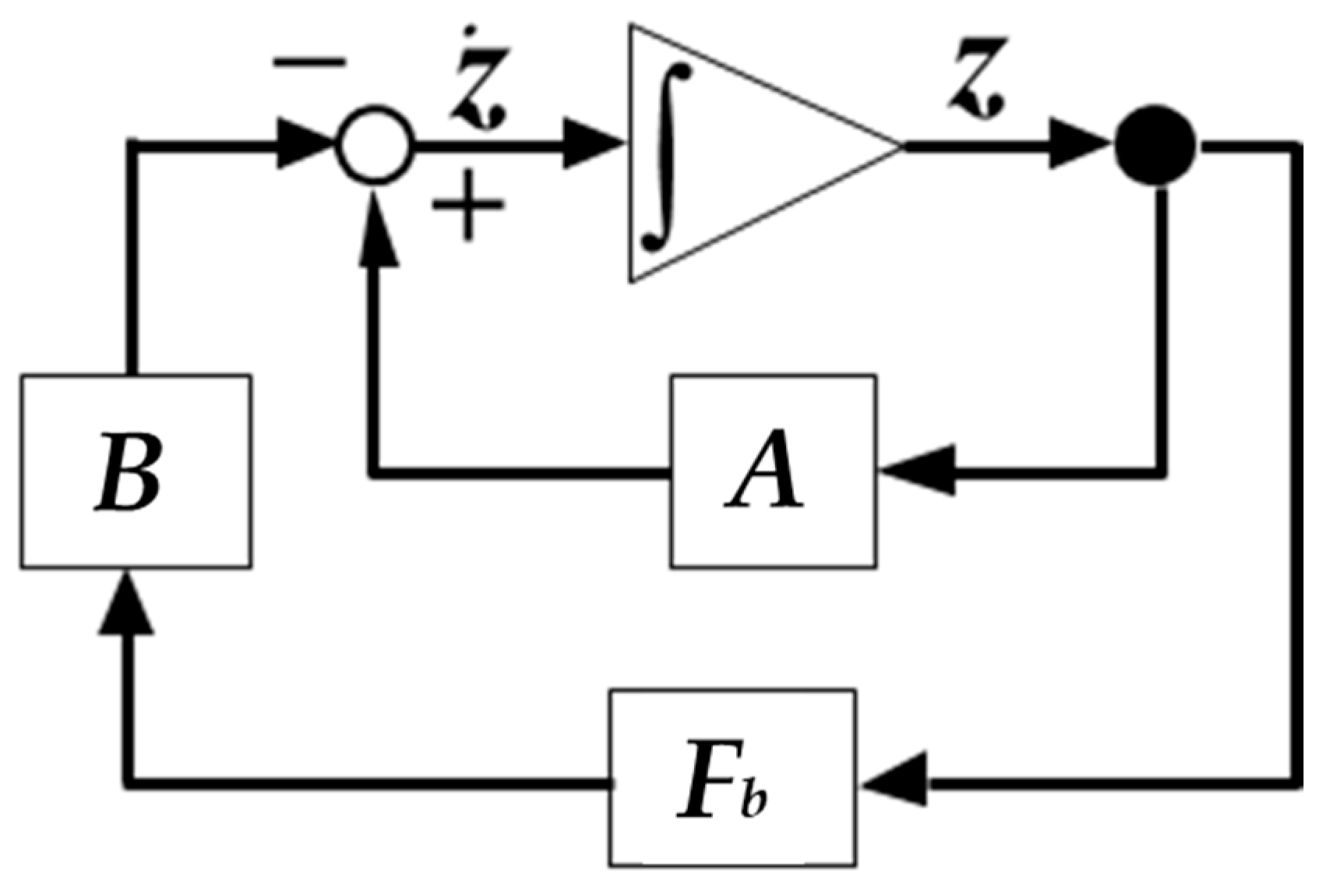
Modeling of Steel Plate
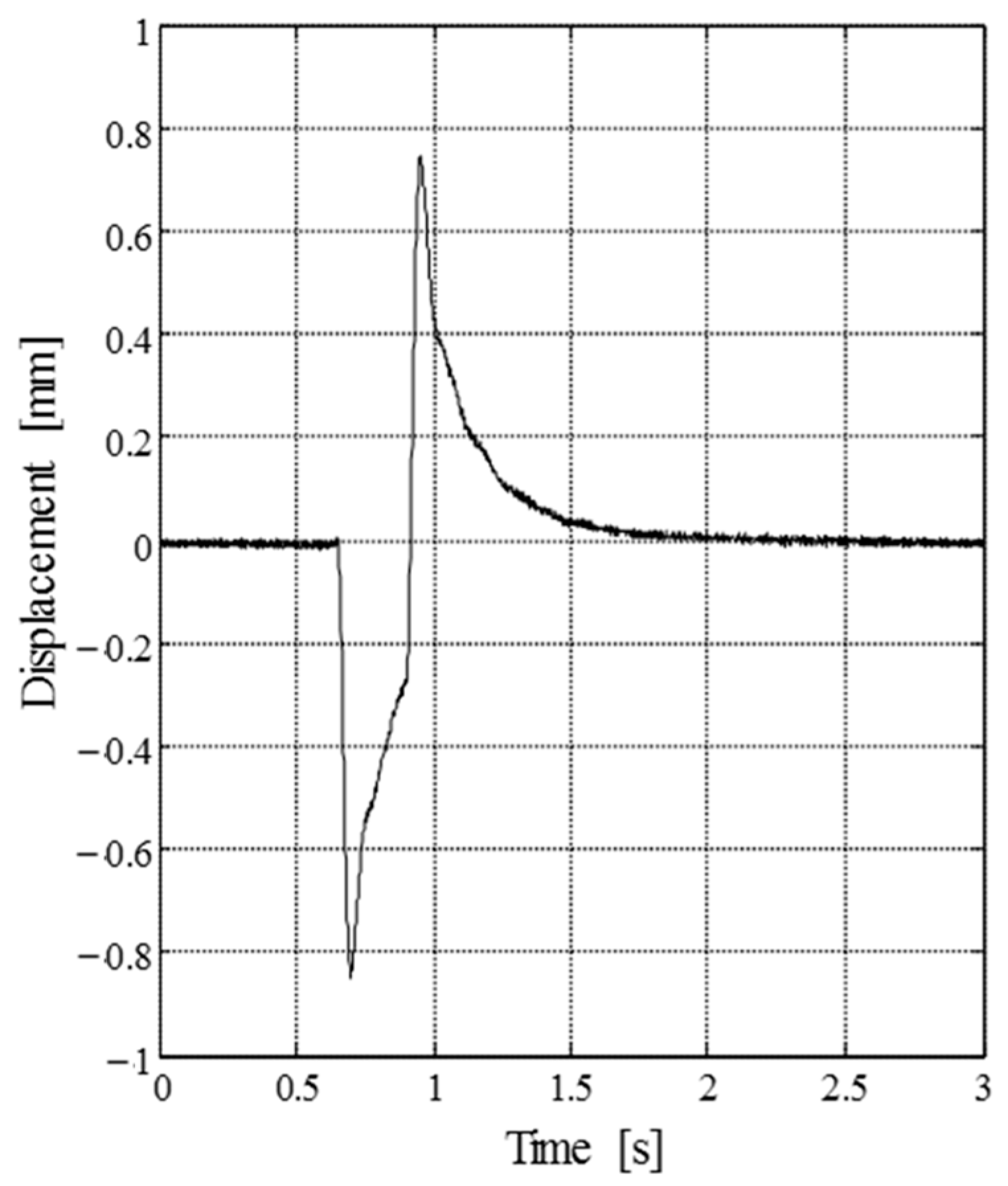
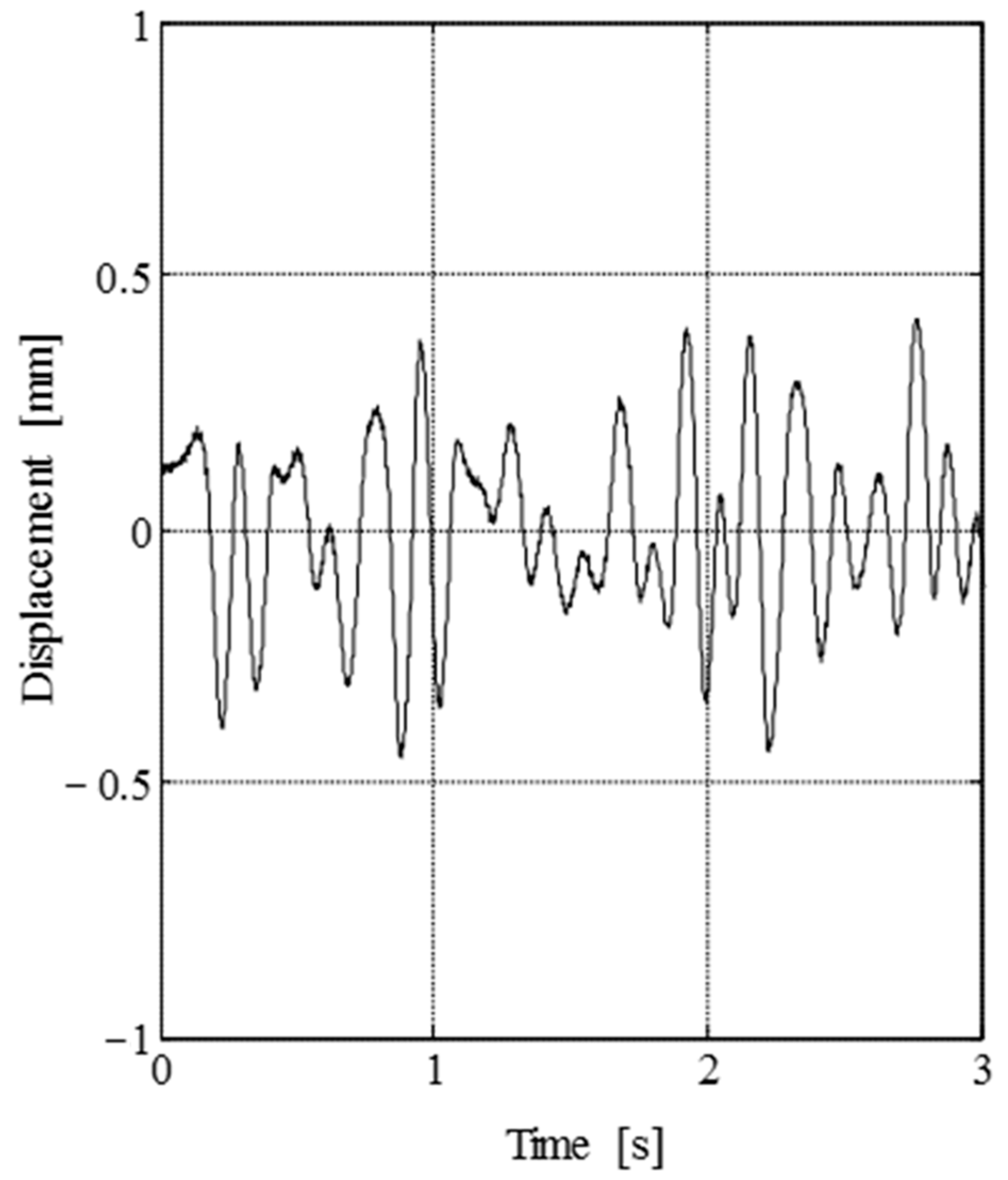
3. Levitation Experiment under Pulse Disturbances
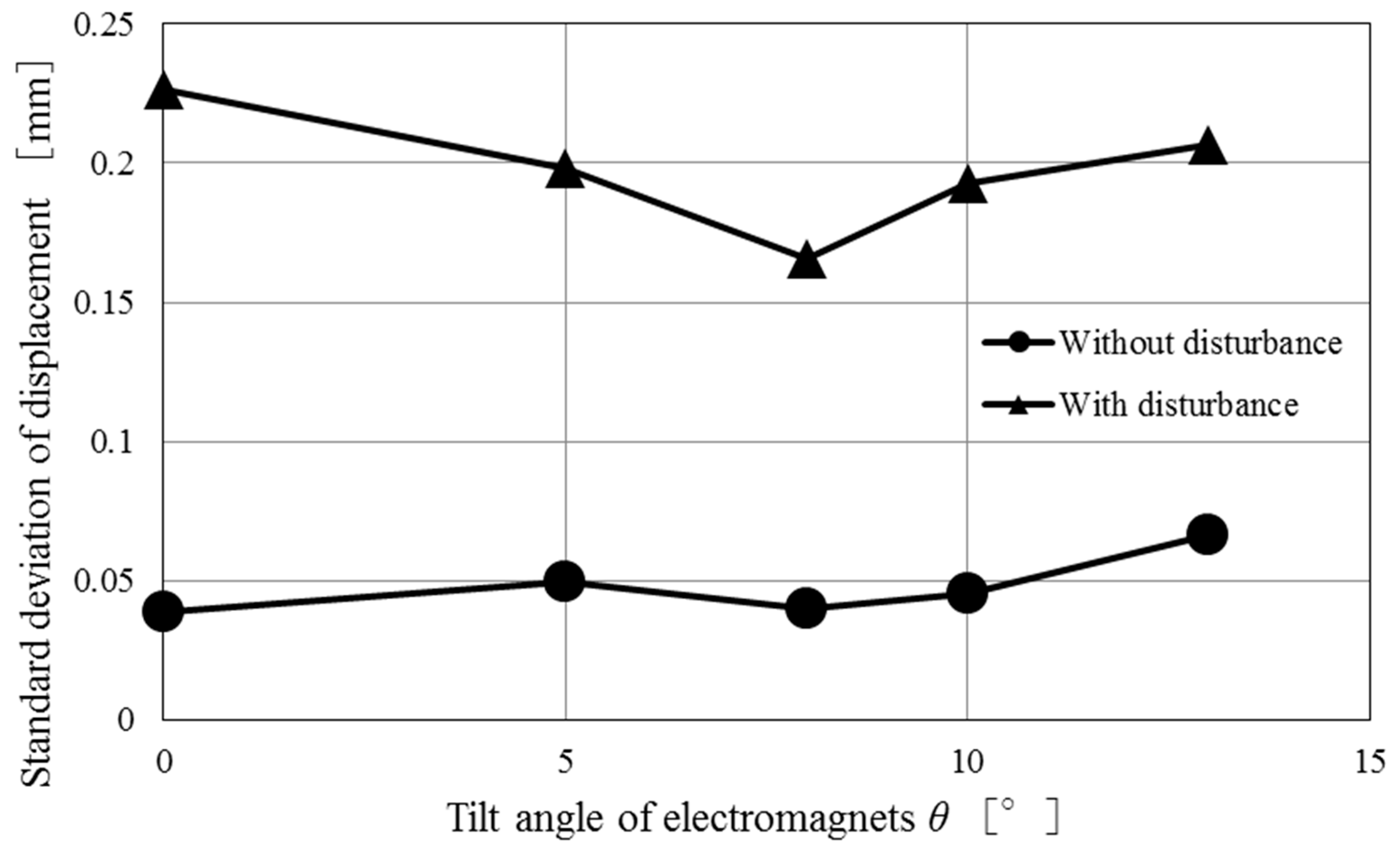
4. Levitation Experiment under Random Disturbances
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Christian, K.; Andreas, K.; Wolfgang, K. Optimal force control of a permanent magnet linear synchronous motor based on a magnetic equivalent circuit model. Control Eng. Pract. 2022, 122, 105076. [Google Scholar]
- Mateo, B.; Dinko, V. Vector control system of a self-excited induction generator including iron losses and magnetic saturation. Control Eng. Pract. 2013, 21, 395–406. [Google Scholar]
- Zhen, S.; Hao, J.; Liu, X.; Wu, Q.; Zhao, H.; Chen, Y.H. A practical robust bounded control for permanent magnet linear motor with inequality constraints. Control Eng. Pract. 2022, 122, 105068. [Google Scholar] [CrossRef]
- Yaojung, S.; Mahendra, B.K.; Chang-Bo, W. New Actuation Control for Hybrid Electromagnetic Valve Train. Appl. Sci. 2022, 12, 10449. [Google Scholar]
- Asano, Y.; Mizuguchi, A.; Amada, M.; Asama, J.; Chiba, A.; Ooshima, M.; Takemoto, M.; Fukao, T.; Ichikawa, O.; Dorrell, D.G. Development of a Four-Axis Actively Controlled Consequent-Pole-Type Bearingless Motor. IEEE Trans. Ind. Appl. 2009, 45, 1378–1386. [Google Scholar] [CrossRef]
- Krzysztof, K. Modification of Electromechanical Coupling in Electromagnetic Harvester. Energies 2022, 15, 4007. [Google Scholar]
- Joanna, B.; Tomasz, T.; Marcin, S.; Zygmunt, K. Modelling and Investigation of Energy Harvesting System Utilizing Magnetically Levitated Permanent Magnet. Sensors 2022, 22, 6384. [Google Scholar]
- Hamidreza, M.; Ali, Z.; Rajesh, R. Magnetic position estimation using optimal sensor placement and nonlinear observer for smart actuators. Control Eng. Pract. 2021, 112, 104817. [Google Scholar]
- Rajiv, T.; Prabhat, K. An innovative virtual trial misalignment approach for identification of unbalance, sensor and active magnetic bearing misalignment along with its stiffness parameters in a magnetically levitated flexible rotor system. Mech. Syst. Sig. Proces. 2022, 167, 1085440. [Google Scholar]
- Murakami, I.; Zhao, Y.; Tashiro, T. Stabilization of a Magnetic Repulsive Levitation Flywheel System Using a High-Efficiency Superconducting Magnetic Bearing. Actuators 2022, 11, 180. [Google Scholar] [CrossRef]
- Georg, S.; Martin, B.; Martin, H.; Josef, Z.; Clenn, G. Control of a magnetic levitation system with communication imperfections: A model-based coupling approach. Control Eng. Pract. 2013, 58, 161–170. [Google Scholar]
- Fengqiu, X.; Kaiyang, Z.; Xianze, X. Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking. Sensors 2022, 22, 4270. [Google Scholar]
- Dahoon, A.; Ji-Won, J.; Hyeeun, Y.; Jaeheon, J. Development of a Novel Dual Servo Magnetic Levitation Stage. Actuators 2022, 11, 147. [Google Scholar]
- Mizuno, T.; Takasaki, M.; Kishita, K.; Hirakawa, K. Vibration isolation system combining zero-power magnetic suspension with springs. Control Eng. Pract. 2007, 15, 187–196. [Google Scholar] [CrossRef]
- Ranhee, Y.; Birhan, A.N.; Wonhee, Y.; Jungyoul, L.; Jinho, L.; Changyoung, L.; Kwansup, L. Capsule Vehicle Dynamics Based on Levitation Coil Design Using Equivalent Model of a Sidewall Electrodynamic Suspension System. Energies 2021, 14, 4979. [Google Scholar]
- Fujita, K.; Sugiura, T. Characterization of LCR Parallel-Type Electromagnetic Shunt Damper for Superconducting Magnetic Levitation. Actuators 2022, 11, 216. [Google Scholar] [CrossRef]
- Laith, S.I.; Ciprian, L.; Hamid, A. Design of Adaptive-RST Controller for Nonlinear Magnetic Levitation System Using Multiple Zone-Model Approach in Real-Time Experimentation. Appl. Syst. Innov. 2022, 5, 93. [Google Scholar]
- Lidia, M.B.; Eva, S.; Antonio, F.C.; José, A.S.; Rafael, M. Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach. Mathematics 2021, 9, 1424. [Google Scholar]
- Nihal, D.; Dipankar, D.; Muyeen, S.M. A Reference Model Assisted Adaptive Control Structure for Maglev Transportation System. Electronics 2021, 10, 332. [Google Scholar]
- Rahul, S.G.; Soundarya, S.; Kavitha, P.; Yuvaraja, T.; Ramya, K.; Shabana, U. Enhanced Model Reference Adaptive Control Scheme for Tracking Control of Magnetic Levitation System. Energies 2021, 14, 1455. [Google Scholar]
- Suzuki, O.; Nagashima, D.; Nishimura, K.; Nakagawa, T. Magnetic Levitation Control by Considering the Twisting Mode of a 0.18 mm Thick Steel Plate. IEEE Trans. Magn. 2015, 51, 8600304. [Google Scholar] [CrossRef]
- Cheng, T.L.; Yung, Y.Y.; Sheng, Y.L. On-line realizations of dynamic gap detection and control for levitated industrial steel plate conveyance system. In Proceedings of the 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA, 7–11 October 2012. [Google Scholar] [CrossRef]
- Kato, H.; Marumori, H.; Yonezawa, H.; Narita, T. Vibration Suppression Effect in a Bending-Levitated Flexible Steel Plate by the Electromagnetic Force. J. Vib. Acoust. 2016, 138, VIB-15-1159. [Google Scholar] [CrossRef]
- Marumori, H.; Yonezawa, H.; Narita, T.; Kato, H.; Oshinoya, Y. Consideration on bentmagnetic levitation apparatus for thin steel plate. Trans. JSME 2015, 81, 14-00471. [Google Scholar] [CrossRef]
- Tada, M.; Yonezawa, H.; Marumori, H.; Narita, T.; Kato, H.; Moriyama, H. Vibration suppression effect in a maglev system for flexible steel plate with curvature. Int. J. Appl. Electromagn. Mech. 2019, 59, 993–1001. [Google Scholar] [CrossRef]









| Electromagnet Number | Displacement | Velocity | Current |
|---|---|---|---|
| 1~4 | 6555.7 | 97.9 | 32.1 |
| 5 | 8084.1 | 120.7 | 32.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogawa, K.; Miyazaki, R.; Uchida, Y.; Kobayashi, I.; Kuroda, J.; Uchino, D.; Ikeda, K.; Kato, T.; Endo, A.; Narita, T.; et al. Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature. Vibration 2022, 5, 817-828. https://doi.org/10.3390/vibration5040048
Ogawa K, Miyazaki R, Uchida Y, Kobayashi I, Kuroda J, Uchino D, Ikeda K, Kato T, Endo A, Narita T, et al. Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature. Vibration. 2022; 5(4):817-828. https://doi.org/10.3390/vibration5040048
Chicago/Turabian StyleOgawa, Kazuki, Riku Miyazaki, Yamato Uchida, Ikkei Kobayashi, Jumpei Kuroda, Daigo Uchino, Keigo Ikeda, Taro Kato, Ayato Endo, Takayoshi Narita, and et al. 2022. "Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature" Vibration 5, no. 4: 817-828. https://doi.org/10.3390/vibration5040048
APA StyleOgawa, K., Miyazaki, R., Uchida, Y., Kobayashi, I., Kuroda, J., Uchino, D., Ikeda, K., Kato, T., Endo, A., Narita, T., & Kato, H. (2022). Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature. Vibration, 5(4), 817-828. https://doi.org/10.3390/vibration5040048









