An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range
Abstract
:1. Introduction
- the type of vehicle and its static wheel loads,
- the mechanical resistance of the track and its layout [1].
2. Materials and Methods
2.1. Finite Element Model of the Track
2.2. Track Loading
- the static wheel loads of the vehicle,
- the vehicle’s dynamic overloads due to irregularities of the track vertical profile.
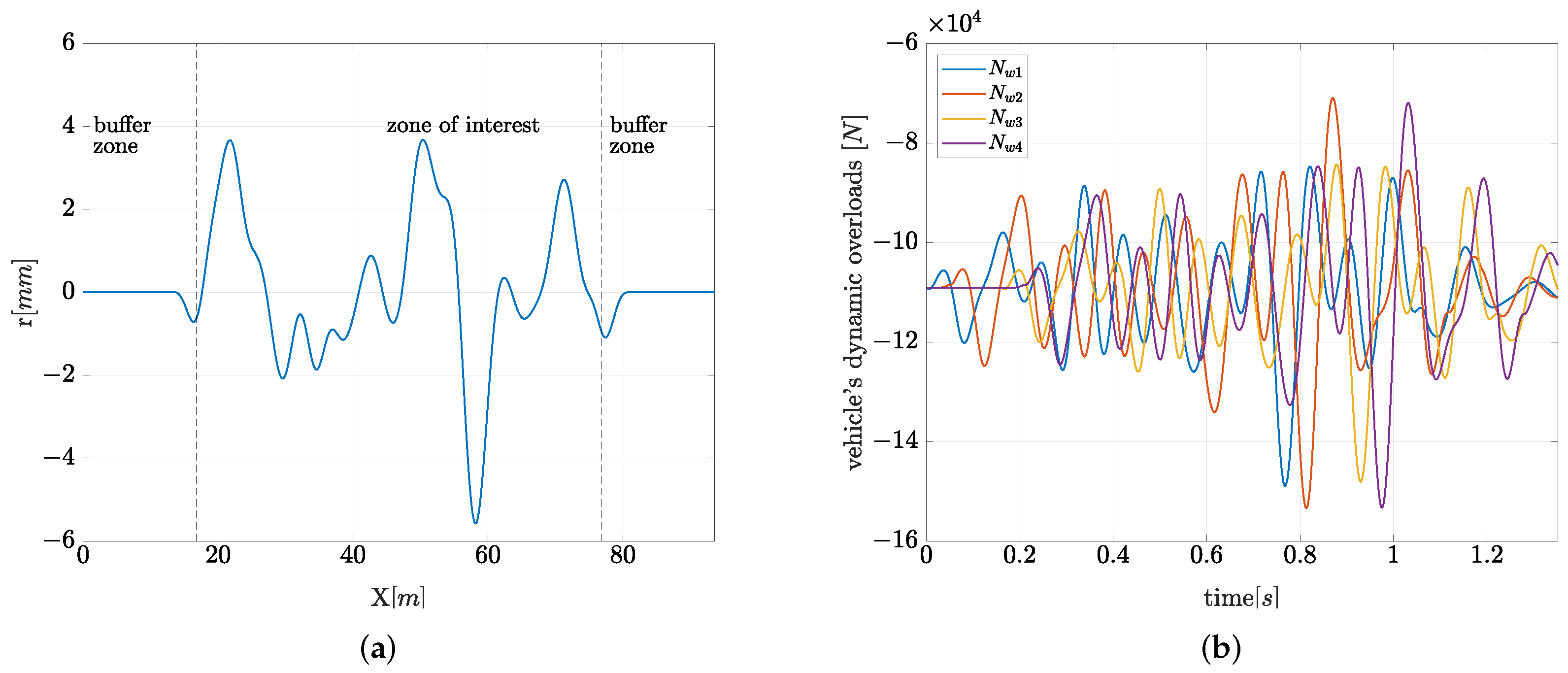
2.2.1. Simulation of a Random Irregularity of the Track Vertical Profile
Track Inspection Techniques in the French Railway Network
Methodology for Generating the Random Irregularity of Track Vertical Profile
- A first preprocessing on the vertical measurements is achieved by removing track zones which are in curves since the modelled track is fully in alignment. is thus the total number of track zones in alignment.
- For each track zone, a discrete Fourier transfom (DFT) of the measured signal is performed with zero padding, where N is the size of the longest signal, is the frequency and i is the imaginary number:
- At each spectral component between 0 and the Nyquist frequency (i.e., ), the maximum amplitude of the DFT among the signals is extracted:
- By creating uniformly distributed random phases in [0;] at each spectral component, one can construct the positive frequency domain signal:The negative frequency domain signal is calculated as the complex conjugate of the positive frequency domain signal. Hence, the DFT H of the random vertical track irregularity is built,
- The track vertical irregularity is recovered by inverse fourier transform:
2.2.2. Multi-Body Model of the Railway Vehicle
3. Results
3.1. Vertical Track Response to a Moving Half Vehicle
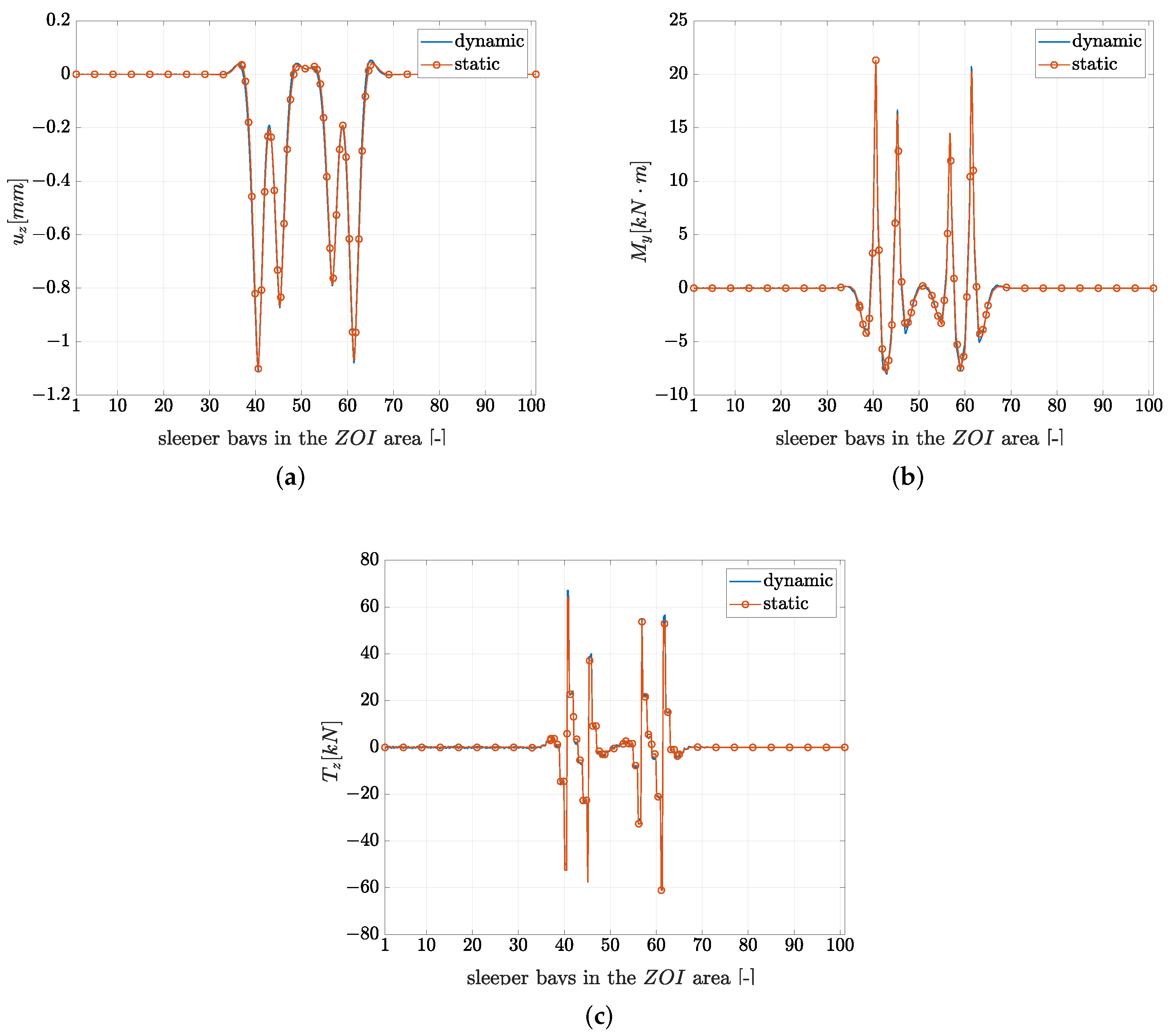
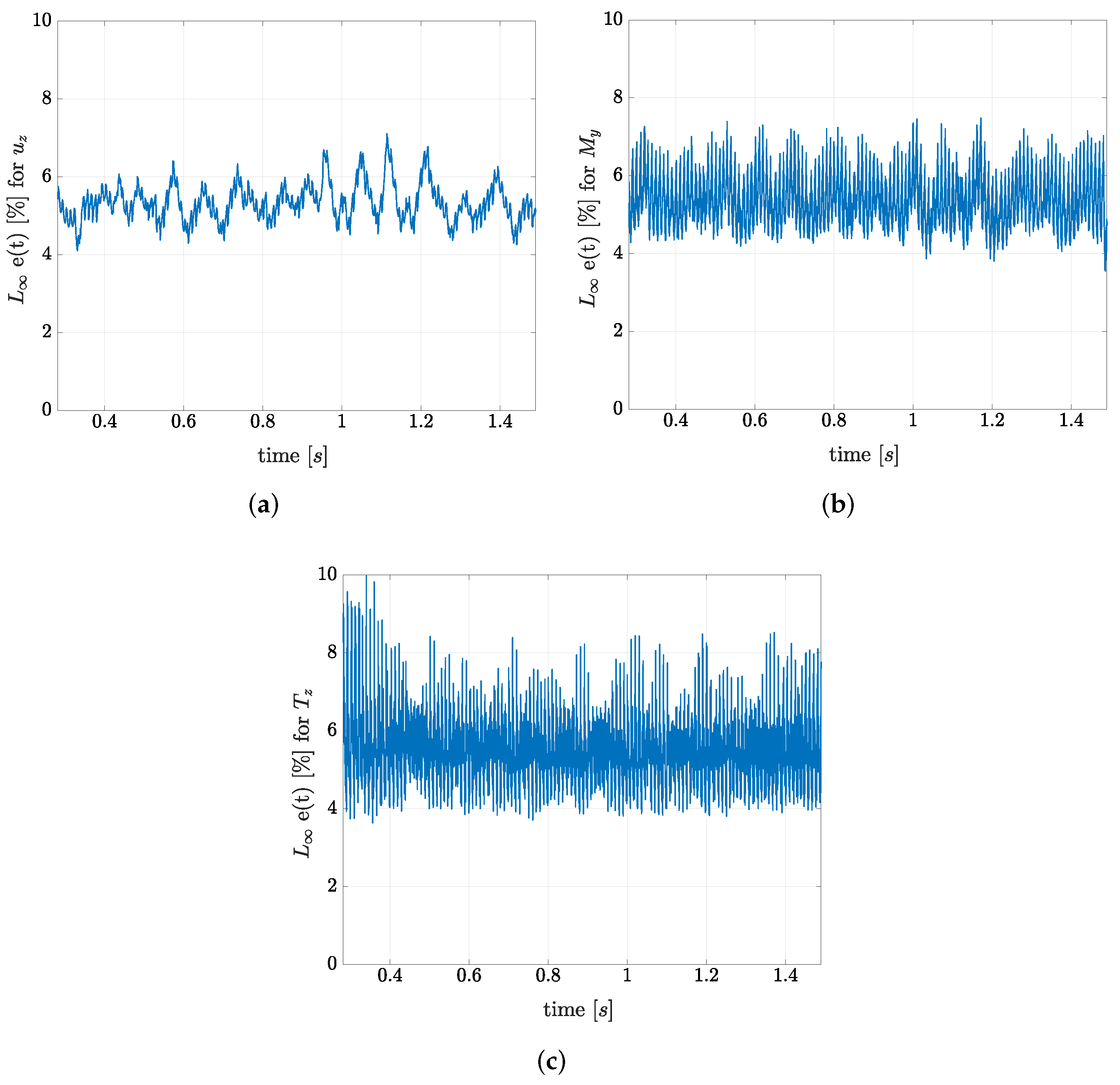
3.1.1. Validation of the Hypothesis of Negligible Inertial Forces at Low Frequency
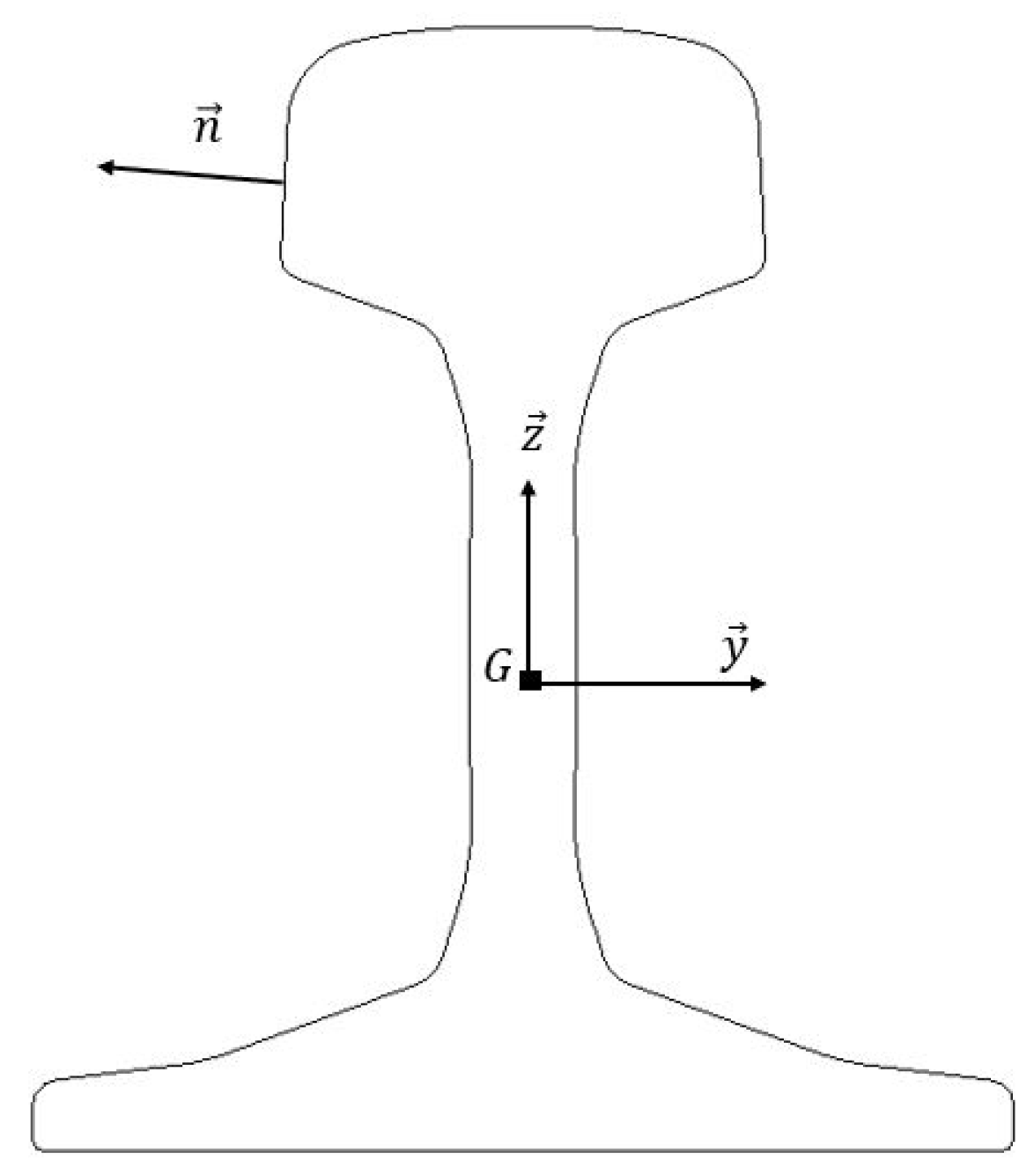
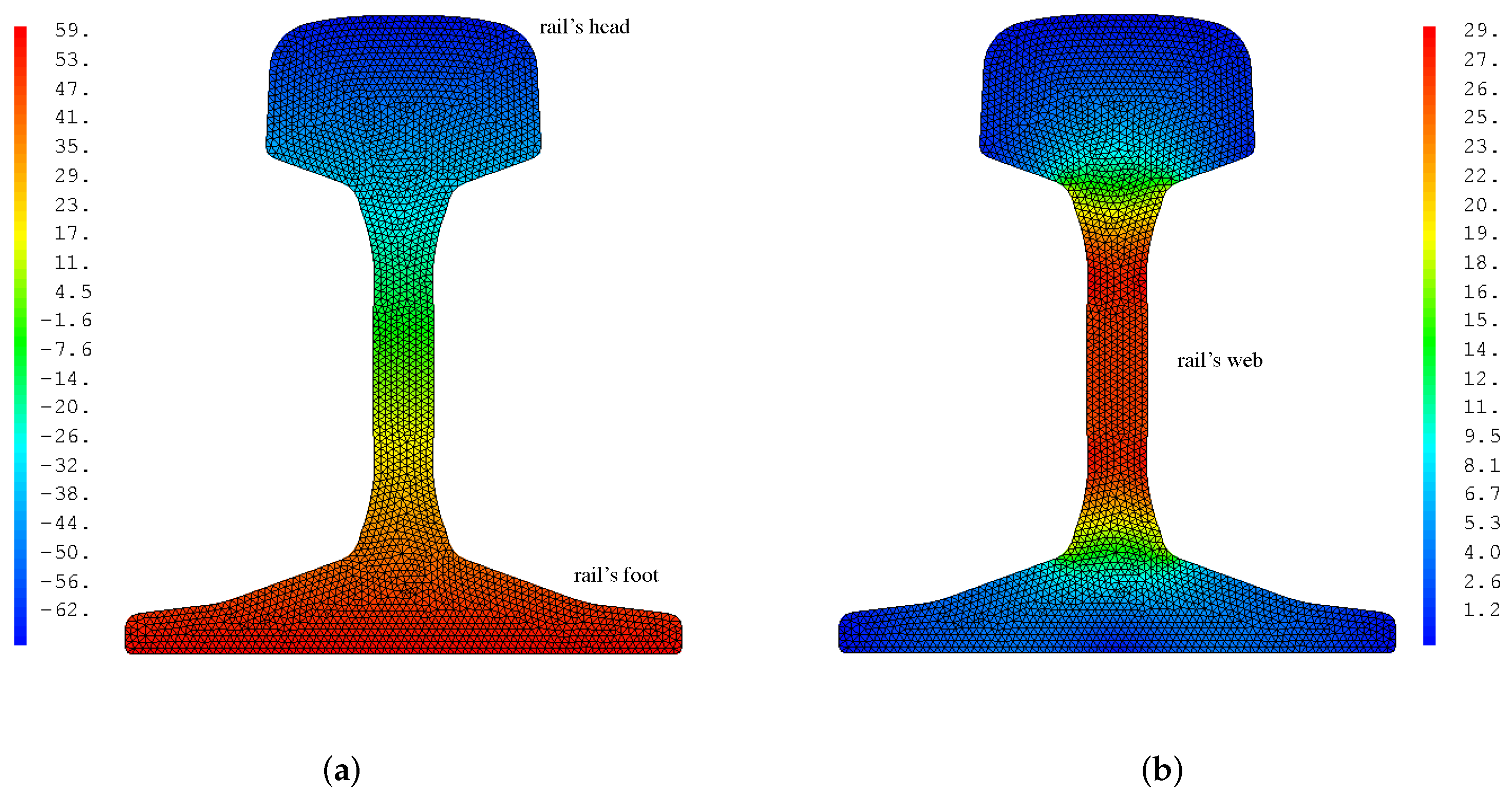
3.1.2. Stress State in the Rail
3.2. Statistical Analysis
4. Conclusions
5. Perspectives
Author Contributions
Funding
Conflicts of Interest
Appendix A. Recall of the Finite Element Matrices of a Two Nodes Timoshenko Beam
References
- SNCF. Règles D’admission des Matériels Roulants sur le RFN en Fonction de la Sollicitation de la Voie; Internal Report; SNCF Division Interaction Véhicule Voie: La Plaine Saint-Denis, France, 2019. [Google Scholar]
- Kraft, S. Parameter Identification for a TGV Model. Ph.D. Thesis, Ecole Centrale de Paris, Paris, France, 2012. [Google Scholar]
- SNCF. Rapport de la Commission Demaux; Internal Report; SNCF: Paris, France, 1944. [Google Scholar]
- Ling, L.; Xiao, X.B.; Xiong, J.Y.; Zhou, L.; Wen, Z.F.; Jin, X.S. A 3D model for coupling dynamics analysis of high-speed train/track system. In China’s High-Speed Rail Technology; Springer: Singapore, 2018; pp. 309–339. [Google Scholar]
- Xu, Y.; Yang, C.; Zhendong, L.; Zhang, W.; Stichel, S. Long-Term High-Speed Train-Track Dynamic Interaction Analysis. In Proceedings of the 27th IAVSD Symposium on Dynamics of Vehicles on Roads and Tracks, Saint-Petersburg, Russia, 16–20 August 2021. [Google Scholar]
- Cai, W.; Chi, M. Study on steady-state responses of high-speed vehicle using infinite long track model. Shock Vib. 2020, 2020, 6878252. [Google Scholar] [CrossRef]
- Mei, H.; Leng, W.; Nie, R.; Liu, W.; Chen, C.; Wu, X. Random distribution characteristics of peak dynamic stress on the subgrade surface of heavy-haul railways considering track irregularities. Soil Dyn. Earthq. Eng. 2019, 116, 205–214. [Google Scholar] [CrossRef]
- Varandas, J.N.; Paixão, A.; Fortunato, E.; Coelho, B.Z.; Hölscher, P. Long-term deformation of railway tracks considering train-track interaction and non-linear resilient behaviour of aggregates—A 3D FEM implementation. Comput. Geotech. 2020, 126, 103712. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Three-dimensional numerical modelling of ballasted railway track foundations for high-speed trains with special reference to critical speed. Transp. Geotech. 2016, 6, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Chebli, H.; Clouteau, D.; Schmitt, L. Dynamic response of high-speed ballasted railway tracks: 3D periodic model and in situ measurements. Soil Dyn. Earthq. Eng. 2008, 28, 118–131. [Google Scholar] [CrossRef]
- Arlaud, E. Modèles Dynamiques Réduits de Milieux Périodiques par Morceaux: Application aux Voies Ferroviaires. Ph.D. Thesis, École Nationale Supérieure d’Arts et Métiers, Paris, France, 2016. [Google Scholar]
- Rhayma, N.; Bressolette, P.h.; Breul, P.; Fogli, M.; Saussine, G. A probabilistic approach for estimating the behavior of railway tracks. Eng. Struct. 2011, 33, 2120–2133. [Google Scholar] [CrossRef]
- Fernandes, V.A.; Lopez-Caballero, F.; d’Aguiar, S.C. Probabilistic analysis of numerical simulated railway track global stiffness. Comput. Geotech. 2014, 55, 267–276. [Google Scholar] [CrossRef]
- Xie, G.; Iwnicki, S.D. Simulation of wear on a rough rail using a time-domain wheel–track interaction model. Wear 2008, 265, 1572–1583. [Google Scholar] [CrossRef]
- Nielsen, J.C.; Igeland, A. Vertical dynamic interaction between train and track influence of wheel and track imperfections. J. Sound Vib. 1995, 187, 825–839. [Google Scholar] [CrossRef]
- Ferrara, R.; Leonardi, G.; Jourdan, F. Numerical modelling of train induced vibrations. Procedia Soc. Behav. Sci. 2012, 53, 155–165. [Google Scholar] [CrossRef]
- Hou, K.; Kalousek, J.; Dong, R. A dynamic model for an asymmetrical vehicle/track system. J. Sound Vib. 2003, 267, 591–604. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Dhanasekar, M. A dynamic model for the vertical interaction of the rail track and wagon system. Int. J. Solids Struct. 2002, 39, 1337–1359. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Vrouwenvelder, A.; Wardenier, J. Numerical simulation of train–bridge interactive dynamics. Comput. Struct. 2001, 79, 1059–1075. [Google Scholar] [CrossRef]
- Lei, X.; Noda, N.A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vib. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Au, F.T.K.; Wang, J.J.; Cheung, Y.K. Impact study of cable-stayed railway bridges with random rail irregularities. Eng. Struct. 2002, 24, 529–541. [Google Scholar] [CrossRef]
- Wang, Y.; Dimitrovová, Z.; Yau, J. Dynamic responses of vehicle ballasted track interaction system for heavy haul trains. MATEC Web Conf. 2018, 148, 05004. [Google Scholar] [CrossRef] [Green Version]
- Arvidsson, T.; Andersson, A.; Karoumi, R. Train running safety on non-ballasted bridges. Int. J. Rail Transp. 2019, 7, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Rodrigo, M.D.; Galvín, P.; Moliner, E.; Romero Ordóñez, A. Rail-Bridge Interaction Effects in Single-Track Multi-Span Bridges. Experimental Results versus Numerical Predictions under Operating Conditions. In Proceedings of the XI International Conference on Structural Dynamics, EURODYN 2020, Athens, Greece, 23–26 November 2020; Papadrakakis, M., Fragiadakis, M., Papadimitriou, C., Eds.; Institute of Structural Analysis and Antiseismic Research, School of Civil Engineering, National Technical University of Athens (NTUA): Athens, Greece, 2020; Volume I, pp. 1652–1665, ISBN 978-618-85072-0-3. [Google Scholar]
- Shan, Y.; Wang, B.; Zhang, J.; Zhou, S. The influence of dynamic loading and thermal conditions on tram track slab damage resulting from subgrade differential settlement. Eng. Fail. Anal. 2021, 128, 105610. [Google Scholar] [CrossRef]
- Punetha, P.; Nimbalkar, S.; Khabbaz, H. Simplified geotechnical rheological model for simulating viscoelasto-plastic response of ballasted railway substructure. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 2019–2047. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Two-layer model of the railway track: Analysis of the critical velocity and instability of two moving proximate masses. Int. J. Mech. Sci. 2022, 217, 107042. [Google Scholar] [CrossRef]
- Sysyn, M.; Przybylowicz, M.; Nabochenko, O.; Liu, J. Mechanism of Sleeper–Ballast Dynamic Impact and Residual Settlements Accumulation in Zones with Unsupported Sleepers. Sustainability 2021, 13, 7740. [Google Scholar] [CrossRef]
- Sysyn, M.; Przybylowicz, M.; Nabochenko, O.; Kou, L. Identification of Sleeper Support Conditions Using Mechanical Model Supported Data-Driven Approach. Sensors 2021, 21, 3609. [Google Scholar] [CrossRef] [PubMed]
- Knothe, K.L.; Grassie, S.L. Modelling of railway track and vehicle/track interaction at high frequencies. Veh. Syst. Dyn. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Iwnicki, S. Handbook of Railway Vehicle Dynamics; CRC Press: Boca Raton, FL, USA, 2006; pp. 147–165. [Google Scholar]
- Dumitriu, M. Analysis of the dynamic response in the railway vehicles to the track vertical irregularities. Part II: The numerical analysis. J. Eng. Sci. Technol. 2015, 8, 32–39. [Google Scholar] [CrossRef]
- Guerin, N. Approche Expérimentale et Numérique du Comportement du Ballast des Voies Ferrées. Ph.D. Thesis, École Nationale des Ponts et Chaussées, Champs-sur-Marne, France, 1996. [Google Scholar]
- Paixão, A.; Fortunato, E.; Calçada, R. The effect of differential settlements on the dynamic response of the train–track system: A numerical study. Eng. Struct. 2015, 88, 216–224. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W.; Gao, J. Extended applications of track irregularity probabilistic model and vehicle–slab track coupled model on dynamics of railway systems. Veh. Syst. Dyn. 2017, 88, 1686–1706. [Google Scholar] [CrossRef]
- Perrin, G.; Soize, C.; Duhamel, D.; Funfschilling, C. Track irregularities stochastic modeling. Probabilistic Eng. Mech. 2013, 34, 123–130. [Google Scholar] [CrossRef] [Green Version]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Cast3M. Available online: http://www-cast3m.cea.fr (accessed on 30 March 2022).
- Nguyen, V.H. Comportement Dynamique de Structures Non-Linéaires Soumises à des Charges Mobiles. Ph.D. Thesis, École Nationale des Ponts et Chaussées, Champs-sur-Marne, France, 2002. [Google Scholar]
- Cai, Z.; Raymond, G.P.; Bathurst, R.J. Natural vibration analysis of rail track as a system of elastically coupled beam structures on Winkler foundation. Comput. Struct. 1994, 53, 1427–1436. [Google Scholar] [CrossRef]
- Cambronero-Barrientos, F.; Díaz-del-Valle, J.; Martínez-Martínez, J.A. Beam element for thin-walled beams with torsion, distortion, and shear lag. Eng. Struct. 2017, 143, 571–588. [Google Scholar] [CrossRef]
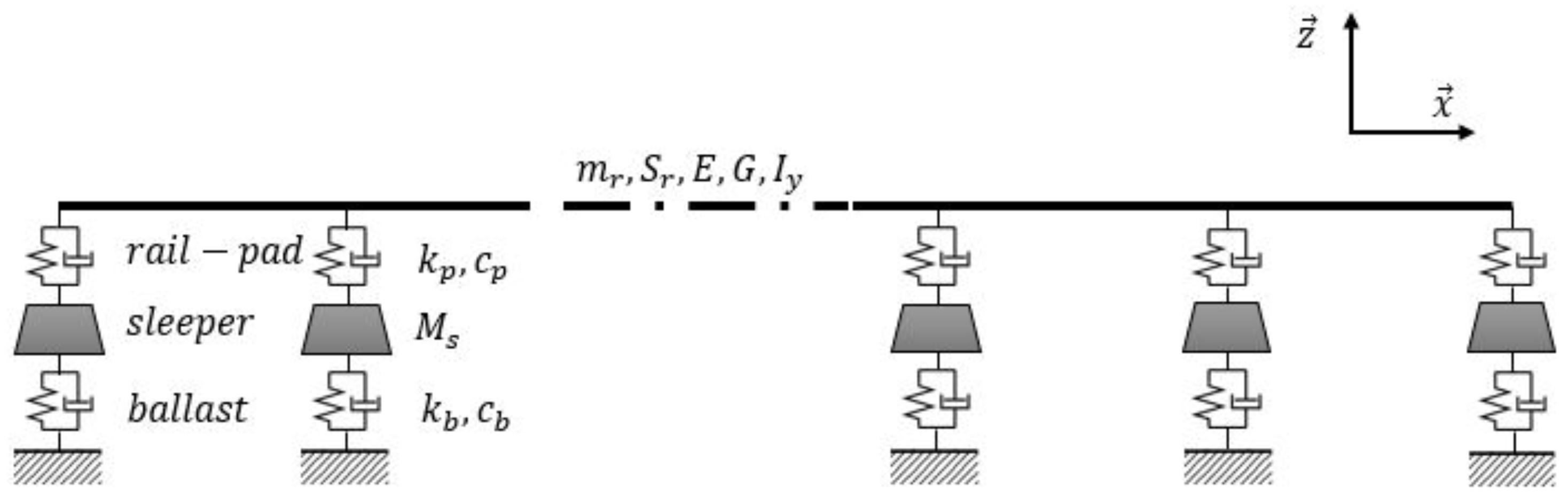
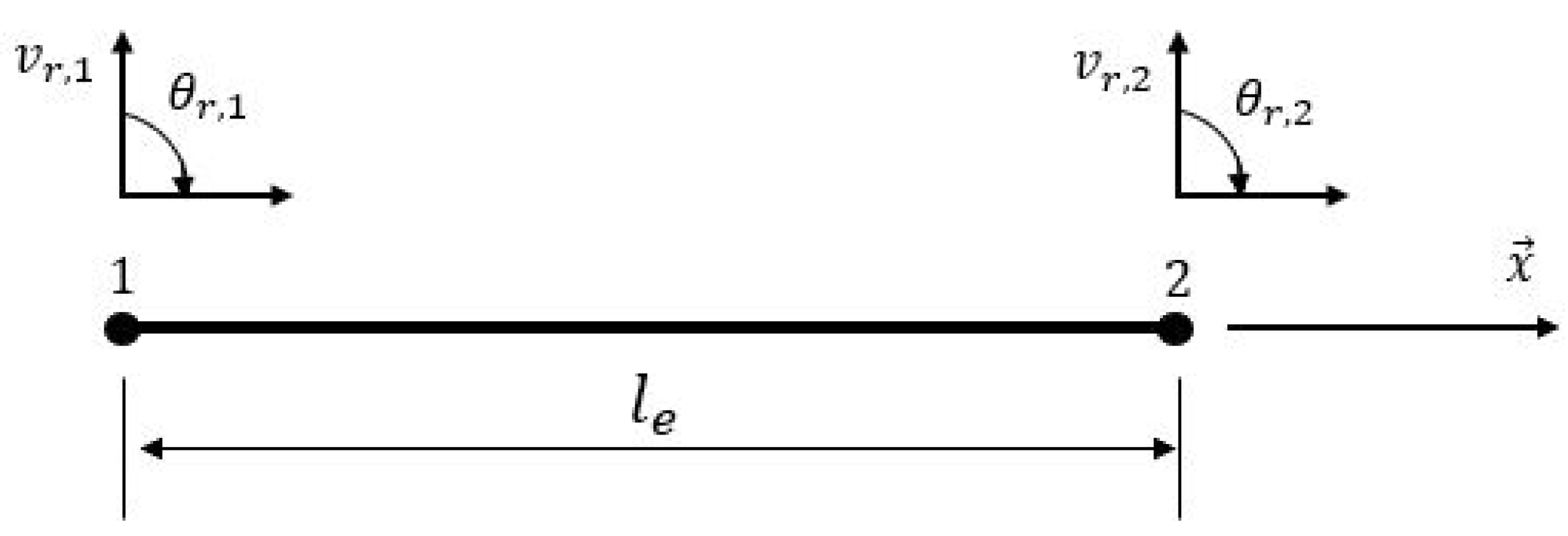

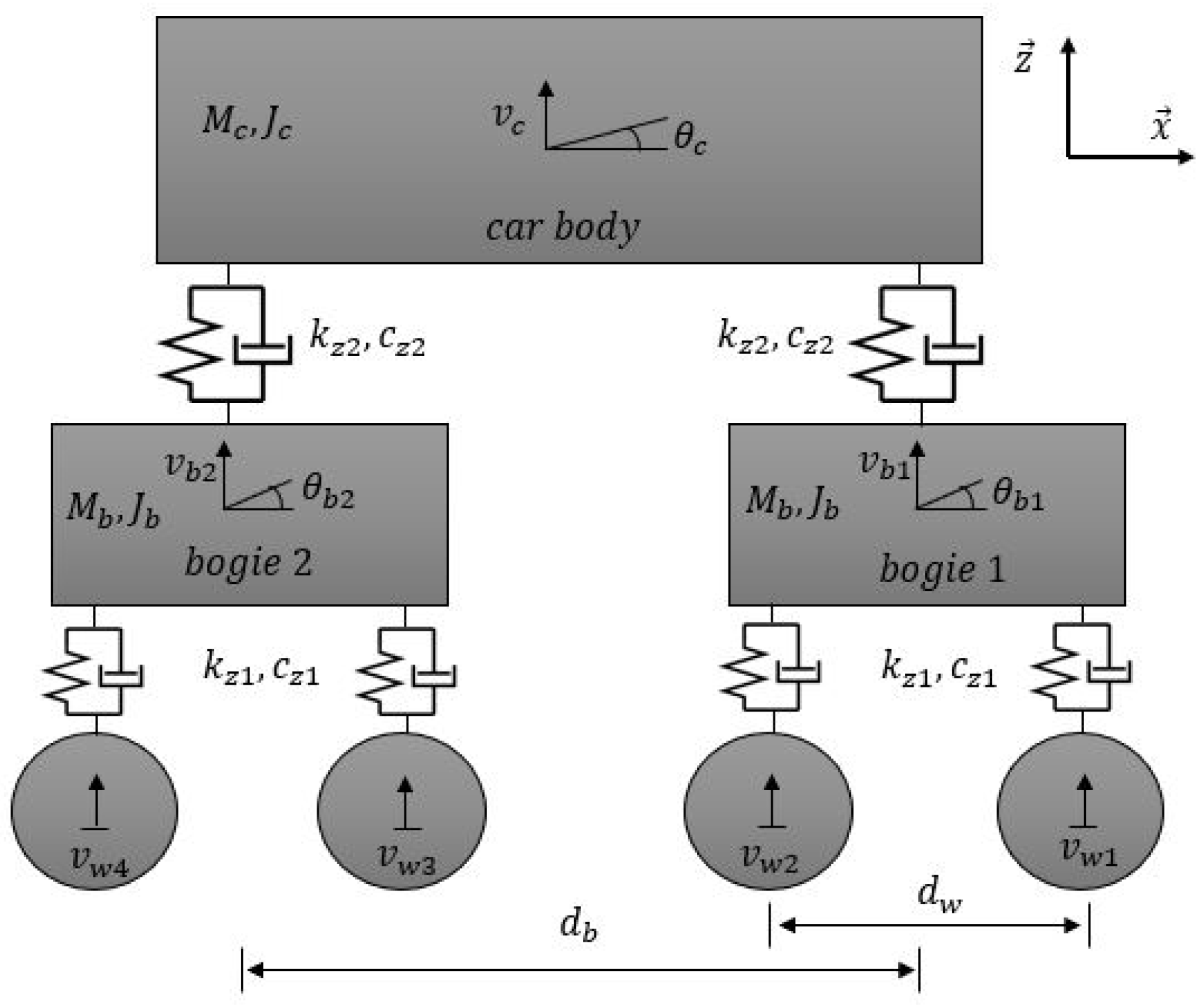


| Parameter | Notation | Numerical Value |
|---|---|---|
| -Track system- | ||
| Rail density | ||
| Rail Young’s modulus | E | |
| Rail cross section | ||
| Rail second moment of area | ||
| Rail-pad vertical stiffness | ||
| Rail-pad vertical damping | ||
| Half sleeper mass | ||
| Sleeper spacing | l | |
| Ballast vertical stiffness | ||
| Ballast vertical damping | ||
| -Half Vehicle system- | ||
| Half car body mass | 23,400 | |
| Half car body pitch moment of inertia | 965,979.7 | |
| Half bogie mass | ||
| Half bogie pitch moment of inertia | ||
| Wheel mass | ||
| Primary suspension vertical stiffness | ||
| Primary suspension vertical damping | ||
| Secondary suspension vertical stiffness | ||
| Secondary suspension vertical damping | ||
| Secondary suspension pitch stiffness | ||
| Secondary suspension pitch damping | ||
| Wheel base | ||
| Distance between the two bogie centrelines |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Moueddeb, M.; Louf, F.; Boucard, P.-A.; Dadié, F.; Saussine, G.; Sorrentino, D. An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration 2022, 5, 326-343. https://doi.org/10.3390/vibration5020019
El Moueddeb M, Louf F, Boucard P-A, Dadié F, Saussine G, Sorrentino D. An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration. 2022; 5(2):326-343. https://doi.org/10.3390/vibration5020019
Chicago/Turabian StyleEl Moueddeb, Maryam, François Louf, Pierre-Alain Boucard, Franck Dadié, Gilles Saussine, and Danilo Sorrentino. 2022. "An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range" Vibration 5, no. 2: 326-343. https://doi.org/10.3390/vibration5020019
APA StyleEl Moueddeb, M., Louf, F., Boucard, P.-A., Dadié, F., Saussine, G., & Sorrentino, D. (2022). An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration, 5(2), 326-343. https://doi.org/10.3390/vibration5020019





