Abstract
In this study, the vibration total value of the acceleration transmitted to the wrist and elbow was measured in the laboratory with a group of 13 male subjects holding a cylindrical handle while modifying the coupling force under varying levels of vibration. The results were used to establish the relationship between hand-transmitted vibration and coupling forces and to compare with the relations proposed as part of an ISO Technical Specification, ISO/TS 15230-2. This was done to determine the suitability of the proposed relationships when variations are introduced on the level of vibration on the handle. While tracing back the origins of the relations proposed in ISO/TS 15230-2, this paper further brings in evidence of the importance of considering the role of coupling forces when evaluating the exposure to hand-transmitted vibration and provides additional evidence to support the relationships which are proposed as part of the ISO Technical Specification. Irrespective of the level of broadband random vibration excitation considered, the agreement with these relationships was found to be best when setting the reference coupling force at 50, 75, 100 and 125 N and whenever the coupling forces applied on the handle were maintained below 150 N.
1. Introduction
Prolonged exposure to hand-transmitted vibration (HTV) is associated with an increased risk of developing vascular, neurological, and musculoskeletal disorders of the hand–arm system known as hand–arm vibration syndrome (HAVS) [1]. This study was conducted within the laboratories of the Institute of Physical Factor Surveillance (IPFS) at the Guangdong Province Hospital for Occupational Disease Prevention and Treatment, a public institution under the Guangdong Provincial Health Commission. The activities of the vibration research group within IPFS are aimed at developing improved assessment tools for hand-transmitted vibration exposure, evaluating the exposure of workers, understanding the pathogenesis of the HAVS, and identifying means of controlling the exposure of workers. This work is concerned with investigating the influence of coupling forces when measuring hand-transmitted vibration exposure.
The prescribed methodology for evaluating the exposure to hand-transmitted vibration as defined in the ISO 5349-1 standard [2] currently relies on the vibration total value of the frequency-weighted root-mean-square (rms) acceleration measured on the vibrating surface with which the hand is in contact. Although the standard requires that the measurements be performed under normal representative conditions, it recognizes that several factors linked with the operating conditions are likely to influence the level of exposure and consequently, the effects of exposure. These factors are identified in Annex D of the ISO 5349-1 standard [2] and include various operating characteristics, such as the working conditions, coupling forces and posture. Considering that the influence of many of these factors on the development of hand-transmitted vibration disorders is not entirely known at this time, it is recommended in Annex F of the ISO 5349–1 standard [2] to document them as much as possible when reporting the exposure. This additional information should serve to provide an improved understanding of the relationship between the hand-transmitted vibration measurements and the observed health effects.
Among the various influencing factors identified in Annex D of the ISO 5349-1 standard [2] are the contact forces between the hand and the gripping zone, which have been shown to affect the vibration energy being transferred to the hand [3,4]. Studies have suggested that both the vibration exposure level and the coupling force should be considered when assessing the potential risk of disorders for vibration workers, especially those using impact tools [5]. The role of the coupling forces in the development of hand-transmitted vibration disorders has still not been clarified, although several studies [6,7,8] have investigated their influence on the biodynamic responses of the hand–arm system, such as the driving-point apparent mass or mechanical impedance and vibration transmissibility. These have generally shown that the hand forces increase the biodynamic responses of the hand–arm system, thus increasing the stresses and strains of the tissues and consequently the injury potential.
Despite the lack of a clear relationship with the coupling forces, it has been suggested that modulation of hand-transmitted vibration exposure is potentially needed when the contact forces are varied over a certain range [9]. It is well known that the operation of a tool by different individuals can lead to quite important differences in the contact forces being exerted on the tool, due to variations in the physiological characteristics and musculature of the operators, their working method, skills, body posture, etc. [10] Yet the magnitude of the frequency-weighted rms acceleration as measured on the handle of the tool would not necessarily reflect the variation of the contact forces used by the different individuals. To account for such variations of contact forces, the International Standardization Organization (ISO) is proposing as part of a Technical Specification (ISO/TS 15230-2 [11], not yet published) an adjustment to be applied to the vibration total value of the frequency-weighted rms acceleration measured on the tool handle, which considers the influence of the coupling force on the exposure level.
It is important to recognize that the relationships, which are proposed in ISO/TS 15230-2 [11], to consider the influence of coupling force on hand-transmitted vibration exposure are not based on any epidemiological data. Rather, they rely on biomechanical relationships between the vibration transmitted to the hand and arm and the forces acting at the interface between the hand and vibrating surface. Consequently, and as stated within ISO/TS 15230-2 [11], the proposed relationships are not intended to be applied for legal purposes or as a substitute to ISO 5349-1 [2] or any other national regulations, but rather to account for the potential influence of coupling forces when performing epidemiological or laboratory research.
The coupling force as defined in ISO/TS 15230-2 [11] refers to the quasi-static force (frequency below 5 Hz) which is needed to control and guide the machine when gripping a handle. It is evaluated by summing the grip and push or pull forces. Guidelines for the measuring procedure of the grip and push forces and the instrumentation requirements are given as part of the ISO 15230-1 standard [12], which provides a description of the forces between the hands of an operator and a machine, to assist in the characterization of the coupling forces when performing hand-transmitted vibration exposure measurements.
The coupling force-adjusted-vibration total value ahwF as proposed in ISO/TS 15230-2 [11] is represented by the following equation:
where ahw represents the frequency-weighted rms acceleration measured on the machine handle as per the ISO 5349-1 standard [2], and ccp is a dimensionless coupling factor which takes on a positive value representing the adjustment of the frequency-weighted rms acceleration as a function of the coupling force Fcp. The coupling factor is taken to be unity whenever the coupling force is considered to be representative of that which is normally applied on the machine handle under most conditions. Above the representative coupling force, the coupling factor takes on a value that is larger than unity, thus, leading to a vibration exposure that is higher than the value of the frequency-weighted rms acceleration measured on the machine handle. Conversely, below the representative coupling force, the coupling factor takes on a value that is lower than 1.0, thus leading to a lower exposure value than measured on the machine handle.
ahwF = ahw × ccp
Figure 1 presents a graphical representation of the coupling factor proposed in ISO/TS 15230-2 [11] as a function of the coupling force for different reference values of the representative coupling force at which the coupling factor is set to unity: 50, 75, 100, 125 and 150 N. These curves represent fourth-order polynomial equations of the form
where the coefficients A, B, C, D and E are numerical constants for which the values are given in Table 1 for each reference value of the representative coupling force.
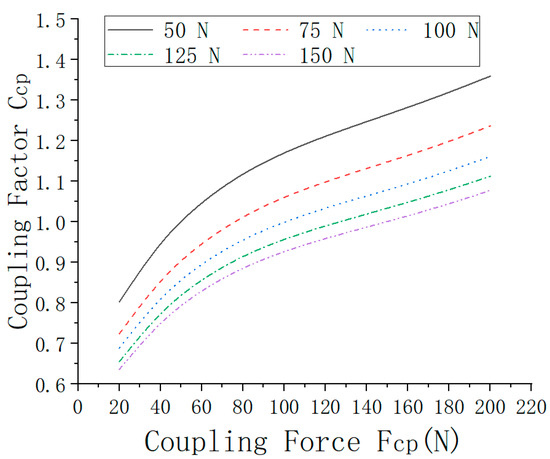
Figure 1.
Coupling factor as a function of coupling force for different values of reference coupling forces as given in ISO/TS 15230-2 [11].

Table 1.
Numerical values of the coefficients for calculating the coupling factor according to ISO/TS 15230-2 [11].
The relations represented in Figure 1 and by Equation (2) were derived mainly from a study by Dupuis and Scheffer (1992) [13], later reported in the works of Hartung, Dupuis and Scheffer (1993) [14] and Riedel (1995) [9], in which the vibration transmitted to the wrist, elbow and shoulder was measured with a group of 10 subjects grasping a cylindrical handle while varying the grip and push forces to give coupling forces of 37, 50, 75, 100, 112, 125, 150 and 200 N. The experiments were conducted by applying uniaxial vibration successively in the xh, yh and zh directions and measuring the vector sum vibration being transmitted simultaneously to the wrist, elbow, and shoulder. A broadband random vibration of single amplitude of 9.5 ms−2 was used as the excitation. To determine the coupling factor for different reference values of the representative coupling force, only the vector sum values of the acceleration measured at the wrist and elbow were retained, considering that the data measured at the elbow showed little resolution. The mean curves shown in Figure 1 were obtained by normalizing the vector sum values of the accelerations measured at the wrist and elbow at the various coupling forces to the vector sum values measured at both these positions for corresponding coupling forces set at 50, 75, 100, 125 and 150 N, respectively. Annex C in ISO/TS 15230-2 [11] further identifies the data that were retained, and shows the mean fitted curves of the coupling factor as a function of the coupling force for each reference value of the representative coupling force, along with the 95% confidence intervals for these curves.
As stated in Annex C of ISO/TS 15230-2 [11], the German study identified above was the only one found in the literature that included as many subjects (10 subjects) and a wide range of coupling forces for investigating the influence of coupling force on the exposure to hand-transmitted vibration. Considering the use of a single broadband random excitation level in the derivation of the relationships, and of data originating from a single source, it was deemed necessary to make available some additional data to verify their conformity with theses curves. In view of the nonlinear nature of the hand–arm vibration system, this study is thus intended to investigate the relationship between the coupling factor and coupling force under varying levels of broadband random vibration excitation.
2. Methodology
2.1. Experimental Setup
The experimental setup is represented schematically in Figure 2.
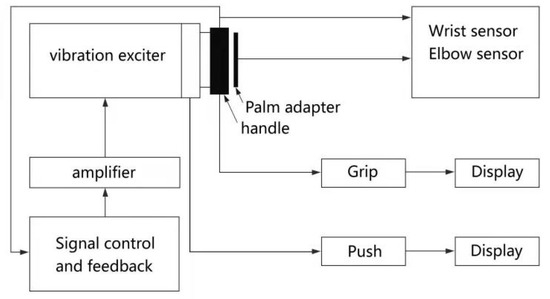
Figure 2.
Schematic diagram of the experimental setup.
It consists of an electrodynamic exciter (China Dong Ling ET 1-150 vibration generator) oriented along the horizontal axis on which is mounted an instrumented cylindrical handle containing force sensors (Kistler 9212) to measure the grip force. The push force is measured using a tri-axial force plate (Kistler 9286BA) on which is standing the subject as illustrated in Figure 3a.
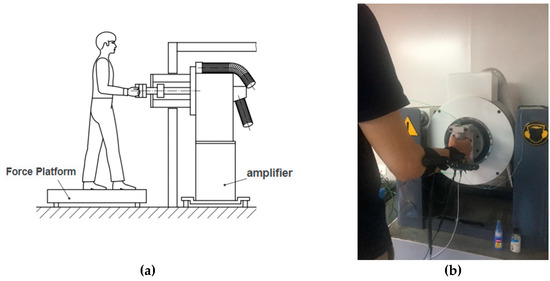
Figure 3.
Vibration excitation system with instrumented handle. (a) Position of subject on force platform; (b) identification of the measuring points on the wrist and elbow.
Both the grip and push forces are monitored in real time, and a display is made available to the subjects to control the required forces. A single-channel Kistler 5018A1002 charge amplifier with single signal control module (5695 B) is used to regulate the required vibration excitation on the exciter. In this study, this was done by fixing the power spectral density of the white noise random excitation to the value that was required over the frequency range from 5 to 1500 Hz to provide the required frequency-weighted rms acceleration on the handle. One miniature tri-axial accelerometer (Meggitt 35B-10) incorporated within the handle is used to monitor the input vibration excitation and provides feedback to the exciter to achieve the required acceleration. Another accelerometer (Kistler 8763B100AB) inserted within a hand adapter held in the palm against the handle is used to measure the vibration input to the hand. Two miniature SV 105B Svantek triaxial accelerometers are attached to the wrist and close to the elbow using Velcro bands to measure the vibration being transmitted to the subjects.
2.2. Test Matrix
The excitation is applied along the horizontal axis on the handle at three levels of broadband white noise random excitations for which the frequency-weighted rms accelerations were set at ah, w = 2.5, 5.0 and 10 ms−2 over the 6.3 to 1250 Hz frequency range. The Wh hand–arm frequency weighting prescribed in the ISO 5349-1 standard [2] was applied to achieve the required accelerations. The experiments were conducted with a group of 13 subjects who were asked to maintain constant the values of grip and push forces during the experiments. The values of the grip force were set at 10, 25, 50 and 75 N and push forces at 25, 50 and 75 N, thus making the coupling force (sum of grip and push forces) vary from 35 to 150 N. During the tests, visual displays were provided to the subjects through video monitors to ensure that both the grip and push forces were kept at the required values. For each subject, level of vibration excitation, and grip and push force combination, the duration of each measurement was set at 30 s. In total, the entire test matrix required 36 tests to be performed by each subject. During the tests, the posture of the subjects was as shown in Figure 3a: standing straight with forearm aligned parallel to the axis of the exciter and making a 90° angle with the upper arm, hand wrapped around the handle with the palm pushing against the handle with the adapter.
2.3. Test Subjects
Thirteen male subjects took part in the experiments. Prior to testing, the subjects were introduced to the functioning of the test setup and performed several trial experiments to become familiarized with the methodology. All the subjects gave their informed consent to participate in the experiments and acknowledged the fact that they were in good health and had not suffered in the past from any health issues that may have been associated with vibration exposure, finger trauma or a circulatory disorder affecting the hand–arm system. The age of the subjects ranged from 21 to 42 years old, their mass ranged from 66 to 92 kg (mean 76.3 ± 8.4 kg) and the mean hand length and circumference were 190.9 mm and 208.5 mm, respectively, as determined using the ISO 21420 standard [15].
2.4. Data Collection and Analysis
For each subject and test condition, two miniature Svantek triaxial accelerometers SV 105 were attached at the wrist and close to the elbow using Velcro bands as shown in Figure 3b. The orientation of the accelerometers was adjusted at each position to ensure that one axis was aligned with the direction of application of the excitation. The accelerometers were connected to two Svantek Model 106 six-channel human vibration meters: one for the wrist, the other for the elbow. Each meter monitored simultaneously the input vibration from the hand adapter in each of the three directions, and the resulting unweighted rms accelerations along each axis, xh, yh and zh, at the set position (wrist or elbow) and the corresponding vibration total value, av over the frequency range from 6.3 to 1250 Hz. The vibration total value was determined by calculating the root-sum-of-squares of the unweighted accelerations axh, ayh and azh measured along each axis according to the following equation:
The analysis consisted in evaluating the influence of the coupling force (sum of grip and push forces) and of the vibration excitation level on the transmission of vibration to the wrist and elbow for the entire subject population. These results were further used for determining how they could relate with the coupling factor relationships given as part of the ISO TS 15230-2 [11] for reference coupling forces set at 50, 75, 100, 125 and 150 N as in the Technical Specification.
3. Results
3.1. Transmission of Vibration to the Wrist and Elbow
For each vibration excitation level and grip and push force combination, the data measured for the entire subject population at the wrist and elbow were tested for normality using the Shapiro–Wilk test. Under most conditions (54/60 data sets), the data were found to satisfy the normality condition at the 5% significance (p > 0.05) for which W > 0.889 and p > 0.095. For each test condition, the mean and standard deviation of the vibration total value measured at the wrist and elbow were thus determined for the entire subject population. The results are presented graphically in Figure 4, along with the fitted curve associated with each vibration level for the measurements at both the wrist and elbow. The fitted curves are in close agreement with a fourth-order polynomial equation as seen by the values of R2 appearing in Figure 4.
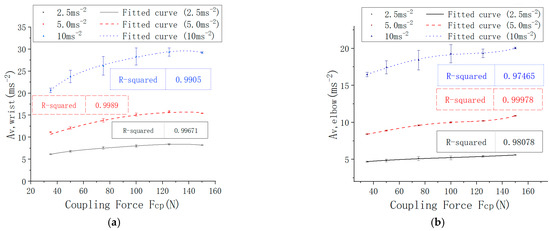
Figure 4.
Influence of the level of vibration excitation on the mean vibration total value measured at (a) the wrist and (b) elbow for different values of the coupling force.
The results further revealed that for the combinations of grip and push forces leading to an equivalent value of the coupling force, the mean measured vibration value at the wrist and elbow were relatively equivalent. Such a situation was encountered for the coupling forces set at 75 N (25 N grip/50 N push and 50 N grip/25 N push), 100 N (75 N grip/25 N push, 50 N grip/50 N push and 25 N grip/75 N push) and 125 N (75 N grip/50 N push and 50 N grip/75 N push). For the combinations of grip and push forces leading to coupling forces of 75 and 125 N, the Levene test was used to test the null hypothesis that the variance is equal across the combinations. Taken across all three vibration excitation levels at both the wrist and elbow, the null hypothesis across the groups proved to be significant for most combinations (p > 0.05). For those combinations leading to a 100 N coupling force, the equality of the variances appeared to be clearer only when the lower vibration excitation level was used. The inclusion of a combination involving equal grip and push forces for the 100 N coupling force could have led to more variability in the results as compared with those obtained with the 75 and 125 N coupling forces.
At both the wrist and elbow, the mean vibration total value was found to increase with the increasing coupling force, the trend following a fourth-order polynomial relation as shown in Figure 4. The higher values of the vibration total value observed for a larger excitation level appear to be roughly in direct proportion with the increase in vibration level. The trends observed, showing an increase with vibration excitation level, were found to be statistically significant at both the wrist and elbow. Calculation of the least significant difference with multiple comparisons between the groups at the various excitation levels proved that the differences were significant at the 0.05 level at both the wrist and elbow.
3.2. Coupling Factor at the Wrist and Elbow
The coupling factor defined in Equation (1) was determined based on the results presented in Figure 4 by normalizing the curves to the mean vibration total value measured at a fixed value of the coupling force taken as the reference coupling force. In conformity with the content of ISO/TS 15230-2 [11], the values for the reference coupling force were set successively at 50, 75, 100, 125 and 150 N, at which the coupling factor was forced to be unity. The resulting curves are shown in Figure 5 for the cases involving the reference coupling force set at 50, 100 and 150 N.
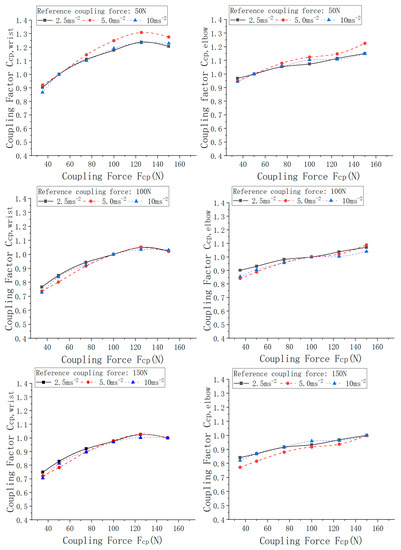
Figure 5.
Mean coupling factor measured at the wrist and elbow under various vibration excitation levels for reference coupling forces set at 50, 100 and 150 N.
The results reveal a negligible influence of the vibration excitation level on the coupling factor at both the wrist and elbow for the various reference coupling forces. The ANOVA analysis of variance reveals F-values ranging from 0.528 to 2.691 when performing the comparisons of the curves for the reference coupling forces set at 50, 100 and 150 N, for which the mean differences were not found to be significant (p > 0.100). Although not shown, the results obtained at 75 and 125 N were found to yield similar trends with no statistical differences being observed between the curves at the various coupling forces.
3.3. Comparison with the ISO/TS 15230–2 Relationships from Total Vibration Ratios at the Various Excitation Levels
To investigate their compliance with the coupling factor relationships recommended in ISO/TS 15230-2 [11], the experimental results are further compared with the fitted curves and 95% confidence intervals presented in that document for the various values of the reference coupling force. Figure 6 provides a representation of these curves for which the ISO upper and lower bounds represent the 95% confidence intervals. The mean coupling factors determined from measurements made at the wrist and the elbow under the various excitation levels are shown along with these curves. For most reference coupling forces, the majority of the measured data were found to follow the recommended trends and fall within the envelopes of values defined by the 95% confidence intervals.
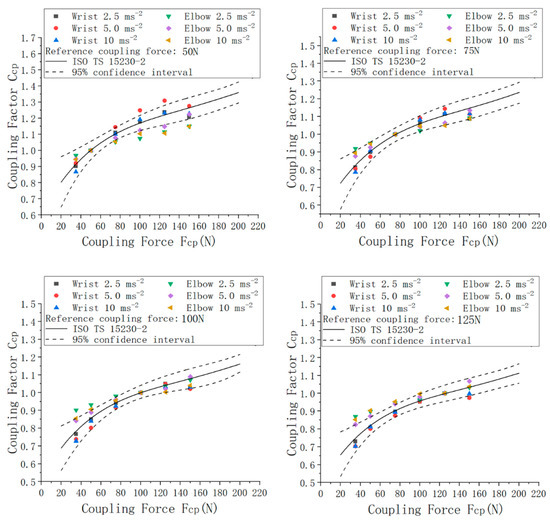
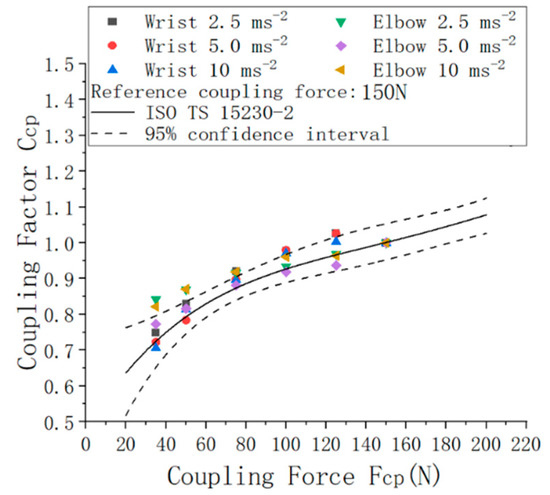
Figure 6.
Comparison of the experimental results with the ISO TS 15230-2 [11] relationships and corresponding 95% confidence intervals for the various values of the reference coupling force.
3.4. Overall Measured Coupling Factors and Comparison with ISO/TS 15230–2
The measured data appearing in Figure 6 at the various values of the coupling force from measurements at the wrist and elbow under the various excitation levels for the different reference coupling forces were further tested for normality using the Shapiro–Wilk test. At each value of the coupling force and for each reference coupling force, the data were found to satisfy the normality condition at the 5% significance (p > 0.05) for which W > 0.828 and p > 0.104. The mean value of all the data appearing in Figure 6 for each coupling force and reference value of the coupling force was thus computed and is shown graphically in Figure 7 along with its corresponding standard deviation values, where it is compared with the curve-fitted relationships proposed in ISO/TS 15230-2 [11].
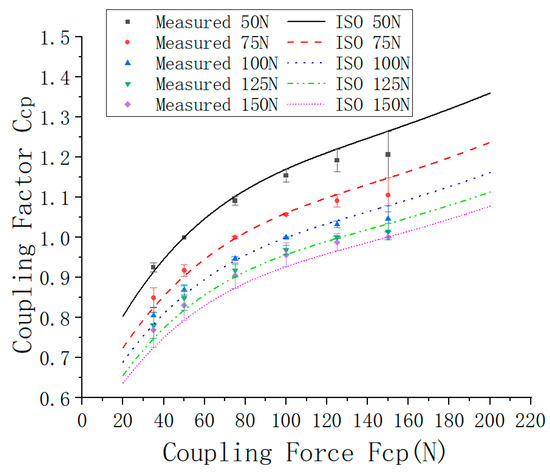
Figure 7.
Overall measured coupling factors and comparison with the recommended curves in ISO TS 15230-2 [11].
The degree of convergence of the mean data with the recommended curves was assessed through the Univariate Statistical Analysis of Variance examining the convergence in slope and intercepts. The analysis revealed an excellent convergence between the measured data and the curve-fitted relationships proposed in ISO/TS 15230-2 [11] for the reference coupling forces set at 50, 75, 100 and 125 N. However, a larger difference was observed with the 150 N reference coupling force. In all cases, the largest difference between the measured data and the curve-fitted relationships was observed on the slope, although the difference was not found to be statistically significant (p > 0.05), except when the reference coupling force was set at 150 N, where p was found to be equal to 0.038. The measured data shown in Figure 7 further suggest that the deviation with the prescribed curves generally tends to be larger with a coupling force set at 150 N, compared with the other lower coupling forces. This perhaps can be explained by the difficulty in maintaining steady the grip and push forces when higher coupling forces are involved.
4. Discussion
The results presented in this study tend to confirm the coupling factor relationships proposed in ISO/TS 15230-2 [11], even when the magnitudes of the broadband random excitations differ from those that were used in their development. The agreement obtained with these curves was found to be best with the reference coupling forces set at 50, 75, 100 and 125 N and whenever the coupling forces applied on the handle were maintained below 150 N. Although the results showed larger differences with a reference coupling force set at 150 N, the corresponding coupling factors were generally found to fall within the envelope formed by the 95% confidence intervals for the fitted curve proposed in ISO/TS 15230-2 [11]. Although this laboratory study has provided much needed supporting evidence for the coupling factor relationships proposed by ISO, it is considered that future investigations should perhaps focus on evaluating their suitability when different types of handheld machines are operated under representative working conditions.
Author Contributions
Investigation, H.L., Y.J. and M.Y.; methodology, P.-E.B. and B.X.; project administration, B.X.; supervision, P.-E.B.; writing—original draft, H.L. and Y.J.; writing—review and editing, P.-E.B. All authors have read and agreed to the published version of the manuscript.
Funding
Guangdong Provincial Key Laboratory of Occupational Disease Prevention and Treatment (2017B030314152); Guangdong Provincial Engineering Research Center of Public Health Detection and Assessment (2019GCZX012); Medical Scientific Research Foundation of Guangdong Province, China (A2022062).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Medical Ethics Committee of Guangdong Province Hospital for Occupational Disease Prevention and Treatment (protocol code GDHOD MEC 2021 No.047 and date of approval 23 November 2021) for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Acknowledgments
We gratefully acknowledge the contribution of our teammates Jianyu Guo, Jiayu Liu and Zhipeng He, who were mainly involved in assisting with the experiments and data collection and analysis. This work could not have been completed in a timely manner without their assistance.
Conflicts of Interest
All authors declare that (i) no support, financial or otherwise, was received from any organization that may have an interest in the submitted work, and (ii) there are no other relationships or activities that could appear to have influenced the submitted work.
References
- Griffin, M.J. Handbook of Human Vibration; Academic Press: London, UK, 1990. [Google Scholar]
- ISO 5349-1: 2001, Mechanical Vibration—Measurement and Evaluation of Human Exposure to Hand-transmitted Vibration—Part 1: General Requirements. International Organization for Standardization. Available online: https://www.iso.org/standard/32355.html (accessed on 18 November 2021).
- Aldien, Y.; Marcotte, P.; Rakheja, S.; Boileau, P.-É. Influence of hand forces and handle size on power absorption of the human hand–arm exposed to zh-axis vibration. J. Sound Vib. 2006, 290, 1015–1039. [Google Scholar] [CrossRef]
- Adewusi, S.; Rakheja, S.; Marcotte, P.; Boutin, J. Vibration transmissibility characteristics of the human hand–arm system under different postures, hand forces and excitation levels. J. Sound Vib. 2010, 329, 2953–2971. [Google Scholar] [CrossRef]
- Dong, R.G.; Welcome, D.E.; McDowell, T.W.; Wu, J.Z.; Schopper, A.W. Frequency weighting derived from power absorption of fingers–hand–arm system under zh-axis vibration. J. Biomech. 2006, 39, 2311–2324. [Google Scholar] [CrossRef] [PubMed]
- Marcotte, P.; Aldien, Y.; Boileau, P.-É.; Rakheja, S.; Boutin, J. Effect of handle size and hand–handle contact force on the biodynamic response of the hand–arm system under zh-axis vibration. J. Sound Vib. 2005, 283, 1071–1091. [Google Scholar] [CrossRef]
- Pan, D.; Xu, X.S.; Welcome, D.E.; McDowell, T.W.; Warren, C.; Wu, J.; Dong, R.G. The relationships between hand coupling force and vibration biodynamic responses of the hand-arm system. Ergon. 2018, 61, 818–830. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.S.; Dong, R.G.; Welcome, D.E.; Warren, C.; McDowell, T.W.; Wu, J.Z. Vibrations transmitted from human hands to upper arm, shoulder, back, neck, and head. Int. J. Ind. Ergon. 2017, 62, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riedel, S. Consideration of grip and push forces for the assessment of vibration exposure. Central Eur. J. Public Health 1995, 3, 139–141. [Google Scholar]
- Saha, S.; Kalra, P. A review on hand-arm vibration exposure and vibration transmissibility from power hand tools to hand-arm system. Int. J. Hum. Factors Ergon. 2016, 4, 10–46. [Google Scholar] [CrossRef]
- ISO/TS 15230-2: (Technical Specification awaiting publication) Mechanical Vibration and Shock- Coupling Forces at the Man-machine Interface for Hand-transmitted Vibration-Part 2: Guidelines for the Evaluation of Coupling Forces. International Organization for Standardization. Available online: https://www.iso.org/standard/77517.html (accessed on 10 February 2022).
- ISO 15230-1: 2021, Mechanical Vibration and Shock—Coupling Forces at the Man-machine Interface for Hand-transmitted Vibration—Part 1: Measurement and Evaluation. International Organization for Standardization. Available online: https://www.iso.org/standard/77516.html (accessed on 18 November 2021).
- Dupuis, H.; Scheffer, M. Wirkung von Greif- und Andruckkraft unter Schwingungsbelastung—Teilprojekt II; Forschungsbericht Hand-Arm-Schwingungen III; Schriftenreihe des Hauptverbandes der gewerblichen Berufsgenossenschaften; Hauptverbandes der gewerblichen Berufsgenossenschaften: Sankt Augustin, Germany, 1992; pp. 1–164. [Google Scholar]
- Hartung, E.; Dupuis, H.; Scheffer, M. Effects of grip and push forces on the acute response of the hand-arm system under vibrating conditions. Int. Arch. Occup. Environ. Health 1993, 64, 463–467. [Google Scholar] [CrossRef] [PubMed]
- ISO 21420: 2020, Protective Gloves—General Requirements and Test Methods. International Organization for Standardization. Available online: https://www.iso.org/standard/69030.html (accessed on 18 November 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).