Damping Behavior of Thermoplastic Organic Sheets with Continuous Natural Fiber-Reinforcement

Abstract

In the field of lightweight construction, the use of natural fibers as reinforcement in composites has been increasingly discussed. Additionally, the damping properties of natural fibers are known from fiber materials such as fiber insulation boards. In the scope of the work presented here, the focus is on identifying the potential of natural fibers for lightweight structures with high vibration damping capacity. For this purpose, test specimens made of flax fiber-reinforced and glass fiber-reinforced thermoplastic composites were manufactured and characterized. Contrary to expectations, the flax fiber-reinforced composite exhibited an almost isotropic damping characteristic. A comparison of the damping and stiffness properties determined by measurement confirms the high potential of natural fiber-reinforced materials for lightweight structures with high damping.

1. Introduction

Due to their physical properties, fiber-reinforced plastics have significant technical advantages over competing materials in a large number of component applications. The use of natural fibers (especially plant fibers) in those components is gaining more and more interest. This is mainly based on the excellent lightweight construction potential of natural fibers and the increasing environmental awareness, since renewable raw materials do have less impact on global warming through CO₂ emissions compared to conventional composites like glass fiber-reinforced plastics [1]. Especially continuous natural fiber-reinforced composites reach excellent mechanical and dynamic mechanical properties, leading to a variety of new fields of applications in the automotive, aerospace industry and building applications. The high specific stiffness and the low cost (in terms of volume) of natural fibers are the main driving forces for using them in highly-stressed components [2].

The present investigations are focused on the damping behavior of continuous natural fiber-reinforced thermoplastic composites. In this context, numerous research studies on natural fiber-reinforced composite materials have been published in recent years.

Many different fibers were used as continuous reinforcing layers. Especially bast fibers like flax and hemp were frequently used [2]. Due to the low cost and low density, polypropylene (PP) and polyethylene (PE) are widely applied as thermoplastic matrix polymer [3,4,5]. The use of biopolymers is steadily increasing. Polymers like polylactic acid (PLA) and polyamide 11 (PA11) combined with natural fibers generate a fully biobased composite [6,7,8].

One of the main challenges is the maximization of the fiber matrix adhesion between hydrophilic natural fibers and hydrophobic matrix systems. Physical pretreatments like fiber stretching or heat treatment change the fiber surface leading to better connection of fibers and matrix [2]. Many different chemical pretreatments have already been studied. Alkaline treatment is one method to remove lignin and natural oils on the fiber surface increasing the tensile strength of the composite [3,8,9,10,11]. Silane treatment affects the surface energy by decreasing the fiber hydrophilicity [9]. Bledzki [12] and Gassan [3] use fiber pre-impregnation with polypropylene functionalized with maleic-acid anhydride (MAH-PP) increasing the fiber-wetting during composite fabrication. Acetylation has also shown to increase natural fiber composites properties. To this effect, Bledzki et al. [13] determined improved fiber surface morphology and enhanced moisture resistance. Their acetylation treatment leads to flax-polypropylene composites (fiber mass ratio of 30%) with up to 18% increased tensile and flexural strength. Loong and Cree [14] received improved tensile strength and modulus of flax-epoxy composites with 55% and 58% respectively, by treating 275 g/m² unidirectional (UD) flax with an acetic anhydride solution (2%).

Depending on the required fiber orientation, there are different types of fabrics to create a continuous fiber reinforcement. Woven fabrics create a bi-directional reinforcement. Dan-Mallam [15] weaves with additional polyethylene terephthalate (PET) yarn to improve the fiber-wetting. The use of woven hybrid yarns is another approach to guarantee optimal fiber-wetting [4,16]. Unidirectional fabrics and weaves made of dry or hybrid natural fibers are commercially available containing natural fibers or polymer yarns as fixation in cross direction [17,18].

The fabrication of continuous reinforced thermoplastic composites is usually divided in two steps. Fully impregnated and consolidated semi-finished products (organic sheets) need to be produced first [19]. This could happen by film stacking using reinforcing layers like UD fabrics or woven fabrics together with thermoplastic films. The impregnation and consolidation of the reinforcing fibers are usually realized by hot pressing. Melt impregnation is also a way to produce fully impregnated reinforcing layers. In a second step, the organic sheets need to be heated up and are transformed to a component via compression molding [20]. Another common way to produce geometrically more complex components is to thermoform the organic sheets by a press process and then combining it with an injection molding process.

It is essential to control the processing temperatures during the whole composite fabrication since natural fibers do not tolerate high temperatures for a long time. Kobayashi [7] determined a thermal decomposition of hemp fibers at 210 °C.

Damping in composites is fundamentally different from that of conventional metals and alloys. The energy dissipation of fiber-reinforced composites is based on the viscoelastic properties of the matrix and the reinforcing fibers and the damping at the interfaces [21]. In this context, dynamic mechanical analysis (DMA) is the most used tool to characterize the dynamic mechanical properties. DMA characterizes the storage modulus (E′), loss modulus (E″) and loss factor (tan δ), which is used to measure the damping of viscoelastic systems with its frequency and temperature dependency (see e.g., [22]). In addition to DMA, there are several possibilities for the determination of damping characteristics by measurement, such as the bending resonance test [23].

Baghaei [16] investigated the influence of the fiber content on the damping properties of a composite made of PLA/hemp co-wrapped hybrid yarns. A decreasing loss factor tan δ with increasing fiber content can be observed. A possible explanation for this is the restriction of the free movement of the polymer chains as a result of the increasing fiber content. In addition to the fiber matrix adhesion and the fiber content, the type of reinforcing fabric has a major influence on the damping properties. In this context Duc [6] noted a reduced loss factor tan δ of woven flax fiber composites and explains these results with the reduction of the sliding surfaces between fibers and matrix due to the ondulation of the fibers in the fabric. Unidirectional reinforced composites were investigated by Amenini [17], using UD flax fabrics and PA11. The loss factor was identified in longitudinal and transverse direction at different frequencies, showing no clear trend. Mahmoudi et al. studied the damping performance of flax fiber reinforced epoxy [24]. They used composite plates and measured the eigenfrequency and modal damping and found that the viscoelastic characteristics are not constant in terms of temperature and frequency.

In summary, there are numerous studies on natural fiber-reinforced thermoplastics. The subjects of the investigation were their production, the characterization of stiffness and strength properties and, in some publications, their damping behavior. However, there are no publications studying the directional dependence of the damping and dynamical stiffness of natural fiber-reinforced composites especially with thermoplastic matrices.

2. Materials and Methods

2.1. Material Selection

The natural fiber reinforcement was a commercial dry roll of unidirectional non-crimp flax fabric (Bcomp AmpliTex 5009; Bcomp Ltd., Fribourg, Switzerland) with a grammage of 300 g/m². As a comparative material a unidirectional non-crimp glass fabric (Suter-Kunststoffe UDO UD EST 220; Suter Kunststoffe AG, Fraubrunnen, Switzerland) with a grammage of 220 g/m² was selected. As matrix a 200 µm thick PLA film based on NatureWorks LLC Ingeo 2003D (NatureWorks LLC, Minnetonka, MN, USA) was used.

2.2. Manufacturing and Test Specimens

The reinforcing fabrics and the PLA matrix film were cut from the rolls and dried (100 °C; 30 min) to ensure a reproducible manufacturing process. Four layers of the unidirectional flax fabric were alternately stacked together with six layers of PLA film resulting in a fiber mass ratio of 43% (fiber volume ratio of 41% for the fully impregnated organic sheet). For the comparative tests, five glass fiber fabrics were combined with six layers of PLA film to achieve a fiber mass ratio of 44% (28 vol.%). The consolidation and impregnation of the reinforcing fibers was realized by a two-step pressing process. During the first pressing process, the hot pressing at 180 °C, the polymer matrix in the form of the PLA films is melted. The application of external pressure of 0.1 MPa during heating (8 min) and an increase of the pressure to 0.85 MPa for one minute allows the matrix to flow and ensures optimal wetting of the reinforcing fibers. The second pressing process, the cold pressing, ensures solidification of the polymer matrix. For this purpose, a constant pressure of 0.85 MPa is applied to an unheated press (25 °C). After solidification of the matrix, a fully consolidated and impregnated organic sheet can be removed. To ensure a full solidification of the matrix, this cold pressing process should last at least 10 min.

For the comparative studies of the dynamic composite characteristics, three specimens of different fiber angles φ (0°, 15°, 30°, 45°, 60°, 75°, 90°) were cut from each of the planar flax/PLA and glass/PLA organic sheets to investigate the directional dependence. The glass/PLA specimens have a length of approximately 213 mm (143 mm free bending length), a width of 17.7 mm and a thickness of 1.5 mm. The flax/PLA specimens are 235 mm long (165 mm free bending length), 14.8 mm wide and have a thickness of 1.8 mm.

2.3. Determination of Dynamic Characteristic Values

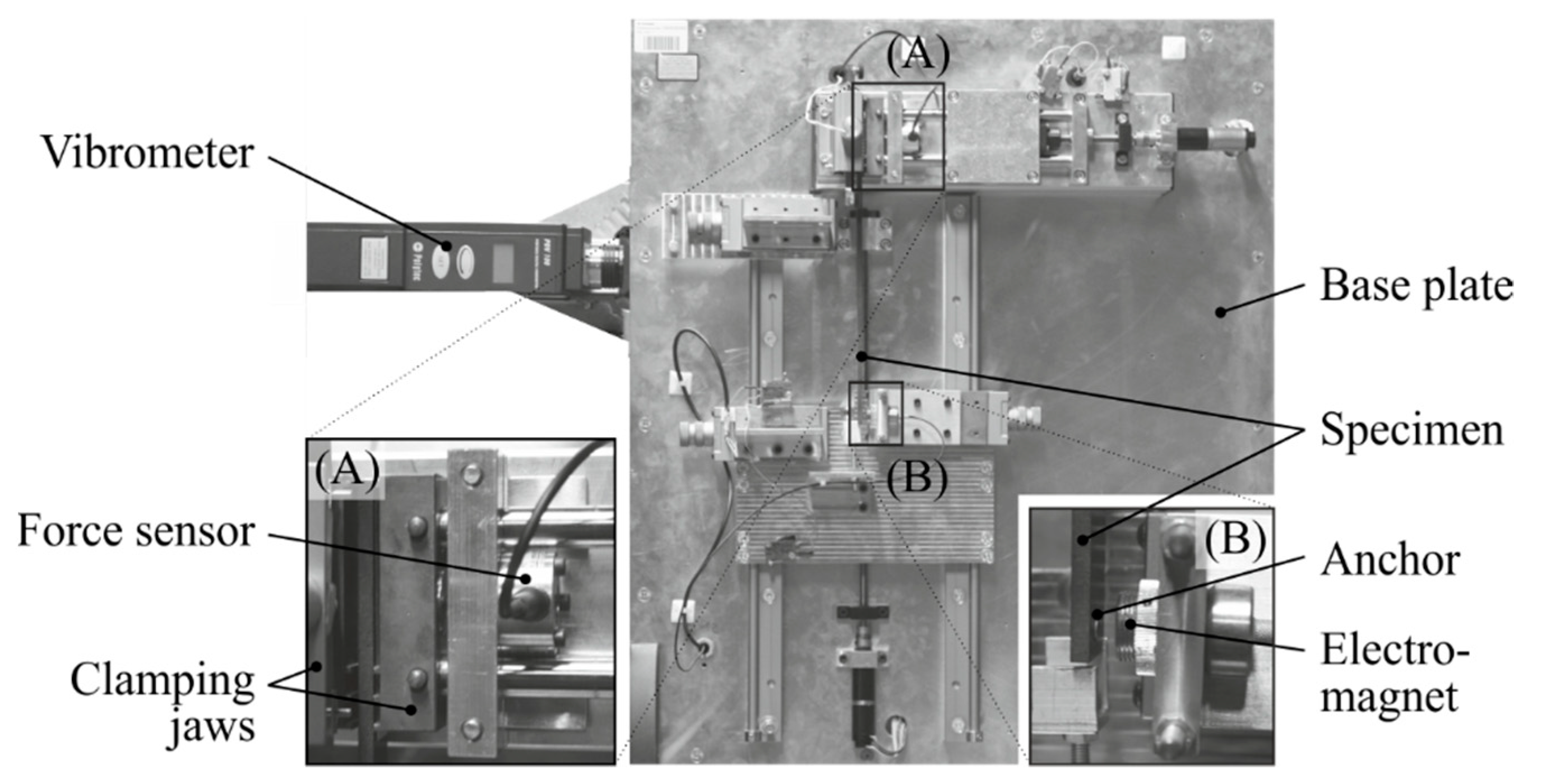
The dynamic characterization of the manufactured specimens was carried out by means of a flexural vibration test using the resonance curve method based on the standard DIN EN ISO 6721-3 [25]. In this test, a specimen clamped on one side is excited to bending vibrations and its dynamic properties modulus of elasticity and loss factor are determined from the vibration response at the first mode, which corresponds to the first bending mode for the dimensions and materials used. All tests were carried out at ambient temperature (approx. 22 °C). The test setup used is shown in Figure 1.

A beam-shaped specimen is clamped at one end (A) using damping minimized clamping jaws. The clamping force is measured for repeatability of the measurement. The excitation of the test specimen is done at the free end (B) by means of an electromagnet. The excitation occurs at the first natural frequency, which in this case was between 17 and 37 Hz. For non-ferromagnetic specimens, an iron washer is attached at the free end in order to allow the electromagnetic excitation. A laser vibrometer is used to measure the vibration amplitude that results from dynamic excitation. This allows contactless and non-interacting detection of the vibration. To reduce noise and increase measurement accuracy, a retroreflective dot was bonded to the specimen at the measurement position. The measured timeseries are then evaluated using curve-fitting algorithms. Measuring the steady-state amplitude at several frequencies allows to determine the frequency of the resonant peak and corresponding 3 dB-bandwidth.

The test is based on the following procedure:

• Clamping of the specimen with a defined clamping force;
• Electromagnetic excitation of the specimens’ free end at defined frequencies;
• Determination of the steady-state-vibration amplitude for each frequency;
• Curve fit of the resulting frequency response;
• Determination of new excitation frequencies on the basis of the fitted curve;
• Repeat points 2–5 until the curve parameters have settled;
• Curve parameters define the eigenfrequency and the 3 dB-bandwidth.

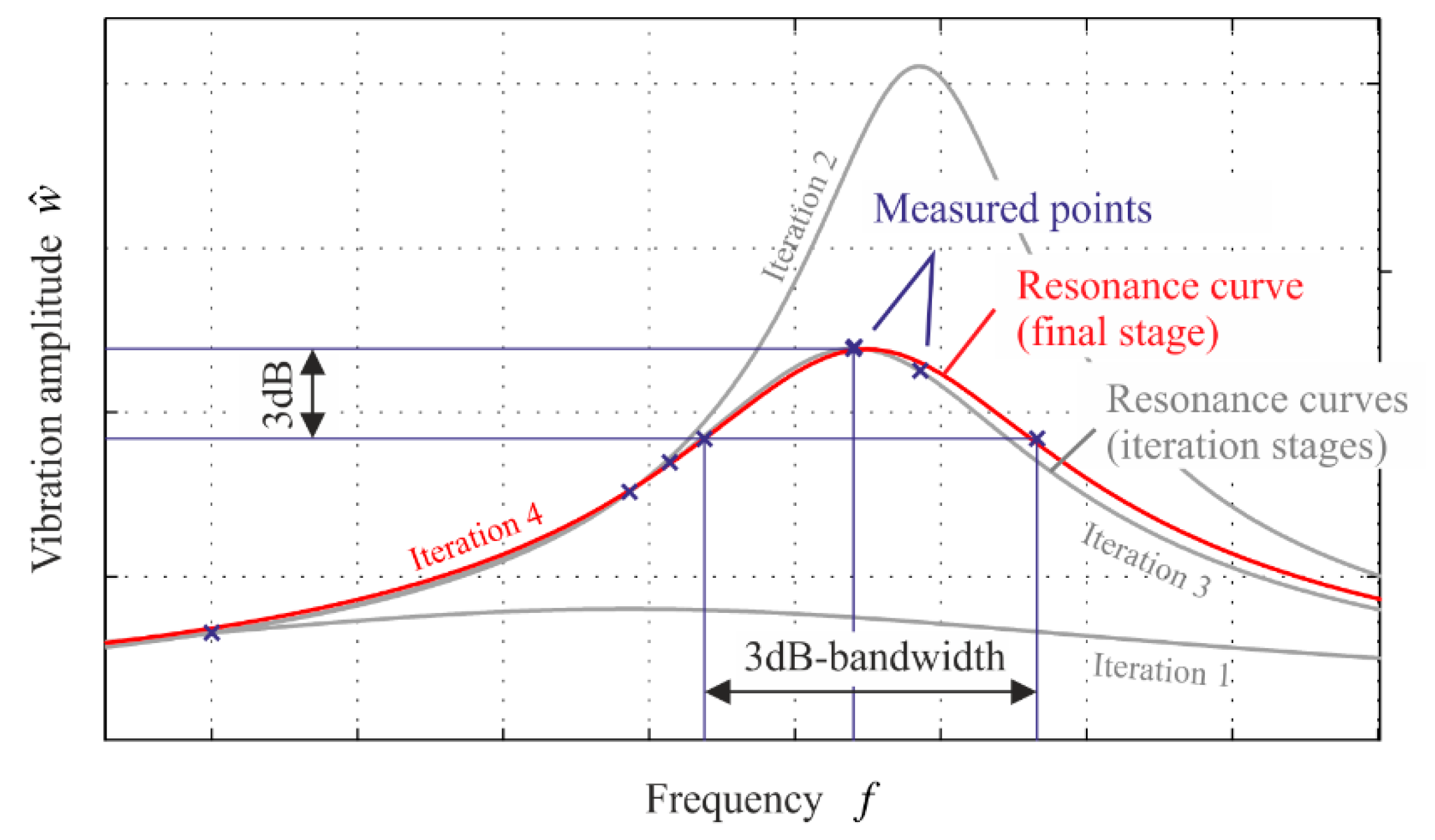
Figure 2 shows the spectrum determined during Steps 4–6 of this procedure. During this step the analytically described resonance curve (see e.g., [25])

$$\widehat{w}\left(f\right)=\frac{{\widehat{w}}_{max}}{\sqrt{1+\frac{{\left(f/f_n-f_n/f\right)}^2}{d_n^2}}}$$

(1)

is fitted to the initially measured points (see curve Iteration 1 in Figure 2). Subsequently, new frequency points to be measured are determined on the basis of the parameters of the fitted curve. The new points are then included into the curve-fitting process (see curves Iteration 2–4 in Figure 2). With this iterative procedure, the parameters of interest, namely the eigenfrequency $f_n$ and the loss factor $d_n$ of the $n$th mode are determined (Step 7).

A complete description of the measurement procedure and evaluation methodology is given in [23].

For the determination of the directional dependence of the dynamic material properties the procedure described above is applied on unidirectional reinforced specimens with different fiber angles. As a result, the first resonance frequencies $f_{1,\phi }$ for each fiber orientation $\phi$ can be obtained. Analytical models were used to estimate the natural frequencies and mode shapes for all fiber angles to ensure that the first mode corresponds to the first flexural mode shape and consequently a comparable loading of the specimens as a result of the vibration excitation. The storage moduli $E_{\phi ,Exp}^{\prime }$ can be obtained from the measured values $f_{1,\phi }$ for each reinforcement angle $\phi$:

$$E_{\phi ,Exp}^{\prime }=\frac{48 {\pi }^2}{{\lambda }_1^4} \frac{l_x^4}{h^2} \rho f_{1,\phi }^2.$$

(2)

These values $E_{\phi ,Exp}^{\prime }$ and the corresponding loss factors $d_{\phi ,Exp}$ have to be measured for at least three different fiber angles. Then, the engineering constants $E_{\parallel }^{\prime }$, $E_{\perp }^{\prime }$ and $G_{⋕}^{\prime }$ in the fiber coordinate system as well as the damping properties $D_{\parallel }$, $D_{\perp }$ and $D_{⋕}$ can be calculated using the well-known polar transformation in combination with the least-squares method [23].

3. Results and Discussion

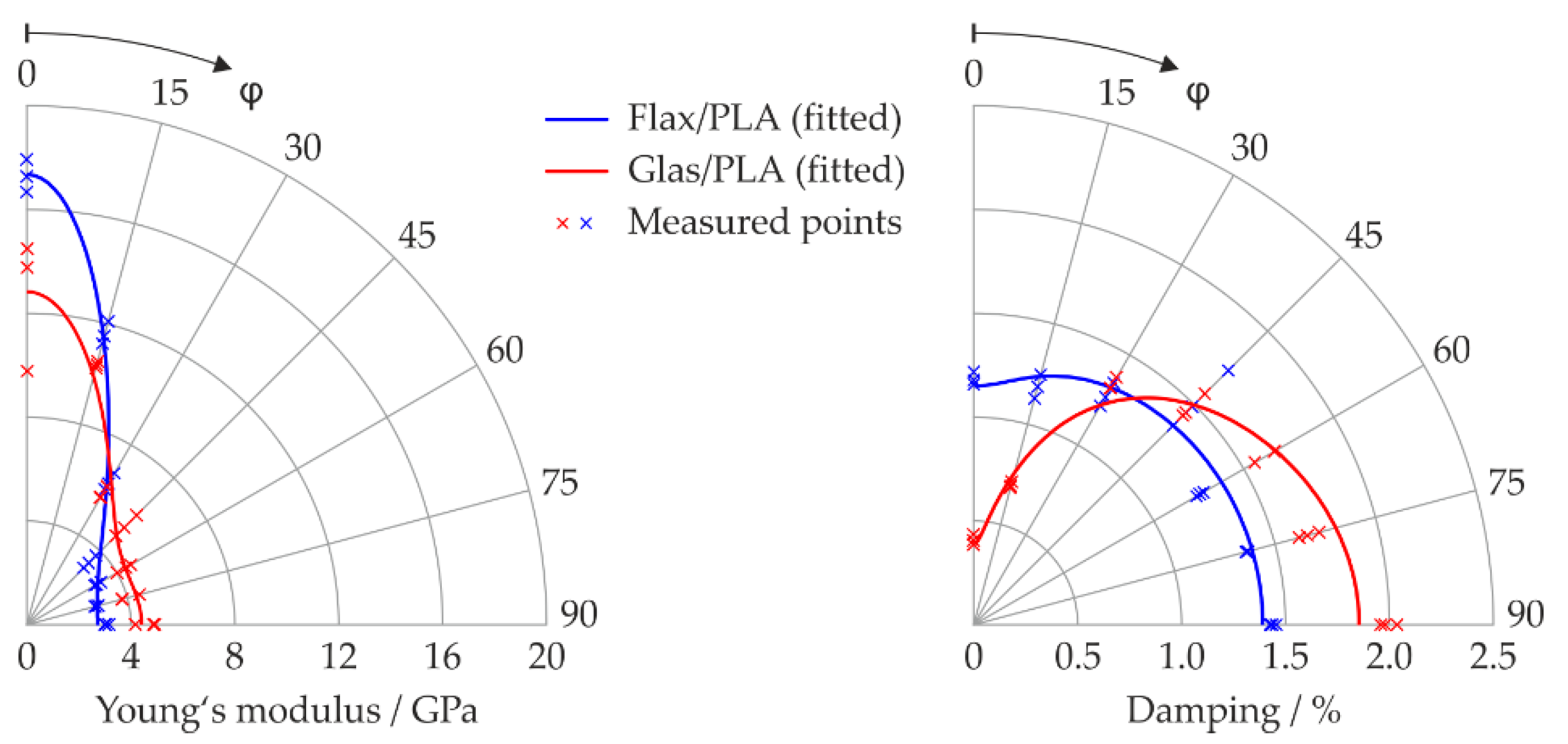
For each fiber angle, three specimens were measured. The resulting directional dependencies are shown in Figure 3. Here, the smaller crosses represent the mean value of the measurements performed on one specimen and the thicker crosses represent the mean value of all measurements at one fiber angle.

The fitted polar transformation is shown as a solid curve. The engineering constants underlying this curve are summarized in

Table 1. Determined properties of the investigated materials.

	Flax/PLA	Glass/PLA
$E_{\parallel }^{\prime }$/GPa	17.54	12.98
$E_{\perp }^{\prime }$/GPa	2.76	4.46
$G_{⋕}^{\prime }$/GPa	1.67	1.80
${\nu }_{\parallel \perp }$/-	0.30	0.30
$d_{\parallel }$/%	1.16	0.40
$d_{\perp }$/%	1.40	1.88
$d_{⋕}$/%	1.37	1.49
$\varrho$/g/cm3	1.24	1.45

. Here $E_{\parallel }^{\prime }$ and $E_{\perp }^{\prime }$ are the storage moduli (real part of the complex Young’s modulus) parallel, perpendicular to the unidirectional fiber direction, respectively. $G_{⋕}^{\prime }$ is the shear modulus and ${\nu }_{\parallel \perp }$ the Poisson’s ratio. Analogous to these elasticity quantities, the quantities $d_{\parallel }$, $d_{\perp }$, and $d_{⋕}$ describe the direction-dependent damping properties of the unidirectional reinforced layer.

The curves in Figure 3 and the material properties in Table 1 allow the following statements to be made:

The glass/PLA composite shows a unidirectional characteristic with an opposite behavior of stiffness and damping as it is expected for unidirectional fiber-reinforced composites. Here, fiber angles with a high modulus of elasticity have low damping values and vice versa. This behavior is consistent with findings from publications [23,26]. The reason for this behavior is the assumption that the composite damping is largely determined by the matrix material, while the reinforcing fibers themselves—such as glass fibers—usually have only negligible damping and mainly determine the composite stiffness in the fiber direction.

The flax/PLA composite not only exhibits a strong anisotropy for the Young’s modulus; the degree of anisotropy for this composite is even higher than for the glass/PLA composite. Contrary to expectations, however, this only applies to the stiffness and not to the damping characteristics. Here, the flax/PLA composite exhibits an almost isotropic behavior. One possible explanation for this is that the natural flax fibers not only have a significant influence on the stiffness, but—in contrast to the glass fibers—also add a considerable amount of damping to the composite. In this respect, the influences of fiber and matrix material on the directional dependence could nearly compensate each other and thus lead to an almost isotropic behavior of the damping. Detailed investigations on this are being planned. This mainly involves tests on flax fibers without embedding them in the composite.

4. Conclusions

The directional dependence of damping and dynamical stiffness of unidirectional flax fiber-reinforced PLA was investigated in this study. This composite with a fiber mass ratio of 44% (28 vol.%) shows the typical strong anisotropy of Young’s modulus. An increasing fiber angle of the unidirectionally reinforced composite leads to a decreasing Young’s modulus. Here, the damping characteristics show a completely different progression. The investigated composite configuration even exhibits almost isotropic behavior in the damping characteristics. The high damping in the fiber dominated longitudinal direction (compared to the investigated glass/PLA composite) is presumably based on the high damping values of the flax fibers. These results reveal that the damping properties of the flax fibers also lead to a higher material damping of the composite without a decrease in Young’s modulus.

The characterization carried out, shows the high potential of natural fiber-reinforced thermoplastics as a sustainable functional material for achieving low-vibration and simultaneously stiff composite structures. The integration of the “passive” function of vibration damping can make a significant contribution to the design of lightweight, quiet and sustainable products.