Finite Element Analysis of Wind Turbine Blade Vibrations

Abstract

The article is devoted to the practical problem of computer simulation of the dynamic behaviour of horizontal axis wind turbine composite rotor blades. This type of wind turbine is the dominant design in modern wind farms, and as such its dynamics and strength characteristics should be carefully studied. For this purpose, in this paper the mechanical model of a rotor blade with a composite skin possessing a stiffener was developed and implemented as a finite element model in ABAQUS. On the basis of this computer model, modal analysis of turbine blade vibrations was performed and benchmark cases for the dynamic response were investigated. The response of the system subjected to a uniform underneath pressure was studied, and the root reaction force and blade tip displacement time histories were obtained from the numerical calculations conducted.

1. Introduction

Today, wind energy along with its green counterpart, solar energy, is considered as a predominant source and a pillar of ‘green’ electricity. Currently, the wind power sector is the fastest growing renewable energy sector and contributes significantly to reducing greenhouse gases and to achieving the emission reduction targets set by the Kyoto Protocol and Paris Agreement. Furthermore, the rapidly developing improvements in wind turbines’ design and efficiency increase their economic competitiveness compared to conventional power generating technologies [1].

Over the past decades of the evolution of wind energy technology, the main tendency has been increasing size of wind turbine rotors. This is driven by both economic and technological demands, as larger turbines have enhanced performance and increased production capacity, giving rise to new high-capacity wind power plants [2,3]. In turn, scaling up wind turbines leads to the emergence of new complex problems in their design and operation, for single turbines as well as in wind farm spacing. The solution of these problems requires, along with immoderate experimental investigations, intensive computer simulation of dynamic processes in all their parts, especially in the blades, which in the case of large turbines are now made of composite materials and have a rather complex structural design. Modern turbines have significantly longer blades than their predecessors (tens of meters) and are much more flexible. These blades are designed as long slender composite shell structures with stiffeners, significantly inhomogeneous and becoming more slender towards the free tip. This necessitates a wide range of studies in blade structural dynamics of the performance of such blades to evaluate deformations and stresses in their structure. The possible intensive vibrations in service conditions may not only cause fatigue damage or affect structural strength and stability, but also have significant influence on power production [4]. Another major and important area where simulation of dynamic processes in wind turbines is needed is the vibration control of wind turbines during operation and at extreme conditions [1,5].

For the computer simulation of blades’ dynamic behavior, a number of modern FEM packages like ANSYS or ABAQUS are widely used. They modelling of blades having high accuracy and simulate their dynamic behaviour, taking into account nonlinear geometric and material effects when necessary [6,7].

Simpler beam-type models can be obtained directly using different methods of the blade behaviour approximation. In the past, models based on advanced variants of theory for thin-walled beams have widely used [8,9,10], or an identification approach has been used based on the data obtained from physical or numerical experiments (the latter was considered in [11]).

The aim of the present study is to investigate dynamic characteristics of a horizontal axis wind turbine (HAWT) rotor blade with a stiffener. For this, a corresponding mechanical model was developed and implemented by means of a finite element package ABAQUS [12]. Then a modal analysis of turbine blade vibrations was carried out in order to obtain an eigenfrequency spectrum and shapes of the turbine blade vibration modes, which can be used in transient modal based dynamic analysis and, in future studies, in building different simplified beam-type by identification methods as in [11]. Besides, benchmark cases for the dynamic response of the blade subjected to uniform underneath pressure pulses of different magnitudes were studied in detail to find the loading value that provides a noticeable effect of geometric nonlinearity. The evaluated root reaction forces allow estimation of strength characteristics of the blade in the root section.

2. Methodology

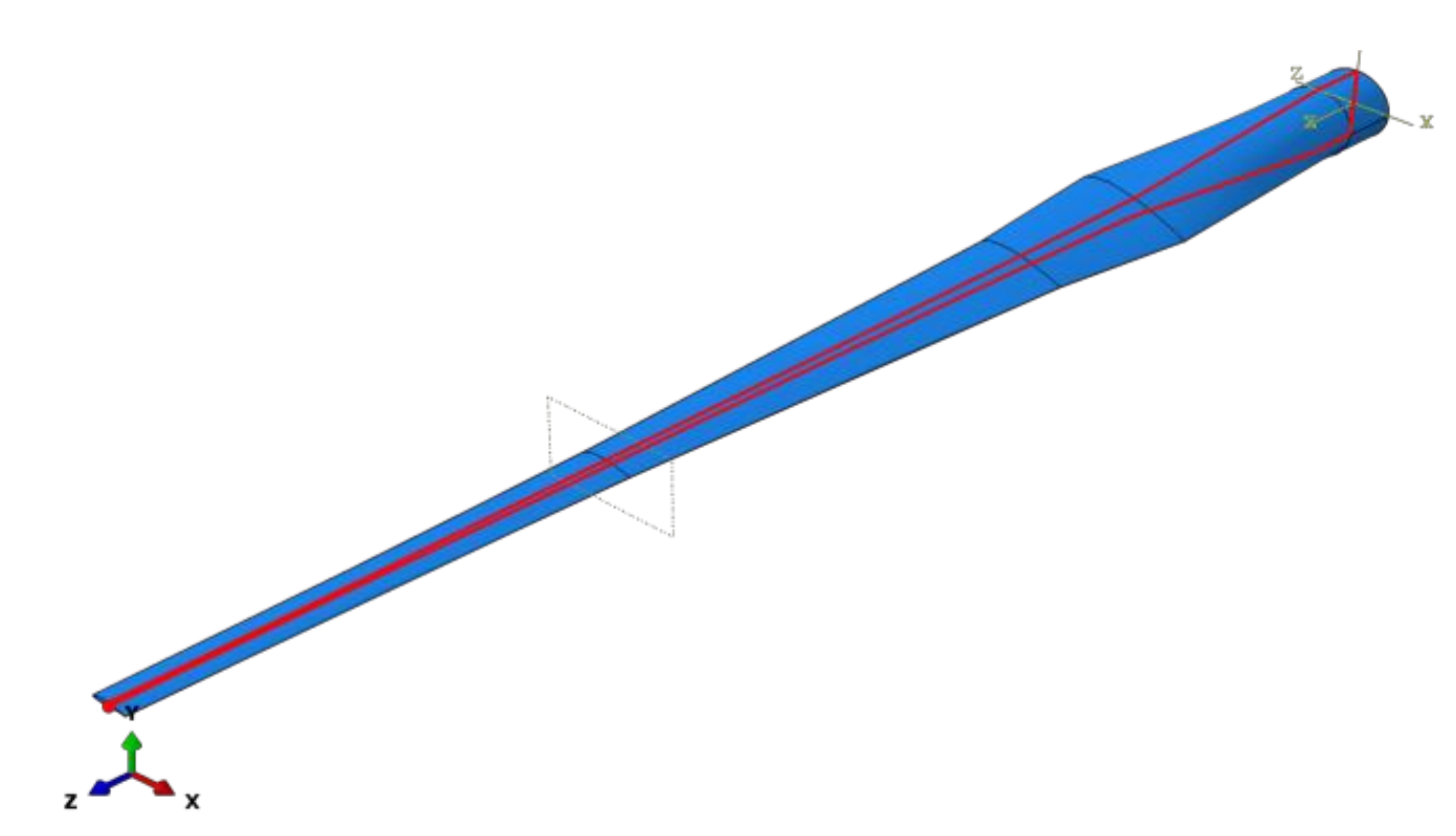
In order to investigate the response of real rotor blades, an ABAQUS shell-type model of the blade was developed to be consistent with industrial demands. Inertial effects due to the rotation were not considered in the present paper but can be taken into account in further investigations. The blade consisted of the skin, a stiffener and a specific attachment zone at the root of the blade. The model incorporated all necessary FEM modeling features for effective simulation of the transient blade response to different types of loading. Blade geometry was a modified version [13] of a 3 MW turbine proposed by [14] and used a scale-up version of the 20.15 m long blade in [15]. The geometry of the model was based on that developed in [11] and is shown in Figure 1.

The rotor blade, which was 44.175 m long, had a circular cross-section at its root attaching the rotor hub to the 1.753-m span location. Then the circular blade cross-sections was gradually transformed to airfoil sections that had NREL airfoil types S818 at the 9.648-m span location, S825 at 32.667-m, and S826 at 41.873-m and 44.175-m (at the blade tip). The shapes of the NREL airfoils used are shown in Figure 1 in [13], and in [16], where data files presenting details of geometry of these airfoils are also given.

Table 1. Section thicknesses along the beam axis (measured from the circular root).

Number of Section	Distance from the Root in z-Direction (mm)	Thickness t (mm)
1	1754	96.02
2	9648	79.04
3	14,251	53.21
4	29,212	13.44
5	44,175	10.34

presents the details of the cross-sections framing the blade, and the constitutive parameters of the blade’s skin material which was considered to be a homogeneous unidirectional composite with fibers oriented along the blade as shown in

Table 2. Stiffness moduli and Poisson ratios for the UD composite (1—fibre direction, 2—transverse direction, 3—through-the-thickness direction).

ρ (kg/m3)	E1	E2	E3	${\mathit{\nu }}_{12}$	${\mathit{\nu }}_{13}$	${\mathit{\nu }}_{23}$	G12	G13	G23
	(GPa)	(GPa)	(GPa)				(GPa)	(GPa)	(GPa)
1860	37.0	18.0	18.0	0.25	0.25	0.3	8.0	8.0	6.9

[11].

For representation of the considered shell structure, ABAQUS S4R 4-node shell elements with reduced integration and hourglass control were utilized. This element type belongs to the class of general-purpose elements suitable for both thin and thick shells and allowed us to take into account finite membrane strains and arbitrarily large rotations [12]. A brief review of different modern approaches to developing shell elements and comparatively evaluating some of them, including S4 and S4R, can be found in [17].

The model was discretized into finite elements by mapped meshing with element size in z direction about 20 cm, and with 16 subdivisions in transverse direction at the top and bottom sides of the blade (overall more than 7000 elements were used).

At the root of the blade the encastre boundary condition was applied which constrains all active structural degrees of freedom (i.e., displacements and rotations): $U_1=U_2=U_3=0$, $U{R}_1=U{R}_2=U{R}_3=0$.

Some computations at early stage of investigation were carried out using S4 shell elements with full integration which led to more expensive models. However, comparison of results with the ones obtained with S4R elements showed small difference between eigenfrequencies (fractions of a percent), so the S4R element was chosen.

The cross-section of the blade was strengthened by a wooden stiffener (made of longleaf pine [18]) with the values of density, stiffness moduli and Poisson ratios listed in

Table 3. Stiffness moduli and Poisson ratios for the longleaf pine.

ρ (kg/m3)	E1	E2	E3	${\mathit{\nu }}_{12}$	${\mathit{\nu }}_{13}$	${\mathit{\nu }}_{23}$	G12	G13	G23
	(GPa)	(GPa)	(GPa)				(GPa)	(GPa)	(GPa)
590	15.07	1.5371	0.8289	0.332	0.365	0.384	1.07	0.9042	0.1808

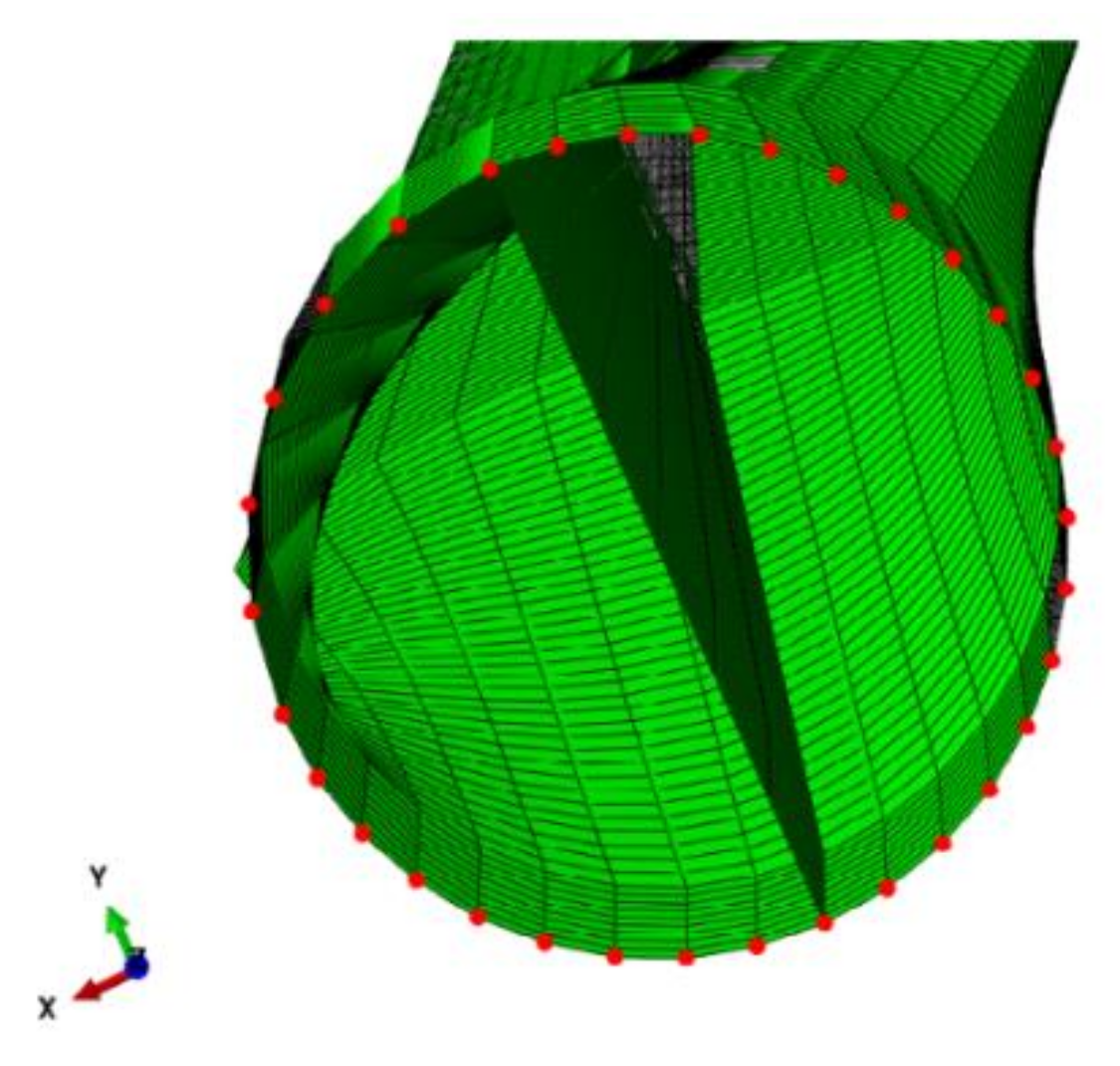
. The stiffener was chosen to be running along the whole blade as shown in Figure 1 by the red line. The rear view of the blade root and the stiffener is depicted in Figure 2.

3. Results

3.1. Modal Analysis of the Wind Turbine Blade Vibrations

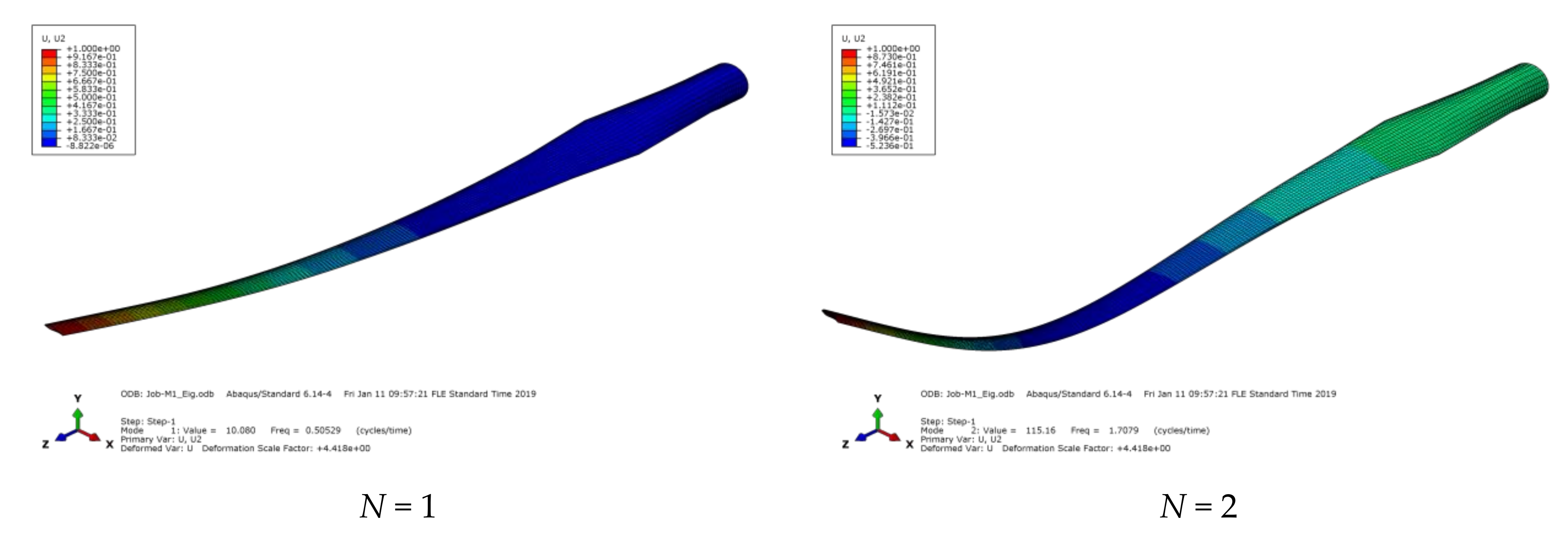
In this subsection modal analysis of a horizontal axis wind turbine (HAWT) composite blade is conducted using the finite element technique. Calculations were performed for three values of the wooden (longleaf pine) stiffener thickness: 100 mm, 150 mm, and 200 mm. Correspondent values of the eigenfrequencies for the eight lowest vibration modes are listed in

Table 4. Eigenfrequencies of the rotor blade (UD composite skin and wooden stiffener) vibration modes for different stiffener thicknesses.

Mode Number N	Eigenfrequency, Hz
	Stiffener Thickness
	100 mm	150 mm	200 mm
1	0.51022	0.50529	0.50076
2	1.73044	1.70793	1.68643
3	2.16916	2.10215	2.04292
4	4.01688	3.97606	3.93519
5	6.52319	6.38345	6.2385
6	7.09087	6.98604	6.90093
7	7.88766	7.97702	8.07623
8	9.56138	9.56842	9.5557

, and their shapes are shown in Figure 3.

Analyses of Table 4 and Figure 3 show that, as can be seen from the vibration mode shapes represented in Figure 3, the modes 1, 2, 4 had a flap character, the 3rd mode was mainly lead-lag, and in the modes 5, 6, 8 flap and lead-lag movements were combined. The vibration mode 7 was a twisting mode.

A blade with a wooden stiffener of 150 mm thickness was chosen for the following simulations and analyses.

3.2. Simulation of Blade Dynamics under Step-Wise Pulse Loading

As mentioned above, a blade consisting of a composite skin along with a wooden stiffener of 150 mm thickness was subjected to step-wise uniform underneath pressure of variable magnitudes. The aim of the simulations performed was to find the loading value that provided a noticeable effect of geometric nonlinearity. Two simulations were run for each particular case of the loading amplitude. The first one was performed using the ABAQUS model, taking into account geometric nonlinearity, while the linear elastic ABAQUS model was employed for the second simulation. The computations were done using an implicit direct-integration dynamic procedure provided in ABAQUS/Standard [12] with constant time steps in linear cases, and with variable steps in nonlinear ones. The different time steps were used for calculations. Stable results were obtained with application of the practical convergence technique for time step choice.

Special attention was paid to the investigation of time histories of the blade tip displacement in the y (flap) direction and the z (longitudinal) component of the root reaction force which were obtained from the results of calculations.

Typical results for the blade tip point deflection time history are shown in Figure 4. In the figures in the sequel, deflection levels are in meters while time is in seconds. The results of calculations showed that for up to a magnitude of pressure (in the case considered here 7 × 10² Pa) the influence of nonlinearity was small and may be neglected. However, for larger values of pressure, nonlinear effects such as increasing of amplitude and time lag of the vibrations were observed.

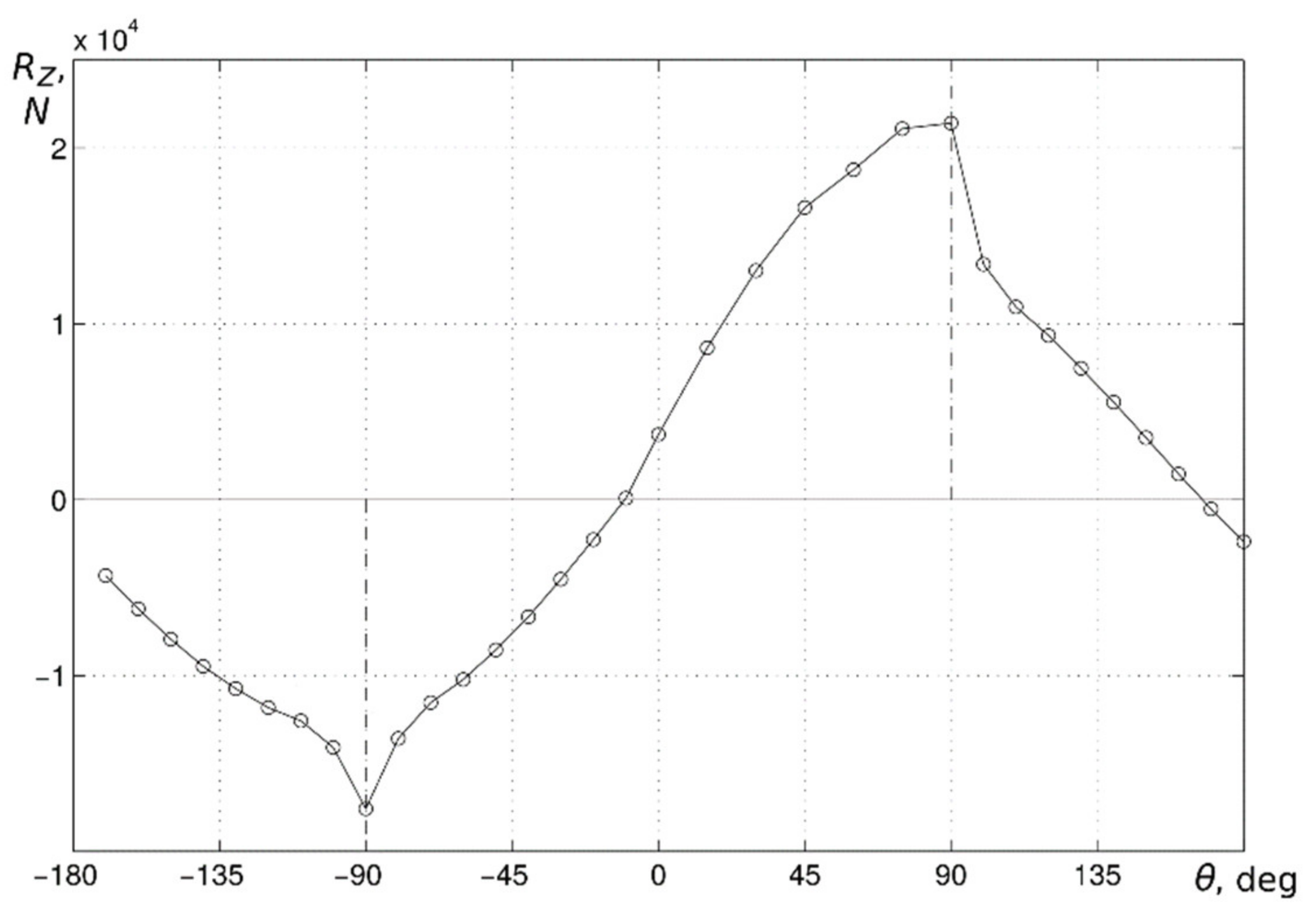
A special procedure was developed to find the corrected distribution of the reaction force results over the root’s circular cross-section because the nodal points of the mesh were not evenly distributed (see red dots in Figure 2). This caused the distribution presented in Figure 5 where the nodal values of reaction forces $R_z$ are in Newtons with respect to azimuth angle θ as shown (calculations were performed for pressure loading magnitude 10² Pa, and this graph corresponds to the time t = 0.9 s when the maximum values of the reaction forces were reached).

For this aim, a standard Fourier series approximation was used:

$$\begin{array}{c}f(\theta )\approx \frac{a_0}{2}+{\displaystyle \sum _{n=1}^N\left(a_n\cos n\theta +b_n\sin n\theta \right)},\\ a_0=\frac{1}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}f(\theta )d\theta },\hspace{1em}\hspace{0.33em}{a}_n=\frac{1}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}f(\theta )\cos n\theta d\theta },\hspace{1em}\hspace{0.33em}{b}_n=\frac{1}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}f(\theta )\sin n\theta d\theta }.\end{array}$$

(1)

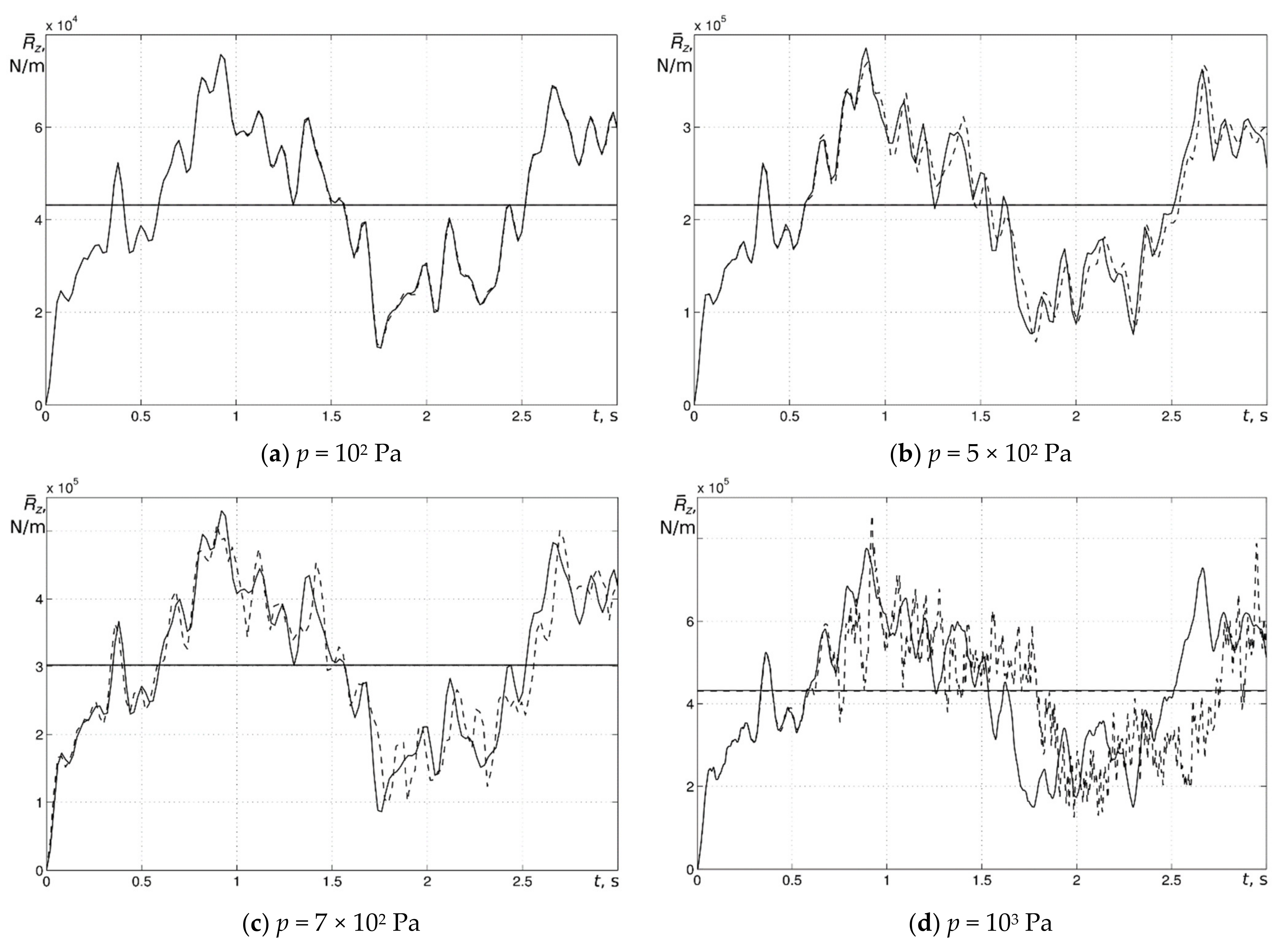
The typical corrected results for the density of membrane reaction force ${\overline{R}}_z$ (N/m) are shown in Figure 6 where the effect of the stiffener is clearly visible as the noticeable rise of the membrane reaction occurred at places of stiffener attachment (90° and −90°). This effect should be taken into account when the strength, fatigue resistance and life prediction of the blade are evaluated.

Graphic representation of the time histories of the reaction force ${\overline{R}}_z$ density at 90° (on y-axis, attachment point of the stiffener and skin) obtained by the Fourier approximation of the 9th order (solid line corresponds to the geometrically linear model while dashed line stands for the nonlinear one) for different pressure loading magnitudes is presented in Figure 7.

It can be seen that both the linear and nonlinear models predicted similar responses for the loads which did not exceed a value of 7 × 10² Pa, which implies insignificant geometric nonlinear effects up to this point in the loading space.

3.3. Simulation of Blade Dynamics under Half-Sine Pulse Loading

Here, the results of response simulation for the wind turbine rotor blade subjected to the uniform underneath pressure pulse of the half-sine shape with a duration of 2 s (see Figure 8) are presented. This pulse imitates the load at a wind gust with a single peak. The investigated blade’s composition was a UD composite skin along with a wooden stiffener 150 mm thick.

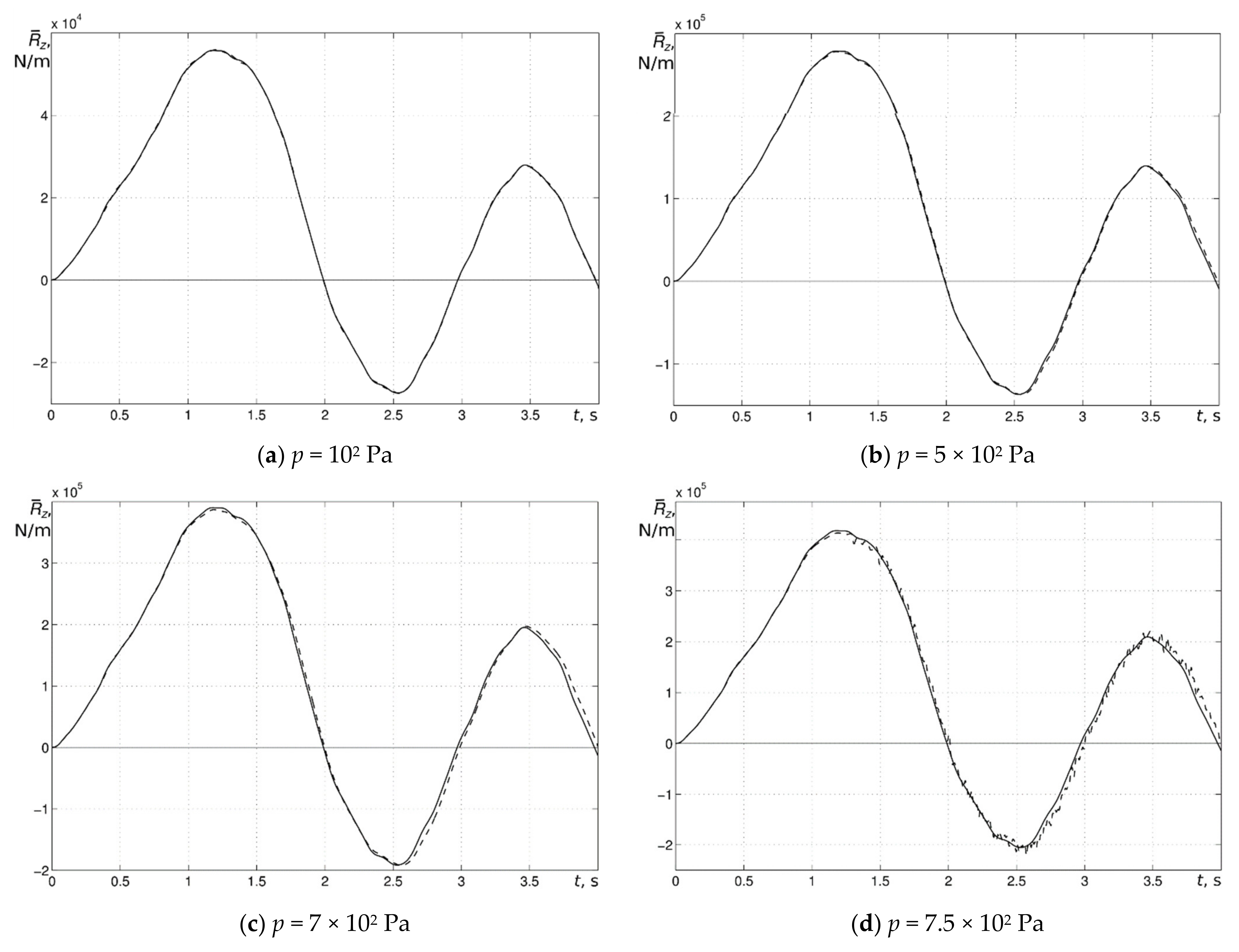
Displacements of the blade tip are shown in Figure 9 for different load levels of the half-sine pulse pressure load. In this figure, the solid lines correspond to linear simulation while dashed lines are used to depict the case when nonlinear geometrical effects are accounted for.

Nonlinearity effects started to become noticeable from the magnitude of pressure p around 7 × 10² Pa upwards. For the loading magnitude of 10³ Pa, the discrepancy between linear and nonlinear cases were more pronounced. It should be mentioned that the nonlinearity level could be estimated by the displacement of nodal points time shift (as well as the displacement extremes). A magnitude of 10³ Pa led to the essential movement of the extreme points of graph along time axis to the right. Thus, both displacement extremes and the nodal displacement shift in time if nonlinearity is taken into account. This is due to the dependence of frequency on amplitude and on considering the deformed configuration derived from the equations of motion.

The membrane reaction force densities at the blade root are depicted in Figure 10a–e, which correspond to load magnitudes of 10², 5 × 10², 7 × 10², 7.5 × 10² and 10³ Pa, respectively. These results are similar to ones obtained in the previous section.

The results were qualitatively similar to the ones shown in Figure 9 for displacements up to those corresponding to the magnitude of pressure p close to the value 7 × 10² Pa. For larger loading amplitudes, fast oscillations due to nonlinear effects occurred (see graphs in Figure 10d,e. The magnitude of the oscillations increased rapidly with the load. Presence of the effect can be explained by the longitudinal vibration of the blade which was taken into account for the nonlinear blade. Thus this additional “shivering effect” can be attributed to geometrical nonlinearity.

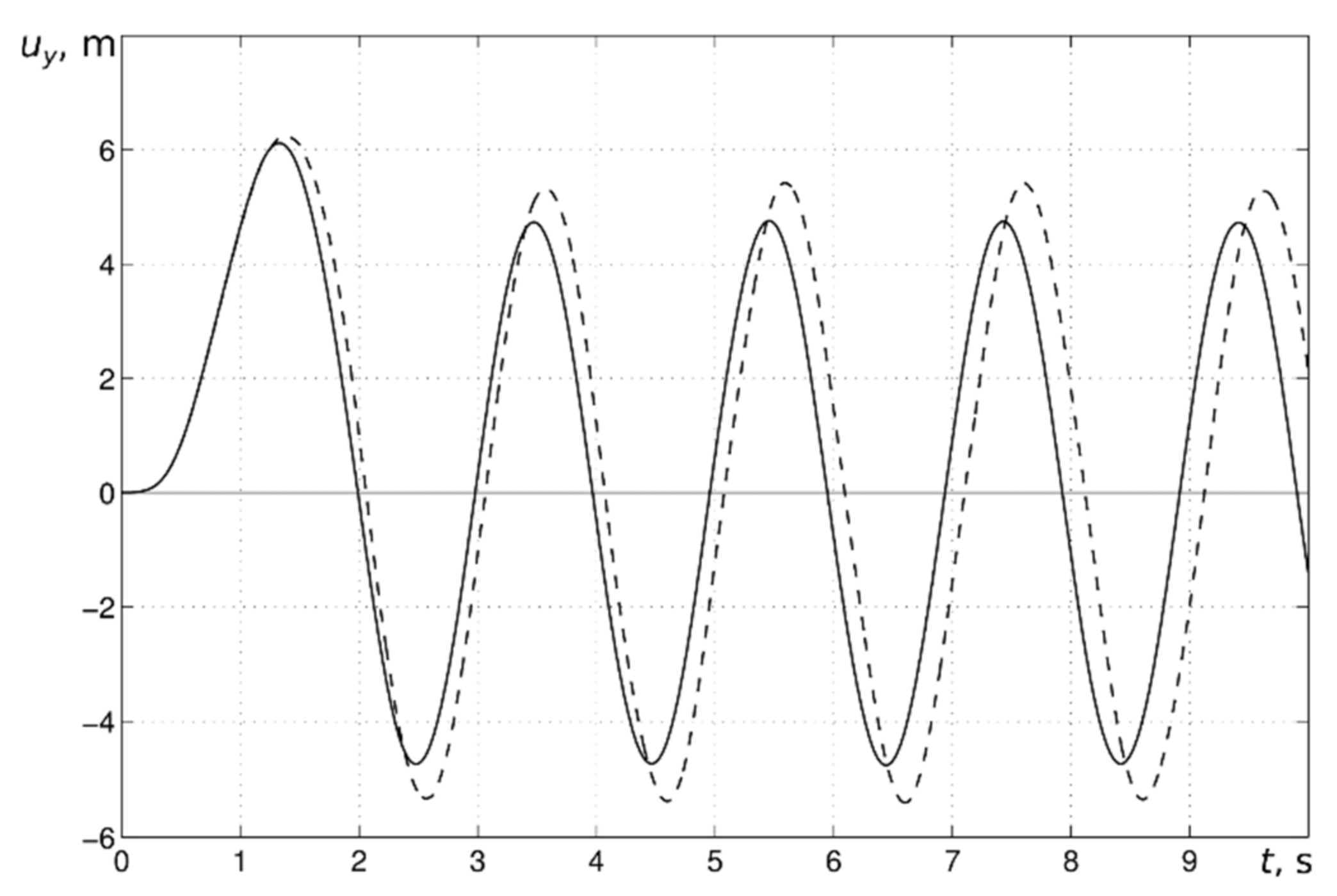
In Figure 11 and Figure 12 the results for simulations up to 10 s for the half-sine pulse with a duration of 2 s with pressure magnitude 10³ Pa are presented. The comparison of Figure 9 and Figure 11 shows that the general tendencies were kept: displacement nodal points shifted to the right (as well as the displacement extremes), i.e., the blade demonstrated nonlinear responses of the soft type. The same was observed for the membrane reaction force graphs in Figure 12 (compare with Figure 10e).

To verify the computation procedure, calculations with different time steps were performed. The results agreed with high accuracy. Therefore, the “shivering effect” was physical and is not introduced by computational instability.

It is worth mentioning here that accounting for the geometrical nonlinearity manifests itself in three effects: (i) increasing of the flap deflection up to about 15 per cent at a load magnitude of 10³ Pa; (ii) gradually increasing time shift in the nodal displacements and their extremes and (iii) “shivering” in the root membrane forces due to excitation of longitudinal vibrations up to about 20 per cent at the load magnitude 10³ Pa.

4. Discussion and Conclusions

In the present study, a shell type mechanical model of a horizontal axis wind turbine (HAWT) rotor blade with a stiffener was developed and implemented in the finite element package ABAQUS. This model allows for detailed investigation of the dynamic response and processes of deformation and evolution of stresses in the rotor blade considered.

Firstly, an eigenvalue modal analysis (linear perturbation analysis) of turbine blade vibrations was carried out. It demonstrated the wide variety of the forms of vibrational motion for the blade, from bending modes in flap and lead-lag directions and twisting modes in their combinations.

Benchmark cases for the dynamic response were investigated. Two types of pulse loading were considered: step-wise, replicating a pulse load as impact or blast, and half-sine shape, which imitates the load at a wind gust. In both cases a uniform pressure pulse was applied to the underneath part of the blade. The computations were performed both in the linear and geometrically nonlinear formulations. Blade tip displacement and root reaction force time histories were obtained from the results of finite element simulation conducted using ABAQUS/Standard. The results of calculations showed that for up to some magnitude of pressure (in the case considered here 7 × 10² Pa) the influence of nonlinearity was small and may be neglected. However, with larger values of pressure, nonlinear effects were observed in the behaviour of reaction forces at the blade’s root, such as gradually increasing amplitude and time lag of the vibrations, and the emergence of high frequency longitudinal vibrations (similar to appearance of overtones in musical instruments).

In general, it was found the geometrical nonlinearity had three main manifestations under the conditions considered: (i) increasing of the flap deflection up to about 15 per cent at the load magnitude 10³ Pa; (ii) gradually increasing time shift in the nodal displacements and their extremes and (iii) “shivering” in the root membrane forces due to excitation of longitudinal vibrations up to about 20 per cent at a load magnitude 10³ Pa.

The developed finite element model of the blade can be modified to investigate behaviour of the blades made of layered composites including different approaches to damage consideration. Using the results of simulation, both modal analysis and transient dynamics and different types of approximated beam-type models of wind turbine blades on the base of identification techniques can be built [12].