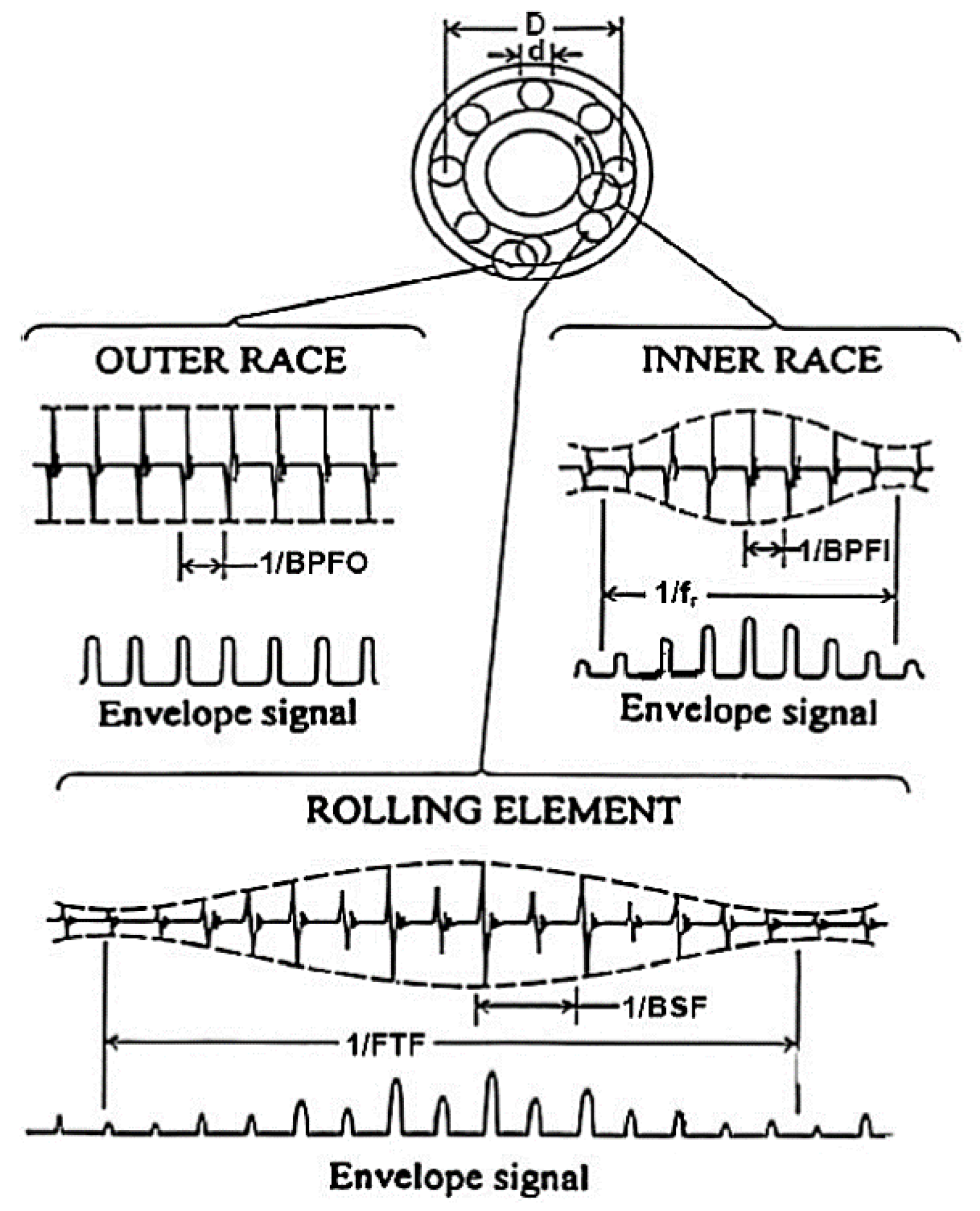
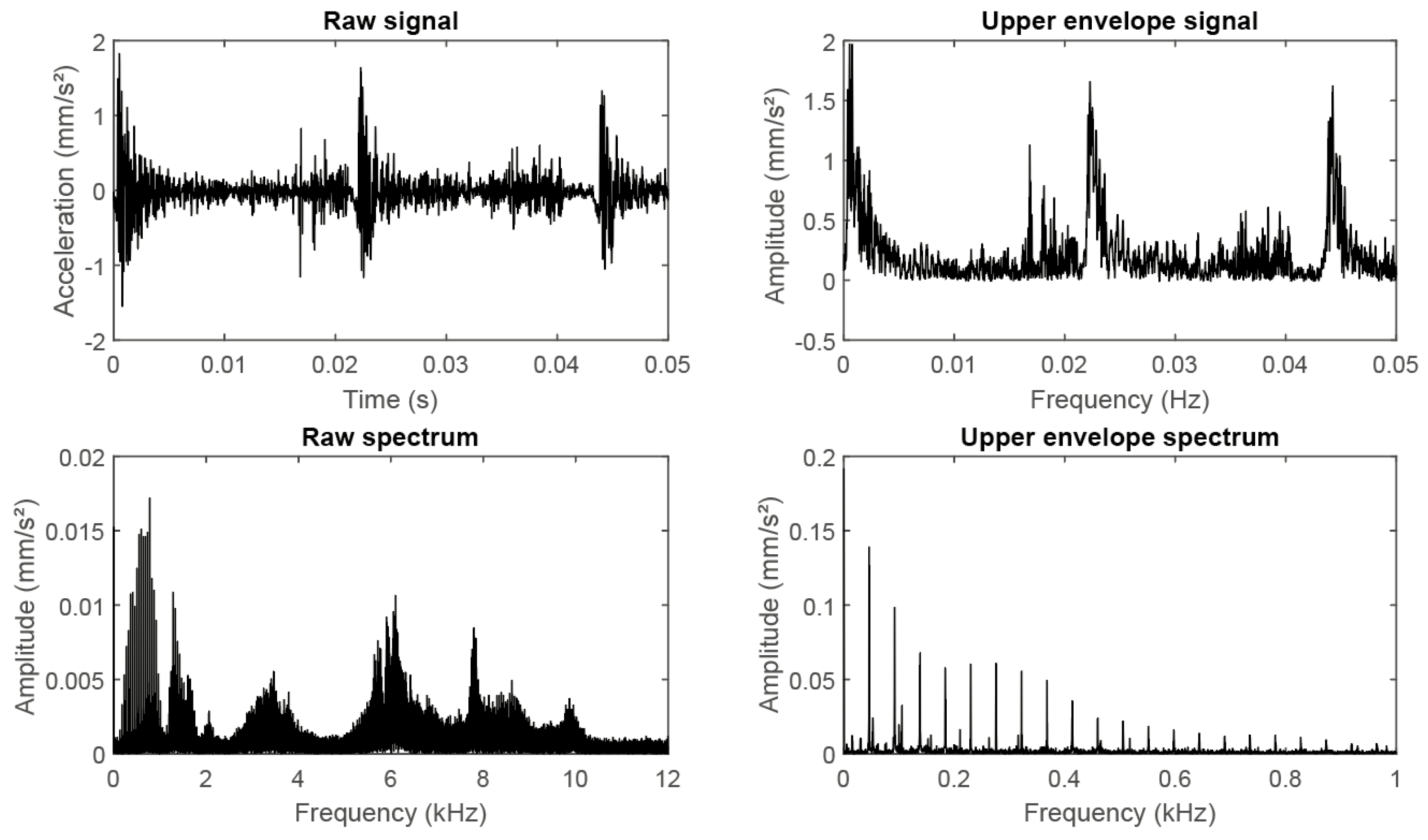
Figure 1.
Typical signals and envelope signals from local faults in rolling element bearings [
19].
Figure 1.
Typical signals and envelope signals from local faults in rolling element bearings [
19].
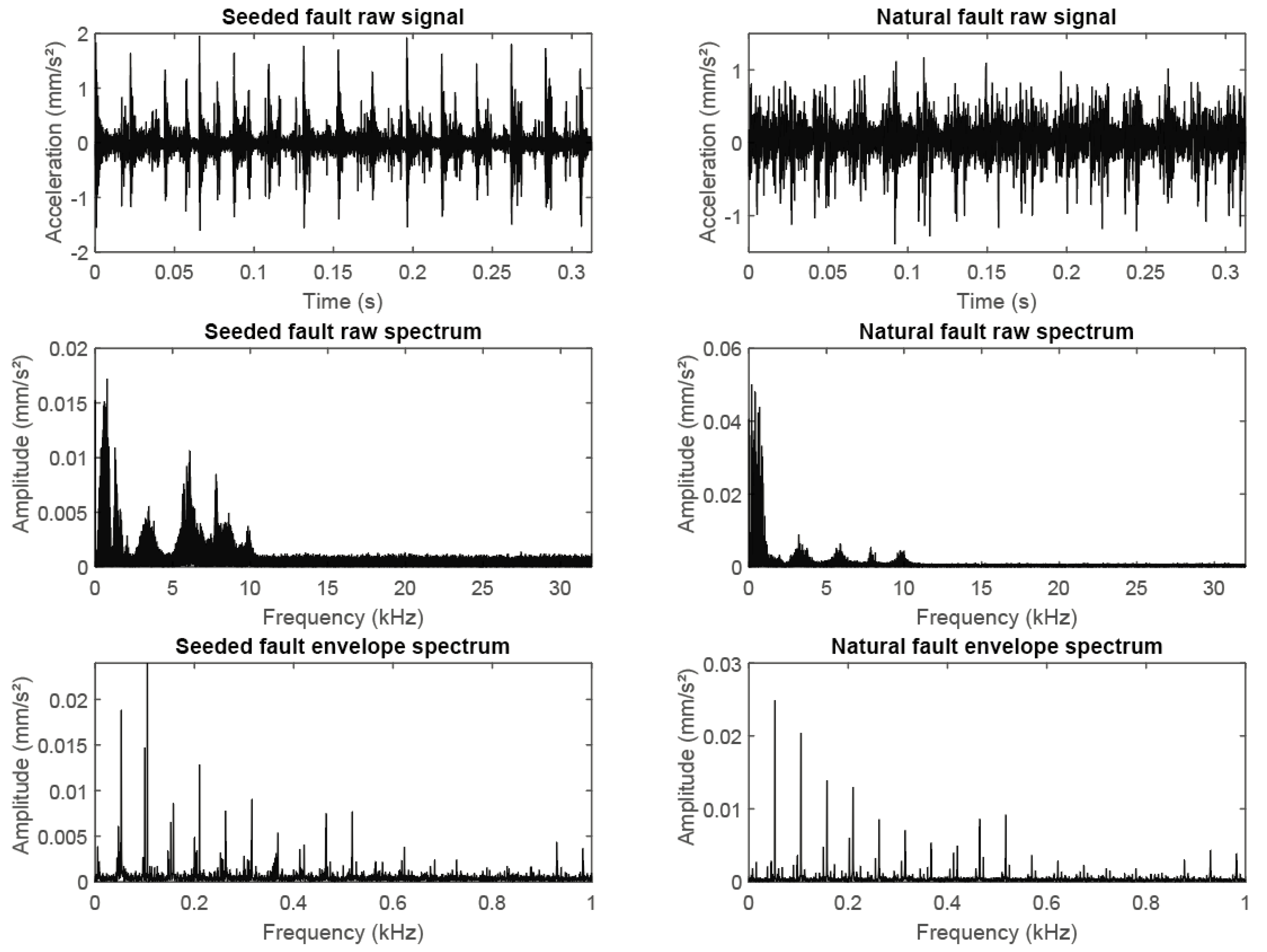
Figure 2.
Comparison of natural faults (left column) and real fault signals (right column) with respect to raw signal (top row), raw frequency spectrum (middle row) and envelope spectrum (bottom row) for identical bearings under the same operating conditions.
Figure 2.
Comparison of natural faults (left column) and real fault signals (right column) with respect to raw signal (top row), raw frequency spectrum (middle row) and envelope spectrum (bottom row) for identical bearings under the same operating conditions.
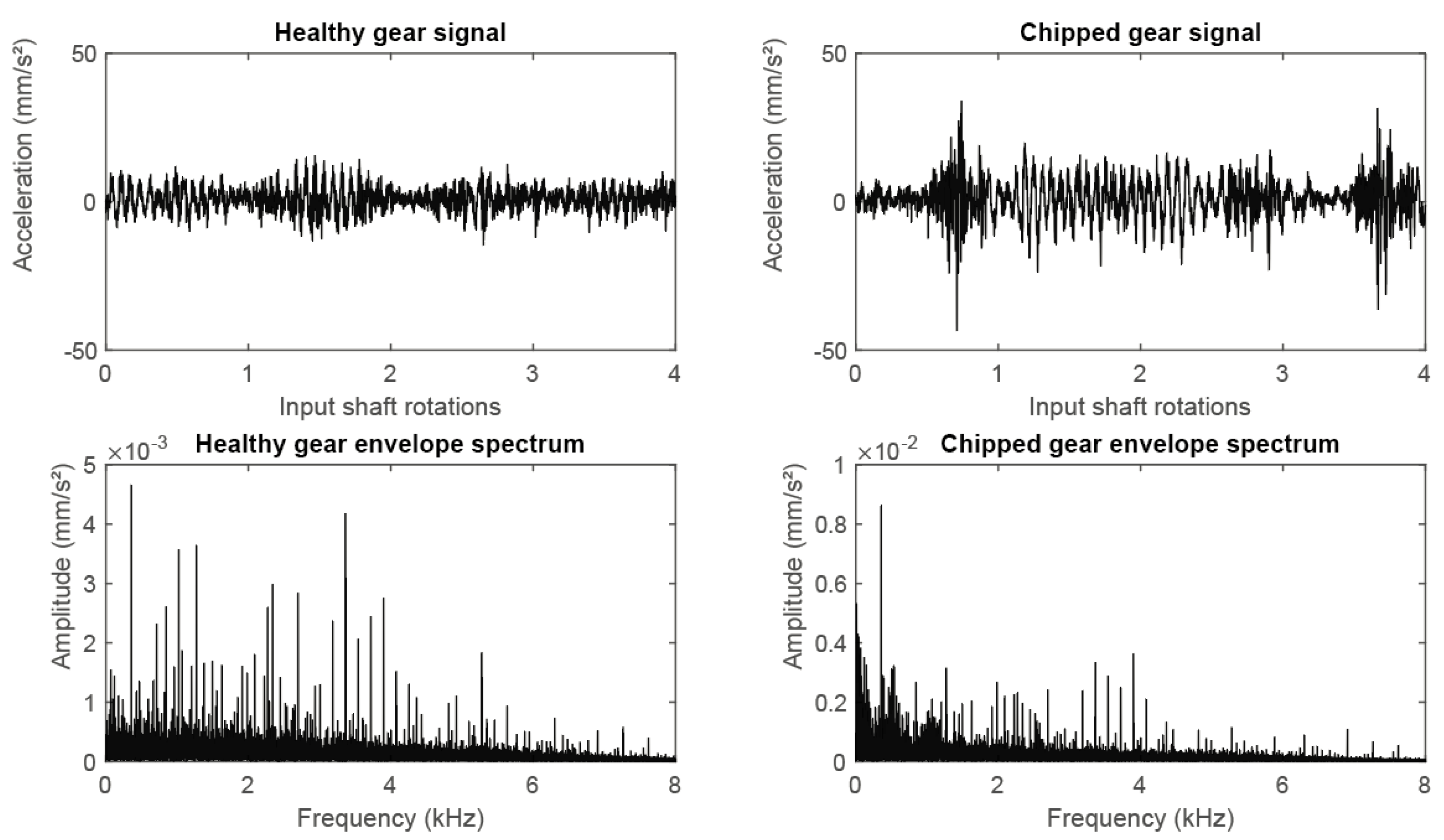
Figure 3.
Raw signal (top) and spectrum of the envelope signal (bottom) for a healthy gear train (left) and one with a chipped tooth at the input gear (right).
Figure 3.
Raw signal (top) and spectrum of the envelope signal (bottom) for a healthy gear train (left) and one with a chipped tooth at the input gear (right).
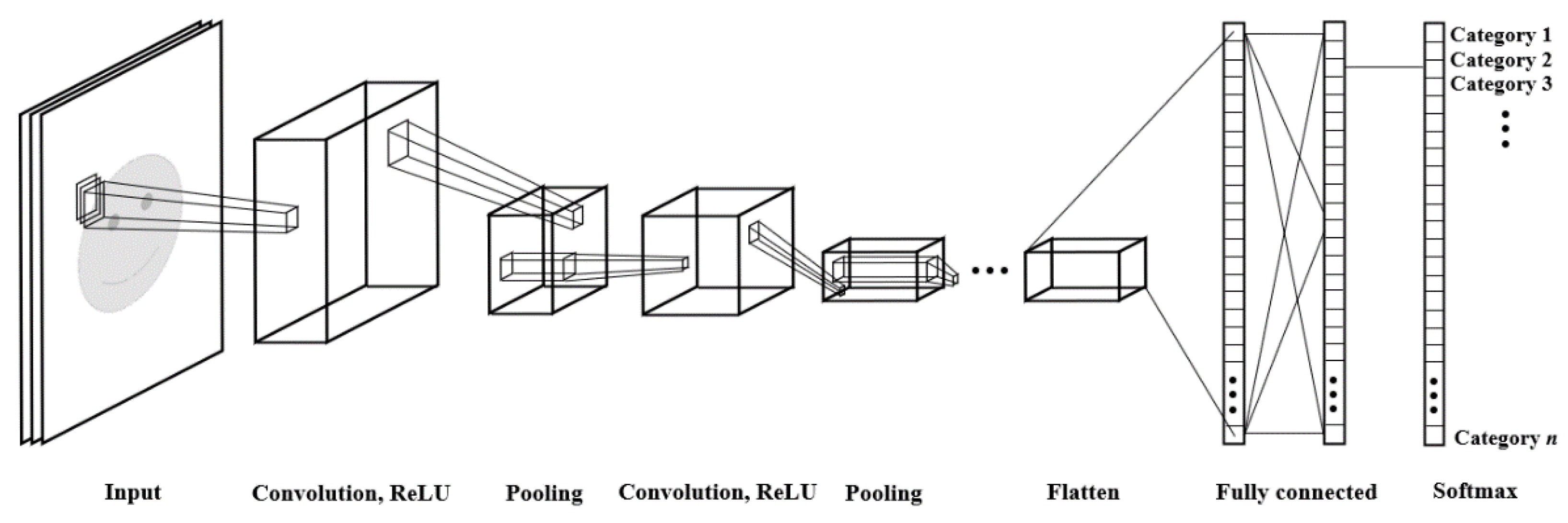
Figure 4.
Architecture, or sequence of layers, for a classical CNN classifier.
Figure 4.
Architecture, or sequence of layers, for a classical CNN classifier.
Figure 5.
Sliding window using the overlap data augmentation technique with the first two extracted training samples shown.
Figure 5.
Sliding window using the overlap data augmentation technique with the first two extracted training samples shown.
Figure 6.
Raw vibration signal for an outer race bearing fault operating at 2900 RPM and sampled at 64 kHz (top) and a chipped tooth fault and a compound fault gear running at 1800 RPM and sampled at 66.6667 kHz.
Figure 6.
Raw vibration signal for an outer race bearing fault operating at 2900 RPM and sampled at 64 kHz (top) and a chipped tooth fault and a compound fault gear running at 1800 RPM and sampled at 66.6667 kHz.
Figure 7.
Raw vibration measurement from a bearing fault test bench with two frequency spectra obtained from windows of 1000 samples with 75% overlap.
Figure 7.
Raw vibration measurement from a bearing fault test bench with two frequency spectra obtained from windows of 1000 samples with 75% overlap.
Figure 8.
Comparison of raw vibration signal, envelope signal, raw spectrum, and envelope spectrum for an outer race fault sampled at 64 kHz from the Padderborn University dataset.
Figure 8.
Comparison of raw vibration signal, envelope signal, raw spectrum, and envelope spectrum for an outer race fault sampled at 64 kHz from the Padderborn University dataset.
Figure 9.
Confusion matrices for (a) raw time, (b) Fourier spectrum, (c) envelope spectrum, and (d) spectrogram as inputs to the CNN.
Figure 9.
Confusion matrices for (a) raw time, (b) Fourier spectrum, (c) envelope spectrum, and (d) spectrogram as inputs to the CNN.
Table 1.
Example CNN specifications for a 8 × 1 filter size, a 2 × 1 stride, and a 1248 × 1 input.
Table 1.
Example CNN specifications for a 8 × 1 filter size, a 2 × 1 stride, and a 1248 × 1 input.
| # | Layer Type | Activations | Learnables |
|---|
| 1 | Input layer | 1248 × 1 × 1 | - |
| 2 | Convolutional layer | 624 × 1 × 16 | Weights 8 × 1 × 1 × 16
Bias 1 × 1 × 16 |
| 3 | ReLU | 624 × 1 × 16 | - |
| 4 | Dropout (50%) | 624 × 1 × 16 | - |
| 5 | Max pooling | 312 × 1 × 16 | - |
| 6 | Convolutional layer | 312 × 1 × 16 | Weights 8 × 1 × 16 × 16
Bias 1 × 1 × 16 |
| 7 | ReLU | 312 × 1 × 16 | - |
| 8 | Dropout (50%) | 312 × 1 × 16 | - |
| 9 | Max pooling | 312 × 1 × 16 | - |
| 10 | Fully connected | 1 × 1 × 7 | Weights 7 × 4992
Bias 7 × 1 |
| 11 | Softmax | 1 × 1 × 7 | - |
| 12 | Class output | - | - |
Table 2.
Training and testing accuracies for various CNN architectures with no preprocessing.
Table 2.
Training and testing accuracies for various CNN architectures with no preprocessing.
| Input Type: Raw Time Series | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1], [2,1] | 72.7 | 68.8 | 64.8 | 71.9 | 68.0 | 72.7 | [4,1], [2,1] | 50.9 | 49.4 | 47.7 | 49.7 | 41.2 | 33.5 |
| [8,1], [2,1] | 82.0 | 86.7 | 83.6 | 59.4 | 65.6 | 49.2 | [8,1], [2,1] | 62.6 | 58.8 | 57.2 | 43.2 | 40.6 | 31.8 |
| [16,1], [4,1] | 89.1 | 86.7 | 89.8 | 82.8 | 83.6 | 67.2 | [16,1], [4,1] | 65.0 | 66.7 | 64.4 | 54.6 | 58.3 | 39.4 |
| [32,1], [4,1] | 93.8 | 87.5 | 97.7 | 86.7 | 41.4 | 46.1 | [32,1], [4,1] | 66.9 | 67.5 | 65.3 | 63.3 | 33.1 | 35.0 |
| [64,1], [4,1] | 89.8 | 93.8 | 96.1 | 83.6 | 56.3 | 50.8 | [65,1], [4,1] | 65.9 | 71.2 | 63.3 | 53.1 | 37.4 | 36.6 |
| [128,1], [1,1] | 81.3 | 61.7 | 54.7 | 61.7 | 42.2 | 31.3 | [128,1], [4,1] | 60.0 | 48.2 | 50.8 | 47.7 | 35.9 | 27.0 |
| [256,1], [4,1] | 89.8 | 87.5 | 68.8 | 40.6 | 28.9 | 34.4 | [256,1], [4,1] | 63.1 | 56.7 | 49.4 | 33.1 | 29.3 | 35.4 |
| Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 3.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
Table 3.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
| Input Type: Fourier Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 96.9 | 97.7 | 98.4 | 100.0 | 99.2 | 99.2 | [4,1] [2,1] | 75.4 | 74.3 | 79.1 | 71.4 | 75.6 | 66.5 |
| [8,1] [2,1] | 99.2 | 96.9 | 98.4 | 99.2 | 97.7 | 97.7 | [8,1] [2,1] | 71.4 | 71.9 | 76.1 | 71.9 | 70.6 | 68.4 |
| [16,1] [4,1] | 85.9 | 88.3 | 93.0 | 93.8 | 94.5 | 69.5 | [16,1] [4,1] | 68.3 | 69.0 | 75.1 | 74.2 | 68.5 | 50.5 |
| [32,1] [4,1] | 71.9 | 88.3 | 73.4 | 82.0 | 79.7 | 22.7 | [32,1] [4,1] | 56.2 | 65.2 | 53.9 | 56.8 | 62.7 | 25.1 |
| [64,1] [4,1] | 40.6 | 45.3 | 39.1 | 45.3 | 34.4 | 23.4 | [64,1] [4,1] | 32.3 | 32.6 | 37.0 | 34.9 | 30.3 | 25.1 |
| [128,1] [4,1] | 52.3 | 48.4 | 47.7 | 30.5 | 30.5 | 20.3 | [128,1] [4,1] | 45.7 | 40.7 | 34.9 | 25.6 | 30.1 | 25.1 |
| [256,1] [4,1] | 42.2 | 39.8 | 32.0 | 38.3 | 31.3 | 27.3 | [256,1] [4,1] | 37.0 | 34.2 | 26.8 | 34.1 | 25.2 | 25.2 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 4.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
Table 4.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
| Input Type: Envelope Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 71.1 | 78.1 | 82.8 | 83.6 | 78.1 | 64.8 | [4,1] [2,1] | 59.4 | 68.1 | 61.3 | 62.9 | 67.6 | 55.7 |
| [8,1] [2,1] | 78.1 | 85.9 | 84.4 | 88.3 | 82.0 | 65.6 | [8,1] [2,1] | 53.9 | 67.2 | 64.0 | 72.0 | 67.0 | 49.9 |
| [16,1] [4,1] | 61.5 | 78.1 | 81.3 | 83.6 | 82.0 | 78.1 | [16,1] [4,1] | 68.0 | 67.8 | 67.6 | 58.5 | 65.1 | 59.7 |
| [32,1] [4,1] | 79.7 | 85.2 | 91.4 | 87.5 | 82.0 | 72.7 | [32,1] [4,1] | 65.5 | 67.5 | 71.0 | 66.0 | 59.7 | 53.9 |
| [64,1] [4,1] | 78.9 | 90.6 | 93.0 | 86.7 | 82.8 | 63.3 | [64,1] [4,1] | 66.9 | 74.6 | 72.4 | 66.9 | 67.5 | 47.0 |
| [128,1] [4,1] | 75.0 | 94.5 | 93.0 | 95.3 | 89.1 | 80.5 | [128,1] [4,1] | 67.7 | 73.4 | 75.7 | 67.7 | 68.6 | 58.5 |
| [256,1] [4,1] | 87.5 | 92.2 | 96.1 | 95.3 | 93.0 | 87.5 | [256,1] [4,1] | 68.8 | 76.9 | 76.7 | 78.0 | 64.5 | 66.7 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 5.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
Table 5.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
| Input Type: Spectrogram (Window = 104) | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [2,2], [1,1] | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | [2,2], [1,1] | 80.0 | 76.1 | 70.5 | 75.1 | 75.5 | 70.9 |
| [4,4], [1,1] | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | [4,4], [1,1] | 75.8 | 73.7 | 71.8 | 71.1 | 74.8 | 66.7 |
| [6,6], [1,1] | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | [6,6], [1,1] | 80.0 | 80.1 | 71.2 | 74.6 | 71.2 | 64.7 |
| [8,8], [1,1] | 100.0 | 99.2 | 100.0 | 100.0 | 61.7 | 53.1 | [8,8], [1,1] | 75.1 | 73.2 | 76.9 | 71.7 | 69.7 | 67.9 |
| Input size: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 | Input length: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 6.
Division of experimental data between training and testing datasets for Case Study 2 part 1.
Table 6.
Division of experimental data between training and testing datasets for Case Study 2 part 1.
| Dataset | Class | Fault Origin | Bearing code |
|---|
| Training | Healthy | None | K002 |
| Training | IR damage | Artificial damage | KI01 |
| Training | IR damage | Artificial damage (electric engraver) | KI05 |
| Training | IR damage | Artificial damage (electric engraver) | KI07 |
| Training | OR damage | Artificial damage (EDM machining) | KA01 |
| Training | OR damage | Artificial damage (electric engraver) | KA05 |
| Training | OR damage | Artificial damage (drilled) | KA07 |
| Testing | Healthy | None | KA001 |
| Testing | IR damage | Overload, wrong viscosity, contamination | KI14 |
| Testing | IR damage | Overload, wrong viscosity, contamination | KI16 |
| Testing | IR damage | Overload, wrong viscosity, contamination | KI17 |
| Testing | IR damage | Overload, wrong viscosity, contamination | KI18 |
| Testing | IR damage | Overload, wrong viscosity, contamination | KI21 |
| Testing | OR damage | Overload, wrong viscosity, contamination | KA04 |
| Testing | OR damage | Overload, wrong viscosity, contamination | KA15 |
| Testing | OR damage | Overload, wrong viscosity, contamination | KA16 |
| Testing | OR damage | Overload, wrong viscosity, contamination | KA22 |
| Testing | OR damage | Overload, wrong viscosity, contamination | KA30 |
Table 7.
Division of experimental data between training and testing datasets for Case Study 2 part 2.
Table 7.
Division of experimental data between training and testing datasets for Case Study 2 part 2.
| Dataset | Class | Fault Origin | Bearing code |
|---|
| Training | Healthy | None | K004 |
| Training | Healthy | None | K005 |
| Training | Healthy | None | K006 |
| Training | IR damage | Artificial damage | KI01 |
| Training | IR damage | Artificial damage (electric engraver) | KI03 |
| Training | IR damage | Artificial damage (electric engraver) | KI05 |
| Training | OR damage | Artificial damage (electric engraver) | KA06 |
| Training | OR damage | Artificial damage (drilled) | KA07 |
| Training | OR damage | Artificial damage (drilled) | KA08 |
| Testing | Healthy | None | K001 |
| Testing | Healthy | None | K002 |
| Testing | Healthy | None | K003 |
| Testing | IR damage | Artificial damage (electric engraver) | KI07 |
| Testing | IR damage | Artificial damage (electric engraver) | KI08 |
| Testing | OR damage | Artificial damage (EDM machining) | KA01 |
| Testing | OR damage | Artificial damage (electric engraving) | KA03 |
| Testing | OR damage | Artificial damage (electric engraving) | KA05 |
Table 8.
Training and testing accuracies for various CNN architectures with no preprocessing.
Table 8.
Training and testing accuracies for various CNN architectures with no preprocessing.
| Input Type: Raw Time Series | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1], [2,1] | 62.5 | 68.8 | 87.5 | 81.3 | 84.4 | 87.5 | [4,1], [2,1] | 47.0 | 46.1 | 47.1 | 37.8 | 43.5 | 35.9 |
| [8,1], [2,1] | 81.3 | 75.0 | 81.3 | 78.1 | 84.4 | 90.6 | [8,1], [2,1] | 49.7 | 46.6 | 49.3 | 48.6 | 48.0 | 31.5 |
| [16,1], [4,1] | 81.3 | 93.8 | 87.5 | 81.3 | 84.4 | 93.8 | [16,1], [4,1] | 49.6 | 50.2 | 51.7 | 49.5 | 52.2 | 52.5 |
| [32,1], [4,1] | 75.0 | 75.0 | 87.5 | 93.8 | 87.5 | 87.5 | [32,1], [4,1] | 47.7 | 49.0 | 48.7 | 49.4 | 51.5 | 52.7 |
| [64,1], [4,1] | 84.4 | 84.4 | 81.3 | 100.0 | 100.0 | 93.8 | [64,1], [4,1] | 47.9 | 49.2 | 49.1 | 49.4 | 55.0 | 50.0 |
| [128,1], [4,1] | 81.3 | 87.5 | 93.8 | 100.0 | 100.0 | 100.0 | [128,1], [4,1] | 45.7 | 45.5 | 46.9 | 46.6 | 47.9 | 51.8 |
| [256,1], [4,1] | 75.0 | 84.4 | 81.3 | 96.9 | 90.6 | 100.0 | [256,1], [4,1] | 45.8 | 45.4 | 48.7 | 49.0 | 48.9 | 49.7 |
| Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 9.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
Table 9.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
| Input Type: Fourier Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 75.0 | 93.8 | 87.5 | 90.6 | 90.6 | 90.6 | [4,1] [2,1] | 37.8 | 39.0 | 41.8 | 38.9 | 39.1 | 41.3 |
| [8,1] [2,1] | 75.0 | 90.6 | 90.6 | 90.6 | 93.8 | 93.8 | [8,1] [2,1] | 38.0 | 36.3 | 40.5 | 43.3 | 37.4 | 43.1 |
| [16,1] [4,1] | 68.8 | 84.4 | 84.4 | 96.9 | 96.9 | 96.9 | [16,1] [4,1] | 36.9 | 42.8 | 40.7 | 34.7 | 48.4 | 44.0 |
| [32,1] [4,1] | 78.1 | 84.4 | 84.4 | 96.9 | 87.5 | 90.6 | [32,1] [4,1] | 37.3 | 35.2 | 42.1 | 41.0 | 48.3 | 46.9 |
| [64,1] [4,1] | 75.0 | 87.5 | 90.6 | 93.8 | 84.4 | 90.6 | [64,1] [4,1] | 38.2 | 43.4 | 40.7 | 39.5 | 32.3 | 55.8 |
| [128,1] [4,1] | 84.4 | 87.5 | 75.0 | 84.4 | 90.6 | 87.5 | [128,1] [4,1] | 40.2 | 41.1 | 42.3 | 41.6 | 39.7 | 41.0 |
| [256,1] [4,1] | 90.6 | 78.1 | 81.3 | 87.5 | 90.6 | 75.0 | [256,1] [4,1] | 37.8 | 42.2 | 37.3 | 41.4 | 40.8 | 50.5 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 10.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
Table 10.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
| Input Type: Envelope Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 53.1 | 71.9 | 68.8 | 84.4 | 78.1 | 87.5 | [4,1] [2,1] | 42.2 | 39.3 | 37.0 | 37.2 | 36.7 | 36.4 |
| [8,1] [2,1] | 59.4 | 71.9 | 59.4 | 75.0 | 78.1 | 78.1 | [8,1] [2,1] | 42.3 | 40.3 | 38.1 | 36.8 | 37.4 | 36.5 |
| [16,1] [4,1] | 65.6 | 68.8 | 62.5 | 78.1 | 87.5 | 90.6 | [16,1] [4,1] | 42.0 | 39.5 | 38.2 | 37.5 | 37.1 | 36.7 |
| [32,1] [4,1] | 56.3 | 71.9 | 81.3 | 81.3 | 71.9 | 90.6 | [32,1] [4,1] | 41.9 | 39.8 | 37.5 | 36.7 | 36.9 | 36.6 |
| [64,1] [4,1] | 75.0 | 59.4 | 68.8 | 75.0 | 84.4 | 75.0 | [64,1] [4,1] | 41.9 | 40.0 | 37.2 | 37.2 | 36.5 | 36.6 |
| [128,1] [4,1] | 53.1 | 90.6 | 78.1 | 84.4 | 71.9 | 81.3 | [128,1] [4,1] | 41.9 | 40.2 | 37.6 | 37.4 | 36.8 | 36.5 |
| [256,1] [4,1] | 59.4 | 78.1 | 75.0 | 78.1 | 90.6 | 78.1 | [256,1] [4,1] | 41.7 | 39.6 | 37.0 | 36.9 | 36.5 | 36.6 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 11.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
Table 11.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
| Input Type: Spectrogram (window = 104) | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [2,2], [1,1] | 81.3 | 87.5 | 84.4 | 78.1 | 93.8 | 96.9 | [2,2], [1,1] | 39.5 | 40.3 | 38.4 | 36.6 | 48.9 | 30.4 |
| [4,4], [1,1] | 78.1 | 78.1 | 84.4 | 87.5 | 96.9 | 96.9 | [4,4], [1,1] | 39.5 | 40.1 | 34.6 | 32.8 | 49.2 | 49.7 |
| [6,6], [1,1] | 68.8 | 84.4 | 93.8 | 90.6 | 93.8 | 90.6 | [6,6], [1,1] | 39.1 | 40.4 | 32.0 | 30.5 | 51.9 | 46.6 |
| [8,8], [1,1] | 75.0 | 87.5 | 84.4 | 84.4 | 90.6 | 96.9 | [8,8], [1,1] | 43.5 | 37.4 | 39.0 | 49.6 | 50.0 | 52.2 |
| Input size: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 | Input length: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 12.
Training and testing accuracies for various CNN architectures with no preprocessing.
Table 12.
Training and testing accuracies for various CNN architectures with no preprocessing.
| Input Type: Raw Time Series | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1], [2,1] | 81.3 | 71.9 | 81.3 | 93.8 | 96.9 | 87.5 | [4,1], [2,1] | 33.8 | 43.2 | 39.7 | 48.5 | 52.3 | 53.6 |
| [8,1], [2,1] | 71.9 | 71.9 | 87.5 | 90.6 | 90.6 | 96.9 | [8,1], [2,1] | 43.8 | 50.3 | 52.5 | 52.0 | 53.2 | 48.8 |
| [16,1], [4,1] | 87.5 | 87.5 | 90.6 | 93.8 | 100.0 | 100.0 | [16,1], [4,1] | 46.3 | 50.6 | 50.1 | 56.2 | 51.7 | 48.3 |
| [32,1], [4,1] | 87.5 | 100.0 | 96.9 | 100.0 | 96.9 | 100.0 | [32,1], [4,1] | 50.6 | 57.3 | 60.5 | 54.2 | 59.6 | 52.1 |
| [64,1], [4,1] | 87.5 | 87.5 | 96.9 | 100.0 | 100.0 | 100.0 | [64,1], [4,1] | 55.0 | 55.1 | 57.6 | 64.2 | 60.1 | 47.2 |
| [128,1], [4,1] | 90.6 | 96.9 | 90.6 | 100.0 | 100.0 | 100.0 | [128,1], [4,1] | 53.6 | 57.1 | 70.0 | 62.1 | 54.3 | 58.7 |
| [256,1], [4,1] | 90.6 | 96.9 | 100.0 | 100.0 | 96.9 | 96.9 | [256,1], [4,1] | 52.5 | 58.7 | 57.1 | 64.2 | 62.5 | 51.7 |
| Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 13.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
Table 13.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
| Input Type: Fourier Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 68.8 | 90.6 | 87.5 | 96.9 | 96.9 | 100.0 | [4,1] [2,1] | 44.7 | 55.6 | 58.9 | 63.7 | 66.1 | 62.2 |
| [8,1] [2,1] | 65.6 | 87.5 | 93.8 | 96.9 | 100.0 | 100.0 | [8,1] [2,1] | 43.9 | 55.3 | 59.4 | 68.3 | 61.9 | 65.2 |
| [16,1] [4,1] | 56.3 | 87.5 | 93.8 | 93.8 | 96.9 | 100.0 | [16,1] [4,1] | 46.2 | 52.0 | 56.0 | 63.9 | 68.7 | 67.8 |
| [32,1] [4,1] | 75.0 | 87.5 | 96.9 | 100.0 | 100.0 | 93.8 | [32,1] [4,1] | 47.9 | 55.7 | 58.9 | 61.8 | 66.4 | 63.6 |
| [64,1] [4,1] | 84.4 | 84.4 | 87.5 | 96.9 | 96.9 | 100.0 | [64,1] [4,1] | 47.1 | 50.3 | 58.0 | 55.2 | 65.2 | 69.1 |
| [128,1] [4,1] | 78.1 | 87.5 | 90.6 | 90.6 | 93.8 | 100.0 | [128,1] [4,1] | 47.9 | 57.7 | 55.2 | 53.9 | 47.2 | 56.0 |
| [256,1] [4,1] | 68.8 | 90.6 | 90.6 | 100.0 | 96.9 | 100.0 | [256,1] [4,1] | 42.4 | 57.6 | 61.9 | 63.5 | 64.0 | 49.8 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 14.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
Table 14.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
| Input Type: Envelope Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 46.9 | 50.0 | 71.9 | 78.1 | 71.9 | 84.4 | [4,1] [2,1] | 31.8 | 25.6 | 22.2 | 23.8 | 27.0 | 31.5 |
| [8,1] [2,1] | 65.6 | 56.3 | 68.8 | 84.4 | 87.5 | 90.6 | [8,1] [2,1] | 28.8 | 26.5 | 18.2 | 20.5 | 19.5 | 15.8 |
| [16,1] [4,1] | 59.4 | 78.1 | 78.1 | 75.0 | 93.8 | 84.4 | [16,1] [4,1] | 32.2 | 30.6 | 32.3 | 21.9 | 23.8 | 31.1 |
| [32,1] [4,1] | 65.6 | 59.4 | 65.6 | 87.5 | 81.3 | 81.3 | [32,1] [4,1] | 23.5 | 23.8 | 21.3 | 32.2 | 38.3 | 38.3 |
| [64,1] [4,1] | 65.6 | 68.8 | 78.1 | 81.3 | 84.4 | 78.1 | [64,1] [4,1] | 29.8 | 32.4 | 29.4 | 37.9 | 38.3 | 37.6 |
| [128,1] [4,1] | 53.1 | 59.4 | 81.3 | 87.5 | 90.6 | 96.9 | [128,1] [4,1] | 25.6 | 27.5 | 30.9 | 32.8 | 31.1 | 31.2 |
| [256,1] [4,1] | 62.5 | 53.1 | 68.8 | 84.4 | 81.3 | 87.5 | [256,1] [4,1] | 25.2 | 36.7 | 24.7 | 39.2 | 32.5 | 51.6 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 15.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
Table 15.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
| Input Type: Spectrogram (window = 104) | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) | |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | | |
| [2,2], [1,1] | 90.6 | 96.9 | 100.0 | 100.0 | 84.4 | 96.9 | [2,2], [1,1] | 49.1 | 57.3 | 58.7 | 56.8 | 59.7 | 60.9 | |
| [4,4], [1,1] | 84.4 | 90.6 | 96.9 | 96.9 | 100.0 | 100.0 | [4,4], [1,1] | 49.9 | 57.9 | 62.8 | 62.8 | 60.9 | 69.5 | |
| [6,6], [1,1] | 93.8 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | [6,6], [1,1] | 50.4 | 57.6 | 60.6 | 61.5 | 60.1 | 63.6 | |
| [8,8], [1,1] | 96.9 | 93.8 | 100.0 | 100.0 | 100.0 | 100.0 | [8,8], [1,1] | 49.6 | 57.5 | 60.8 | 66.8 | 58.5 | 69.0 | |
| Input size: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 | Input length: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 | |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | |
Table 16.
Summary of gearbox component condition in various labeled states [
4].
Table 16.
Summary of gearbox component condition in various labeled states [
4].
| | Gear | Bearing | | | | | | Shaft | |
|---|
| Case | 32T | 96T | 48T | 80T | IS:IS | ID:IS | OS:IS | IS:OS | ID:OS | OS:OS | Input | Output |
|---|
| Spur 1 | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good | Good |
| Spur 2 | Chipped | Good | Eccentric | Good | Good | Good | Good | Good | Good | Good | Good | Good |
| Spur 3 | Good | Good | Eccentric | Good | Good | Good | Good | Good | Good | Good | Good | Good |
| Spur 4 | Good | Good | Eccentric | Broken | Ball | Good | Good | Good | Good | Good | Good | Good |
| Spur 5 | Chipped | Good | Eccentric | Broken | Inner | Ball | Outer | Good | Good | Good | Good | Good |
| Spur 6 | Good | Good | Good | Broken | Inner | Ball | Outer | Good | Good | Good | Imbalance | Good |
| Spur 7 | Good | Good | Good | Good | Inner | Good | Good | Good | Good | Good | Good | Keyway Sheared |
| Spur 8 | Good | Good | Good | Good | Good | Ball | Outer | Good | Good | Good | Imbalance | Good |
Table 17.
Training and testing accuracies for various CNN architectures with no preprocessing.
Table 17.
Training and testing accuracies for various CNN architectures with no preprocessing.
| Input Type: Raw Time Series | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1], [2,1] | 41.7 | 56.3 | 54.2 | 89.6 | 100.0 | 100.0 | [4,1], [2,1] | 34.3 | 27.7 | 31.4 | 27.1 | 27.2 | 20.3 |
| [8,1], [2,1] | 45.8 | 77.1 | 83.3 | 100.0 | 100.0 | 100.0 | [8,1], [2,1] | 44.7 | 53.5 | 52.2 | 46.4 | 31.5 | 24.7 |
| [16,1], [4,1] | 39.6 | 66.7 | 79.2 | 85.4 | 95.8 | 100.0 | [16,1], [4,1] | 53.4 | 64.0 | 67.7 | 68.1 | 55.3 | 49.2 |
| [32,1], [4,1] | 68.8 | 85.4 | 81.3 | 95.8 | 100.0 | 100.0 | [32,1], [4,1] | 64.2 | 75.7 | 80.0 | 74.4 | 80.2 | 51.6 |
| [64,1], [4,1] | 72.9 | 93.8 | 85.4 | 93.8 | 100.0 | 100.0 | [64,1], [4,1] | 73.2 | 84.9 | 93.8 | 93.1 | 83.6 | 59.7 |
| [128,1], [4,1] | 77.1 | 97.9 | 97.9 | 93.8 | 100.0 | 100.0 | [128,1], [4,1] | 78.2 | 90.9 | 96.1 | 91.7 | 93.2 | 69.0 |
| [256,1], [4,1] | 89.6 | 97.9 | 100.0 | 97.9 | 100.0 | 100.0 | [256,1], [4,1] | 79.2 | 91.5 | 96.4 | 98.1 | 96.7 | 92.6 |
| Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Input length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 18.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
Table 18.
Training and testing accuracies for various CNN architectures with FFT preprocessing.
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | | | | | | Kernel Size, Stride | | | | | | |
| [4,1] [2,1] | 85.4 | 95.8 | 100.0 | 100.0 | 100.0 | 100.0 | [4,1] [2,1] | 81.3 | 94.1 | 97.5 | 99.7 | 99.9 | 100.0 |
| [8,1] [2,1] | 79.2 | 95.8 | 100.0 | 100.0 | 100.0 | 100.0 | [8,1] [2,1] | 82.3 | 95.1 | 97.9 | 99.6 | 99.8 | 100.0 |
| [16,1] [4,1] | 77.1 | 97.9 | 100.0 | 100.0 | 100.0 | 100.0 | [16,1] [4,1] | 81.4 | 93.8 | 98.6 | 99.2 | 99.0 | 99.8 |
| [32,1] [4,1] | 77.1 | 91.7 | 97.9 | 100.0 | 100.0 | 100.0 | [32,1] [4,1] | 84.4 | 95.1 | 98.3 | 99.3 | 99.5 | 99.8 |
| [64,1] [4,1] | 81.3 | 95.8 | 97.9 | 100.0 | 100.0 | 100.0 | [64,1] [4,1] | 85.6 | 96.2 | 98.8 | 99.6 | 99.7 | 99.0 |
| [128,1] [4,1] | 87.5 | 95.8 | 100.0 | 100.0 | 100.0 | 100.0 | [128,1] [4,1] | 87.3 | 96.7 | 98.9 | 99.0 | 99.0 | 99.9 |
| [256,1] [4,1] | 83.3 | 95.8 | 100.0 | 97.9 | 95.8 | 100.0 | [256,1] [4,1] | 88.4 | 97.0 | 99.1 | 98.0 | 98.0 | 99.7 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 19.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
Table 19.
Training and testing accuracies for various CNN architectures with envelope spectrum preprocessing.
| Input Type: Envelope Spectrum | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [4,1] [2,1] | 31.3 | 52.1 | 60.4 | 89.6 | 100.0 | 100.0 | [4,1] [2,1] | 20.8 | 24.9 | 28.1 | 34.3 | 43.0 | 58.6 |
| [8,1] [2,1] | 20.8 | 39.6 | 56.3 | 97.9 | 100.0 | 100.0 | [8,1] [2,1] | 21.9 | 24.6 | 27.3 | 32.5 | 40.5 | 55.6 |
| [16,1] [4,1] | 31.3 | 31.3 | 56.3 | 89.6 | 100.0 | 100.0 | [16,1] [4,1] | 21.8 | 26.2 | 29.6 | 35.8 | 46.8 | 58.8 |
| [32,1] [4,1] | 31.3 | 52.1 | 45.8 | 81.3 | 97.9 | 100.0 | [32,1] [4,1] | 22.8 | 27.3 | 29.8 | 37.0 | 46.0 | 59.1 |
| [64,1] [4,1] | 31.3 | 47.9 | 54.2 | 77.1 | 100.0 | 100.0 | [64,1] [4,1] | 22.7 | 27.1 | 30.8 | 36.3 | 46.0 | 63.0 |
| [128,1] [4,1] | 25.0 | 47.9 | 52.1 | 83.3 | 97.9 | 100.0 | [128,1] [4,1] | 21.7 | 25.8 | 30.1 | 37.8 | 45.4 | 65.4 |
| [256,1] [4,1] | 35.4 | 54.2 | 70.8 | 89.6 | 95.8 | 100.0 | [256,1] [4,1] | 19.5 | 26.0 | 29.1 | 36.6 | 46.1 | 63.3 |
| Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 | Input length: | 208 | 416 | 832 | 1248 | 2496 | 4992 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 20.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
Table 20.
Training and testing accuracies for various CNN architectures with spectrogram preprocessing.
| Input Type: Spectrogram (window = 104) | | | | | | | |
|---|
| Training Accuracy: (%) | Testing Accuracy: (%) |
|---|
| Kernel Size, Stride | | Kernel Size, Stride | |
| [2,2], [1,1] | 95.8 | 97.9 | 100.0 | 100.0 | 100.0 | 100.0 | [2,2], [1,1] | 75.9 | 87.4 | 95.8 | 96.1 | 98.4 | 97.2 |
| [4,4], [1,1] | 95.8 | 97.9 | 100.0 | 100.0 | 100.0 | 100.0 | [4,4], [1,1] | 81.7 | 92.5 | 97.3 | 98.8 | 98.6 | 99.0 |
| [6,6], [1,1] | 95.8 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | [6,6], [1,1] | 82.3 | 93.6 | 97.8 | 99.2 | 99.2 | 98.2 |
| [8,8], [1,1] | 91.7 | 97.9 | 100.0 | 100.0 | 100.0 | 100.0 | [8,8], [1,1] | 83.9 | 92.2 | 97.2 | 99.1 | 98.7 | 92.8 |
| Input size: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 | Input length: | 129 × 7 | 129 × 15 | 129 × 23 | 129 × 47 | 129 × 95 | 129 × 191 |
| Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 | Original signal length: | 416 | 832 | 1248 | 2496 | 4992 | 9984 |
Table 21.
Details of best CNNs from each case study.
Table 21.
Details of best CNNs from each case study.
| | Validation Accuracy (%) | Preprocessor | Original Signal Length | Kernel Size/Stride |
|---|
| Case Study 1 | 80.1 | Spectrogram | 832 | [6,6]/[1,1] |
| Case Study 2–part 1 | 55.8 | FFT | 9984 | [64,1]/[4,1] |
| Case Study 2–part 2 | 70.0 | None | 1248 | [128,1]/[4,1] |
| Case Study 3 | 99.2 | Spectrogram | 4992 | [6,6]/[1,1] |