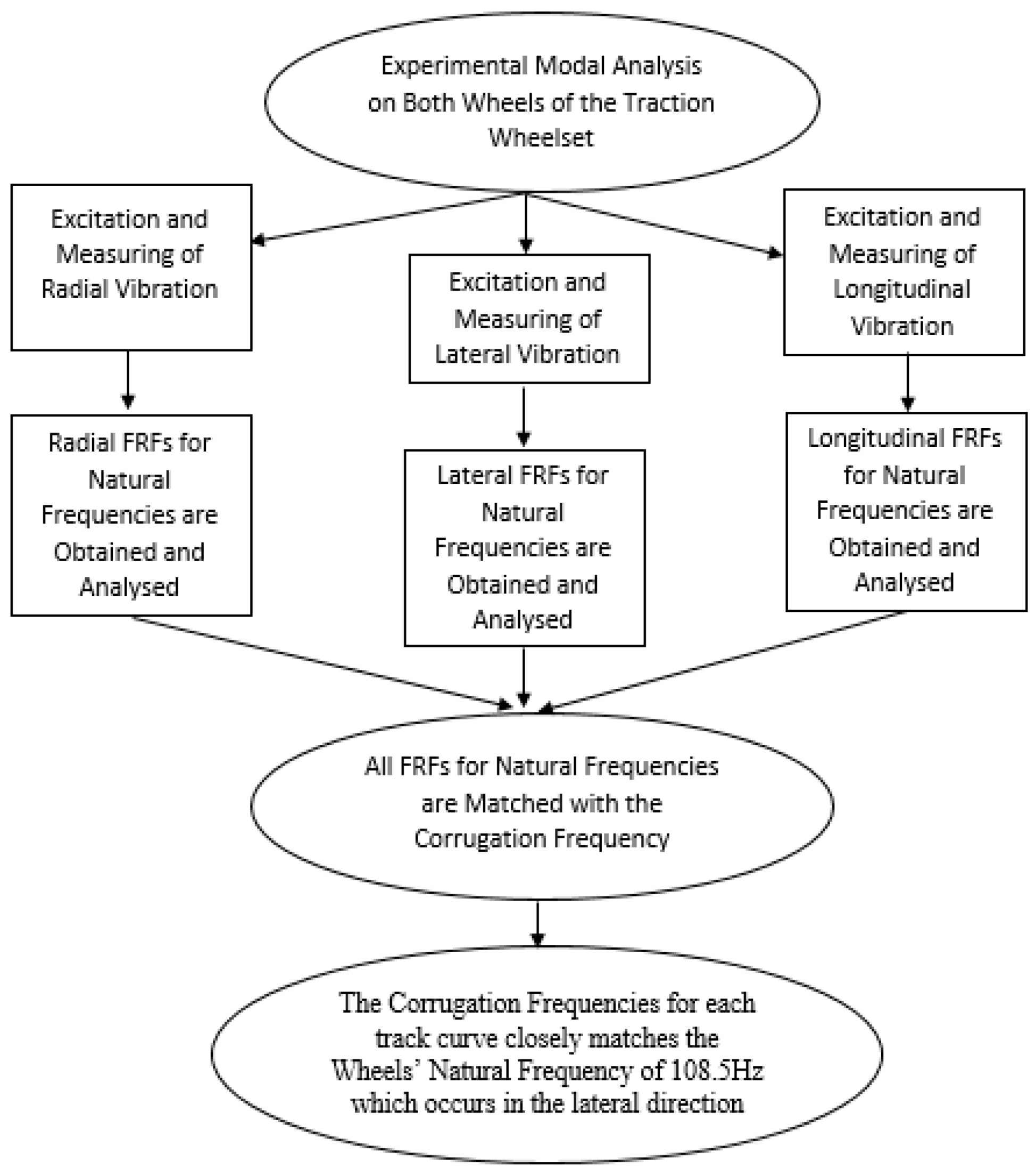
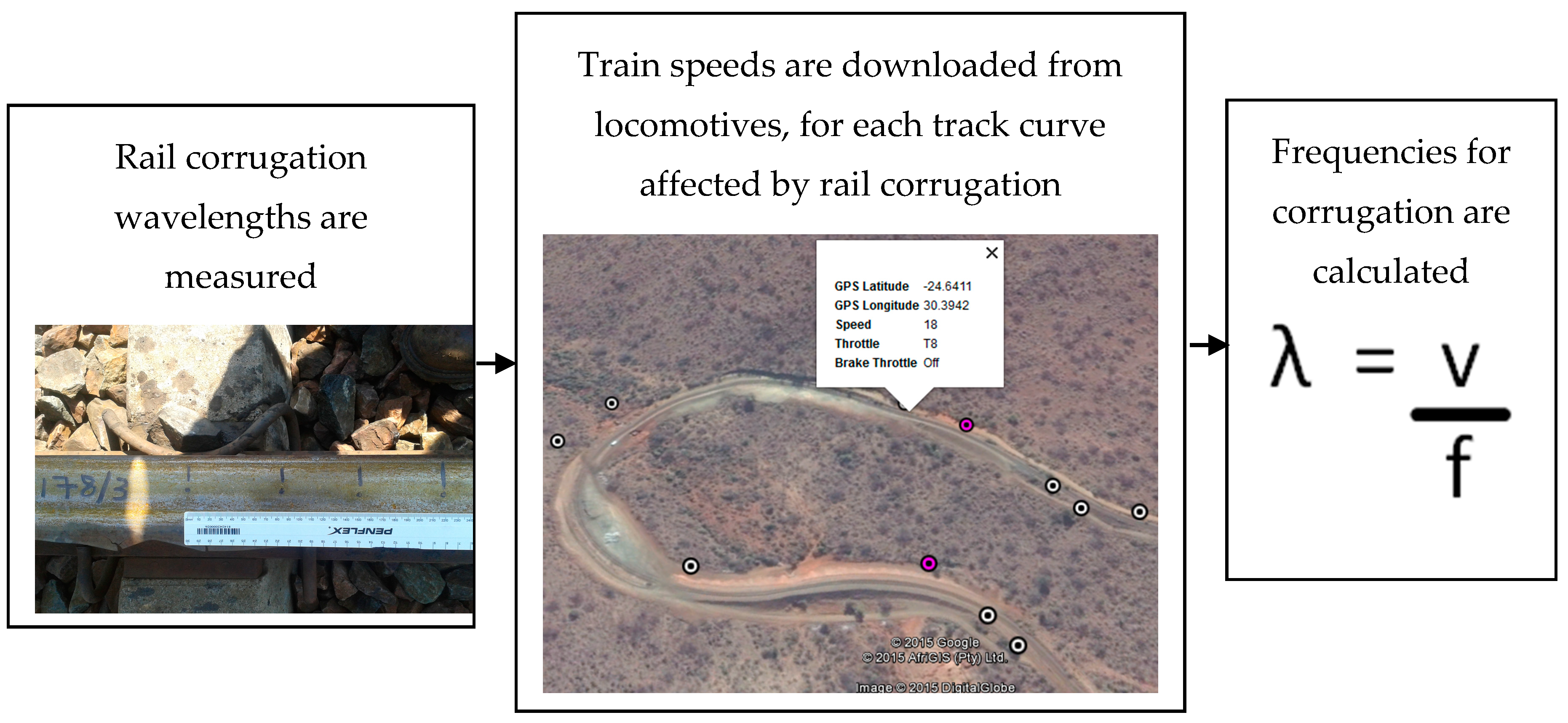
Figure 1.
Illustration of the analytical method to determine corrugation frequencies per track curve.
Figure 1.
Illustration of the analytical method to determine corrugation frequencies per track curve.
Figure 2.
(a) Modal analysis on wheel profile. (b) Suspended wheelset prepared for modal analysis. (c) Wheel profile locations where accelerometer was stuck. (d) Steel block stuck on wheel profile for circumferential excitation.
Figure 2.
(a) Modal analysis on wheel profile. (b) Suspended wheelset prepared for modal analysis. (c) Wheel profile locations where accelerometer was stuck. (d) Steel block stuck on wheel profile for circumferential excitation.
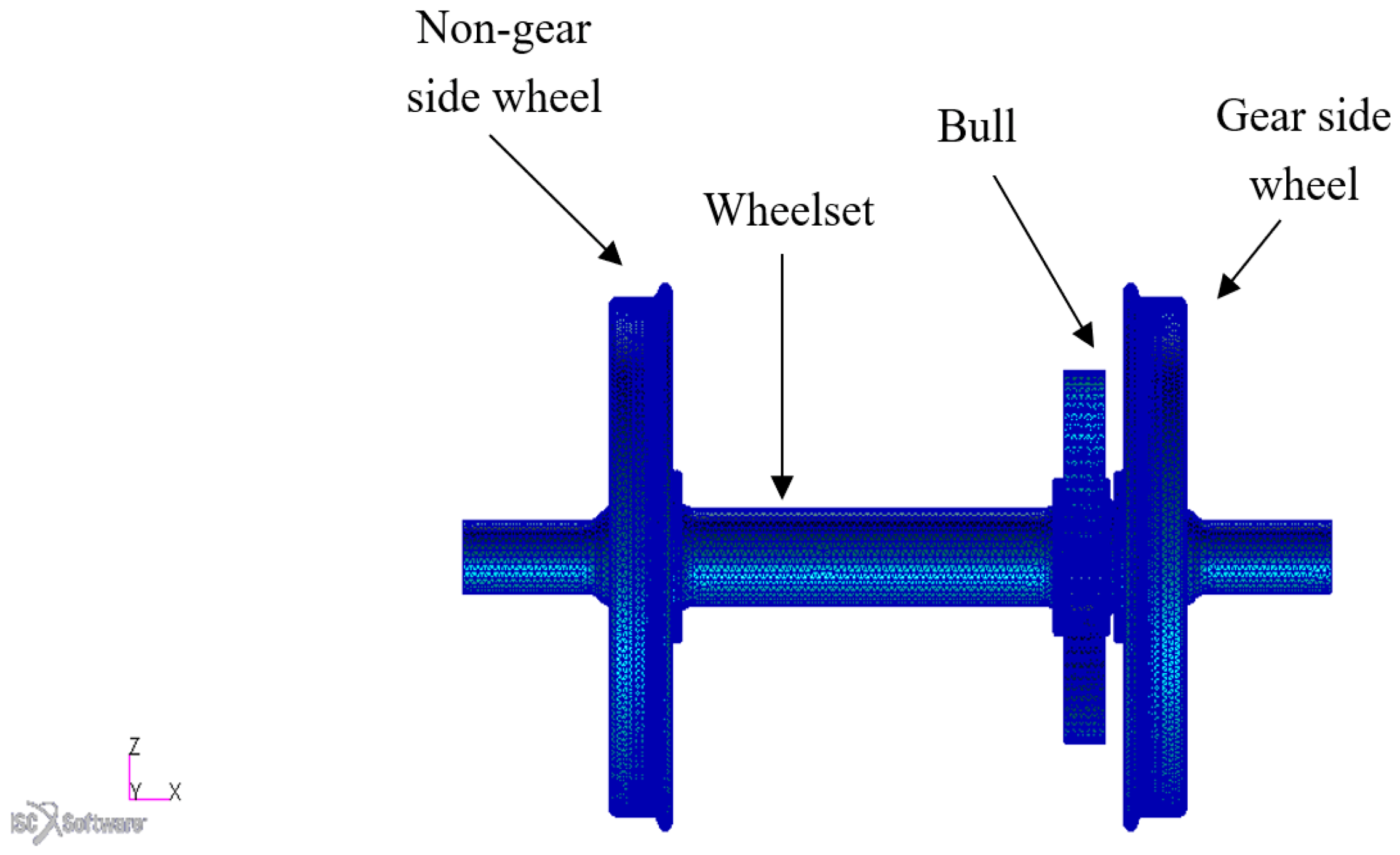
Figure 3.
Finite Element Analysis (FE)A model for a D39200 locomotive class wheelset.
Figure 3.
Finite Element Analysis (FE)A model for a D39200 locomotive class wheelset.
Figure 4.
(a) Exploded view of the FY-type concrete sleeper with a FISTclip rail fastening system. (b) assembled view of the FY-type concrete sleeper with a FISTclip rail fastening system. (c) Exploded view of the PY-type concrete sleeper with an e-clip rail fastening system. (d) Assembled view of the PY-type concrete sleeper with an e-clip rail fastening system. (e) Rail on steel sleeper with its fastening system. (f) Mid-span and on top of sleeper point rail preparation. (g) Accelerometer and impact hammer.
Figure 4.
(a) Exploded view of the FY-type concrete sleeper with a FISTclip rail fastening system. (b) assembled view of the FY-type concrete sleeper with a FISTclip rail fastening system. (c) Exploded view of the PY-type concrete sleeper with an e-clip rail fastening system. (d) Assembled view of the PY-type concrete sleeper with an e-clip rail fastening system. (e) Rail on steel sleeper with its fastening system. (f) Mid-span and on top of sleeper point rail preparation. (g) Accelerometer and impact hammer.
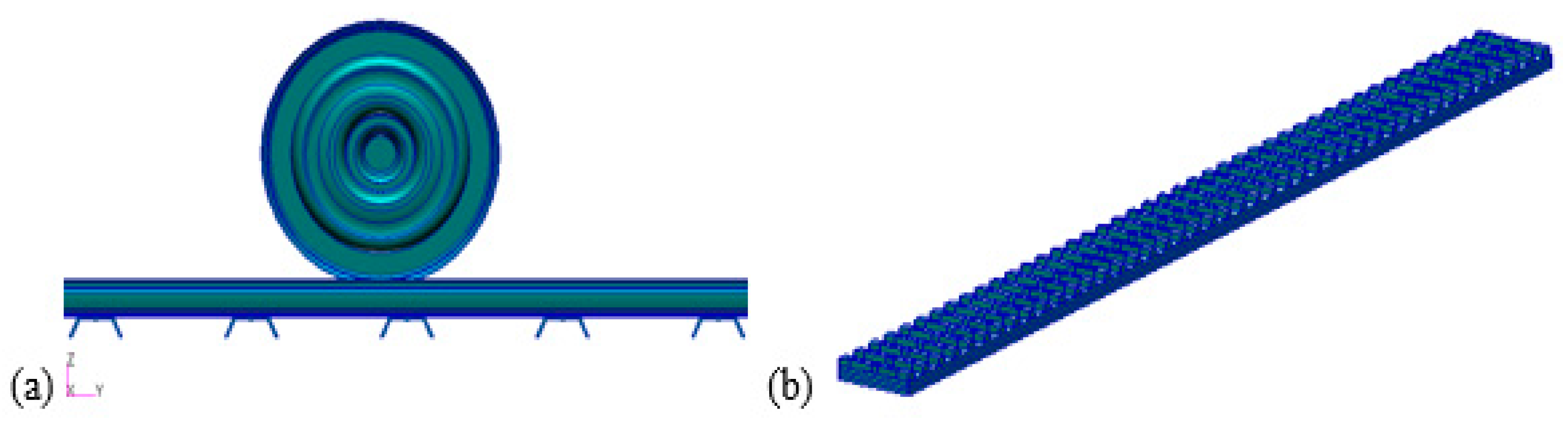
Figure 5.
(a) Rail track model with steel sleepers; (b) ballast underneath sleepers.
Figure 5.
(a) Rail track model with steel sleepers; (b) ballast underneath sleepers.
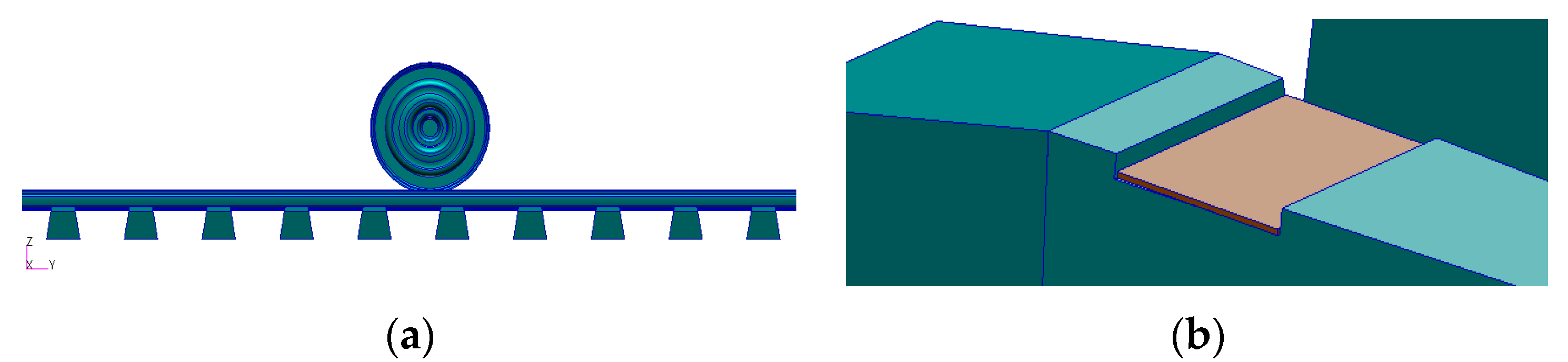
Figure 6.
Concrete sleeper track. (a) Rail track model with concrete sleepers; (b) rail pad (coloured in brown) on a concrete sleeper.
Figure 6.
Concrete sleeper track. (a) Rail track model with concrete sleepers; (b) rail pad (coloured in brown) on a concrete sleeper.
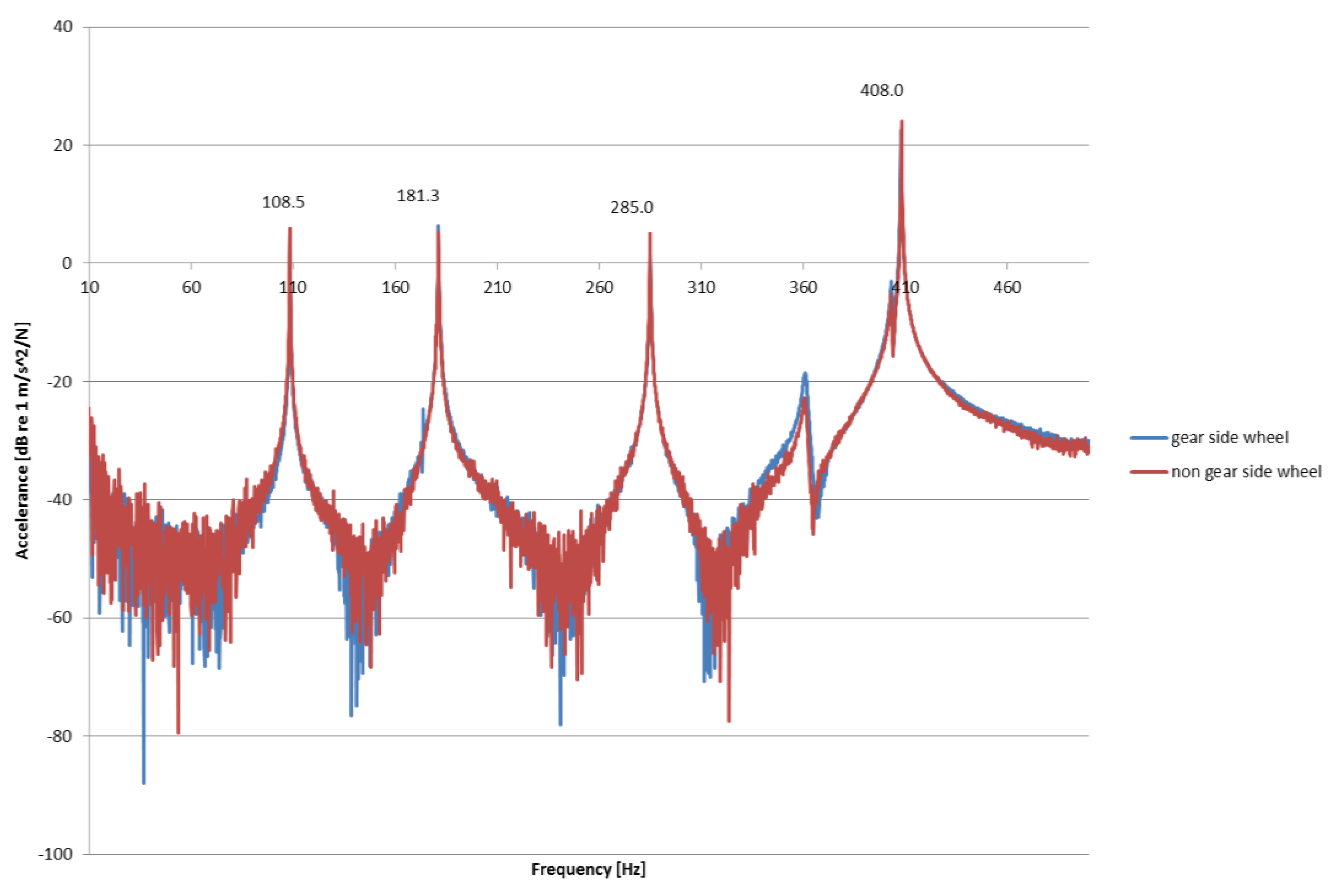
Figure 7.
Point Frequency Response Functions (FRFs) for the gear and non-gear side wheels for response of wheels in the lateral direction.
Figure 7.
Point Frequency Response Functions (FRFs) for the gear and non-gear side wheels for response of wheels in the lateral direction.
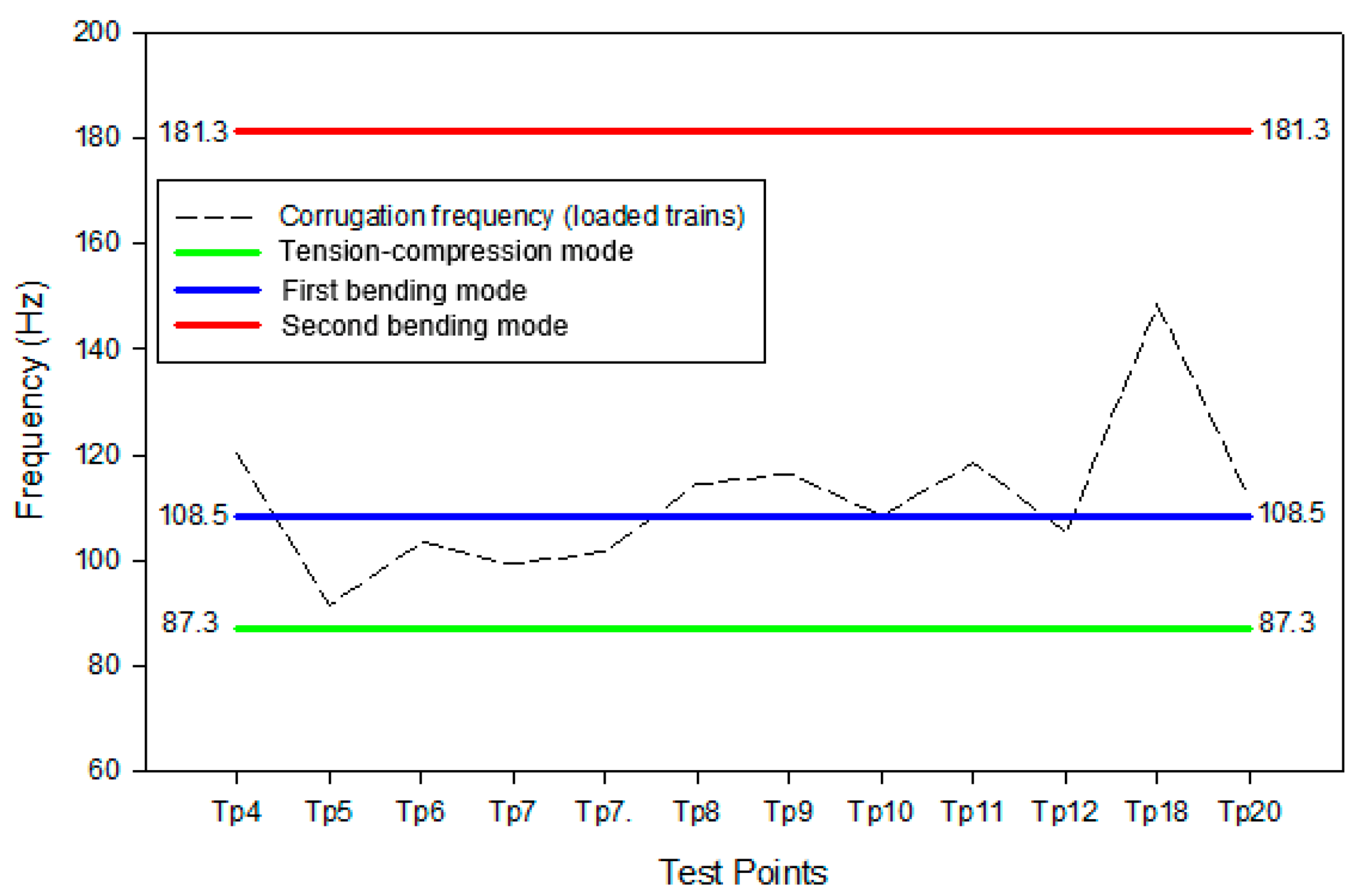
Figure 8.
Correlation of wheelset natural frequencies to corrugation frequencies for track curves.
Figure 8.
Correlation of wheelset natural frequencies to corrugation frequencies for track curves.
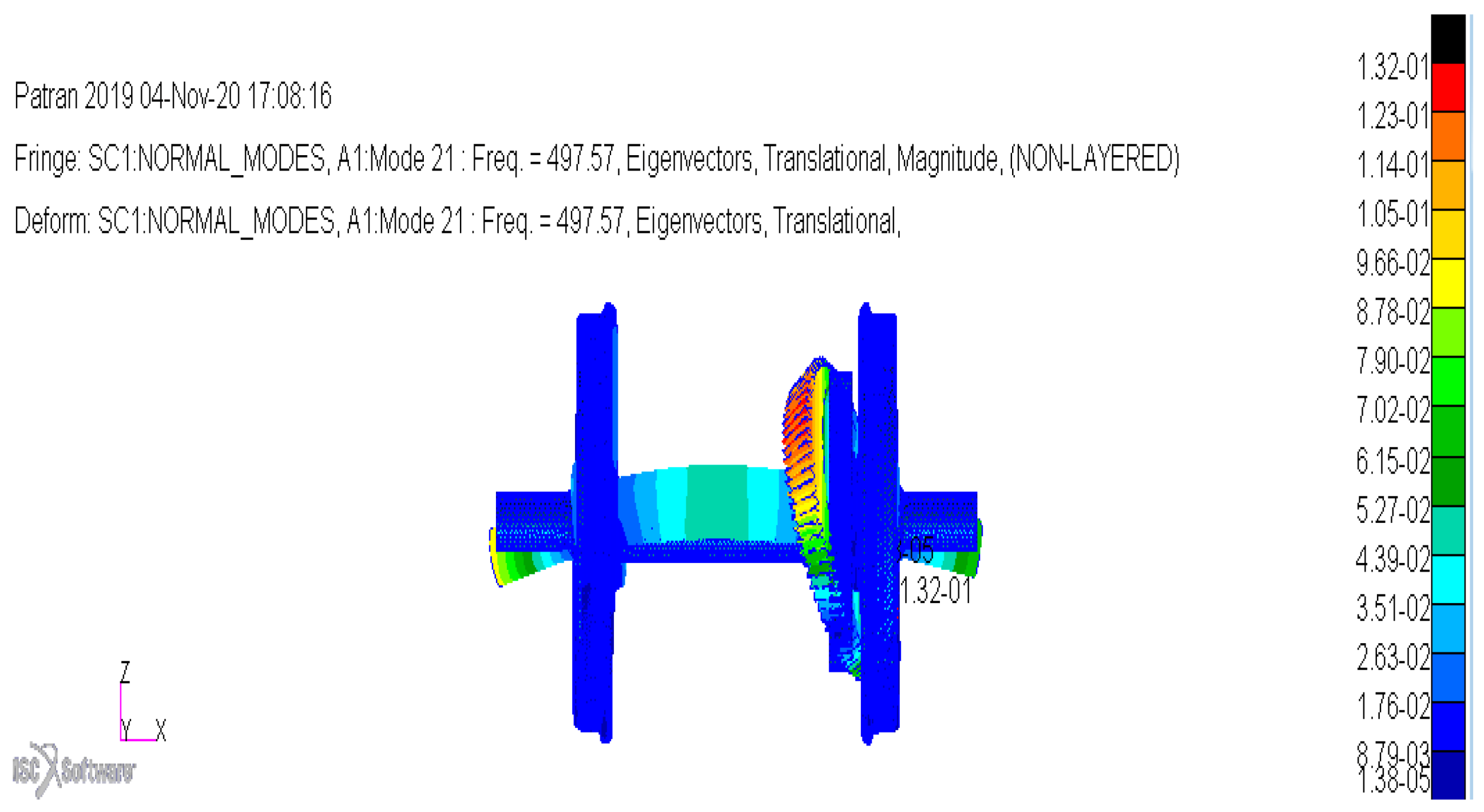
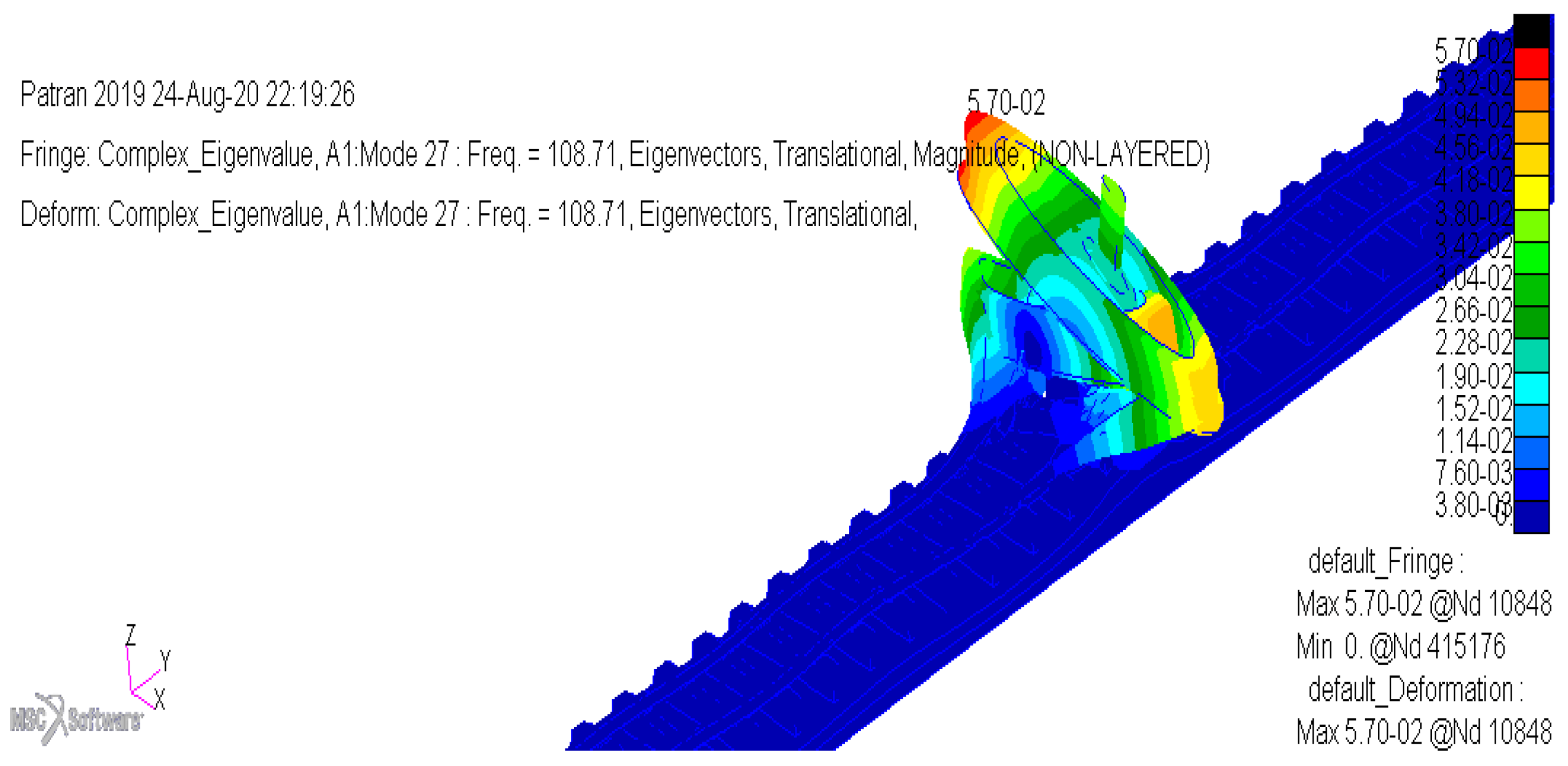
Figure 9.
D39 200 wheelset FEM results.
Figure 9.
D39 200 wheelset FEM results.
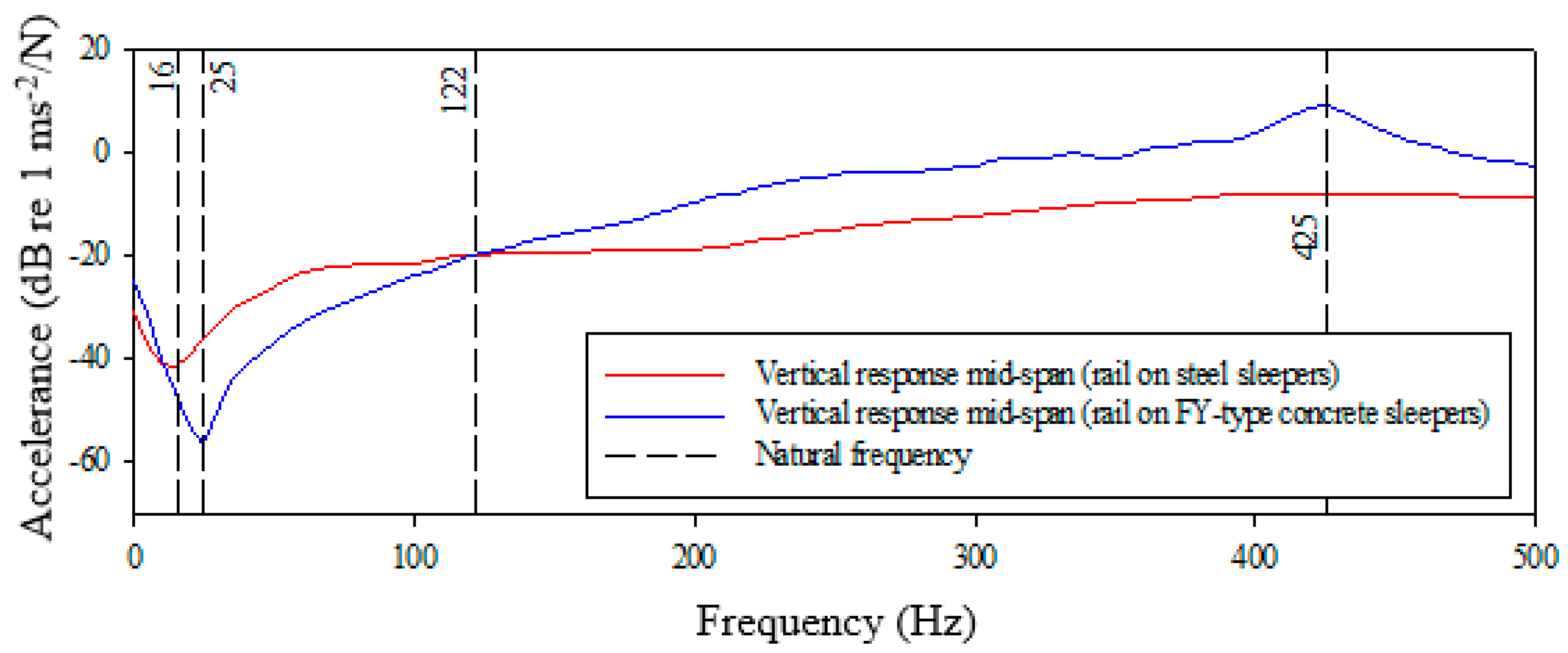
Figure 10.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the vertical direction mid-span.
Figure 10.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the vertical direction mid-span.
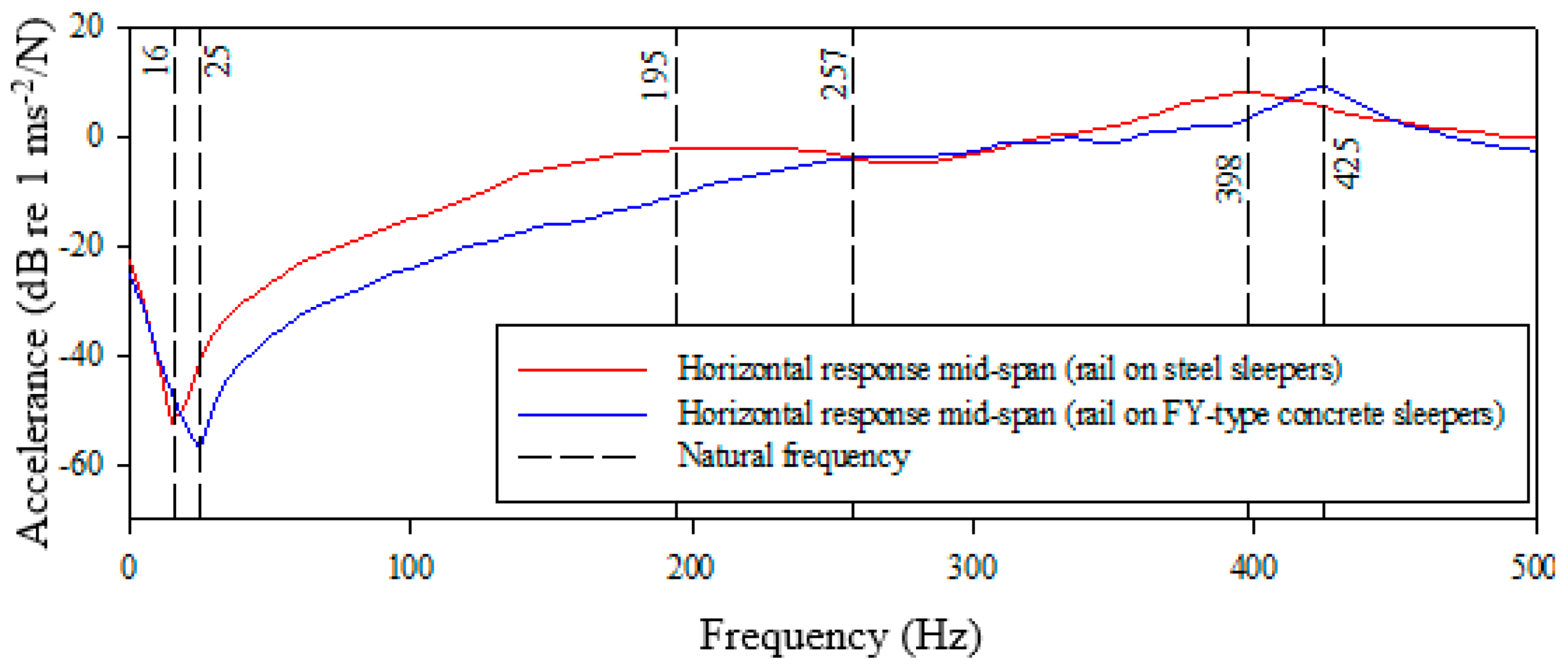
Figure 11.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the horizontal direction mid-span.
Figure 11.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the horizontal direction mid-span.
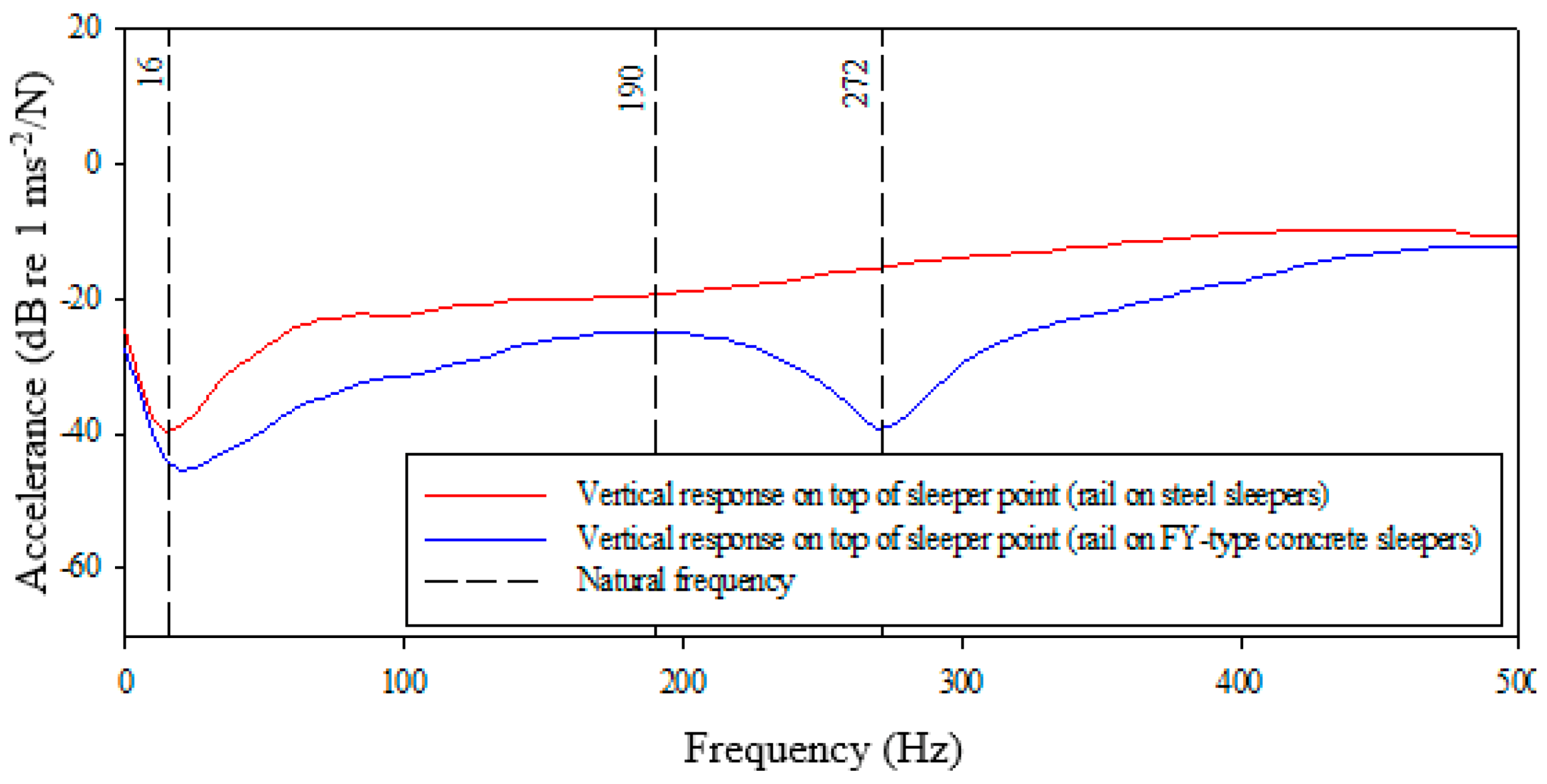
Figure 12.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the vertical direction on top of sleeper point.
Figure 12.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the vertical direction on top of sleeper point.
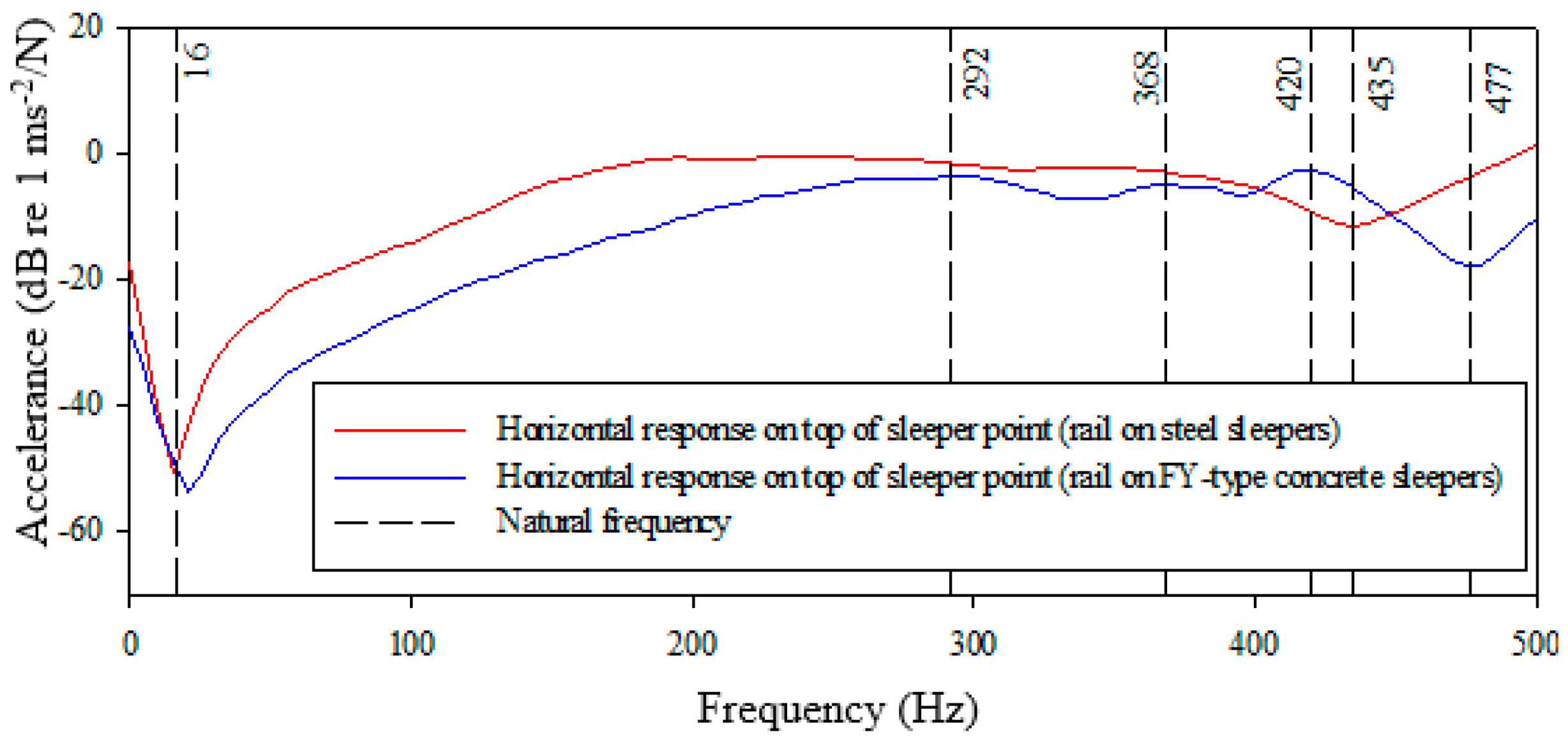
Figure 13.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the horizontal direction on top of sleeper point.
Figure 13.
Comparison of FRFs for rail vibration response, rails are laying on FY-Type concrete and on steel sleepers. Vibration measured in the horizontal direction on top of sleeper point.
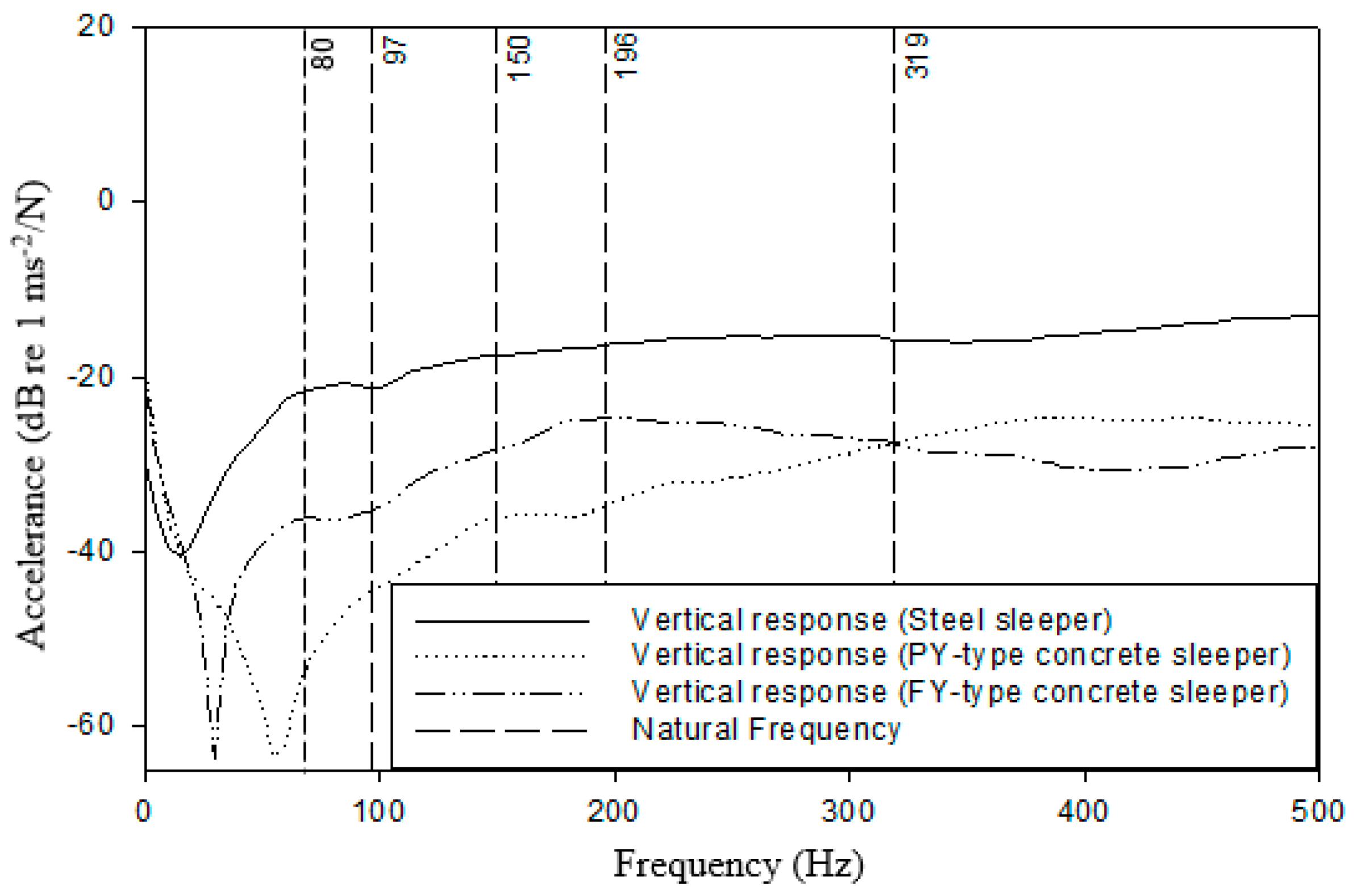
Figure 14.
Comparison of FRFs for vibration response of sleepers. Vibration measured in the vertical direction, on the top face of sleeper, by the field side of the rail.
Figure 14.
Comparison of FRFs for vibration response of sleepers. Vibration measured in the vertical direction, on the top face of sleeper, by the field side of the rail.
Figure 15.
Comparison of FRFs for vibration response of sleepers. Vibration measured in the horizontal direction, on the top face of sleeper, by the field side of the rail.
Figure 15.
Comparison of FRFs for vibration response of sleepers. Vibration measured in the horizontal direction, on the top face of sleeper, by the field side of the rail.
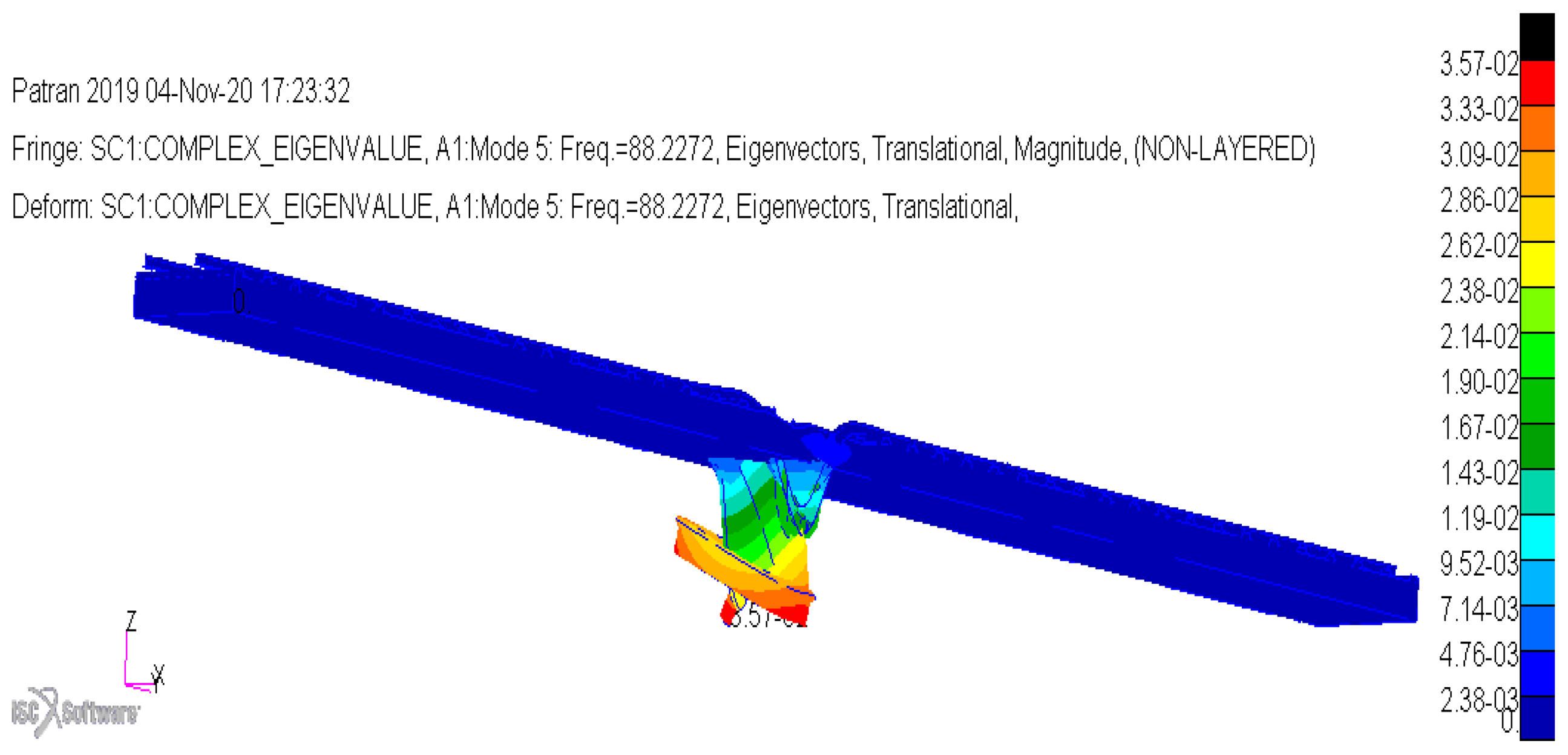
Figure 16.
Bending mode for rail track with steel sleepers and ballast.
Figure 16.
Bending mode for rail track with steel sleepers and ballast.
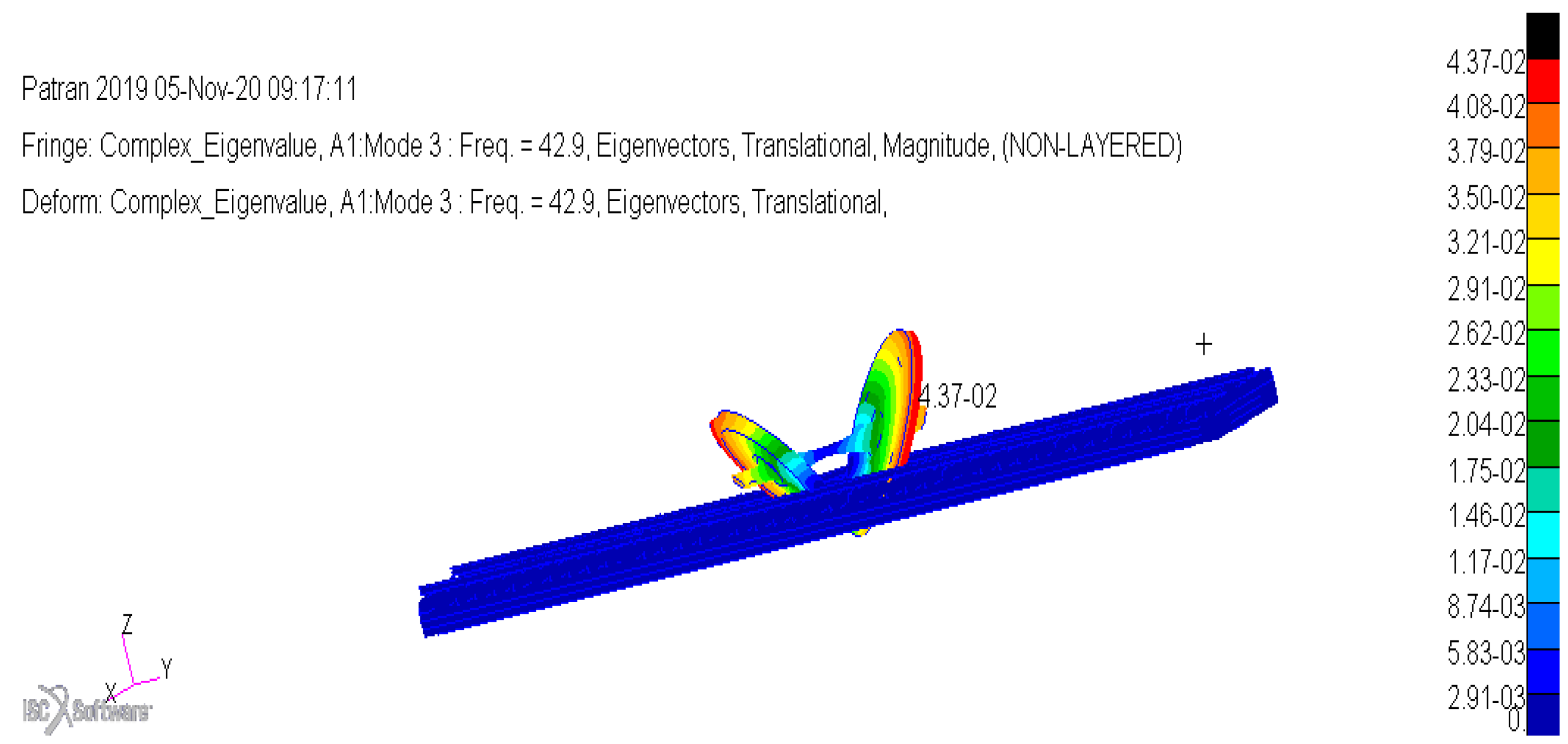
Figure 17.
Bending mode for rail track with steel sleepers, no ballast.
Figure 17.
Bending mode for rail track with steel sleepers, no ballast.
Figure 18.
Bending mode for rail track with concrete sleepers.
Figure 18.
Bending mode for rail track with concrete sleepers.
Table 1.
Mesh details for wheelset FEM.
Table 1.
Mesh details for wheelset FEM.
| Mesh Item | Mesh Details |
|---|
| Mesh type | Solid |
| Element type | Tetrahedron |
| Mesher | TetMesh |
| Topology | Tet 10 |
Table 2.
Mesh convergence for wheelset model.
Table 2.
Mesh convergence for wheelset model.
| Element Global Edge Length (mm) | Number of Nodes | Maximum Displacement (mm) |
|---|
| 250 | 48,188 | 42.3 |
| 50 | 182,346 | 43.8 |
| 10 | 763,491 | 54.7 |
| 5 | 823,157 | 57.3 |
| 4 | 834,568 | 57.7 |
| 3.5 | 869,498 | 58.1 |
| 3 | 905,567 | 58.1 |
Table 3.
Material properties of the FEA model.
Table 3.
Material properties of the FEA model.
| Material | Young’s Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio |
|---|
| Steel | 210 | 7850 | 0.3 |
Table 4.
Mesh details for rail track FEM with steel sleepers.
Table 4.
Mesh details for rail track FEM with steel sleepers.
| Mesh Item | Mesh Details |
|---|
| Mesh type | Solid |
| Element type | Tetrahedron |
| Mesher | TetMesh |
| Topology | Tet 10 |
Table 5.
Mesh convergence for the rail FEM in the rail track model with steel sleepers.
Table 5.
Mesh convergence for the rail FEM in the rail track model with steel sleepers.
| Element Global Edge Length (mm) | Number of Nodes | Maximum Displacement (mm) |
|---|
| 170 | 68,156 | 7.8 |
| 50 | 134,872 | 10.9 |
| 30 | 202,658 | 11.6 |
| 10 | 327,956 | 12.9 |
| 5 | 449,676 | 13.7 |
| 4.5 | 449,853 | 14.4 |
| 4 | 449,981 | 14.4 |
Table 6.
Material properties for FEMs on rail track model with steel sleepers.
Table 6.
Material properties for FEMs on rail track model with steel sleepers.
| FEM Solid | Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Shear Modulus (GPa) |
|---|
| Axle | Steel | 7850 | 210 | 0.3 | |
| Wheel | Steel | 7850 | 210 | 0.3 | |
| Rail | Steel | 7800 | 210 | 0.3 | |
| Sleeper | Steel | 7870 | 205 | 0.29 | 80 |
Table 7.
Mesh details for rail track FEM with steel sleepers.
Table 7.
Mesh details for rail track FEM with steel sleepers.
| Mesh Item | Mesh Details |
|---|
| Mesh type | Solid |
| Element type | Tetrahedron |
| Mesher | TetMesh |
| Topology | Tet 10 |
Table 8.
Material properties for ballast FEM.
Table 8.
Material properties for ballast FEM.
| FEM Solid | Material | Density (kg/m3) | Young’s Modulus (MPa) | Poisson’s Ratio | Structural Damping |
|---|
| Top layer ballast | Stones | 2500 | 256 | 0.2 | 0.01 |
| Middle layer ballast | Stones | 2600 | 276 | 0.2 | 0.01 |
| Bottom layer ballast | Stones | 2700 | 300 | 0.2 | 0.01 |
Table 9.
Contacts, loads and boundary conditions for rail track model on steel sleepers.
Table 9.
Contacts, loads and boundary conditions for rail track model on steel sleepers.
| Geometry (In Contact) | Geometry (In Contact with) | Contact | Fix Translation | Fix Rotation |
|---|
| Top layer ballast | Middle layer ballast | Glue | | |
| Middle layer ballast | Bottom layer ballast | Glue |
| Bottom layer ballast | 0, 0, 0 | 0, 0, 0 |
Table 10.
Material properties for FEMs on rail track model with concrete sleepers.
Table 10.
Material properties for FEMs on rail track model with concrete sleepers.
| FEM Solid | Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|
| Axle | Steel | 7850 | 210 | 0.3 |
| Wheel | Steel | 7850 | 210 | 0.3 |
| Rail | Steel | 7800 | 210 | 0.3 |
| Pad | Rubber | 1300 | 0.08 | 0.45 |
| Sleeper | Concrete | 2400 | 36.406 | 0.2 |
Table 11.
Mesh convergence for the rail FEM in the rail track model with concrete sleepers.
Table 11.
Mesh convergence for the rail FEM in the rail track model with concrete sleepers.
| Element Global Edge Length (mm) | Number of Nodes | Maximum Displacement (mm) |
|---|
| 190 | 73,224 | 16.4 |
| 50 | 151,421 | 23.1 |
| 30 | 223,687 | 28.6 |
| 10 | 346,872 | 34.2 |
| 5 | 483,277 | 51.8 |
| 4.5 | 572,183 | 57.6 |
| 4 | 581,186 | 57.0 |
Table 12.
Calculated corrugation frequencies per track curve.
Table 12.
Calculated corrugation frequencies per track curve.
| Corrugation Frequencies Per Track Curve |
|---|
| Test Point | Track Kilometer Point | Average Wavelength (m) | Average Loaded Trains’ Speeds (m/s) | Average Empty Trains’ Speeds (m/s) | Corrugation Frequency Associated with Loaded Trains (Hz) | Corrugation Frequency Associated with Empty Trains (Hz) |
|---|
| 4 | 165/8 | 0.09 | 10.83 | 13.33 | 120.37 | 148.15 |
| 5 | 169/3 | 0.082 | 7.5 | 10 | 91.46 | 121.95 |
| 6 | 172/14 | 0.086 | 8.89 | 10.56 | 103.36 | 122.74 |
| 7 | 178/3 | 0.084 | 8.33 | 10.83 | 99.21 | 128.97 |
| 7 | 178/3 | 0.082 | 8.33 | 10.83 | 101.63 | 132.11 |
| 8 | 181/13 | 0.068 | 7.78 | 11.39 | 114.38 | 167.48 |
| 9 | 183/3 | 0.074 | 8.61 | 10.28 | 116.37 | 138.89 |
| 10 | 183/7 | 0.082 | 8.89 | 7.78 | 108.4 | 94.85 |
| 11 | 184/4 | 0.068 | 8.06 | 9.17 | 118.46 | 134.8 |
| 12 | 184/13 | 0.082 | 8.61 | 8.06 | 105.01 | 98.24 |
| 18 | 215/15 | 0.058 | 8.61 | 9.17 | 148.47 | 158.05 |
| 20 | 216/18 | 0.077 | 8.61 | 9.17 | 111.83 | 119.05 |
Table 13.
Difference between experimental and FEA frequencies for first bending mode.
Table 13.
Difference between experimental and FEA frequencies for first bending mode.
| Firs Bending Mode Experimental Frequency (Hz). | First Bending Mode FEA Frequency (Hz). | Difference in Frequencies (Hz) | Percentage Error (%) |
|---|
| 108.5 | 100.68 | 7.82 | 7.77 |