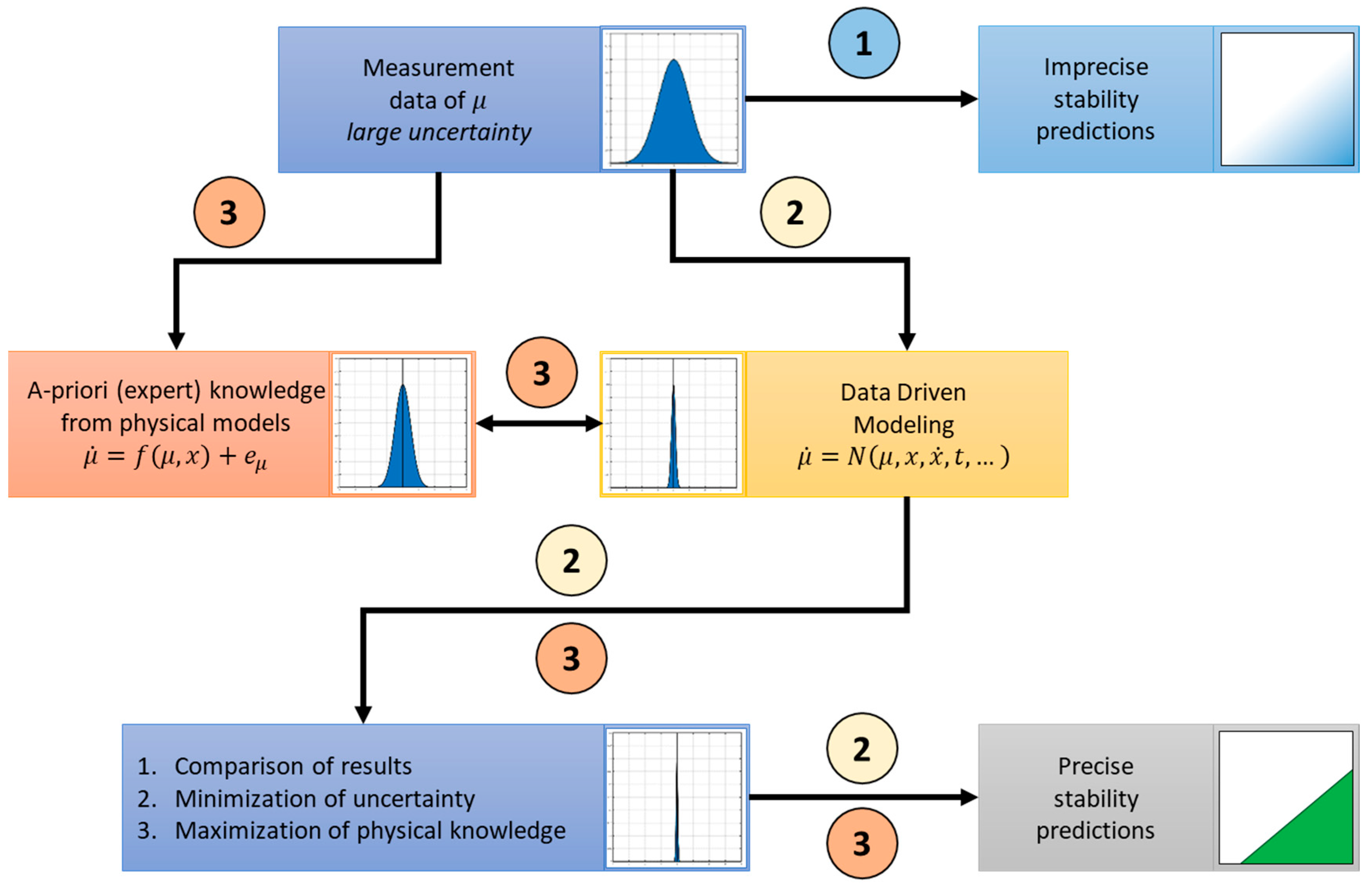
In this paper, models with polymorphic uncertainty are applied to a minimal model for instabilities of NVH phenomena. In the following subsections, the system to be investigated and the inclusion of the measurement data are presented.
2.1. The Method of Augmented Dimensioning
Concerning the brake dynamics in this study, the friction is not only treated as one uncertain parameter, but also as a dynamic system variable incorporated as a differential equation (also see
Section 1.2 and
Section 2.2). Here, the authors follow the new concept where the system state space is expanded by the dynamic state variables representing the friction, the so-called Method of Augmented Dimensioning (MAD) [
26]. The MAD considers the system as a coupled system of brake dynamics and friction dynamics. The stability of this coupled system is different compared to the single uncoupled brake dynamics. With
and
, the general form of this coupled system can be written for an eigenvalue analysis (where only the homogenous part is necessary), as follows:
where the first line in Equation (1) represents the system of the brake dynamics, while the second line represents the friction dynamics, and
describes the mechanical degrees of freedom. Similarly,
represents the degrees of freedom for the friction system and its time-derivative
takes into account the existence of dynamic friction behaviour. The coupling term
in the damping matrix contains the friction model with respect to the velocity dependence, such as a falling characteristic or a Stribeck-like effect. The term
combines the normal force resulting from the mechanical deformations with the COF in the contact, i.e., it primarily considers the normal force dependence of the COF. Finally, the coupling term
takes into account the friction force resulting from the COF. For all CEA calculations, the derivatives must be provided in a linearized form; for this purpose, the generally non-linear functions must be linearized at the respective equilibrium points. Further details on this method and its effects can be found in [
26].
Based on the equations in Equation (1), the CEA is performed and provides eigenvalues in the complex form, i.e., , where is the real part and is the imaginary part of the jth eigenvalues.
The sign of the real part eigenvalues is the well-known criterion for the stability evaluation of the investigated system. If any of the eigenvalues’ real parts are positive, the system is unstable, corresponding to increasing oscillation amplitudes. Only if all real parts are negative is this a stable system with decaying oscillating amplitudes. The imaginary part depicts the corresponding frequency, whereas the corresponding eigenvector represents the oscillation’s shape. The CEA computations are performed by using the polynomial eigenvalues solver in MATLAB R2017b.
2.2. Eigenvalue Analysis with an NVH Minimal Model for Brakes
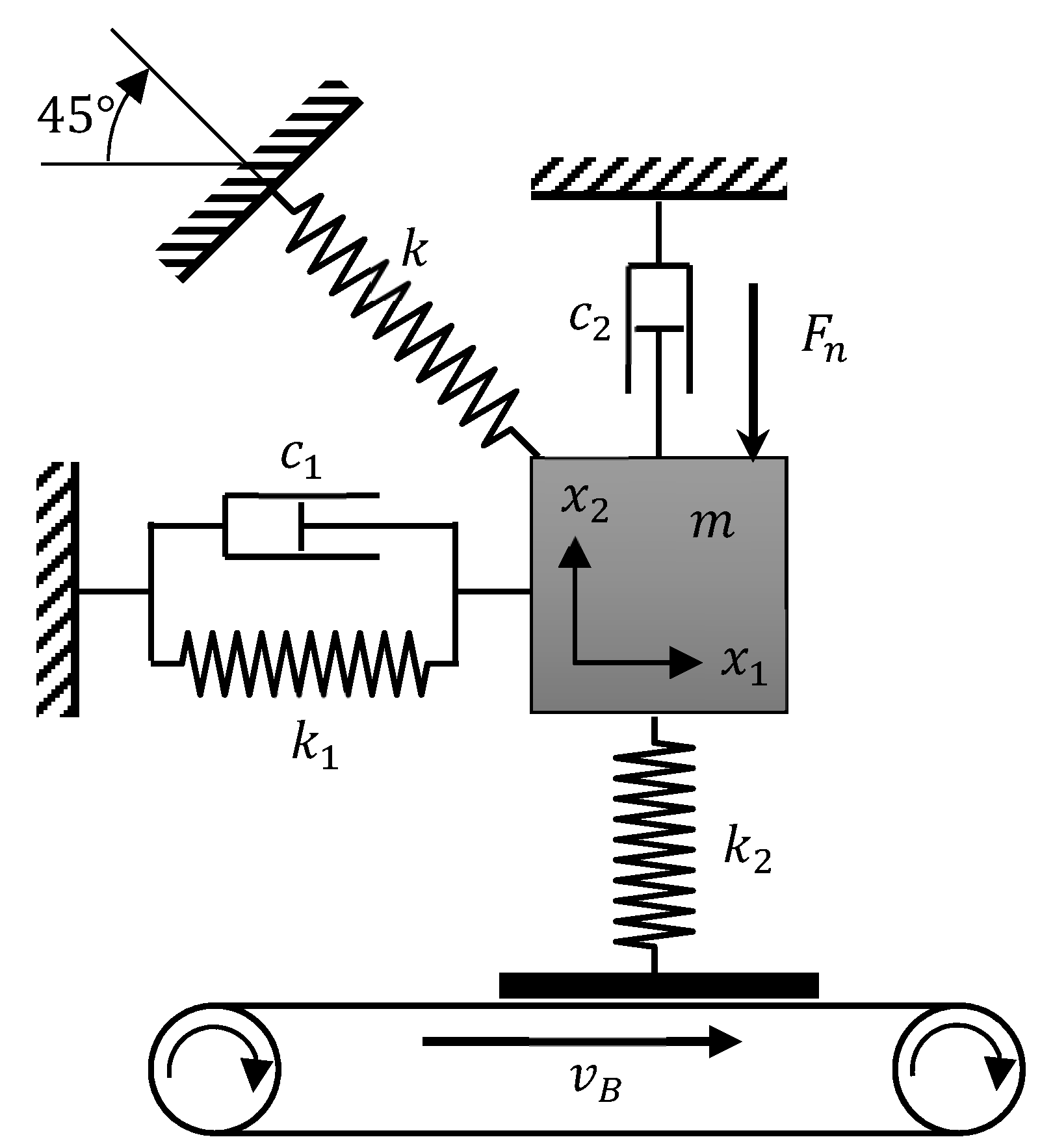
In the present study, the primary goal is to incorporate uncertainty models for friction into eigenvalue questions. For this reason, these first studies are carried out on a minimal model for NVH phenomena in brake systems. For this purpose, the well-established model originally introduced by Hamabe [
27] and further developed by Hoffmann et al., [
11,
12] with two degrees of freedom that is shown in
Figure 3 is used.
The conceptual model concerns a single mass sliding on a rotational belt. This mass is supported by a spring with a stiffness in the parallel direction to the belt surface and a spring with stiffness , which accounts for the physical contact stiffness of the object’s mass and sliding surface. These springs are accompanied by the dampers c1 and c2, respectively. An additional spring acts at an angle of relative to the horizontal line. This spring with the stiffness represents the elasticity of the brake pad and brake disk and supports the occurrence of mode-coupling instabilities. The normal force acts downwards and causes a force resisting the motion of the mass in the horizontal direction (the friction force ), so that the COF can be computed according to .
The paper’s objective is to evaluate the quality of the conclusions on stability, including a priori knowledge by using uncertainty modeling techniques for the friction. For this purpose, two different hypotheses are used to describe the COF:
● Hypothesis 1: Coulomb friction model
This hypothesis represents the most common and simplest friction model that practically does not include any expert knowledge.
● Hypothesis 2: Ostermeyer friction model [
1,
21]
where
is the contact temperature,
is the normal force,
is the relative velocity, and (
are the corresponding system parameters. This model was developed especially for brake systems, is based on measurements and theories, and therefore contains a very high degree of expert knowledge.
According to Equation (1), the NVH minimal model described above [
11], and the extended formulations by the MAD, the governing equations for the coupled system incorporating the Coulomb friction model can be written as follows [
26]:
where
is the friction force, and the stiffness matrix entries are
,
, and
.
In this study, all the corresponding parameters are selected and assumed to be invariable, except for the COF, which is considered as a variable parameter in the CEA. The constant parameter values are defined as follows:
. These values are based on the (also roughly estimated) values from [
11], whereby
and
have been adjusted for the present study in order to illustrate the uncertainty effects more clearly.
For the case of the coupled NVH model with the Ostermeyer friction model (hypothesis 2), the equations of motion for the coupled system read [
26,
28]:
with the terms
These also include the parameters (
) corresponding to the stationary solution, i.e., the equilibrium point at which the system is linearized. These terms read as follows:
Since the Coulomb friction model is a 0th order differential equation and the Ostermeyer model is a 2nd order differential equation, the latter obviously results in two more eigenvalues. In addition, the existing eigenvalues shift, especially with the increasing influence of the friction dynamics. Equations (4) and (5) serve as the basis for the eigenvalue analyses for all further investigations found in
Section 3.
2.3. Data Modeling
The following subsection documents the COF measurement data obtained for the studies and their exploitation for uncertainty studies.
2.3.1. Considered Data Set
In the present case, the COF characteristic is performed on an automated tribometer, the so-called Automated Universal Tribotester (AUT), available at the Institute of Dynamics and Vibrations at Braunschweig University of Technology [
29], (see
Figure 4). These are measurements in which a 2 cm² (height: 2 cm (tangential to sliding velocity), width: 1 cm (perpendicular to sliding velocity)) part of the pad material (pin) is pressed against a rotating disk. Here, the forces in the pin and the temperature of the disk near the contact are measured. The COF is calculated from the ratio of tangential force to normal force.
The normal force and rotational speed are specified for each application. This specification is made according to a certain scheme in which the frictional power is increased successively from application to application. This results in a procedure consisting of a total of 461 applications. These two controlled variables are also measured during the application, whereby, in [
29], it has been demonstrated that the automation can very well maintain these specified values over the entire procedure.
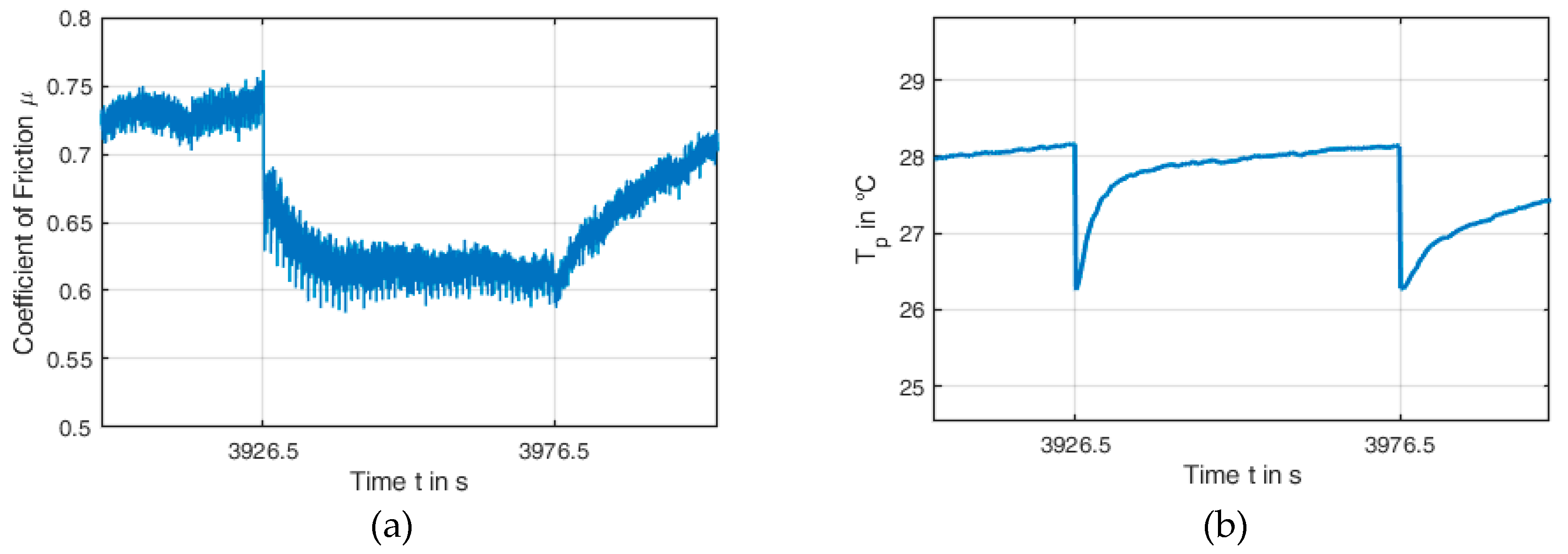
Much greater variation during an application can be observed for the COF and the temperature.
Figure 5 shows the corresponding values at application 78 as an example of this.
Application #77 ends at t = 3926.5 s, application #78 lasts from t = 3926.5 s to t = 3976.5 s, and from t = 3976.5 s, application #79 begins. An application takes about 50 seconds; at a sampling rate of 100 Hz, this corresponds to 5000 samples per application. These curves already clearly show that both the COF and the temperature within an application and also from application to application can change considerably.
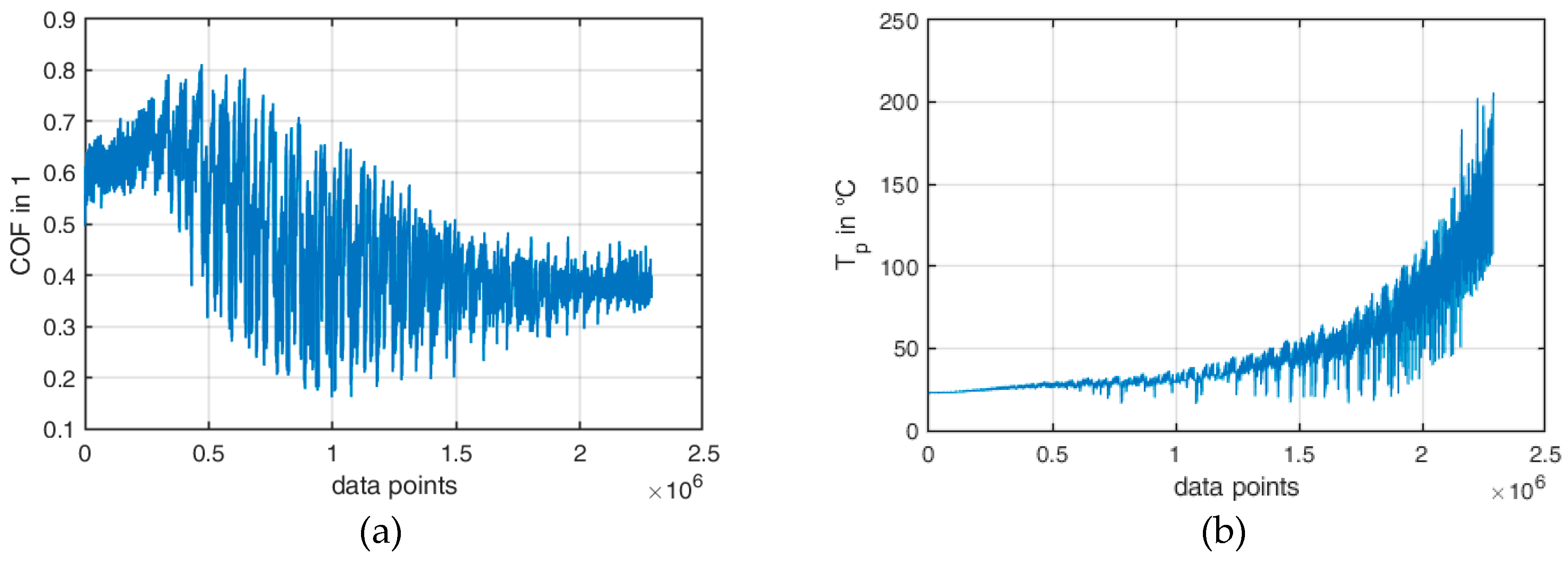
Figure 6 shows the measured values for the entire procedure (461 applications), plotted over the data point number (the total number of samples is approximately 2.3 million).
For this project, these data were reprocessed and prepared for the identification of friction models and their uncertainty quantifications. The applied techniques for this step are briefly summarized in the following section.
2.3.2. Model Identification via Data Driven Methods
The friction measurement curves presented in the previous section are to be implemented in the form of differential equations. In recent years, Data Driven Methods (DDM) [
30,
31] have become firmly established for this purpose. In principle, they are capable of extracting such functional relationships from measurement data. This methodology will also be used in the context of this study. Special attention must be paid to the fact that these methods could also identify mathematical artifacts instead of physical models, which is disadvantageous for the understanding of the system [
32]. The corresponding backgrounds and mathematical approaches are explained below.
This model identification method refers to the research field of Machine Learning (ML) and has recently been the focus in different fields of applications.
In the present work, the DDM chosen by the authors is based on optimization with sparse regression techniques [
30], which is applicable to identifying Ordinary Differential Equations or even Partial Differential Equations. The governing equations for complex physical systems are oftentimes unknown or only partially known, due to, e.g., nonlinearities, unknown parameter dependencies, coupled multiphysics, or multiscale phenomena, etc.
The starting point for the model identification is the very general formulation of a physical model in the following form:
where the left hand side of Equation (18) is the time derivative of a variable (u), and the right hand side contains the function
which can represent various linear and nonlinear terms, as well as operators (such as spatial derivatives) and corresponding parameters
. The main objective of DDM is to identify
when only time series of measurement data representing the system are available.
To determine the
terms, a library
of all possible candidate terms and the time derivative of measurement data
will be evaluated directly from the collected data. The correlation between
and
can be formulated according to [
30]
where
contains the coefficients associated with the candidate terms. In Equation (19), the time derivative vector
is a column vector with the length
, where
is the number of measured state variables and
is the number of collected time steps. Similarly, for the library
, the matrix has the dimension of
columns and
rows, where
equals the number of candidate terms:
Typically, Equation (20) can be solved for
by means of a least square optimizer. Without further conditionings, however, it is difficult to realize a proper solution, as
will be full of non-zero terms. To avoid this effect, it is the aim to keep
sparse, with only a few non-zero terms. For this purpose, the optimization process of the least square method is extended by adding the following regularization term:
where
denotes the condition number of the matrix
and
is a constant value to control the balance between the first (data fidelity term) and second term (regularization term). The regularization will force the solutions vector
to become sparse [
30]. This approach allows one to identify the dominant system-determining terms, which is not only numerically efficient, but can also be of great use for the interpretation of measurement data.
2.3.3. Tracking Information of Noisy Data via Total Variation Regularization (TVR)
In order to perform the identification of a physical model and its parameters via DDMs described in the previous section, it is very important to appropriately consider time-derivatives for values that could be influenced by noisy data (
). Let
where
contains physical information and
contains uncorrelated random noise. To calculate the derivative value of noisy data via the typical finite difference method is obviously unsuitable and might result in very large errors. Oftentimes, the methods used to calculate derivatives after denoising also do not produce satisfactory results. Therefore, regularization should take place directly in the processes of differentiation, as it can guarantee that the derivative will have a higher degree of regularity. This method, the so—called method of Total Variation Regularization (TVR), was further developed by Rick Chartrand [
33] and followed up the methods of Tikhonov [
34]. The associated ideas are briefly explained below.
The evaluation of the derivation of data
in a time interval
can be completed by minimizing the following functional:
The functional
is defined on the interval
, where
is the noisy and possibly non-smooth data,
(in this context it can be understood as an analogy to
in Equation (18)) is the required differentiation of
, and
is the first derivative of
. The usage of the TVR accomplishes two advantages. It suppresses the noise as the noise function would have a large total variation. It also does not suppress jump discontinuities, unlike the typical regularizations. This allows for the computation of discontinuous derivatives, and detection of corners and edges in noisy data [
33].
To find the minimum of the functional
, the well-known Euler-Lagrange equation is applied:
where
is the adjoint of the operator A. The approach continues with the iterative Gradient Descent procedure. In this method, it is assumed that the variation parameter
is changed along with artificial time evolution. Therefore, Equation (24) can be rewritten in the following form:
Substituting the term
with
, while
, introduces a small number for avoiding the (otherwise possible) dividing by zero:
Typically, Equation (26) can be efficiently solved with an explicit time marching scheme, discretized as
for fixed values of
, and
, where
characterizes the discretized right side term of Equation (26) at the current iteration step (n) [
33,
34].
When
is small, the convergence is rather slow, while with increasing
, divergence might occur. The optimum of
should not be greater than the inverse of the Hessian (second-order partial derivation)
of
In this case,
is replaced by
and the iteration steps are then performed according to Equation (27):
To construct and , it is firstly assumed that is defined on a uniform grid . The derivatives of are computed halfway between two grid points as centered difference ; this procedure defines the differentiation matrix . The integrals of are likewise computed halfway between two grid points, using the trapezoid rule to define matrix . Let be the diagonal matrix whose entry is , and . Then, the term becomes . The approximation of the Hessian of is derived according to: .
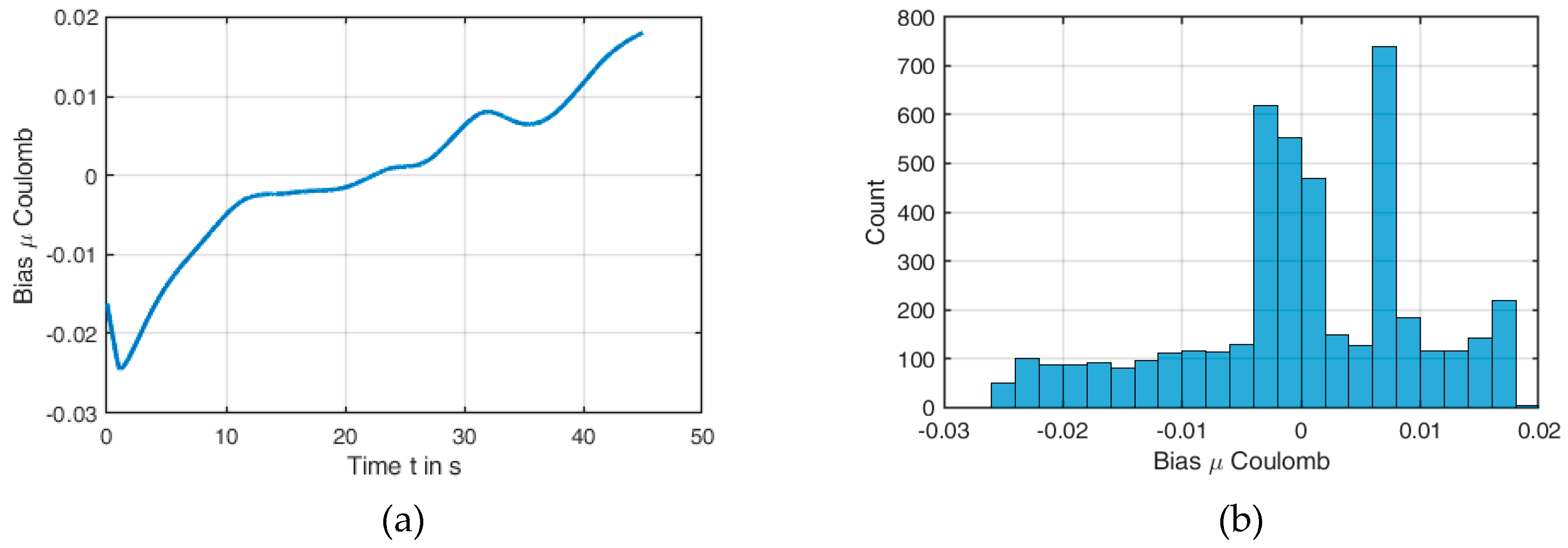
With these two methods (DDM and TVR), the measurement data of the COF and the contact temperature are processed. Especially for the signal of the COF , TVR produces a reasonable smoothing and reduces the strong noise very well.
2.4. Polymorphic Uncertainty Modeling
In general terms, uncertainty can be classified into two classes with respect to its characteristics. One is an irreducible uncertainty, namely aleatory uncertainty, which refers to the natural stochastics in system processes, e.g., the variations of manufacturing processes, material properties, geometry properties, etc. In contrast to this, uncertainty with reducible characteristics is known as epistemic uncertainty. This may refer to, i.e., the lack of knowledge (model uncertainty), lack of statistical information (statistical uncertainty), or accuracy of data (perceptual uncertainty), etc. This type of uncertainty can be significantly reduced when, e.g., better knowledge, more statistical information, or an improved measurement accuracy are available. This concept has already been applied to simple COF formulations for eigenvalue problems in brake systems [
35].
The occurrence of only one uncertainty (aleatory or epistemic) can also be referred to as monomorphic uncertainty, whereas the joint occurrence is called polymorphic uncertainty. The uncertainty quantification could be carried out based on, e.g., a probabilistic approach, a possibilistic approach, or even a combination of both techniques. In general, the probabilistic approach is used for aleatory uncertainty analysis, when the informative variation is available, e.g., in a typical stochastic process.
The possibilistic approach has proven to be an adequate description, if the range or interval of the statistical output is of particular interest or statistical data or knowledge are limited etc., so the probabilistic approach would not provide much more information [
36]. In these cases, fuzzy-like algorithms can improve the informative value of the possibilistic approach by using the fuzzy membership function instead of only a simple interval.
The transition between the usefulness of a probabilistic and possibilistic description is sometimes fluent and primarily linked to the available amount of data and knowledge. Thus, in some cases, the possibilistic approach can be replaced by the probabilistic approach. For example, when the incompleteness (statistical uncertainty) is based on a low volume of available data, the possibilistic approach is suitable. However, if more statistical data are collected, the probabilistic approach can be used instead of the possibilistic one, as more informative statistical outputs can be obtained.
For the probabilistic approach, the Monte Carlo simulation is often used. This methodology spreads a large number of sampling data over the design parameter space, and forwards them through the analysis of the model or mapping function.
The epistemic uncertainty analysis is carried out via the possibilistic approach; the fuzzy method [
37] is used in this study. The fuzzy members are defined as the convex set of fuzzy values over the universal set
). The membership function is generally defined with
and at the nominal point
, the fuzzy value is
, which represents the true value for the case of no epistemic uncertainty. The form of the membership function can be defined as the corresponding kernel, in which the distribution of epistemic (when information is available) data can be well-described. For a simplified example, the fuzzy number can be defined as a triangular kernel, for which only three points of information are required. Between these three points, a linear interpolation is carried out, as shown in Equation (28):
where
denote the minimum, nominal, and maximum point of the interval, respectively. This kernel function can take on other forms based on the characteristic information inside the interval, and more information on this aspect can be found in [
36,
37].
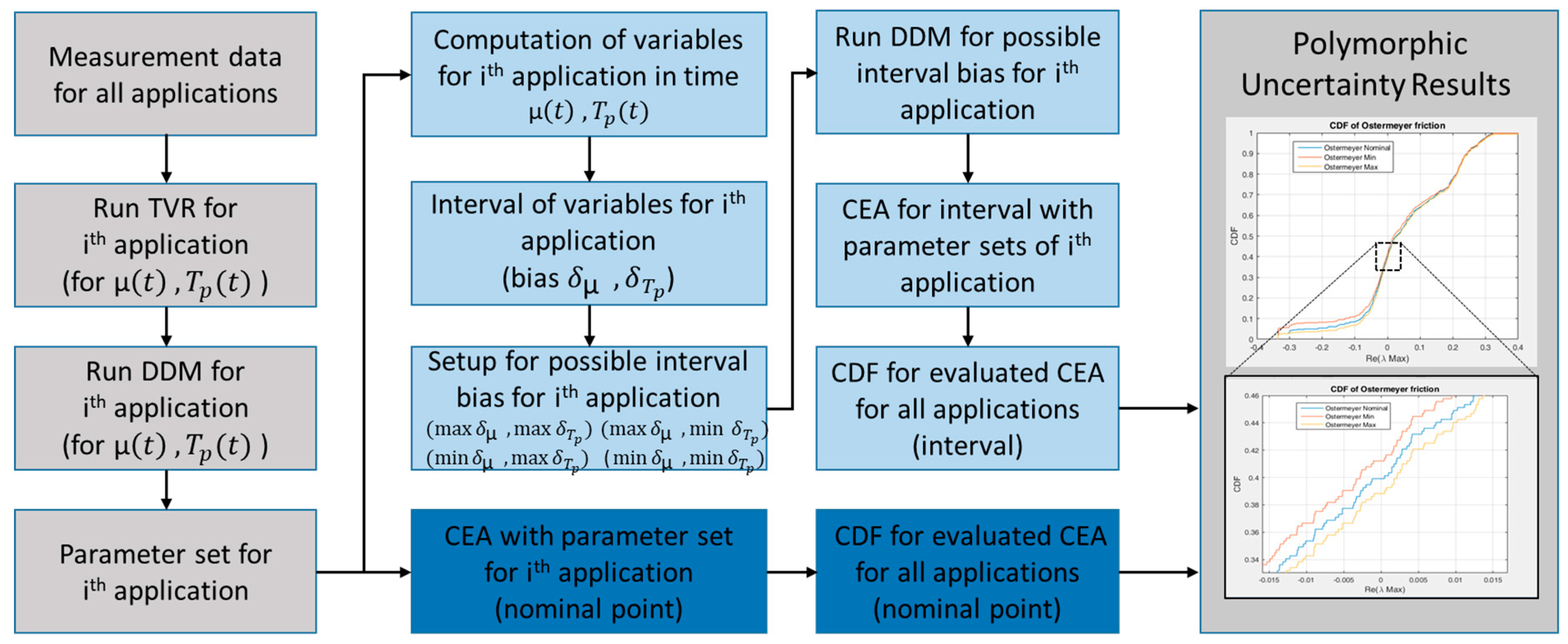
In the present study, polymorphic uncertainty modeling shall be performed. The problem to be considered is the calculation of eigenvalues, which are influenced by different forms of uncertainty. The basis of the calculations is provided by the measurement data introduced in
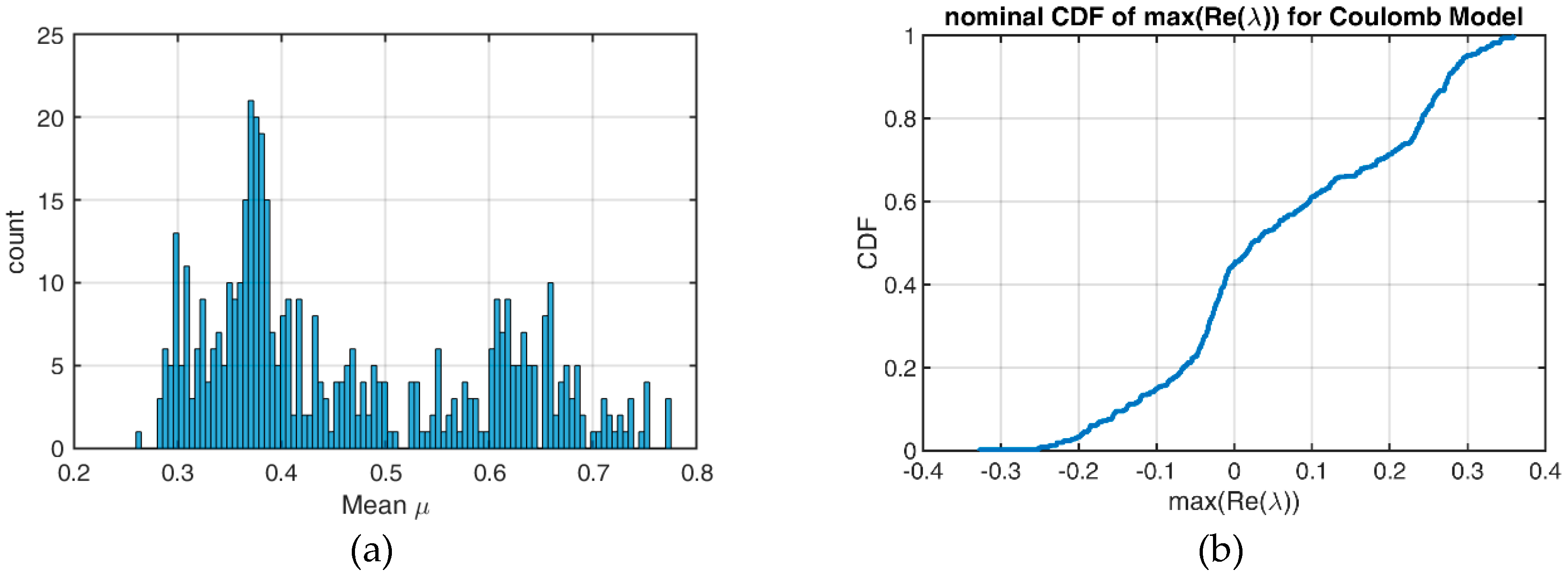
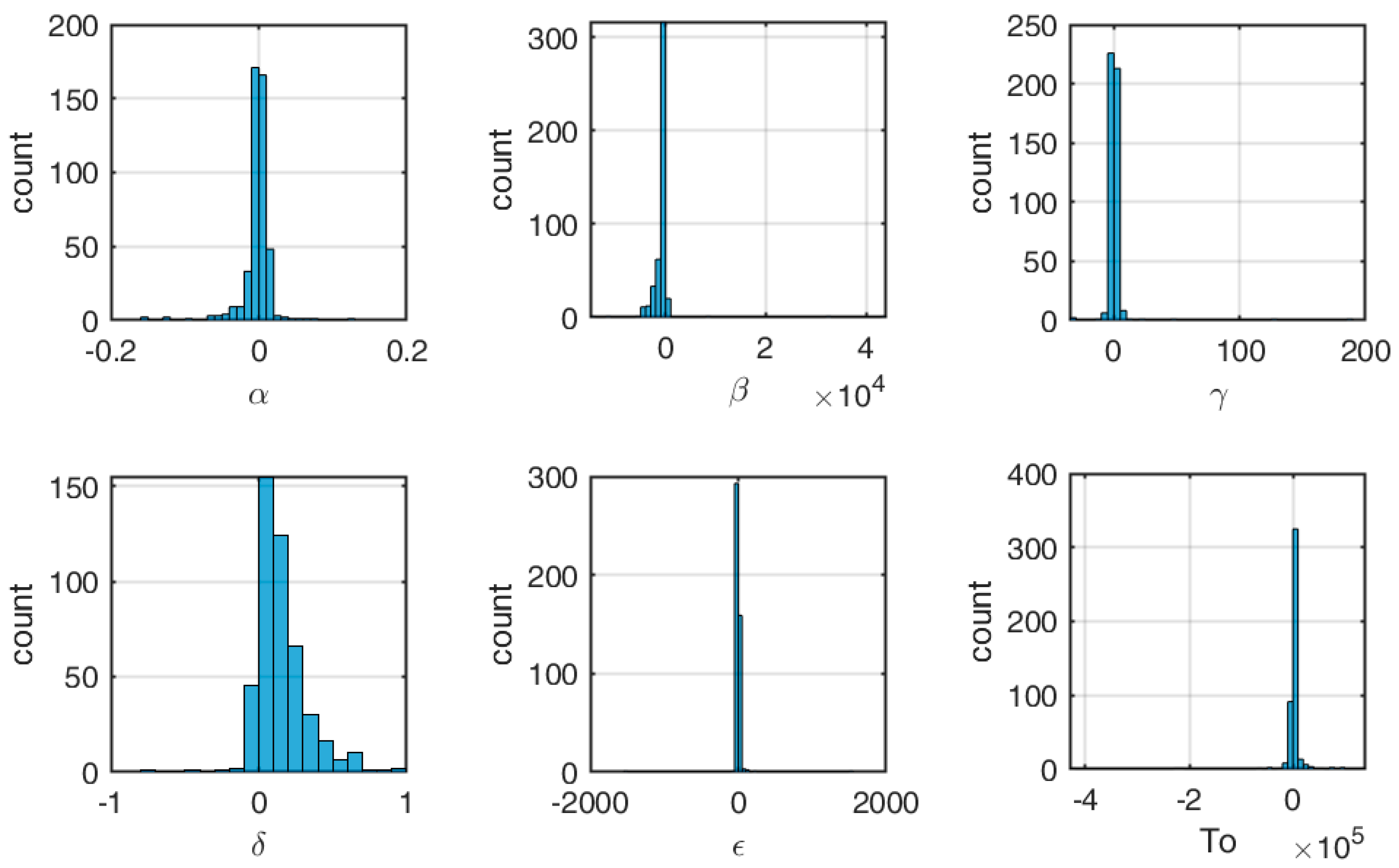
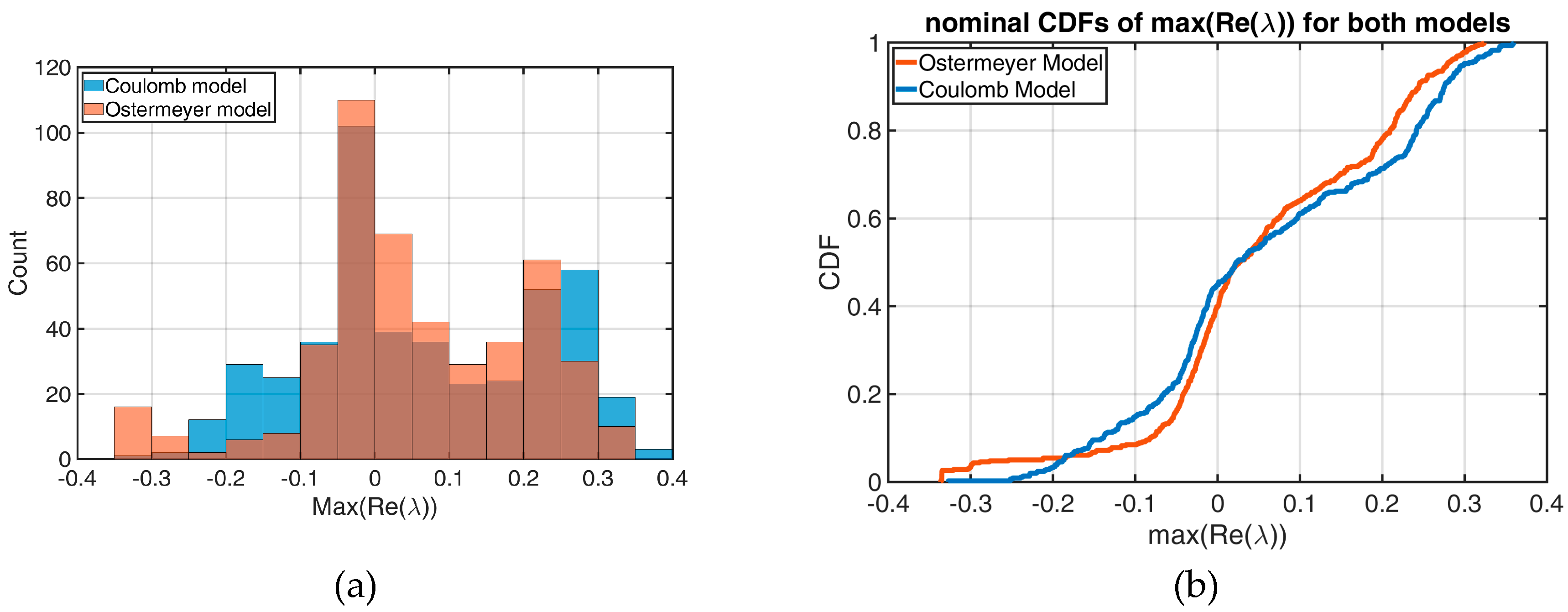
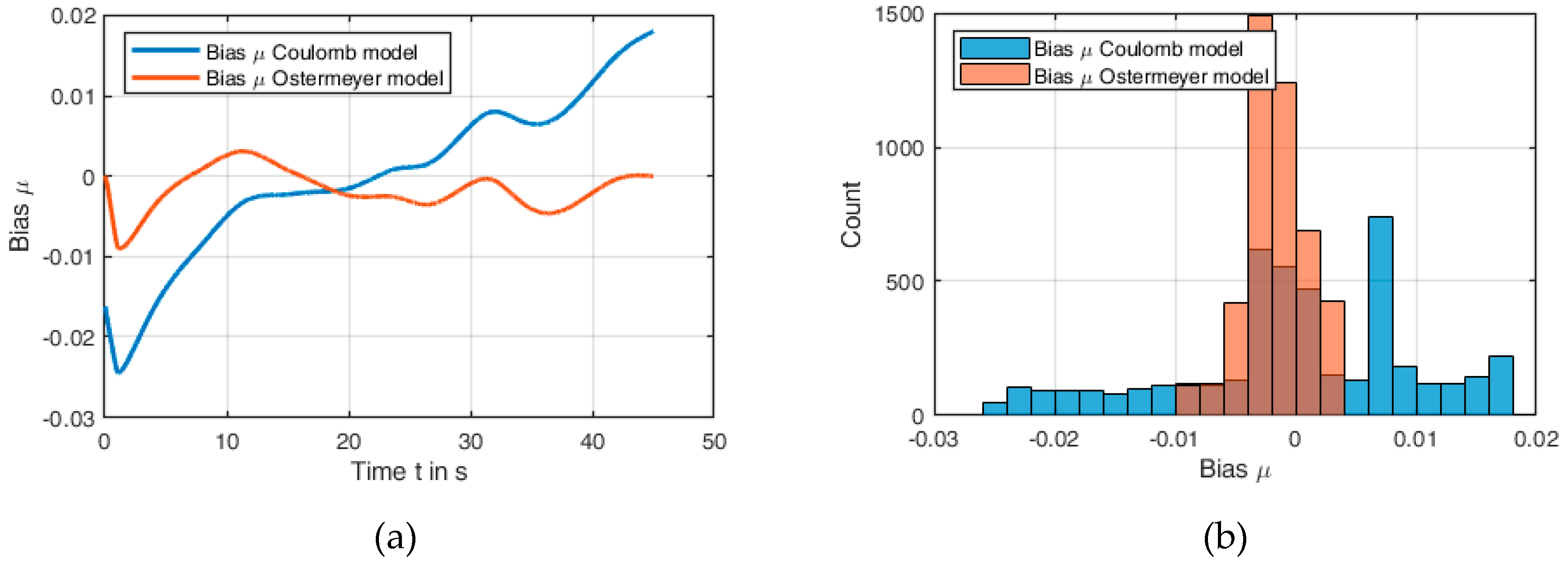
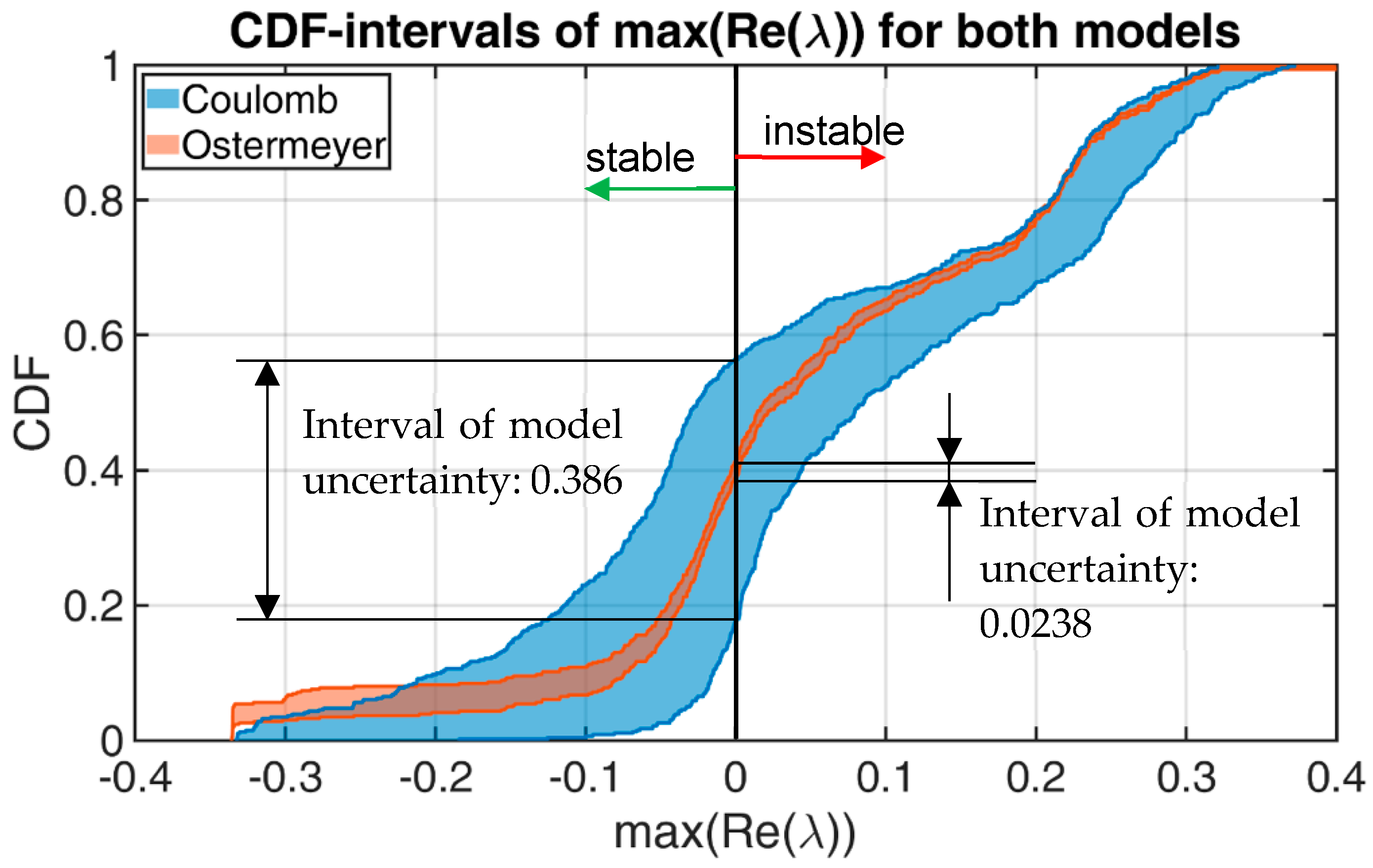
Section 2.3.1. For this purpose, the parameters for two different friction models (Coulomb, Ostermeyer) are calculated for each of the 461 measurement applications. The parameters determining the friction characteristics vary between the individual applications so that there are 461 parameter sets for each friction model. These parameter sets should be regarded as aleatory uncertainties, since it is assumed here that the cause of these uncertainties is primarily of a physical nature, i.e., no significant reduction of the uncertainty can be expected from further measurements. As a result of the aleatory uncertainty model, a corresponding probability density function for the eigenvalues is determined.
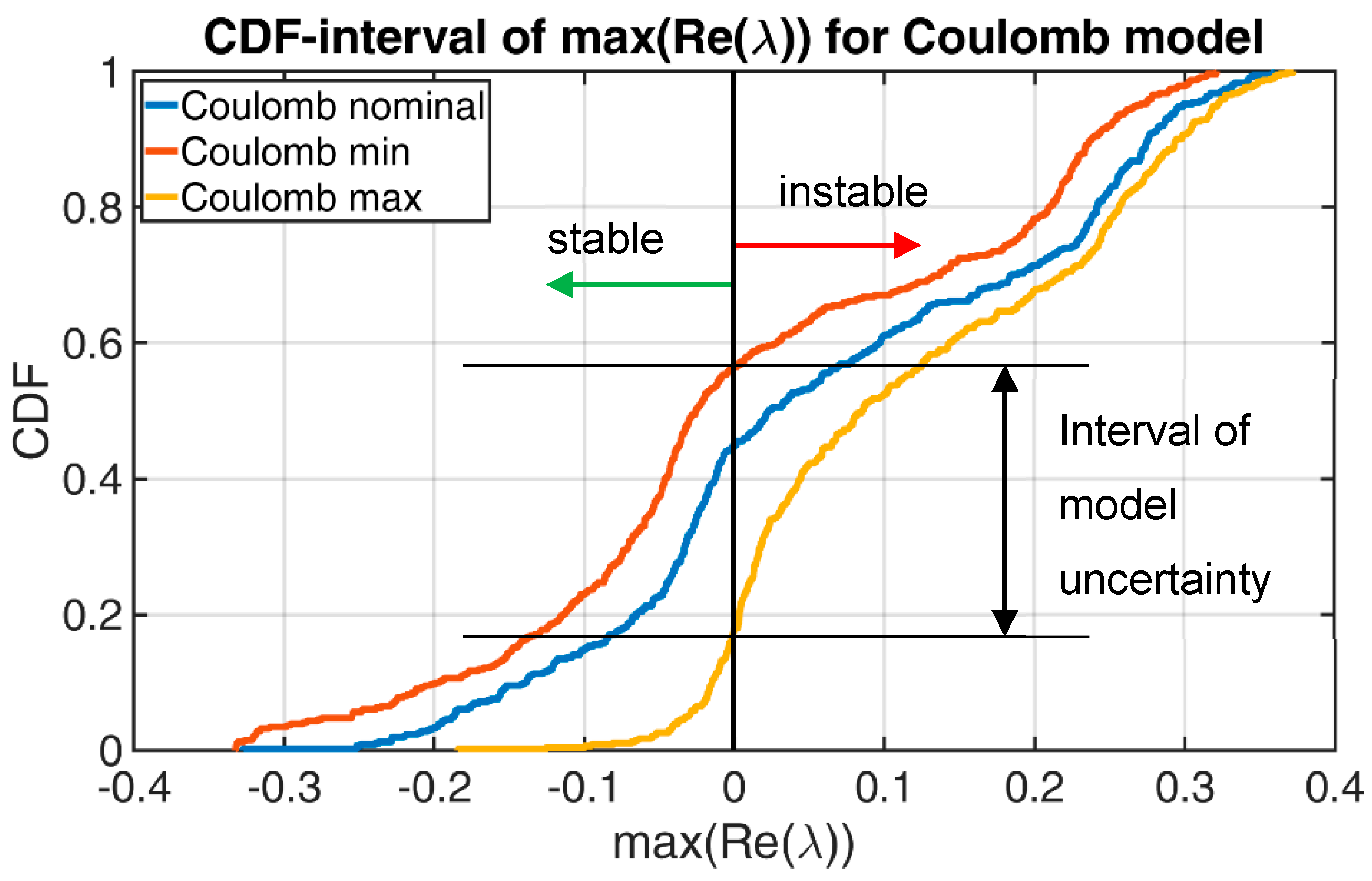
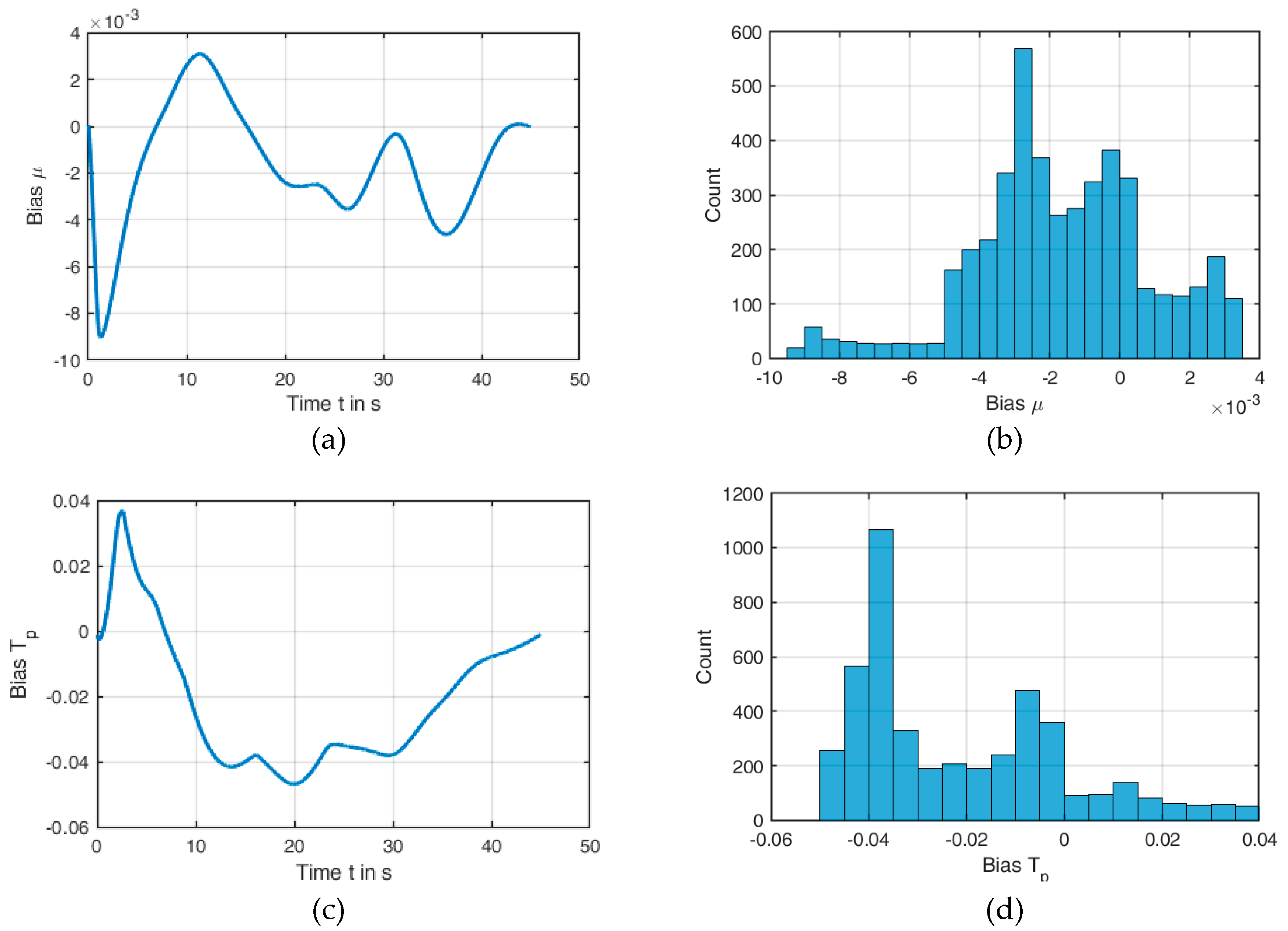
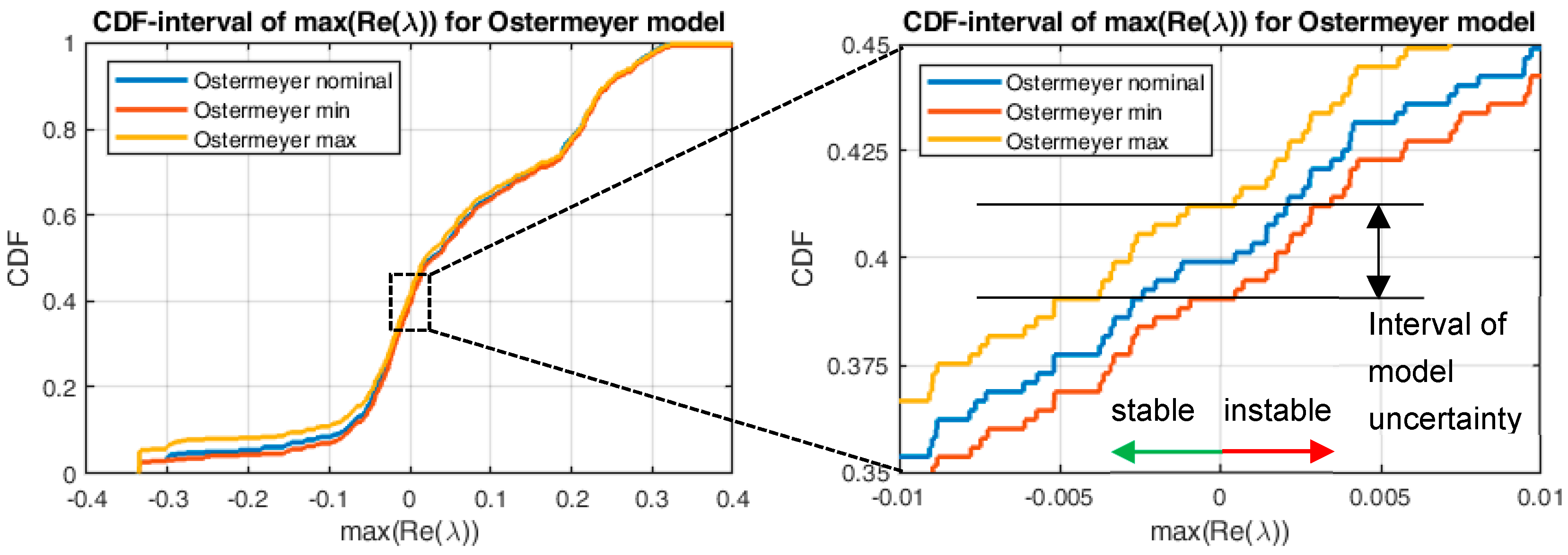
Neither friction models are able to reproduce the measured COFs exactly over time. This results in a “band of uncertainty” for each individual application. The reason of this can be understood as a lack of knowledge, since even more suitable friction models can further reduce this band. Thus, this aspect represents an epistemic uncertainty and the implementation of this band can be carried out with fuzzy methods. The exact procedures and results are discussed in
Section 3.