A Wideband Piezoelectric Energy Harvester Design by Using Multiple Non-Uniform Bimorphs

Abstract

This paper presents an analytical approach for the development of a new wideband piezoelectric energy harvesting system. The proposed model is based on Adomian decomposition method to derive the dynamic response of the general non-uniform smart structures under external environmental excitations over a wide frequency domain efficiently harvesting the subsequent vibrational energy. The steady-state response of a nonlinearly tapered piezoelectric harvester subjected to harmonic base motion is obtained, and the higher potential electromechanical outputs compared with traditional uniform harvester are analytically derived. Afterward, a group of nonlinearly tapered cantilevers with the same volume and length but different taper ratios and surface bonded piezoelectric layers are assembled together in order to build a broadband piezoelectric energy harvester. Through numerical studies, it is proven that with the proposed non-uniform configuration, the new energy harvester design can function effectively and efficiently with high voltage output over a wide frequency range. The designed wideband harvester can automatically activate one of the non-uniform bimorphs to resonate at particular ambient vibration frequencies and eventually reach the maximum electromechanical output. Based on the proposed theoretical model, an optimum structural design for the wideband piezoelectric energy harvester in the required operational frequency range can be efficiently achieved.

1. Introduction

Energy harvesting from environment energy sources has become a vibrant study field and attracted huge attention in recent years due to numerous applications. Powering wireless electronics and sensors with very low electrical power requirements at the location without the limitations of batteries is pleasing for various automation and monitoring systems. Consequently, energy harvesters are designed to transform the ambient energy into a usable power form to supply the small wireless systems throughout their lifespan.

Recently, vibration-based energy harvesting has become more appealing and has received further attention. The three mechanical conversion mechanisms of vibration energy to electrical energy are: electrostatic, electromagnetic, and piezoelectric [1]. The small dimension, custom shape fabrication capability, and great power conversion potential are the major benefits of the piezoelectric methodology for vibration-based energy harvesting [2]. Even a minor external excitation results in significant amount of produced voltage without demanding any low-efficient initiation mechanical mechanism [3]. The principal characteristic of piezoelectric materials is to generate electrical charge from an external mechanical stimulation (direct effect) and to sense deformation from an applied external electrical polarization (reverse effect). The direct piezoelectric effect is good for harvesting environment energy and transforming it to electrical energy to supply smart systems.

There are quite a few literature reviews on piezoelectric harvesters with abundant suggested methodologies and designs [4,5,6,7]. The most common design is the transversely vibrating cantilever beam with surface bonded piezoelectric layers which has a simple and cost-efficient configuration. They mostly function on the resonance mechanism to increase the strain distribution in the piezoelectric layer and ultimately raise the electrical power output. Moreover, geometry refinement of the harvester itself is a key advancement area. Roundy et al. [8] pointed that a trapezoidal geometry can distribute the strain consistently to attain the maximum strain at every point in the piezoelectric energy harvester. They have indicated that a harvester with a trapezoidal profile can produce more than twice the energy compared to a rectangular harvester. Thus, they recommended a trapezoidal shape harvester with wider cross-section, smaller size, and lower weight. Baker et al. [9] showed up to 50% greater generated power by using a cantilever piezoelectric harvester with trapezoidal profile. Additionally, Xie et al. [10] reported 70 times larger power output than the uniform configuration by using a linearly tapered bimorph energy harvester. Recently, Keshmiri et al. [11] presented a theoretical model for piezoelectric energy harvesters with nonlinearly tapered geometry and functionally graded material properties. Based on their model, up to 20 times higher output voltage can be obtained.

One of the biggest drawbacks of the common vibration energy harvesters is the very limited practical bandwidths over which energy can be hunted. In order to increase the frequency range of energy harvesters, two approaches of tuning the resonant frequency and widening the bandwidth are suggested in the literature [12]. Based on the widen bandwidth method, the operational frequency range of the vibration energy generator can be expanded by using an array of harvesters with different natural frequencies. In other words, the piezoelectric energy harvester should have the appropriate bandwidth in the range of peak-power frequencies of the ambient vibrations which can be easily measured in different environments. As one of the pioneers works in this area, Shahruz [13] used an ensemble of cantilever beams with proof mass to build a mechanical bandpass filter and showed a systematic procedure for designing energy harvesters which can efficiently harvest energy from a variety of vibration sources with various peak-power frequencies. He has called the proposed device a mechanical bandpass filter. Moreover, several other researchers have benefited from a similar configuration to design a wideband energy harvester as well [14,15,16]. Hajati and Kim [17,18] designed and tested a novel pie-shaped piezoelectric energy harvester which harvests energy from parasitic environment vibrations with a wide range of amplitude and frequency. Their design utilizes the tensile stretching strain in beams that enables wideband resonance and robust power generation. Yang and Zu [19] developed an energy harvester working in the compressive mode. Their multi-stage force amplification mechanism has considerably increased the electrical outputs and bandwidth. More recently, Li et al. [20] investigated an interdigital-shaped oscillator including a rectangular flexible frame and groups of cantilever beams interdigitally attached to reach low frequency and wide-bandwidth energy harvesting. Based on their designed device, they have reported a 460% increase in bandwidth below 80 Hz and achieved maximum open-circuit voltage and power of 65 V and 4.5 mW, respectively.

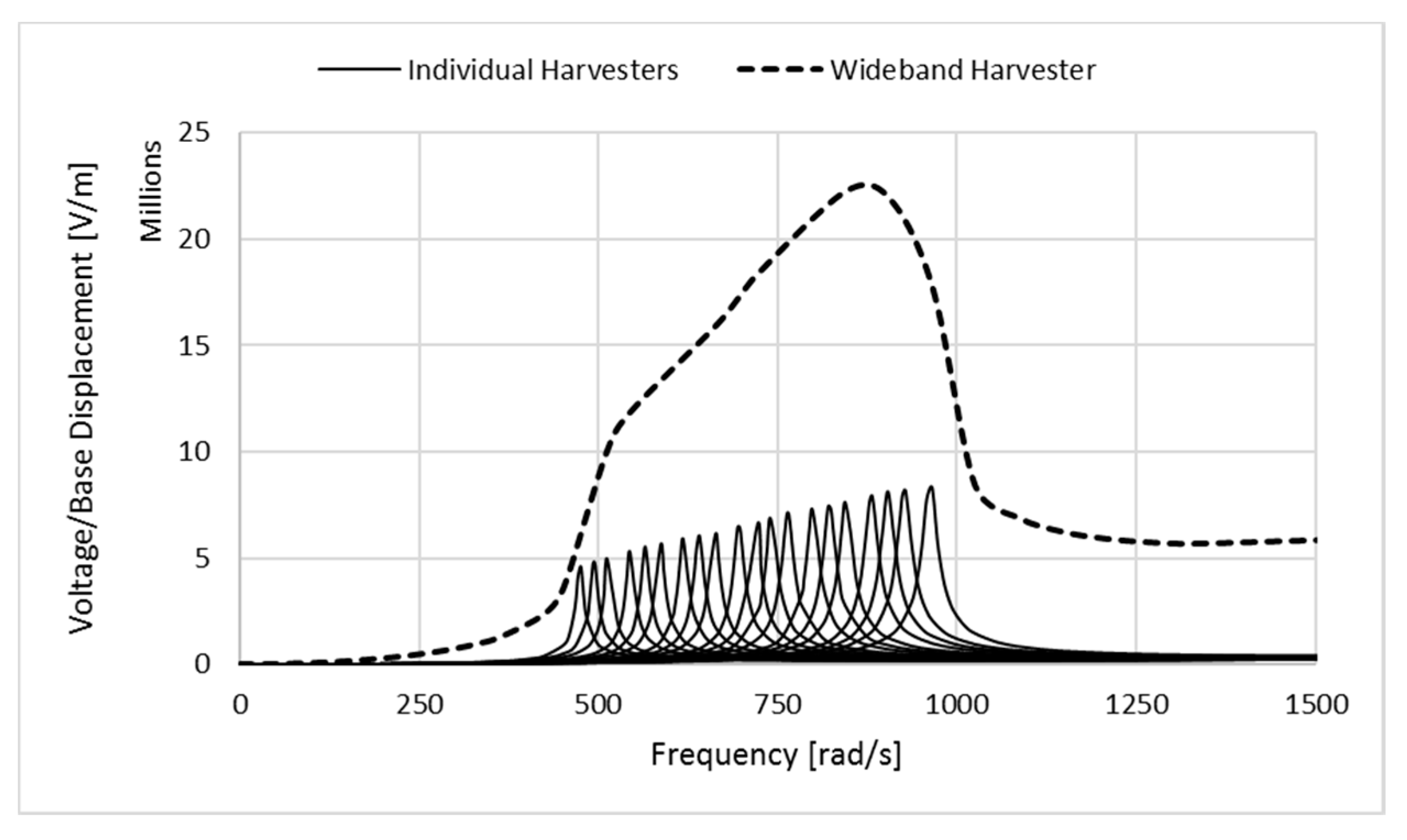
This work investigates the new design and theoretical development of a wideband piezoelectric energy harvesting system with efficient electromechanical outputs. The current study endeavors to challenge earlier energy harvesting designs and engineer a novel and advanced energy harvester system with adequate bandwidth in the range of ambient vibration frequencies by considering nonlinear geometry design. The steady-state dynamic solution of the harmonic base excitation problem for lateral vibration of a single nonlinearly tapered piezoelectric-coupled cantilever beam with strain rate damping is presented and electromechanical outputs are analytically derived and compared with the traditional uniform design. The wideband harvester is then proposed by combining non-uniform piezoelectric-coupled cantilevers with different taper ratios. The mathematical model is developed based on Adomian decomposition method (ADM) and the mechanical model is applicable to any slender beam which allows neglecting shear deformation and rotatory inertia effects. The proposed approach is numerically tested with two sample structures made of 20 and 10 non-uniform piezoelectric-coupled cantilevers with different geometries, but it can be generalized to various numbers of beams and different conversion principles.

2. Materials and Methods

The proposed bimorph piezoelectric energy harvester includes beams with general geometry configuration with piezoelectric patches bonded on the top and bottom surfaces, Figure 1. L is the length of the beam, 2b0 is the width of the beam at the fixed end, 2h0 is the thickness of the beam at the fixed end, and hp is the thickness of the piezoelectric layer. y(t) = Ye^jφt is defined as the harmonic base motion excitation, where Y is the amplitude of the base displacement, φ is the angular frequency of the harmonic excitation, and j is the unit imaginary number. The dynamic governing equation of the lateral vibration under base motion for a piezoelectric coupled beam with non-uniform geometry and structural strain rate damping can be expressed by,

$$\rho A(x)\frac{{\partial }^{2}w(x,t)}{\partial t^2}+\frac{{\partial }^2}{\partial x^2}\left[EI(x)\frac{{\partial }^{2}w(x,t)}{\partial x^2}+C_{s}I(x)\frac{{\partial }^{3}w(x,t)}{\partial x^2\partial t}\right]=-\rho A(x){\phi }^{2}Y{e}^{j\phi t},$$

(1)

where x is position variable along length of the beam, t is time variable, 𝜌 is the equivalent mass density, A(x) is cross-sectional area, w(x,t) is the deflection function, E is the equivalent elasticity modulus, I(x) is the second moment of area, and C_s is the strain rate damping coefficient. Moreover, boundary conditions for the non-uniform cantilever beam are defined as,

$$\begin{array}{l}{\left[w(x,t)\right]}_{x=0}=0,\\ {\left[\frac{\partial w(x,t)}{\partial x}\right]}_{x=0}=0,\\ {\left[EI(x)\frac{{\partial }^{2}w(x,t)}{\partial x^2}\right]}_{x=L}=0,\\ {\left[\frac{\partial }{\partial x}\left(EI(x)\frac{{\partial }^{2}w(x,t)}{\partial x^2}\right)\right]}_{x=L}=0\end{array}$$

(2)

By using the normal mode analysis for a linear system, the solution of Equation (1) is supposed to be a linear combination of the vibration solutions corresponding to normal modes of the beam,

$$w(x,t)={\displaystyle \sum _{i=1}^{\infty }{X}_i(x)T_i(t)},$$

(3)

where X_i(x) are mass normalized eigenfunctions and T_i(t) are modal participation coefficients for the ith vibration mode. Since the system is proportionally damped, eigenfunctions represented by X_i(x) are normal mode eigenfunctions of the corresponding undamped free vibration problem [21,22]. By inserting Equation (3) into the governing equation of the problem, Equation (1), normal modes can be calculated by solving,

$$EI(x)\frac{d^4{X}_i(x)}{d{x}^4}+2E\frac{dI(x)}{dx}\frac{d^3{X}_i(x)}{d{x}^3}+E\frac{d^{2}I(x)}{d{x}^2}\frac{d^2{X}_i(x)}{d{x}^2}-\rho A(x){\omega }_i^2{X}_i(x)=0,$$

(4)

where 𝜔_i² are the undamped natural frequencies of the structure.

Now, ADM is employed to solve the Equation (4). ADM is an operative technique obtaining analytical solution of vibrational systems without linearization or nonlinearity assumptions. Hence, it is physically more precise and realistic. The solution presented by ADM is an infinite series; an n-term approximation which often works as a practical answer. An exact solution could be found with very small values of n [23]. For numerical purposes, the response can be improved by adding more terms which would be the exact solution of the problem if it exists [24]. Details of the mathematical model have been completely discussed in [23,25]. By applying ADM and replacing the decomposition form of X(x), the mode shape function in the recurrence format is expressed as,

$$\begin{gathered} X_0(x)=C_1+C_{2}x+C_3\frac{x^2}{2!}+C_4\frac{x^3}{3!}, \\ {X}_{k+1}(x)=-L_x^{-1}\left[2\frac{\frac{dI(x)}{dx}}{I(x)}\frac{d^3{X}_k(x)}{d{x}^3}+\frac{\frac{d^{2}I(x)}{d{x}^2}}{I(x)}\frac{d^2{X}_k(x)}{d{x}^2}-\frac{\rho A(x)}{EI(x)}{\omega }^2{X}_k(x)\right]k\ge 0 \end{gathered}$$

(5)

where the inverse operator L_x⁻¹ is a fourfold integration with respect to x. Additionally, C₁ to C₄ are constants which should be evaluated from the system boundary conditions. As a result, all X_k components are calculated.

Clearly, normal mode eigenfunctions satisfy the orthogonality conditions,

$$\begin{array}{l}{\displaystyle {\int }_{x=0}^L\rho A(x)X_i(x)X_{i^{\prime }}(x)}dx=\{\begin{array}{cc}1& i=i^{\prime }\\ 0& i\ne i^{\prime }\end{array},\\ {\displaystyle {\int }_{x=0}^{L}EI(x)\frac{d^4{X}_i(x)}{d{x}^4}{X}_{i^{\prime }}(x)}dx=\{\begin{array}{cc}{\omega }_i^2& i=i^{\prime }\\ 0& i\ne i^{\prime }.\end{array}\end{array}$$

(6)

Therefore, the modal participation coefficients T_i(t) are the solution of the ordinary differential equation,

$$\frac{d^2{T}_i(t)}{d{t}^2}+2{\xi }_i{\omega }_i\frac{d{T}_i(t)}{dt}+{\omega }_i^2{T}_i(t)=Q_i(t)=\rho {\phi }^{2}Y\left[{\displaystyle {\int }_{x=0}^{L}A(x)X_i(x)}dx\right]e^{j\omega t},$$

(7)

where 2ξ_i𝜔_i = C_s𝜔_i²/E and ξ_i is the structural strain rate damping ratio of ith vibration mode. Finally, the vibration response can be obtained by Duhamel integral,

$$T_i(t)=\frac{1}{{\omega }_{d_i}}{\displaystyle {\int }_{\tau =0}^t{Q}_i(\tau )e^{-{\xi }_i{\omega }_i(t-\tau )}\sin }{\omega }_{d_i}(t-\tau )d\tau ,$$

(8)

where 𝜔_di is the ith mode damped natural frequency. However, the steady state solution of Equation (7) is expressed as,

$$T_i(t)=\frac{\rho {\phi }^{2}Y\left[{\displaystyle {\int }_{x=0}^{L}A(x)X_i(x)}dx\right]}{{\omega }_i^2-{\phi }^2+j2{\xi }_i{\omega }_i\phi }{e}^{j\omega t}.$$

(9)

As a result, normal mode eigenfunctions in Equation (5) and modal participation coefficients in Equation (9) are used in Equation (3) to derive the dynamic steady-state response of the smart structure relative to its base as,

$$w(x,t)={\displaystyle \sum _{i=1}^{\infty }{X}_i(x)T_i(t)}={\displaystyle \sum _{i=1}^{\infty }{X}_i(x)}\frac{\rho {\phi }^{2}Y\left[{\displaystyle {\int }_{x=0}^{L}A(x)X_i(x)}dx\right]}{{\omega }_i^2-{\phi }^2+j2{\xi }_i{\omega }_i\phi }{e}^{j\omega t}.$$

(10)

In order to find the electromechanical responses of the piezoelectric coupled beam in an open-circuit condition, the Erturk and Inman [21] method is used here. The constitutive relation for piezoelectric materials is,

$$D_3(x,t)=d_{31}{\sigma }_1(x,t)+e_{33}^{\sigma }{E}_3(t),$$

(11)

where D₃ is the electrical displacement, d₃₁ (Coulomb/N or m/V) is the piezoelectric coefficient with polarization in direction 3 due to the external stress in direction 1, 𝜎₁ is the axial stress along 1-axis, e₃₃^𝜎 is the permittivity at constant stress, and E₃ is the electrical field along 3-axis. It should be noted that 1, 2, and 3 directions are aligned with x, y, and z axes, respectively.

By replacing the axial stress 𝜎₁ with bending strain 𝜀₁, changing the component permittivity at constant stress into constant strain [26] and knowing that due to assumed uniform electric field E₃(t) = V(t)/h_p, Equation (11) can be rewritten as,

$$D_3(x,t)=d_{31}{E}_p{\epsilon }_1(x,t)-e_{33}^{\epsilon }\frac{V(t)}{h_p},$$

(12)

where E_p is the piezoelectric elasticity modulus and V(t) is the electric voltage over the piezoelectric area. Furthermore, the longitudinal bending strain 𝜀₁(x,t) in the structure can be calculated as,

$${\epsilon }_1(x,t)=-h_c\frac{{\partial }^{2}w(x,t)}{\partial x^2}=-\left(h(x)+\frac{h_p}{2}\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2},$$

(13)

where h_c is the distance between the center of the piezoelectric layer and the beam’s neutral axis. Consequently, the electric displacement becomes,

$$D_3(x,t)=-d_{31}{E}_p\left(h(x)+\frac{h_p}{2}\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2}-e_{33}^{\epsilon }\frac{V(t)}{h_p}.$$

(14)

The electric displacement D₃(x,t) is related to the output electric charge q(t) by integration over the electrode area as,

$$q(t)=-{\displaystyle {\int }_{x=0}^L\left[d_{31}{E}_p\left(h(x)+\frac{h_p}{2}\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2}+e_{33}^{\epsilon }\frac{V(t)}{h_p}\right]}b(x)dx.$$

(15)

It is noted that the piezoelectric layers should cover the whole surface of the beam. Since the vibration mode of the energy harvester is not limited to the first mode, segmented piezoelectric patches and electrodes are used to avoid the charge offset at higher vibration modes. This is because using continuous electrodes leads to phase difference in the strain distribution and results in charge cancellation at different locations of a piezoelectric layer [21]. Thus, Equation (15) is rephrased in a segmented format as,

$$q(t)=-{\displaystyle \sum _{u=1}^{N_p}\left\{{\displaystyle {\int }_{(u-1)L_p}^{u{L}_p}\left[d_{31}{E}_p\left(h(x)+\frac{h_p}{2}\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2}+e_{33}^{\epsilon }\frac{V(t)}{h_p}\right]}b(x)dx\right\}},$$

(16)

where N_p is the number of piezoelectric patches bonded to the surface of the beam and clearly N_pL_p = L. Considering each piezoelectric patch as an individual harvester, absolute charge values from each piezoelectric patch are added to build the total charge generated by the harvester.

According to Ref. [27], the capacitance of the piezoelectric is represented by C_p. Additionally, the goal of this research is to estimate the open circuit voltage across the piezoelectric layers. Hence, the backward coupling in the relations is ignored. Finally, the generated voltage v(t) can be calculated as,

$$v(t)=-\frac{d_{31}{E}_p}{C_p}{\displaystyle \sum _{u=1}^{N_p}\left[{\displaystyle {\int }_{(u-1)L_p}^{u{L}_p}b(x)\left(h(x)+\frac{h_p}{2}\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2}}dx\right]}.$$

(17)

In order to provide a more general form of steady-state responses, frequency response functions (FRFs) of the electromechanical outputs are obtained and presented. Firstly, the voltage FRF is defined as the ratio of the steady state voltage output to the base displacement. By using Equations (3), (5), (9) and (17), voltage FRF is described as,

$$\frac{v(t)}{-Y{e}^{j\phi t}}=-{\displaystyle \sum _{i=1}^{\infty }\frac{d_{31}{E}_p}{C_p}\left\{{\displaystyle \sum _{u=1}^{N_p}\left[{\displaystyle {\int }_{(u-1)L_p}^{u{L}_p}b(x)\left(h(x)+\frac{h_p}{2}\right)\frac{d^2{X}_i(x)}{\partial x^2}}dx\right]}\frac{\rho {\phi }^2\left[{\displaystyle {\int }_{x=0}^{L}A(x)X_i(x)}dx\right]}{{\omega }_i^2-{\phi }^2+j2{\xi }_i{\omega }_i\phi }\right\}}.$$

(18)

Equation (18) is a modified version of an equation analytically derived and experimentally validated by Erturk and Inman [28]. They have presented that the FRFs from the analytical solution can predict the voltage output of a uniform bimorph precisely.

Secondly, the relative tip motion FRF is presented as the ratio of the beam’s tip to the base displacement. It is noted that the presented model is not limited to the motion at the tip and can be applied to any point along the beam. By using Equation (10), tip motion FRF is defined as,

$$\frac{w(L,t)}{Y{e}^{j\phi t}}=-{\displaystyle \sum _{i=1}^{\infty }{X}_i(L)\frac{\rho {\phi }^2\left[{\displaystyle {\int }_{x=0}^{L}A(x)X_i(x)}dx\right]}{{\omega }_i^2-{\phi }^2+j2{\xi }_i{\omega }_i\phi }}$$

(19)

3. A Piezoelectric Cantilever Harvester with Non-Uniform Design

Now, electromechanical outputs of the nonlinearly tapered energy harvester are analytically obtained to study the effect of different parameters and subsequently harvest the maximum electrical energy from the environment vibration energy. Firstly, a uniform beam with PZT4 piezoelectric sensors bonded to its surface is considered with the geometric dimensions, material properties, and electromechanical coefficients listed in

Table 1. Geometry, material, and electromechanical properties of the piezoelectric energy harvester.

L (m)	b0 (m)	h0 (m)	hp (m)	E (GPa)	𝜌 (kg/m3)	Ep (GPa)	𝜌p (kg/m3)	d31 (pm/V)	e33𝜀 (nF/m)
0.2	0.02	0.005	0.004	100	7165	66	7800	−190	15.93

. The piezoelectric energy harvester is excited by a harmonic base translation and the steady-state dynamic response of the system is of interest. Moreover, structural strain rate damping ratios for the first two vibration modes are assumed to be ξ₁ = ξ₂ = 0.01. Lastly, two steady-state frequency responses, voltage output and tip motion, are investigated. According to the same mathematical model and convergence study for vibration analysis of non-uniform beams provided by Ref. [10], 20 terms of mode shape function series (n = 20) are used to accurately present the final vibration mode shape function for the first two vibration modes.

Although the non-uniformity function in the methodology is not limited to any particular type of function and is a general definition, here, an exponential variation function g(x) = g₀e^−mx/L is considered where g₀ is the initial value, m is the taper ratio and 0 ≤ x ≤ L. It is noted that taper/variation function is defined from fixed to the free end of the cantilever structure. In order to effectively compare the electromechanical outputs, all of the beams in this section have similar length, volume, and mass.

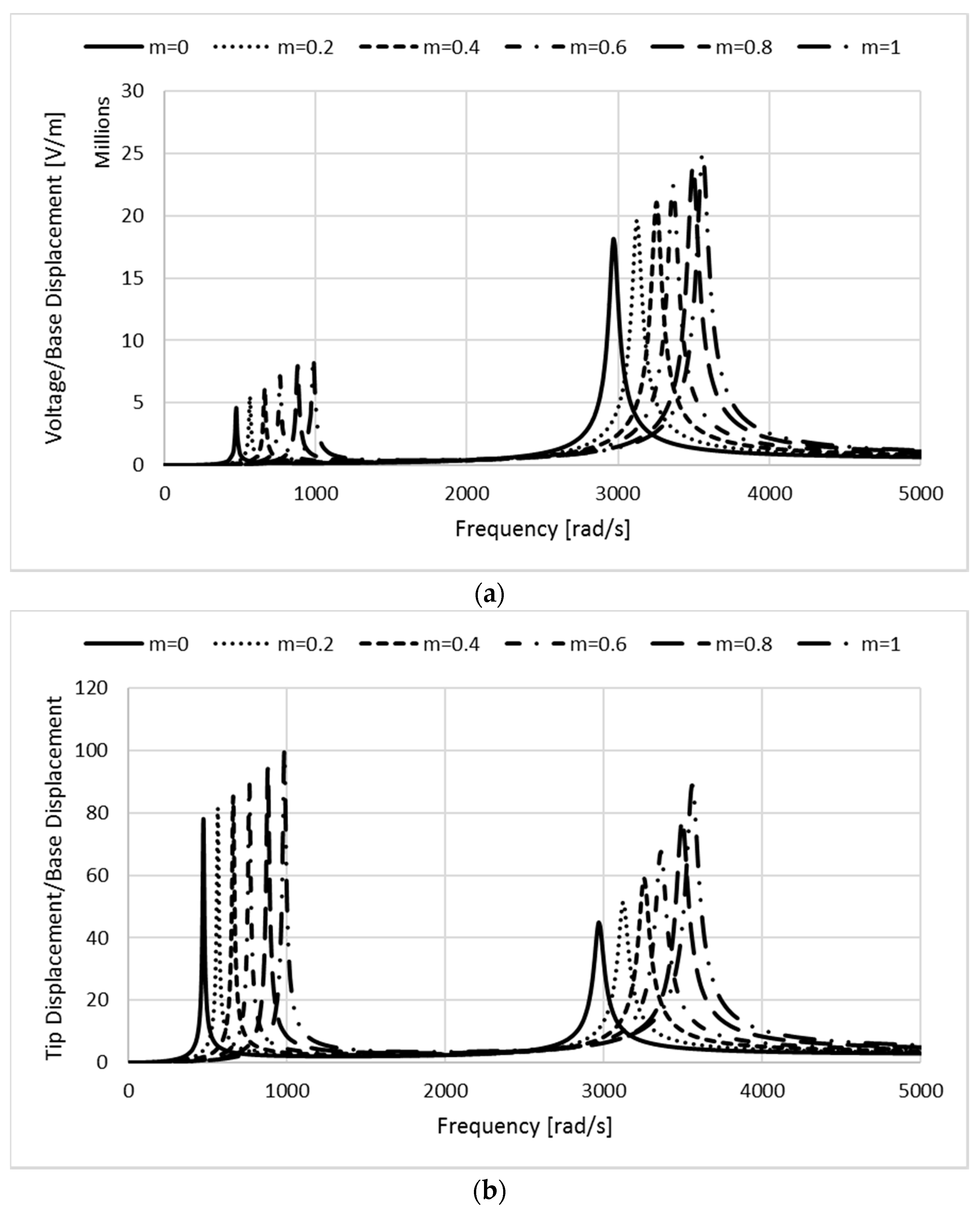
Figure 2a gives the effect of decaying taper geometry on the voltage output in the frequency domain. As shown Figure 2, higher tapering nonlinearity of the harvester leads to significant rise of the voltage output. By changing the taper ratio from 0 to 1, the peak voltage for the first and second vibration modes shows 1.89 and 1.37 times higher values compared to the uniform configuration. For excitation frequencies around φ = 984 rad/s, the non-uniform piezoelectric energy harvester with same length, volume and material properties but with m = 1 geometrical taper ratio generates up to 51 times higher voltage output than the traditional uniform design, Figure 2a. Furthermore, the nonlinear taper effect on the tip displacement is shown in Figure 2b. The nonlinear decaying profile of the piezoelectric energy harvester has a substantial positive effect on the electromechanical outputs [11].

4. Wideband Piezoelectric Energy Harvester

In this section, the probability of designing a wideband energy harvesting system from an array of non-uniform cantilever bimorphs is investigated. The basic idea of an ensemble of the beam-mass structure is borrowed from Ref. [13] and further developed. An energy harvesting system including several nonlinearly tapered piezoelectric-coupled cantilever beams, each of which has the same volume and length but different taper ratios and hence different resonance frequencies, is considered. A schematic illustration of the proposed wideband energy harvester configuration is shown in Figure 3.

As shown in the previous section, the electromechanical outputs have a local maximum at the resonance frequencies of the harvester. A tapered structure has different natural frequencies and higher peak voltage output compared with traditional uniform design with the same length and volume. This makes the natural frequencies of a beam harvester with same size and weight tunable by adjusting the cantilever geometrical taper ratios. For the certain desired voltage output, the non-uniform design can help to reduce the weight of the harvester. By combining single bimorph piezoelectric cantilevers with different taper ratios on a base with a shape as shown in Figure 3, a wide resonance frequency range of the energy harvesting system can be obtained. Additionally, it is very critical to place bimorph natural frequencies sufficiently close to have a steady and continuous bandwidth for wideband operation. The assembled system has a wide-ranging operational frequency which can automatically choose one harvester to resonate at one particular ambient vibration frequency. As a result, the whole system can work as a wideband piezoelectric energy harvester.

4.1. Wideband Energy Harvester with Decaying Tapered Design

In this design, the geometrical variation function is the decaying exponential one like what was presented in Section 3. The geometrical taper ratio increments are chosen as 0.05. The electromechanical outputs of a wideband energy harvesting system including 20 non-uniform bimorph cantilevers with the same length, volume, and mass are presented in Figure 4. As depicted, a slight difference in the geometry of the non-uniform harvester can lead to a considerable alteration in the natural frequencies and electromechanical outputs. In fact, steeper nonlinearity in the geometry of the structure results in higher natural frequencies and peak voltage outputs. Figure 4 shows the estimated voltage output of the wideband energy harvesting system within an input excitation range of [𝜔_min–𝜔_max] = (475–965) rad/s ≈ (75–155) Hz. The bottom plots show the individual output of each harvester whereas the top plot displays the superimposed overall voltage. As shown in Figure 4, high peak voltage outputs (>10 V) at resonance can be obtained in a wide frequency range from 500 rad/s to 950 rad/s by employing 20 nonlinearly tapered cantilever harvesters. Increasing the excitation frequency leads to higher peak voltage output (10 V to 22 V) due to the higher natural frequencies and peak voltage outputs of the bimorph cantilevers with greater taper ratios in the wideband harvesting system.

In addition, it should be noted that all piezoelectric harvesters with decaying tapered geometry have higher natural frequencies than the uniform cantilever with the same length and volume. This limits the application of the wideband harvester under excitations in the low frequency range. Therefore, the increasing tapered design leading to lower natural frequencies will be discussed in the following section.

4.2. Wideband Energy Harvester with Increasing Tapered Design

For the second proposed design, the geometrical variation function is the increasing exponential function as g(x) = g₀e^mx/L where g₀ is the initial value, m is the taper ratio, and 0 ≤ x ≤ L. Again, the geometrical taper ratio increments are chosen as 0.05. By employing 10 non-uniform bimorph energy harvesters with the same length, volume, and mass, the voltage output of a wideband energy harvester is obtained and presented in Figure 5. In contrast to the decaying geometry, the increasing profile decreases the natural frequencies of the cantilever structure which is definitely beneficial for energy harvesting from environmental vibration signals with very low frequencies like HVAC systems. The overall voltage output of the wideband energy harvester within an input excitation range of [𝜔_min–𝜔_max] = (300–475) rad/s ≈ (45–75) Hz changes from 4.5 V to 8 V as shown in Figure 5. The bottom plots show the individual output of each harvester, whereas the top plot displays the superimposed voltage output.

In summary, a wideband harvester comprising two non-uniform configurations can be designed to effectively cover a large bandwidth based on the ambient vibration peak power frequency range covering both low and high frequencies. For the cases in Section 4.1 and Section 4.2, a wideband piezoelectric energy harvester consisting of 30 nonlinearly tapered beams (−0.45 ≤ m ≤ 0.95) with similar length, volume, and mass can efficiently function over a wide frequency range which roughly covers (45–155) Hz with voltage output changes from 5.5 V to 23.4 V. The final result is depicted in Figure 6. Higher voltage output is obtained at higher excitation frequency in the case that constant amplitude of the base motion at different frequencies is considered. In addition to the wideband frequency coverage, it is demonstrated that the peak voltage output for the wideband harvester is roughly 5 times higher than the traditional uniform bimorph design (m = 0).

5. Conclusions

In this paper, an analytic model for a wideband energy harvesting system combining nonlinearly tapered cantilevers is presented. By using ADM, the steady-state dynamic behavior of the smart structures with non-uniform geometry and structural strain-rate damping under harmonic motion is obtained and the closed-form expressions for the electromechanical outputs as frequency response functions are derived. A wideband piezoelectric energy harvester comprising a group of nonlinearly tapered piezoelectric-coupled bimorph cantilevers, each of which has a different geometrical taper ratio and hence different resonance frequencies, is presented and studied.

In conclusion, a new approach to realize high efficiency energy harvesting from ambient vibration with varying frequency by widening the bandwidth of the harvester is developed and presented. This is achieved by combining an array of cantilever non-uniform piezoelectric harvesters with different taper ratios and resonance frequencies. The new wideband energy harvesting system can increase the electromechanical outputs compared with the traditional single bimorphs through a combination of multiple nonlinearly tapered beams with the same volume and length. This research challenges previous energy harvesting designs and formulates an innovative wideband energy-harvesting configuration which functions efficiently in an extensive range of ambient excitation frequencies. Currently, the work is at the theoretical development level. The research direction is generally toward the theoretical optimum design, and the next step is the experimental validation of the new design.