Abstract
Metamaterials are materials with an artificially tailored internal structure and unusual physical and mechanical properties such as a negative refraction coefficient, negative mass inertia, and negative modulus of elasticity, etc. Due to their unique characteristics, metamaterials possess great potential in engineering applications. This study aims to develop new acoustic metamaterials for applications in semi-active vibration isolation. For the proposed state-of-the-art structural configurations in metamaterials, the geometry and mass distribution of the crafted internal structure is employed to induce the local resonance inside the material. Therefore, a stopband in the dispersion curve can be created because of the energy gap. For conventional metamaterials, the stopband is fixed and unable to be adjusted in real-time once the design is completed. Although the metamaterial with distributed resonance characteristics has been proposed in the literature to extend its working stopband, the efficacy is usually compromised. In order to increase its adaptability to time-varying disturbance, several semi-active metamaterials have been proposed. In this study, the incorporation of a tunable shape memory alloy (SMA) into the configuration of metamaterial is proposed. The repeated resonance unit consisting of SMA beams is designed and its theoretical formulation for determining the dynamic characteristics is established. For more general application, the finite element model of this smart metamaterial is also derived and simulated. The stopband of this metamaterial beam with different configurations in the arrangement of the SMA absorbers was investigated. The result shows that the proposed model is able to predict the unique dynamic characteristics of this smart metamaterial beam. Moreover, the tunable stopband of the metamaterial beam with controlling the state of SMA absorbers was also demonstrated.
1. Introduction
Metamaterials are artificially fabricated structural materials with special physical properties, such as a negative refraction index of the electromagnetic wave [], negative effective mass, and negative effective elastic modulus [], etc. Their potential applications include an invisibility cloak, vibration, acoustic control in structures, and metadevices []. Usually, the materials with a periodic distribution of elastic constant or mass density are known as phononic crystals. With analogy to photonic crystal, it is found that when an elastic wave propagates through phononic crystal or an elastic composite with a periodic structure, a similar stopband or bandgap is formed in its transmission [,,].
Low frequency flexural wave band gaps in Timoshenko beams with locally resonant structures were studied theoretically and experimentally by Yu et al. []. They concluded that the existence of low frequency band gaps in the beams provides a method for the flexural vibration control of beams. For broadband vibration absorption, Pai [], by varying the attached absorber’s characteristics along its wave propagating axis, numerically showed the feasibility of the design of a broadband elastic wave absorber in the axial vibration of a longitudinal metamaterial bar. With regards to other structures, the multi-stopband metamaterial beam [] and plate [,] were designed by employing local resonance between the multi-frequency absorbers and external excitation. Moreover, a Helmholtz resonator with an adjustable size [], a 3-D kagome-sphere lattice with tuned dimensional sizes [], a chiral elastic lattice with different column materials [], and a lattice with sinusoidally-shaped ligaments [] were also employed, respectively, to alter the bandgap of the materials. He and coworkers [] reported that composite laminate acoustic metamaterials manifested were more effective for broadband vibration absorption with the superior strength to weight ratio of carbon fiber reinforced polymer (CFRP). The design of a layered mechanical metamaterial having implemented negative stiffness inclusions has been presented and its acoustic wave propagation properties have been modeled for beam [] and plate [] structures, respectively. A superior performance in a broadband frequency range when compared to a viscoelastic damping constraint layer of equivalent mass was demonstrated using the proposed configurations.
Although the above studies proposed the designs of metamaterial which were effective in demonstrating their stopband characteristics in vibration or acoustic control, their designs were unable to be adapted to the change in external excitation source, e.g., machinery which needs to operate at different rotational speeds. Therefore, a variety of metamaterial designs have been incorporated with a tunable capability to be adapted to environmental changes. Wang and co-workers [] proposed a design of locally tunable resonant acoustic metamaterials composed of easy-to-buckle elastic beams. The controlled static loading induced buckling dramatically alters the stiffness of the beams and consequently the natural frequency of the resonating units, which in turn determines the frequency range of the band gap. The designs of tunable acoustic metamaterials by altering the resonant frequency via piezo shunting [,] were also proposed. The performance of this class of design was verified experimentally by Zhu et al. []. In addition, Casadei et al. [] proposed a metamaterial consisting of a slender beam featuring a periodic array of airfoil-shaped masses supported by linear and torsional springs. The resonance characteristics of the airfoils lead to strong attenuation at frequencies defined by the properties of the airfoils and the speed on the incident fluid. There are also designs incorporating the use of tunable smart materials, such as magnetorheological elastomer (MRE) [], electrorheological fluid (ERF) [], and shape memory polymer (SMP) [].
Although the use of smart materials such as MRE and ERF in the design of tunable metamaterials has been proposed, as mentioned previously, the mechanical property change upon activation by the magnetic field or electric field is still limited due to their rubber-like nature. On the other hand, a shape memory alloy (SMA) is metallic in nature and undergoes significant stiffness change upon the thermally activated martensite to austenite transformation []. Nevertheless, there is a thermal hysteresis in the phase transformation. Thus, a superlattice material consisting of alternate layers of a shape memory Ni-rich NiAl alloy and NiAl B2 alloy has been proposed to reduce this thermal hysteresis []. In general, SMA has been employed in the tunable vibration absorber design for vibration control [,]. Therefore, in this study, a theoretical analysis of the feasibility of using SMA cantilevers in the design of a tunable metamaterial beam structure was performed. The geometrical dimensions and configuration of the periodic arrangement on the stopband of vibration transmission were investigated through finite element analysis.
2. Modeling
A schematic diagram for the proposed metamaterial beam with shape memory material (SMM) absorbers is shown in Figure 1. Two types of plausible SMM absorber are shown in Figure 1: an absorber with a helical spring and an absorber with cantilevers. Either type can be applied in the construction of the metamaterial beam. l denotes the pitch of the attached absorbers along the axial direction of the beam. In mathematical modeling, each absorber can be represented by a one-degree-of-freedom mass-damper-spring system. However, the helical spring can usually be made with lower stiffness than the cantilever. The different configurations can be considered for different ranges of stopbands. A suitable design can be chosen for individual application. By controlling the temperature of the SMM via electric current or other means, the stiffness and subsequently, the natural frequency of the absorber, can be tuned accordingly.
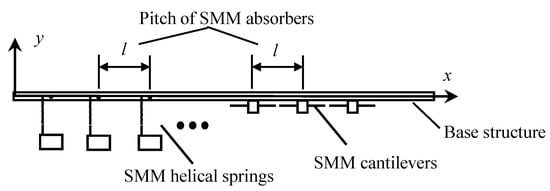
Figure 1.
The schematic diagram of the proposed metamaterial beam consisting of different types of shape memory material absorbers.
2.1. Metamaterial Beam with Infinite Length
Figure 2 shows a schematic diagram of the repeated unit element for the metamaterial beam. ma, ca, and ka denote the equivalent mass, damping, and stiffness of the SMM absorber, respectively, while l represents the pitch length of the element. Similar modeling can be found in the work of Pai et al. []. However, in this study, it should be noted that ca and ka can be adjusted by controlling the temperature of the SMM. According to Euler-Bernoulli’s beam theory, if the damping for both the beam and absorber can be neglected, the governing equations for the beam and absorber can be written as:
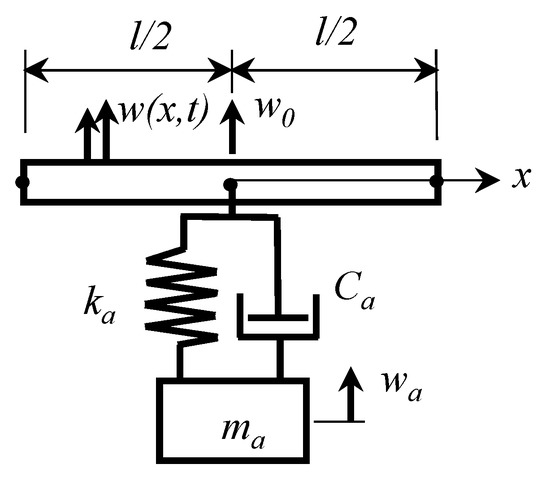
Figure 2.
The schematic diagram of the repeated unit element for the metamaterial beam.
In Equation (1), ρ, A, I, and E are the mass density, cross-sectional area, second area moment of inertia, and Young’s modulus of the beam structure. δ(x) is the Kroneckler delta function. For a metamaterial beam of an infinite length, the representative repeat unit should satisfy the conditions of periodicity at both ends. Therefore, under harmonic excitation, the lateral displacement functions of the beam structure w(x, t) and the absorber wa(t) can be expressed, respectively, as:
In the above equations, β and Ω are the wave number and frequency of the propagating waves, respectively, and . Substituting Equation (3) into Equation (1) and performing the integration over the pitch length l, we can have:
where
By further substituting Equations (3) and (4) into Equations (5) and (2), and solving for the nontrivial solution of the resulting homogeneous equations, an equation to determine the wave number β can be obtained:
Given a vibration frequency Ω, the stopband of this metamaterial beam lies within the range when no real β solution exists in Equation (7).
2.2. Finite Element Formulation of the Metamaterial Beam
The equations established in the previous section are based on a metamaterial beam of an infinite length. For practical applications, the beam should be of a finite length and different boundary conditions. Moreover, if multiple stopbands are to be implemented in this metamaterial beam, the absorbers should be tunable in their parameters. The resort to finite element analysis has its necessity. In this study, the structural beam was discretized as an Euler-Bernoulli beam element and the base of each 1-DOF absorber was attached to its node. The corresponding mass matrix and stiffness matrices of the beam element can be found in the standard textbook of the finite element method, e.g., Bathe []. As for the damping matrix of the beam element, a proportional damping approach was assumed if considered. The viscous damping of the absorber was appended in the system damping matrix accordingly. By following the standard procedure in finite element analysis, the system matrices and equations of motion could be assembled as in the following equation, where and denote the nodal force vector and nodal displacement vector, respectively.
A sweep sine analysis was performed in Equation (8). The frequency response function of the metamaterial beam over the required frequency span was obtained.
For simulating the time response of the metamaterial beam, the Newmark method [] was adopted in this study:
In the above equations, α and δ are the parameters for adjusting the accuracy and stability of the integration, respectively. The trapezoidal rule of α = 1/4 and δ = 1/2 was adopted in this study. A time incremental step of was employed in the calculation.
Table 1 presents the dimensions and material properties of the structural beam and the parameters of the absorbers used in the numerical simulation. The structural beam was made of aluminum and the absorber was designed to damp out the vibration at 2500 Hz, which was within an acoustic range. If calculated, it is found that the mass of the absorber was about one tenth of a beam element.

Table 1.
The dimensions and material properties of the structural beam and the parameters of the absorbers used in the simulation of the metamaterial beam.
As for the possible experimental implementation, Figure 3 shows an SMA cantilevered beam configuration. Two parallel SMA wires were clamped symmetrically at their half lengths by an insulating fixture pad. The wires were separated along their lengths, except at the two extreme ends. The ends were electrically connected to form a circuit loop where the control current was brought in through the tabs in the fixture pad. The direction of current flow through this absorber was also schematically shown in the figure. The control current provided resistance heating to the SMA wires and tuned their phase transformation from martensite to austenite through temperature manipulation. Therefore, the stiffness of the absorber could be changed from the lower martensitic phase to the higher austenitic phase. Under the assumption of Euler beam theory, the fundamental frequency of the cantilever beam can be calculated as []:
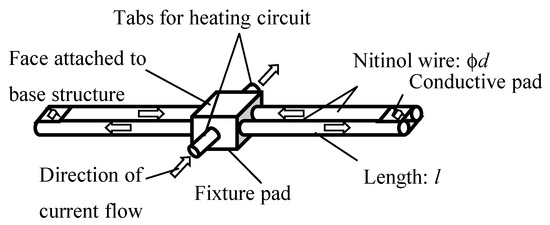
Figure 3.
An exemplary implementation of the proposed absorber with SMA wires clamped in double-cantilevered configuration.
For instance, if Nitinol wire with a diameter of 0.8 mm and length of 10 mm is used, based on its mass density of 6450 kg/m3 and Young’s moduli for martensite and austenite phases of 75 GPa and 28 GPa, respectively, the calculated fundamental frequencies of the cantilevered beam are 2332 Hz and 3816 Hz before and after the martensite-austenite transformation. The estimated working frequency of this proposed absorber configuration seems to fit the parameter presented in Table 1.
3. Results and Discussion
3.1. The Stopband of the Metamaterial Beam with Infinite Length
Figure 4 presents the frequency dispersion curves of the metamaterial beam of an infinite length. It is clearly seen that around the natural frequency, the absorber existed as a stopband. No vibration wave in this frequency band can propagate through this metamaterial beam. When the mass ratio of the absorber to the beam element increased, the stopband widened. On the other hand, as the natural frequency of the absorber changed, the stopband of the frequency ratio remained unchanged. However, the stopband of the actual frequency of vibration Ω shifted accordingly with ωa. In other words, the mass ratio of the absorber changed the bandwidth of the stopband, while the natural frequency of the absorber shifted the frequency of the stopband without alteration of its frequency ratio. The simulation of changing the natural frequency of the absorber was conducted to examine the possible influence of switching SMA from martensite to austenite, which generates a change in the Young’s modulus of three folds [].
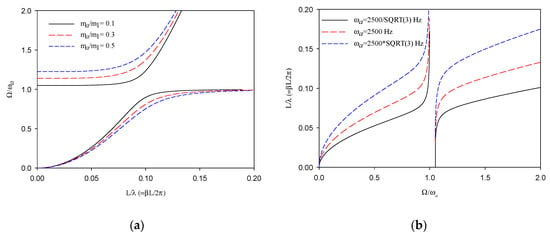
Figure 4.
The frequency dispersion curves of metamaterial beams: (a) with the appended absorbers of different mass ratios; (b) with the appended absorbers of different natural frequencies.
3.2. The Response of the Metamaterial Beam with Finite Length
For the beam with a finite length, the boundary conditions should influence its vibration characteristics. Before considering the effect of adding SMM absorbers, the reliability of the finite element model for the pristine beam should be verified. Table 2 presents some calculated natural frequencies from the finite element model along with their theoretical results obtained from the Euler beam theory []. For the beam in three different boundary configurations, only the natural frequencies from the first three modes were calculated. However, for the beam in simply-supported boundary conditions, its 19th and 20th natural frequencies close to the interested frequency range of 2500 Hz were also calculated due to its simpler effort in calculation. The calculation for the higher modes of the beam in other configurations was not attempted because the theoretical results were not readily available from the vibration textbook. It is seen that the accuracy of the finite element model in calculating the natural frequencies of the structural beam under different boundary conditions was reasonably good, even for the higher frequency modes within the interested frequency range of this study.

Table 2.
The calculated natural frequencies of the structural beam from the finite element model along with their theoretical results obtained from the Euler beam theory.
The frequency response function of the metamaterial beam in cantilevered configuration was calculated first from Equation (8) by using sweep sine technique. The beam with 32 equally spaced absorbers was discretized into 32 elements in the finite element model. With the linear nature of the governing equation, the steady state response was calculated under a sinusoidal input force of unit magnitude at x = 0.03125 m. The input excitation near to the fixed end was applied to leave more room for observing the vibration propagation toward to the free end. The frequency response spectra of this cantilevered metamaterial beam are shown in Figure 5. It is noted that there was a discrete stopband and the response of the beam reduced drastically within the stopband. The stopband was around 2500 Hz, which was the designed working frequency of this metamaterial beam presented in Table 1. Moreover, because of the attached absorbers to the beam structure, there were several resonance peaks around the stopband. For the frequency response of the beam away from the stopband, the displacement amplitude was lower at location x = 0.0625 m, which was nearer the cantilevered end than at the free end (x = 1.0 m). This fits the characteristics of a cantilevered beam in usual vibrations. However, at frequency near the stopband, the response at the free end was lower than that near the cantilevered end. The accumulated vibration reduction effect through the action of absorbers effectively reduced the vibration of the beam. Therefore, it is clearly seen that the stopband was present more obviously at the free end. As regards to the vibration of the absorber, the displacement amplitude was always higher than its beam counterpart. Nonetheless, the frequency response followed closely with that of its beam counterpart.
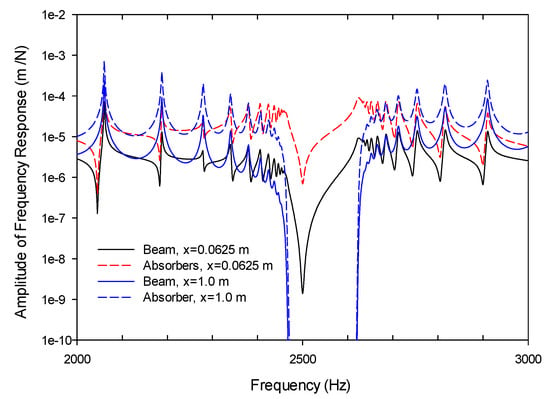
Figure 5.
The frequency response spectra near the fixed end (x = 0.0625 m) and at the free end of a cantilevered metamaterial beam with the SMA spring in martensite phase.
By using the Newmark method mentioned previously, the time responses of a cantilevered metamaterial beam at different downstream locations were simulated and shown in Figure 6. For the beam excited with a sinusoidal disturbance at x = 31.25 mm near the fixed end, the response component with the same frequency of excitation showed a quick decay at farer downstream locations. Nevertheless, the vibration of lower frequency was still observed. This result reveals that the vibration components in the stopband can be effectively diminished after a certain distance away from the excitation. This was consistent with the lower magnitude in frequency response spectra at a further downstream location from the disturbance presented in Figure 5.
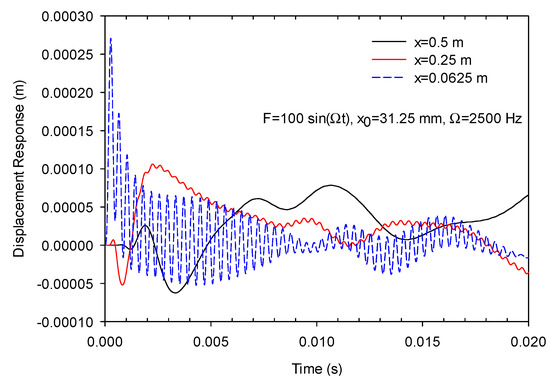
Figure 6.
Time responses of a cantilevered metamaterial beam at different downstream locations.
Figure 7 presents the variations of displacement amplitudes along the downstream direction for the metamaterial beams having 16 and 32 absorbers, respectively. For the metamaterial beam with 32 absorbers equally-spaced along its full length, it is seen that both the displacement amplitudes of the beam and absorber decayed drastically away from the location of external disturbance. Because the absorber took over the vibration energy from the beam, it had a larger displacement amplitude than the base beam at all locations. For the metamaterial beam with only 16 absorbers equally-spaced in the first half of its length, the decay in displacement amplitude leveled after the last absorber. Even under this circumstance, the attenuation in vibration still reached an applicable level for engineering application. Therefore, the configuration design of this metamaterial beam should be an interesting topic to be further explored.
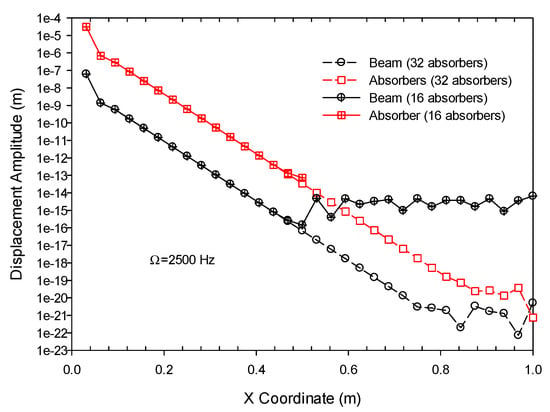
Figure 7.
The variations in displacement amplitudes along the length of the cantilevered metamaterial beams having different numbers of absorbers.
3.3. The Stopband Tunability of the Metamaterial Beam
Figure 8 presents the calculated frequency response spectra of a cantilevered metamaterial beam with the SMA spring in martensite and austenite phases, respectively. As mentioned previously, the Young’s modulus of the Nitinol changed from 28 GPa of martensite phase to 75 GPa of austenite phase upon complete transformation in heating. The corresponding change in the stiffness of the absorber as given in Table 1 was adjusted accordingly. The finite element analysis clearly showed that the stopband was tuned to a higher frequency when the absorbers were heated into austenite phase. Theoretically, if the SMA was heated to a temperature wherein only partial austenite transformation was completed, the stopband could be tuned between the two extremes of simple martensite and simple austenite. Another possibility would be that the absorbers were tuned in a distributed fashion, i.e., the absorbers were divided into several groups and the SMA in each group had different degrees of austenite transformation. In this case, a metamaterial beam with very wide stopband could probably be made.
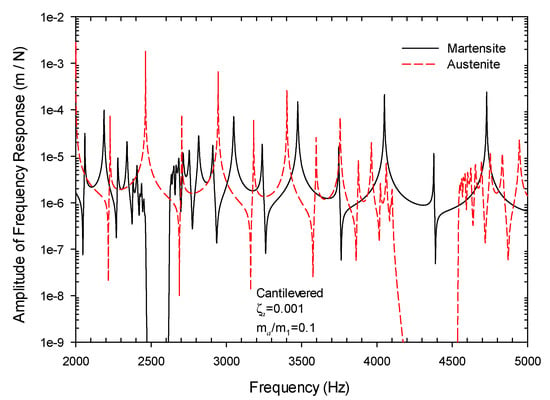
Figure 8.
The frequency response spectra of a cantilevered metamaterial beam with the SMA spring in martensite and austenite phases, respectively.
For the metamaterial beams in simply-supported configuration, Figure 9 shows their frequency responses when the absorbers were arranged in different spacing. These frequency responses were calculated from the sinusoidal input at x = 0.03125 m and steady state output at x = 0.96875 m. For these four metamaterial beams, the stopband near the designed frequency of 2500 Hz occurred. However, only the metamaterial beam with absorber spacing of 0.03125 m showed the complete stopband around 2500 Hz. The other metamaterial beams with larger absorber spacing ≥0.0625 m either presented a smaller or offset stopband. As seen from Table 2, the mode shape of the simply-supported beam with frequency close to 2500 Hz was the 19th mode, which had a wave length of about 0.05 m. Therefore, it is suspected that the spacing of the absorbers in a metamaterial beam should be less than the wave length of the corresponding mode shape at the designed working frequency. More detailed study is needed in this respect.
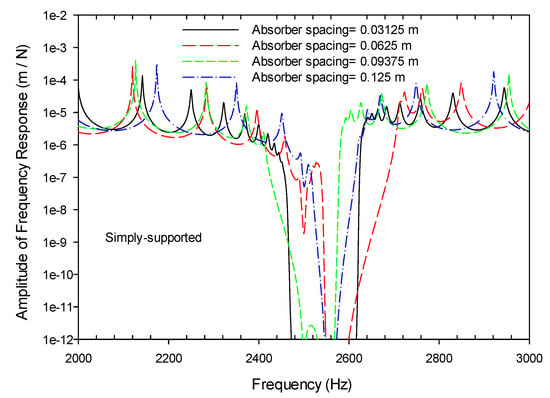
Figure 9.
The frequency responses of the simply-supported metamaterial beams having absorbers in different spacing.
Figure 10 presents the frequency response spectra of the simply-supported metamaterial beam having the absorbers activated in different states. For the absorbers in an inactivated state, i.e., martensitic phase, the stopband around 2500 Hz was seen, as expected from a previous example. As all the absorber springs were activated or heated to fully austenitic phase, the Young’s modulus of the Nitinol was raised to 75 GPa and the spring constants of the absorber increased accordingly. The stopband of this simply-supported beam having all absorbers activated shifted to a higher frequency around 4200 Hz, similar to that of the cantilevered beam shown in Figure 6. In order to explore the effect of the tunable capability of the SMA absorber, only alternating absorbers were activated along the beam. The frequency response shown in Figure 10 for this beam with alternatingly activated absorbers demonstrated two discrete stopbands, around 2500 and 4200 Hz, respectively. Although their bandwidths were somewhat compromised, these two stopbands were very distinctive. It is therefore believed that distributed activation of the absorbers along the beam’s axis could present more capabilities of the metamaterial beam in active broadband control.
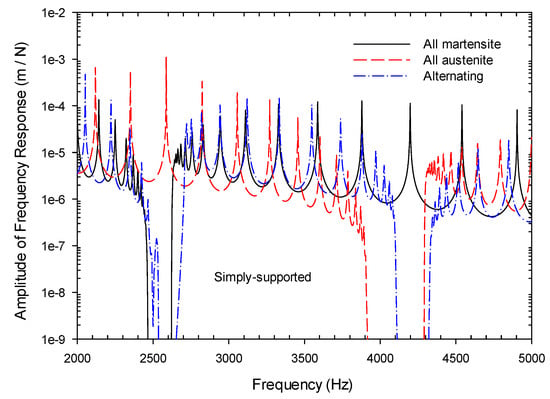
Figure 10.
The frequency responses of the simply-supported metamaterial beam having the absorbers activated in different states.
4. Conclusions
The finite element formulation on a metamaterial beam which features distributed SMM absorbers was established. Based on the theoretical analyses, the tuning in absorber mass was more effective in increasing the bandwidth of the stopband in vibration transmission, while both mass and stiffness tuning had the capability to shift the stopband. The simulation results of both cantilevered and simply-supported metamaterial beams showed the shift of the stopband to a higher frequency by the controlled phase transformation from martensite to austenite of the SMA absorber spring. This proposed design could constitute another class of smart acoustic metamaterial structure. Moreover, installation of the absorbers along a partial segment was able to dampen out the harmonic disturbance of target frequency with an acceptable performance. Thus, the configuration design of this metamaterial beam can be an interesting topic to be further explored.
Author Contributions
Conceptualization, C.-Y.L.; Methodology, H.-L.H.; Programming, J.-W.P.; Writing-Original Draft Preparation, H.-L.H.; Writing-Review & Editing, C.-Y.L.
Funding
This research was funded by Ministry of Science and Technology, Taiwan, under Grant No. MOST 106-2221-E-027-054.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | cross-sectional area of the beam structure |
| damping matrix of the metabeam in finite element formulation | |
| ca | the equivalent stiffness of the SMM absorber |
| E | Young’s modulus of the beam structure |
| external force vector of the metabeam in finite element formulation | |
| I | second area moment of inertia of the beam structure |
| stiffness matrix of the metabeam in finite element formulation | |
| ka | the equivalent stiffness of the SMM absorber |
| equivalent spring constant defined in Equation (6) | |
| l | pitch length between the absorbers |
| mass matrix of the metabeam in finite element formulation | |
| ma | the equivalent mass of the SMM absorber |
| equivalent mass defined in Equation (6) | |
| w(x, t) | the lateral displacement function of the beam structure |
| amplitude of the lateral displacement of the beam structure | |
| wa(t) | the displacement function of the absorber |
| amplitude of the lateral displacement of the absorber | |
| nodal displacement vector of the metabeam in finite element formulation | |
| α | the parameter used in Newmark method |
| β | wave number of the propagating waves |
| δ(x) | is the Kroneckler delta function |
| δ | the parameter used in Newmark method |
| ρ | the mass density of the beam structure |
| Ω | frequency of the propagating waves |
| ωa | natural frequency of the absorber |
References
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Findeisen, C.; Hohe, J.; Kadic, M.; Gumbsch, P. Characteristics of mechanical metamaterials based on buckling elements. J. Mech. Phys. Solids 2017, 102, 151–164. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A. Elastic metamaterials and dynamic homogenization: A review. Int. J. Smart Nano Mater. 2015, 6, 41–60. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, X.N.; Hu, G.K.; Yuan, F.G.; Huang, G.L. Microstructural designs of plate-type elastic metamaterial and their potential applications: A review. Int. J. Smart Nano Mater. 2015, 6, 14–40. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Zhao, H.; Qiu, J. Flexural vibration band gaps in Timoshenko beams with locally resonant structures. J. Appl. Phys. 2006, 100, 124901. [Google Scholar] [CrossRef]
- Pai, P.F. Metamaterial-based broadband elastic wave absorber. J. Intell. Mater. Syst. Struct. 2010, 21, 517–528. [Google Scholar] [CrossRef]
- Pai, P.F.; Peng, H.; Jiang, S. Acoustic metamaterial beams based on multi-frequency vibration absorbers. Int. J. Mech. Sci. 2014, 79, 195–205. [Google Scholar] [CrossRef]
- Peng, H.; Pai, P.F. Acoustic metamaterial plates for elastic wave absorption and structural vibration suppression. Int. J. Mech. Sci. 2014, 89, 350–361. [Google Scholar] [CrossRef]
- Peng, H.; Pai, P.F.; Deng, H. Acoustic multi-stop band metamaterial plates design for broadband elastic wave absorption and vibration suppression. Int. J. Mech. Sci. 2015, 103, 104–114. [Google Scholar] [CrossRef]
- Li, J.-B.; Wang, Y.-S.; Zhang, C. Tuning of acoustic bandgaps in phononic crystals with Helmholtz resonators. J. Vib. Acoust. 2013, 135, 031015. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, X.-Z.; Jiang, W.-Z.; Gu, Y. Tuning of bandgap structures in three-dimensional kagome-sphere lattice. J. Vib. Acoust. 2014, 136, 021016. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, X.N.; Hu, G.K.; Sun, C.T.; Huang, G.L. A chiral elastic metamaterial beam for broadband vibration suppression. J. Sound Vib. 2014, 333, 2759–2773. [Google Scholar] [CrossRef]
- Chen, Y.; Qian, F.; Zuo, L.; Scarpa, F.; Wang, L. Broadband and multiband vibration mitigation in lattice metamaterials with sinusoidally-shaped ligaments. Extreme Mech. Lett. 2017, 17, 24–32. [Google Scholar] [CrossRef]
- He, Z.C.; Xiao, X.; Li, E. Design for structural vibration suppression in laminate acoustic metamaterials. Compos. Part B 2017, 131, 237–252. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Antoniadis, I.; Collet, M.; Ichchou, M. Enhancement of wave damping within metamaterials having embedded negative stiffness inclusions. Wave Motion 2015, 58, 165–179. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Antoniadis, I.; Ampatzidis, T. Enhanced acoustic insulation properties of composite metamaterials having embedded negative stiffness inclusions. Extreme Mech. Lett. 2017, 12, 48–54. [Google Scholar] [CrossRef]
- Wang, P.; Casadei, F.; Shan, S.; Weaver, J.C.; Bertoldi, K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys. Rev. Lett. 2014, 113, 014301. [Google Scholar] [CrossRef] [PubMed]
- Airoldi, L.; Ruzzene, M. Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos. New J. Phys. 2011, 13, 113010. [Google Scholar] [CrossRef]
- Casadei, F.; Delpero, T.; Bergamini, A.; Ermanni, P.; Ruzzene, M. Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials. J. Appl. Phys. 2012, 112, 064902. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, Y.Y.; Barnhart, M.V.; Hu, G.K.; Sun, C.T.; Huang, G.L. Experimental study of an adaptive elastic metamaterial controlled by electric circuits. Appl. Phys. Lett. 2016, 108, 011905. [Google Scholar] [CrossRef]
- Casadei, F.; Bertoldi, K. Harnessing fluid-structure interactions to design self-regulating acoustic metamaterials. J. Appl. Phys. 2014, 115, 034907. [Google Scholar] [CrossRef]
- Xu, Z.; Tong, J.; Wu, F. Magnetorheological elastomer vibration isolation of tunable three-dimensional locally resonant acoustic metamaterial. Solid State Commun. 2018, 271, 51–55. [Google Scholar] [CrossRef]
- Yeh, J.-Y. Control analysis of the tunable phononic crystal with electrorheological material. Physical B 2007, 400, 137–144. [Google Scholar] [CrossRef]
- Rossiter, J.; Takashima, K.; Scarpa, F.; Walters, P.; Mukai, T. Shape memory polymer hexachiral auxetic structures with tunable stiffness. Smart Mater. Struct. 2014, 23, 045007. [Google Scholar] [CrossRef]
- Churchill, C.B.; Shaw, J.A.; Iadicola, M.A. Tips and tricks for characterizing shape memory alloy wire: Part 2-fundamental isothermal responses. Exp. Tech. 2009, 33, 51–62. [Google Scholar] [CrossRef]
- Guda Vishnu, K.; Strachan, A. Shape memory metamaterials with tunable thermo-mechanical response via hetero-epitaxial integration: A molecular dynamics study. J. Appl. Phys. 2013, 113, 103503. [Google Scholar] [CrossRef]
- Williams, K.; Chiu, G.; Bernhard, R. Adaptive-passive absorbers using shape-memory alloys. J. Sound Vib. 2002, 249, 835–848. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chen, C.C.; Yang, T.H.; Lin, C.J. Structural vibration control using a tunable hybrid shape memory material vibration absorber. J. Intell. Mater. Syst. Struct. 2012, 23, 1725–1734. [Google Scholar] [CrossRef]
- Bathe, K.-J. Finite Element Procedures in Engineering Analysis; Prentice-Hall: Upper Saddle River, NJ, USA, 1982. [Google Scholar]
- Thomson, W.T. Theory of Vibration with Applications, 2nd ed.; George Allen and Unwin: London, UK, 1981. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).