Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation
Abstract
:1. Introduction
2. Theory
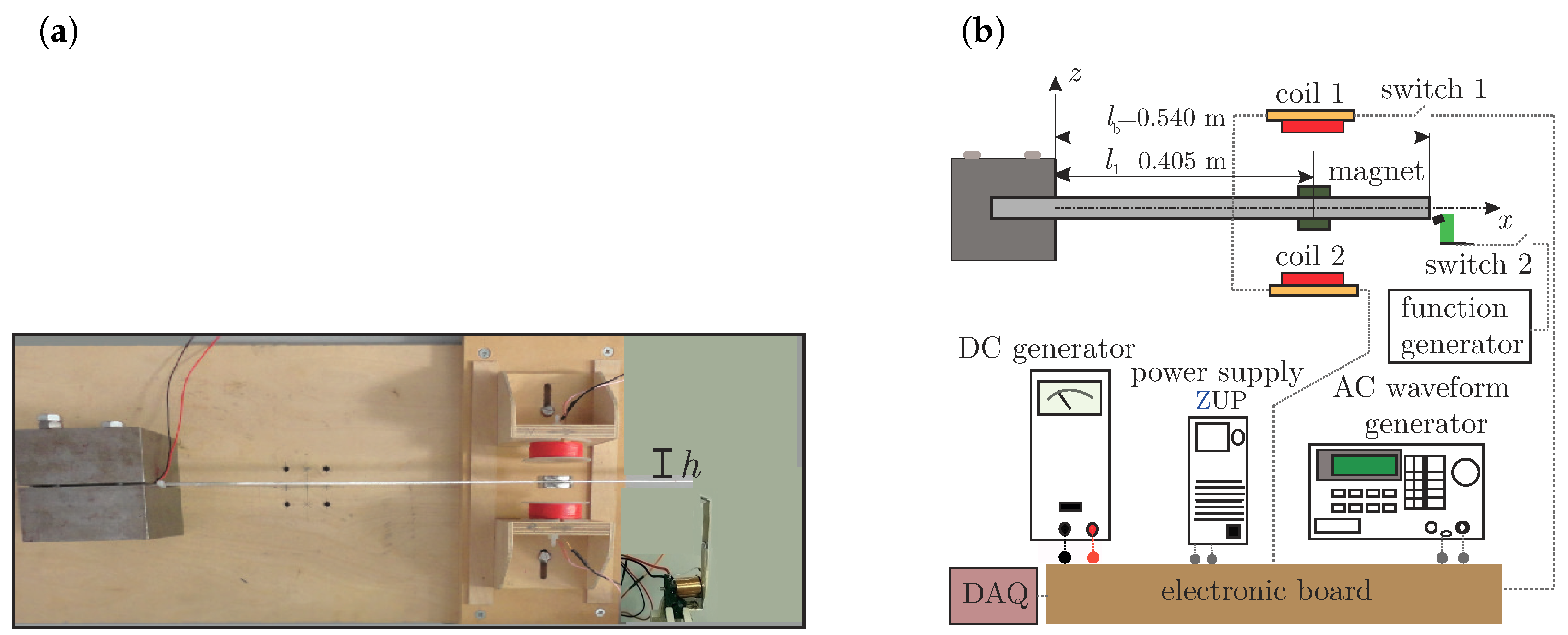
2.1. Apparatus
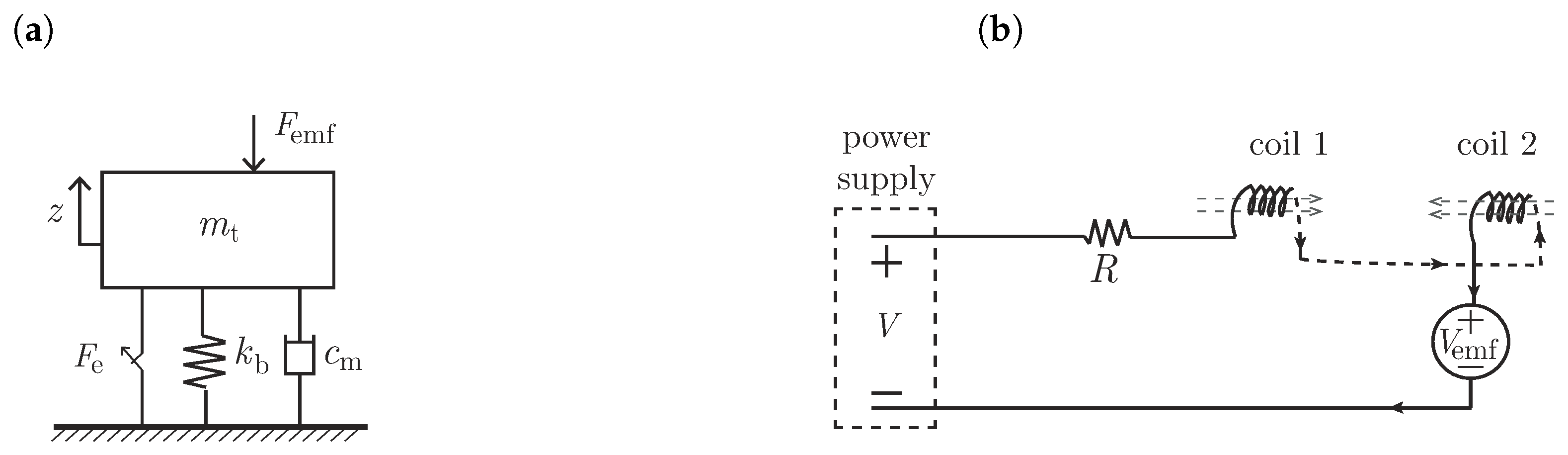
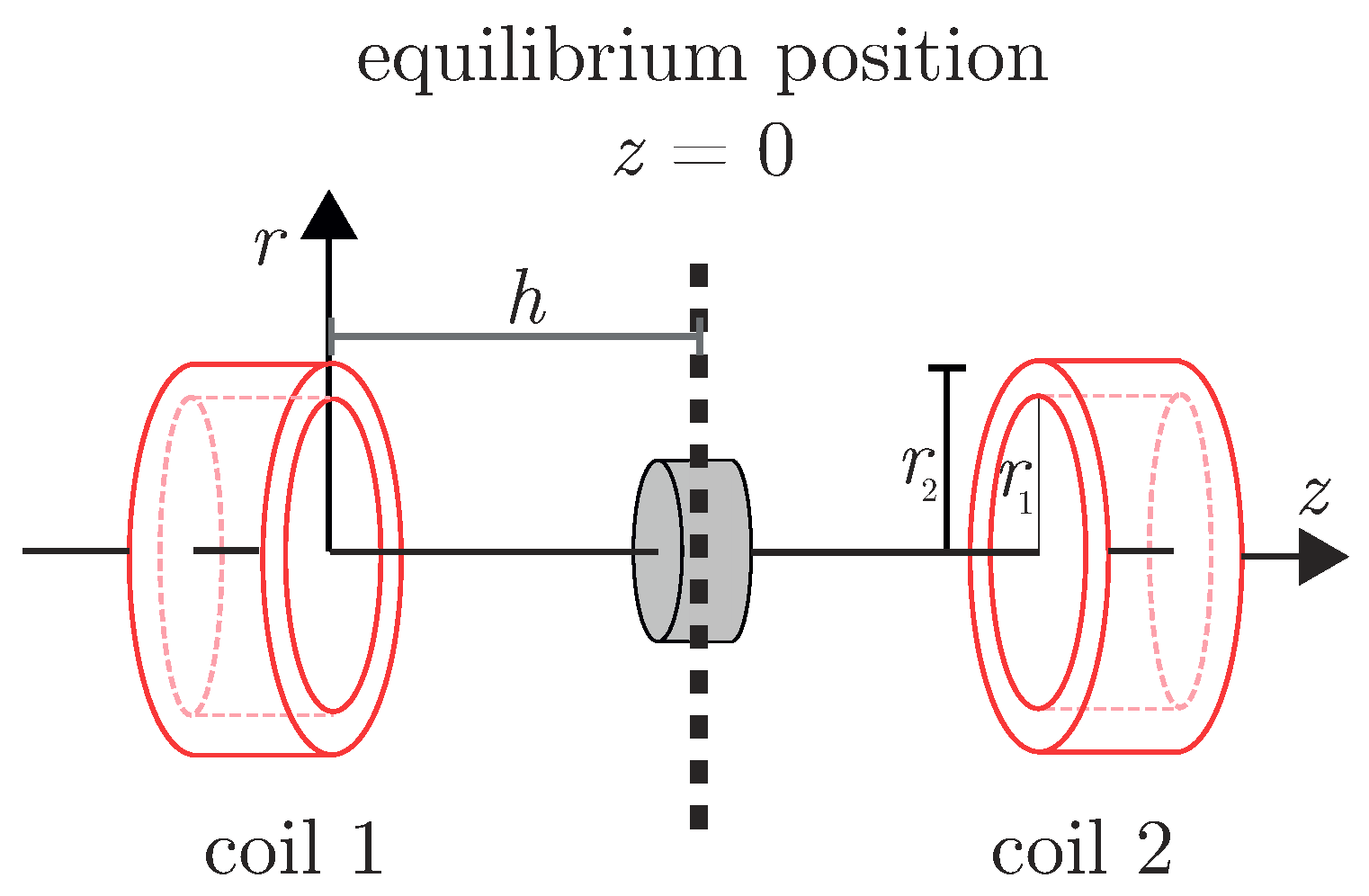
2.2. Mathematical Model
2.3. Parameter Identification
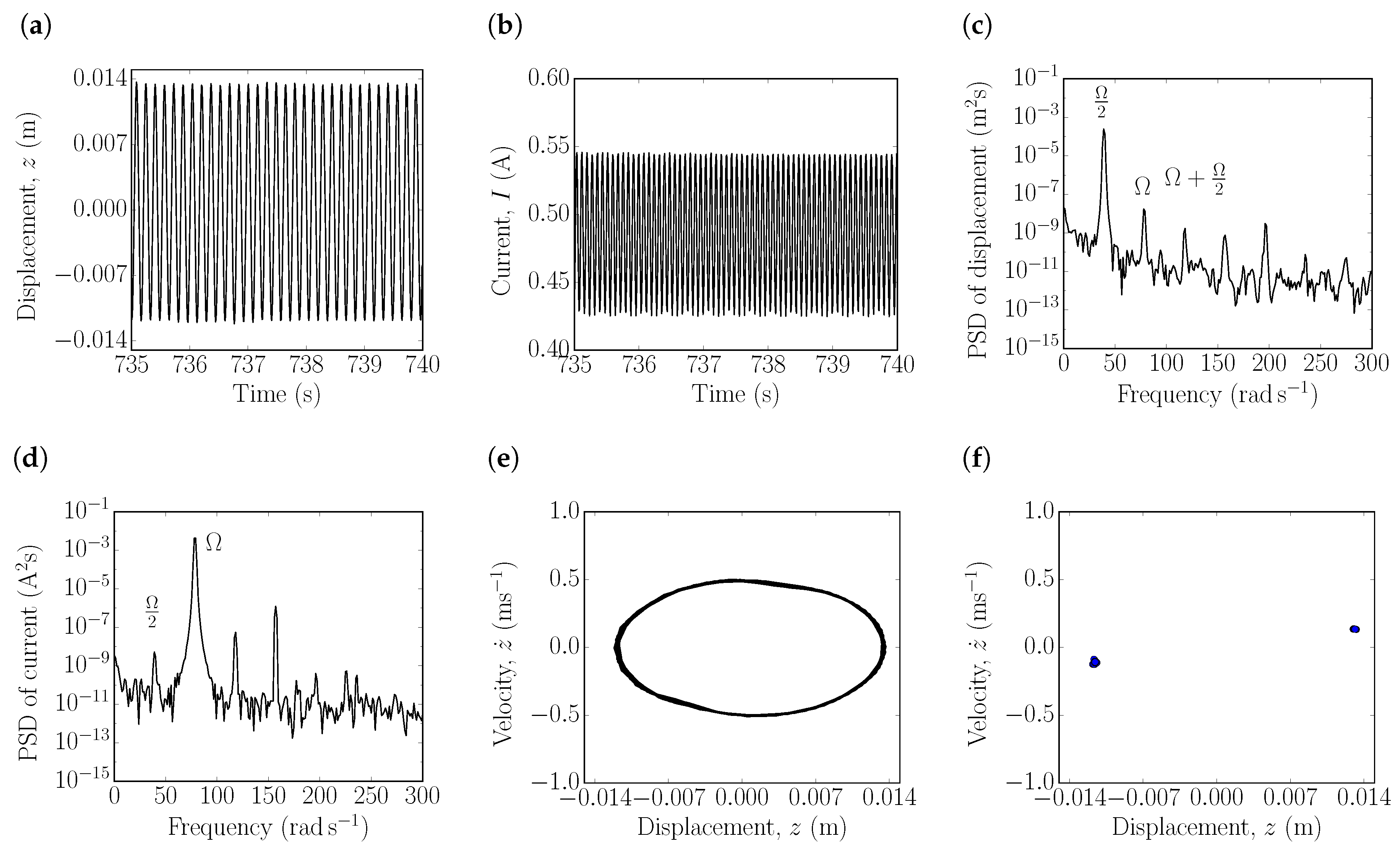
3. Free Response of the NPE System
3.1. Experimental Results
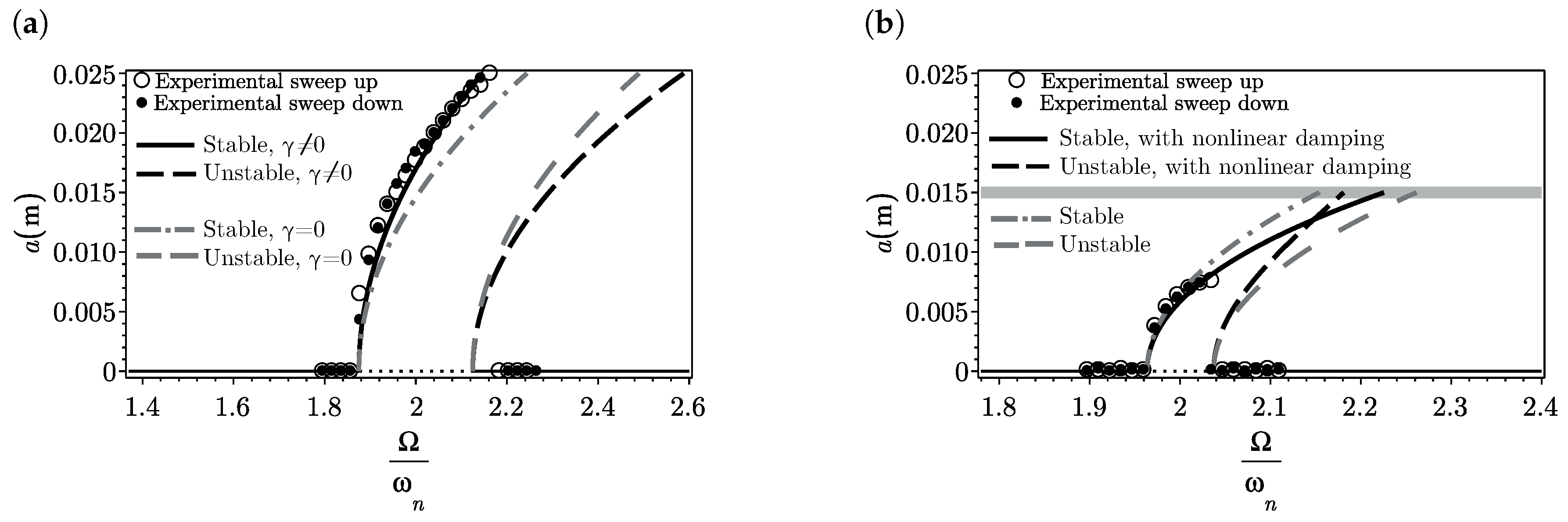
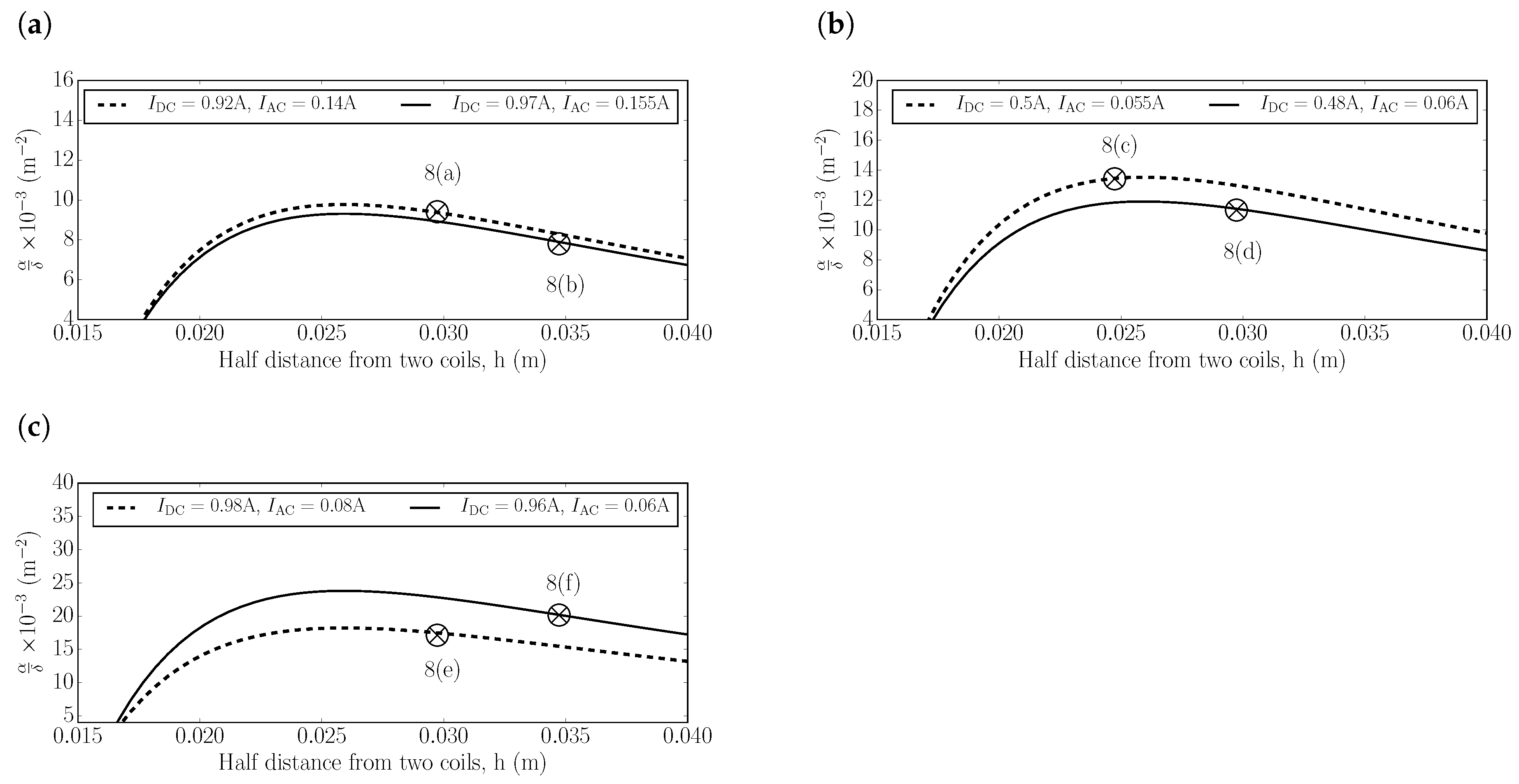
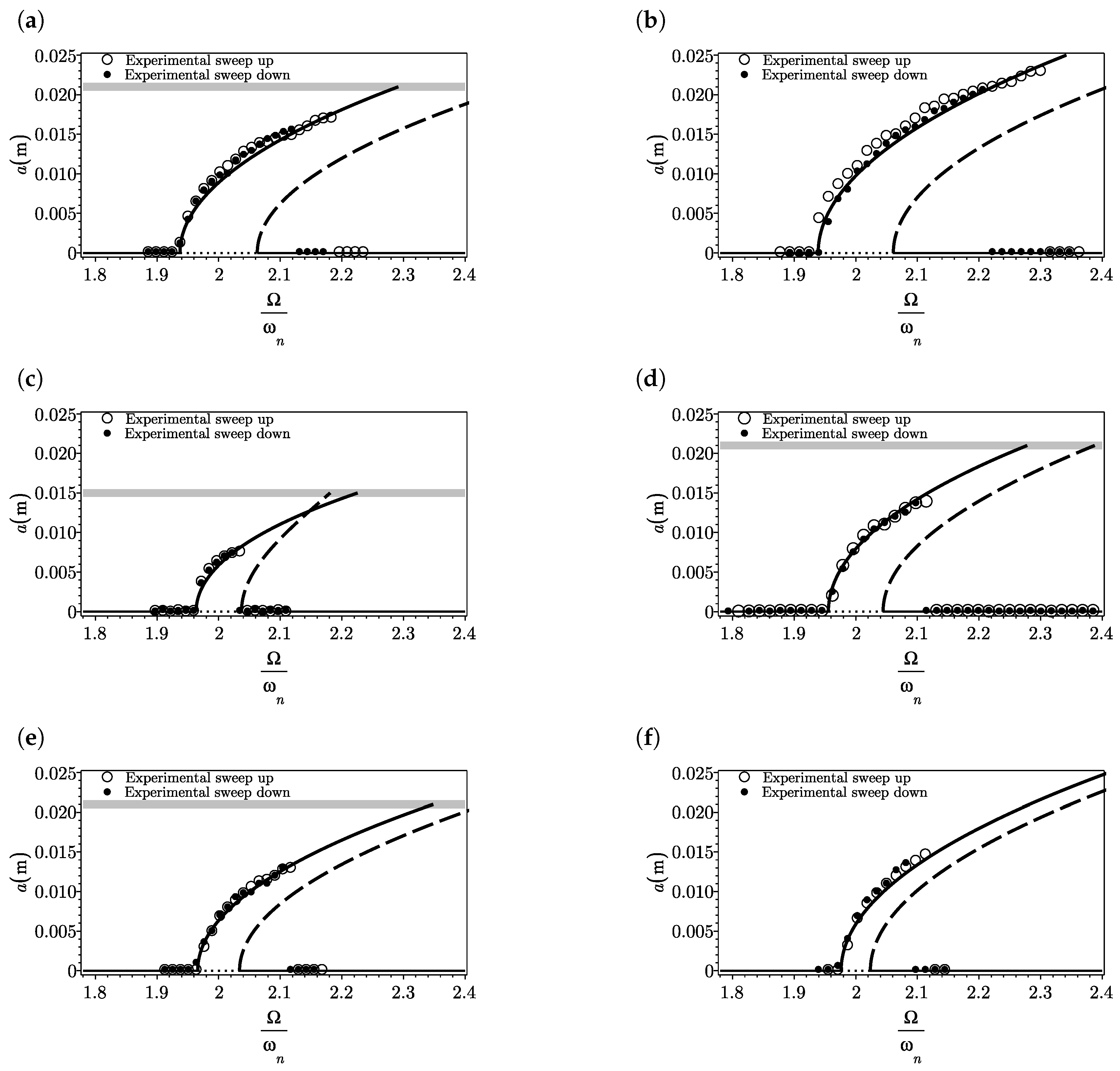
3.2. Effects of Cubic Parametric Stiffness and Nonlinear Damping
3.3. The Effects of Cubic Stiffness
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chivukula, V.B.; Rhoads, J.F. Microelectromechanical bandpass filters based on cyclic coupling architectures. J. Sound Vib. 2010, 329, 4313–4332. [Google Scholar] [CrossRef]
- Dohnal, F. Experimental studies on damping by parametric excitation using electromagnets. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2015–2027. [Google Scholar] [CrossRef]
- Faraday, M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 1831, 121, 299–340. [Google Scholar] [CrossRef]
- Rayleigh, F.L. On maintained vibrations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1883, 15, 229–235. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Ghandchi Tehrani, M. An experimentally validated parametrically excited vibration energy harvester with time-varying stiffness. In SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; pp. 1–13. [Google Scholar]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L.; Baskaran, R. Tunable microelectromechanical filters that exploit parametric resonance. J. Vib. Acoust. 2005, 127, 423–430. [Google Scholar] [CrossRef]
- Welte, J.; Kniffka, T.J.; Ecker, H. Parametric excitation in a two degree of freedom MEMS system. Shock Vib. 2013, 20, 1113–1124. [Google Scholar] [CrossRef]
- Ghandchi Tehrani, M.; Kalkowski, M.K. Active control of parametrically excited systems. J. Intell. Mater. Syst. Struct. 2015, 27, 1218–1230. [Google Scholar] [CrossRef] [Green Version]
- Baskaran, R.; Turner, K. Mechanical domain non-degenerate parametric resonance in torsional mode micro electro mechanical oscillator. TRANSDUCERS 2003. In Proceedings of the 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Boston, MA, USA, 8–12 June 2003; Volume 1, pp. 863–866. [Google Scholar]
- Abou-Rayan, A.M.; Nayfeh, A.H.; Mook, D.T.; Nayfeh, M.A. Nonlinear response of a parametrically excited buckled beam. Nonlinear Dyn. 1993, 4, 499–525. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Bode, D. Exploring the parametric amplification phenomenon for energy harvesting. Proc. Inst. Mech. Eng. 2011, 225, 456–466. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Pai, P.F. Non-linear non-planar parametric responses of an inextensional beam. Int. J. Non-Linear Mech. 1989, 24, 139–158. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Stabler, C.; Qaroush, Y.; Seuaciuc-Osorio, T. Investigation of Power Harvesting via Parametric Excitations. J. Intell. Mater. Syst. Struct. 2009, 20, 545–557. [Google Scholar] [CrossRef]
- Ghaderi, P.; Dick, A.J. Parametric resonance based piezoelectric micro-scale resonators: modeling and theoretical analysis. J. Comput. Nonlinear Dyn. 2013, 8, 011004. [Google Scholar] [CrossRef]
- Dolev, A.; Bucher, I. Tuneable, non-degenerated, nonlinear, parametrically-excited amplifier. J. Sound Vib. 2016, 361, 176–189. [Google Scholar] [CrossRef]
- Cugat, O.; Delamare, J.; Reyne, G. Magnetic micro-actuators and systems (MAGMAS). Trans. Magn. 2003, 39, 3607–3612. [Google Scholar] [CrossRef]
- Chen, C.C.; Yeh, M.K. Parametric instability of a beam under electromagnetic excitation. J. Sound Vib. 2001, 240, 747–764. [Google Scholar] [CrossRef]
- Yeh, M.K.; Kuo, Y.T. Dynamic instability of composite beams under parametric excitation. Compos. Sci. Technol. 2004, 64, 1885–1893. [Google Scholar] [CrossRef]
- Han, Q.; Jianjun, W.; Qihan, L. Experimental study on dynamic characteristics of linear parametrically excited system. Mech. Syst. Signal Process. 2011, 25, 1585–1597. [Google Scholar] [CrossRef]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Transient responses. J. Sound Vib. 2014, 333, 4859–4880. [Google Scholar] [CrossRef]
- Verhulst, F. Nonlinear Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Dohnal, F.; Mace, B.R. Amplification of damping of a cantilever beam by parametric excitation. In Proceedings of the CD MOVIC 2008, Munich, Germany, 15–18 September 2008. [Google Scholar]
- Zaghari, B. Dynamic Analysis of a Nonlinear Parametrically Excited System Using Electromagnets. PhD Thesis, University of Southampton, Southampton, UK, 2016. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wheeler, H.A. Simple inductance formulas for radio coils. Proc. Inst. Radio Eng. 1928, 16, 1398–1400. [Google Scholar] [CrossRef]
- Sneller, A.J.; Mann, B.P. On the nonlinear electromagnetic coupling between a coil and an oscillating magnet. J. Phys. D Appl. Phys. 2010, 43, 295005. [Google Scholar] [CrossRef] [Green Version]
- Wei-Chau, X. Dynamic Stability of Structures; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
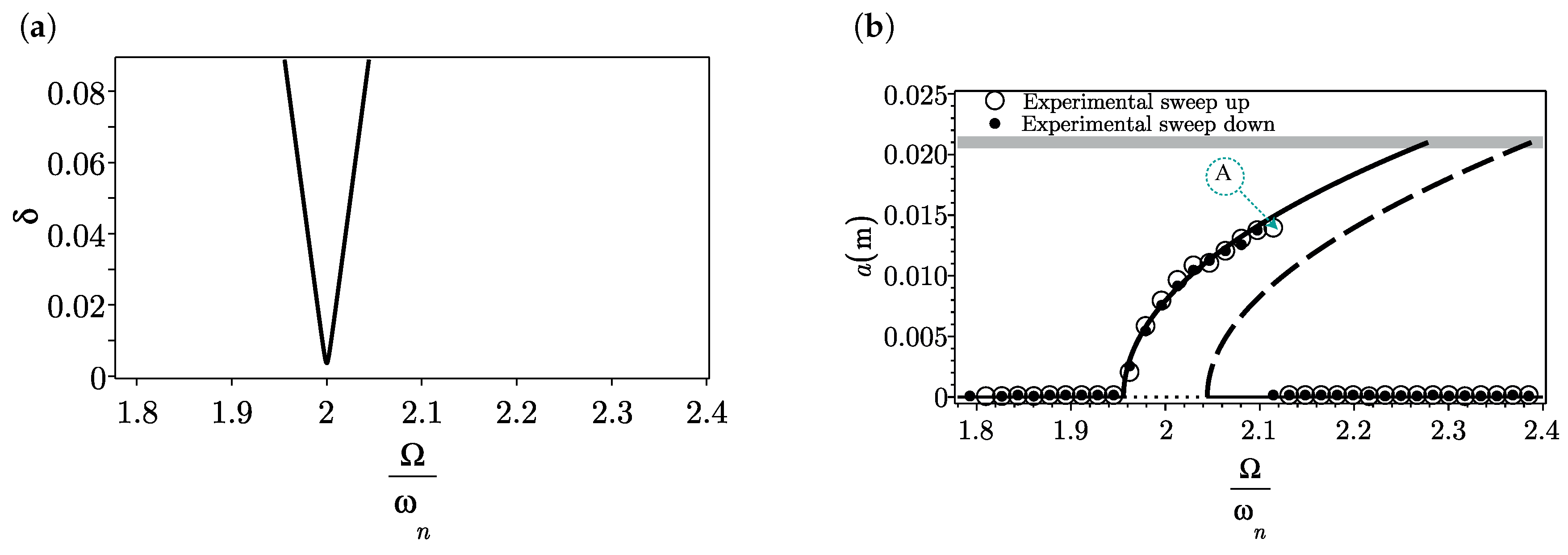
| Property | Value | Units |
|---|---|---|
| Radius of the Neodymium (N42) disc magnets | ||
| Residual magnetic flux density of the permanent magnet () | T | |
| Permeability () | ||
| Inner radius of the coil type L71-3,30 from Mundorf () | ||
| Outer radius of the coil () | ||
| Mean radius of the coil () | ||
| Number of turns of in coil (N) | 485 | - |
| Length of wire in one rotation () | 0.078 | |
| Diameter of the coil () | 0.00071 | |
| Height of the coil with shield () | 0.02 | |
| Coordinate for coil () | 0.007 | |
| Coordinate for coil () | −0.007 | |
| Measured electrical resistance of the coil and extra wiring () | 1.91 | Ohm |
| Resistor (R) | 0.1 | Ohm |
| Width of the beam () | ||
| Thickness of the beam () | ||
| Total physical mass (the effective mass of the beam and magnets) () | ||
| Static stiffness of the beam with magnets and coils when () | 32.84 | |
| Measured first natural frequency of the beam with magnets and coils when () | 17.76 | |
| Measured second natural frequency of the beam with magnets and coils when | 202 | |
| Mechanical damping coefficient of the beam with magnets and coils when () | 0.011 |
| Tests | Measured Parameters | Calculated Parameters from Equations (23)–(28) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| h (m) | () | ||||||||
| Figure 6a | 0.035 | 0.001 | 30.77 | 78.46 | 14.18 | 17762.4 | 0.25 | 782.63 | Refer to Figure 6a |
| Figure 6b | 0.025 | 0.001 | 50.3 | Refer to Figure 6b | 0.093 | 1262.17 | 138.83 | ||
| Tests | Measured Parameters | Calculated Parameters from Equations (23)–(28) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| h (m) | (A) | (A) | () | ||||||||
| Figure 8a | 0.03 | 0.92 | 0.14 | 0.001 | 48.60 | 146 | 17.44 | 24,761.7 | 0.129 | 1203.19 | 183.1 |
| Figure 8b | 0.035 | 0.97 | 0.155 | 0.001 | 40.12 | 60.16 | 8.93 | 11,188.82 | 0.122 | 956.40 | 152.82 |
| Figure 8c | 0.025 | 0.50 | 0.055 | 0.001 | 50.3 | 430.26 | 56.33 | 83,508.47 | 0.093 | 1262.17 | 138.83 |
| Figure 8d | 0.03 | 0.48 | 0.06 | 0.001 | 37.11 | 191.26 | 28.82 | 40,897.67 | 0.092 | 1055.86 | 131.98 |
| Figure 8e | 0.03 | 0.98 | 0.08 | 0.001 | 49.23 | 144.17 | 16.55 | 23,497.5 | 0.069 | 1214.5 | 99.14 |
| Figure 8f | 0.035 | 0.96 | 0.06 | 0.001 | 39.81 | 60.64 | 9 | 11,277.63 | 0.047 | 954.05 | 59.62 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaghari, B.; Rustighi, E.; Ghandchi Tehrani, M. Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation. Vibration 2018, 1, 157-171. https://doi.org/10.3390/vibration1010012
Zaghari B, Rustighi E, Ghandchi Tehrani M. Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation. Vibration. 2018; 1(1):157-171. https://doi.org/10.3390/vibration1010012
Chicago/Turabian StyleZaghari, Bahareh, Emiliano Rustighi, and Maryam Ghandchi Tehrani. 2018. "Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation" Vibration 1, no. 1: 157-171. https://doi.org/10.3390/vibration1010012
APA StyleZaghari, B., Rustighi, E., & Ghandchi Tehrani, M. (2018). Improved Modelling of a Nonlinear Parametrically Excited System with Electromagnetic Excitation. Vibration, 1(1), 157-171. https://doi.org/10.3390/vibration1010012





