Study of Temperature Distribution in U-Shaped Underwater Tunnel Fires Under the Influence of Induced Airflow
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Model Design
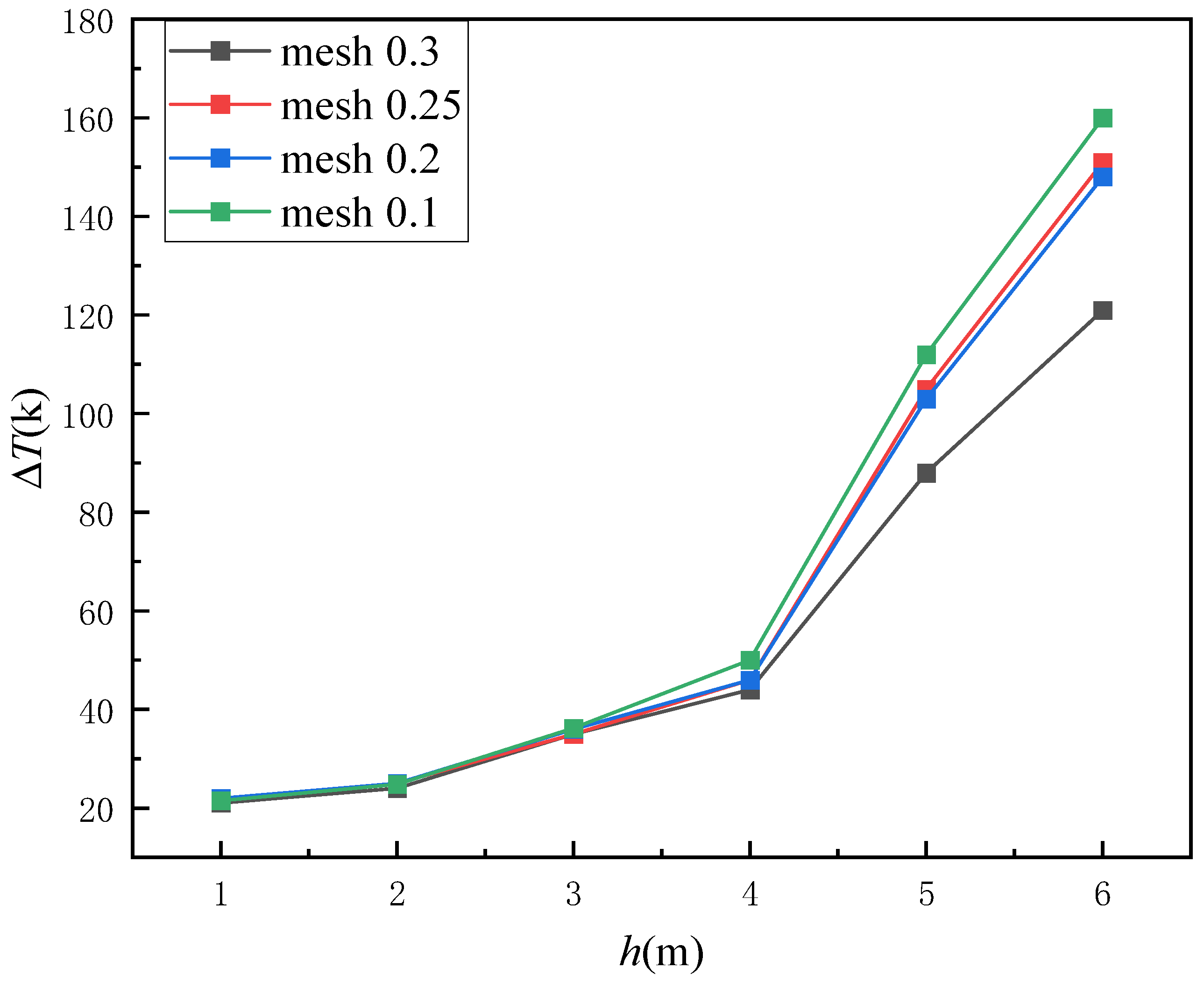
2.2. Mesh Size Setting
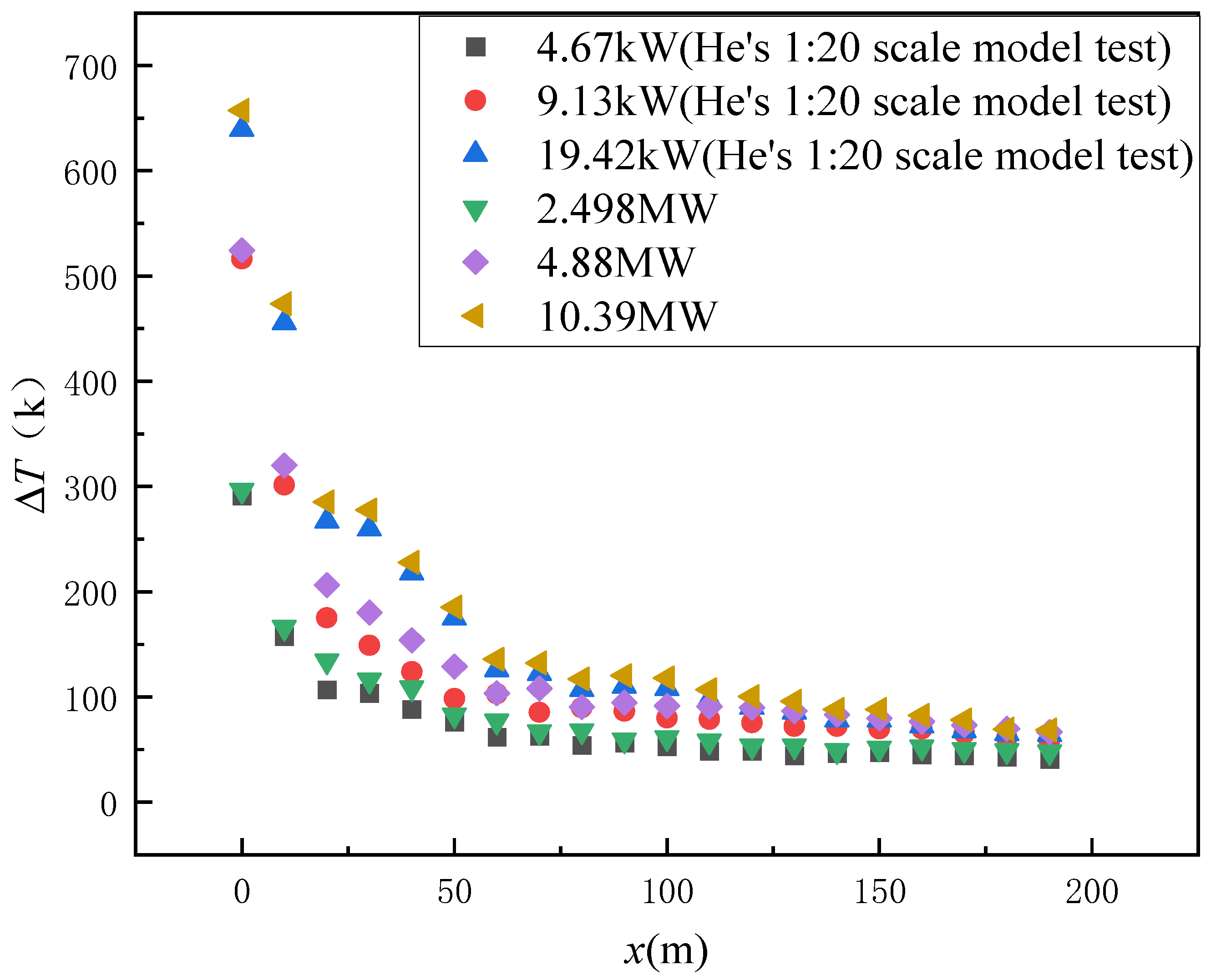
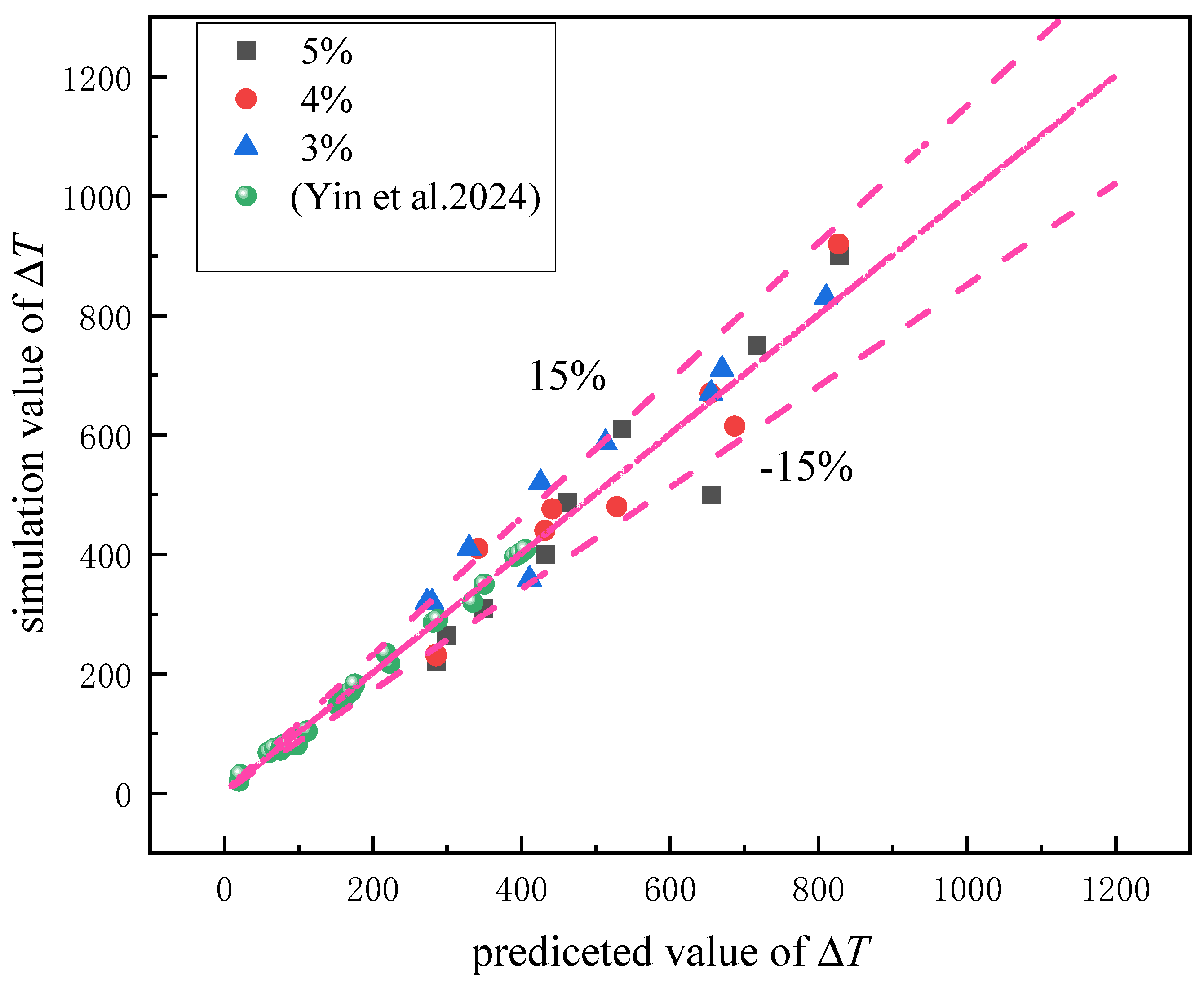
2.3. Mesh Accuracy Verification
3. Result and Discussion
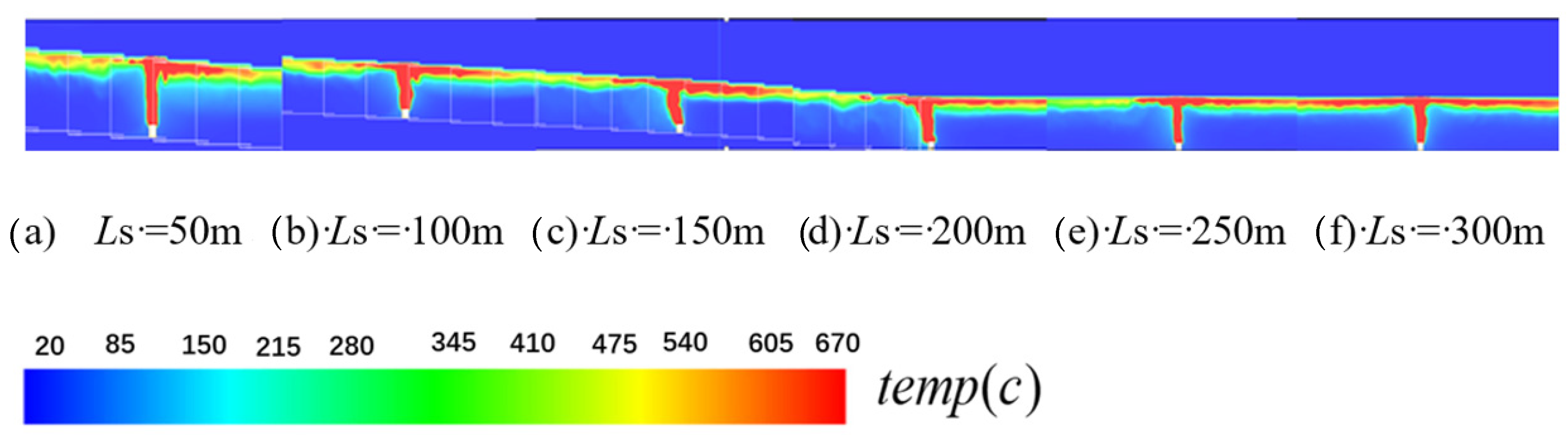
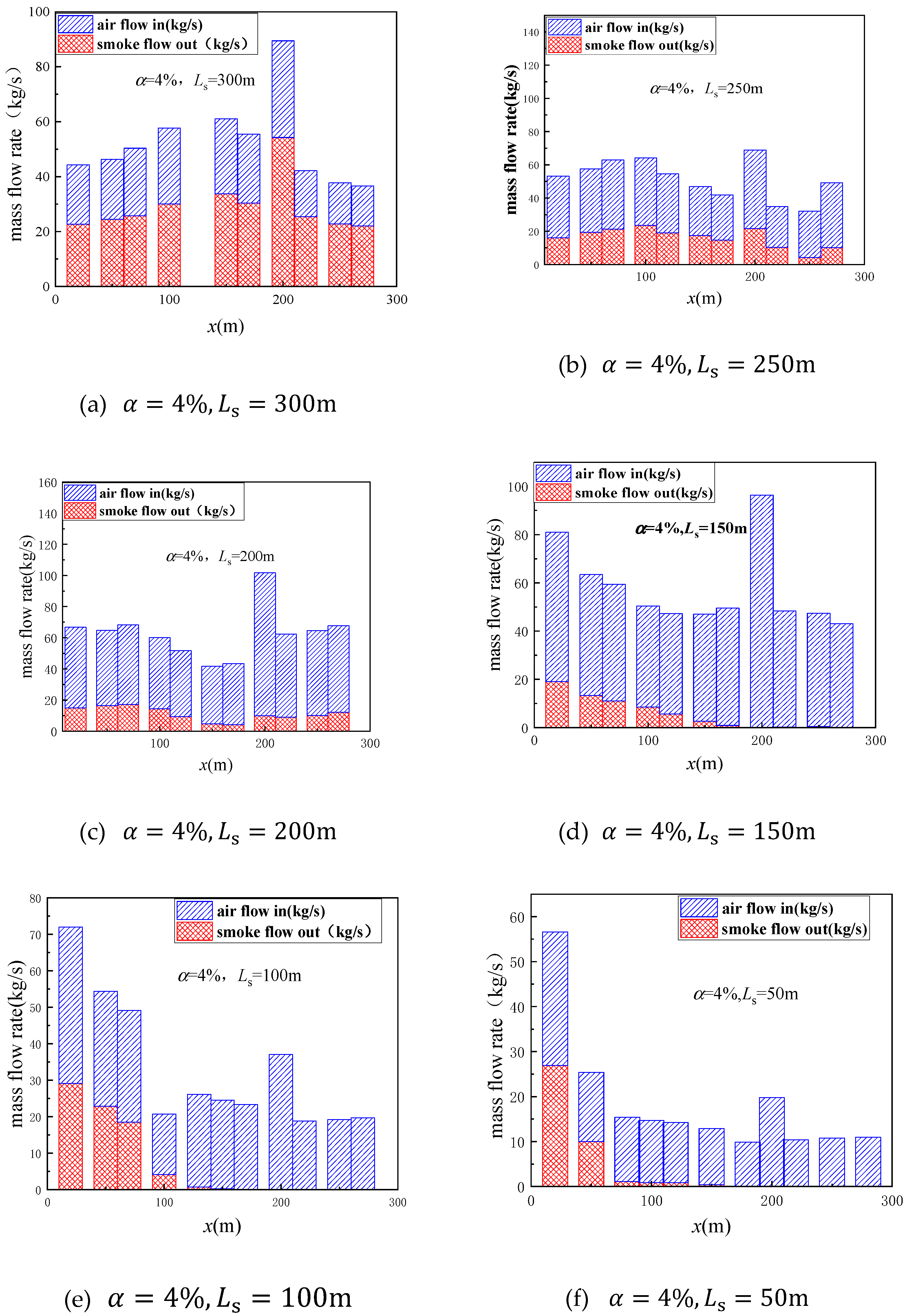
3.1. Changes in the Heat Transfer Proportion Under Induced Airflow
- (1)
- Temperature variation of 5 MW
- (2)
- Mass flow distribution after longitudinal position change of 5 MW fires
- (3)
- Changes in heat transfer proportion under the influence of induced airflow
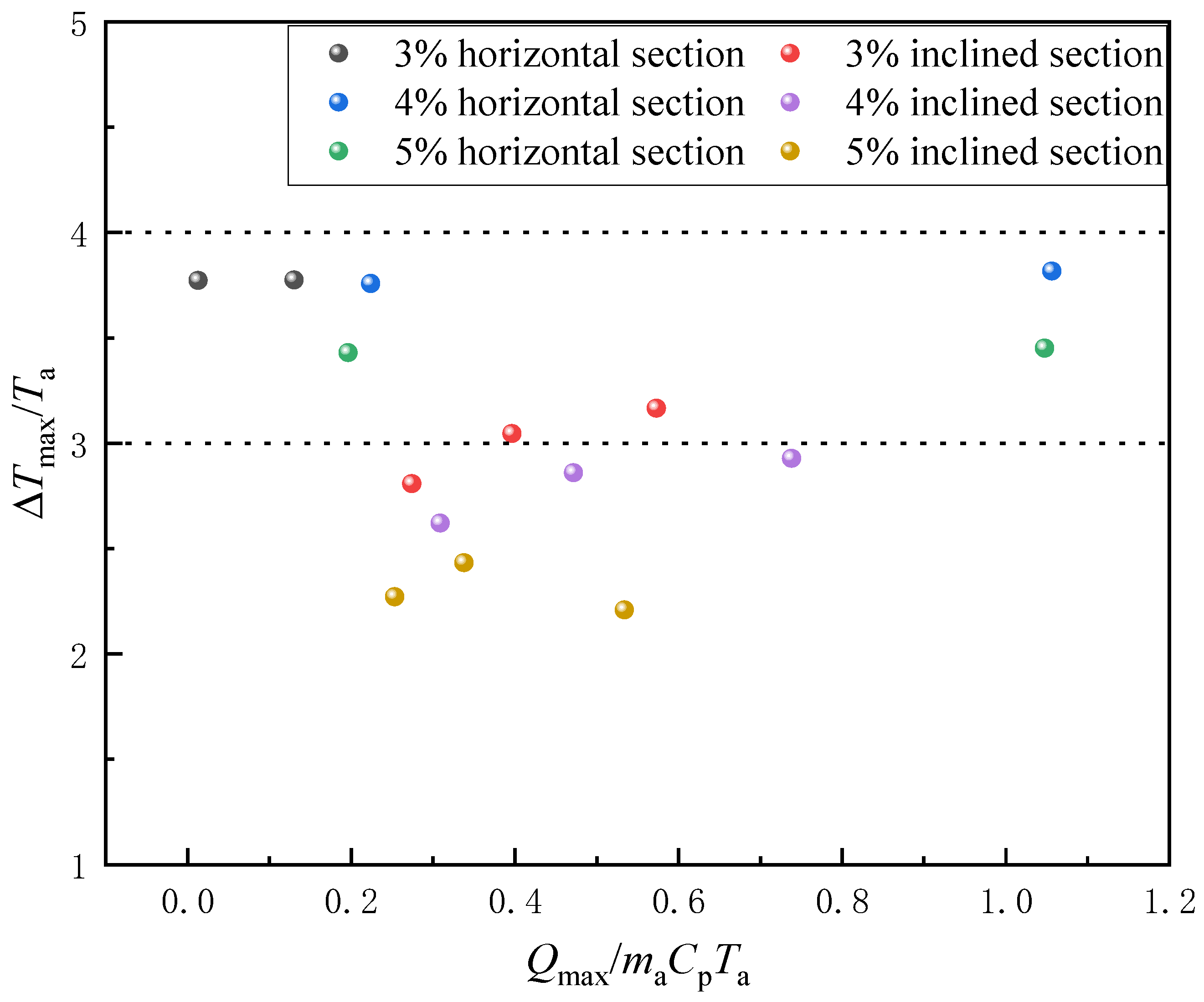
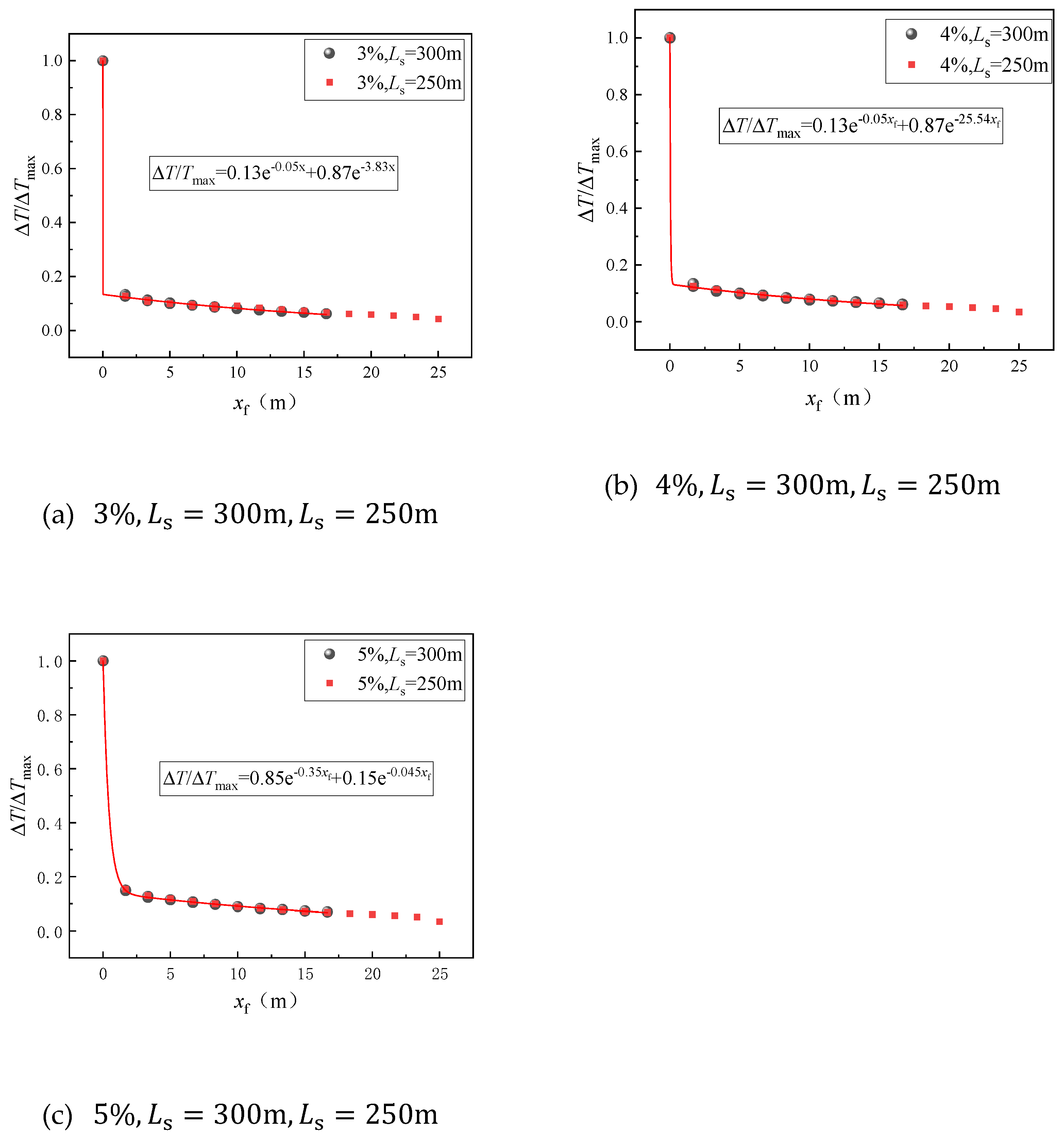
3.2. Temperature Field Under the Influence of Weak Induced Airflow
- (1)
- Maximum excess temperature under weak induced airflow
- (2)
- Longitudinal temperature decay under weak induced airflow
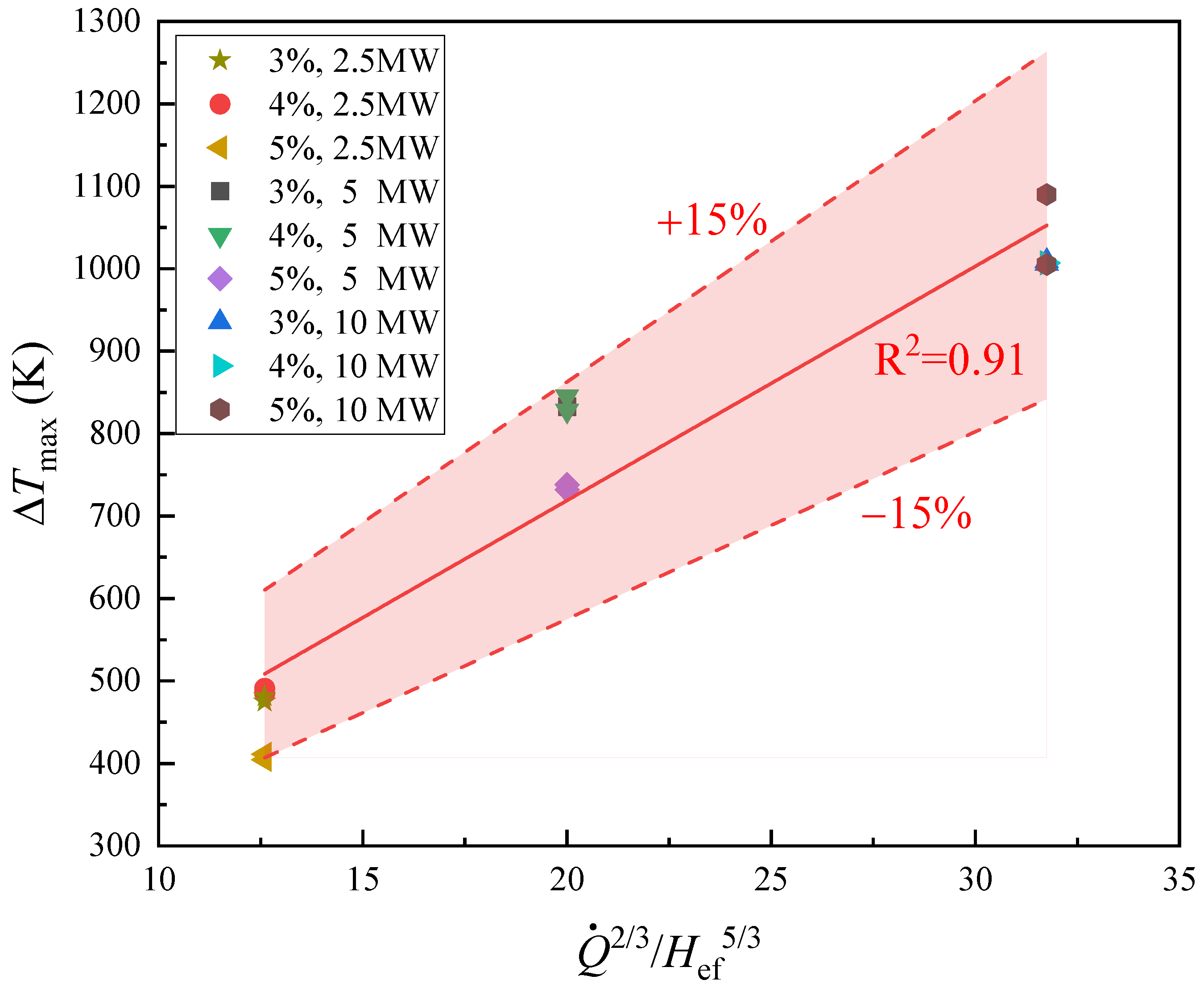
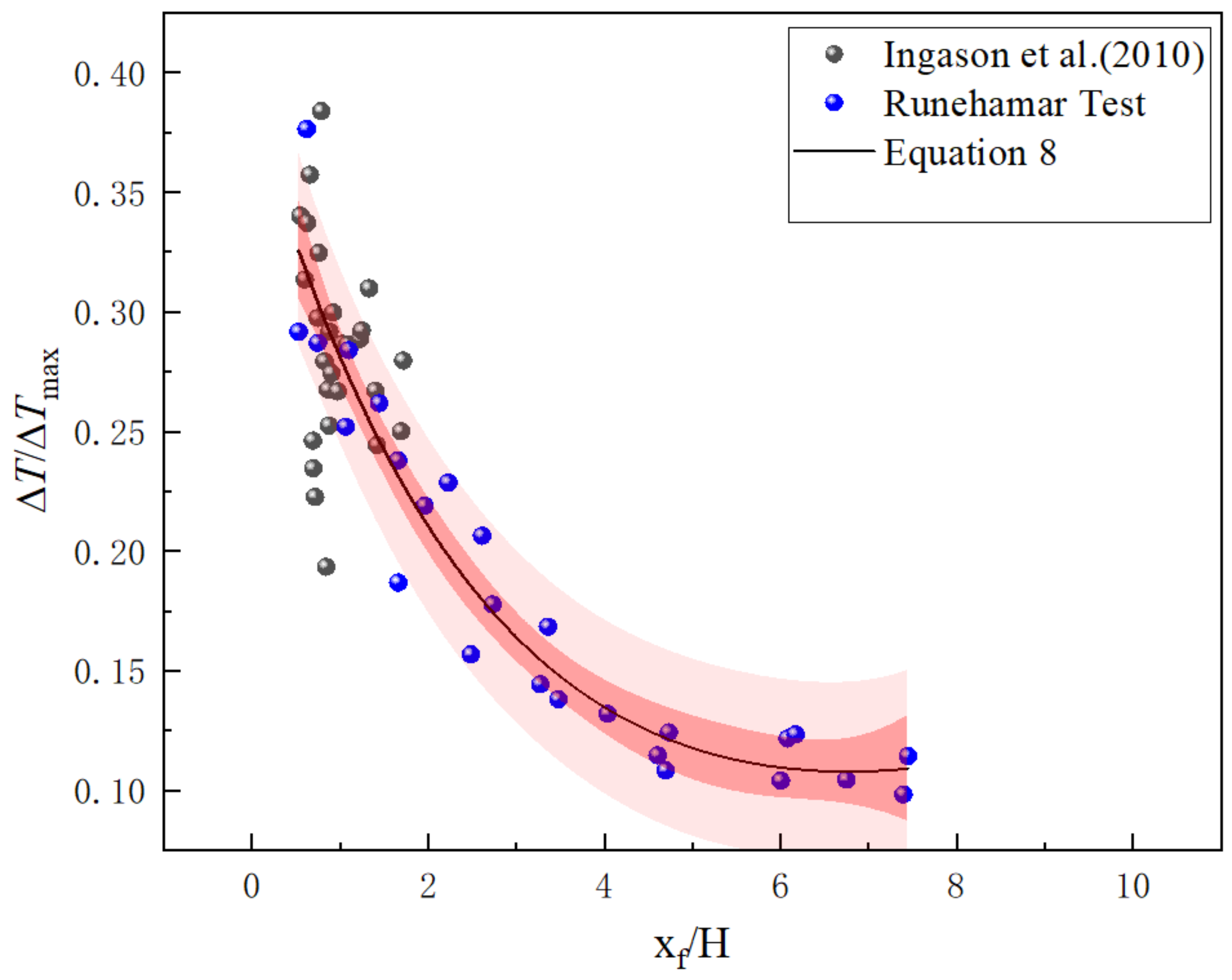
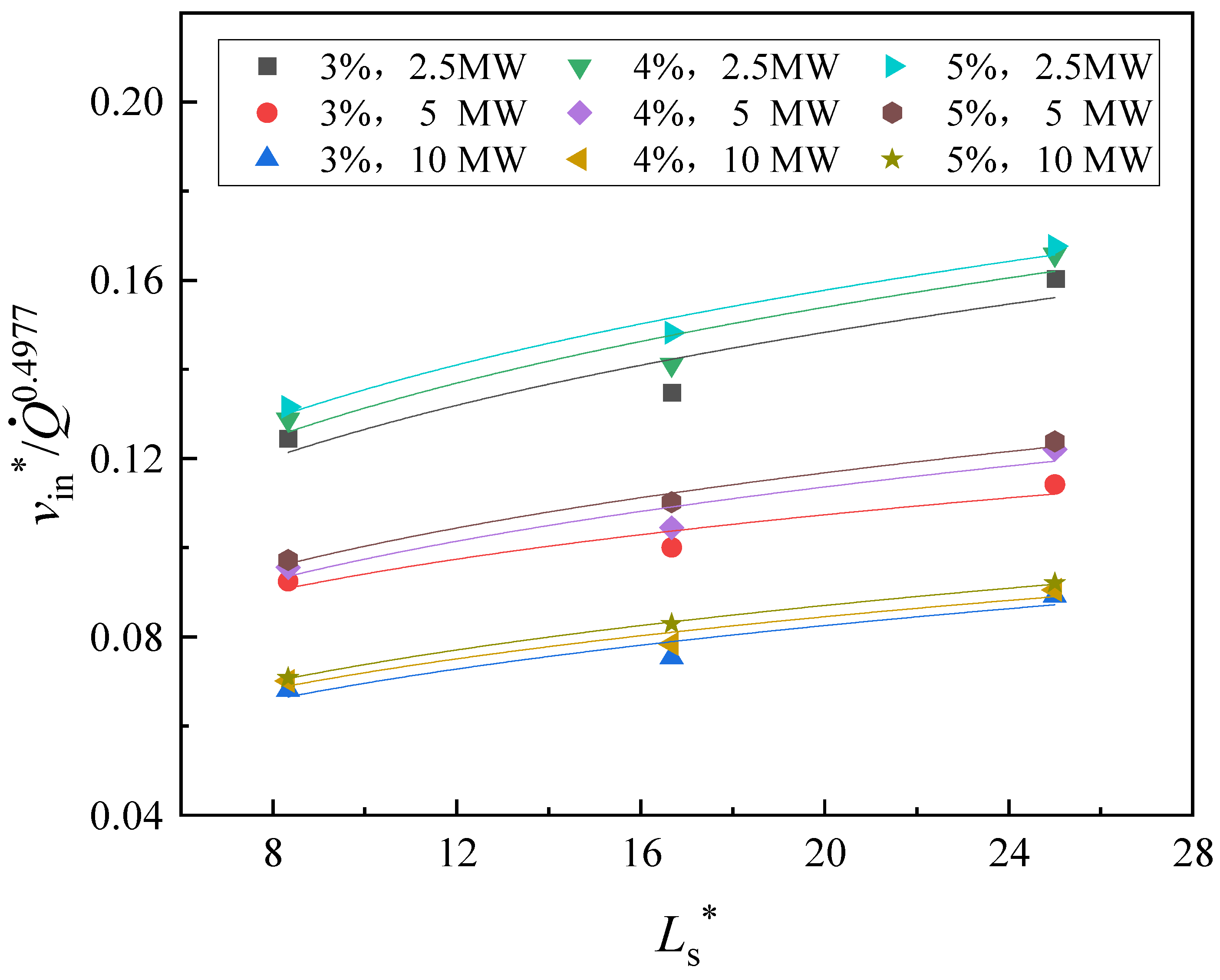
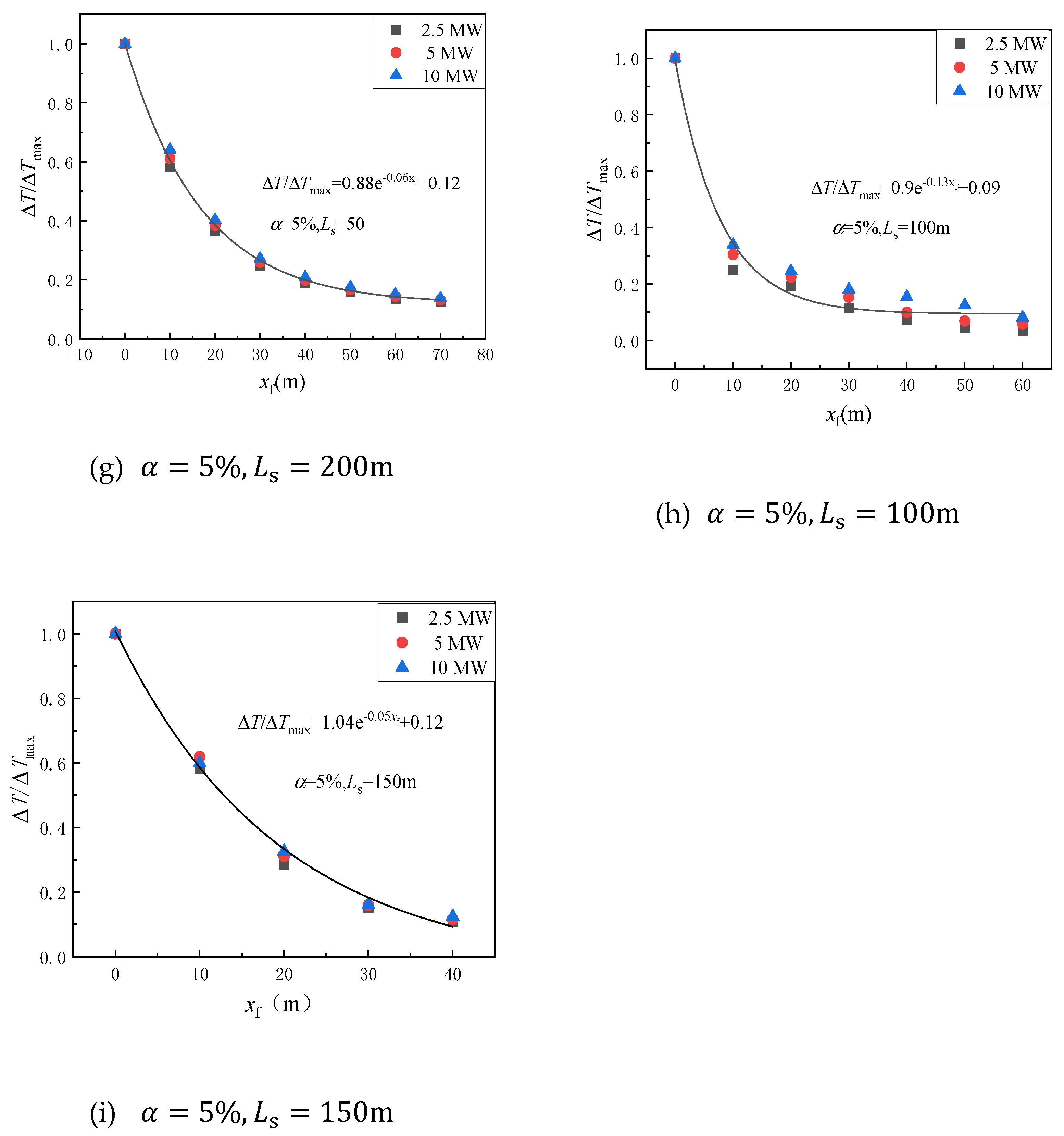
3.3. Temperature Field Under the Influence of Strong Induced Airflow
- (1)
- Maximum excess temperature under strong induced airflow
- (2)
- Longitudinal temperature decay under strong induced airflow
4. Conclusions
- (1)
- In the U-shaped tunnel, as the fire moves towards the left opening, the stack effect upstream of the fire source becomes more pronounced, and the temperature decays more rapidly. At the same time, there is a critical transition point for the change between strong and weak induced airflow near the corner. When the inclination angle is small, this position is located above the corner. As the inclination angle increases, the position gradually moves towards the fire-source side.
- (2)
- In the case where the fire-source location is in the horizontal section of the tunnel, heat transfer within the tunnel is primarily dominated by thermal radiation. In this scenario, weak induced airflow occurs, making ventilation challenging. A prediction model for the maximum excess temperature and longitudinal temperature decay is developed, considering the impact of varying HRRs of the fire, various inclination angles, and different longitudinal positions.
- (3)
- In the case where the fire-source location is in the inclined section of the tunnel, the heat transfer mechanism is dominated by convective heat transfer, indicating strong induced airflow. The mass flow rate of incoming air is used to predict temperature under the influence of two factors: distinct longitudinal locations of the fire source and varying inclination angles. Prediction models are proposed for longitudinal temperature decrease and maximum excess temperature, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Heat release rate (kW) | |
| Maximum of heat release rate (kW) | |
| Convection of the HRR (kW) | |
| Dimensionless heat release rate | |
| Tunnel height (m) | |
| Effective height of tunnel (m) | |
| Tunnel width (m) | |
| Tunnel perimeter (m) | |
| Distance from the fire source to the left opening (m) | |
| Distance from fire source (m) | |
| Mesh size (m) | |
| Dimensionless fire-source characteristic diameter | |
| Slope angle | |
| Ambient pressure (pa) | |
| Total heat transfer coefficient (kW/m2⋅k) | |
| χr | Percentage of radiation of heat transfer |
| Maximum excess temperature (K) | |
| Temperature difference between smoke and ambient air (K) | |
| Average temperature difference between smoke and ambient air (K) | |
| Temperature of ambient air (K) | |
| Density of ambient air (kg/m3) | |
| Specific heat capacity (J/kg·g) | |
| Induced airflow velocity (m/s) | |
| Dimensionless induced airflow velocity | |
| Coefficients related to the angle | |
| Gravitational acceleration (m/s2) | |
| Mass flow rate of air (kg/s) | |
| Mass flow rate of smoke (kg/s) |
References
- Alpert, R.L. Calculation of response time of ceiling-mounted fire detectors. Fire Technol. 1972, 8, 181–195. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Huo, Y.; Gao, Y.; Chow, W.K. A study on ceiling jet characteristics in an inclined tunnel. Tunn. Undergr. Sp. Tech. 2015, 50, 32–46. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Yao, Y.; Zhu, K.; Zhou, Y.; Shi, L.; Cheng, X. Numerical Investigation of Back-Layering Length and Critical Velocity in Curved Subway Tunnels with Different Turning Radius. Fire Technol. 2017, 53, 1765–1793. [Google Scholar] [CrossRef]
- Chow, W.K.; Gao, Y.; Zou, J.F.; Liu, Q.K.; Chow, C.L.; Miao, L. Numerical Studies on Thermally-Induced Air Flow in Sloping Tunnels with Experimental Scale Modelling Justifications. Fire Technol. 2018, 54, 867–892. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Y.Z.; Kumm, M.; Ingason, H.; Liu, F. Re-direction of smoke flow in inclined tunnel fires. Tunn. Undergr. Sp. Tech. 2019, 86, 113–127. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.; Xu, Q.; Yang, L. The inclination effect on CO generation and smoke movement in an inclined tunnel fire. Tunn. Undergr. Sp. Tech. 2012, 29, 78–84. [Google Scholar] [CrossRef]
- Ji, J.; Wan, H.; Li, K.; Han, J.; Sun, J. A numerical study on upstream maximum temperature in inclined urban road tunnel fires. Int. J. Heat. Mass. Tran. 2015, 88, 516–526. [Google Scholar] [CrossRef]
- Fan, C.G.; Li, X.Y.; Mu, Y.; Guo, F.Y.; Ji, J. Smoke movement characteristics under stack effect in a mine laneway fire. Appl. Therm. Eng. 2017, 110, 70–79. [Google Scholar] [CrossRef]
- He, L.; Liao, K.; Zhu, G. Study on the influence of the longitudinal position of fire source and tunnel width on the maximum ceiling gas temperature. Case Stud. Therm. Eng. 2023, 52, 103731. [Google Scholar] [CrossRef]
- Huang, P.; Ye, S.; Xie, J.; Chen, M.; Liu, C.; Yu, L. Study on the maximum and longitudinal distribution of ceiling gas temperature in a naturally ventilated tunnel: The effect of longitudinal fire location. Int. J. Therm. Sci. 2023, 185, 108037. [Google Scholar] [CrossRef]
- Chen, C.; Jiao, W.; Zhang, Y.; Shi, C.; Lei, P.; Fan, C. Experimental investigation on the influence of longitudinal fire location on critical velocity in a T-shaped tunnel fire. Tunn. Undergr. Sp. Tech. 2023, 134, 104983. [Google Scholar] [CrossRef]
- Li, X.; Zhu, G.; He, L. Study on the smoke mass flow in T-shaped tunnel fire. Case Stud. Therm. Eng. 2024, 61, 104848. [Google Scholar] [CrossRef]
- Qie, Y.; Li, J.; Li, Y.; Zhao, H.; Lin, X.; Li, D.; Hou, S.; Wang, Z. Experimental Study on the Impact of Smoke Exhaust Rate and Exhaust Vent Opening Mode on the Smoke Control Effect of the Point Smoke Exhaust System in an Asymmetric V-Shaped Tunnel. Fire 2025, 8, 162. [Google Scholar] [CrossRef]
- Wang, J.; Gao, D.; Kong, X.; Jiang, X.; Lu, K. Water spray effects on fire smoke temperature distribution beneath a symmetrical V-shaped tunnel ceiling. Case Stud. Therm. Eng. 2023, 51, 103568. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Yang, D. Experimental study on the effects of exhaust vent layout on plug-holing for ceiling central smoke extraction in road tunnel fires. Tunn. Undergr. Sp. Tech. 2022, 126, 104550. [Google Scholar] [CrossRef]
- Hu, L.H.; Xu, Y.; Zhu, W.; Wu, L.; Tang, F.; Lu, K.H. Large eddy simulation of pollutant gas dispersion with buoyancy ejected from building into an urban street canyon. J. Hazard. Mater. 2011, 192, 940–948. [Google Scholar] [CrossRef]
- Ko, J.; Yoon, C.; Yoon, S.; Kim, J. Determination of the applicable exhaust airflow rate through a ventilation shaft in the case of road tunnel fires. Saf. Sci. 2010, 48, 722–728. [Google Scholar] [CrossRef]
- Kong, J.; Xu, Z.; You, W.; Wang, B.; Liang, Y.; Chen, T. Study of smoke back-layering length with different longitudinal fire locations in inclined tunnels under natural ventilation. Tunn. Undergr. Sp. Tech. 2021, 107, 103663. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, X.; Xiao, N.; Liao, X.; Fan, C. Influence of the competitive effect of V-shaped slope tunnel on smoke characteristics. Tunn. Undergr. Sp. Tech. 2021, 118, 104193. [Google Scholar] [CrossRef]
- Tilley, N.; Rauwoens, P.; Merci, B. Verification of the accuracy of CFD simulations in small-scale tunnel and atrium fire configurations. Fire Saf. J. 2011, 46, 186–193. [Google Scholar] [CrossRef]
- He, L.; Liao, K.; Zhou, Y.; Tao, H.; Ming, Y.; Wang, X.; Zhang, H.; Zhu, G. Study on the influence of the longitudinal position of the fire source on the movement behavior of the asymmetric flow field. Therm. Sci. Eng. Prog. 2023, 39, 101753. [Google Scholar] [CrossRef]
- Hu, L.H.; Fong, N.K.; Yang, L.Z.; Chow, W.K.; Li, Y.Z.; Huo, R. Modeling fire-induced smoke spread and carbon monoxide transportation in a long channel: Fire Dynamics Simulator comparisons with measured data. J. Hazard. Mater. 2007, 140, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Z.; Lei, B.; Ingason, H. Scale modeling and numerical simulation of smoke control for rescue stations in long railway tunnels. J. Fire Prot. Eng. 2012, 22, 101–131. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, F.; Chen, L.; Wang, Q.; Xu, X. Effect of lateral concentrated smoke extraction on the smoke back-layering length and critical velocity in a longitudinal ventilation tunnel. J. Wind. Eng. Ind. Aerod 2020, 207, 104403. [Google Scholar] [CrossRef]
- Ming, Y.; Zhu, G.; He, L.; Liu, X.; Zhou, Y.; Ding, J. Study on the maximum excess temperature and temperature distribution under the influence of lateral smoke exhaust in tunnel fires. Therm. Sci. Eng. Prog. 2023, 40, 101713. [Google Scholar] [CrossRef]
- Weng, M.; Lu, X.; Liu, F.; Du, C. Study on the critical velocity in a sloping tunnel fire under longitudinal ventilation. Appl. Therm. Eng. 2016, 94, 422–434. [Google Scholar] [CrossRef]
- Ji, J.; Guo, F.; Gao, Z.; Zhu, J. Effects of ambient pressure on transport characteristics of thermal-driven smoke flow in a tunnel. Int. J. Therm. Sci. 2018, 125, 210–217. [Google Scholar] [CrossRef]
- Merci, B. One-dimensional analysis of the global chimney effect in the case of fire in an inclined tunnel. Fire Saf. J. 2008, 43, 376–389. [Google Scholar] [CrossRef]
- Wan, H.; Gao, Z.; Han, J.; Ji, J.; Ye, M.; Zhang, Y. A numerical study on smoke back-layering length and inlet air velocity of fires in an inclined tunnel under natural ventilation with a vertical shaft. Int. J. Therm. Sci. 2019, 138, 293–303. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. Study of critical velocity and backlayering length in longitudinally ventilated tunnel fires. Fire Saf. J. 2010, 45, 361–370. [Google Scholar] [CrossRef]
- Oka, Y.; Kakae, N.; Imazeki, O.; Inagaki, K. Temperature Property of Ceiling Jet in an Inclined Tunnel. Procedia Eng. 2013, 62, 234–241. [Google Scholar] [CrossRef]
- Yin, Y.; Xu, Z.; Lei, Z.; Xie, B.; Liu, Q. Study of air supplement velocity by thermal stack effect and critical velocity under longitudinal ventilation in the uniclinal V-shaped tunnel. Case Stud. Therm. Eng. 2024, 60, 104723. [Google Scholar] [CrossRef]


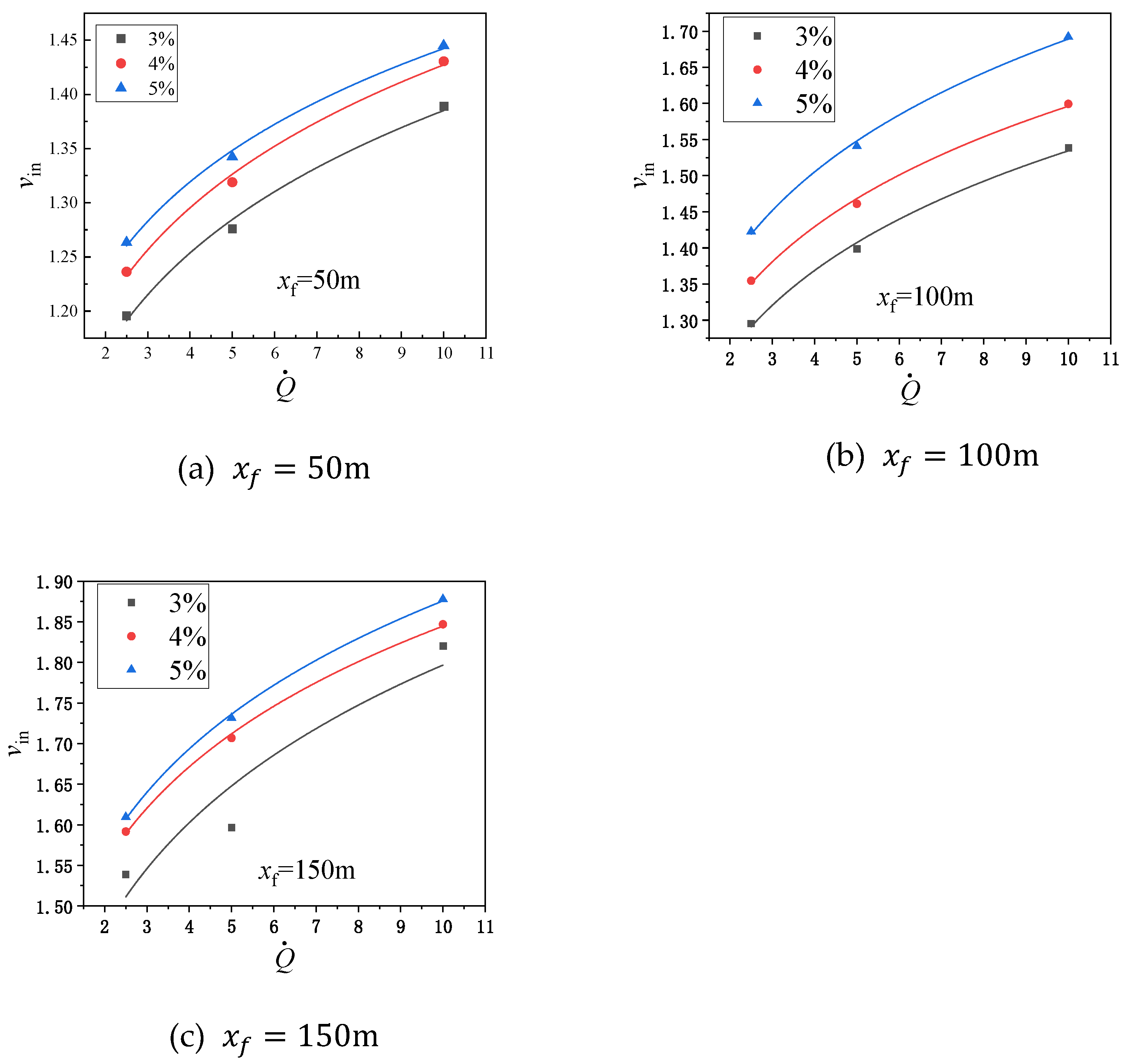

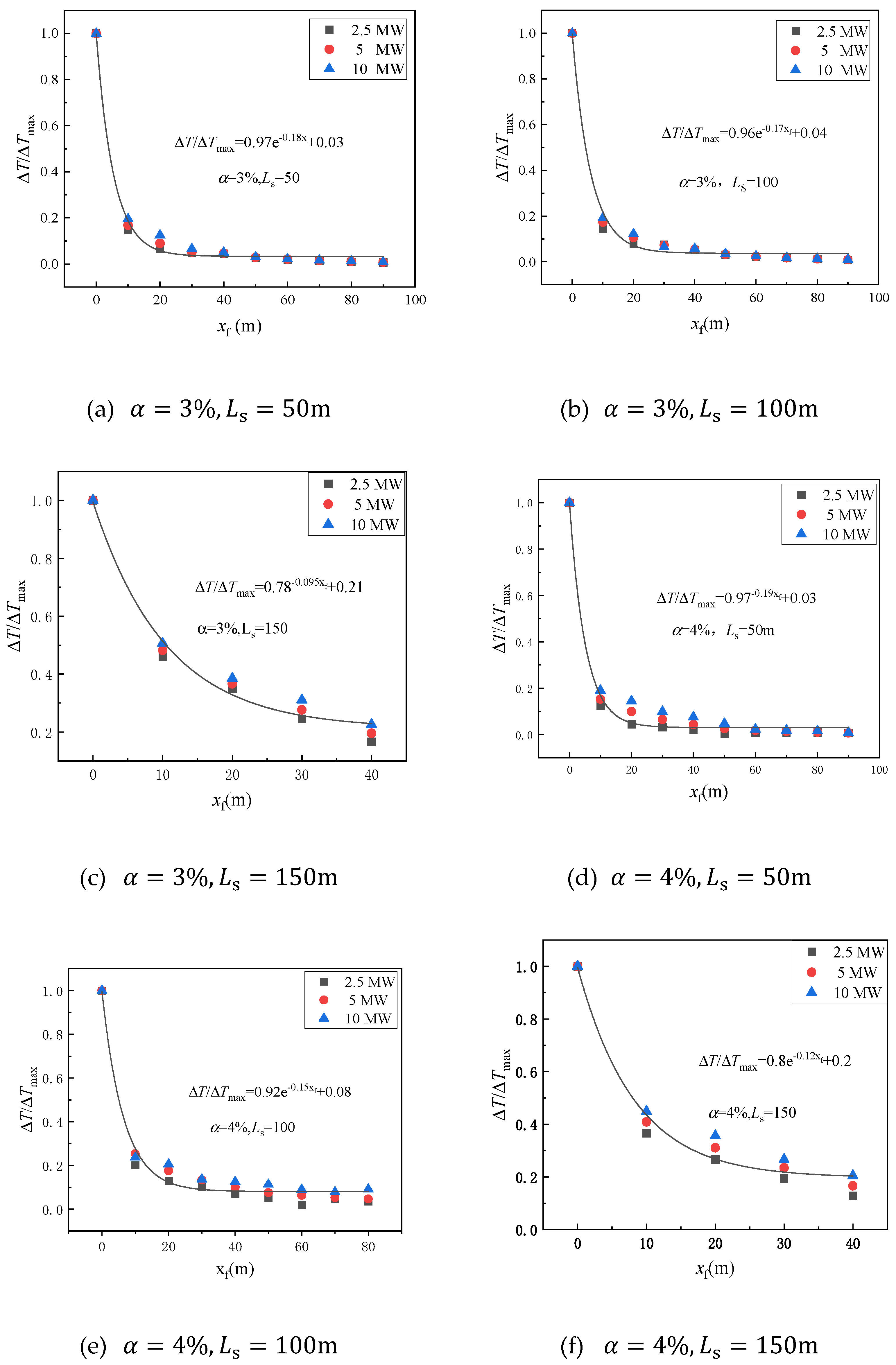
| No. | Distance from the Left Opening (m) | Angle | HRR (MW) |
|---|---|---|---|
| 1–18 | 50, 100, 150, 200, 250, 300 | 3% | 2.5, 5, 10 |
| 19–36 | 50, 100, 150, 200, 250, 300 | 4% | 2.5, 5, 10 |
| 37–54 | 50, 100, 150, 200, 250, 300 | 5% | 2.5, 5, 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhu, G.; Ming, Y.; Wang, X.; Li, X.; Wang, L. Study of Temperature Distribution in U-Shaped Underwater Tunnel Fires Under the Influence of Induced Airflow. Fire 2025, 8, 185. https://doi.org/10.3390/fire8050185
Zhou Y, Zhu G, Ming Y, Wang X, Li X, Wang L. Study of Temperature Distribution in U-Shaped Underwater Tunnel Fires Under the Influence of Induced Airflow. Fire. 2025; 8(5):185. https://doi.org/10.3390/fire8050185
Chicago/Turabian StyleZhou, Yuhang, Guoqing Zhu, Yuyang Ming, Xinyu Wang, Xuming Li, and Liang Wang. 2025. "Study of Temperature Distribution in U-Shaped Underwater Tunnel Fires Under the Influence of Induced Airflow" Fire 8, no. 5: 185. https://doi.org/10.3390/fire8050185
APA StyleZhou, Y., Zhu, G., Ming, Y., Wang, X., Li, X., & Wang, L. (2025). Study of Temperature Distribution in U-Shaped Underwater Tunnel Fires Under the Influence of Induced Airflow. Fire, 8(5), 185. https://doi.org/10.3390/fire8050185





