Correlation Between the Load-Bearing Capacity, Fire Resistance, and the Price of Glued Laminated Timber
Abstract
1. Introduction
2. Materials and Methods
2.1. The Limit States Method
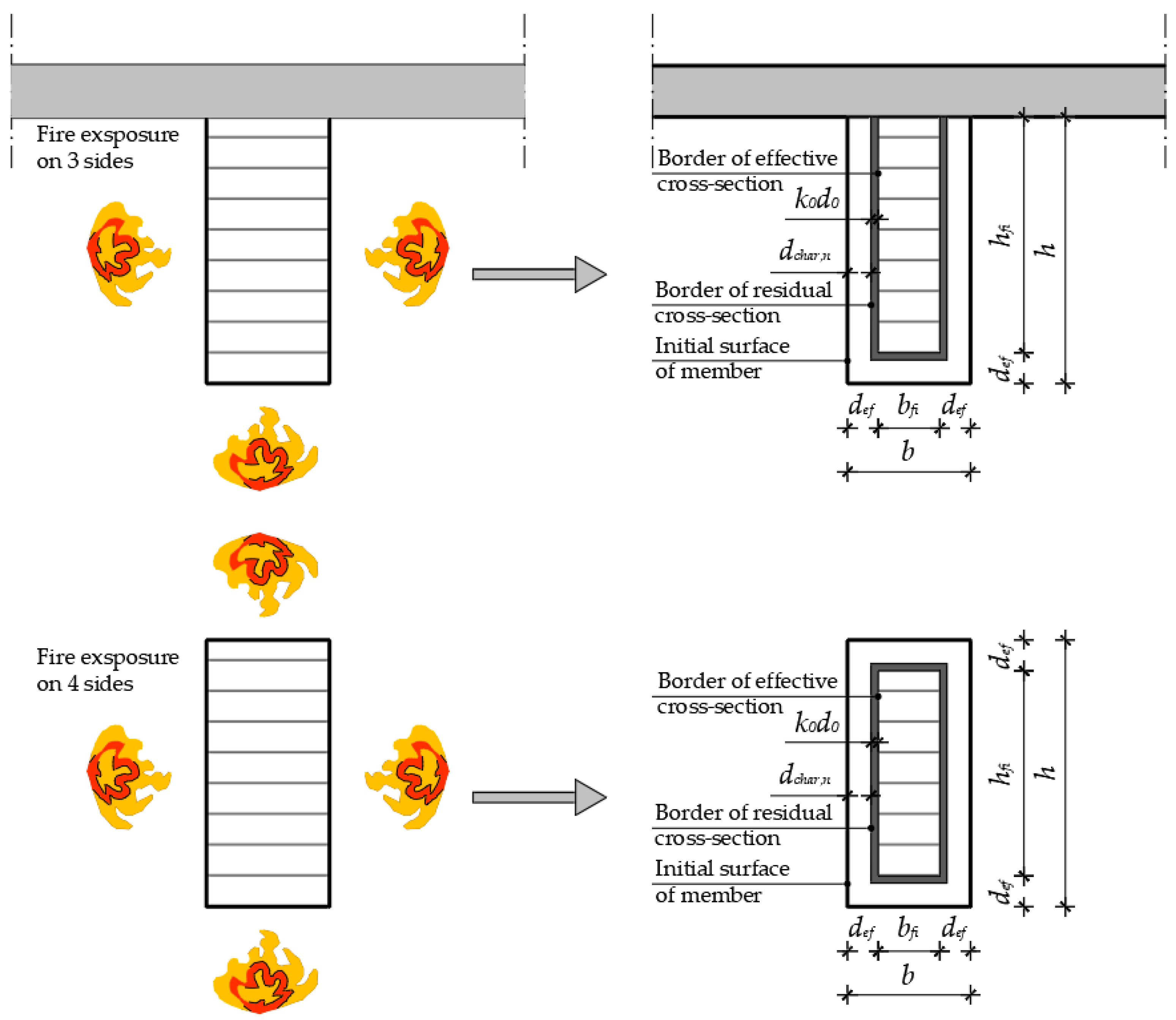
2.2. Reduced Cross-Section Method
- -
- Fire coefficient kfi = 1.15;
- -
- The modification factor for fire, kmod,fi = 1.0, and
- -
3. Results
3.1. Results of the Limit States Method
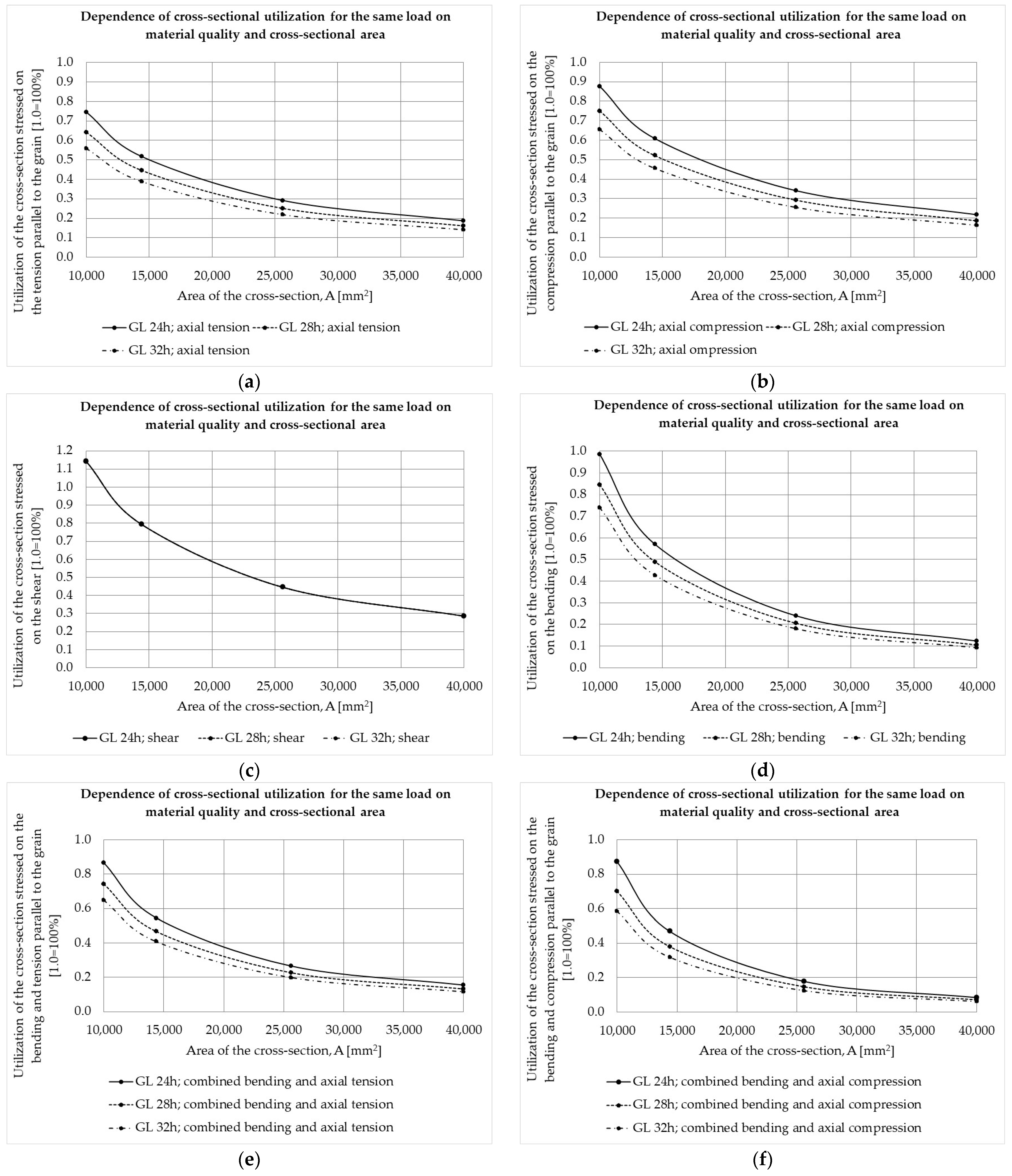
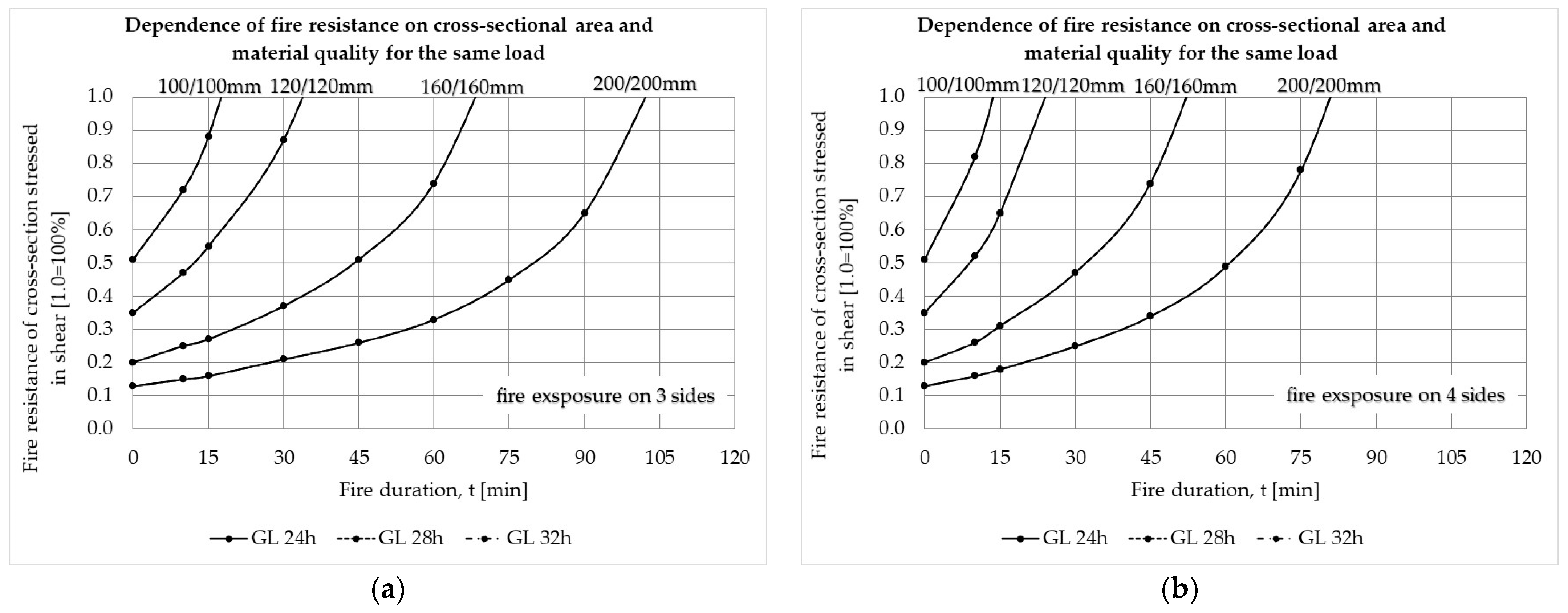
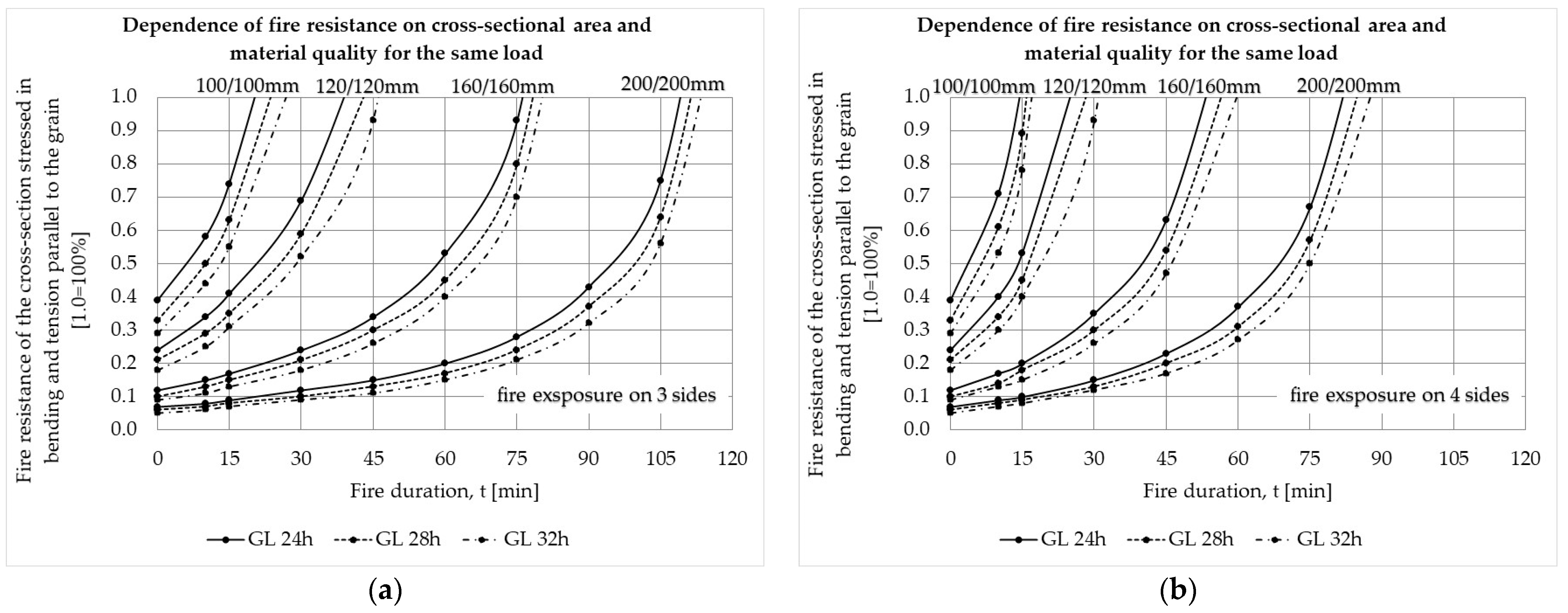
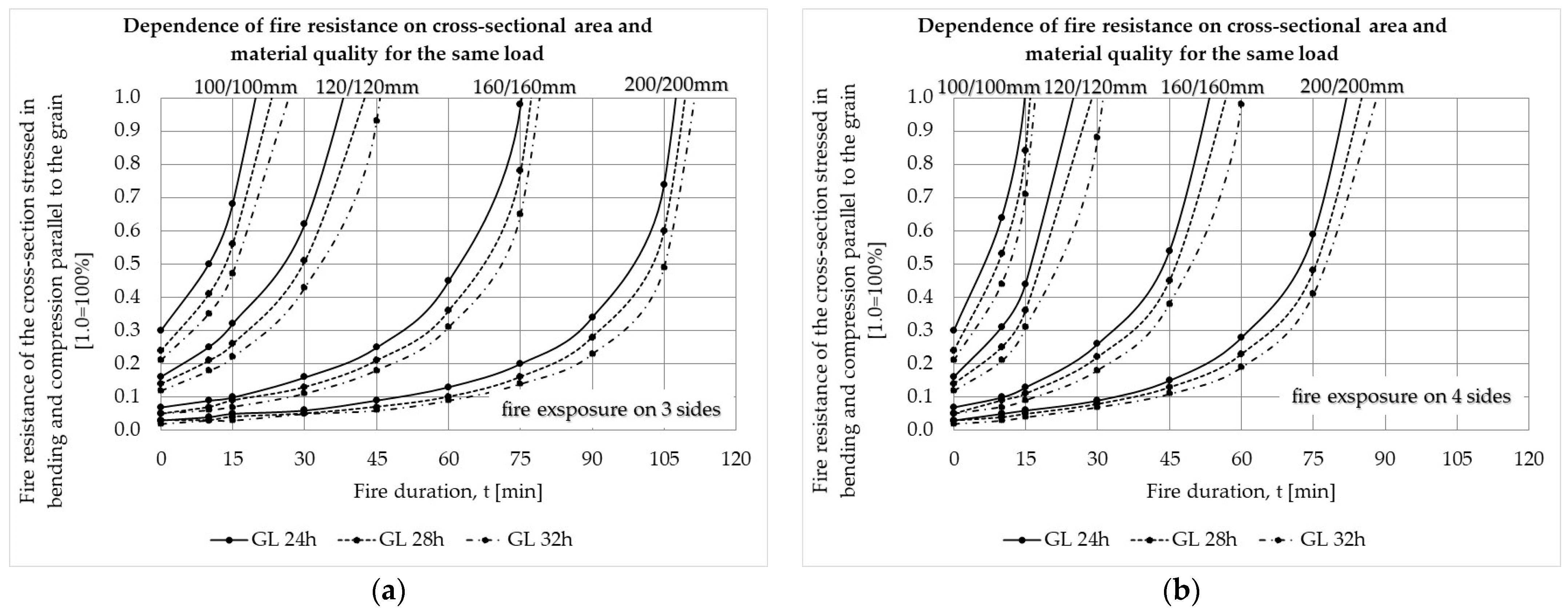
3.2. Results of the Reduced Cross-Section Method
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 | |
| Axial tension—ULS [1.0 = 100%] | 0.745 | 0.517 | 0.291 | 0.186 | 0.641 | 0.445 | 0.250 | 0.160 | 0.558 | 0.388 | 0.218 | 0.140 | |
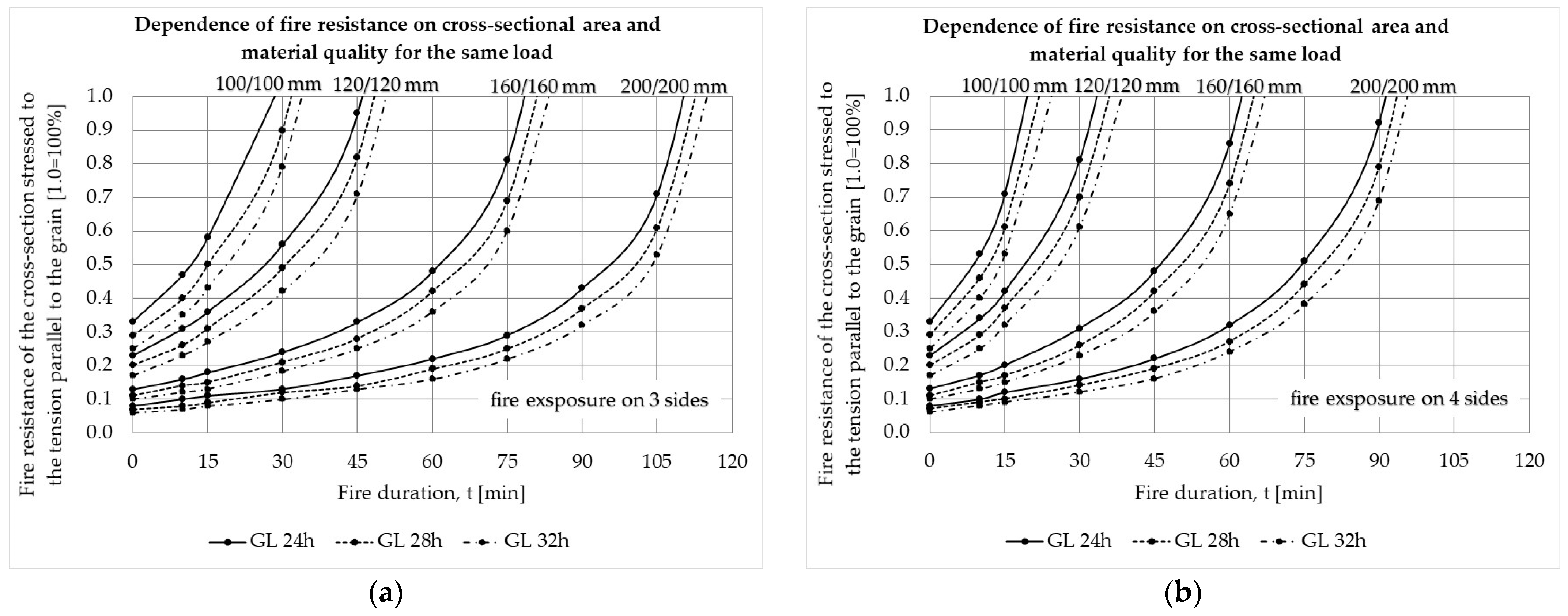
| Fire resistance (fire exposure on 3 sides), R [min] | 0 | 0.33 | 0.23 | 0.13 | 0.08 | 0.29 | 0.20 | 0.11 | 0.07 | 0.25 | 0.17 | 0.10 | 0.06 |
| 10 | 0.47 | 0.31 | 0.16 | 0.10 | 0.40 | 0.26 | 0.14 | 0.08 | 0.35 | 0.23 | 0.12 | 0.07 | |
| 15 | 0.58 | 0.36 | 0.18 | 0.11 | 0.50 | 0.31 | 0.15 | 0.09 | 0.43 | 0.27 | 0.13 | 0.08 | |
| 30 | 1.05 | 0.56 | 0.24 | 0.13 | 0.90 | 0.49 | 0.21 | 0.12 | 0.79 | 0.42 | 0.18 | 0.10 | |
| 45 | 0.95 | 0.33 | 0.17 | 2.02 | 0.82 | 0.28 | 0.14 | 1.76 | 0.71 | 0.25 | 0.13 | ||
| 60 | 2.13 | 0.48 | 0.22 | 1.83 | 0.42 | 0.19 | 1.59 | 0.36 | 0.16 | ||||
| 75 | 0.81 | 0.29 | 0.69 | 0.25 | 0.60 | 0.22 | |||||||
| 90 | 1.84 | 0.43 | 1.59 | 0.37 | 1.38 | 0.32 | |||||||
| 105 | 0.71 | 0.61 | 0.53 | ||||||||||
| 120 | 1.69 | 1.46 | 1.27 | ||||||||||
| Fire resistance (fire exposure on 4 sides), R [min] | 0 | 0.33 | 0.23 | 0.13 | 0.08 | 0.29 | 0.20 | 0.11 | 0.07 | 0.25 | 0.17 | 0.10 | 0.06 |
| 10 | 0.53 | 0.34 | 0.17 | 0.10 | 0.46 | 0.29 | 0.15 | 0.09 | 0.40 | 0.25 | 0.13 | 0.08 | |
| 15 | 0.71 | 0.42 | 0.20 | 0.12 | 0.61 | 0.37 | 0.17 | 0.10 | 0.53 | 0.32 | 0.15 | 0.09 | |
| 30 | 1.72 | 0.81 | 0.31 | 0.16 | 1.48 | 0.70 | 0.26 | 0.14 | 1.29 | 0.61 | 0.23 | 0.12 | |
| 45 | 1.80 | 0.48 | 0.22 | 1.55 | 0.42 | 0.19 | 1.35 | 0.36 | 0.16 | ||||
| 60 | 0.86 | 0.32 | 0.74 | 0.27 | 0.65 | 0.24 | |||||||
| 75 | 1.98 | 0.51 | 1.70 | 0.44 | 1.48 | 0.38 | |||||||
| 90 | 0.92 | 0.79 | 0.69 | ||||||||||
| 105 | 2.18 | 1.88 | 1.64 | ||||||||||
| 120 | |||||||||||||
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 | |
| Axial compression—ULS [1.0 = 100%] | 0.875 | 0.608 | 0.342 | 0.219 | 0.750 | 0.521 | 0.293 | 0.187 | 0.656 | 0.456 | 0.256 | 0.164 | |
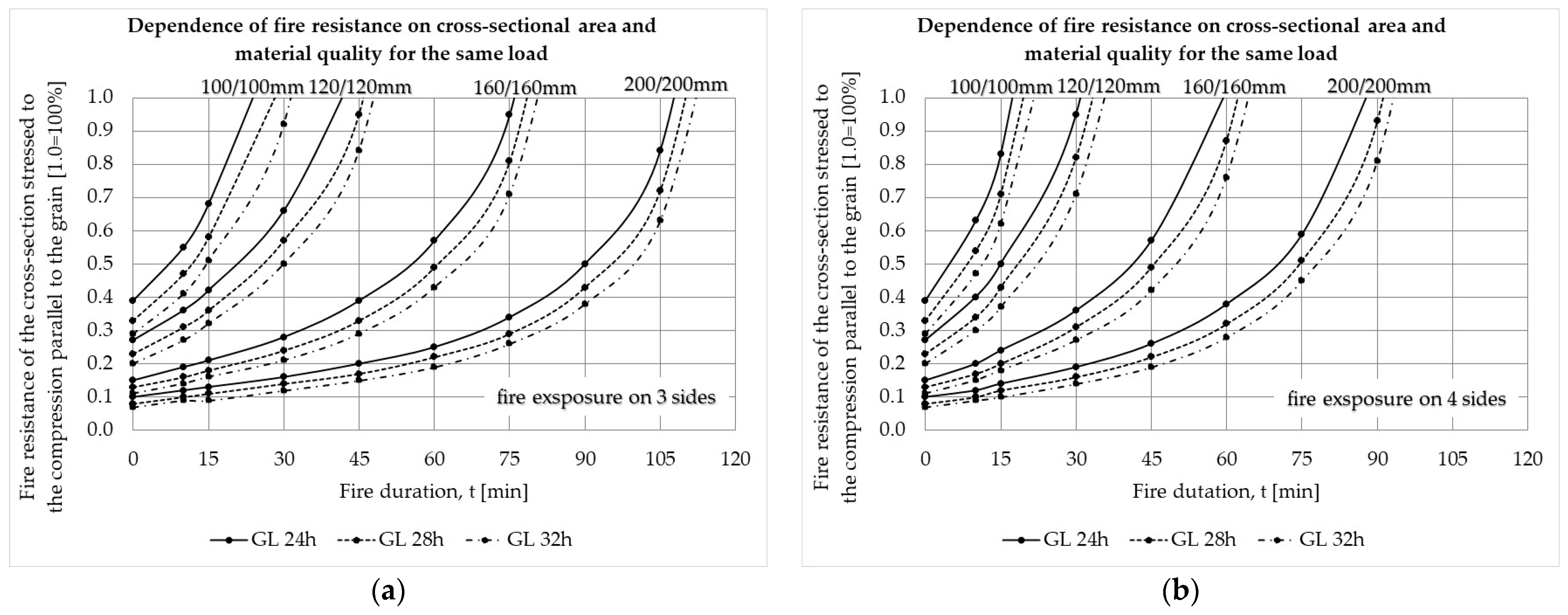
| Fire resistance (fire exposure on 3 sides). R [min] | 0 | 0.39 | 0.27 | 0.15 | 0.10 | 0.33 | 0.23 | 0.13 | 0.08 | 0.29 | 0.20 | 0.11 | 0.07 |
| 10 | 0.55 | 0.36 | 0.19 | 0.12 | 0.47 | 0.31 | 0.16 | 0.10 | 0.41 | 0.27 | 0.14 | 0.09 | |
| 15 | 0.68 | 0.42 | 0.21 | 0.13 | 0.58 | 0.36 | 0.18 | 0.11 | 0.51 | 0.32 | 0.16 | 0.09 | |
| 30 | 1.23 | 0.66 | 0.28 | 0.16 | 1.06 | 0.57 | 0.24 | 0.14 | 0.92 | 0.50 | 0.21 | 0.12 | |
| 45 | 1.11 | 0.39 | 0.20 | 0.95 | 0.33 | 0.17 | 2.07 | 0.84 | 0.29 | 0.15 | |||
| 60 | 0.57 | 0.25 | 2.14 | 0.49 | 0.22 | 1.87 | 0.43 | 0.19 | |||||
| 75 | 0.95 | 0.34 | 0.81 | 0.29 | 0.71 | 0.26 | |||||||
| 90 | 2.17 | 0.50 | 1.86 | 0.43 | 1.63 | 0.38 | |||||||
| 105 | 0.84 | 0.72 | 0.63 | ||||||||||
| 120 | 1.99 | 1.70 | 1.49 | ||||||||||
| Fire resistance (fire exposure on 4 sides). R [min] | 0 | 0.39 | 0.27 | 0.15 | 0.10 | 0.33 | 0.23 | 0.13 | 0.08 | 0.29 | 0.20 | 0.11 | 0.07 |
| 10 | 0.63 | 0.40 | 0.20 | 0.12 | 0.54 | 0.34 | 0.17 | 0.10 | 0.47 | 0.30 | 0.15 | 0.09 | |
| 15 | 0.83 | 0.50 | 0.24 | 0.14 | 0.71 | 0.43 | 0.20 | 0.12 | 0.62 | 0.37 | 0.18 | 0.10 | |
| 30 | 2.02 | 0.95 | 0.36 | 0.19 | 1.73 | 0.82 | 0.31 | 0.16 | 1.51 | 0.71 | 0.27 | 0.14 | |
| 45 | 2.11 | 0.57 | 0.26 | 1.81 | 0.49 | 0.22 | 1.58 | 0.42 | 0.19 | ||||
| 60 | 1.02 | 0.38 | 0.87 | 0.32 | 0.76 | 0.28 | |||||||
| 75 | 0.59 | 1.99 | 0.51 | 1.74 | 0.45 | ||||||||
| 90 | 1.08 | 0.93 | 0.81 | ||||||||||
| 105 | 2.20 | 1.92 | |||||||||||
| 120 | |||||||||||||
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 | |
| Shear—ULS [1.0 = 100%] | 1.143 | 0.794 | 0.446 | 0.286 | 1.143 | 0.794 | 0.446 | 0.286 | 1.143 | 0.794 | 0.446 | 0.286 | |
| Fire resistance (fire exposure on 3 sides), R [min] | 0 | 0.51 | 0.35 | 0.20 | 0.13 | 0.51 | 0.35 | 0.20 | 0.13 | 0.51 | 0.35 | 0.20 | 0.13 |
| 10 | 0.72 | 0.47 | 0.25 | 0.15 | 0.72 | 0.47 | 0.25 | 0.15 | 0.72 | 0.47 | 0.25 | 0.15 | |
| 15 | 0.88 | 0.55 | 0.27 | 0.16 | 0.88 | 0.55 | 0.27 | 0.16 | 0.88 | 0.55 | 0.27 | 0.16 | |
| 30 | 1.61 | 0.87 | 0.37 | 0.21 | 1.61 | 0.87 | 0.37 | 0.21 | 1.61 | 0.87 | 0.37 | 0.21 | |
| 45 | 1.45 | 0.51 | 0.26 | 1.45 | 0.51 | 0.26 | 1.45 | 0.51 | 0.26 | ||||
| 60 | 0.74 | 0.33 | 0.74 | 0.33 | 0.74 | 0.33 | |||||||
| 75 | 1.24 | 0.45 | 1.24 | 0.45 | 1.24 | 0.45 | |||||||
| 90 | 0.65 | 0.65 | 0.65 | ||||||||||
| 105 | 1.09 | 1.09 | 1.09 | ||||||||||
| 120 | |||||||||||||
| Fire resistance (fire exposure on 4 sides), R [min] | 0 | 0.51 | 0.35 | 0.20 | 0.13 | 0.51 | 0.35 | 0.20 | 0.13 | 0.51 | 0.35 | 0.20 | 0.13 |
| 10 | 0.82 | 0.52 | 0.26 | 0.16 | 0.82 | 0.52 | 0.26 | 0.16 | 0.82 | 0.52 | 0.26 | 0.16 | |
| 15 | 1.09 | 0.65 | 0.31 | 0.18 | 1.09 | 0.65 | 0.31 | 0.18 | 1.09 | 0.65 | 0.31 | 0.18 | |
| 30 | 1.24 | 0.47 | 0.25 | 1.24 | 0.47 | 0.25 | 1.24 | 0.47 | 0.25 | ||||
| 45 | 0.74 | 0.34 | 0.74 | 0.34 | 0.74 | 0.34 | |||||||
| 60 | 1.33 | 0.49 | 1.33 | 0.49 | 1.33 | 0.49 | |||||||
| 75 | 0.78 | 0.78 | 0.78 | ||||||||||
| 90 | 1.42 | 1.42 | 1.42 | ||||||||||
| 105 | |||||||||||||
| 120 | |||||||||||||
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9,36 | 16,64 | 26,00 | |
| Bending—ULS [1.0 = 100%] | 0.985 | 0.570 | 0.240 | 0.123 | 0.844 | 0.489 | 0.206 | 0.106 | 0.739 | 0.427 | 0.180 | 0.092 | |
| Fire resistance (fire exposure on 3 sides). R [min] | 0 | 0.44 | 0.25 | 0.11 | 0.05 | 0.38 | 0.22 | 0.09 | 0.05 | 0.33 | 0.19 | 0.08 | 0.04 |
| 10 | 0.69 | 0.37 | 0.14 | 0.07 | 0.59 | 0.32 | 0.12 | 0.06 | 0.52 | 0.28 | 0.11 | 0.05 | |
| 15 | 0.90 | 0.46 | 0.16 | 0.08 | 0.77 | 0.39 | 0.14 | 0.07 | 0.68 | 0.34 | 0.12 | 0.06 | |
| 30 | 1.93 | 0.81 | 0.24 | 0.10 | 1.65 | 0.69 | 0.21 | 0.09 | 1.44 | 0.61 | 0.18 | 0.08 | |
| 45 | 1.54 | 0.36 | 0.14 | 1.32 | 0.31 | 0.12 | 1.15 | 0.27 | 0.10 | ||||
| 60 | 0.57 | 0.19 | 0.49 | 0.16 | 0.43 | 0.14 | |||||||
| 75 | 1.06 | 0.27 | 0.91 | 0.24 | 0.80 | 0.21 | |||||||
| 90 | 0.43 | 2.32 | 0.37 | 2.03 | 0.32 | ||||||||
| 105 | 0.79 | 0.68 | 0.59 | ||||||||||
| 120 | 2.05 | 1.76 | 1.54 | ||||||||||
| Fire resistance (fire exposure on 4 sides). R [min] | 0 | 0.44 | 0.25 | 0.11 | 0.05 | 0.38 | 0.22 | 0.09 | 0.05 | 0.33 | 0.19 | 0.08 | 0.04 |
| 10 | 0.89 | 0.45 | 0.16 | 0.08 | 0.76 | 0.39 | 0.14 | 0.07 | 0.67 | 0.34 | 0.12 | 0.06 | |
| 15 | 1.37 | 0.63 | 0.21 | 0.09 | 1.17 | 0.54 | 0.18 | 0.08 | 1.02 | 0.48 | 0.16 | 0.07 | |
| 30 | 1.68 | 0.39 | 0.15 | 1.44 | 0.33 | 0.13 | 1.26 | 0.29 | 0.11 | ||||
| 45 | 0.77 | 0.24 | 0.66 | 0.20 | 0.58 | 0.18 | |||||||
| 60 | 1.84 | 0.41 | 1.58 | 0.35 | 1.38 | 0.31 | |||||||
| 75 | 0.83 | 0.71 | 0.62 | ||||||||||
| 90 | 2.03 | 1.74 | 1.52 | ||||||||||
| 105 | |||||||||||||
| 120 | |||||||||||||
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 | |
| Comb. Md and Nt,d—ULS [1.0 = 100%] | 0.865 | 0.544 | 0.266 | 0.155 | 0.743 | 0.467 | 0.228 | 0.133 | 0.649 | 0.408 | 0.199 | 0.116 | |
| Fire resistance (fire exposure on 3 sides), R [min] | 0 | 0.39 | 0.24 | 0.12 | 0.07 | 0.33 | 0.21 | 0.10 | 0.06 | 0.29 | 0.18 | 0.09 | 0.05 |
| 10 | 0.58 | 0.34 | 0.15 | 0.08 | 0.50 | 0.29 | 0.13 | 0.07 | 0.44 | 0.25 | 0.11 | 0.06 | |
| 15 | 0.74 | 0.41 | 0.17 | 0.09 | 0.63 | 0.35 | 0.15 | 0.08 | 0.55 | 0.31 | 0.13 | 0.07 | |
| 30 | 1.49 | 0.69 | 0.24 | 0.12 | 1.28 | 0.59 | 0.21 | 0.10 | 1.12 | 0.52 | 0.18 | 0.09 | |
| 45 | 1.24 | 0.34 | 0.15 | 1.07 | 0.30 | 0.13 | 0.93 | 0.26 | 0.11 | ||||
| 60 | 0.53 | 0.20 | 0.45 | 0.17 | 2.28 | 0.40 | 0.15 | ||||||
| 75 | 0.93 | 0.28 | 0.80 | 0.24 | 0.70 | 0.21 | |||||||
| 90 | 2.28 | 0.43 | 1.96 | 0.37 | 1.71 | 0.32 | |||||||
| 105 | 0.75 | 0.64 | 0.56 | ||||||||||
| 120 | 1.87 | 1.61 | 1.40 | ||||||||||
| Fire resistance (fire exposure on 4 sides), R [min] | 0 | 0.39 | 0.24 | 0.12 | 0.07 | 0.33 | 0.21 | 0.10 | 0.06 | 0.29 | 0.18 | 0.09 | 0.05 |
| 10 | 0.71 | 0.40 | 0.17 | 0.09 | 0.61 | 0.34 | 0.14 | 0.08 | 0.53 | 0.30 | 0.13 | 0.07 | |
| 15 | 1.04 | 0.53 | 0.20 | 0.10 | 0.89 | 0.45 | 0.18 | 0.09 | 0.78 | 0.40 | 0.15 | 0.08 | |
| 30 | 1.24 | 0.35 | 0.15 | 2.95 | 1.07 | 0.30 | 0.13 | 2.58 | 0.93 | 0.26 | 0.12 | ||
| 45 | 0.63 | 0.23 | 0.54 | 0.20 | 2.74 | 0.47 | 0.17 | ||||||
| 60 | 1.35 | 0.37 | 1.16 | 0.31 | 1.01 | 0.27 | |||||||
| 75 | 0.67 | 0.57 | 0.50 | ||||||||||
| 90 | 1.48 | 1.27 | 1.11 | ||||||||||
| 105 | |||||||||||||
| 120 | |||||||||||||
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 | |
| Comb. Md and Nc,d—ULS [1.0 = 100%] | 0.875 | 0.470 | 0.179 | 0.085 | 0.703 | 0.380 | 0.146 | 0.070 | 0.585 | 0.318 | 0.123 | 0.060 | |
| Fire resistance (fire exposure on 3 sides), R [min] | 0 | 0.30 | 0.16 | 0.07 | 0.03 | 0.24 | 0.14 | 0.05 | 0.03 | 0.21 | 0.12 | 0.05 | 0.02 |
| 10 | 0.50 | 0.25 | 0.09 | 0.04 | 0.41 | 0.21 | 0.07 | 0.03 | 0.35 | 0.18 | 0.06 | 0.03 | |
| 15 | 0.68 | 0.32 | 0.10 | 0.05 | 0.56 | 0.26 | 0.09 | 0.04 | 0.47 | 0.22 | 0.07 | 0.03 | |
| 30 | 1.72 | 0.62 | 0.16 | 0.06 | 1.38 | 0.51 | 0.13 | 0.05 | 1.15 | 0.43 | 0.11 | 0.05 | |
| 45 | 1.39 | 0.25 | 0.09 | 1.11 | 0.21 | 0.07 | 0.93 | 0.18 | 0.06 | ||||
| 60 | 0.45 | 0.13 | 0.36 | 0.10 | 3.24 | 0.31 | 0.09 | ||||||
| 75 | 0.98 | 0.20 | 0.78 | 0.16 | 0.65 | 0.14 | |||||||
| 90 | 3.71 | 0.34 | 2.89 | 0.28 | 2.34 | 0.23 | |||||||
| 105 | 0.74 | 0.60 | 0.49 | ||||||||||
| 120 | 3.00 | 2.33 | 1.88 | ||||||||||
| Fire resistance (fire exposure on 4 sides), R [min] | 0 | 0.30 | 0.16 | 0.07 | 0.03 | 0.24 | 0.14 | 0.05 | 0.03 | 0.21 | 0.12 | 0.05 | 0.02 |
| 10 | 0.64 | 0.31 | 0.10 | 0.05 | 0.53 | 0.25 | 0.09 | 0.04 | 0.44 | 0.21 | 0.07 | 0.03 | |
| 15 | 1.03 | 0.44 | 0.13 | 0.06 | 0.84 | 0.36 | 0.11 | 0.05 | 0.71 | 0.31 | 0.09 | 0.04 | |
| 30 | 4.61 | 1.29 | 0.26 | 0.09 | 3.70 | 1.05 | 0.22 | 0.08 | 3.08 | 0.88 | 0.18 | 0.07 | |
| 45 | 0.54 | 0.15 | 0.45 | 0.13 | 3.32 | 0.38 | 0.11 | ||||||
| 60 | 1.44 | 0.28 | 1.17 | 0.23 | 0.98 | 0.19 | |||||||
| 75 | 0.59 | 0.48 | 3.91 | 0.41 | |||||||||
| 90 | 1.60 | 1.30 | 1.09 | ||||||||||
| 105 | |||||||||||||
| 120 | |||||||||||||
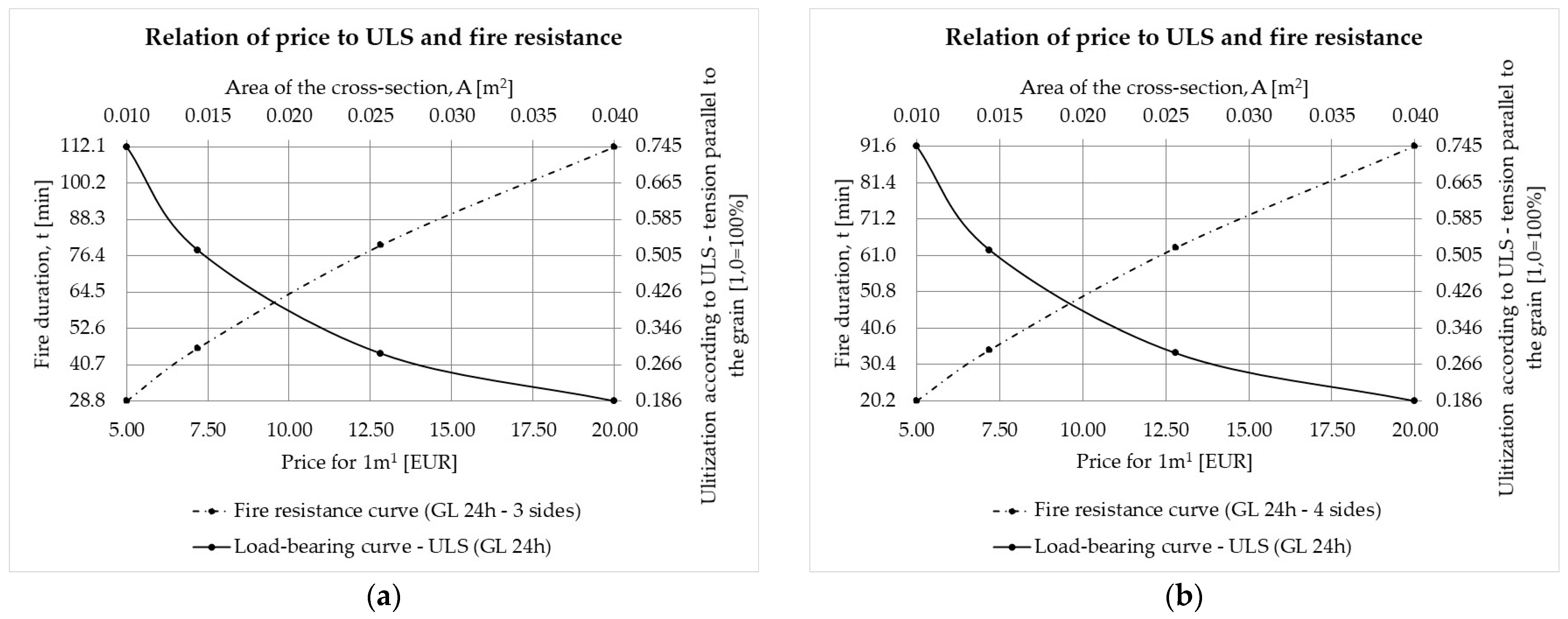
3.3. Variation in Price on ULS and Fire Resistance
4. Conclusions
- The fire resistance of timber structures made of GLT calculated with the reduced cross-section method tends to be directly affected by the load bearing capacity proving procedure, which is not the case with structures made of other structural materials like concrete or steel.
- Utilization of the element’s cross-section has a particular impact on its fire resistance. Namely, if the element’s CS is utilized at 87.50% for any load action or their combination and for any GLT strength class, it does not meet a fire resistance higher than R15 in case that the fire acts on its three sides. Increasing the cross-sectional area has, as a result, decreased the utilization of the element’s CS. At the same time, fire resistance increases as well as the price of the material.
- Fire resistance obviously depends on the cross-section’s exposure to fire. For example, if one specific CS satisfies the fire resistance class of R30 and the fire acts on its three sides, the same CS will not meet the stated fire resistance if the fire acts on its all four sides.
- The increase in the GLT strength class for any action or stress state does not contribute significantly to fire resistance. The contribution of the increase in the strength class is manifested only in the improved utilization of the cross-section’s bearing capacity for the same fire exposure class. The only exception is in the case of shear, where the increase in the GLT strength class has no effect on fire resistance at all.
- To achieve a certain fire resistance according to the load-bearing criterion R, the price of the timber material might also have a deciding impact. By variating the specific fire resistance class for a given stress state of the CS, the corresponding timber material price might increase by up to four times.
- By correlating the load limit state capacity proof and the corresponding fire resistance functions, it is quite easy for any stress state case to obtain the optimal price for timber material as their intersection point. For example, if the CS is subjected to tension parallel to the grain and the fire acts on its three or four sides, the optimal price can be obtained if that section is utilized approximately to 40% of the bearing capacity. It is expected, in that case, that CS will withstand the fire action duration on the section’s three sides of approximately 60 minutes and 45 minutes if the fire acts on the section’s all four sides.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GLT | Glued laminated timber |
| CS | Cross-section |
| ULS | Ultimate limit state |
References
- EN 14080:2013; Timber Structures—Glued Aminated Timber and Glued Solid Timber—Requirements. European Committee for Standardization (CEN): Brussels, Belgium, 2013.
- Jirouš-Rajković, V.; Miklečić, J. Fire retardants for wood. Drv. Ind. 2009, 60, 111–121. [Google Scholar]
- EN 1995-1-2:2004+AC:2009; Eurocode 5: Design of Timber Structures—Part 1-2: General-Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 2009.
- Klippel, M.; Frangi, A. Fire safety of glued-laminated timber beams in bending. J. Struct. Eng. 2017, 143, 04017052. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Mei, F.; Liao, J.; Li, W. Experimental and numerical analysis on fire behavior of loaded cross-laminated timber panels. Adv. Struct. Eng. 2020, 23, 22–36. [Google Scholar]
- Pečenko, R.; Svensson, S.; Hozjan, T. Modelling heat and moisture transfer in timber exposed to fire. Int. J. Heat Mass Transf. 2015, 87, 598–605. [Google Scholar] [CrossRef]
- Yang, T.; Wang, S.; Tsai, M.; Lin, C. Temperature distribution within glued laminated timber during a standard fire exposure test. Mater. Des. 2009, 30, 518–525. [Google Scholar] [CrossRef]
- Yang, T.; Wang, S.; Tsai, M.; Lin, C. The charring depth and charring rate of glued laminated timber after a standard fire exposure test. Mater. Des. 2009, 44, 518–525. [Google Scholar] [CrossRef]
- Firmanti, A.; Subiyanto, B.; Kawai, S. Evaluation of the fire endurance of mechanically graded timber in bending. J. Wood Sci. 2006, 52, 25–32. [Google Scholar]
- Frangi, A.; Fontana, M.; Mischler, A. Shear behavior of bond lines in glued laminated timber beans at high temperature. Wood Sci. Technol. 2004, 38, 119–126. [Google Scholar] [CrossRef]
- Yang, T.; Wang, S.; Tsai, M.; Lin, C.; Chuang, Y. Effect of fire exposure on the mechanical properties of glued laminated timber. Mater. Des. 2009, 30, 698–703. [Google Scholar] [CrossRef]
- Huang, J.; Wang, L. Experimental and numerical study on progressive collapse of the midcolumn in a glulam timber frame exposed to fire. Fire 2023, 6, 374. [Google Scholar] [CrossRef]
- Schmid, J.; Klippel, M.; Just, A.; Frangi, A. Review and analysis of fire resistance tests of timber members in bending, tension and compression with respect to the Reduced Cross-Section Method. Fire Saf. J. 2014, 68, 81–99. [Google Scholar] [CrossRef]
- Kucíková, L.; Janda, T.; Sýkora, J.; Šejnoha, M.; Marseglia, G. Experimental and numerical investigation of the response of GLT beams exposed to fire. Constr. Build. Mater. 2021, 299, 123846. [Google Scholar] [CrossRef]
- Tang, Z.; Yue, K.; Lu, D.; Shi, X.; Chu, Y.; Tian, Z.; Lu, W. Experimental investigation into fire performance of mixed species glulam beams under three-side fire exposure. Eur. J. Wood Wood Prod. 2022, 80, 235–245. [Google Scholar] [CrossRef]
- Ulusoy, S. Optimum design of timber structures under fire using metaheuristic algorithm. Građevinar 2022, 74, 115–124. [Google Scholar] [CrossRef]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures-Part 1-1: General-Common Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2013.
- EN 1995-1-1:2004/A2:2014; Eurocode 5: Design of Timber Structures-Part 1-1: General-Common Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2014.
- HRN EN 1995-1-1:2013/NA:2013; Eurokod 5: Projektiranje Drvenih Konstrukcija–Dio 1-1: Općenito-Opća Pravila i Pravila za Zgrade-Nacionalni Dodatak Eurocode 5: Design of Timber Structures-Part 1-1: General-Common Rules and Rules for Buildings-National Annex. Hrvatski Zavod za Norme: Zagreb, Hrvatska, 2013.
- CEN. EN 1990 Eurocode-Basis of Structural and Geotechnical Design; European Committee for Standardization (CEN): Brussels, Belgium, 2023. [Google Scholar]
- HRN EN 1995-1-2:2013/NA:2013; Eurokod 5: Projektiranje Drvenih Konstrukcija-Dio 1-2: Općenito-Proračun Konstrukcija na Djelovanje Požara-Nacionalni Dodatak Eurocode 5: Design of Timber Structures-Part 1-2: General-Structural Fire Design-National Annex. Hrvatski Zavod za Norme: Zagreb, Hrvatska, 2013.
- EN 1363-1; Fire Resistance Tests—Part 1: General Requirements. European Committee for Standardization (CEN): Brussels, Belgium, 2020.


| Strength Classes | Characteristic Strengths [N/mm2] | Characteristic Density [kg/m3] | |||
|---|---|---|---|---|---|
| Tension | Compression | Shear | Bending | ||
| ft,0,k | fc,0,k | fv,k | fm,k | ρk | |
| GL 24 h | 19.2 | 24.0 | 3.5 | 24.0 | 385 |
| GL 28 h | 22.3 | 28.0 | 3.5 | 28.0 | 425 |
| GL 32 h | 25.6 | 32.0 | 3.5 | 32.0 | 440 |
| Strength Classes | Dimensions of Cross-Section, b/h [mm] | |||
|---|---|---|---|---|
| GL 24 h | 100/100 | 120/120 | 160/160 | 200/200 |
| GL 28 h | ||||
| GL 32 h | ||||
| Cross-section area, A [mm2] | 10,000 | 14,400 | 25,600 | 40,000 |
| Strength Classes | CS, b/h | Internal Forces Obtained for Basic Load Combinations | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tension, Ft,d | Compression, Fc,d | Shear, Vd | Bending, My,d | Bending + Tension | Bending + Compression | ||||
| 0.50·My,d | 0.50·Ft,d | 0.50·My,d | 0.707·Fc,d | ||||||
| [mm/mm] | [kN] | [kN] | [kN] | [kNm] | [kNm] | [kN] | [kNm] | [kN] | |
| GL 24 h GL 28 h GL 32 h | 100/100 120/120 160/160 200/200 | 108.88 | 145.38 | 12.37 | 3.00 | 1.50 | 54.44 | 1.50 | 102.81 |
| Strength Classes | CS, b/h | Internal Forces Used for Fire Resistance Proof | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tension, Ft,d,fi | Compression, Fc,d,fi | Shear, Vd,fi | Bending, My,d,fi | Bending + Tension | Bending + Compression | ||||
| 0.50·My,d,fi | 0.50·Ft,d,fi | 0.5·My,d,fi | 0.707·Fc,d,fi | ||||||
| [mm/mm] | [kN] | [kN] | [kN] | [kNm] | [kN] | [kNm] | [kN] | [kNm] | |
| GL 24 h GL 28 h GL 32 h | 100/100 120/120 160/160 200/200 | 80.65 | 107.69 | 9.16 | 2.22 | 1.11 | 40.33 | 1.11 | 76.16 |
| Strength Classes | GL 24 h | GL 28 h | GL 32 h | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area of the CS [mm2] | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 | 10,000 | 14,400 | 25,600 | 40,000 |
| Price for 1 m [EUR] | 5.00 | 7.20 | 12.80 | 20.00 | 5.50 | 7.92 | 14.08 | 22.00 | 6.50 | 9.36 | 16.64 | 26.00 |
| Axial tension | 0.745 | 0.517 | 0.291 | 0.186 | 0.641 | 0.445 | 0.250 | 0.160 | 0.558 | 0.388 | 0.218 | 0.140 |
| Axial compression | 0.875 | 0.608 | 0.342 | 0.219 | 0.750 | 0.521 | 0.293 | 0.187 | 0.656 | 0.456 | 0.256 | 0.164 |
| Shear | 1.143 | 0.794 | 0.446 | 0.286 | 1.143 | 0.794 | 0.446 | 0.286 | 1.143 | 0.794 | 0.446 | 0.286 |
| Bending | 0.985 | 0.570 | 0.240 | 0.123 | 0.844 | 0.489 | 0.206 | 0.106 | 0.739 | 0.427 | 0.180 | 0.092 |
| Combined bending and axial tension | 0.865 | 0.544 | 0.266 | 0.155 | 0.743 | 0.467 | 0.228 | 0.133 | 0.649 | 0.408 | 0.199 | 0.116 |
| Combined bending and axial compression | 0.875 | 0.470 | 0.179 | 0.085 | 0.703 | 0.380 | 0.146 | 0.070 | 0.585 | 0.318 | 0.123 | 0.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zovkić, J.; Dolaček-Alduk, Z.; Guljaš, I. Correlation Between the Load-Bearing Capacity, Fire Resistance, and the Price of Glued Laminated Timber. Fire 2025, 8, 123. https://doi.org/10.3390/fire8040123
Zovkić J, Dolaček-Alduk Z, Guljaš I. Correlation Between the Load-Bearing Capacity, Fire Resistance, and the Price of Glued Laminated Timber. Fire. 2025; 8(4):123. https://doi.org/10.3390/fire8040123
Chicago/Turabian StyleZovkić, Jurko, Zlata Dolaček-Alduk, and Ivica Guljaš. 2025. "Correlation Between the Load-Bearing Capacity, Fire Resistance, and the Price of Glued Laminated Timber" Fire 8, no. 4: 123. https://doi.org/10.3390/fire8040123
APA StyleZovkić, J., Dolaček-Alduk, Z., & Guljaš, I. (2025). Correlation Between the Load-Bearing Capacity, Fire Resistance, and the Price of Glued Laminated Timber. Fire, 8(4), 123. https://doi.org/10.3390/fire8040123








