Abstract
Square steel tube (SST) columns are widely applied, and fire resistance is a critical issue in its design. Current research on the fire resistance of the SST column predominantly assumes that it is uniformly exposed to fire, ignoring the thermal insulation of the surrounding walls under actual fire conditions. The heat transfer and mechanical finite element model (FEM) for SST columns embedded in walls under an ISO 834 standard fire are established in this study, and the accuracy of the FEM is verified by existing experimental results. Subsequently, the wall effect on the temperature distribution and fire resistance of the SST columns exposed to fire is analyzed, the stress mechanisms of the SST column embedded in walls is investigated and further parametric analyses are performed. The results show that, for SST columns embedded in walls, the temperature rise rate of the wall-embedded region is significantly reduced, and the fire resistance is improved by 25.3% compared with the case of uniform exposure to fire. Under two fire conditions, the SST columns exhibit compressive bending failure, and when considering the wall effect, the uneven temperature distribution induces material strength eccentricity, causing the buckling direction to deviate toward the wall-thickness direction. Reducing the fire-resistive coating thickness of the wall-embedded region can mitigate the uneven stress distribution, thereby lowering construction costs while concurrently preserving fire resistance. Increasing the steel tube thickness can significantly improve the fire resistance, but the high steel strength and slenderness ratio result in the accelerated failure of the SST column when exposed to fire.
1. Introduction
Assembled steel structures present significant advantages, including expedited construction timelines, excellent seismic resistance, high industrialization degrees and material recyclability, collectively embodying the principles of green and low-carbon construction [1,2]. The promotion of assembled steel structures and the establishment of a standardized production system for assembled buildings have emerged as key trends in national green building initiatives. This development represents a crucial strategy for the construction industry to achieve the goals of “carbon emissions peak and carbon neutrality” [3,4,5].
Within assembled steel structure system, square steel tube (SST) columns are one of the preferred cross-sectional forms for steel frame columns owing to their regular shape, high torsional stiffness and load-bearing capacity; these attributes not only enhance their suitability for construction but also underscore their significant potential for standardization [6,7,8,9]. Currently, extensive experimental and theoretical studies have been carried out on the static and dynamic properties of SST columns in normal temperatures [10,11,12,13], and the Standard for Design of Steel Structures GB 50017-2017 [14] has provided the design method for this type of members in normal temperatures. However, as columns are the principal vertical load-bearing components in frame structures and due to the poor fire resistance of steel materials and the high frequency of building fires, fire-protection design has emerged as a critical aspect of the design process for SST columns [15,16,17,18,19].
Current standards and research regarding the fire resistance of SST columns primarily operate under the assumption of uniform exposure to fire. The Code for Fire Safety of Steel Structures in Buildings GB 51249-2017 [20] addressed only the comprehensive emissivity of steel columns exposed to fire from four sides. Li [21] conducted full-scale fire-resistance tests on SST columns featuring composite fire protection with fire-resistant gypsum board and aluminum silicate cotton in a four-sided fire environment; the local buckling failure of the whole cross-section was identified, and a simplified theoretical model was proposed to effectively solve the temperature rise of the composite fire-protected SST columns. Both Zong [22] and Dashdemberel [23] compared the fire resistance of SST columns based on different fire-protection measures as well as bare SST columns under uniform fire conditions. They concluded that a well-designed protective layer can significantly mitigate the temperature rise rate of the SST columns, with the encapsulation method using aluminum silicate cotton outperforming fire-resistant boards and the SST column treated with fire-resistive coatings demonstrating a 149% improvement in fire resistance compared with that with surface mortar.
However, in actual building structures, SST columns are predominantly integrated with the walls. When exposed to fire, the walls serve as the natural barriers, effectively partitioning and impeding the flames’ spread. This interaction modifies the fire boundary conditions for the SST columns, which results in a thermal gradient across the cross-section of the SST columns. Currently, some scholars have investigated the effect of this thermal gradient on the fire resistance of H-section steel columns [24,25,26,27], and the results show that, in many cases, uniformly heated columns reach the critical temperature earlier than unevenly heated columns. In terms of failure modes, columns with a thermal gradient along the flange plate show overall buckling around the weak axis. However, columns with thermal gradients along the web fail through overall buckling around the strong axis or through flexural torsional buckling around the weak axis. It can be seen that the effect of the thermal gradient created by the wall on the fire resistance of the column members cannot be ignored.
Therefore, building upon existing research regarding the fire resistance of SST columns, a sequentially coupled thermal-mechanical FEM is established to evaluate the fire resistance of SST columns embedded in walls, and the influences of various parameters, such as fire resistive coating thickness, steel tube thickness, steel strength and slenderness ratio, are further investigated, with a view to providing valuable references for the design of SST columns exposed to fire in practical applications.
2. FEM Building and Validation
2.1. FEM Building
The finite element analysis model is performed using the ABAQUS software (Version 6.14-1). There are two commonly used methods for simulating temperature distribution and performing stress mechanism analysis in ABAQUS, including the fully coupled thermal–mechanical method and the sequentially coupled thermal–mechanical method. For the structural fire-resistance analysis, since it is a unidirectional coupling case (temperature affects deformation, but deformation has a negligible effect on temperature), and considering the efficiency, flexibility and convergence for simulation, the sequentially coupled thermal–mechanical model is selected [28,29].
Regarding the common design parameters of the SST columns in the actual project, the height of the SST columns is set at 3300 mm, with cross-sectional dimensions of 300 mm × 300 mm × 12 mm. The material used for the specimens is Q355. The walls are fabricated using autoclaved lightweight concrete (ALC) blocks measuring 200 mm in thickness. The thickness of the fire-resistive coating for the SST columns is 30 mm; this value is commonly used in practical engineering. The arrangement of the wall and SST column is aligned along one side of their cross-sections.
In the heat-transfer model, reasonable thermal property is vital for the heat-transfer analysis. The thermal parameters (thermal conductivity and specific heat ) of the SST column provided by Lie [30] are employed, specifically as shown in Equations (1) and (2). The density of steel material varies slightly with increasing temperature and is generally taken as 7850 kg/m3.
The density of ALC is 650 kg/m3, and its variation rules for the specific heat and thermal conductivity with increasing temperature are shown in Equations (3) and (4), respectively [31].
In the above equations, is the thermal conductivity of water, taken as 0.58 W/(m·°C); is the thermal conductivity of ALC in the completely dry state, taken as 0.131 W/(m·°C); is the thermal conductivity of lightweight concrete in a completely dry state when unaerated, taken as 0.5 W/(m·°C); is the volume ratio of water in ALC, taken as 0.1677; is the porosity of ALC, taken as 75%; is the thermal conductivity of the pore air in ALC; is the equivalent diameter of the pores, taken as 0.72 mm; and is the Stefan–Boltzmann constant.
The fire-resistive coating adopted in this study is a gypsum-based non-intumescent type, and the thermal characteristics of the fire-resistive coating are based on measured values from commercially available products, with a bulk density of 450 kg/m3, a thermal conductivity of 0.106 W/(m·°C) and a specific heat of 1024 J/(kg·°C). In the heat-transfer analysis of steel components coated with non-intumescent fire-resistive coatings, the thermal conductivity of the coating is generally taken as a constant value [32,33]. The temperature increases according to the ISO 834 standard fire curve [34], with the initial temperature set at 20 °C. Heat transfer between the surrounding environment, the fire-resistive coating and the outer surface of the walls occurs through thermal convection and radiation, characterized by a constant convective coefficient of 25 W/(m·°C), emissivity of 0.5 and the Stefan–Boltzmann constant at 5.67 × 10−8 W/(m2·K4), with absolute zero defined as −273 °C. The SST columns, fire-resistive coating and walls are modeled using eight-node three-dimensional solid heat-transfer elements (DC3D8). “Tie” constraints are applied at the interfaces between the fire-resistive coating and the SST column, as well as between the fire-resistive coating and the walls, disregarding any interface thermal resistance and assuming complete heat transfer. The mesh size for the cross-section of the SST column and fire-resistive coating is determined by their thickness, while the height direction has a mesh size of 100 mm. The wall element is divided by taking 1/10 of the side length in two directions. The mesh sensitivity analysis is carried out as shown in Figure 1. The results indicate that halving or doubling the present mesh size yields minor variations; therefore, the median mesh size is chosen to reach a balance between accuracy and efficiency.
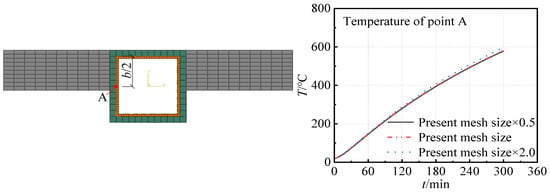
Figure 1.
Mesh sensitivity analysis.
In a building fire, flames may spread to a single side or to both sides of the walls. A comparison of the fire resistance of SST columns embedded in walls in the case of interior-only fire and a two-sided fire is provided in Figure 2. Since two-sided fires are more hazardous than interior-only fires, two-sided fires are considered in this study. Figure 3a,b present the heat transfer models of the SST columns under uniform exposure to fire (ideal fire conditions) and considering the wall effect (actual fire conditions), respectively.
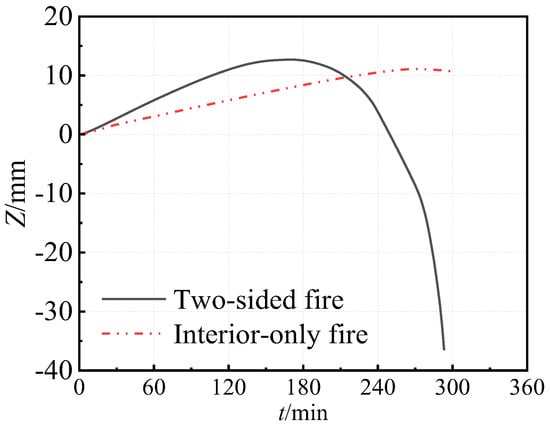
Figure 2.
Comparison of fire resistance in the case of an interior-only fire and a two-sided fire.
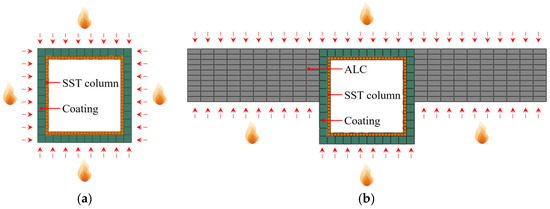
Figure 3.
Heat-transfer model. (a) Ideal fire conditions. (b) Actual fire conditions.
In the mechanical model, the thermodynamic parameters of the steel are based on the model provided by Eurocode 3 [35]. The reduction coefficients for the strength and elastic modulus of steel material at increased temperatures are shown in Table 1.

Table 1.
Reduction coefficients for steel mechanical properties.
The stress–strain relationship of steel material at high temperatures is modeled as follows:
In the above equations, is the yield strength at temperature T; is the proportional limit at temperature T; is the initial elastic modulus at temperature T; is the proportional limit strain at temperature T; is the yield strain at temperature T, which is taken as 0.02; is the maximum strain corresponding to the yield strength at temperature T, which is taken as 0.15; and is the ultimate strain at temperature T, which is taken as 0.20. a, b and c are calculation coefficients.
The expansion and contraction of steel material in response to temperature changes are expressed by the thermal expansion coefficient, which is calculated by Equation (11)
Poisson’s ratio for the steel is minimally affected by temperature and is maintained at a constant value of 0.3. Steel plates are installed at both ends of the SST columns to apply a load, and to prevent significant deformation at the column ends, the steel plates are considered as a rigid body, with their physical movement represented by the corresponding reference points (RP-1 and RP-2 in Figure 4). The load ratio takes the common value of 0.5. The fire-resistive coating and walls mainly affect the heat transfer, while their effects on the deformation and stress of the columns are neglected. The SST column employs eight-node linear reduced-integration solid elements (C3D8R). To ensure that the temperature data from the heat-transfer model can be accurately incorporated into the mechanical model, the mesh division of the mechanical model is aligned with that of the heat-transfer model. The first-order buckling mode, representing 1/1000 of the column length, is applied as the initial defect of the column component and corresponds to the selection of the first-order sinusoidal half-wave in the finite element buckle analysis for the buckling mode [36,37]. Figure 4 shows the mechanical model for the SST column.
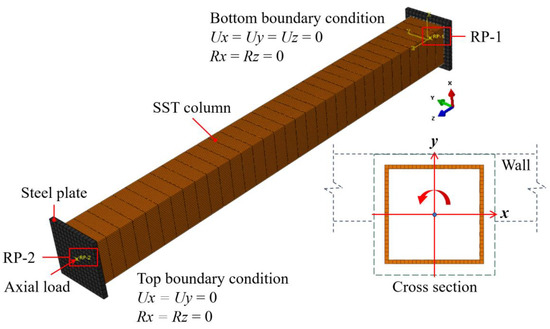
Figure 4.
Mechanical model.
2.2. FEM Validation
In the absence of experimental studies on the fire resistance of SST columns embedded in walls, the test data obtained by Li [21] are employed to validate the modeling methods for the heat transfer and mechanical model of the SST columns under ideal fire conditions. Z1 and Z2 are two different SST column specimens in reference [21]; the main difference is that the thickness of the fire-resistive gypsum board in specimen Z1 is 12 mm, while that of specimen Z2 is 24 mm. The comparative results of the temperature measurements (T) and the axial displacement (Z) versus time (t) curves are presented in Figure 5 and Figure 6. For the temperature versus time curves, during the initial test period, the test temperature is higher than that of the finite element results, which is probably due to the uneven temperature distribution in the test furnace. Overall, taking 1 min as the statistical interval of the data, the average temperature difference between the finite element and the test results is only 15.5 °C, which verifies the reasonableness of the heat-transfer model. For the axial displacement versus time curves, the main reason for the curve deviation is that the constraint conditions at the column end in the finite element model are more satisfactory, and the variations between the calculated and experimental fire resistance for specimens Z1 and Z2 are within 5%, so that the accuracy of the mechanical model is also verified.
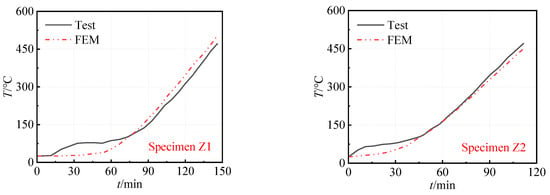
Figure 5.
Validation of the heat-transfer model calculation results.

Figure 6.
Validation of the mechanical calculation results.
3. Simulation Results Analysis
3.1. Heat-Transfer Model
The calculated temperature results for the SST columns under ideal and actual fire conditions are illustrated in Figure 7. Under ideal fire conditions, the temperature distribution of the SST column exhibits biaxial symmetry, whereas the temperature distribution becomes uniaxial symmetric when considering the wall effect. Based on the symmetry, typical measurement points (see Figure 8) are selected for detailed analysis, with the temperature–time curves and comparative analysis for each measurement point depicted in Figure 9 and Figure 10.
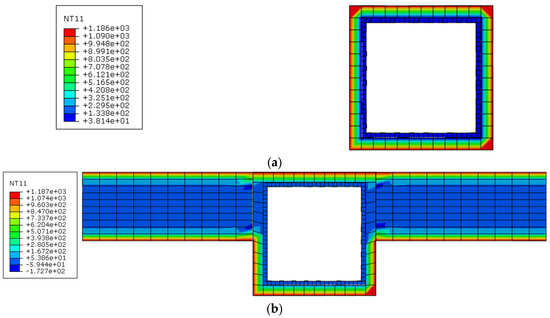
Figure 7.
Temperature distribution of the SST columns: (a) ideal fire conditions; (b) actual fire conditions.
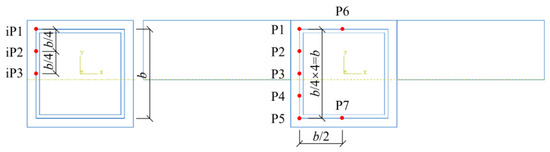
Figure 8.
Typical measurement points.

Figure 9.
Temperature–time curves of the measurement points. (a) Ideal fire conditions. (b) Actual fire conditions: (A) Wall-thickness direction; (B) Wall-length direction.
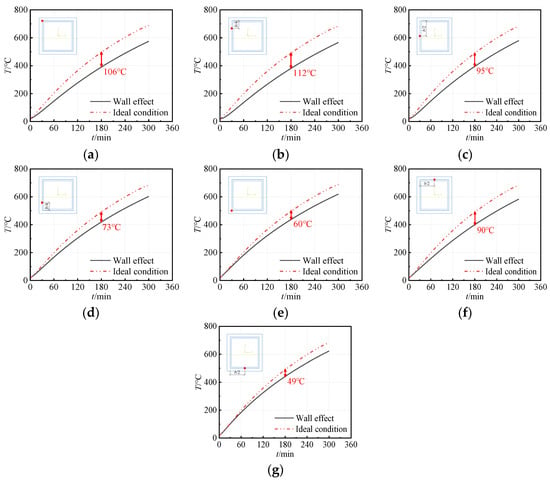
Figure 10.
Comparison of temperature–time curves at different measurement points: (a) P1/iP1; (b) P2/iP2; (c) P3/iP3; (d) P4; (e) P5; (f) P6; (g) P7.
The temperature rise curves for each measurement point are illustrated in Figure 9. It is evident that when fire-resistive coating is applied, the maximum temperature of the SST column reaches 496 °C and 442 °C when heating for 3 h under ideal and actual fire conditions, respectively, both temperatures remain below 538 °C, thus satisfying the 3 h fire-resistance requirements outlined in Fire Resistive Coating for Steel Structure GB 14907-2018 [38].
Under ideal fire conditions, due to the heat transfer by the convection and radiation of the surrounding air being relatively uniform, this results in nearly identical temperature rise curves across various measurement points. Consequently, based on the symmetry, the temperature throughout the entire cross-section of the column remains largely consistent. In contrast, for SST columns embedded in walls, the wall effect on the temperature distribution is significant, which is analyzed as follows:
- (1)
- Along the wall-thickness direction, the non-embedded region of the SST column experiences a higher heating rate than that of the embedded region, i.e., points P4/P5 > points P1/P2/P3, and the temperature of point P5 is 14.7% higher than that of point P2 after 3 h of heating. The temperature variation trend is mainly due to the different heat-transfer mechanisms, with the non-embedded region of the SST column being directly affected by the heat radiation from the fire source, while the temperature rise of the embedded region is mainly through the heat conduction between the SST column and the walls. For the measurement points located on the embedded region of the SST column, the temperature of the measurement point near the middle of the wall (P3) is lowest, and as the measurement point approaches the wall edges, the temperature increases gradually, i.e., point P3 < points P1/P4, while for the measurement points located outside the walls, the pattern is reversed, i.e., point P5 > point P4. This is mainly due to the high thickness and relatively high thermal conductivity of the walls, which results in heat dispersion in the walls, and the measurement points near the walls are subject to the “cooling effect” by the walls.
- (2)
- Along the wall-length direction, the temperature of the measurement point near the wall is relatively low, as evidenced by the fact that point P1 < point P6, point P5 < point P7, and the temperature difference between point P1 and point P6 is greater than that between point P5 and point P7; this is attributable to the same underlying reasons previously discussed.
- (3)
- The wall effect results in a non-uniform temperature distribution along the SST column, and the degradation of the material’s properties varies across different positions within the column cross-section, resulting in material strength eccentricities. In practical engineering, considering the economic aspects and standard fire-protection requirements, it may be advantageous to reduce the fire-resistive coating thickness on the embedded region of the SST column.
The temperature comparison of the SST columns under ideal and actual fire conditions is shown in Figure 10. Due to alterations in the heat-transfer mechanisms and fire boundary conditions, under the ISO 834 standard fire conditions, the overall temperature rise rate for SST columns embedded in walls is diminished compared with those subjected to ideal fire conditions. Significantly, the temperature at the most affected point (P2) decreases by 22.8%, while even the least affected point (P7) recorded a reduction of 10.0%. This finding further emphasizes the importance of considering wall effects in the fire-resistance design of SST columns.
3.2. Mechanical Model
Based on the temperature distribution of the SST columns derived from the transient thermal-transfer analysis, in this section, the temperature data of various nodes are imported into the mechanical model for further thermodynamic analysis.
3.2.1. Axial Deformation
The axial deformation versus time (Z-t) curves for the SST columns subjected to thermal–stress coupling under ideal and actual fire conditions are depicted in Figure 11. The Z-t curves are clearly delineated into the expansion phase (OA/OA’) and the compression failure phase (AB/A’B’).
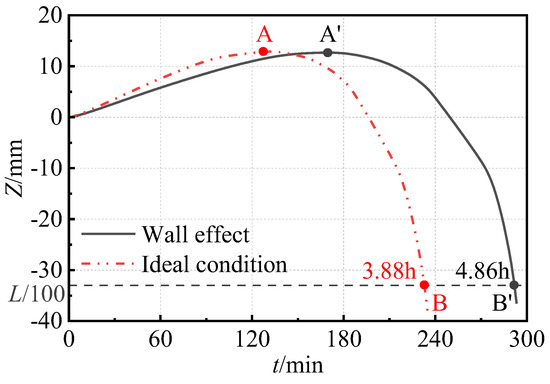
Figure 11.
Axial deformation versus time curves of the SST columns under different fire conditions.
- (1)
- Expansion phase (OA/OA’): At the initial heating, the overall temperature of the SST columns remains relatively low, which leads to minimal degradation of the material’s properties. Due to the high thermal-expansion coefficient of the steel, the columns undergo pronounced thermal expansion. During this phase, the deformation due to thermal expansion exceeds that of compressive deformation, resulting in an upward axial displacement of the columns. Under ideal fire conditions, the column experiences a more rapid temperature increase, resulting in a steeper slope of the axial deformation curve compared with that observed under actual fire conditions at this phase. As the columns temperature rises, the steel strength progressively deteriorates, accelerating the compressive deformation rate under axial loading, which is reflected in a gradual decrease in the slope of the Z-t curves. When the overall compressive deformation rate coincides with the thermal-expansion deformation rate, the Z-t curves attain their peak points (A/A’).
- (2)
- Compression failure phase (AB/A’B’): With the increasing temperature of the columns, degradation of the material’s properties becomes markedly pronounced. Concurrently, due to the initial defects and the stress redistribution induced by the thermal expansion, localized buckling or plastic deformation may manifest, resulting in a substantial reduction in the load-bearing capacity of the columns. During this phase, the overall compressive deformation rate significantly exceeds that of thermal expansion. According to the criteria for determining fire resistance outlined in Fire-Resistance Tests-Elements of Building Construction-Part 7: Specific Requirements for Columns GB/T 9978.1-2008 [39], for axial load bearing components, when the axial compressive deformation reaches 1/100 of its length, it is considered that the components undergo failure (B/B’).
Under ideal and actual fire conditions, SST columns can satisfy the fire-resistance requirements (3 h) stipulated in Code for Fire Protection Design of Building GB 50016-2014 (2018 edition) [40]. When considering the wall effect, the fire resistance of the SST column is enhanced by 25.3% compared with that observed under ideal conditions. This enhancement primarily arises from the significantly reduced temperature rise rate of the column that is influenced by the walls, which serves to effectively mitigate the deterioration of the steel material’s properties.
3.2.2. Lateral Deformation
The lateral deformation versus time (C-t) curves for the SST columns under different fire conditions are presented in Figure 12. During the initial heating, the lateral deformation remains relatively negligible under the two conditions. However, as the steel strength deteriorates, lateral buckling becomes evident. When considering the wall effect, the increase rate in lateral deformation for the SST column is significantly less than that recorded under ideal fire conditions; after 3 h of exposure to fire, the lateral deformation along the x-axis and y-axis directions for the SST column embedded in the wall is reduced by 28.9% and 15.6%, respectively, in comparison with that under ideal fire conditions, thereby highlighting the considerable wall effects.
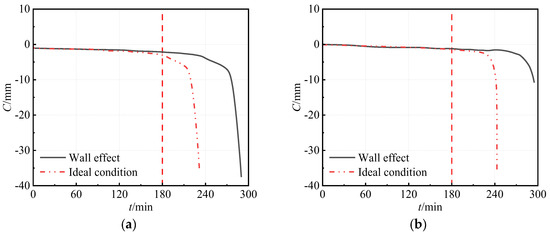
Figure 12.
Lateral deformation versus time curves of the SST columns under different fire conditions: (a) x-axis (Ux); (b) y-axis (Uy).
Furthermore, combining this with the deformation contour (Figure 13), it can be inferred that, under ideal fire conditions, the lateral deformation of the SST column along the x-axis direction is primarily attributed to the local buckling of the steel tube, with the direction of the local buckling coinciding with the assumed initial defect direction, while the lateral deformation along the y-axis direction is the outward expansion caused by the buckling of the steel tube in the x-axis direction.
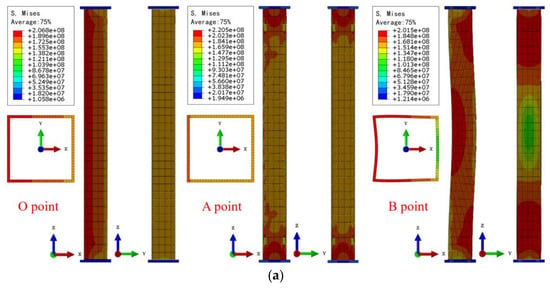
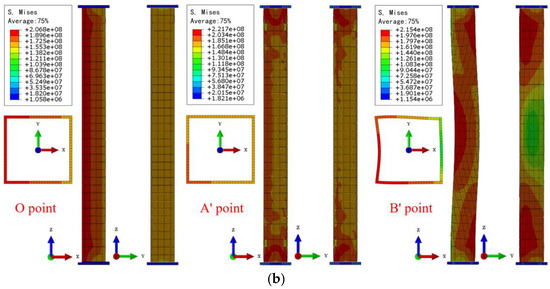
Figure 13.
The stress and deformation contours of the SST columns under different fire conditions: (a) ideal fire conditions; (b) actual fire conditions.
3.2.3. Stress Distribution
Figure 13 illustrates the stress and deformation contours for the SST columns at points O, A/A’ and B/B’ under the two fire conditions. It is apparent that at point O, the stress distribution along the y-axis direction is uniformly distributed under the two fire conditions. Nonetheless, owing to the existence of the initial defect, the overall stress state along the x-axis direction displays a compressive bending characteristic, while the lateral deformation remains minimal.
When point A/A’ is reached, the axial expansion is up to the maximum value. Under ideal fire conditions, the SST column is still in the compressive bending stress state along the x-axis direction due to the uniform heating across its entire cross-section. In contrast, for the SST columns embedded in walls, localized stress concentration begins to emerge along the y-axis direction.
Following point A/A’, the local compressive stress under the two fire conditions exceeds the yield strength of the steel material, and the columns commence to develop obvious lateral bending deformation. The stress contours demonstrate a large plastic deformation region, and the lateral deformation gradually increases as the temperature rises. Upon reaching point B/B’, the column ultimately succumbs to failure. The stress distribution analysis reveals that the wall effect introduces a significant asymmetry in the material degradation of the SST column. The embedded region experiences a lower temperature rise, preserving higher material strength, while the exposed region undergoes accelerated softening. This differential degradation induces an eccentricity in the strength centroid, shifting the neutral axis and modifying the internal moment equilibrium. Consequently, the critical buckling stress is reduced, leading to premature failure in the direction of the wall thickness. Such an effect is superposed with the initial buckling, which results in the buckling direction at the fire-resistance point occurring along an angle between the x-axis and y-axis directions.
4. Parametric Analyses
The comprehensive parameter analysis of the fire resistance of SST columns embedded in walls is performed in this section. The studied parameters include the fire-resistive coating thickness, steel tube thickness, steel strength and slenderness ratio, which provide valuable references for the fire-resistant design of SST columns in practical engineering.
4.1. Fire-Resistive Coating Thickness
Drawing upon the preceding analysis, it is evident that the temperature rise rate of the embedded region of the SST columns is relatively slow under fire conditions. To facilitate uniform heating across the entire cross-section, adjustment is applied solely to the fire-resistive coating thickness for the embedded region. Figure 14 illustrates the influence of coating thickness of the embedded region (hereinafter referred as “coating thickness”) on the fire resistance of the SST columns; as the coating thickness decreases, there is an overall downward trend in the fire resistance. When the coating thickness ranges from 10 mm to 30 mm, the fire resistance of the SST columns embedded in walls remains largely unchanged; correspondingly, as depicted in Figure 14c, the stress distribution at the failure points also exhibits minimal variation. Notably, in this study, the column achieves an optimal fire resistance of 4.89 h when the coating thickness is 15 mm.

Figure 14.
The effect of coating thickness on the fire resistance of SST columns embedded in walls. (a) Axial deformation versus time curves. (b) Fire resistance. (c) Stress and deformation contours of the cross-section of the SST columns reaching fire resistance.
Moreover, even in the absence of fire-resistive coating in the embedded region, the SST column still satisfies the Class I fire-resistance requirements stipulated in the relevant standard [40]. In practical engineering applications, optimizing the coating thickness can help balance fire-resistance performance while reducing construction costs.
Furthermore, from observing the stress and deformation contours of the cross-section of the SST column, as the coating thickness decreases, the temperature gradient along the y-axis reverses. This phenomenon causes a shift in the failure mode from buckling along an angle between the −y and −x directions to buckling along an angle between the y and −x directions; this behavior is attributed to an initial defect defined around the y-axis (Ry).
4.2. Steel Tube Thickness
The impact of steel tube thickness on the fire resistance of the SST columns embedded in walls is depicted in Figure 15a. The fire resistance increases from 3.34 h to 6.05 h as the steel tube thickness increases from 8 mm to 20 mm. This is mainly due to the fact that a thicker steel tube serves to effectively impede the initial heat transfer to the interior, thereby diminishing the overall temperature rise rate of the columns and prolonging the degradation process of the material’s properties. As a result, thick-walled SST columns can sustain an elevated yield strength and elastic modulus for extended durations under high-temperature conditions. Additionally, under the same load ratio, the enhanced rigidity of thick-walled steel tube enables them to more efficiently withstand deformations induced by thermal stress and external loads during a fire, reducing the likelihood of localized stress concentrations and buckling instabilities. Consequently, increasing the steel tube thickness can significantly extend the fire resistance of the SST column and improve structural safety.
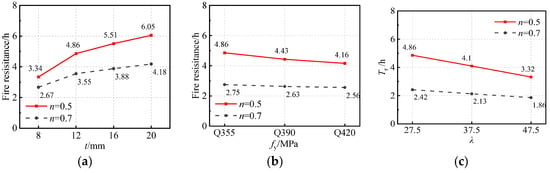
Figure 15.
The effect of various parameters on the fire resistance of SST columns embedded in walls. (a) Steel tube thickness. (b) Steel strength. (c) Slenderness ratio.
4.3. Steel Strength
Steel strength exerts a dual effect on the fire resistance of the SST columns embedded in walls under fire conditions. On one hand, high-strength steel offers enhanced load-bearing capacity in the initial phase exposed to fire. Conversely, as illustrated in Figure 15b, an increase in steel strength correlates with a decline in fire resistance. For example, by improving the steel strength from Q355 to Q420, the fire resistance of SST columns embedded in walls reduces by 14.40%. The reason for this is because the enhanced normal-temperature load-bearing capacity allows for higher specified loads under an identical load ratio. At elevated temperatures, the rapid degradation in both strength and stiffness of high-strength steel may result in a significant reduction in load-bearing capacity during the later phase of exposure to fire, ultimately shortening the fire resistance of the columns. Consequently, in the fire-resistant design of SST columns, it would be prudent to prioritize increasing the steel tube thickness to ensure adequate load-bearing capabilities.
4.4. Slenderness Ratio
Under normal temperature conditions, low-slenderness-ratio columns primarily exhibit compressive failure, while high-slenderness-ratio columns demonstrate reduced stability and heightened buckling risk, with the “second-order” effect becoming increasingly prominent. In such cases, the predominant failure mode is compressive bending failure, which is controlled by the component’s bending stiffness. Under fire conditions, these detrimental factors are further amplified. Elevated temperatures induce significant thermal stress and thermal deformation, rendering high-slenderness-ratio columns more prone to local buckling and overall instability due to the coupled thermal–stress effects. As shown in Figure 15c, the fire resistance of SST columns embedded in walls decreases linearly with an increasing slenderness ratio. As the slenderness ratio increases from 27.5 to 47.5, the fire resistance decreases by 31.69%. Moreover, as the load ratio diminishes, the linear correlation between the fire resistance and slenderness ratio becomes increasingly apparent; this conclusion is also supported by reference [41].
5. Conclusions
In this study, the heat transfer and mechanical FEM of the SST columns under ideal and actual fire conditions are established to analyze the influence of the wall on the temperature distribution and stress mechanism of the SST columns, and further parametric analysis is carried out on the fire resistance of SST columns embedded in walls. The following conclusions can be drawn:
- (1)
- Under ideal fire conditions, the temperature distribution across the whole cross-section of the SST column is uniform. However, when considering the wall effect, the temperature rise rate of the embedded region is considerably lower than that of the non-embedded region. Consequently, degradation of the material’s properties varies at different locations, resulting in eccentricity in the material’s strength.
- (2)
- The axial deformation trends of the SST column under ideal and actual fire conditions are consistent. In the initial heating, the temperature of the columns remains low, and the material’s properties exhibit minimal deterioration, resulting in significant thermal expansion. As the temperature escalates, the degradation of the material’s properties occurs, leading to an increased rate of compressive deformation and local buckling, which ultimately leads to the column’s failure. When considering the wall effect, the fire resistance of the SST column is enhanced by 25.3% compared with that under ideal fire conditions.
- (3)
- Under ideal fire conditions, the buckling direction of the SST column under failure is in the direction of the initial defect setting, whereas when considering the wall effect, the buckling direction of the SST column deviates toward the wall-thickness direction due to the eccentricity of the material strength induced by the non-uniform temperature distribution.
- (4)
- In a practical assembled steel-structure design, the thermal insulation effect of the wall should be considered. By reducing the fire-resistive coating thickness on the embedded region, the uniformity of stress distribution within the column can be ameliorated, which can ensure the fire resistance of the column members and reduce the cost at the same time. When a high load-bearing capacity is required, prioritizing an increase in the steel tube thickness over enhancing steel strength is advisable. Components with high slenderness ratios are more susceptible to local buckling and overall instability in fire conditions.
- (5)
- For the fire-resistance design of SST columns embedded in walls, when the demand for the fire-resistance level is Class I, it is recommended that the fire-resistive coating thickness on the embedded region be reduced to 10 mm, the steel tube thickness be no less than 8 mm and the load ratio and slenderness ratio not exceed 0.5 and 47.5, respectively.
However, there are still certain limitations in this study. Due to the randomness of the initial defects of the SST columns, the conclusions drawn in this study are limited to cases where the initial defects are around the y-axis. Additionally, the heat transfer between the walls and the SST columns in actual fire conditions requires further experimental investigation. Overall, the findings of this study can provide a reference for the fire-protection design of SST columns in practical engineering.
Author Contributions
Conceptualization, W.S. and J.W.; methodology, S.T.; software, S.T.; validation, J.W.; formal analysis, S.T.; investigation, W.S.; resources, W.S.; data curation, T.W.; writing—original draft, W.S.; writing—review & editing, X.W. and T.W.; visualization, S.T.; supervision, T.W.; project administration, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (No. 2022YFC3006300).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Authors Wanyu Shen and Tao Wang were employed by the company Anhui Fuhuang Steel Structure Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Hao, J.P.; Sun, X.L.; Xue, Q.; Fan, C.L. Research and applications of prefabricated steel structure building systems. Eng. Mech. 2017, 34, 1–13. [Google Scholar]
- Hou, J.W.; Wang, X.D.; Liu, J.D.; Chen, Z.; Zhong, X. Study on the stability bearing capacity of multi-column wall in modular steel building. Eng. Struct. 2020, 214, 110648. [Google Scholar] [CrossRef]
- Seyedabadi, M.R.; Karrabi, M.; Shariati, M.; Karimi, S.; Maghrebi, M.; Eicker, U. Global building life cycle assessment: Comparative study of steel and concrete frames across European union, USA, Canada, and Australia building codes. Energy Build. 2024, 304, 113875. [Google Scholar] [CrossRef]
- Li, J.W.; Wang, X.Y.; Chen, L.; Lu, W.B. Bearing capacity of light-steel compound section and steel columns under axial compression. Adv. Civ. Eng. 2022, 2022, 8061015. [Google Scholar] [CrossRef]
- Cai, K.H.; Wang, H.X.; Wang, J.S.; Bai, J.; Zuo, J.; Chan, K.; Lai, K.; Song, Q. Mitigating lifecycle GHG emissions of building sector through prefabricated light-steel buildings in comparison with traditional cast-in-place buildings. Resour. Conserv. Recycl. 2023, 194, 107007. [Google Scholar] [CrossRef]
- Zhang, C.T.; Hu, S.H.; An, R.B.; Wang, Z.S. Seismic performance of a newly assembled joint between shaped steel beams and square steel tubular columns. J. Build. Eng. 2025, 100, 111748. [Google Scholar] [CrossRef]
- Xu, J.H.; Zhou, T.; Chen, Z.H.; Liu, X.S.; Qiao, W.T. Experimental research on H-section beam-square steel column joints connected by self-tapping screws. Thin-Walled Struct. 2024, 200, 111923. [Google Scholar] [CrossRef]
- Liu, J.F.; Cheng, X.; Lei, H.Q.; An, Y. An experimental study on seismic behavior of square hollow section column-truss beam connections. J. Vib. Shock 2023, 42, 237–244. [Google Scholar]
- Chang, H.F.; Li, Z.W.; Qian, Y.L.; Xia, J.W. Experimental and parametric study on flexural performance of transverse reverse channel connections between square hollow section column and H-beam. J. Build. Struct. 2021, 42, 92–102. [Google Scholar]
- Yamada, S.; Ishida, T. Collapse behavior of weak column type steel moment resisting frames built with square hollow section columns subjected to bi-directional horizontal ground motion. J. Build. Eng. 2022, 48, 103960. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, Y.; Takeuchi, T.; Zhao, S. Comprehensive stress-strain model of square steel tube stub columns under compression. Eng. Struct. 2017, 131, 503–512. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, Q.Y.; Xue, H.; Liu, X.K. Low cycle fatigue behavior and damage model analysis of bolted endplate connections to square hollow section columns. J. Build. Struct. 2016, 37, 151–159+173. [Google Scholar]
- Liu, H.; Yao, Y.; Deng, Y.J.; Chu, Y.P. Study on influence of width-to-thickness ratios on static performance of the thin-wall square steel tube columns to axial loads. Build. Sci. 2013, 29, 88–94. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. National Standard of the People’s Republic of China: Beijing, China, 2017.
- Yang, J.J.; Wang, W.Y.; Shi, Y.; Xu, L. Experimental study on fire resistance of cold-formed steel built-up box columns. Thin-Walled Struct. 2020, 147, 106564. [Google Scholar] [CrossRef]
- ElSabbagh, A.; Nassef, W.; El-Ghandour, M.; Sharaf, T. Inelastic buckling analysis of steel columns at different fire scenarios. Eng. Struct. 2023, 291, 116464. [Google Scholar] [CrossRef]
- Qi, H.-H.; Hou, J.; Lou, G.-B.; Jiang, Y.; Zhong, B.; Li, G.-Q. Experimental and numerical study on fire-induced collapse of unprotected steel framed structures. J. Constr. Steel Res. 2024, 218, 108730. [Google Scholar] [CrossRef]
- Shan, S.D.; Pan, W. Collapse mechanisms of multi-story steel-framed modular structures under fire scenarios. J. Constr. Steel Res. 2022, 196, 107419. [Google Scholar] [CrossRef]
- Ruan, S.P.; Zhao, J.C.; Song, Z.S.; Duan, L.P. Experimental investigation of the structural response of a steel-framed building subjected to traveling fire. J. Struct. Eng. 2022, 148, 4021269. [Google Scholar] [CrossRef]
- GB 51249-2017; Code for Fire Safety of Steel Structures in Buildings. National Standard of the People’s Republic of China: Beijing, China, 2018.
- Li, R.; Chen, W.; Ye, J.H.; Jiang, W. Fire resistance test and simplified theoretical model of square steel tubular columns with composite fire protection. Eng. Mech. 2025, 1–12. [Google Scholar] [CrossRef]
- Zong, J.H.; Li, H.C.; Yu, F.Z.; Huang, Y.L. Numerical analysis of the fire-resistance capacity for mouth-section steel columns with external cladding. J. Hebei Agric. Univ. 2016, 39, 126–130. [Google Scholar]
- Dashdemberel, N.; Han, S.-G.; Kim, S.-H.; Chung, K.-S.; Choi, S.-M. Experimental and analytical study on fire resistance performance of mid-high rise modular rectangular steel tube columns using a 3 h fireproof cladding method. Int. J. Steel Struct. 2024, 24, 1178–1188. [Google Scholar] [CrossRef]
- Agarwal, A.; Choe, L.; Varma, A.H. Fire design of steel columns: Effects of thermal gradients. J. Constr. Steel Res. 2014, 93, 107–118. [Google Scholar] [CrossRef]
- Quiel, S.E.; Garlock, M.E.M.; Dwaikat, M.M.S.; Kodur, V.K.R. Predicting the demand and plastic capacity of axially loaded steel beam–columns with thermal gradients. Eng. Struct. 2014, 58, 49–62. [Google Scholar] [CrossRef]
- Moura Correia, A.J.P.; Rodrigues, J.P.C.; Real, P.V. Thermal bowing on steel columns embedded on walls under fire conditions. Fire Saf. J. 2014, 67, 53–69. [Google Scholar] [CrossRef]
- Rocha, F.M.; Rodrigues, J.P.C.; Neto, J.M. Fire behavior of steel and partially encased composite columns embedded on walls. J. Constr. Steel Res. 2018, 149, 105–118. [Google Scholar] [CrossRef]
- Liu, X.-C.; Feng, X.-Z.; Chen, X.; Zhou, W.; Xu, B.; Yin, Z. Fire resistance performance of L-section fireproof board and thin concrete encased skeleton steel column. Eng. Struct. 2025, 327, 119629. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, S.; Ahmed, M.; Liang, Q.Q. Experimental and numerical investigations of circular concrete filled steel double-skin and double-tube columns exposed to fire. Thin-Walled Struct. 2024, 198, 111766. [Google Scholar] [CrossRef]
- Lie, T.T. Fire resistance of circular steel columns filled with bar-reinforced concrete. J. Struct. Eng. 1994, 120. [Google Scholar] [CrossRef]
- Othuman, M.A.; Wang, Y.C. Elevated-temperature thermal properties of lightweight foamed concrete. Constr. Build. Mater. 2011, 25, 705–716. [Google Scholar] [CrossRef]
- GB 50936-2014; Technical Code for Concrete Filled Steel Tubular Structures. National Standard of the People’s Republic of China: Beijing, China, 2014.
- Duan, B.C.; Yang, D.D.; Liu, F.Q.; Yang, H. Analysis and design on fire performance of circular steel tube confined reinforced concrete columns with fire protection. Eng. Mech. 2024, 41, 118–129. [Google Scholar]
- ISO 834-11: 2014; Fire Resistance Tests-Elements of Building Construction-Part 11: Specific Requirements for the Assessment of Fire Protection to Structural Steel Elements. British Standards Institution: London, UK, 2014.
- Eurocede 3; Design of Steel Structures. McGraw Hill: New York, NY, USA, 1993.
- Mao, W.-J.; Wang, W.-D.; Zhou, K. Fire performance on steel-reinforced concrete-filled steel tubular columns with fire protection. J. Constr. Steel Res. 2022, 199, 107580. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Y.; Su, A.; Su, M.; Zhao, O. Post-fire flexural buckling and resistances of square recycled aggregate concrete-filled stainless steel tube (RACFSST) columns. Thin Walled Struct. 2024, 205, 112490. [Google Scholar] [CrossRef]
- GB 14907-2018; Fire Resistive Coating for Steel Structure. National Standard of the People’s Republic of China: Beijing, China, 2019.
- GB/T 9978.1-2008; Fire-Resistance Tests-Elements of Building Construction-Part 7: Specific Requirements for Columns. National Standard of the People’s Republic of China: Beijing, China, 2009.
- GB 50016-2014 (2018 edition); Code for Fire Protection Design of Building. National Standard of the People’s Republic of China: Beijing, China, 2018.
- Liu, F.Q.; Yang, H.; Yang, D.D.; Zhang, S.M. Fire safety design method of circular steel tube confined reinforced concrete columns. J. Build. Struct. 2017, 38, 150–156. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).