Effect of Initial Temperature on Flame Spread over a Sand Bed Wetted with Transformer Oil
Abstract
1. Introduction
2. Experimental Setup
3. Results and Discussion
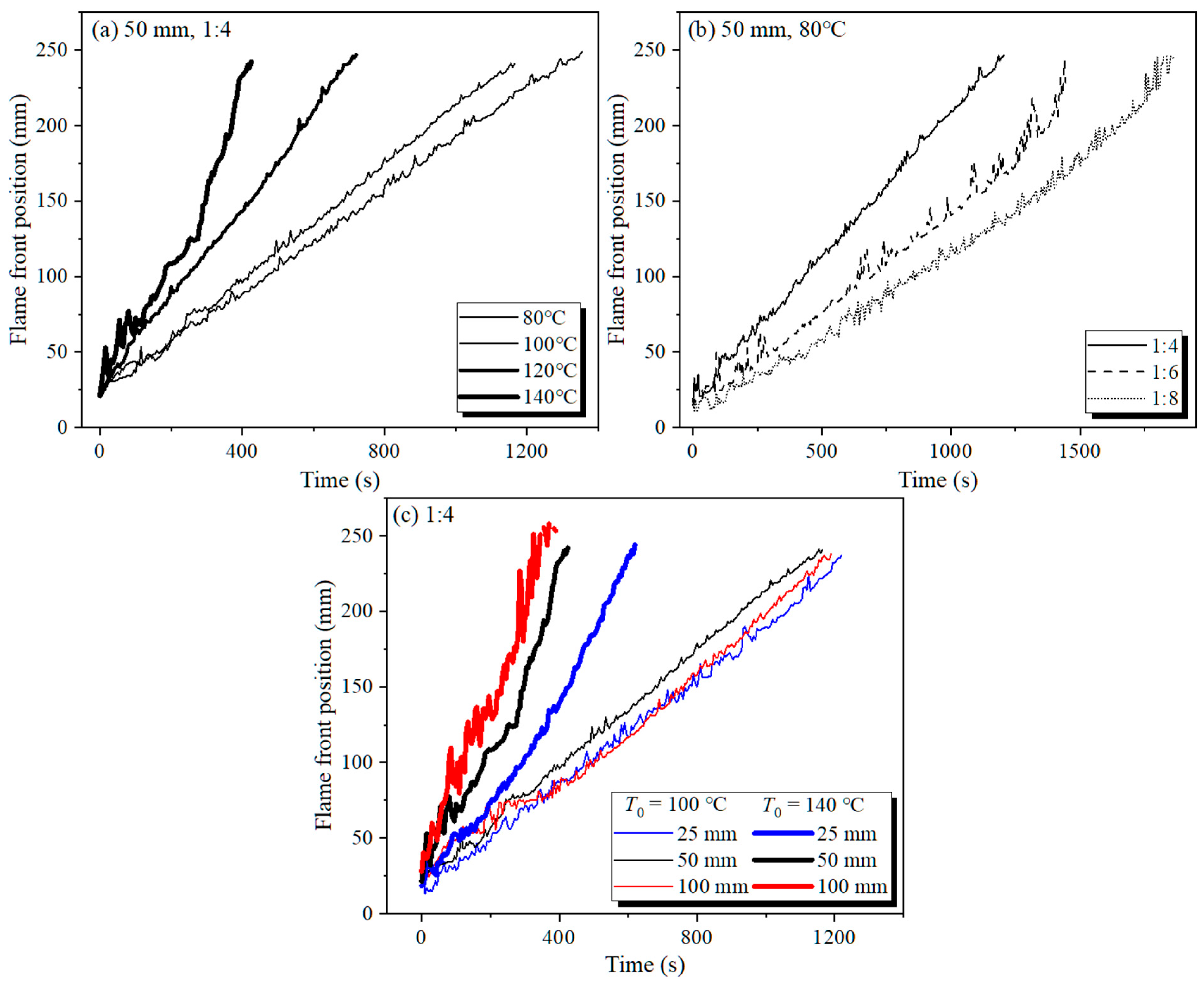
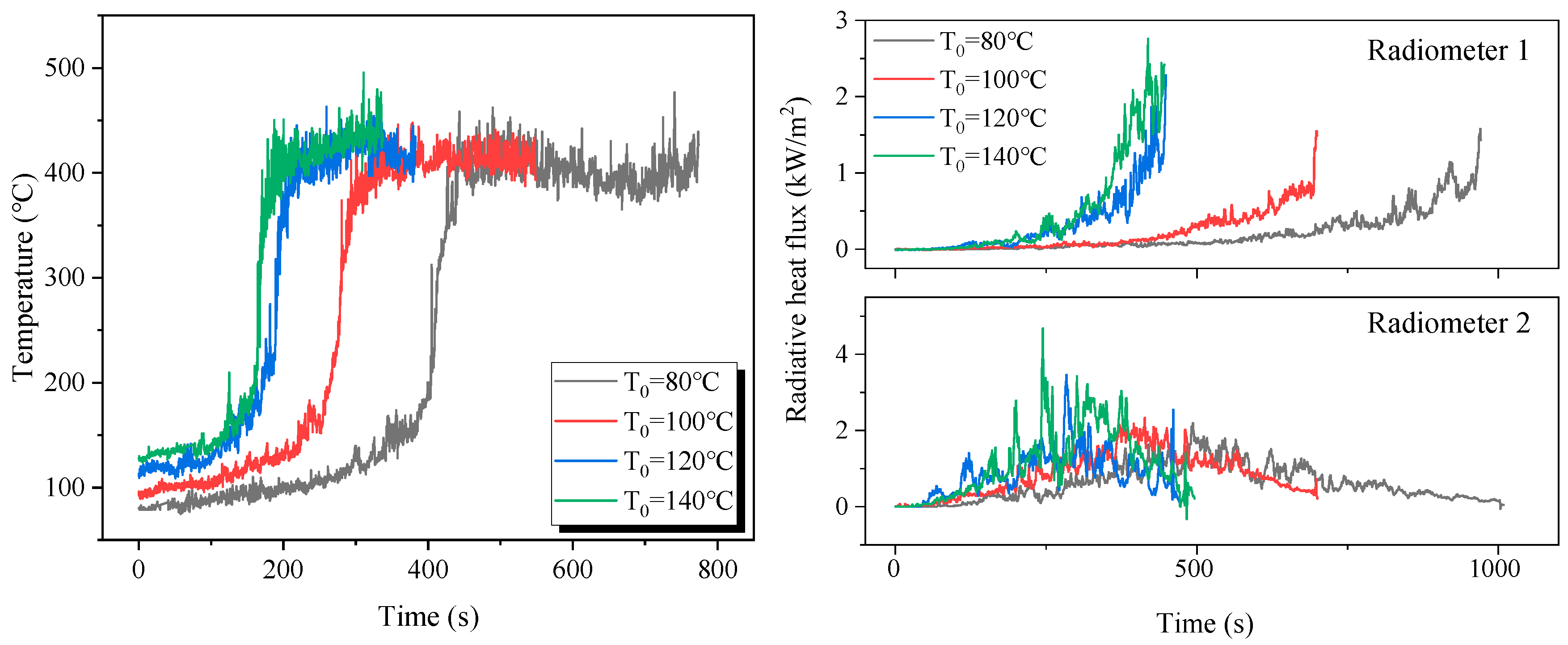
3.1. Flame Spread Process over Sand Bed Wetted with Transformer Oil
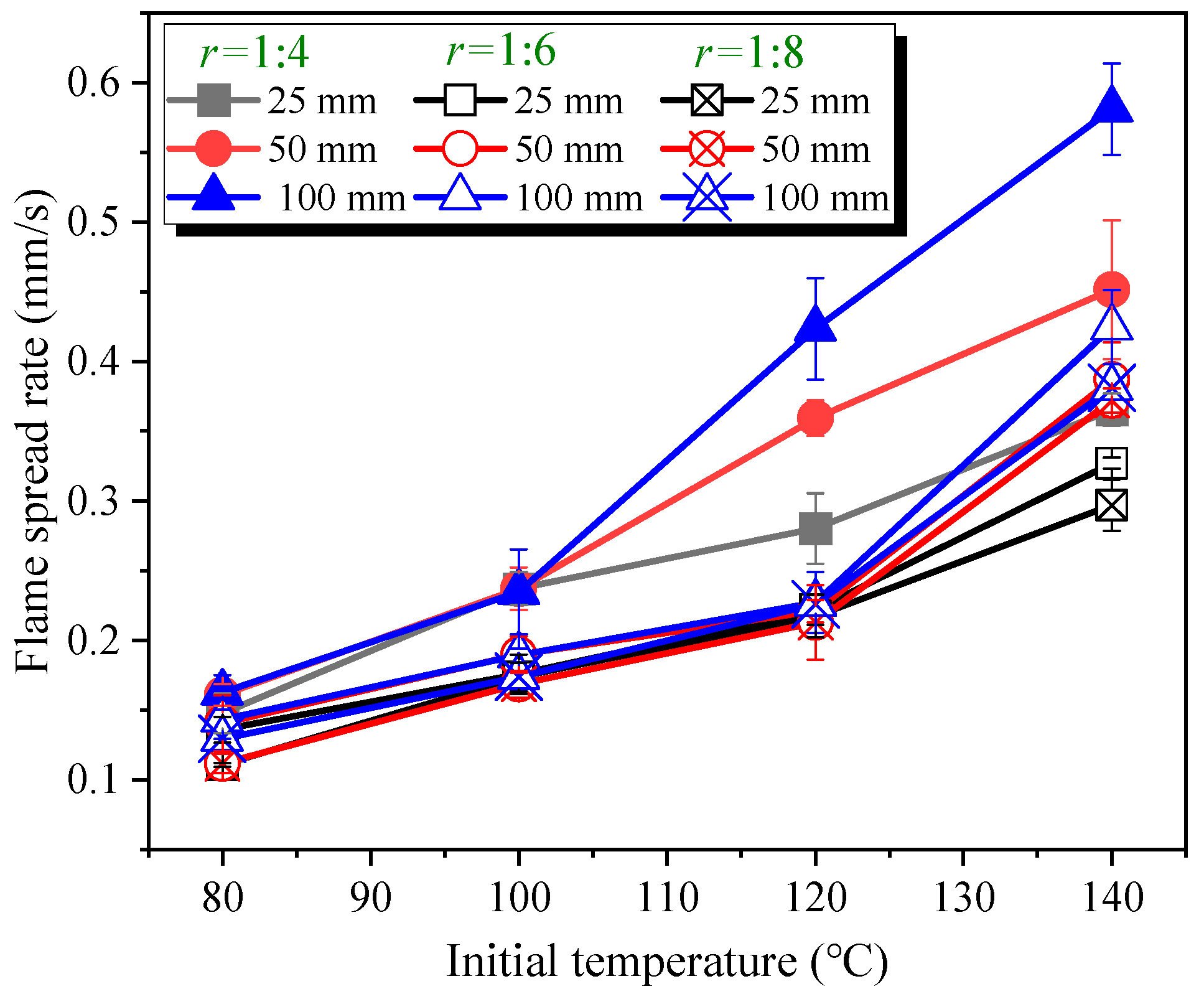
3.2. Flame Spread Rate
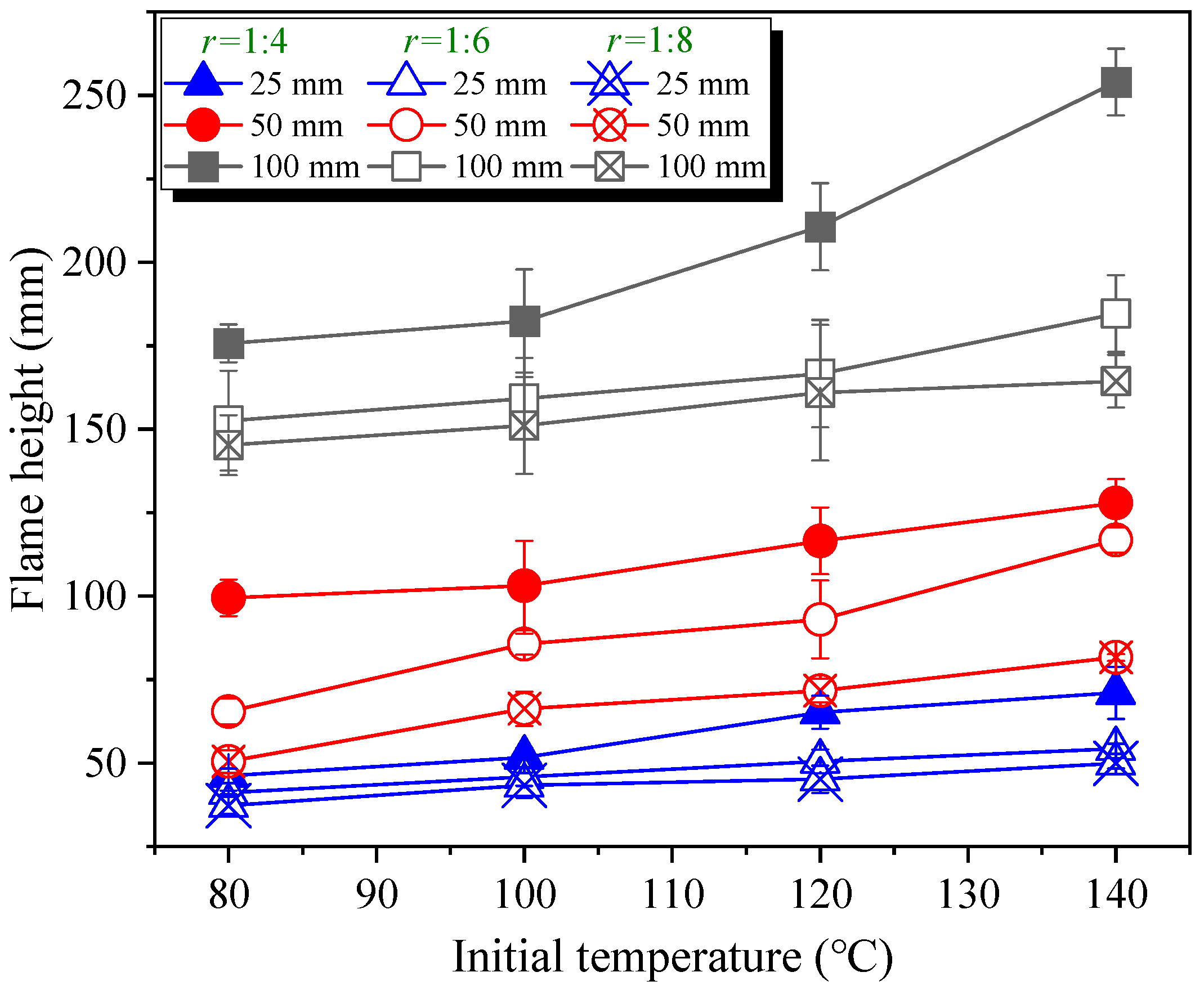
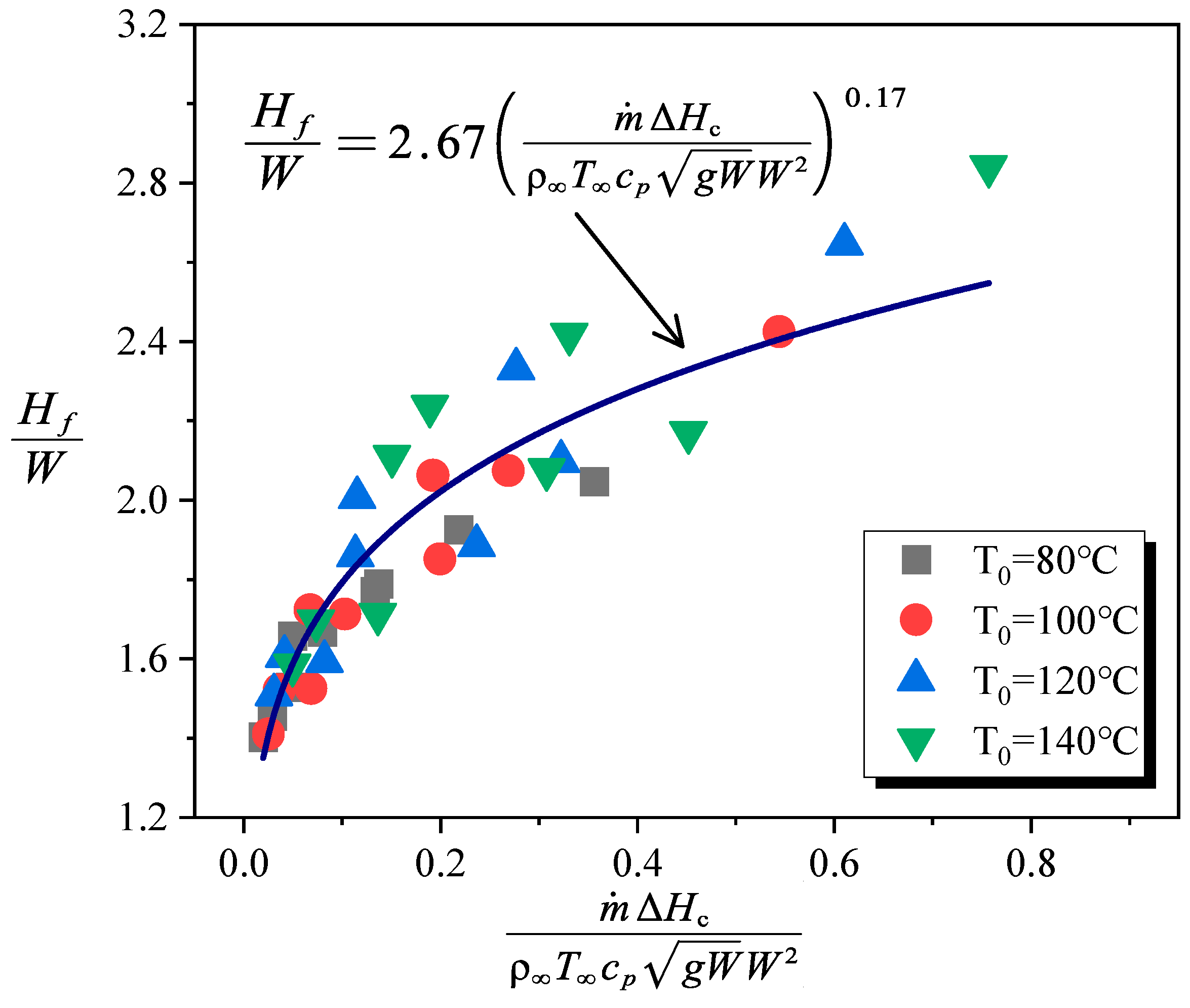
3.3. Flame Height in the Quasi-Steady Stage
4. Conclusions
- (1)
- The flame spread rate over the fine sand bed wetted with transformer oil depends mainly on the fuel–sand mass ratio and initial temperature. At low initial temperatures, the flame spread rate increases with initial temperature and the effect of sand bed width is negligible. Due to the combined effect of enhanced capillary effect and increased heat feedback, width effects become apparent at initial temperatures close to the flash point.
- (2)
- The flame height in the quasi-steady stage is related to the sand bed width and fuel–sand mass ratio but is insensitive to the initial temperature of the sand bed.
- (3)
- An empirical correlation between the normalized flame height and the dimensionless heat release rate is proposed, as given in Equation (4).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Chen, C. An experimental study on burning characteristics and temperature distribution of inert porous sand bed soaked by leaked combustible liquid. Int. J. Therm. Sci. 2022, 179, 107594. [Google Scholar] [CrossRef]
- Zhao, J.; He, Y.; Xiao, J.; Su, Z.; Ma, H.; Zhai, X. Experimental Investigation of the Spread and Burning Behaviors of Diesel Spill Fires on a Water Surface. Fire 2024, 7, 402. [Google Scholar] [CrossRef]
- Ding, C.; Ma, S.; Yan, Z.; He, L.; Li, Y.; Fang, T.; Jiao, Y. Experimental Study on the Effect of Sub-Flash Point Fuel Temperature on the Spread Characteristics of Spill Fire. Fire 2023, 6, 284. [Google Scholar] [CrossRef]
- Xu, T.; Lei, P. Experimental study on flame height and heat release rate estimation of diesel-wetted wood powder fire. Case Stud. Therm. Eng. 2022, 33, 101906. [Google Scholar] [CrossRef]
- Chen, C.; Lei, P.; Zhang, Y.; Xiao, H.; Xu, T.; Jiao, W. Experimental study of influence of fuel ratio on combustion characteristics of diesel-wetted wood powder. J. Therm. Sci. 2020, 29, 884–892. [Google Scholar] [CrossRef]
- Ross, H.D. Ignition of and flame spread over laboratory-scale pools of pure liquid fuels. Prog. Energy Combust. Sci. Technol. 1994, 20, 17–63. [Google Scholar] [CrossRef]
- Chao, C.Y.H.; Wang, J.H.; Kong, W. Effects of fuel properties on the combustion behavior of different types of porous beds soaked with combustible liquid. Int. J. Heat Mass Transf. 2004, 47, 5201–5210. [Google Scholar] [CrossRef]
- Zanganeh, J.; Moghtaderi, B.; Ishida, H. Combustion and flame spread on fuel-soaked porous solids. Prog. Energy Combust. Sci. 2013, 39, 320–339. [Google Scholar] [CrossRef]
- Ishida, H. Flame spread over ground soaked with highly volatile liquid fuel. Fire Saf. J. 1988, 13, 115–123. [Google Scholar] [CrossRef]
- Kong, W.; Chao, C.Y.; Wang, J. Burning characteristics of non-spread diffusion flames of liquid fuel soaked in porous beds. J. Fire Sci. 2002, 20, 203–225. [Google Scholar] [CrossRef]
- Li, M.; Lu, S.; Guo, J.; Chen, R.; Tsui, K.-L. Initial fuel temperature effects on flame spread over aviation kerosene in low-and high-altitude environments. Fire Technol. 2015, 51, 707–721. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, Z.; Ji, J.; Li, K.; Zhang, Y. Experimental study of flame spread over diesel and diesel-wetted sand beds. Fuel 2017, 204, 54–62. [Google Scholar] [CrossRef]
- Zanganeh, J.; Moghtaderi, B. Effect of fuel soaked time and fuel ratio on the flame spread rate over a porous bed wetted with liquid fuel. Fire Saf. J. 2013, 59, 151–159. [Google Scholar] [CrossRef]
- Suzuki, T.; Kawamata, M.; Hirano, T. Flame spread over fuel soaked sand in an opposed air stream. Fire Saf. Sci. 1989, 2, 199–208. [Google Scholar] [CrossRef]
- Ishida, H. Flame tip propagation with assisted flow along fuel-soaked ground. J. Fire Sci. 2011, 29, 99–110. [Google Scholar] [CrossRef]
- Ishida, H.; Kenmotsu, Y. Flame spread in opposed flow along the ground soaked with high-volatile liquid fuel. J. Fire Sci. 2009, 27, 285–297. [Google Scholar] [CrossRef]
- Zanganeh, J.; Moghtaderi, B. Flame spread over porous sand beds wetted with propenol. Fire Mater. 2011, 35, 61–70. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, J.; Huang, Y.; Wang, Q.; Yu, Z.; Fan, M. Burning process and fire characteristics of transformer oil: A study focusing on the effects of oil type. J. Therm. Anal. Calorim. 2020, 139, 1839–1848. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, W.; Yoshioka, H.; Chen, T.; Wang, K.; Hao, D.; Jiang, C.; Cui, K. Research on suppression effectiveness of compressed air foam for oil-immersed transformer hot oil fire. Case Stud. Therm. Eng. 2023, 49, 103272. [Google Scholar] [CrossRef]
- Sorte, S.; Salgado, A.; Monteiro, A.F.; Ventura, D.; Martins, N.; Oliveira, M.S. Advancing Power Transformer Cooling: The Role of Fluids and Nanofluids—A Comprehensive Review. Materials 2025, 18, 923. [Google Scholar] [CrossRef]
- Li, L.; Zhai, X.; Wang, J.; Chen, P.; Shi, C. Experimental study on vertical spill fire characteristics of transformer oil under continuous spill condition. Process Saf. Environ. Prot. 2021, 156, 521–530. [Google Scholar] [CrossRef]
- Li, L.; Guo, X.; Lu, R.; Chen, P.; Shi, C. Experimental study on horizontal fire spread characteristics of transformer oil. J. Energy Resour. Technol. 2022, 144, 012107. [Google Scholar] [CrossRef]
- Huang, Y.; Guo, Y.; Shang, F.; Zhang, J. Effect of oil immersion on the horizontal flame spread over transformer insulating paperboard with different sizes. Case Stud. Therm. Eng. 2025, 70, 106076. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Li, M.; Shu, Z.; Yi, L.; Chen, B.; Zhao, Y.; Geng, S. Combustion behavior and oscillatory regime of flame spread over ethanol aqueous solution with different proportions. Fuel 2019, 253, 220–228. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Z.; Ma, S.; Ju, X.; Guo, P.; Cao, X. Experimental study on the diffusion burning and radiative heat delivery of two adjacent heptane pool fires. Int. J. Therm. Sci. 2022, 171, 107246. [Google Scholar] [CrossRef]
- Bergman, T.L. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhao, K.; Zhou, Y.; Li, S.; Lin, Z. Experimental and numerical study on the burning and opposed flame spread behaviors over PMMA under different flow conditions. Int. Commun. Heat Mass Transf. 2025, 165, 108989. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Jiao, W.; Lu, T. Experimental study on burning characteristic of liquid fuel immersed in porous media bed: Effect of particle gradation. Fuel 2023, 344, 128103. [Google Scholar] [CrossRef]
- Gao, S.; Zhu, G.; Gao, Y.; Zhou, J. Experimental study on width effects on downward flame spread over thin PMMA under limited distance condition. Case Stud. Therm. Eng. 2019, 13, 100382. [Google Scholar] [CrossRef]
- Zhao, K.; Zhou, X.; Liu, X.; Lu, L.; Wu, Z.; Peng, F.; Ju, X.; Yang, L. Prediction of Three-Dimensional Downward Flame Spread Characteristics over Poly (methyl methacrylate) Slabs in Different Pressure Environments. Materials 2016, 9, 948. [Google Scholar] [CrossRef]
- Wu, Z.; Peng, M.; Chai, G.; Zhou, J.; Zhou, Y.; Zhu, G. Experimental study on the influence of restricted distance on the discrete flame spread of different widths. Case Stud. Therm. Eng. 2024, 54, 103973. [Google Scholar] [CrossRef]
- Tu, K.-M.; Quintiere, J.G. Wall flame heights with external radiation. Fire Technol. 1991, 27, 195–203. [Google Scholar] [CrossRef]
- Zhao, K.; Yang, L.; Tang, W.; Liu, Q.; Ju, X.; Gong, J. Effect of orientation on the burning and flame characteristics of PMMA slabs under different pressure environments. Appl. Therm. Eng. 2019, 156, 619–626. [Google Scholar] [CrossRef]
- Gollner, M.; Williams, F.; Rangwala, A. Upward flame spread over corrugated cardboard. Combust. Flame 2011, 158, 1404–1412. [Google Scholar] [CrossRef]
- Hu, L. A review of physics and correlations of pool fire behaviour in wind and future challenges. Fire Saf. J. 2017, 91, 41–55. [Google Scholar] [CrossRef]
- Heskestad, G. Luminous heights of turbulent diffusion flames. Fire Saf. J. 1983, 5, 103–108. [Google Scholar] [CrossRef]
- Jeong, J.-J.; Mizuno, M.; Park, K.-W.; Lim, H.-J.; Cho, C.-G. Fire properties of bed mattresses focusing on the fire growth rate and flame height. Materials 2022, 15, 3757. [Google Scholar] [CrossRef]
- Huang, X.; Ding, H.; Zhang, X.; Li, X.; Wang, M.; Zhang, P. Effects of wind speed, spacing distance and heat release rate on the combustion and flame merging characteristics of two extra-thin line fires. Case Stud. Therm. Eng. 2024, 60, 104676. [Google Scholar] [CrossRef]
- Jiang, L.; Miller, C.H.; Gollner, M.J.; Sun, J. Sample width and thickness effects on horizontal flame spread over a thin PMMA surface. Proc. Combust. Inst. 2016, 36, 2987–2994. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Mao, S.; Wang, X.; Lu, K.; Li, B. Experimental study on burning characteristic of liquid fuel-immersed porous media bed in cross airflow. Int. J. Therm. Sci. 2025, 210, 109677. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Li, J.; Sun, J.; Wang, Q.; Huang, X. Effects of altitude and sample width on the characteristics of horizontal flame spread over wood sheets. Fire Saf. J. 2012, 51, 120–125. [Google Scholar] [CrossRef]
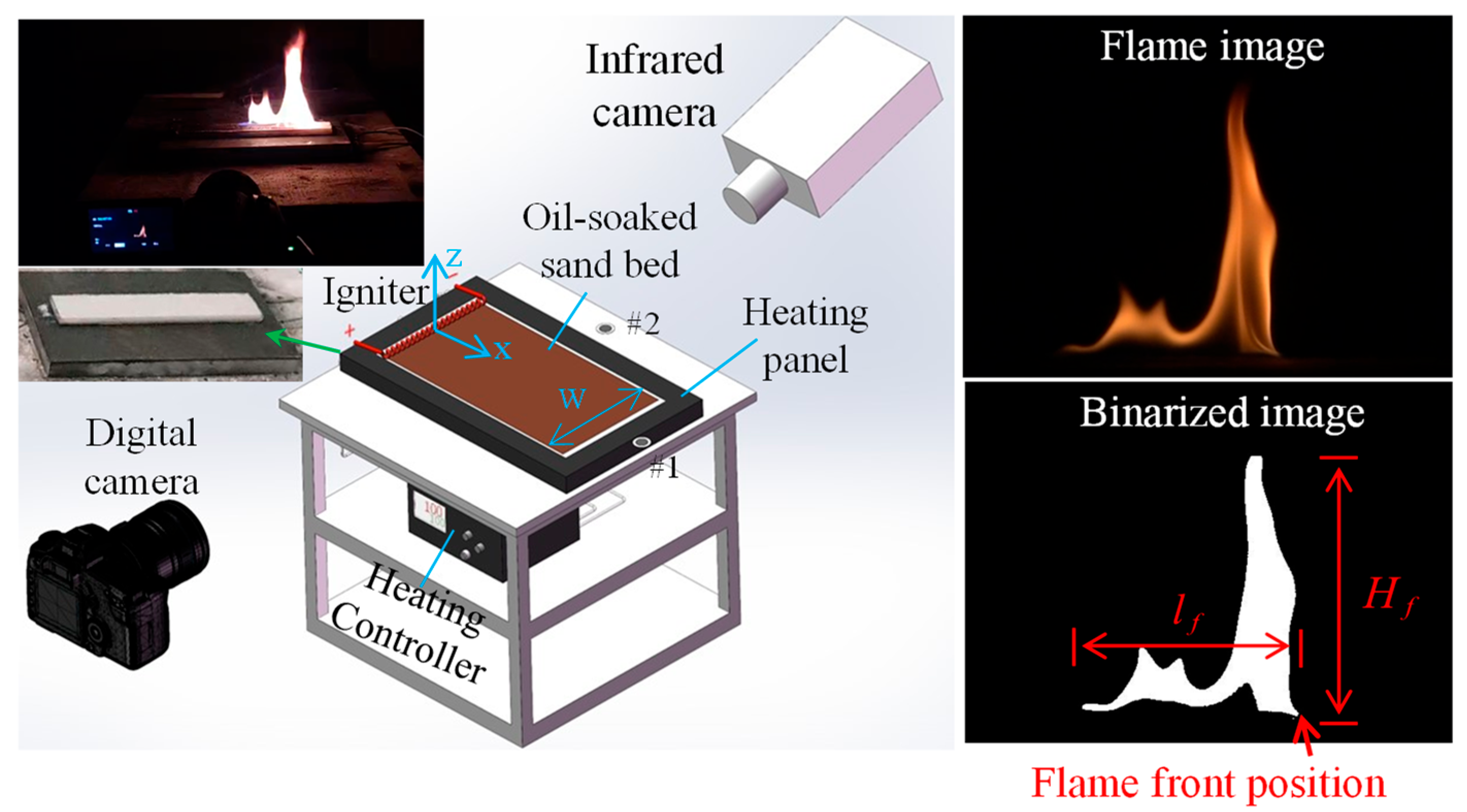
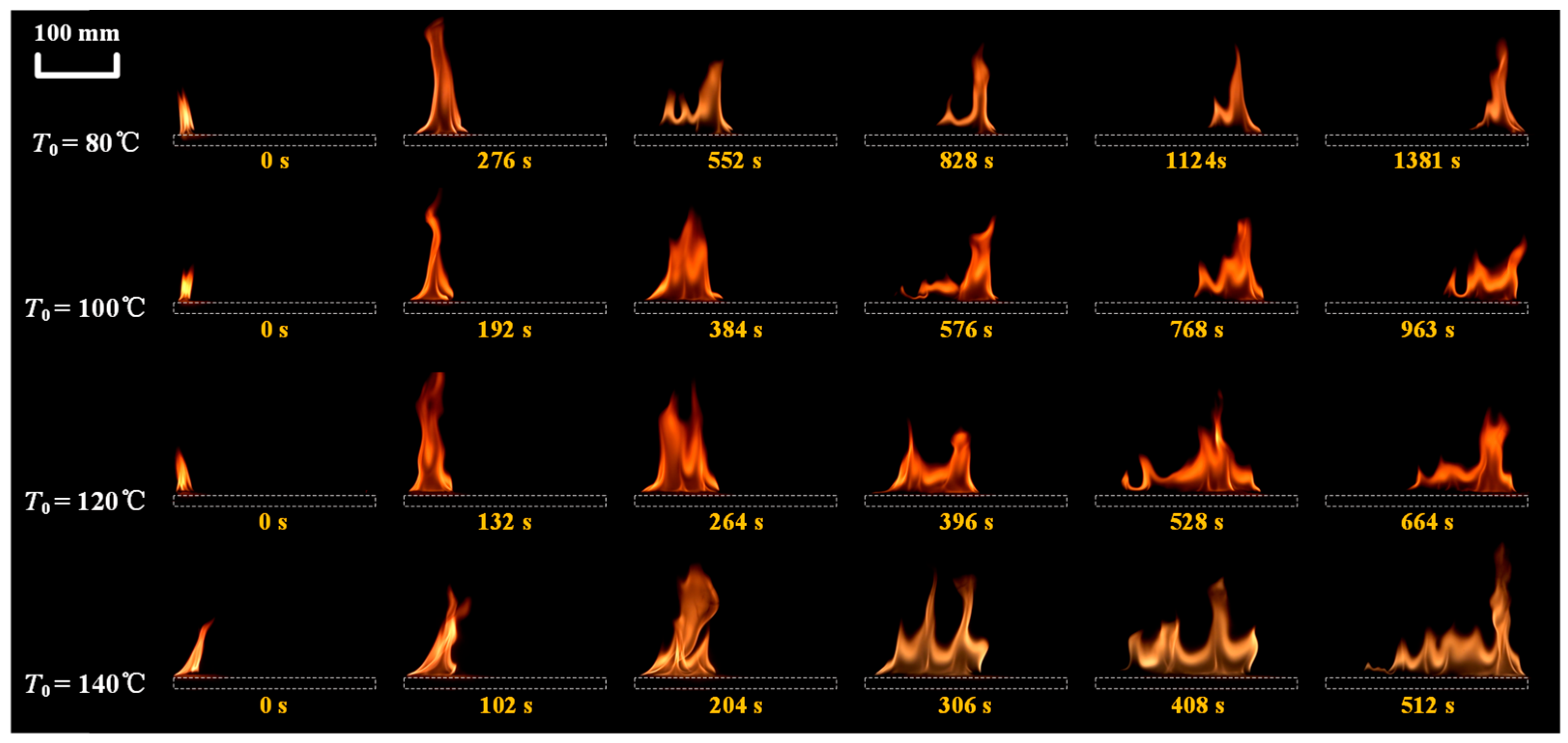
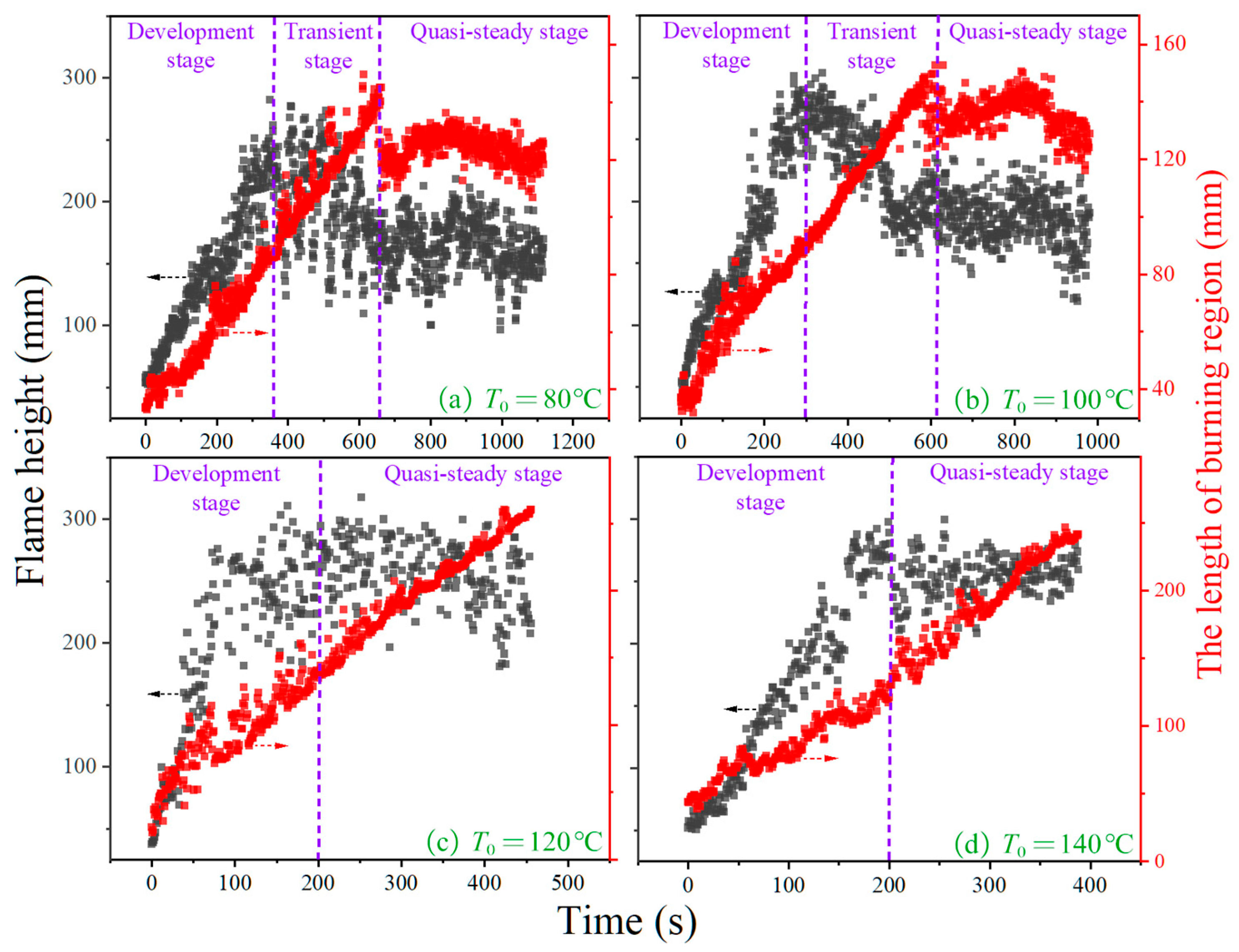
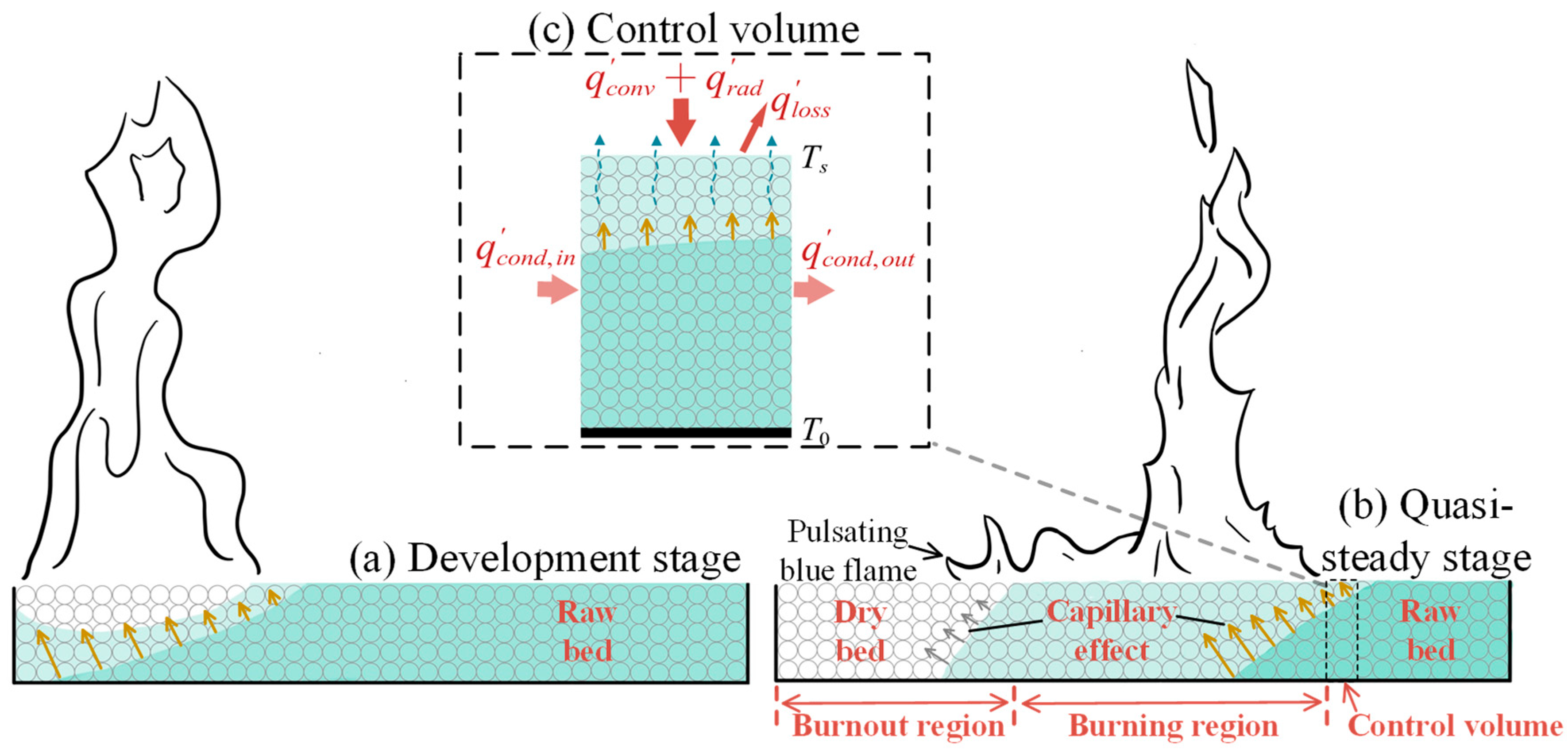
| (mm) | (mm) | (mm) | Fuel–Sand Mass Ratio, r | (°C) |
|---|---|---|---|---|
| 25, 50, 100 | 8 | 250 | 1:4, 1:6, 1:8 | 80, 100, 120, 140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Huang, Y.; Guo, Y.; Ding, G. Effect of Initial Temperature on Flame Spread over a Sand Bed Wetted with Transformer Oil. Fire 2025, 8, 193. https://doi.org/10.3390/fire8050193
Zhang J, Huang Y, Guo Y, Ding G. Effect of Initial Temperature on Flame Spread over a Sand Bed Wetted with Transformer Oil. Fire. 2025; 8(5):193. https://doi.org/10.3390/fire8050193
Chicago/Turabian StyleZhang, Jiaqing, Yubiao Huang, Yi Guo, and Guocheng Ding. 2025. "Effect of Initial Temperature on Flame Spread over a Sand Bed Wetted with Transformer Oil" Fire 8, no. 5: 193. https://doi.org/10.3390/fire8050193
APA StyleZhang, J., Huang, Y., Guo, Y., & Ding, G. (2025). Effect of Initial Temperature on Flame Spread over a Sand Bed Wetted with Transformer Oil. Fire, 8(5), 193. https://doi.org/10.3390/fire8050193






