Study on Leakage and Diffusion Law Under the Combined Laying of Gas Pipelines and Power Channels
Abstract
1. Introduction
2. Model Building
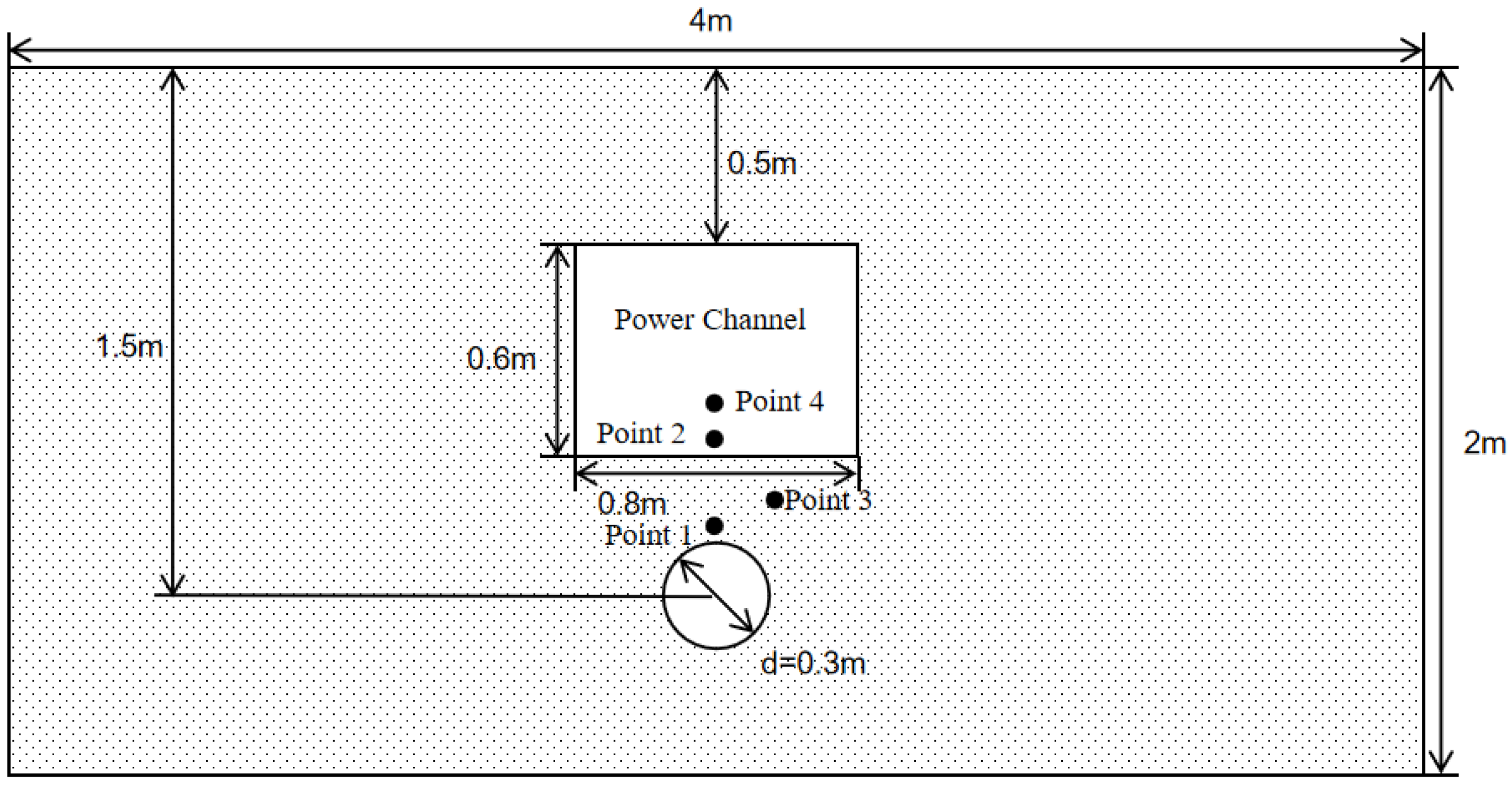
2.1. Physical Model
2.2. Theoretical Basis
- 1.
- Continuity Equation:
- 2.
- Momentum Equation:
- 3.
- Energy Equation:
2.3. Initial and Boundary Condition Setup
2.4. Grid Partitioning and Irrelevance Verification
3. Experimental Validation of the Model
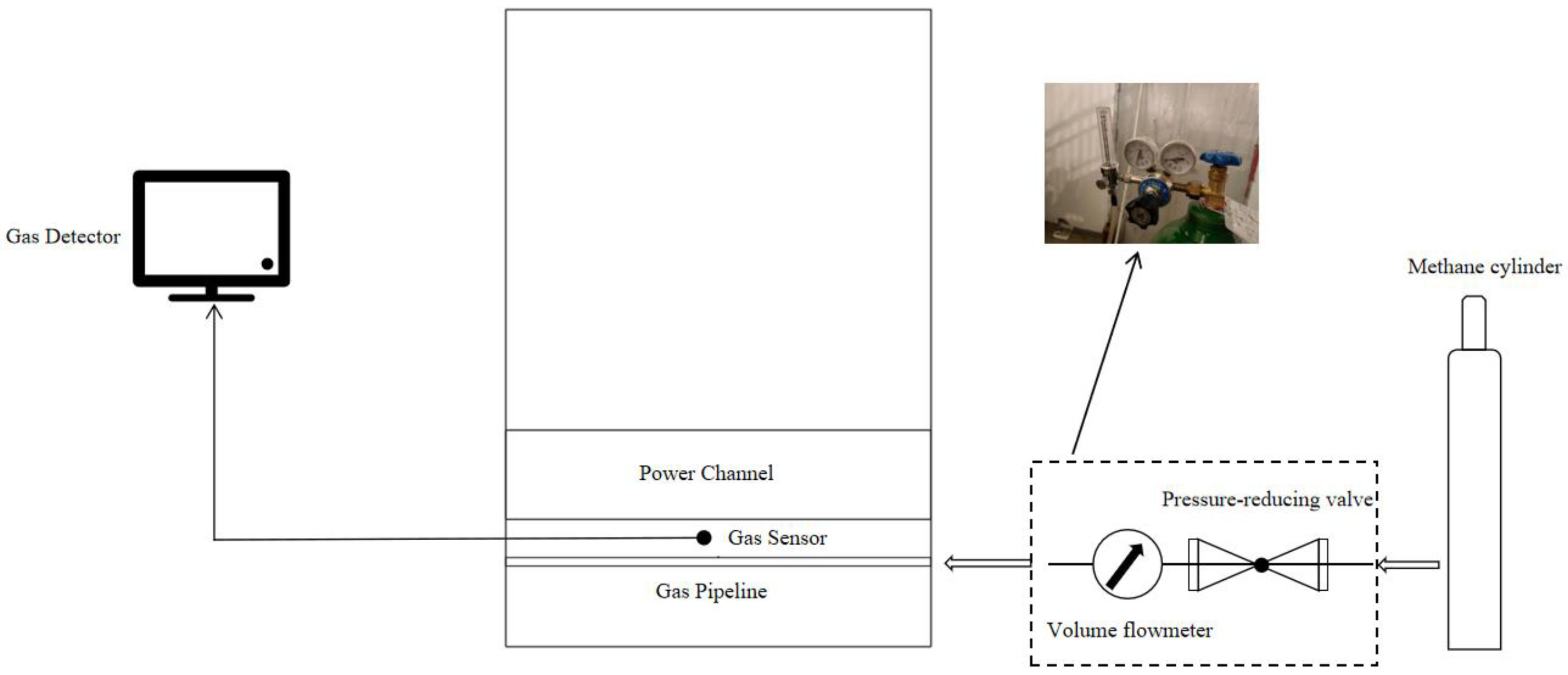
3.1. Design of the Experimental Platform
3.2. Experimental Procedure
- Conduct preliminary experiments to determine optimal conditions for the formal experiment and verify the scientific validity and feasibility of the experimental design.
- Open the methane cylinder, adjust the pipeline pressure, and begin recording changes in methane concentration at the measurement point under different operating conditions.
- Stop recording, close the methane cylinder, and wait for methane gas to dissipate from the soil.
- Repeat the above steps until experiments under all operating conditions are completed.
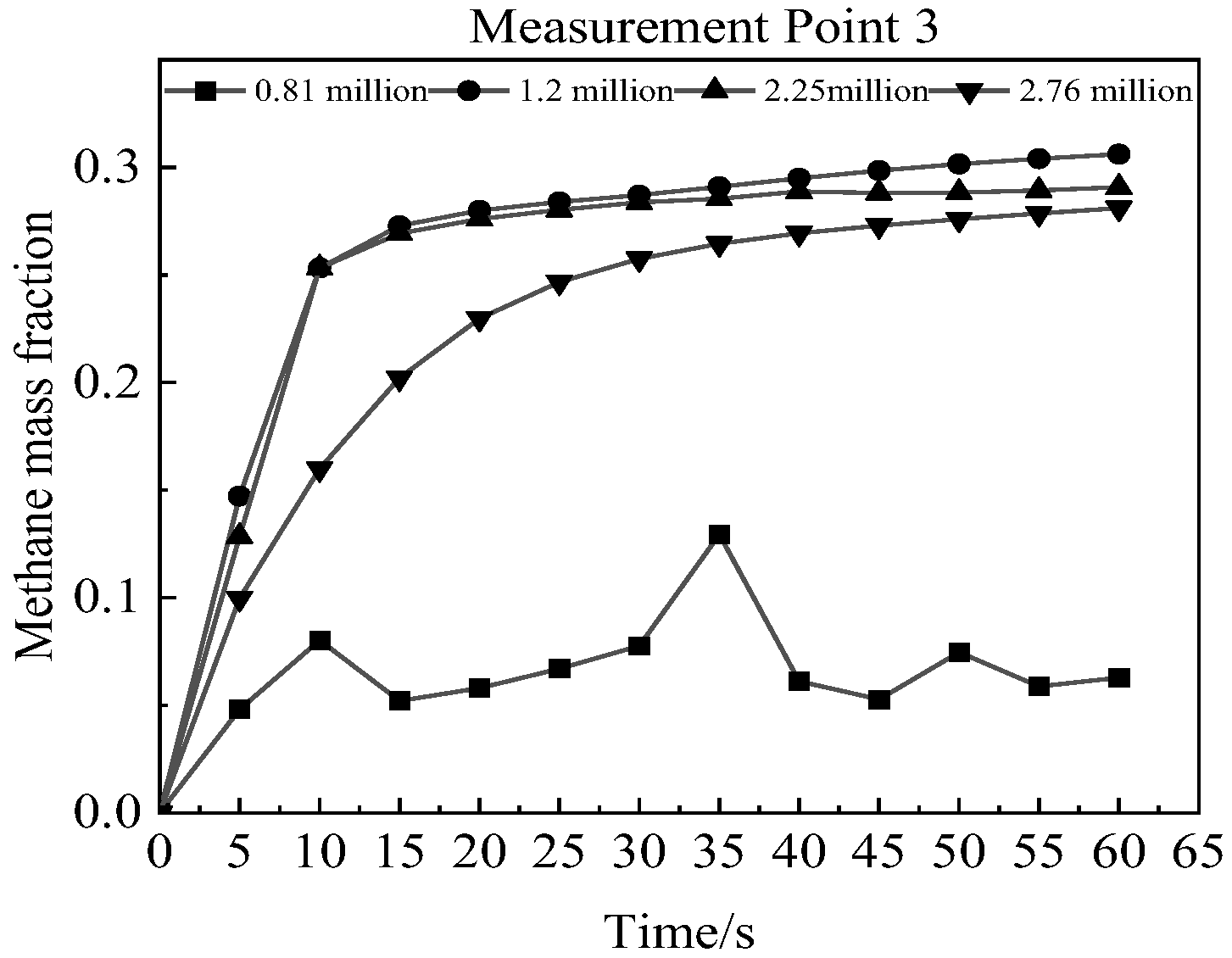
3.3. Model Validation
4. Analysis of Numerical Simulation Results
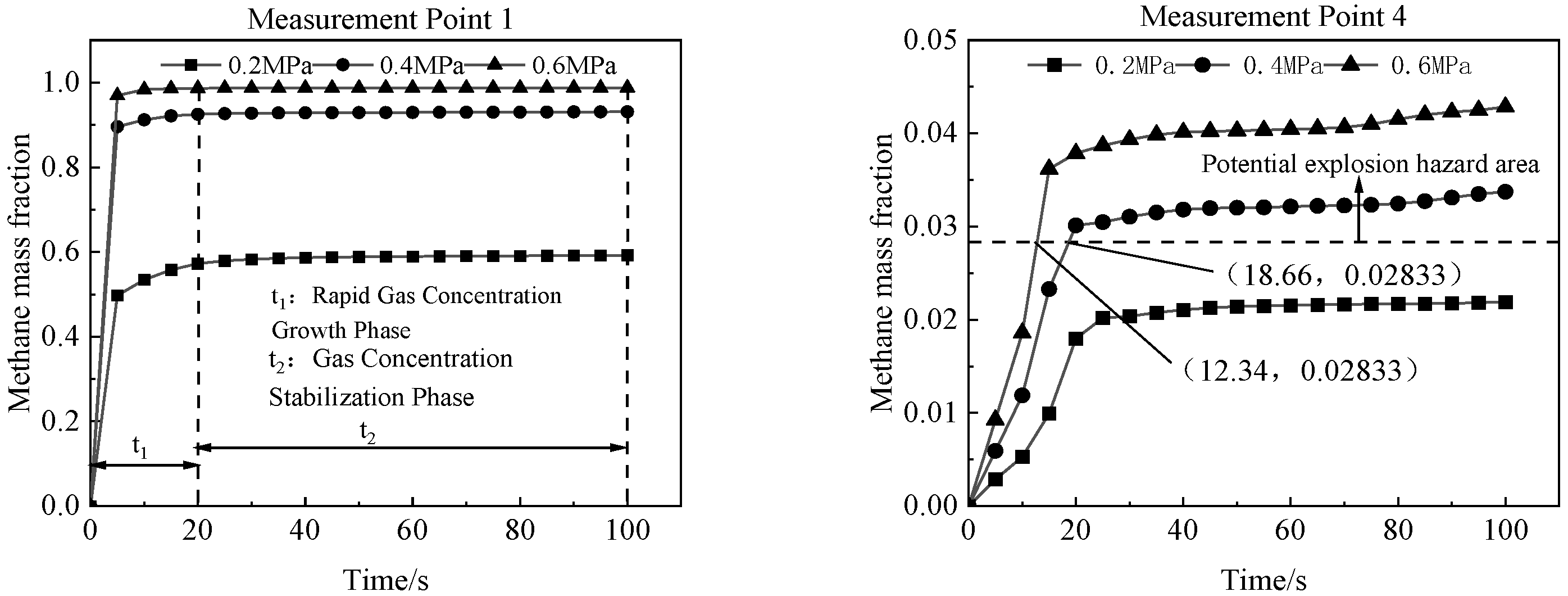
4.1. Simulation Results at Different Pressures
4.2. Simulation Results for Different Leak Hole Sizes
4.3. Simulation Results for Different Buried Soils
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Zhao, X.; Fang, W.; Wang, J.; Tang, F. Numerical simulation study on leakage and diffusion of urban buried gas pipeline adjacent to electric pipeline. J. Saf. Sci. Technol. 2024, 20, 125–131. [Google Scholar]
- Zhu, Q.; Yi, S.; Chen, Y.; Liu, Y. Time effect early warning model for failure risk of buried gas pipeline. Fire Sci. Technol. 2021, 40, 1780–1784. [Google Scholar]
- Luo, T.; Ma, H.; Hu, K.; Han, J.; Deng, R. Analysis of gas diffusion mechanism of gas leakage in buried gas pipeline. Chin. J. Appl. Mech. 2021, 38, 2405–2410. [Google Scholar]
- Jayarathne, J.R.R.N.; Kolodziej, R.S.; Riddick, S.N.; Zimmerle, D.J.; Smits, K.M. Influence of soil-gas diffusivity on expansion of leaked underground natural gas plumes and application on simulation efforts. J. Hydrol. 2023, 625, 130049. [Google Scholar] [CrossRef]
- Mynarz, M.; Tulach, A.; Bojko, M. CFD-based simulation of flammable gas dispersion in a complex geometry. J. Loss Prev. Process Ind. 2025, 94, 105551. [Google Scholar] [CrossRef]
- Parvini, M.; Gharagouzlou, E. Gas leakage consequence modeling for buried gas pipelines. J. Loss Prev. Process Ind. 2015, 37, 110–118. [Google Scholar] [CrossRef]
- Dadkani, P.; Noorzai, E.; Ghanbari, A.; Gharib, A. Risk analysis of gas leakage in gas pressure reduction station and its consequences: A case study for Zahedan. Heliyon 2021, 7, e6911. [Google Scholar] [CrossRef]
- Bonnaud, C.; Cluzel, V.; Corcoles, P.; Dubois, J.-P.; Louvet, V.; Maury, M.; Narbonne, A.; Orefice, H.; Perez, A.; Ranty, J.; et al. Experimental study and modelling of the consequences of small leaks on buried transmission gas pipeline. J. Loss Prev. Process Ind. 2018, 55, 303–312. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Deymi-Dashtebayaz, M. Correlations for estimating natural gas leakage from above-ground and buried urban distribution pipelines. J. Nat. Gas Sci. Eng. 2016, 34, 185–196. [Google Scholar] [CrossRef]
- Houssin-Agbomson, D.; Blanchetiere, G.; Mccollum, D.; Saint-Macary, C.; Mendes, R.F.; Jamois, D.; Barbalat, M.; Foissac, A.; Lubet, T. Consequences of a 12-mm diameter high pressure gas release on a buried pipeline. Experimental setup and results. J. Loss Prev. Process Ind. 2018, 54, 183–189. [Google Scholar] [CrossRef]
- Wakoh, H.; Hirano, T. Diffusion of leaked flammable gas in soil. J. Loss Prev. Process Ind. 1991, 4, 260–264. [Google Scholar] [CrossRef]
- Wilkening, H.; Baraldi, D. CFD modelling of accidental hydrogen release from pipelines. Int. J. Hydrogen Energy 2007, 32, 2206–2215. [Google Scholar] [CrossRef]
- Bai, M.; Liu, Q. Evaluating Urban Fire Risk Based on Entropy-Cloud Model Method Considering Urban Safety Resilience. Fire 2023, 6, 62. [Google Scholar] [CrossRef]
- Żakowski, K.; Szociński, M.; Krakowiak, S. Assessment Methods for DC Stray Current Corrosion Hazards in Underground Gas Pipelines: A Review Focused on Rail Traction Systems. Energies 2025, 18, 5570. [Google Scholar] [CrossRef]
- Torno, S.; Toraño, J. Methane Emission Outbursts in the Mine Face of Two Galleries: Computational Fluid Dynamics Analysis and On-Site Calibration. Energies 2023, 16, 7298. [Google Scholar] [CrossRef]
- Komarov, A.; Korolchenko, D.; Gromov, N.; Korolchenko, A.; Jafari, M.; Gravit, M. Specific Aspects of Modeling Gas Mixture Explosions in the Atmosphere. Fire 2023, 6, 201. [Google Scholar] [CrossRef]
- Moloudi, R.; Abolfazli Esfahani, J. Modeling of gas release following pipeline rupture: Proposing non-dimensional correlation. J. Loss Prev. Process Ind. 2014, 32, 207–217. [Google Scholar] [CrossRef]
- Malakhov, A.A.; Avdeenkov, A.V.; du Toit, M.H.; Bessarabov, D.G. CFD simulation and experimental study of a hydrogen leak in a semi-closed space with the purpose of risk mitigation. Int. J. Hydrogen Energy 2020, 45, 9231–9240. [Google Scholar] [CrossRef]
- Mahgerefteh, H.; Oke, A.; Atti, O. Modelling outflow following rupture in pipeline networks. Chem. Eng. Sci. 2006, 61, 1811–1818. [Google Scholar] [CrossRef]
- Abhulimen, K.E.; Susu, A.A. Liquid pipeline leak detection system: Model development and numerical simulation. Chem. Eng. J. 2004, 97, 47–67. [Google Scholar] [CrossRef]
- Gupta, P.; Thein Zan, T.T.; Wang, M.; Dauwels, J.; Ukil, A. Leak detection in low-pressure gas distribution networks by probabilistic methods. J. Nat. Gas Sci. Eng. 2018, 58, 69–79. [Google Scholar] [CrossRef]
- Tauseef, S.M.; Rashtchian, D.; Abbasi, S.A. CFD-based simulation of dense gas dispersion in presence of obstacles. J. Loss Prev. Process Ind. 2011, 24, 371–376. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, P.; Lu, Y.; Yang, M.; Zhang, J.; Liu, K. Research on Pipeline Leakage Calculation and Correction Method Based on Numerical Calculation Method. Energies 2023, 16, 7255. [Google Scholar] [CrossRef]
- Silgado-Correa, K.J.; Ferreira, T.D.; Vianna, S.S.V. Leak release momentum and the convective flow influence on the calculation of flammable cloud. J. Loss Prev. Process Ind. 2020, 65, 104123. [Google Scholar] [CrossRef]
- Yassin, K.; Kelm, S.; Reinecke, E. Numerical Simulation of Dispersion and Ventilation of Hydrogen Clouds in Case of Leakage Inside a Large-Scale Industrial Building. Hydrogen 2025, 6, 40. [Google Scholar] [CrossRef]
- Mohanty, S.; Brennan, S.; Molkov, V. CFD modelling of methane dispersion from buried pipeline leaks: Experimental validation and hazard distance estimation. Process Saf. Environ. Prot. 2024, 187, 1540–1557. [Google Scholar] [CrossRef]
- Srour, O.; Kakosimos, K.E.; Vechot, L.N. Toward a high-fidelity model for the identification of underground gas flow regimes resulting from buried pipeline releases. J. Nat. Gas Sci. Eng. 2022, 108, 104832. [Google Scholar] [CrossRef]
- Penchev, M.; Martinez-Morales, A.A.; Lim, T.; Raju, A.S.K.; Yilmaz, M.; Akinci, T.C. Leakage rates of hydrogen-methane gas blends under varying pressure conditions. Int. J. Hydrogen Energy 2025, 143, 912–920. [Google Scholar] [CrossRef]
- Bagheri, M.; Sari, A. A time-dependent CFD approach to consequence assessment of sour natural gas leakage from buried high-pressure transmission pipelines. J. Loss Prev. Process Ind. 2024, 91, 105389. [Google Scholar] [CrossRef]
- Moghadam Dezfouli, A.; Saffarian, M.R.; Behbahani-Nejad, M.; Changizian, M. Experimental and numerical investigation on development of a method for measuring the rate of natural gas leakage. J. Nat. Gas Sci. Eng. 2022, 104, 104643. [Google Scholar] [CrossRef]
- Bagheri, M.; Sari, A. Study of natural gas emission from a hole on underground pipelines using optimal design-based CFD simulations: Developing comprehensive soil classified leakage models. J. Nat. Gas Sci. Eng. 2022, 102, 104583. [Google Scholar] [CrossRef]
- Venkata Rao, G.; Kolodziej, R.S.; Zimmerle, D.J.; Smits, K.M. Performance of mobile survey solutions for natural gas pipeline leaks under different soil type and moisture conditions. Gas Sci. Eng. 2025, 140, 205650. [Google Scholar] [CrossRef]
- Bezaatpour, J.; Fatehifar, E.; Rasoulzadeh, A. CFD investigation of natural gas leakage and propagation from buried pipeline for anisotropic and partially saturated multilayer soil. J. Clean. Prod. 2020, 277, 123940. [Google Scholar] [CrossRef]
- Agarwal, A.; Molwane, O.B.; Pitso, I. Analytical investigation of the influence of natural gas leakage & safety zone in a pipeline flow. Mater. Today Proc. 2021, 39, 547–552. [Google Scholar]
- Liang, J. Study on Leakage Estimation and Diffusion Characteristics of Buried Gas Transmission Pipeline. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2019. [Google Scholar]




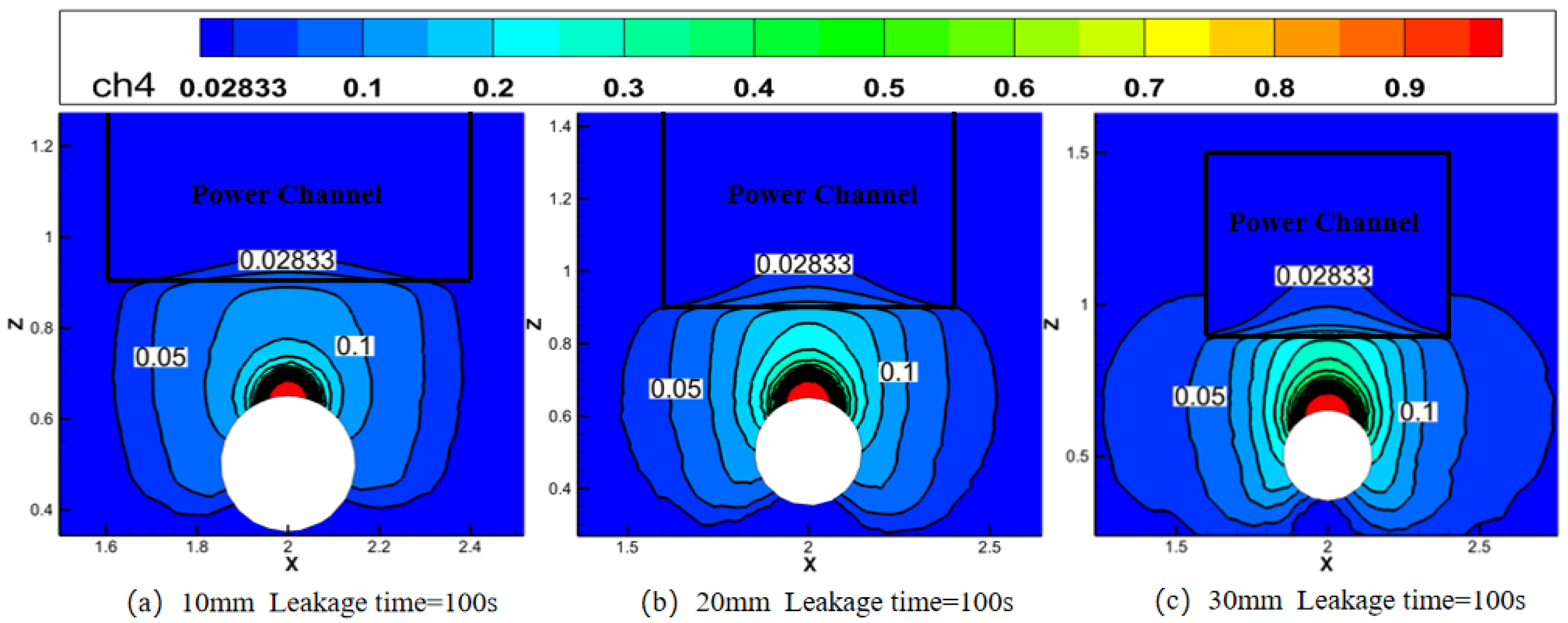
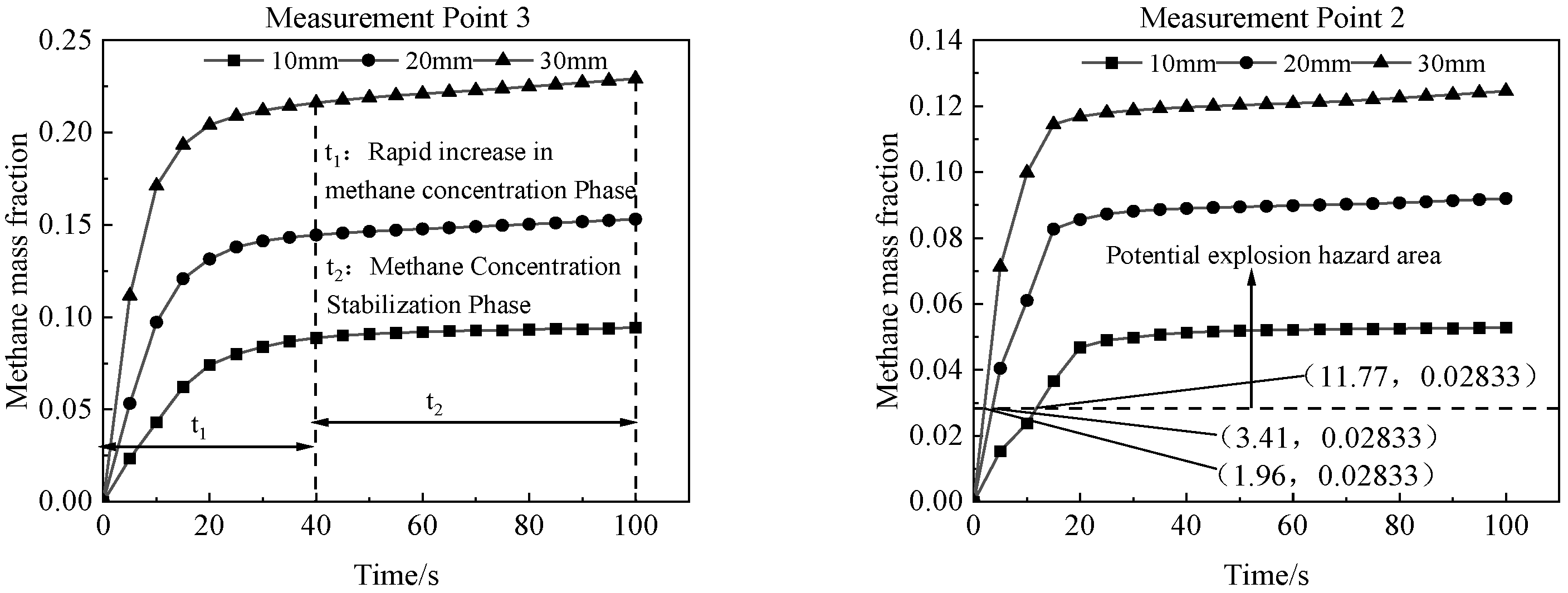

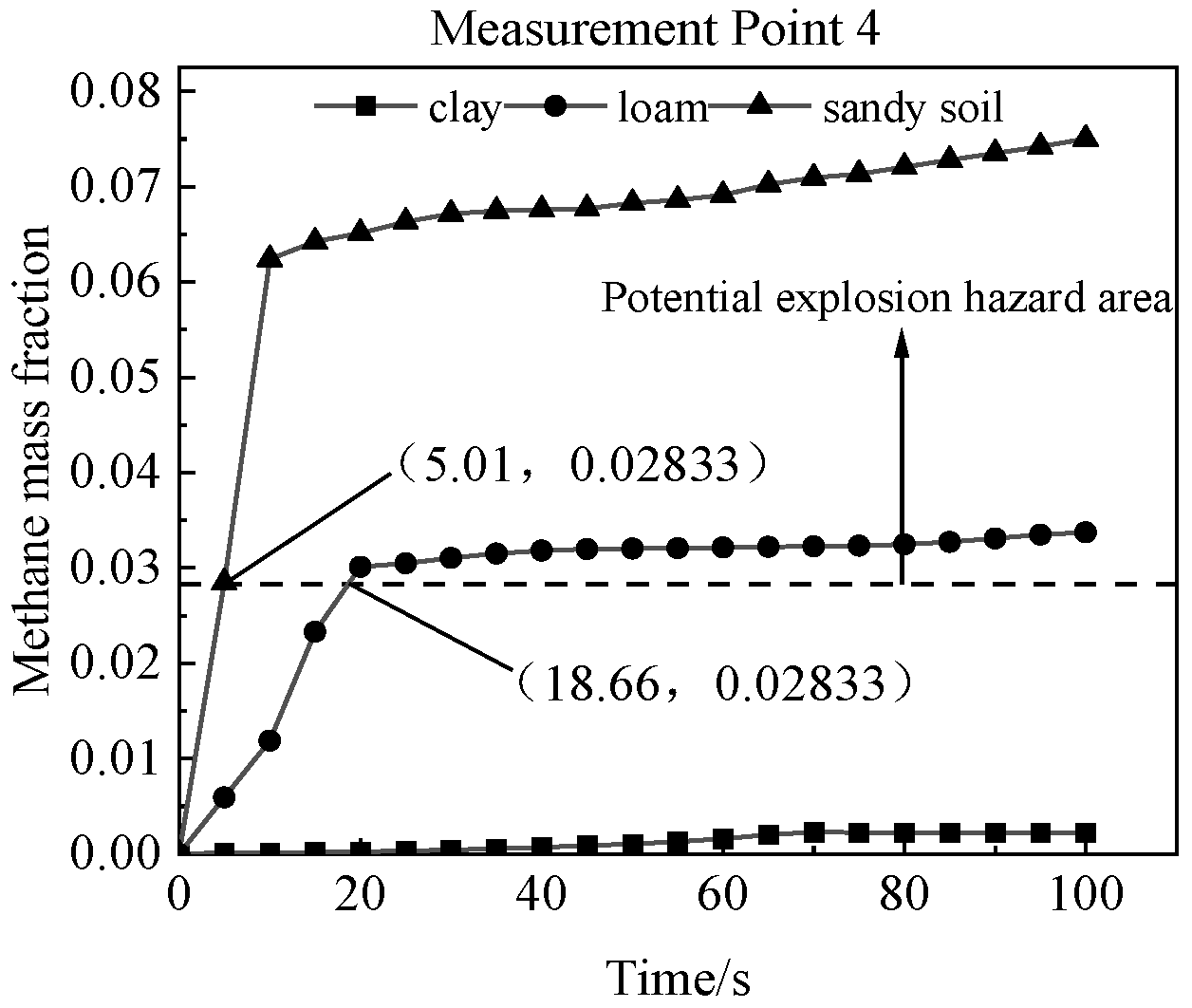
| Serial Number | Time | Brief Description of the Incident | Cause of the Accident |
|---|---|---|---|
| 1 | 13 March 2024 | An explosion occurred in Yanjiao Town, Sanhe City, Langfang, resulting in seven deaths and 27 injuries. | A gas leak occurred during transportation, ultimately leading to an explosion. |
| 2 | 24 October 2023 | An explosion occurred at Cuiyuan Residential Community in Heping Subdistrict, Meihekou City, Jilin Province, resulting in one fatality, one person seriously injured, and 15 others sustaining minor abrasions. | Improper operation by residents during gas usage ultimately led to the accident. |
| 3 | 21 June 2023 | A major gas explosion occurred at Fuyang Barbecue Restaurant in Xingqing District, Yinchuan City, Ningxia Hui Autonomous Region, resulting in 31 deaths and seven injuries. | Improper handling of liquefied petroleum gas cylinders caused a leak and an explosion. |
| 4 | 29 October 2022 | An explosion occurred in a shop in Ganzhou, Jiangxi Province, resulting in four deaths and 18 injuries. | The gas pipeline leaked under overpressure conditions, ultimately leading to an explosion. |
| 5 | 21 June 2022 | A gas explosion occurred near the intersection of Beicheng East Road and Wusu Road in Baodi District, Tianjin, resulting in 23 injuries. | The accident was caused by non-compliant construction practices. |
| 6 | 10 September 2021 | A pipeline liquefied petroleum gas leak and explosion occurred on Commercial Street in Pulandian District, Dalian City, Liaoning Province. The incident resulted in nine fatalities and four injuries. | Indoor gas leaked due to corrosion and exploded upon contact with an open flame. |
| Soil Types | Average Diameter (mm) | Porosity | Viscous Resistance Coefficient | Inertial Resistance Coefficient |
|---|---|---|---|---|
| sandy soil | 0.5 | 0.25 | 2.14 × 1010 | 3.34 × 105 |
| loam | 0.05 | 0.43 | 2.43 × 1011 | 5.01 × 105 |
| clay | 0.01 | 0.3 | 2.71 × 1013 | 9.06 × 106 |
| Number | Pipeline Pressure (MPa) | Leakage Hole Diameter (mm) | Leakage Hole Orientation | Soil Types |
|---|---|---|---|---|
| 1 | 0.2 | 20 | Upward | loam |
| 2 | 0.4 | 20 | Upward | loam |
| 3 | 0.6 | 20 | Upward | loam |
| 4 | 0.4 | 10 | Upward | loam |
| 5 | 0.4 | 30 | Upward | loam |
| 6 | 0.4 | 20 | Upward | clay |
| 7 | 0.4 | 20 | Upward | sandy soil |
| Number | Leak Pressure (MPa) | Leakage Time | Leakage Aperture |
|---|---|---|---|
| 1 | 0.1 | 3 min | 3 mm |
| 2 | 0.15 | 3 min | 3 mm |
| 3 | 0.2 | 3 min | 3 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, C.; Chen, J.; Fan, M.; Niu, G.; Zhu, L.; Zhao, X. Study on Leakage and Diffusion Law Under the Combined Laying of Gas Pipelines and Power Channels. Fire 2025, 8, 454. https://doi.org/10.3390/fire8120454
Ge C, Chen J, Fan M, Niu G, Zhu L, Zhao X. Study on Leakage and Diffusion Law Under the Combined Laying of Gas Pipelines and Power Channels. Fire. 2025; 8(12):454. https://doi.org/10.3390/fire8120454
Chicago/Turabian StyleGe, Chenghao, Jie Chen, Minghao Fan, Guoqing Niu, Lin Zhu, and Xiaolong Zhao. 2025. "Study on Leakage and Diffusion Law Under the Combined Laying of Gas Pipelines and Power Channels" Fire 8, no. 12: 454. https://doi.org/10.3390/fire8120454
APA StyleGe, C., Chen, J., Fan, M., Niu, G., Zhu, L., & Zhao, X. (2025). Study on Leakage and Diffusion Law Under the Combined Laying of Gas Pipelines and Power Channels. Fire, 8(12), 454. https://doi.org/10.3390/fire8120454






