Density-Based Spatial Clustering of Vegetation Fire Points Based on Genetic Optimization of Threshold Values
Abstract
1. Introduction
2. Materials
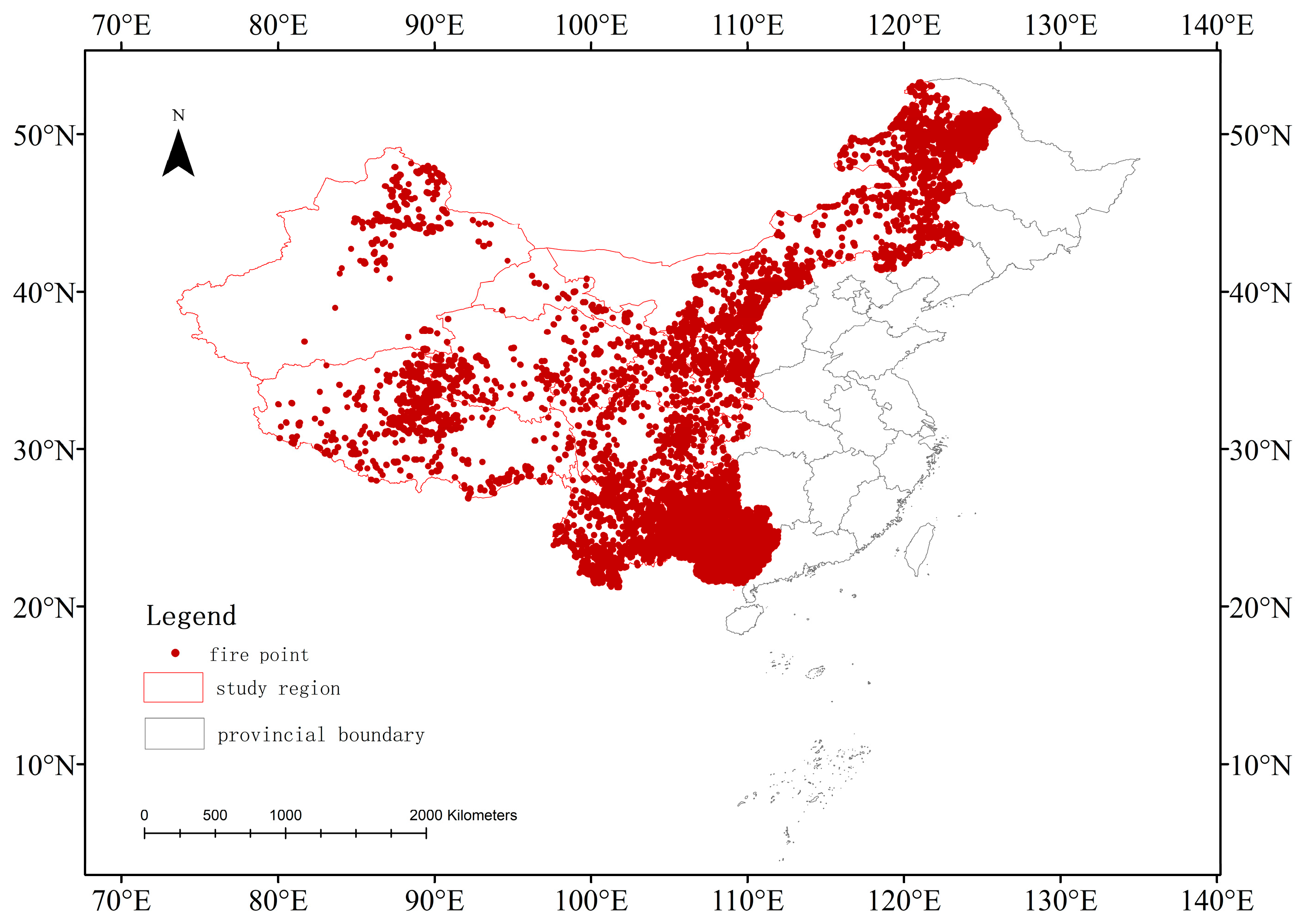
2.1. Study Area
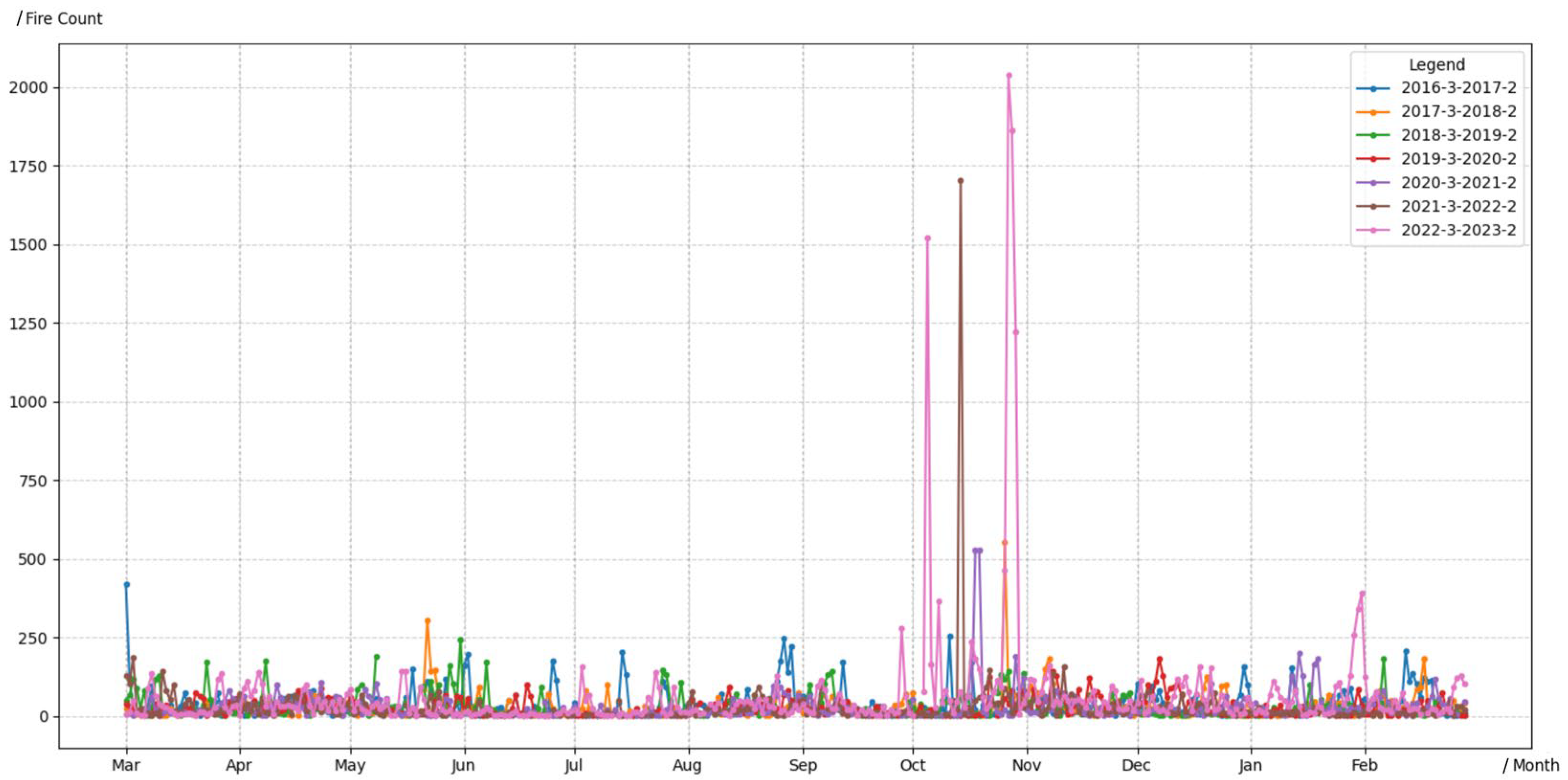
2.2. Research Data
3. Methods
3.1. DBSCAN Clustering Method
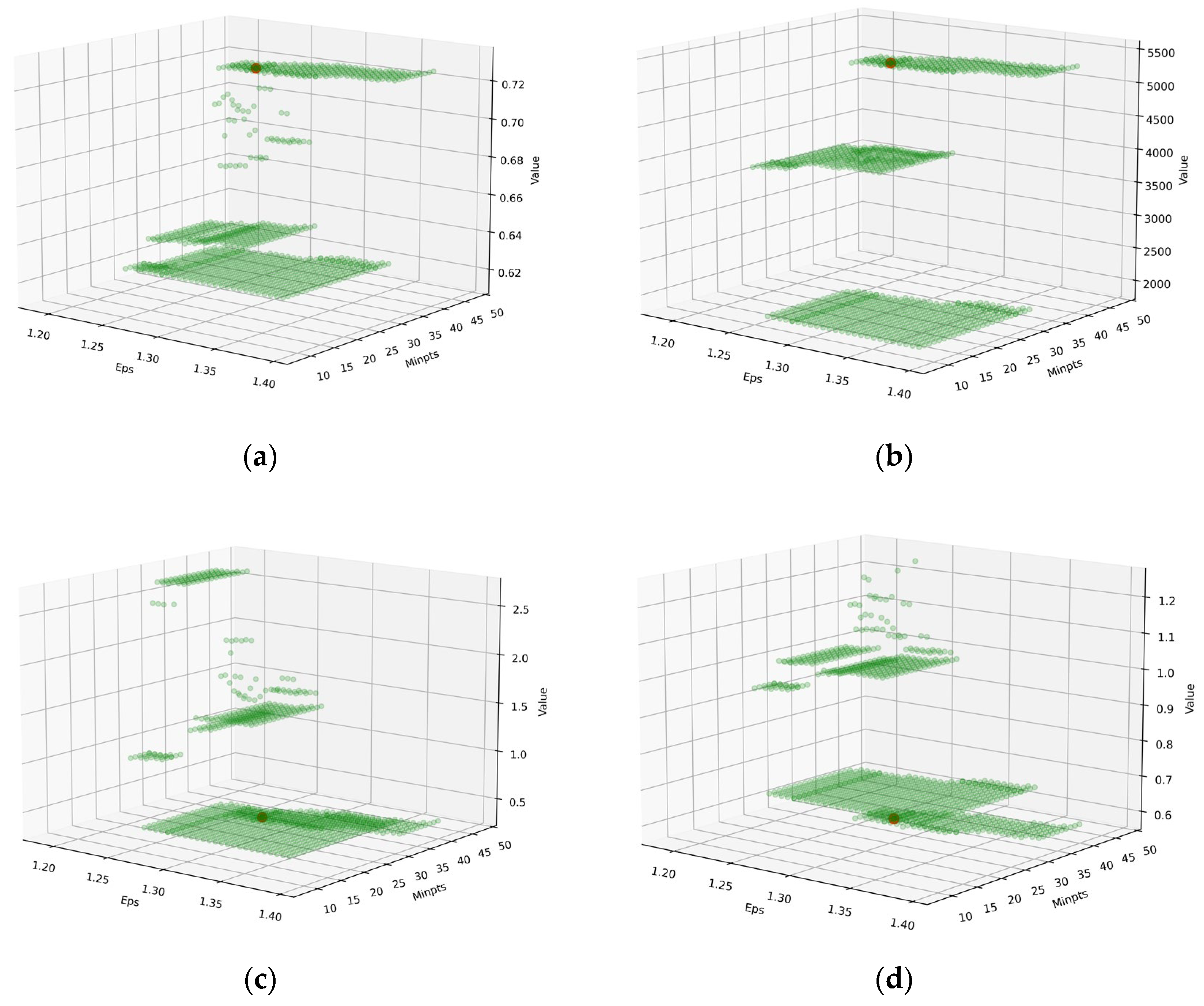
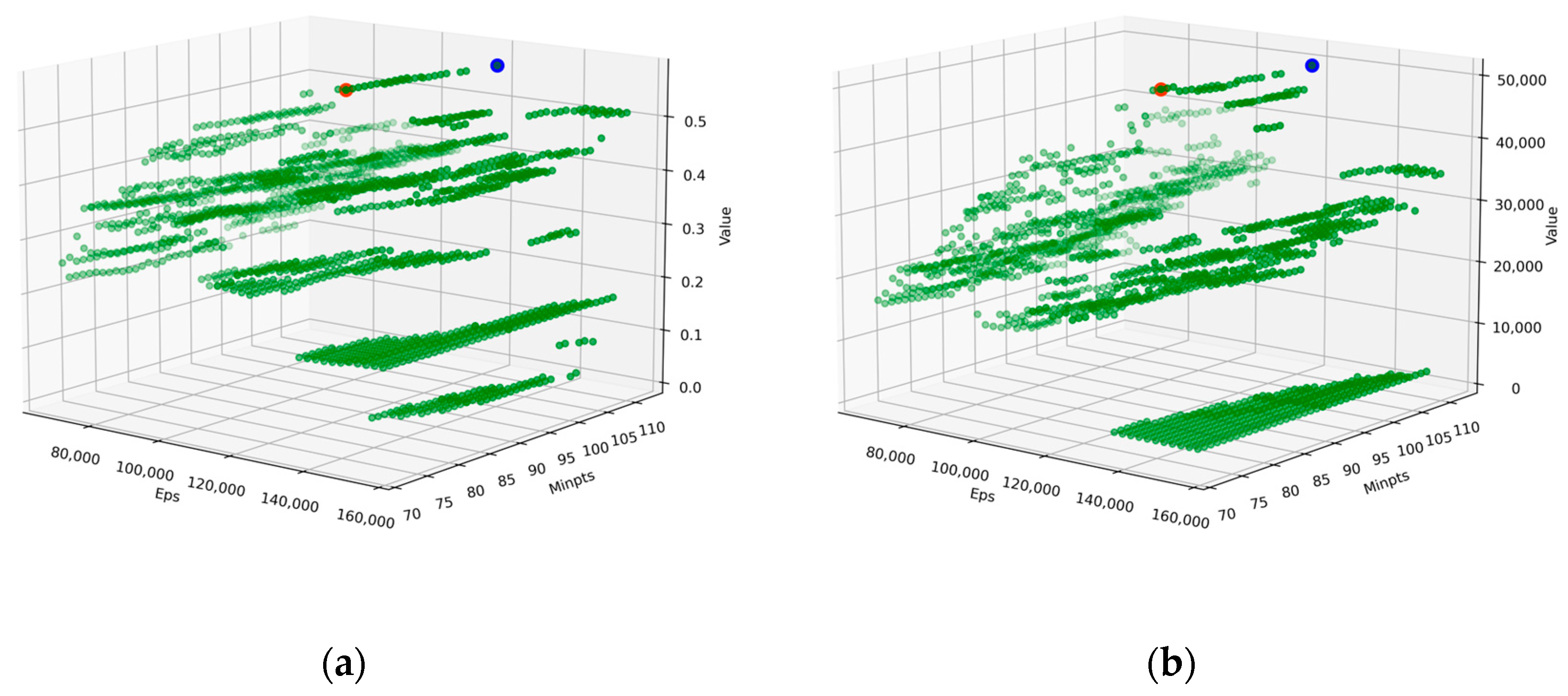
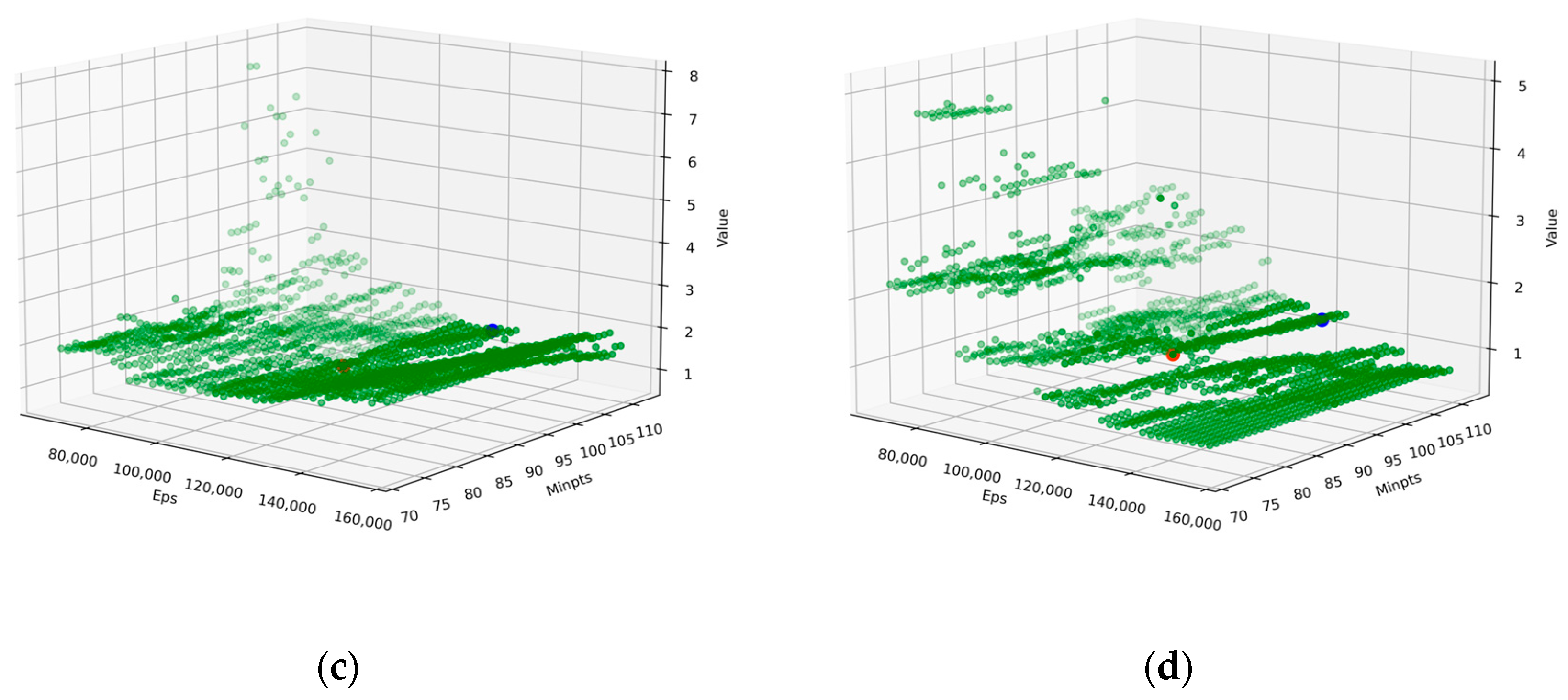
3.2. Dual-Population Genetic Algorithm for DBSCAN Optimization
3.3. Evaluation Metrics
3.4. Performance Evaluation
3.5. Distance Metrics
4. Results
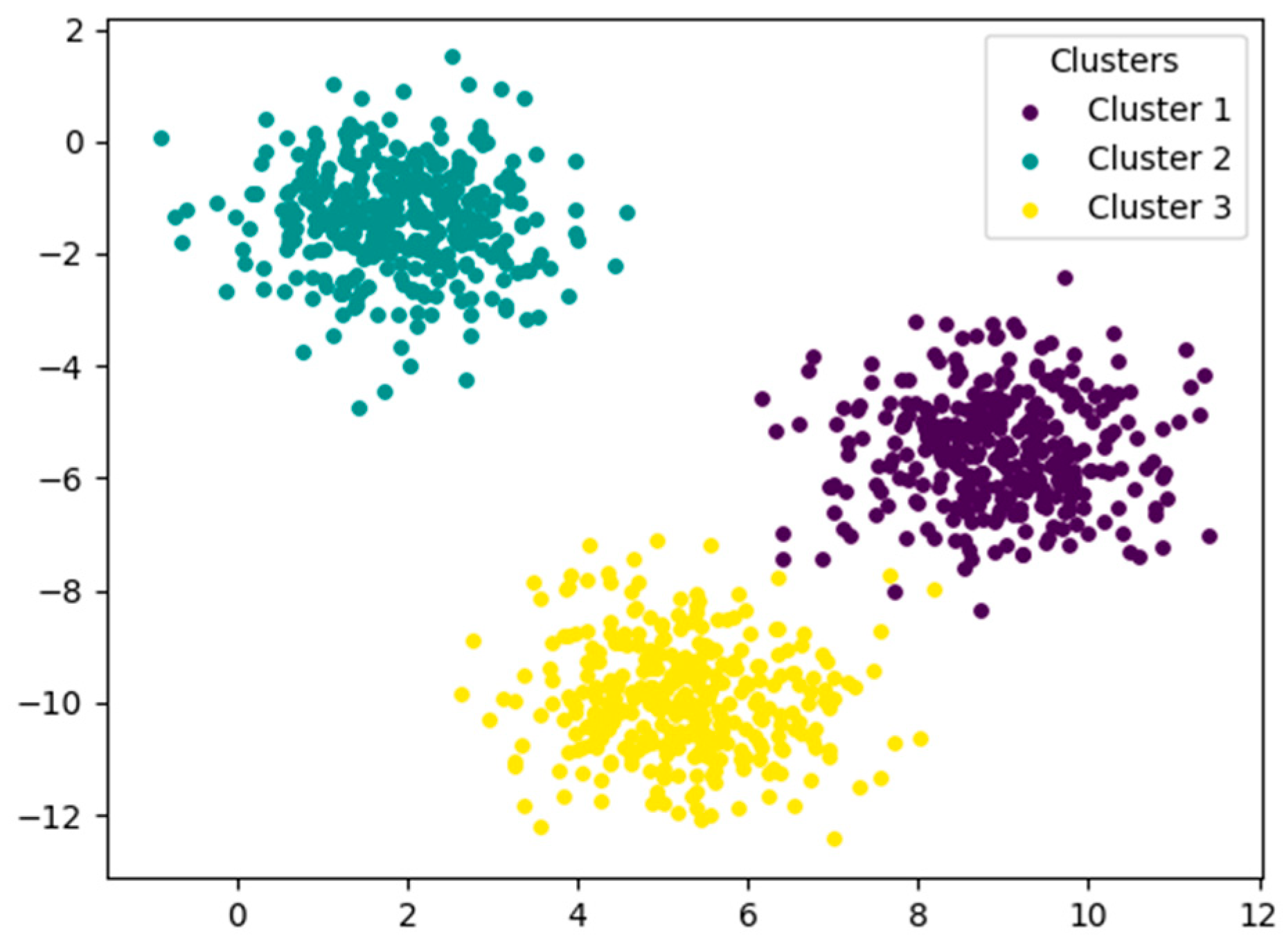
4.1. Validation of Synthetic Data
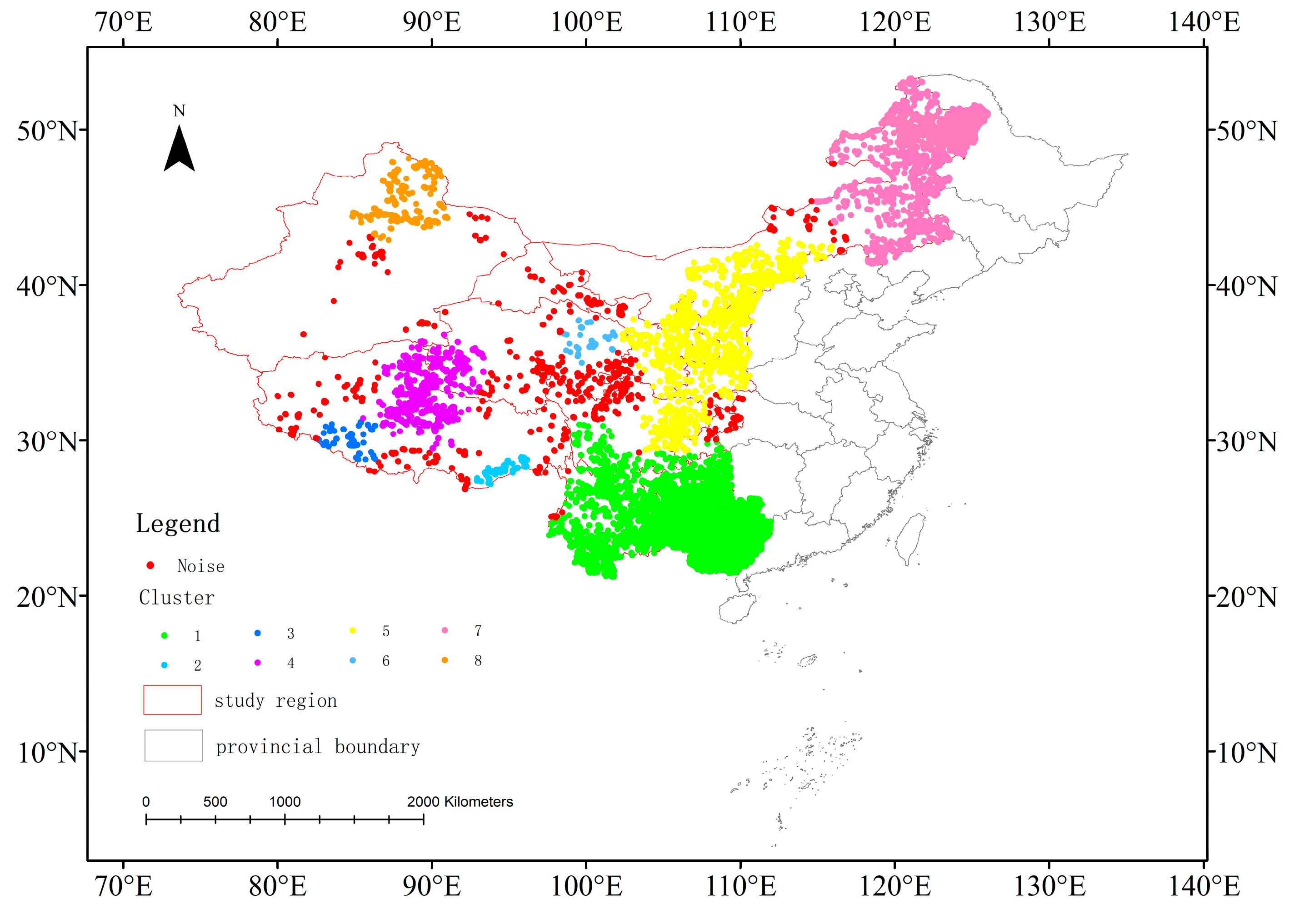
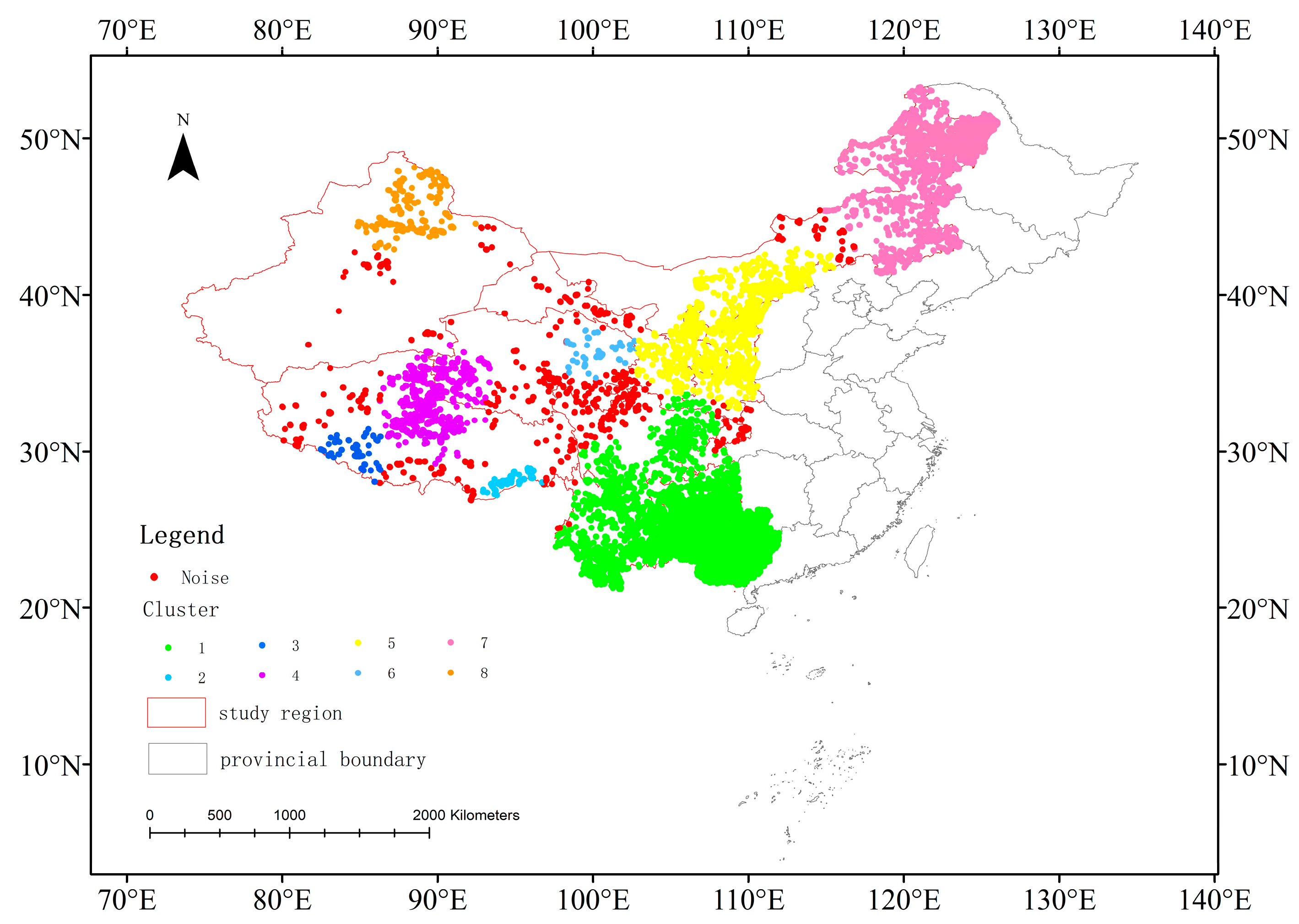
4.2. Experiment Results of Vegetation Fire Point Clustering
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scholten, R.C.; Veraverbeke, S.; Chen, Y.; Randerson, J.T. Spatial variability in Arctic-boreal fire regimes influenced by environmental and human factors. Nat. Geosci. 2024, 17, 866–873. [Google Scholar] [CrossRef]
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef]
- Bal, Y.; Wang, B.; Wu, Y.D.; Liu, X.D. A review of global forest fires in 2021. Fire Sci. Technol. 2022, 41, 705–709. [Google Scholar]
- Brys, C.; Martínez, D.; Marinelli, M. Machine learning methods for wildfire risk assessment. Earth Sci. Inform. 2025, 18, 148. [Google Scholar] [CrossRef]
- Bowman, D.M.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; van der Werf, G.R.; Flannigan, M. Vegetation fires in the Anthropocene. Nat. Rev. Earth Environ. 2020, 1, 500–515. [Google Scholar] [CrossRef]
- van der Werf, G.R.; Randerson, J.T.; Giglio, L.; van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.; van Marle, M.J.E.; Morton, D.C.; Collatz, G.J.; et al. Global fire emissions estimates during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Li, S.; Meng, C.; Zhu, Y.P. Temporal and spatial distribution of economic losses and casualties of forest fires in China. Fire Sci. Technol. 2023, 42, 387–391. [Google Scholar]
- Yi, K.; Bao, Y.; Zhang, J. Spatial distribution and temporal variability of open fire in China. Int. J. Wildland Fire 2016, 26, 122–135. [Google Scholar] [CrossRef]
- Donovan, V.M.; Crandall, R.; Fill, J.; Wonkka, C.L. Increasing large wildfire in the eastern United States. Geophys. Res. Lett. 2023, 50, e2023GL107051. [Google Scholar] [CrossRef]
- Reddy, C.S.; Bird, N.G.; Sreelakshmi, S.; Manikandan, T.M.; Asra, M.; Krishna, P.H.; Jha, C.S.; Rao, P.V.N.; Diwakar, P.G. Identification and characterization of spatio-temporal hotspots of forest fires in South Asia. Environ. Monit. Assess. 2020, 191 (Suppl. 3), 791. [Google Scholar] [CrossRef]
- Feltman, J.A.; Straka, T.J.; Post, C.J.; Sperry, S.L. Geospatial Analysis Application to Forecast Wildfire Occurrences in South Carolina. Forests 2012, 3, 265–282. [Google Scholar] [CrossRef]
- Prasertsri, N.; Littidej, P. Spatial Environmental Modeling for Wildfire Progression Accelerating Extent Analysis Using Geo-Informatics. Pol. J. Environ. Stud. 2020, 29, 3249–3261. [Google Scholar] [CrossRef] [PubMed]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Ma, C.; Pu, R.; Downs, J.; Jin, H. Characterizing Spatial Patterns of Amazon Rainforest Wildfires and Driving Factors by Using Remote Sensing and GIS Geospatial Technologies. Geosciences 2022, 12, 237. [Google Scholar] [CrossRef]
- Bhadoria, R.S.; Pandey, M.K.; Kundu, P. RVFR: Random vector forest regression model for integrated & enhanced approach in forest fires predictions. Ecol. Inform. 2021, 66, 101471. [Google Scholar]
- Li, Z.Y.; Chen, E.X.; Guo, Y.; Tian, X.; Liu, Q.W.; Sun, B.; Zhao, L.; Cai, X.S.; Du, L.M.; Yu, L.F.; et al. Research and application of forestry and grassland remote sensing technology in China: Recent progress, challenges and countermeasures. Natl. Remote Sens. Bull. 2025, 29, 1804–1830. [Google Scholar]
- Grubesic, T.H.; Wei, R.; Murray, A.T. Spatial Clustering Overview and Comparison: Accuracy, Sensitivity, and Computational Expense. Ann. Assoc. Am. Geogr. 2014, 104, 1134–1156. [Google Scholar] [CrossRef]
- Varghese, B.; Unnikrishnan, A.; PouloseJacob, K. Spatial clustering algorithms-an overview. Asian J. Comput. Sci. Inf. Technol. 2013, 3, 1–8. [Google Scholar]
- Hohl, A.; Zheng, M.; Tang, W.; Delmelle, E.; Casas, I. Spatiotemporal Point Pattern Analysis Using Ripley’s K Function. Geospatial Data Science Techniques and Applications, 1st ed.; Karimi, H.A., Karimi, B., Eds.; Taylor & Francis Group: Oxford, UK, 2018; pp. 155–176. [Google Scholar]
- Tian, Y.; Wu, Z.; Bian, S.; Zhang, X.; Wang, B.; Li, M. Study on spatial-distribution characteristics based on fire-spot data in Northern China. Sustainability 2022, 14, 6872. [Google Scholar] [CrossRef]
- Baykal, T.M. Performance assessment of GIS-based spatial clustering methods in forest fire data. Nat. Hazards 2025, 121, 8445–8477. [Google Scholar] [CrossRef]
- Khairani, N.A.; Sutoyo, E. Application of K-Means Clustering Algorithm for Determination of Fire-Prone Areas Utilizing Hotspots in West Kalimantan Province. Int. J. Adv. Data Inf. Syst. 2020, 1, 9–16. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X.W. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD), Menlo Park, CA, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Gan, J.; Tao, Y. DBSCAN revisited: Mis-claim, un-fixability, and approximation. In Proceedings of the SIGMOD ‘15: Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 27 May 2015; pp. 519–530. [Google Scholar]
- Ahajjam, A.; Allgaier, M.; Chance, R.; Chukwuemeka, E.; Putkonen, J.; Pasch, T. Enhancing prediction of wildfire occurrence and behavior in Alaska using spatio-temporal clustering and ensemble machine learning. Ecol. Inf. 2025, 85, 102963. [Google Scholar] [CrossRef]
- Song, M.; Chen, D.M. A Comparison of Three Heuristic Optimization Algorithms for Solving the Multi-Objective Land Allocation (MOLA) Problem. Ann. GIS 2018, 24, 19–31. [Google Scholar] [CrossRef]
- Gebril, I.H.; El-Mouadib, F.A.; Mansori, H.A. Automatic Generation of Epsilon (Eps) value for DBSCAN Using Genetic Algorithms. In Proceedings of the 2024 IEEE 4th International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering (MI-STA), Tripoli, Libya, 19–21 May 2024. [Google Scholar]
- Wei, X.; Liu, R.; Liu, Y.; He, J.; Chen, J.; Qi, L.; Zhou, Y.; Qin, Y.; Wu, C.; Dong, J.; et al. Forest areas in China are recovering since the 21st century. Geophys. Res. Lett. 2024, 51, e2024GL110312. [Google Scholar] [CrossRef]
- Yin, J.; He, B.; Fan, C.; Chen, R. Fire has become a major disturbance agent in the forests of Southwest China. Ecol. Indic. 2024, 160, 111885. [Google Scholar] [CrossRef]
- Li, W.; Shu, L.F.; Wang, M.Y.; Li, W.K.; Yuan, S.B.; Si, L.Q.; Zhao, F.J.; Song, J.J.; Wang, Y.H. Temporal and Spatial Distribution and Dynamic Characteristics of Lightning Fires in the Daxing’anling Mountains from 1980 to 2021. Sci. Silvae Sin. 2023, 59, 22–31. [Google Scholar]
- Zhang, J.H.; Wang, X.J.; Qian, Y.H.; Pei, S.Y. Environmental factor analysis of grassland fire in Qinghai Province. J. Nat. Disasters 2007, 16, 71–75. [Google Scholar]
- Zhou, W.; Tang, B.H.; He, Z.W.; Huang, L.; Chen, J. Identification of forest fire points under clear sky conditions with Himawari-8 satellite data. Int. J. Remote Sens. 2024, 45, 214–234. [Google Scholar] [CrossRef]
- Na, L.; Zhang, J.; Bao, Y.; Bao, Y.; Na, R.; Tong, S.; Si, A. Himawari-8 Satellite Based Dynamic Monitoring of Grassland Fire in China-Mongolia Border Regions. Sensors 2018, 18, 276. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, C.; Gu, J.; Hou, J.; Zhang, Y.; Han, W.; Dou, P.; Feng, Y. Real-Time Wildfire Detection Algorithm Based on VIIRS Fire Product and Himawari-8 Data. Remote Sens. 2023, 15, 1541. [Google Scholar] [CrossRef]
- Scikit-Learn. Available online: https://scikit-learn.org/ (accessed on 23 October 2025).
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 27, 27–0936. [Google Scholar]
- Park, J.; Park, M.-W.; Kim, D.-W.; Lee, J. Multi-Population Genetic Algorithm for Multilabel Feature Selection Based on Label Complementary Communication. Entropy 2020, 22, 876. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Shi, L.; Du, K.J.; Chen, C.H.; Wang, H.; Zhang, J.; Zhan, Z.H. A Multi-Population Genetic Algorithm for Multiobjective Recommendation System. In Proceedings of the 2023 IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; pp. 998–1003. [Google Scholar]
- Shahapure, K.R.; Nicholas, C. Cluster Quality Analysis Using Silhouette Score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, Australia, 6–9 October 2020. [Google Scholar]
- Rousseeuw, P. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Comm. Stat. 1974, 3, 1–27. [Google Scholar]
- Davies, D.; Bouldin, D. A cluster separation measure. IEEE PAMI 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Halkidi, M.; Vazirgiannis, M.; Batistakis, Y. Quality scheme assessment in the clustering process. In Proceedings of the PKDD, London, UK, 14–18 September 2000; pp. 265–276. [Google Scholar]
- Zhang, L.; Zhang, Q.; Yang, Q.; Yue, L.; He, J.; Jin, X.; Yuan, Q. Near-Real-Time Wildfire Detection Approach with Himawari-8/9 Geostationary Satellite Data Integrating Multi-Scale Spatial-Temporal Feature. Int. J. Appl. Earth Obs. Geoinf. 2025, 137, 104416. [Google Scholar] [CrossRef]
- Chen, Y.; Morton, D.C.; Randerson, J.T. Remote sensing for wildfire monitoring: Insights into burned area, emissions, and fire dynamics. One Earth 2024, 7, 1022–1028. [Google Scholar] [CrossRef]
- Fang, K.; Yao, Q.; Guo, Z.; Zheng, B.; Du, J.; Qi, F.; Yan, P.; Li, J.; Ou, T.; Liu, J.; et al. ENSO modulates wildfire activity in China. Nat. Commun. 2021, 12, 1764. [Google Scholar] [CrossRef]
- Sohel, S.I.; Marshall, A.R. Why the world needs a wildfire risk prediction system based on plant functional traits and moisture-before fires ignite. npj Nat. Hazards 2025, 2, 95. [Google Scholar] [CrossRef]


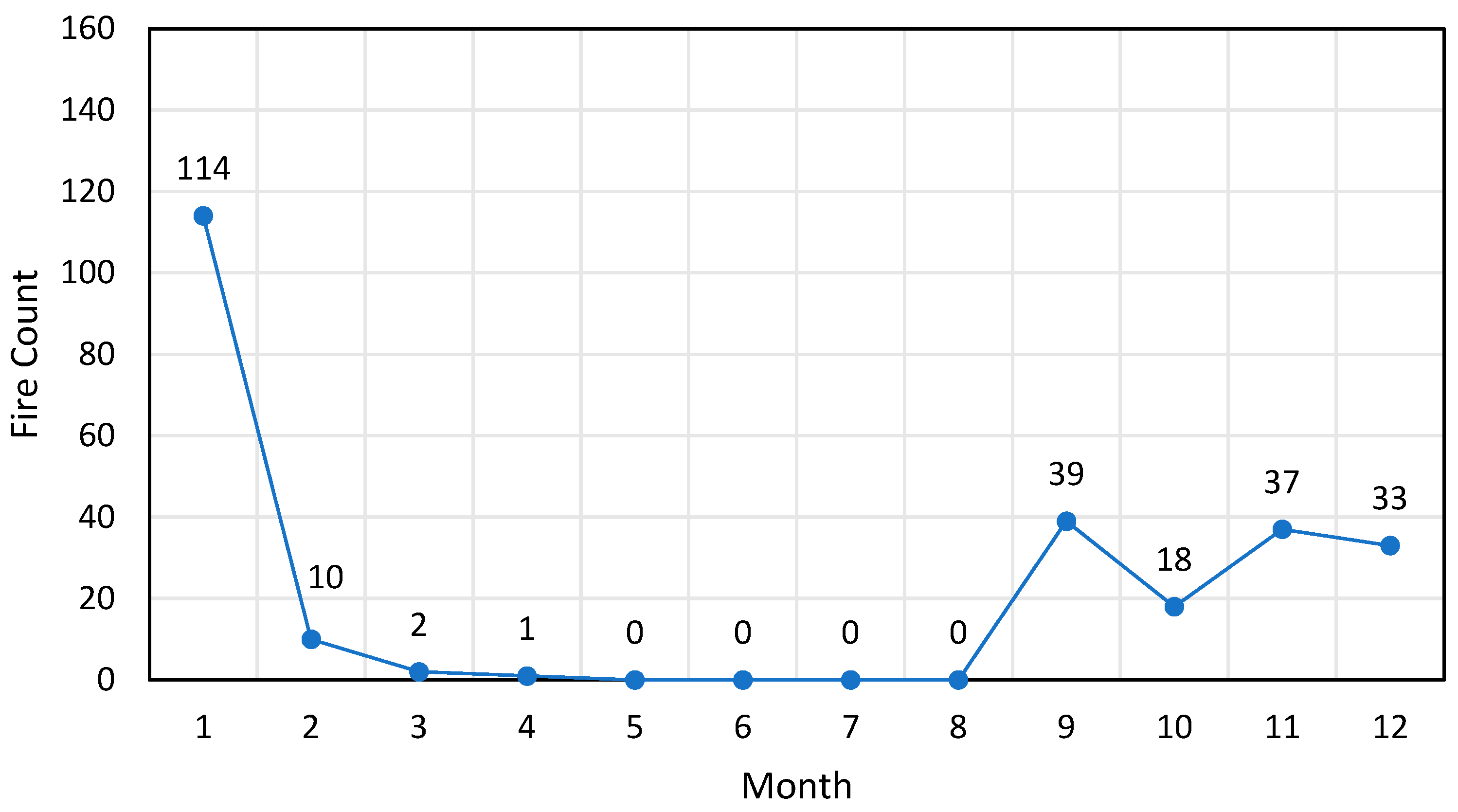
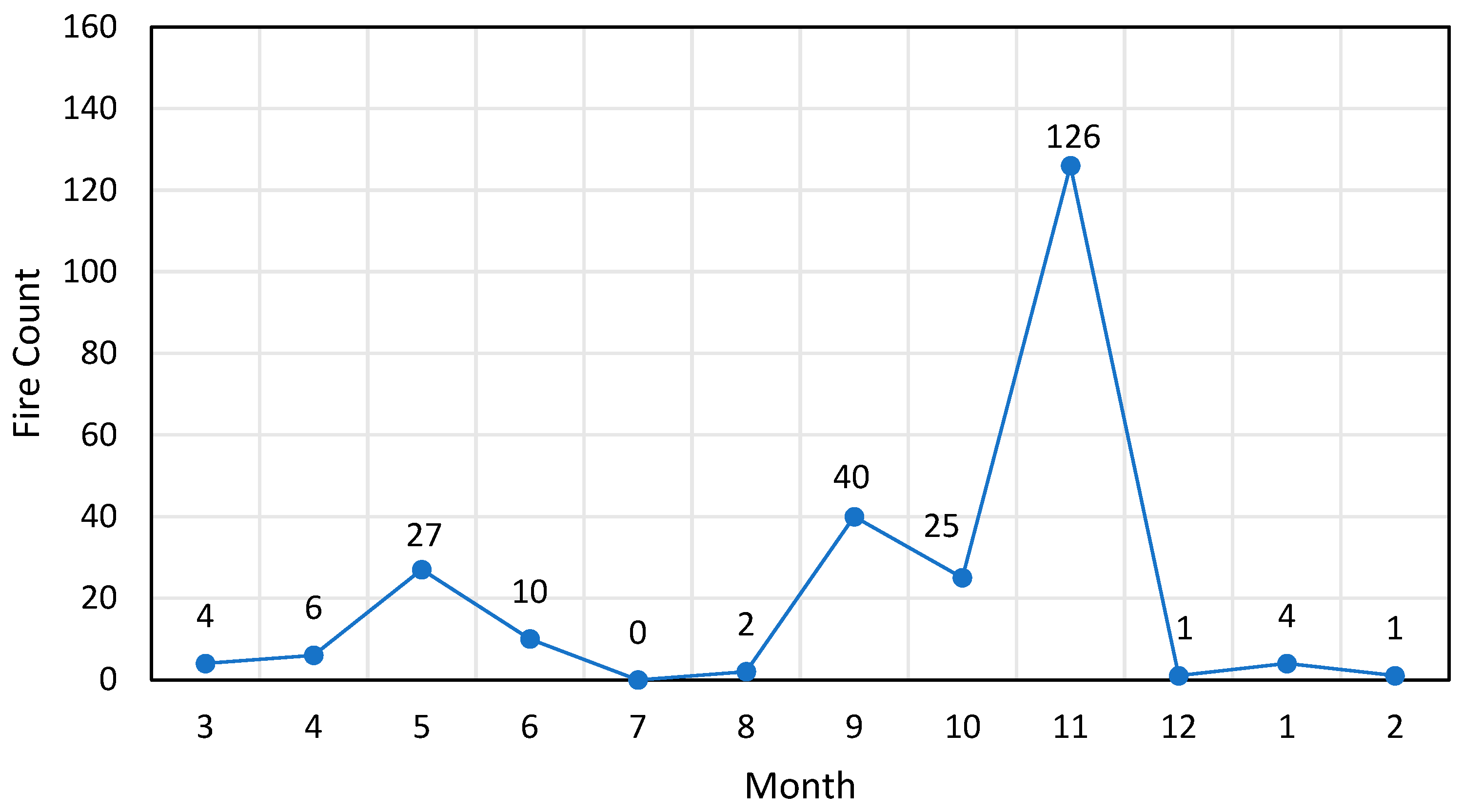
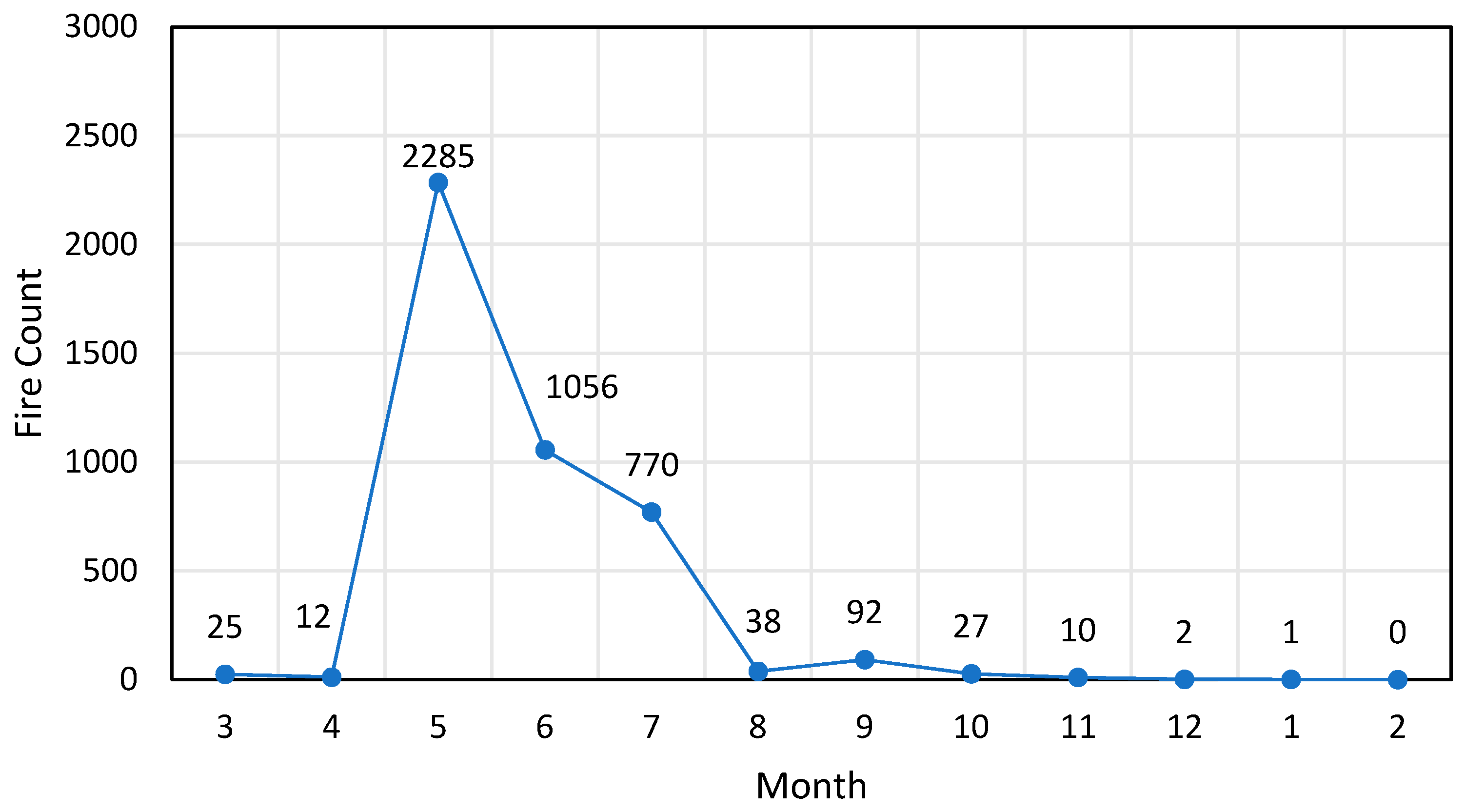
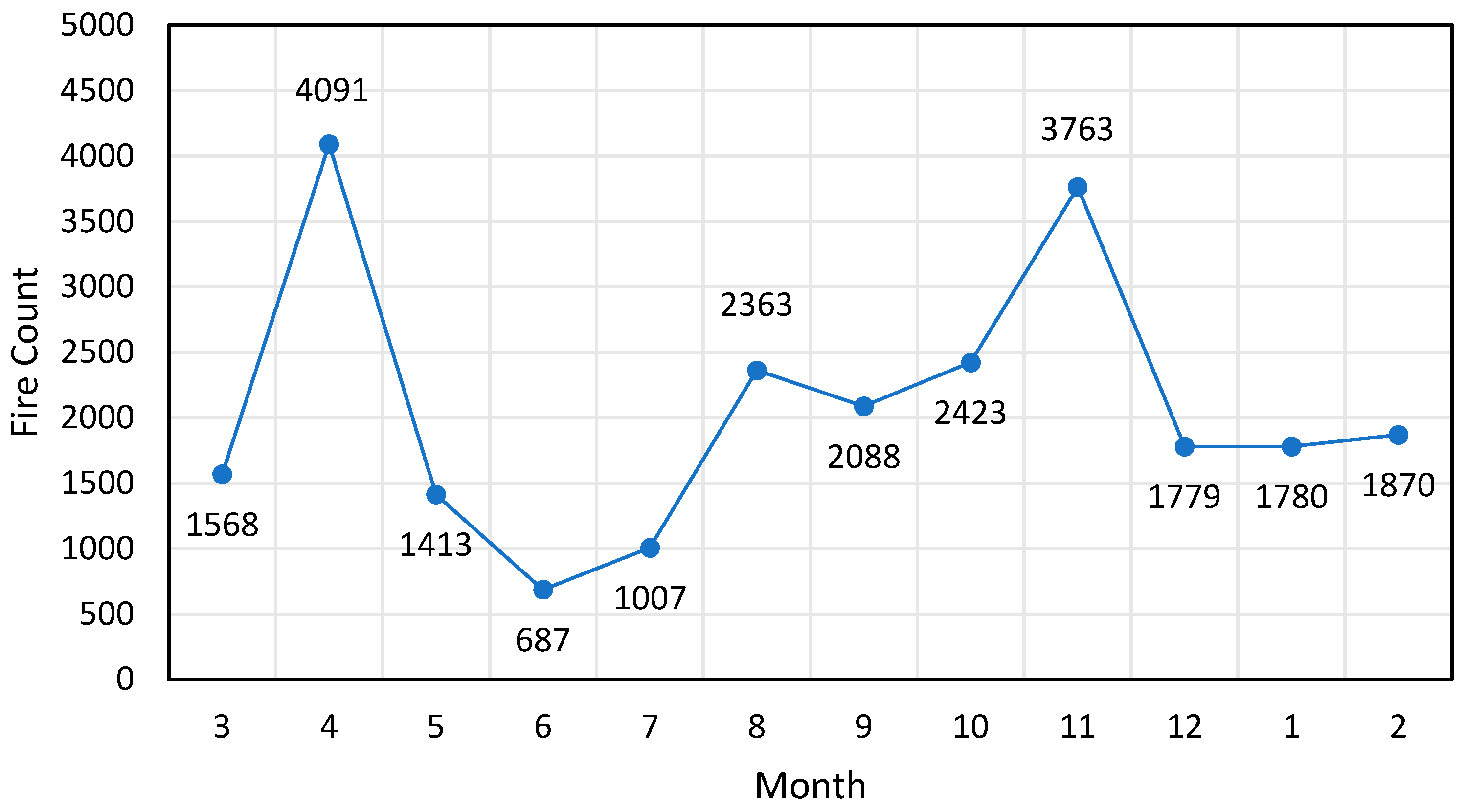
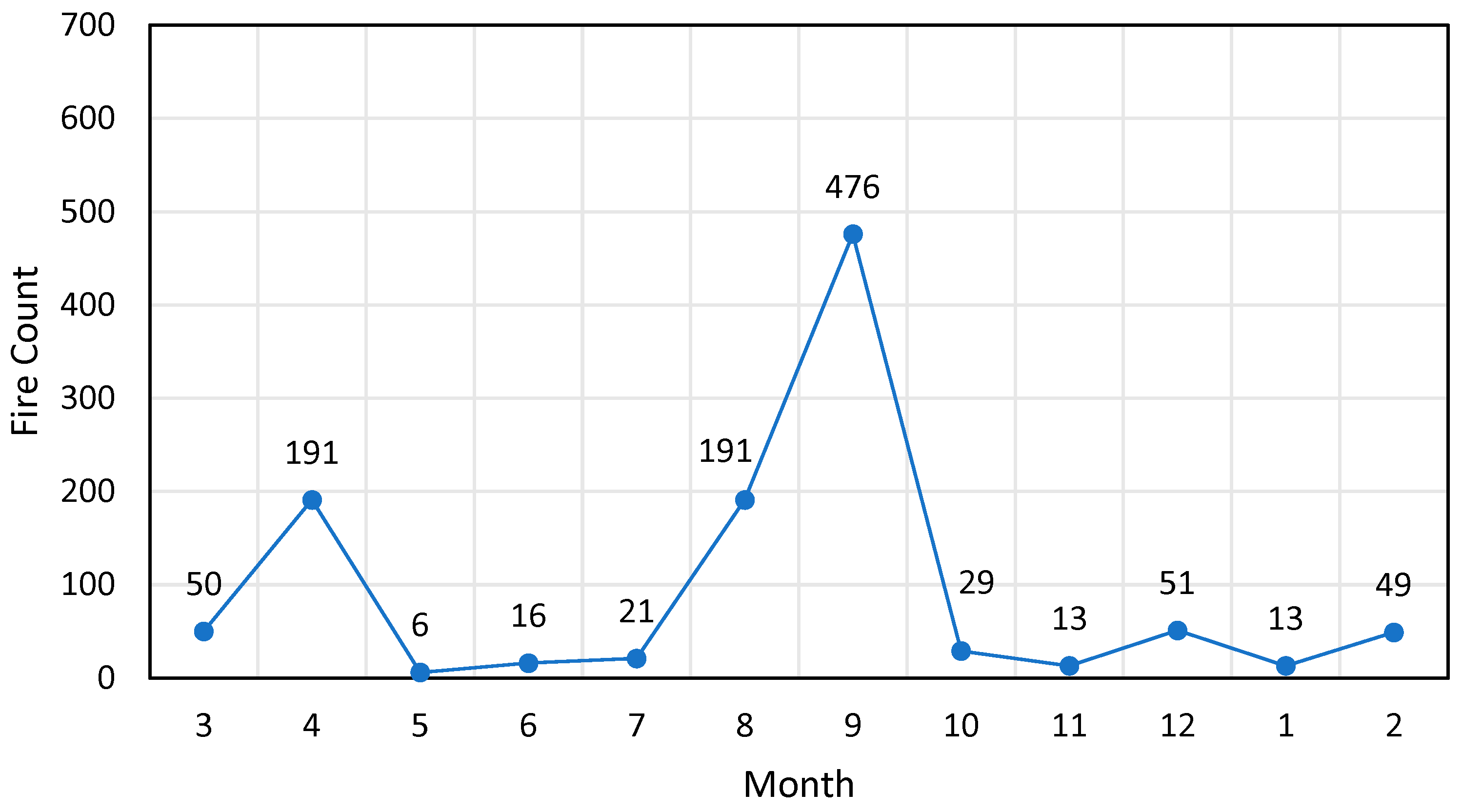
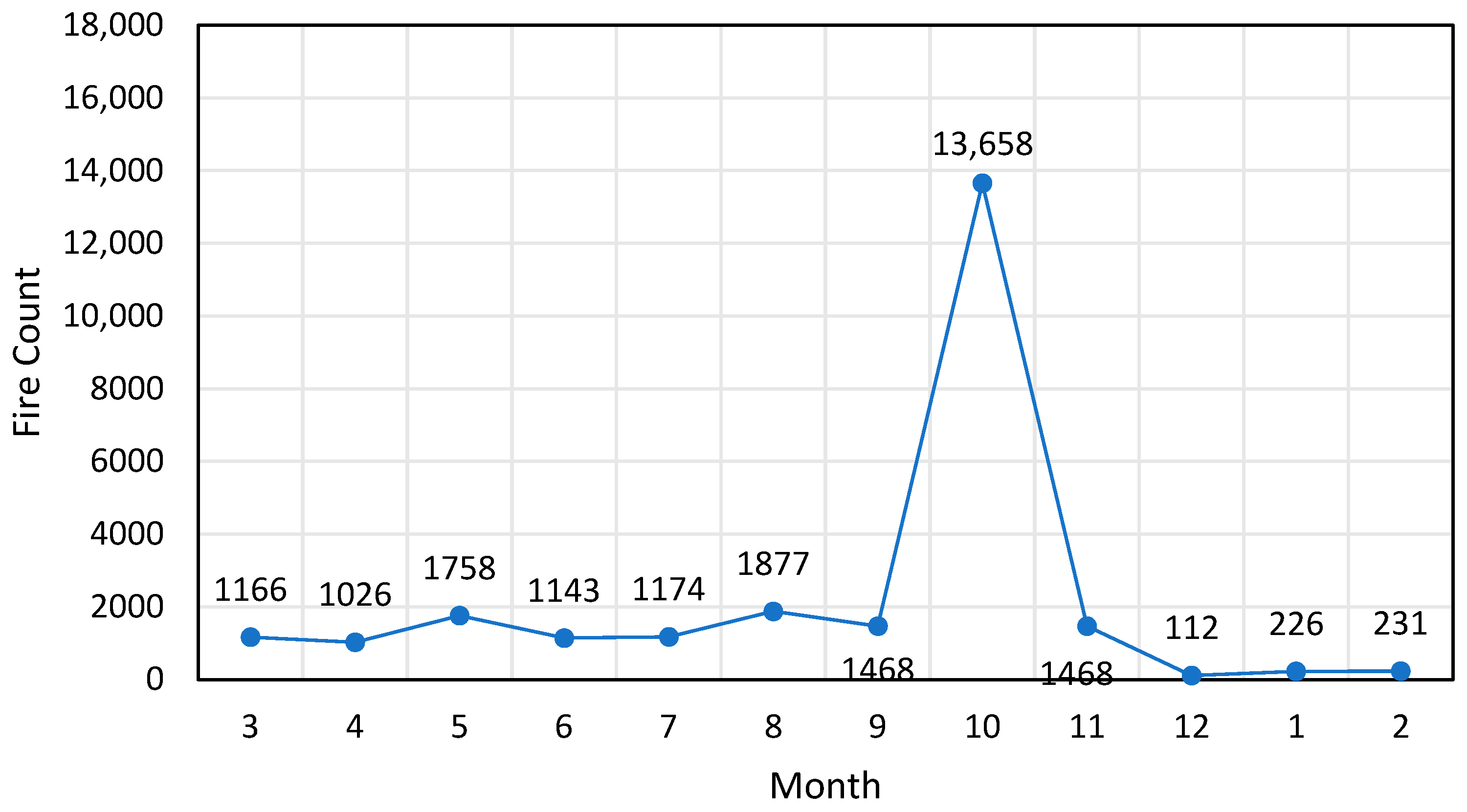
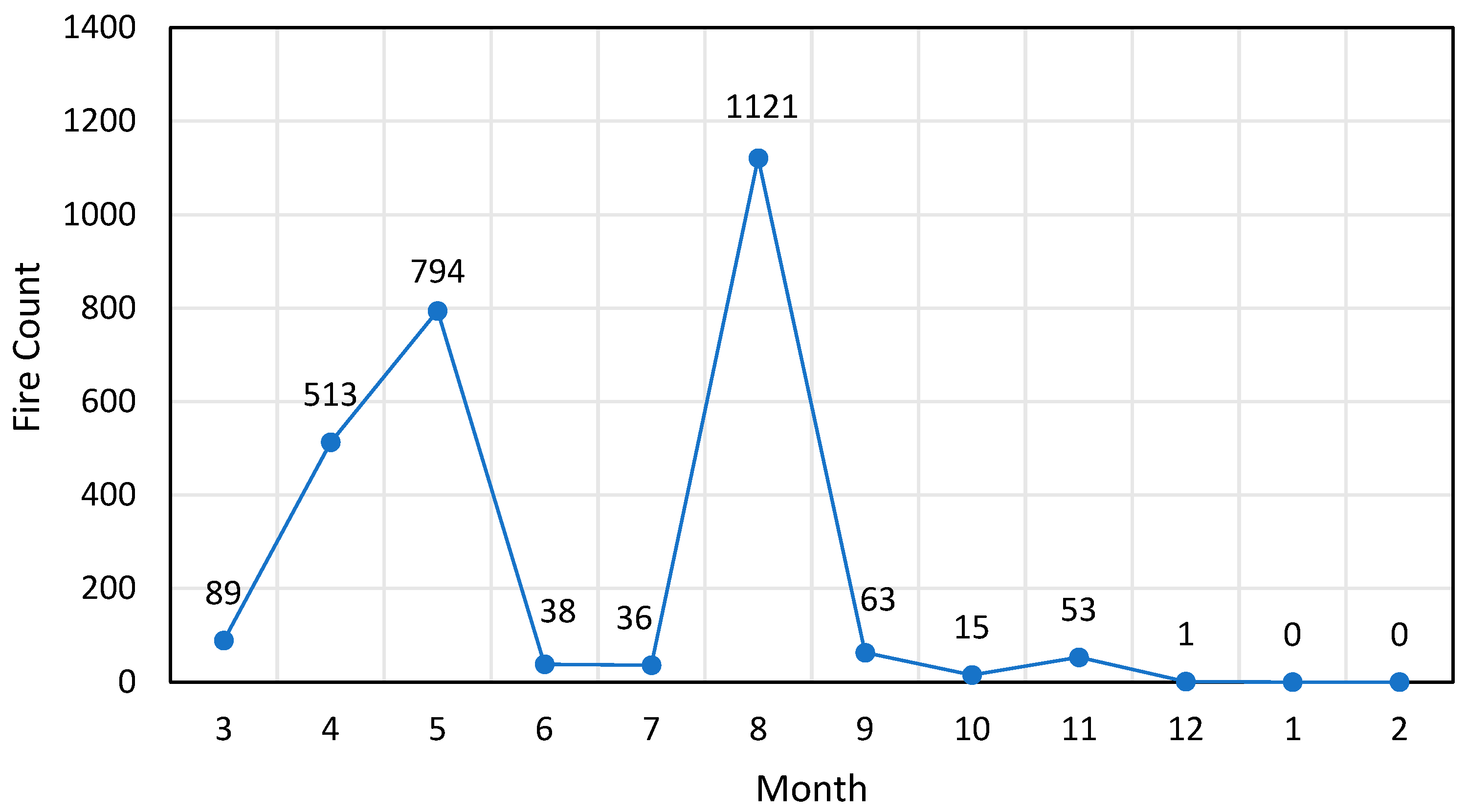
| Internal Indices | Clustering by Genetic Optimized Thresholds | Clustering by Stepwise Search Thresholds |
|---|---|---|
| S | 0.56111 | 0.56576 |
| CH | 48,839.19421 | 49,113.84489 |
| DB | 1.29882 | 1.40942 |
| SD | 1.05276 | 1.11991 |
| Cluster | Clustering by Genetic Optimized Thresholds | Clustering by Stepwise Search Thresholds | ||||||
|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Fall | Winter | Spring | Summer | Fall | Winter | |
| 1 | 4914 | 349 | 3767 | 13,107 | 5027 | 462 | 3907 | 13,353 |
| 2 | 126 | 1 | 37 | 88 | 126 | 1 | 39 | 88 |
| 3 | 37 | 11 | 186 | 3 | 37 | 12 | 191 | 6 |
| 4 | 2320 | 1858 | 125 | 3 | 2322 | 1864 | 129 | 3 |
| 5 | 7282 | 4229 | 8417 | 5687 | 7072 | 4057 | 8274 | 5429 |
| 6 | 245 | 224 | 489 | 107 | 247 | 228 | 518 | 113 |
| 7 | 3964 | 4197 | 16,594 | 569 | 3950 | 4194 | 16,594 | 569 |
| 8 | 1394 | 1193 | 131 | 1 | 1396 | 1195 | 131 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Wang, T.; Xie, K. Density-Based Spatial Clustering of Vegetation Fire Points Based on Genetic Optimization of Threshold Values. Fire 2025, 8, 431. https://doi.org/10.3390/fire8110431
Gao X, Wang T, Xie K. Density-Based Spatial Clustering of Vegetation Fire Points Based on Genetic Optimization of Threshold Values. Fire. 2025; 8(11):431. https://doi.org/10.3390/fire8110431
Chicago/Turabian StyleGao, Xuan, Tao Wang, and Ke Xie. 2025. "Density-Based Spatial Clustering of Vegetation Fire Points Based on Genetic Optimization of Threshold Values" Fire 8, no. 11: 431. https://doi.org/10.3390/fire8110431
APA StyleGao, X., Wang, T., & Xie, K. (2025). Density-Based Spatial Clustering of Vegetation Fire Points Based on Genetic Optimization of Threshold Values. Fire, 8(11), 431. https://doi.org/10.3390/fire8110431





