Forest Fires: Silvicultural Prevention and Mathematical Models for Predicting Fire Propagation in Southern Italy
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Analysis
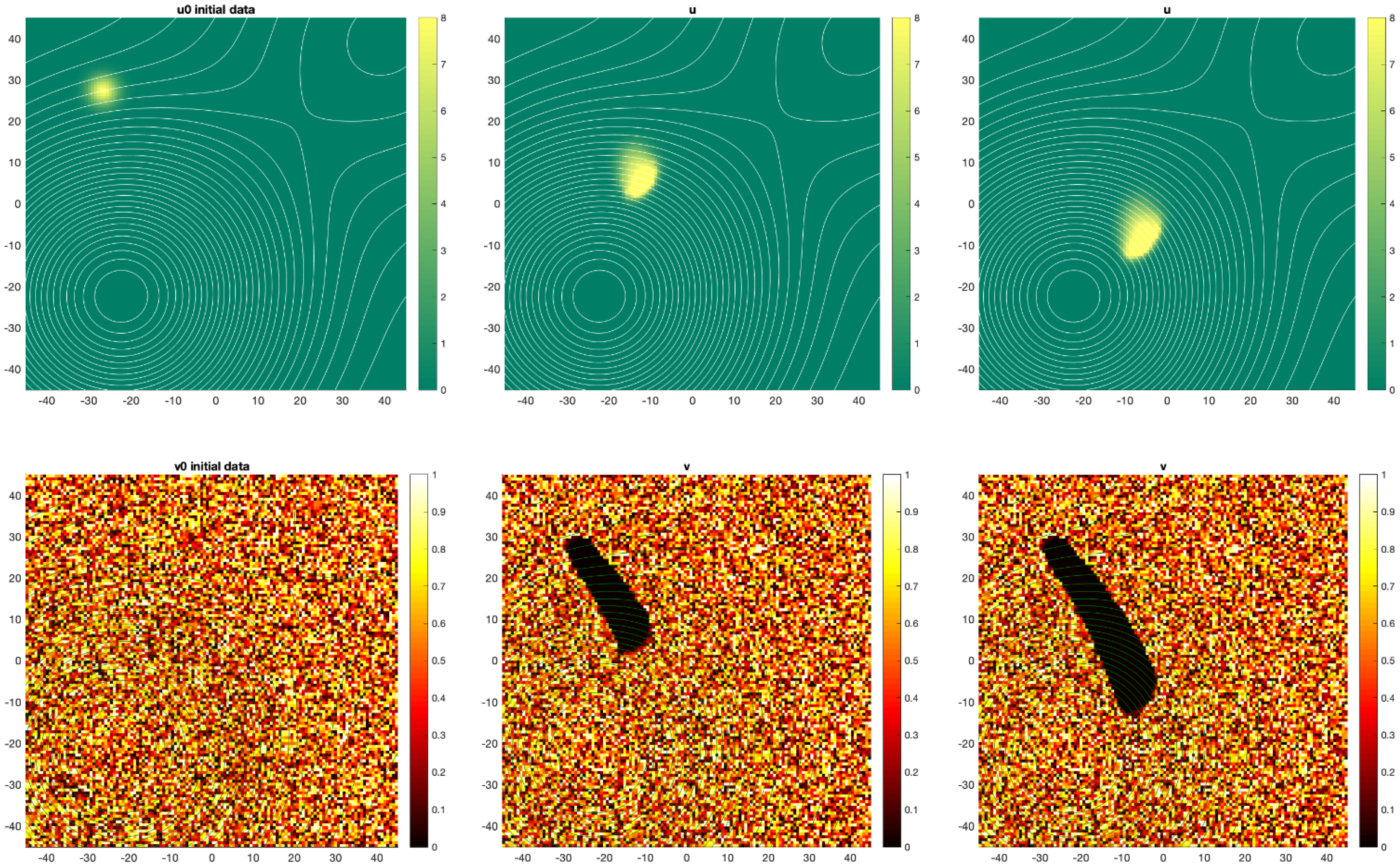
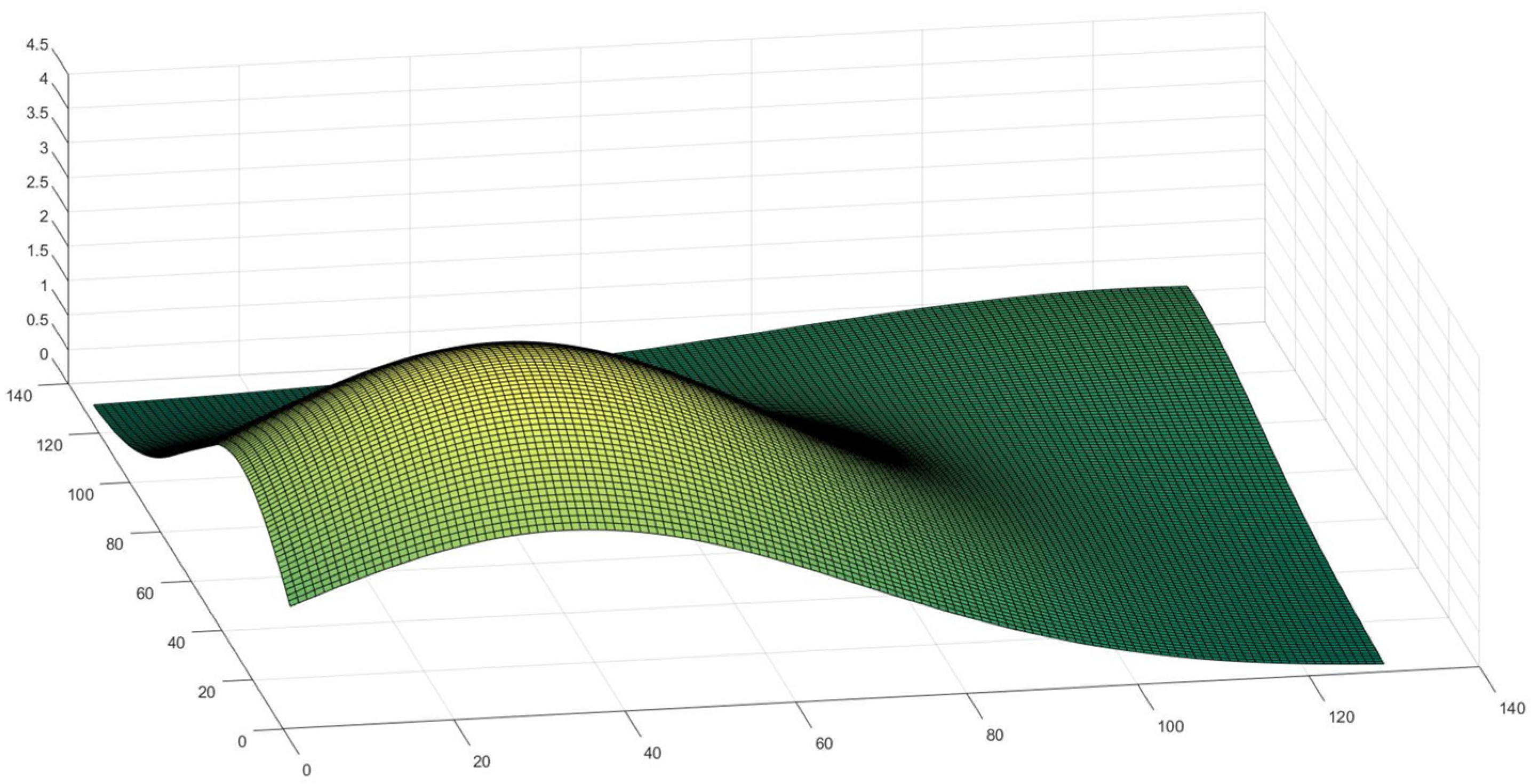
2.3. Mathematical Model Proposed
- Empirical Data: The model incorporates historical data on fire occurrences, fuel types and weather conditions. These data serve as the foundation for understanding the basic patterns and behaviors of forest fires.
- Differential Equations: These describe the physical processes involved in fire spread, including heat transfer, combustion and fluid dynamics. By solving these equations, the model can predict how a fire will spread under specific conditions.
- Finite Difference Solutions: This numerical method is employed to solve the differential equations that govern fire behavior. By discretizing the equations, the model can simulate fire spread over a grid representing the forest landscape.
- Fuel Characteristics: Different types of vegetation and their distribution across the landscape are considered. The model includes parameters for fuel moisture content, density and combustibility.
- Weather Conditions: Wind speed and direction, temperature and humidity are critical inputs. The model uses these variables to predict their influence on fire spread and intensity.
- Topography: The physical features of the landscape, such as slopes and elevation, are included in the model. These features affect how quickly a fire can move and in which direction.
3. Results
3.1. Silvicultural Approach
3.2. Numerical Solution of the Mathematical Model and Numerical Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iovino, F. La ricostruzione boschiva in Calabria. In Modello di Riferimento del Passato on Approcci Attuali in Tema di Tutela del Territorio e Dell’ambiente; Rubbettino Università. Rubbettino Editore s.r.l. Soveria Mannelli: Catanzaro, Italy, 2021; 185p. [Google Scholar]
- Novaco, I. Relazione introduttiva, Seduta speciale dell’Accademia Italiana di Scienze Forestali a Reggio Calabri. Ital. For. Mont. 1984, 2–3, 68–94. [Google Scholar]
- Dimase, A.C.; Iovino, F. Capacità D’uso dei Suoli dei Bacini Idrografici del Trionto, Nicà e Torrenti Limitrofi (Calabria); CNR, Istituto di Ecologia e Idrologia Forestale: Cosenza, Italy, 1988; 56p. [Google Scholar]
- Iovino, F.; Mengazzuto, G. Il ruolo dei rimboschimenti nella lotta alla desertificazione. In Proceedings of the Atti del III Congresso SISEF IP Office/2003, Viterbo, Italy, 15–18 October 2001; pp. 105–109. [Google Scholar]
- Coletta, V.; Menguzzato, G.; Pellicone, G.; Veltri, A.; Marziliano, P.A. Effect of thinning on above-ground biomass accumulation in a Douglas-fir plantation in southern Italy. J. For. Res. 2016, 27, 1313–1320. [Google Scholar] [CrossRef]
- Iovino, F.; Nicolaci, A.; Marziliano, P.A.; Pignataro, F.; Sanesi, G. Lessons learned from the past: Forestry initiatives for effective carbon stocking in Southern Italy. Ann. Silvic. Res. 2021, 46, 99–111. [Google Scholar] [CrossRef]
- Harrington, M. What kind of cutting and thinning can prevent crown fires. In EcoReport; Ritter, S., Ed.; Forest Service, Bitterroot Ecosystem Management Research Project; U.S. Department of Agriculture: Missoula, MT, USA, 2008; pp. 7–12. [Google Scholar]
- Goldammer, J. Wildfire management in forests and other vegetation: A global perspective. Disaster Manag. 1993, 5, 3–10. [Google Scholar]
- Archibold, O.W. Ecologia Della Vegetazione Mondiale; Chapman & Hall: Loondon, UK, 1995. [Google Scholar]
- Pausas, J.G.; Keeley, J.E. Wildfires and global change. Front. Ecol. Env. 2021, 19, 387–395. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Williams, A.P.; Boschetti, L.; Zubkova, M.; Kolden, C.A. Global patterns of interannual climate–fire relationships. Glob. Chang. Biol. 2018, 24, 5164–5175. [Google Scholar] [CrossRef] [PubMed]
- Lucas-Borja, M.E.; Plaza-Àlvarez, P.A.; Uddin, S.M.; Parhizkar, M.; Zema, D.A. Short-term hydrological response of soil after wildfire in a semi-arid landscape covered by Macrochloa tenacissima (L.) Kunth. J. Arid. Environ. 2022, 198, 104702. [Google Scholar] [CrossRef]
- Keeley, J. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Zavala, L.M.M.; de Celis Silvia, R.; López, A.J. How wildfires affect soil properties. A brief review. Cuad. Investig. Geogr. Geogr. Res. Lett. 2014, 40, 311–331. [Google Scholar] [CrossRef]
- Kukavskaya, E.A.; Buryak, L.V.; Ivanova, G.A.; Conard, S.G.; Kalenskaya, O.P.; Zhila, S.V.; McRae, D.J. Influence of logging on the effects of wildfire in Siberia. Environ. Res. Lett. 2013, 8, 045034. [Google Scholar] [CrossRef]
- Lovreglio, R.; Meddour-Sahar, O.; Leone, V. Goat grazing as a wildfire prevention tool: A basic review. Iforest-Biogeosci. For. 2014, 7, 260. [Google Scholar] [CrossRef]
- Johnson, E.A.; Miyanishi, K. (Eds.) Forest Fires Behavior and Ecological Effects; Academic Press: Cambridge, MA, USA, 2001; p. 594. [Google Scholar]
- Keller, F.; Lischke, H.; Mathis, T.; Möhl, A.; Wick, L.; Ammann, B.; Kienast, F. Effects of climate, fire, and humans on forest dynamics: Forest simulations compared to the palaeological record. Ecol. Model. 2002, 152, 109–127. [Google Scholar] [CrossRef]
- Romeo, F.; Marziliano, P.A.; Turrión, M.B.; Muscolo, A. Short-term effects of different fire severities on soil properties and Pinus halepensis regeneration. J. For. Res. 2020, 31, 1271–1282. [Google Scholar] [CrossRef]
- Garfì, V.; Marziliano, P.A.; Chirici, G.; Nicolaci, A.; Iovino, F. Forest management scenarios to reduce the fire risk in chestnut coppices in the Mediterranean area. Ann. Silvic. Res. 2022, 47, 63–77. Available online: https://creajournals.crea.gov.it/asr/ (accessed on 18 March 2024).
- Turco, M.; Rosa-Cánovas, J.J.; Bedia, J.; Jerez, S.; Montávez, J.P.; Llasat, M.C.; Provenzale, A. Exacerbated fires in Mediterranean Europe due to anthropogenic warming projected with non-stationary climate-fire models. Nat. Commun. 2018, 9, 3821. [Google Scholar] [CrossRef]
- Corona, P.; Ascoli, D.; Barbati, A.; Bovio, G.; ColanGelo, M.; Elia, V.; Garfì, F.; Iovino, R.; Lafortezza, V.; Leone, V.; et al. Integrated forest management to prevent wildfires under Mediterranean environments. Ann. Silvic. Res. 2015, 39, 24–45. [Google Scholar]
- Fernandes, P.M. Forest fires in Galicia (Spain): The outcome of unbalanced fire management. J. For. Econ. 2008, 14, 155–157. [Google Scholar] [CrossRef]
- Fernandes, P.M. Fire smart management of forest landscapes in the Mediterranean basin under global change. Landsc. Urban Plan. 2013, 110, 175–182. [Google Scholar] [CrossRef]
- McKelvey, K.S.; Skinner, C.N.; Chang, C.; Erman, D.C.; Husari, S.J.; Parsons, D.J.; Van Wagtendonk, J.W.; Weatherspoon, C.P. An overview of fire in the Sierra Nevada. In Sierra Nevada Ecosystem Project: Final Report to Congress, Vol. II: Assessments and Scientific Basis for Management Options; Water Resources Center Report No. 37; Centers for Water and Wildland Resources, University of California: Davis, CA, USA, 1996; pp. 1033–1040. [Google Scholar]
- Graham, R.T.; Harvey, A.E.; Jain, T.B.; Tonn, J.R. The Effects of Thinning and Similar Stand Treatments on Fire Behavior in Western Forests; Gen. Tech. Rep. PNW-GTR-463; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1999.
- Allen, C.D.; Savage, M.; Falk, D.A.; Suckling, K.F.; Swetnam, T.W.; Schulke, T.; Stacey, P.B.; Morgan, P.; Hoffman, M.; Klingel, J.T. Ecological restoration of southwestern ponderosa pine ecosystems: A broad perspective. Ecol. Appl. 2002, 12, 1418–1433. [Google Scholar] [CrossRef]
- Pollet, J.; Omi, P.N. Effect of thinning and prescribed burning on crown fire severity in ponderosa pine forest. Int. J. Wildland Fire 2002, 11, 1–10. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. For. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Skog, K.E.; Barbour, R.J.; Abt, K.L.; Bilek, E.M.; Burch, F.; Fight, R.J.; Hugget, R.J.; Miles, P.D.; Reinhardt, E.D.; Sheppard, W.D. Evaluation of Silvicultural Treatments and Biomass Use for Reducing Fire Hazard in Western States; Paper FPL-RP-634; USDA Forest Service Research: Washington, DC, USA, 2006.
- Reinhardt, E.D.; Keane, R.E.; Calkin, D.E.; Cohen, J.D. Objectives and considerations for wildland fuel treatment in forested ecosystems of the interior western United States. For. Ecol. Manag. 2008, 256, 1997–2006. [Google Scholar] [CrossRef]
- Foresta, M.; Carranza, M.L.; Garfì, V.; Di Febbraro, M.; Marchetti, M.; Loy, A. A systematic conservation planning approach to fire risk management in Natura 2000 sites. J. Environ. Manag. 2016, 181, 574–581. [Google Scholar] [CrossRef] [PubMed]
- Moreira, F.; Ascoli, D.; Safford, H.; Adams, M.A.; Moreno, J.M.; Pereira, J.M.; Catry, F.X.; Armesto, J.; Bond, W.; González, M.E.; et al. Wildfire management in Mediterranean-type regions: Paradigm change needed. Environ. Res. Lett. 2020, 15, 011001. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Schulte, E.; Schmuck, G.; Camia, A.; Strobl, P.; Liberta, G.; Amatulli, G. Comprehensive monitoring of wildfires in Europe: The European forest fire information system (EFFIS). In Approaches to Managing Disaster-Assessing Hazards, Emergencies and Disaster Impacts; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Pastor, E.; Zarate, L.; Planas, E.; Arnaldos, J. Mathematical models and calculations systems for the study of wildland fire behavior. Prog. Energy Combust. Sci. 2003, 29, 139–153. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 11th ed.; Natural Resources Conservation Service, USDA: Washington, DC, USA, 2010; p. 338. Available online: https://webpages.uidaho.edu/soil454/2010_keys_to_soil_taxonomy.pdf (accessed on 15 April 2024).
- Regione Calabria. Piano Regionale per la Prevenzione e la Lotta Attiva Agli Incendi Boschivi. Reggio Calabria, 2023, 181p. Available online: https://www.regione.calabria.it/website/portalmedia/decreti/2023-05/Piano-AIB-2023_CV_rev05.pdf (accessed on 20 March 2024).
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons: New York, NY, USA, 1983; 333p. [Google Scholar]
- Corona, P.; Marziliano, P.A.; Scotti, R. Top-down growth modelling: A prototype for poplar plantations in Italy. For. Ecol. Manag. 2002, 161, 65–73. [Google Scholar] [CrossRef]
- Marziliano, P.A.; Tognetti, R.; Lombardi, F. Is tree age or tree size reducing height increment in Abies alba Mill. at its southernmost distribution limit? Ann. For. Sci. 2019, 76, 17. [Google Scholar] [CrossRef]
- INFC. Linee generali del progetto per il secondo inventario forestale nazionale italiano. In Inventario Nazionale Delle Foreste e dei Serbatoi Forestali di Carbonio; De Natale, F., Floris, A., Gasparini, P., Scrinzi, G., Tabacchi, G., Tosi, V., Eds.; MiPAF—Ispettorato Generale del Corpo Forestale dello Stato ISAFA: Trento, Italy, 2005. [Google Scholar]
- Tabacchi, G.; Di Cosmo, L.; Gasparini, P. Aboveground tree volume and phytomass prediction equations for forest species in Italy. Eur. J. For. Res. 2011, 130, 911–934. [Google Scholar] [CrossRef]
- Hellrigl, B. Il potere calorifico del legno. In Proceedings of the Atti del Convegno “Le Biomasse Agricole e Forestali Nello Scenario Energetico Nazionale”, Progetto Fuoco, Verona, Italy, 18–19 March 2004; pp. 1–14. [Google Scholar]
- Van Wagner, C.E. Prediction of crown fire behavior in conifer stands. In Proceedings of the 10th Conference on Fire and Forest Meteorology; Ottawa, ON, Canada, 17–21 April 1989, MacIver, D.C., Auld, H., Whitewood, R., Eds.; Environment Canada, Forestry Canada: Gatineau, QC, Canada, 1989; pp. 207–212. [Google Scholar]
- Cruz, M.G.; Alexander, M.E. Assessing crown fire potential in coniferous forests of western North America: A critique of current approaches and recent simulation studies. Int. J. Wildland Fire 2010, 19, 377–398. [Google Scholar] [CrossRef]
- Agee, J.K.; Bahro, B.; Finney, M.; Omi, P.; Sapsis, D.B.; Skinner, C.N.; van Wagtendonk, J.W.; Weatherspoon, C.P. The use of shaded fuelbreaks in landscape fire management. For. Ecol. Manag. 2000, 127, 55–66. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, E.D. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire; Res. Pap. RMRS-RP-29; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2001.
- Marotta, F.; Mossa Verre, M. Un modello unificato per il dimensionamento degli impianti antincendio ad acqua nell’industria. In Proceedings of the Convegno Nazionale “Valutazione e Gestione del Rischio negli Insediamenti Civili e Industriali”, Pisa, Italy, 6–8 October 1998. [Google Scholar]
- Delle Chiaie, M. Compendio di Idraulica Applicata All’ingegneria Antincendi; Scuole Centrali Antincendi: Rome, Italy, 1976. [Google Scholar]
- Richards, G.D. An elliptical growth model of forest fire fronts and its numerical solution. Int. J. Numer. Methods Eng. 1990, 30, 1163–1179. [Google Scholar] [CrossRef]
- Finney, M.A.; Ryan, K.C. Use of the FARSITE fire growth model for fire prediction in US National Parks. In International Emergency Management and Engineering Conference; Sullivan, J.D., Wybo, J.L., Buisson, L., Eds.; International Emergency Management and Engineering Society: Paris, France, 1995; pp. 183–189. [Google Scholar]
- Tymstra, C.; Bryce, R.W.; Wotton, B.M.; Taylor, S.W.; Armitage, O.B. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model; Information Report NOR-X-417; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2010.
- Boychuk, D.; Braun, W.J.; Kulperger, R.J.; Krougly, Z.L.; Stanford, D.A. A stochastic forest fire growth model. Environ. Ecol. Stat. 2009, 16, 133–151. [Google Scholar] [CrossRef]
- Hillen, T.; Greese, B.; Martin, J.; De Vries, G. Birth-jump processes and application to forest fire spotting. J. Biol. Dyn. 2015, 9 (Suppl. S1), 104–127. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Martin, J.; Hillen, T. The spotting distribution of wildfires. Appl. Sci. 2016, 6, 177. [Google Scholar] [CrossRef]
- Beneduci, R.; Mascali, G. Forest fire spreading: A nonlinear stochastic model continuous in space and time. arXiv 2023, arXiv:2309.0066. [Google Scholar] [CrossRef]
- Fosdick, R.; Foti, P.; Fraddosio, A.; Piccioni, M.D. A lower bound estimate of the critical load for compressible elastic solids. Contin. Mech. Thermodyn. 2010, 22, 77–97. [Google Scholar] [CrossRef]
- Mandel, J.; Bennethum, L.S.; Beezley, J.D.; Coen, J.L.; Douglas, C.C.; Kim, M.; Vodacek, A. A wildland fire model with data assimilation. Math. Comput. Simul. 2008, 79, 584–606. [Google Scholar] [CrossRef]
- Asensio, M.I.; Ferragut, L. On a wildland fire model with radiation. Int. J. Numer. Methods Eng. 2002, 54, 137–157. [Google Scholar] [CrossRef]
- Alì, G.; Demarco, F.; Gaudio, D.; Fusaro, P.A.; Olivito, R.S.; Scuro, C. A mathematical model for the propagation of wildfires. In 2023 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv); IEEE: Piscataway, NJ, USA, 2023; pp. 257–260. [Google Scholar]
- Alì, G.; Lamonaca, F.; Scuro, C.; Torcicollo, I. On a one-dimensional hydrodynamic model for semiconductors with field-dependent mobility. Mathematics 2021, 9, 2152. [Google Scholar] [CrossRef]
- Alì, G.; Demarco, F.; Scuro, C. Propagation of Elastic Waves in Homogeneous Media: 2D Numerical Simulation for a Concrete Specimen. Mathematics 2022, 10, 2673. [Google Scholar] [CrossRef]
- San Martín, D.; Torres, C.E. Ngen-Kütral: Toward an open source framework for Chilean wildfire spreading. In Proceedings of the 37th International Conference of the Chilean Computer Science Society, Santiago, Chile, 5–9 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Fernandes, P.; Davies, M.; Ascoli, D.; Fernandez, C.; Moreira, F.; Rigolot, E.; Stoof, C.; Vega, J.A.; Molina, D. Prescribed burning in southern Europe: Developing fire management in a dynamic landscape. Front. Ecol. Environ. 2013, 11, e4–e14. [Google Scholar] [CrossRef] [PubMed]
- Grund, K.; Conedera, M.; Schroder, H.; Walther, G.R. The role of fire in the invasion process of evergreen broad-leaved species. Basic Appl. Ecol. 2005, 6, 47–56. [Google Scholar] [CrossRef]
- Pezzatti, G.; Zumbrunnen, T.; Burgi, T.; Ambrosetti, P.; Conedera, M. Fire regime shifts as a consequence of fire policy and socioeconomic development: An analysis based on the change point approach. For. Policy Econ. 2013, 29, 7–18. [Google Scholar] [CrossRef]
- San Roman Sanz, A.; Fernandez, C.; Mouillot, F.; Ferrat, L.; Istria, D.; Pasqualini, V. Long-term Forest dynamics and land-use abandonment in the Mediterranean mountains, Corsica, France. Ecol. Soc. 2013, 18, 38. [Google Scholar] [CrossRef]
- Bombino, G.; D’Agostino, D.; Marziliano, P.A.; Pérez Cutillas, P.; Praticò, S.; Proto, A.R.; Manti, L.M.; Lofaro, G.; Zimbone, S.M. A Nature-Based Approach Using Felled Burnt Logs to Enhance Forest Recovery Post-Fire and Reduce Erosion Phenomena in the Mediterranean Area. Land 2024, 13, 236. [Google Scholar] [CrossRef]
- Khabarov, N.; Krasovskii, A.; Obersteiner, M.; Swart, R.; Dosio, A.; San-Miguel-Ayanz, J.; Durrant, T.; Camia, A.; Migliavacca, M. Forest fires and adaptation options in Europe. Reg. Environ. Chang. 2016, 16, 21–30. [Google Scholar] [CrossRef]
- Crotteau, J.S.; Keyes, C.R.; Sutherland, E.K.; Wright, D.K.; Egan, J.M. Forest fuels and potential fire behaviour 12 years after variable retention harvest in lodgepole pine. Int. J. Wildland Fire 2016, 25, 633–645. [Google Scholar] [CrossRef]
- Covington, W.W.; Moore, M.M. Southwestern ponderosa forest structure: Changes since Euro-American settlement. J. For. 1994, 92, 39–47. [Google Scholar] [CrossRef]
- Iovino, F.; Ascoli, D.; Laschi, A.; Marchi, E.; Marziliano, P.A.; Nicolaci, A.; Bovio, G. Thinning and prescribed burning for fire hazard reduction in Pinus halepensis plantations. L′Italia J. For. Mt. Environ. 2014, 69, 213–229. [Google Scholar] [CrossRef][Green Version]
- Compostella, G.; Iovino, F. Studio sull’umidità del suolo in relazione ai diradamenti in popolamenti di Pino laricio. L’Italia For. Mont. 1999, 6, 308–323. [Google Scholar]
- Garfì, V.; Iovino, F.; Pellicone, G. Influenza della densità del popolamento sulle variazioni di umidità del suolo in rimboschimenti di Pino d’Aleppo. In Atti del Terzo Congresso Nazionale di Selvicoltura per il Miglioramento e la Conservazione dei Boschi Italiani, Taormina, Italy, 16–19 Ottobre 2008; Accademia Italiana di Scienze Forestali Firenze: Firenze, Italy, 2009; Volume 1, pp. 503–510. [Google Scholar]
- Moghaddas, J.J.; Craggs, L. A fuel treatment reduces fire severity and increases suppression efficiency in a mixed conifer forest. Int. J. Wildland Fire 2007, 16, 673–678. [Google Scholar] [CrossRef]
- Duguy, B.; Alloza, J.A.; Roder, A.; Vallejo, R.; Pastor, F. Modelling the effects of landscape fuel treatments on fire growth and behaviour in a Mediterranean landscape (eastern Spain). Int. J. Wildland 2007, 16, 619–632. [Google Scholar] [CrossRef]
- Bovio, G.; Camia, A. Variabilità degli Incendi Boschivi. In Incendi e Complessità Ecosistemica. Dalla Pianificazione Forestale al Recupero Ambientale; Blasi, C., Bovio, G., Corona, P., Marchetti, M., Maturani, A., Eds.; Ministero dell’Ambiente e della Tutela del Territorio, Direzione per la Protezione della Natura: Rome, Italy, 2004; Volume 61–62, 353p. [Google Scholar]
- Bovio, G.; Ceccato, R.; Francesetti, A.; Marzano, R. La Pianificazione Forestale Territoriale. Stato dell’arte e prospettive di sviluppo. In Presentazione e discussione dei primi risultati Ri.selv.Italia; Consiglio per la Ricerca e la Sperimentazione in Agricoltura–MIPAF: Milano, Italy, 2004. [Google Scholar]
- Leone, V.; Lovreglio, R. Pre and post-fire treatments in Aleppo pine stands: Prevention sylviculture and restoration. In Proceedings of the “II Conferencia Internacional sobre Estrategias de Prevención de Incendios en el Sur de Europa. Gestión Forestall como Herramienta para la Prevención de Incendios”, Barcelona, Spain, 9–11 May 2005; CFC-COSE, USSE Y CTFC. p. 182. [Google Scholar]
- Pausas, J.; Fernandez-Muñoz, S. Fire regime changes in the western Mediterranean basin: From fuel limited to drought driven fire regime. Clim. Chang. 2012, 110, 215–226. [Google Scholar] [CrossRef]
- Seijo, F.; Millington, J.D.A.; Gray, R.; Mateo, L.H.; Sangüesa-Barreda, G.; Camarero, J.J. Divergent Fire Regimes in Two Contrasting Mediterranean Chestnut Forest Landscapes. Hum. Ecol. 2017, 45, 205–219. [Google Scholar] [CrossRef]
- Nocentini, S. La rinaturalizzazione come strumento di recupero dei sistemi forestali semplificati nell’Italia Meridionale. L’Italia For. Mont. 2001, 5, 344–351. [Google Scholar]
- Felton, A.; Lindbladh, M.; Brunet, J.; Fritz, O. Replacing coniferous monocultures with mixed-species production stands: An assessment of the potential benefits for forest biodiversity in northern Europe. For. Ecol. Manag. 2010, 260, 939–947. [Google Scholar] [CrossRef]
- Huuskonen, S.; Domisch, T.; Finér, L.; Hantula, J.; Hynynen, J.; Matala, J.; Miina, J.; Neuvonen, S.; Nevalainen, S.; Niemistö, P.; et al. What is the potential for replacing monocultures with mixed-species stands to enhance ecosystem services in boreal forests in Fennoscandia? For. Ecol. Manag. 2021, 479, 118558. [Google Scholar] [CrossRef]
- Paletto, A.; Pieratti, E.; De Meo, I.; Agnelli, A.E.; Cantiani, P.; Chiavetta, U.; Mazza, G.; Lagomarsino, A. A multi-criteria analysis of forest restoration strategies to improve the ecosystem services supply: An application in Central Italy. Ann. For. Sci. 2021, 78, 7. [Google Scholar] [CrossRef]
- Reisch, C.; Navas-Montilla, A.; Özgen-Xian, I. Analytical and numerical insights into wildfire dynamics: Exploring the advection–diffusion–reaction model. Comput. Math. Appl. 2024, 158, 179–198. [Google Scholar] [CrossRef]
- Demarco, F.; Bertacchini, F.; Scuro, C.; Bilotta, E.; Pantano, P. The development and application of an optimization tool in industrial design. Int. J. Interact. Des. Manuf. (IJIDeM) 2020, 14, 955–970. [Google Scholar] [CrossRef]
- Tiberti, S.; Scuro, C.; Codispoti, R.; Olivito, R.S.; Milani, G. Masonry structures built with fictile tubules: Experimental and numerical analyses. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2017; Volume 1906. [Google Scholar] [CrossRef]
- Tiberti, S.; Scuro, C.; Codispoti, R.; Olivito, R.S.; Milani, G. Traditional masonry arches and domes with fictile tubules in Mediterranean seismic areas: Advanced numerical models and experimentation. In Proceedings of the 6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; pp. 2431–2448. [Google Scholar] [CrossRef][Green Version]
- European Commission. Land-Based Wildfire Prevention—Principles and Experiences on Managing Landscapes, Forests and Woodlands for Safety and Resilience in Europe; Nuijten, D., Onida, M., Lelouvier, R., Eds.; Publications Office of the European Union: Luxembourg, 2021; Available online: https://data.europa.eu/doi/10.2779/695867 (accessed on 26 March 2024).
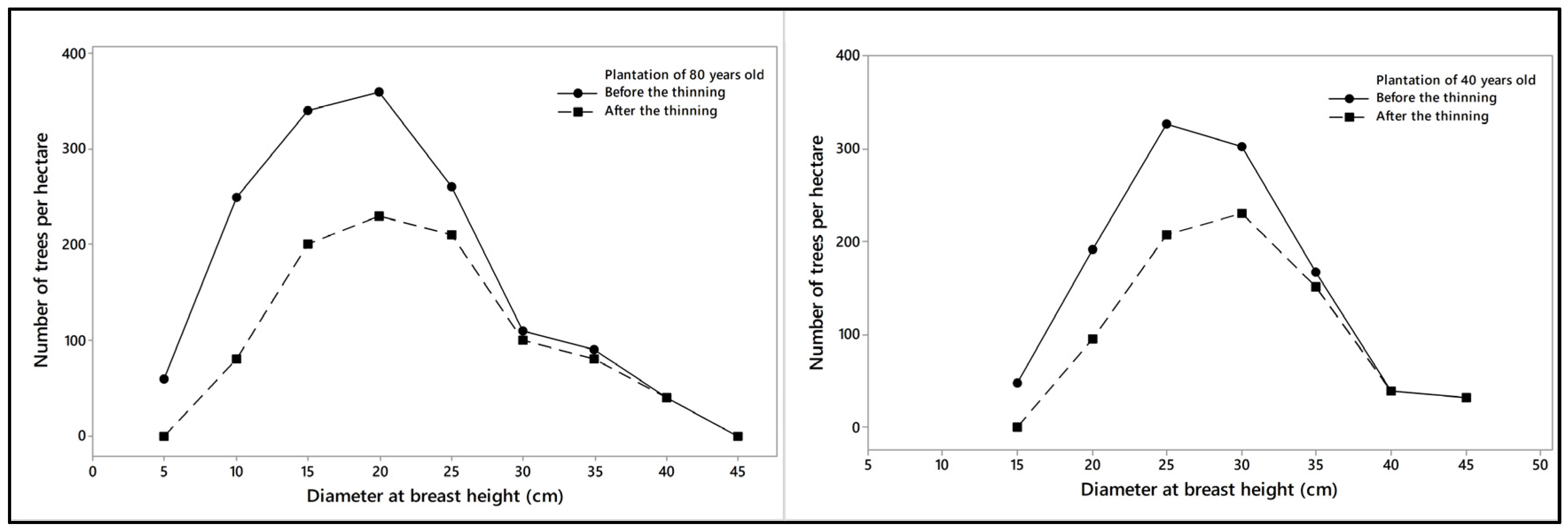
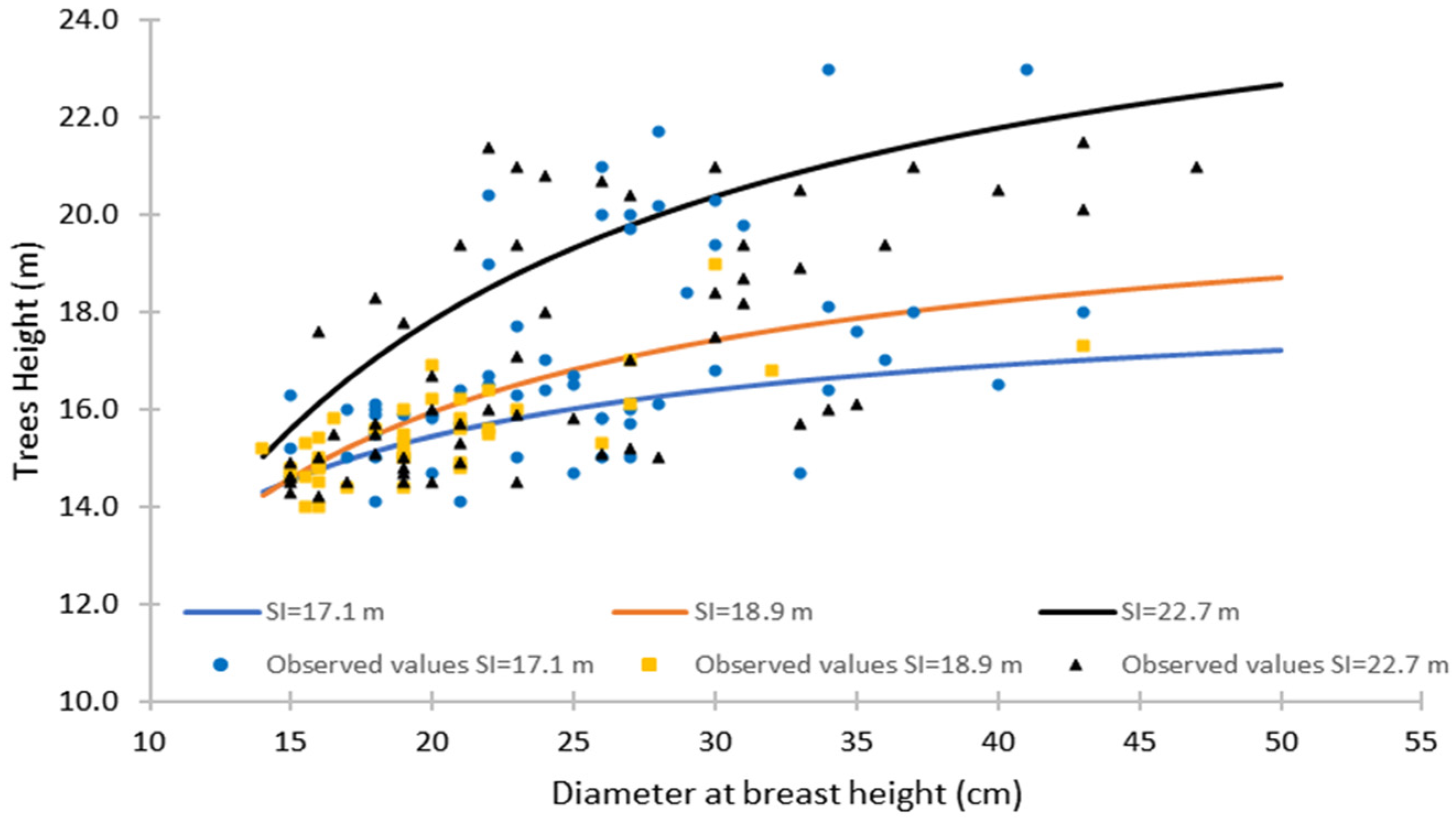

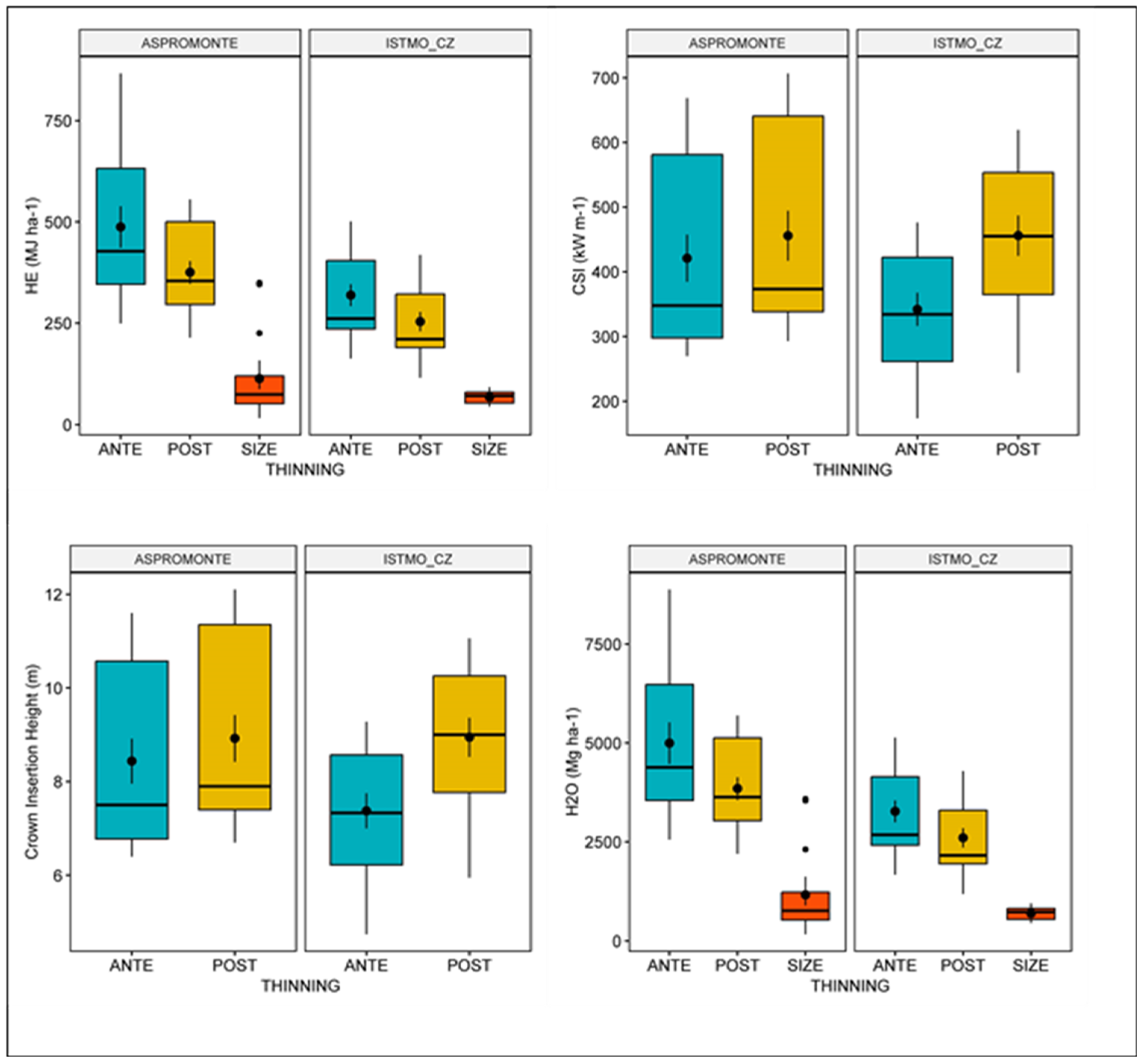
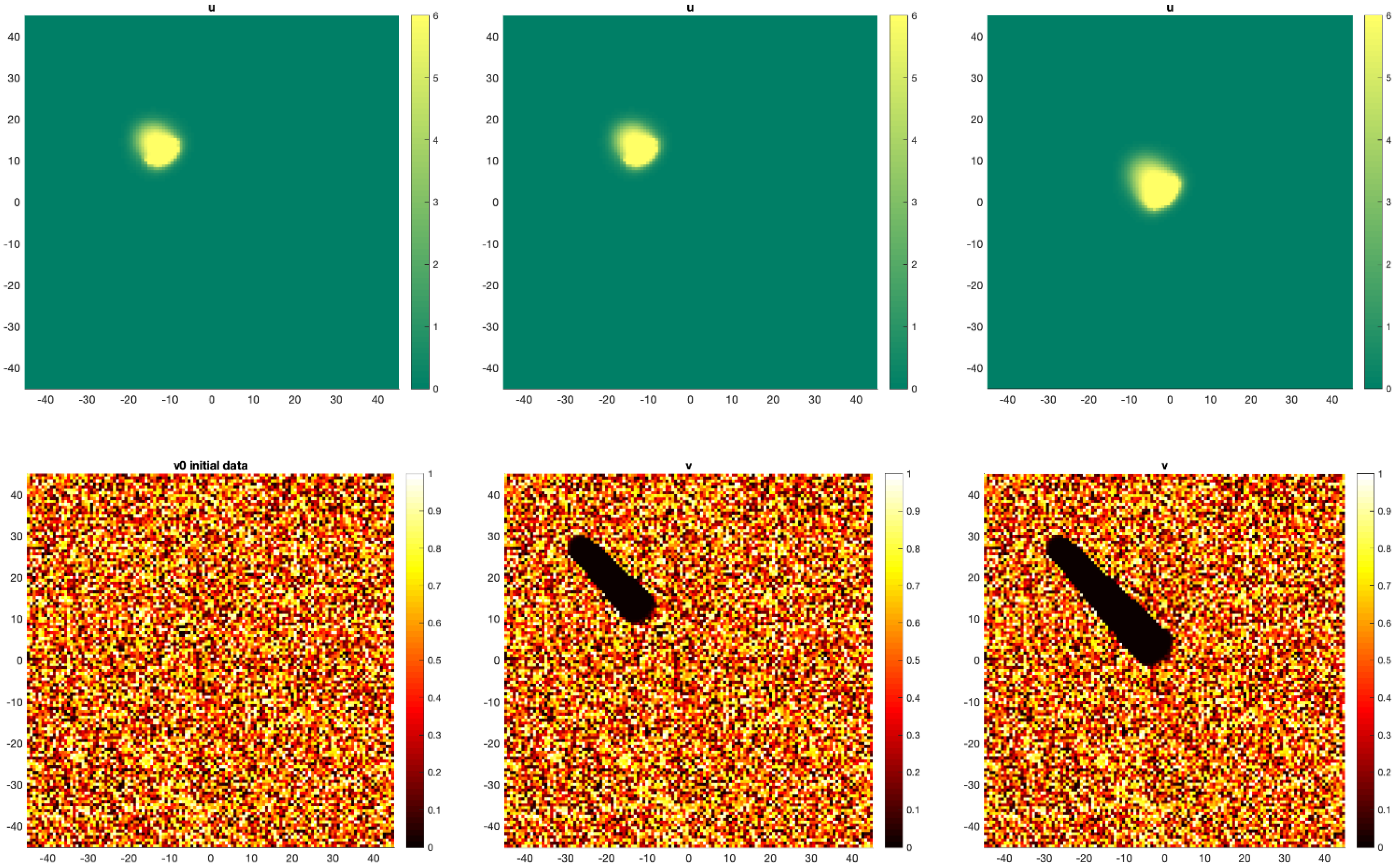
| 80-Year-Old Stand | 40-Year-Old Stand | |||||
|---|---|---|---|---|---|---|
| Thinning | Thinning | |||||
| Before | After | Diff % | Before | After | Diff % | |
| Number of trees [N° ha−1] | 1107 | 757 | −31.6 | 1510 | 940 | −37.8 |
| Mean Diameter [cm] | 28.5 | 30.4 | 6.7 | 21.3 | 23.7 | 11.5 |
| Mean Height [m] | 17.3 | 17.5 | 1.2 | 15.4 | 15.8 | 3.1 |
| Crown Insertion Height [m] | 7.8 | 8.1 | 3.8 | 7.4 | 8.9 | 19.9 |
| Basal Area [m2 ha−1] | 70.6 | 54.8 | −22.4 | 53.6 | 41.5 | −22.6 |
| Volume [m3 ha−1] | 523.2 | 410.6 | −21.5 | 354.2 | 290.2 | −18.1 |
| Above-ground biomass [Mg ha−1] | 254.6 | 199.3 | −21.7 | 175.7 | 142.6 | −18.8 |
| Heat energy [MJ ha−1] | 453.2 | 354.8 | −21.7 | 312.7 | 253.9 | −18.8 |
| Critical Surface Intensity [kW m−1] | 369.0 | 389.9 | 5.7 | 339.5 | 445.6 | 31.3 |
| WH2O [Mg ha−1] | 4643 | 3635 | −21.7 | 3204 | 2601.3 | −18.8 |
| Model Equation | β0 | β1 | β2 | β3 | R2 | RMSE | |
|---|---|---|---|---|---|---|---|
| Equation (1) (Ht) | Parameter | 1.807 | 0.065 | −21.387 | 303.701 | 0.702 | 0.0681 |
| 80-year-old stand | S.E. | 0.0157 | 0.008 | 3.483 | 62.483 | ||
| T | 11.522 | 7.892 | −6.141 | 4.861 | |||
| Sig. | <0.001 | <0.001 | <0.001 | <0.001 | |||
| Equation (1) (Hbc) | Parameter | 0.662 | 0.105 | −39.352 | 423.213 | 0.677 | 0.189 |
| 80-year-old stand | S.E. | 0.434 | 0.023 | 9.640 | 172.951 | ||
| T | 1.525 | 4.605 | −4.082 | 2.447 | |||
| Sig. | 0.129 | <0.001 | <0.001 | 0.16 | |||
| Equation (2) (Ht) | Parameter | 4.721 | −66.806 | −101.660 | 0.703 | 0.0902 | |
| 40-year-old stand | S.E. | 0.072 | 2.958 | 6.802 | |||
| T | 65.854 | −22.587 | −14.946 | ||||
| Sig. | <0.001 | <0.001 | <0.001 | ||||
| Equation (2) (Hbc) | Parameter | 3.630 | −30.353 | −277.096 | 0.397 | 0.2555 | |
| 40-year-old stand | S.E. | 0.203 | 8.375 | 19.260 | |||
| T | 17.883 | −3.624 | −14.387 | ||||
| Sig. | <0.001 | <0.001 | <0.001 |
| Ambient Temperature | 300 | K | |
|---|---|---|---|
| Activation Energy | E | 83.68 | kJ/mol |
| Heat of Combustion | Q | 15,900 | kcal/kg |
| Pre-exponential coefficient | 109 | s−1 | |
| Density | ρ | 100 | kg/m3 |
| Specific heat | C | 1 | kJ kg−1 K−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marziliano, P.A.; Lombardi, F.; Cataldo, M.F.; Mercuri, M.; Papandrea, S.F.; Manti, L.M.; Bagnato, S.; Alì, G.; Fusaro, P.; Pantano, P.S.; et al. Forest Fires: Silvicultural Prevention and Mathematical Models for Predicting Fire Propagation in Southern Italy. Fire 2024, 7, 278. https://doi.org/10.3390/fire7080278
Marziliano PA, Lombardi F, Cataldo MF, Mercuri M, Papandrea SF, Manti LM, Bagnato S, Alì G, Fusaro P, Pantano PS, et al. Forest Fires: Silvicultural Prevention and Mathematical Models for Predicting Fire Propagation in Southern Italy. Fire. 2024; 7(8):278. https://doi.org/10.3390/fire7080278
Chicago/Turabian StyleMarziliano, Pasquale A., Fabio Lombardi, Maria F. Cataldo, Michele Mercuri, Salvatore F. Papandrea, Leonardo M. Manti, Silvio Bagnato, Giuseppe Alì, Pierpaolo Fusaro, Pietro S. Pantano, and et al. 2024. "Forest Fires: Silvicultural Prevention and Mathematical Models for Predicting Fire Propagation in Southern Italy" Fire 7, no. 8: 278. https://doi.org/10.3390/fire7080278
APA StyleMarziliano, P. A., Lombardi, F., Cataldo, M. F., Mercuri, M., Papandrea, S. F., Manti, L. M., Bagnato, S., Alì, G., Fusaro, P., Pantano, P. S., & Scuro, C. (2024). Forest Fires: Silvicultural Prevention and Mathematical Models for Predicting Fire Propagation in Southern Italy. Fire, 7(8), 278. https://doi.org/10.3390/fire7080278










