Abstract
Wildfire spread models are an essential tool for mitigating catastrophic effects associated with wildfires. However, current operational models suffer from significant limitations regarding accuracy and transferability. Recent advances in the availability and capability of Earth observation data and artificial intelligence offer new perspectives for data-driven modeling approaches with the potential to overcome the existing limitations. Therefore, this study developed a data-driven Deep Learning wildfire spread modeling approach based on a comprehensive dataset of European wildfires and a Spatiotemporal Graph Neural Network, which was applied to this modeling problem for the first time. A country-scale model was developed on an individual wildfire time series in Portugal while a second continental-scale model was developed with wildfires from the entire Mediterranean region. While neither model was able to predict the daily spread of European wildfires with sufficient accuracy (weighted macro-mean IoU: Portugal model 0.37; Mediterranean model 0.36), the continental model was able to learn the generalized patterns of wildfire spread, achieving similar performances in various fire-prone Mediterranean countries, indicating an increased capacity in terms of transferability. Furthermore, we found that the spatial and temporal dimensions of wildfires significantly influence model performance. Inadequate reference data quality most likely contributed to the low overall performances, highlighting the current limitations of data-driven wildfire spread models.
1. Introduction
Wildfires are natural disasters that shape our ecosystems [1], and they are frequently associated with negative effects on the environment [1,2], economy [3], infrastructure [4], and human lives [5]. Globally, climatic changes are leading to an intensification of fire activity and fire weather conditions [6], which are especially present in the fire-prone Mediterranean region, where research projects an increase in the frequency, size, and intensity of wildfires over the next decade [7,8]. This growing threat necessitates innovative strategies for wildfire management in the Mediterranean region [9]. In this context, wildfire spread models are an essential tool for predicting and understanding wildfire behavior [10], providing critical insights that enable fire management authorities and emergency responders to make informed decisions regarding evacuation plans, resource allocation, and fire suppression strategies [11].
A wildfire spread model predicts the behavior and propagation of a wildfire by considering the complex interactions of various environmental factors, e.g., weather conditions, terrain, fuel, and land cover [10,12,13]. Traditionally, conventional wildfire spread models have been based on physical [14], semi-empirical [15], empirical, or simulation models [16]. Physical models simulate the physical and chemical processes of wildfires but are not intended for operational use [14]. Semi-empirical models, such as the widely used Rothermel model [17], combine physical principles with statistical methods and are more practical for operational applications [11,15]. However, they face challenges in heterogeneous environments [10], require specialized input data, and are difficult to transfer to regions outside their development context [15,18]. Purely empirical or simulation models, despite their use in operational systems [11], have limitations, such as high computational costs and dependency on input data [16], leading to inaccuracies and transferability issues [19]. Until today, no operationally used conventional wildfire spread model achieved satisfactory results under all situations in a timely and accurate manner while offering a complete solution for fire management activities [12,15,18].
Recent advances in the availability and capability of Earth observation data, artificial intelligence, and computational resources have resulted in an unprecedented quantity and quality of wildfire spread-related data products [11,19]. This provides a novel opportunity for the development of data-driven wildfire spread models that have the potential to overcome the prevailing accuracy and transferability issues of conventional wildfire spread models [19,20]. However, data-driven approaches are only being slowly adopted in the research field of wildfire spread modeling [19].
Deep Learning (DL) architectures can learn highly complex and non-linear dependencies from large amounts of data [21] and should therefore apply to the wildfire spread modeling problem; however, DL is still considered experimental in this research field [19]. Qiao et al. [22] used a transformer-based neural network to simulate the wildfire spread backwards in order to identify the location of the initial ignition point. Only a few studies have used DL techniques to model the forward propagation of wildfires. Hodges and Lattimer [23] formulated the wildfire spread prediction as an image segmentation problem, while similar studies by Radke et al. [24] and Huot et al. [25] developed a Convolutional Neural Network (CNN) based on various environmental variables to predict the wildfire spread in small test regions in the USA. However, these studies did not achieve sufficient results and were solely focused on making spatial predictions, neglecting the temporal component of the wildfire spread process. On the other hand, some studies tried to model the spread of wildfires using time-series-adapted DL learning techniques, e.g., Recurrent Neural Networks (RNNs) [26,27,28,29], but did not incorporate spatial information into the modeling process. Only the study of Burge et al. [30] accounted for the spatiotemporal nature of wildfires by applying a Convolutional Recurrent Neural Network (ConvRNN). Their spatiotemporal wildfire spread model achieved high accuracies but was only developed on artificial wildfire data.
A great challenge in the spatiotemporal modeling of wildfire spread lies in the creation of a dataset that displays individual wildfires in both the spatial and temporal dimensions. An efficient way to represent such data is through spatiotemporal graphs. A spatio-temporal graph consists of a collection of nodes which can hold dynamically changing data features. The graph’s nodes are connected through edges, which define the relationship between the nodes [21]. The theory of graphs has already been used in wildfire applications. Jiang et al. [31] used an irregular graph to predict the propagation time of a wildfire, while Yemshanov et al. [32] tried to identify the critical nodes of a graph for effective fuel reduction treatments. Ge et al. [33] built a spatiotemporal knowledge graph to predict wildfire occurrence in a test region in China, while Chen et al. [34] used a similar approach to forecast the total burned area in a Portuguese national park.
To apply DL techniques to spatiotemporal graph data, Spatiotemporal Graph Neural Networks (STGNNs) have been developed over the last decade. STGNNs implement a spatial (e.g., a Graph Convolutional Network (GCN)) and a temporal modeling component (e.g., an RNN) to simultaneously learn spatial and temporal data dependencies within a graph [21]. This allows for modeling spatiotemporal systems with high accuracy and efficiency [21] and results in improved results in various domains, e.g., traffic forecasting, recommendation systems, or social network analysis [35,36]. The application of STGNNs for modeling natural hazards is, however, still limited, with only a few studies focusing on the prediction of urban floodings [37], typhoon intensity [38], or the location and magnitude of earthquakes [39]. However, no study has yet applied STGNNs to model the daily wildfire spread on a regional or continental scale in Europe.
Inspired by the new opportunities arising from the increasing data availability and advances in the development of spatiotemporal DL techniques, this study built a data-driven DL-based wildfire spread model to predict the daily spread of European wildfires. In a research field where data-driven methods are only slowly being adopted, this study uses a STGNN to model the wildfire spread for the first time. For this, a comprehensive dataset containing the daily burned areas of wildfires in Europe from 2016 to 2022, coupled with relevant wildfire driver variables, was built and used to train two different models.
First, a country-scale STGNN model was developed for Portugal by training and testing on a Portuguese wildfire time series from 2016 to 2022. With this, we tested the general ability of a STGNN architecture and assessed how the spatial and temporal dimensions of wildfires influence the model performance.
Secondly, a STGNN model was developed for the entire Mediterranean region by training and testing it on wildfire time series from 2016 to 2022 from various Mediterranean countries. This addresses the existing transferability issues of conventional models by leveraging the generalizing power of DL techniques. The Mediterranean model was therefore used to assess how the performance of a generalized wildfire spread model varies in different countries with varying environmental conditions and fire regimes.
2. Data and Materials
A comprehensive dataset including the daily time series of European wildfires from 2016 to 2022 was constructed for this study. Daily burned area perimeters of individual wildfires mapped by the burned area detection algorithm of the German Aerospace Center (DLR) [40] were combined with a set of dynamic and static predictor variables. The discrete H3 Hexagonal Hierarchical Geospatial Indexing System (hereafter referred to as “H3 grid system”) [41] was used to combine the input variables in a uniform grid covering Europe. The H3 grid system represents the Earth’s surface using discrete hexagonal cells in different hierarchical spatial resolutions. Each H3 cell has a unique identifier that encodes the positional information, facilitating spatial queries and neighbor identifications. In addition, the hexagonal cell geometry is particularly valuable for spatial modeling because of the six equally distanced neighbors [42], which is why other studies have used discrete hexagonal grid systems to model the behavior of wildfires [32,43].
2.1. Input Variables
2.1.1. Burned Area Perimeters
The wildfire time series dataset (2016–2022) is built upon the individual burned area perimeters derived from a satellite-based burned area monitoring system developed by the DLR [40]. The system uses the Sentinel-3 constellation (S3) Ocean and Land Color Instrument (OLCI) to map the daily burned area perimeters in Europe at 300 m spatial resolution. The monitoring system processes each available S3 satellite scene, which are acquired during the daily overflights over Europe. The mapping procedure utilizes active fire data from the Moderate Resolution Imaging Spectroradiometer (MODIS) and Visible Infrared Imaging Radiometer Suite (VIIRS) sensors in combination with an S3-based pre- and post-fire Normalized Difference Vegetation Index (NDVI) derived from the red and near-infrared (NIR) bands. Using this contextual information, a growing Morphological Active Contour region derives the daily burned area perimeters, which are progressively refined with each newly acquired S3 scene (for a detailed description of the methodology, see Nolde et al. [40]). All detected daily burned area perimeters mapped by the S3 burned area monitoring system from 2016 to 2022 in Europe were selected for this study. By labeling each wildfire with a unique identifier, contiguous daily burned area perimeters representing a wildfire’s spatial expansion over time were created.
2.1.2. ERA5-Land—Historic Weather Data
The behavior of wildfires is closely related to the prevailing weather conditions [44]. While wind direction and speed are the main factors driving a fire across a landscape [13,45], other meteorological variables, such as temperature, precipitation, or relative humidity, correlate with fuel moisture content, which affects the total burned area and the rate of fire spread [29,46]. Therefore, historical weather information, matching the date of the burn, was included in the wildfire time series dataset. This information was retrieved from the ERA5-Land dataset [47] of the European Center for Medium-Range Weather Forecasts (ECMWF). The ERA5-Land dataset offers a continuous record of weather variables from 1950 to the present day at an hourly temporal resolution and a 0.1° horizontal resolution. The main meteorological driver variables for wildfires were selected for the entire region of Europe from 2016 to 2022, including the total precipitation [m], 2 m temperature [K], 2 m dewpoint temperature [K], 10 m u-component of wind [ms−1], and 10 m v-component of wind [ms−1].
2.1.3. Fire Weather Index
Fuel moisture is an important driver of wildfires, as it determines the combustibility of the available fuel. It is highly variable over time and closely linked to the preceding weather conditions [13]. To incorporate this dynamic wildfire driver variable into the wildfire time series dataset, the global Fire Weather Index (FWI) product [48] of the ECMWF is used. The FWI assesses the wildfire danger under the preceding and current weather conditions by calculating and combining fuel moisture and fire behavior codes [49]. For this, it considers the temperature, humidity, wind speed, and precipitation. The used FWI product is calculated from the historical ERA5 meteorological variables and produces daily numerical estimations of the wildfire danger at a spatial resolution of 0.25° [48]. For this study, the daily FWI from 2016 to 2022 was acquired for the extent of Europe.
2.1.4. Active Fire Data
Information on active fires or hotspots sensed by the VIIRS sensor on the Suomi National Polar-Orbiting Partnership (Suomi-NPP) satellite was included in the wildfire time series dataset. The VIIRS active fire product [50] delineates the thermal anomalies up to twice a day (depending on the latitude) on a sub-pixel level at 375 m spatial resolution in nadir. Five high-resolution bands, covering the visible to infrared wavelengths (0.64 μm–11.45 μm), are used to detect the hotspots and calculate their respective Fire Radiative Power (FRP) [MW], measuring the radiative energy emission rate per unit of time [50]. This provides important information for the wildfire spread modeling process, as it helps to visualize the active flaming front and thermal characteristics of a fire over time [27].
2.1.5. Fuel Type
A critical variable for wildfire spread models is the fuel type, which serves as a proxy for the combustibility of a landscape [51]. Therefore, the global fuel type classification product of Pettinari and Cuvieco [51] was integrated into the dataset. This product maps six main fuelbeds—trees, shrubs, grasses, woody surface fuels, litter, and ground fuels—in different biomes resulting in a total of 274 fuelbed classes. The classification was generated from various remote sensing land cover products and regional Land Use and Land Cover (LULC) databases (for a detailed description of the methodology, see [51]). The fuel type classification was downloaded for the extent of Europe and encoded into the wildfire time series dataset as a static variable.
2.1.6. CORINE Land Cover
The distribution of LULC types in a landscape indicates differences in the availability of fuel and reveals landscape heterogeneity, which highly influences the propagation of a fire (e.g., urban areas, roads, or water bodies can act as a natural barrier [32,52]).
To include such information in the wildfire time series dataset, the 2018 CORINE Land Cover (CLC) classification [53] provided by the Copernicus Land Monitoring Service (CLMS) was downloaded for the extent of Europe. The CLC has a spatial resolution of 100 m and consists of 44 LULC classes, including artificial surfaces (e.g., urban areas, industrial sites), agricultural areas (e.g., arable land, pastures), forests, semi-natural areas (e.g., broadleaved forests, heathland), wetlands (e.g., marshes, peat bogs), and water bodies (e.g., rivers, lakes).
2.1.7. Digital Elevation Model
A landscape’s topography strongly influences the behavior of a wildfire. Slopes or local topographic winds can drastically increase the fire’s rate of spread [10,13]. The altitudinal level and aspect of a slope are strongly connected to the fuel type and fuel moisture content [13]. For this reason, a Digital Elevation Model (DEM) was used to incorporate topographic information into the wildfire time series dataset. The globally available Copernicus GLO-90 DEM of the European Space Agency (ESA) [54] was therefore downloaded at 90 m spatial resolution for the extent of Europe.
2.2. Feature Engineering and Construction of Wildfire Time Series
An individual Area of Interest (AOI) was created for each European wildfire that occurred from 2016 to 2022. This was established based on the size of each fire’s burned area perimeter on the last day of fire activity. All H3 hexagonal cells of the resolution 9 (approx. 350 m cell diameter) in this area represented a wildfire’s AOI within the discrete H3 grid system. To spatially expand a wildfire’s AOI beyond the burned area perimeter, a buffer ring of one H3 cell was added to the AOI’s edge H3 cells.
The burn status of an AOI over time was then defined by intersecting the centroids of all H3 cells with the respective burned area perimeter derived by the S3 burned area monitoring system. If a cell was burned at a time step , it was labeled accordingly and maintained its status over the following days of the time series. The variable “burned” therefore displayed the accumulated daily burned area over time (see Figure 1a). Additionally, a second burned area variable (“burned_new”) was introduced that indicated if a previously unburned cell on day was burned on the following day . The “burned_new” variable therefore represented wildfire propagation over time (see Figure 1b). Occasionally, some burned area time series contained days without any detected burned areas due to cloud or smoke contaminations in the S3 scenes. To ensure the continuity of a daily sequence in every wildfire time series, days without any detected burned area were filled with the burned area of the previous day. To encode this case in the wildfire time series dataset, a variable “no_observation” was set for all cells of the AOI.
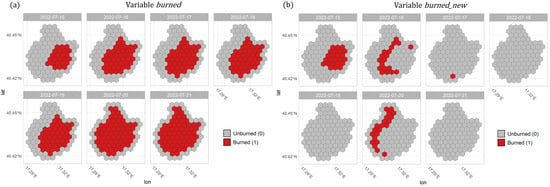
Figure 1.
Burned area variables within the H3 grid for an example wildfire AOI. (a) Time series of the total burned area (variable “burned”). (b) Time series of the daily new burned cells displaying the wildfire propagation (variable “burned_new”).
Feature engineering was conducted for some of the ERA5-Land weather variables. The hourly 2 m temperature and 2 m dewpoint temperature were used to calculate the hourly relative humidity [%]. The hourly wind speed [ms−1] and direction [°] were calculated from the hourly u- and v- wind components. The wind direction was further reclassified into eight classes of 45° intervals. To match the daily resolution of the burned area time series while still preserving the diurnal variation of some weather variables, daily descriptive statistics were computed based on the hourly weather variables, as detailed in Table 1. The daily aggregated weather statistics and the FWI raster layers were then converted to the H3 grid system and joined to the cells of each wildfire AOI.

Table 1.
Input features of the reference dataset for wildfire spread modeling.
Hotspot points were intersected with each daily H3 cell of each wildfire AOI. The daily count of intersecting hotspots per cell was included in the dataset (see Table 1). In addition to the number of active fires, thermal information was incorporated into the dataset by including the daily FRP values for each H3 cell. If a cell contained more than one hotspot, the FRP values were aggregated to daily descriptive statistics (see Table 1).
Feature engineering was also applied to the temporally static variables. The DEM was used to calculate the slope and aspect. All static variables (fuel type, CLC, elevation, slope, and aspect) were then converted into H3 cells and joined to the cells of each fire AOI. The new H3 cell values were determined by using a majority aggregation function for the discrete classification variables (fuel type, CLC) and a mean aggregation function for the continuous topographic layers (elevation, slope, aspect) (see Table 1).
After feature engineering and data aggregation, consecutive daily time series of all H3 cells in a fire’s AOI were constructed. The time series are also displayable as a three-dimensional datacube, with the 1st dimension being the H3 cells within the fire’s AOI, the 2nd dimension being the dynamic (burned area variables, ERA5-Land weather statistics, FWI, hotspot statistics), and static (fuel type, CLC, elevation, slope, aspect) variables and the 3rd dimension being the daily timesteps (see Figure 2). Finally, such a datacube was built for each wildfire event in Europe from 2016 to 2022.
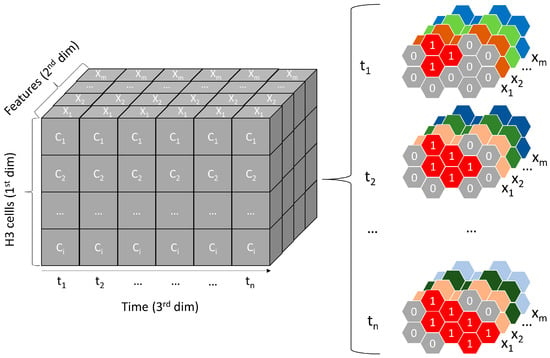
Figure 2.
Datacube representation of a wildfire time series containing all H3 cells (c) (1st dimension), with all static and dynamic features (X) (2nd dimension) over the time steps (t) (3rd dimension). The datacube can also be represented as an ordered sequence of two-dimensional H3 grids over time.
3. Methodology
3.1. Experimental Setup
Based on the comprehensive wildfire time series dataset, we developed a data-driven DL model to predict the next day’s burned area of European wildfires. For this task, a graph-based DL architecture was chosen. STGNNs can solve complex spatiotemporal modeling problems by combining a spatial modeling component (e.g., GCN) with a temporal modeling component (e.g., RNN) to simultaneously learn multidimensional patterns from data [21]. This has resulted in superior results compared to traditional DL architectures in a variety of research fields [36]. In theory, this architecture can be applied to the complex and non-linear wildfire spread process, where multiple fire driver variables interact along different temporal and spatial scales [10,13,55].
Given the prevailing accuracy and transferability limitations of established semi-empirical and empirical wildfire spread models, a data-driven approach using such an STGNN architecture can be expected to yield improved results. To test this assumption, the following experimental setup was chosen.
The first model was developed on a country-scale to test the general applicability of a STGNN architecture for wildfire spread modeling. We selected Portugal as a test region, as it is one of the most fire-prone countries in Europe and experienced substantial wildfire events during the period 2016−2022 [56]. The respective STGNN was trained and tested with the historic wildfire time series from this period. The development of the Portugal model also allowed us to retrieve insights about the model’s predictive capabilities concerning a wildfire’s spatial and temporal dimensions.
Following this, a second STGNN wildfire spread model was developed for the entire Mediterranean region. This model was trained on the historic wildfire time series of various Mediterranean countries with differing environmental conditions and fire regimes. With this, the generalization and transferability of the developed data-driven approach could be assessed.
3.2. Pre-Processing and Reference Data Sampling
We created two separate reference datasets for both a Portugal and Mediterranean study region. The Portugal AOI was defined by the country’s boundary (see Figure S1). The Mediterranean AOI was defined by using the Köppen–Geiger climate zone classes BSk (arid, steppe, cold arid), Csa (temperate, dry summer, hot summer), Csb (temperate, dry summer, warm summer), and Cfa (temperate, no dry season, hot summer) [57], which predominantly cover the fire activity in the Mediterranean [56] (see Figure S2).
To exclude too small and short fire time series, all wildfires that occurred in each AOI between 2016 and 2022 were filtered by size and length. A fire was included in the Portugal or Mediterranean reference dataset if the burned area perimeter at the final stage of burning covered a minimum of ten H3 cells and the fire was active for a minimum of five days. Furthermore, all fires with no or only sporadic growth were excluded from the reference datasets by applying a moving average filter over the time of a wildfire time series. After filtering, the Portugal and Mediterranean reference datasets included 332 and 3020 wildfire time series, respectively.
The STGNN model is trained with equal-length input sequences. To maintain this, all wildfire time series with more than the minimum five days of activity were trimmed to equal-length sequences of five days. To prevent a loss of data while also augmenting the total number of samples in the reference datasets, a rolling window approach using a step size of one day was applied to each time series. Thus, wildfire time series with more than five days of activity were split into multiple artificial time series with an equal length of five days. After this temporal trimming process, the total number of samples in the Portugal and Mediterranean reference datasets increased to 1181 and 11,082, respectively (see Table 2).

Table 2.
Sample distribution in Portugal and Mediterranean reference datasets.
All variables included in the reference datasets are transformed to a range between 0 and 1 using minimum−maximum scaling. Consecutively, all wildfire time series are converted to spatiotemporal graph structures. A spatiotemporal graph is defined as:
where represents a set of nodes (vertices), represents a set of edges between the graph’s nodes, represents the adjacency matrix, which mathematically describes the connections between nodes, and describes a feature matrix containing a feature vector for each node at a timestep . Within the H3 grid system, the conversion of the wildfire time series is straightforward. For each time step in a time series, a graph object is retrieved by using all H3 cells of wildfire AOIs as nodes . Edges and the respective adjacency matrix are delineated by identifying each cell’s six first-order neighboring cells within the H3 grid system (see Figure 3). The graphs are implemented with self-loops for all nodes, ensuring that each node’s features are included in the graph convolution, and undirected edges without weighting, allowing for a bidirectional information flow between nodes. Lastly, the daily graph’s nodes were populated with the feature matrices of the respective days. The variable “burned_new”, representing the daily wildfire spread, is defined as the node’s target variable. This results in a time series of fixed graph structures with dynamically changing node features for each wildfire event in the Portugal and Mediterranean reference datasets.
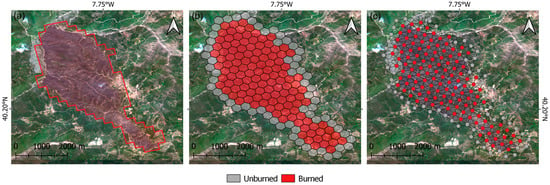
Figure 3.
Different data representations of the burned area of a wildfire in Portugal. Background: Sentinel-2 RGB image from the 07.08.2020. (a) Burned area perimeter derived by the Sentinel-3 mapping algorithm. (b) Burned area perimeter displayed in H3 cells (resolution 9). (c) Burned area perimeter displayed as a graph.
Training, validation, and testing datasets were created from the Portugal and Mediterranean reference datasets using a 70:15:15 split (see Table 2). Sampling for the training, validation, and testing datasets was conducted using stratified random sampling considering the seasonality (summer, winter), year, and location of the wildfire time series.
3.3. Model Architecture and Training
Given the limited research on STGNN architectures for modeling natural hazards, we chose a STGNN from the traffic forecasting domain, where STGNNs proved to be a capable methodology [35]. The process of wildfire propagation and traffic systems indeed have some parallels regarding their spatiotemporal behavior, as they experience similar spatial-growing patterns and non-linear temporal changes [10,35]. For this reason, the well-known Temporal Graph Convolutional Network (TGCN) architecture developed by Zhao et al. [58] was selected to be applied to the wildfire spread modeling problem. The TGCN can model spatiotemporal dependencies using multivariate features and showed strong performances in predicting traffic flows [36]. Figure 4a describes the TGCN architecture schematically. A detailed mathematical description of the architecture can be found in [58]. The TGCN consists of a spatial component that obtains and transforms the node features in a defined neighborhood within the graph using a spectral graph convolution. This is followed by a temporal component, where an RNN receives the outputs of the spatial component to learn the temporal dependencies between the graph’s nodes.
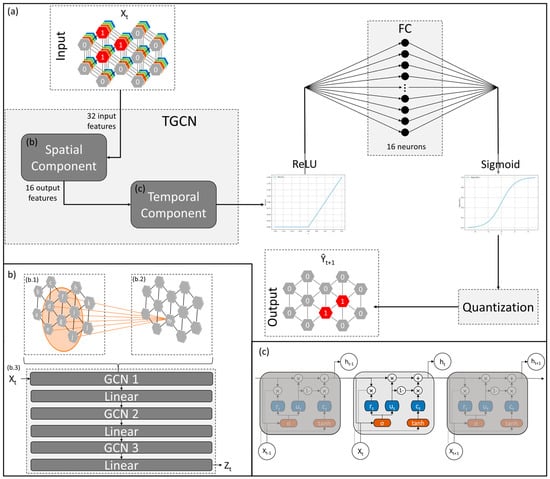
Figure 4.
Schematic display of the STGNN wildfire spread model and its subcomponents. (a) Workflow of the STGNN model. (b) Spatial subcomponent of the TGCN model with a schematic representation of the graph convolution process of the GCN (b.1,b.2) and the GCN layer stacking (b.3). (c) Temporal subcomponent of the TGCN with a schematic representation of the GRU cell.
At first, the TGCN receives a graph structure at the time step Xt as input and passes it to the spatial modeling component (see Figure 4b). This consists of an implementation of the GCN by Kipf and Welling [59] which uses a spectral filter in the Fourier domain on the graph’s nodes to capture spatial features between all nodes in the first-order neighborhood (Figure 4(b.1,b.2)). In the TGCN, a stack of three subsequent GCN layers is used to increase the spatial component’s receptive field up to the third-order neighborhood nodes [58] (see Figure 4(b.3)). This results in a new feature-embedding matrix containing transformed feature vectors for each node.
The temporal component implements a Gated Recurrent Unit (GRU) first introduced by Cho et al. [60] (see Figure 4c). The GRU addresses the vanishing gradient problem of traditional RNNs through gated mechanisms for memorizing past input information. It receives the output feature-embedding matrix of the GCN for a time step , as well a hidden state from the previous time step . An update gate controls how much of the previous hidden state should be retained and how much of the new information from the input should be added to the current hidden state . The reset gate works in tandem with the update gate to control how much of the past information the model should forget when calculating the updated hidden state . The input and the scaled previous hidden state are then used to calculate a candidate hidden state . The final hidden state is then computed from the previous hidden state and the candidate hidden state . The output of the temporal component is transformed by a Rectified Linear Unit (ReLU) activation function and passed to a Fully Connected (FC) layer with 16 neurons which produces the final one-dimensional output for each of the graph’s nodes (Figure 4a). Finally, binary classification results are achieved by scaling each node’s output between 0 and 1 using a Sigmoid function and quantization with a threshold of 0.5.
The model was developed and trained using the Pytorch Geometric Temporal library (v0.54.0) [61]. Hyperparameter tuning was performed for the Portugal and Mediterranean models using a grid search of potential values for learning rate, batch size, and output channels (number of neurons in the FC layer). This resulted in the optimal learning rate (0.00001), batch size (1) and output channel number (16) for both the Portugal and Mediterranean models. Both models were trained for 2500 epochs with an early stopping with a patience of 10 epochs using stochastic gradient descent. Since both the Portugal and Mediterranean datasets were highly imbalanced, a customized binary cross-entropy loss function (weig. BCE) was used to account for this:
where and are the weights for the positive and negative class, is the reference label, and is the predicted sigmoid probability of the positive class that is the output for each node. The weights for the positive and negative class were calculated based on the inverse class frequency, resulting in the weights (unburned) and (burned).
Figure 5 displays the model training workflow schematically. The models perform a binary node classification to predict the newly burned cells for each future day. The dependent targets are the newly burned cells (“burned_new”) of the day , which are predicted using the independent features of the current day . For every epoch, the model iterates over the temporal dimension of a training wildfire time series, receiving the input of the first day and an empty hidden state . Based on the input features of the first day , the STGNN cell then produces a prediction for the next day, labeling all cells that will be affected by the wildfire’s propagation. Furthermore, an updated hidden state is passed onto the next STGNN cell, preserving the temporal information from previous time steps. The daily weighted loss is calculated using the prediction and the reference of the respective day .The mean batch loss is computed after all iterations and used to update the model’s weights.
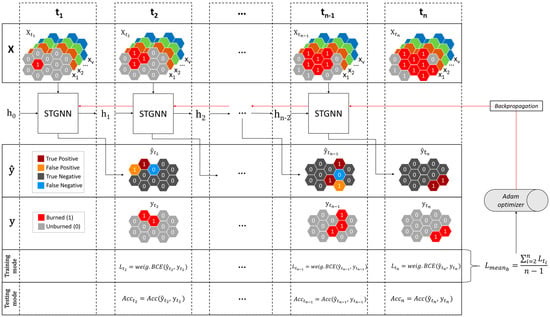
Figure 5.
Model workflow in training and testing mode.
3.4. Model Testing and Evaluation
The respective testing datasets were used to evaluate the performance of the Portugal and Mediterranean models. The developed model framework allowed predictions of the wildfire spread up to days, with being the input length of a wildfire time series (5 days). In testing mode, the model received the first day of a testing wildfire time series and produced subsequent predictions for the next four days (see Figure 5). For each daily prediction, the following accuracy metrics were calculated:
All metrics were set between 0 and 1 and were chosen by their suitability in imbalanced binary classification problems and computed for both the positive and negative predictions using the respective true positive (TP), false positive (FP), and false negative (FN) samples. Because of the spatiotemporal nature of the wildfire spread predictions, a more complex validation framework was needed to assess the true predictive capabilities of the Portugal and Mediterranean models.
On numerous prediction days, edge cases arose without any positive samples, either being caused by excessively overpredicting the wildfire spread (e.g., all cells are predicted positive but the testing cells are all negative) or by perfectly predicting only true negatives (e.g., the model correctly predicted that, on a particular day, no wildfire spread occurs). Both scenarios lead to no data values when computing the accuracy metric precision, recall, and F1-score for the positive class. To obtain a more meaningful accuracy assessment and account for both these edge case scenarios, the macro-average was calculated for each of the accuracy metrics. The macro-average computed the unweighted mean of the positive and negative class accuracy metrics. In the imbalanced reference datasets, the macro-average therefore weighted the underrepresented (positive) class more heavily, which allowed for a more valid evaluation of the daily wildfire spread predictions.
To produce comparable accuracy metrics between the models, the accuracy assessment was conducted on three different levels. At Level-1, the daily prediction accuracy for an individual test wildfire was calculated by the macro-average of all accuracy metrics (precision, recall, F1-score, IoU) (see Table 3). At Level-2, the model performance in predicting the entire time series of an individual wildfire was computed by calculating the fire’s weighted macro-mean accuracy metrics (see Table 3). This referred to the weighted average of the daily macro-mean accuracies from Level-1 over the entire wildfire time series. Since days with substantial wildfire spread were viewed as more important, the daily union of the positive class was used as a weight during the calculation of the Level-2 accuracy metrics (see Table 3). To assess the model performances on the entire testing dataset, the Level-3 overall weighted macro-mean was calculated. This was achieved by computing the average of all Level-2 fire-weighted macro-mean accuracy metrics (see Table 3).

Table 3.
Used evaluation techniques to assess the model performance at different scales.
4. Results
4.1. Overall Model Performance
The Portugal model achieved overall weighted macro mean accuracy metrics (Level-3) of 0.59 (precision), 0.69 (recall), 0.57 (F1-score), and 0.37 (IoU) (see Table 4). Because of its robustness and balanced evaluation between false positive and false negative predictions, the IoU was chosen as the main accuracy metric for evaluating the model performance. The Portugal model trained for the maximum 2500 epochs with a continuous loss decrease (see Figure S3).

Table 4.
Overall model performance of the Portugal and Mediterranean model.
Figure 6 exemplifies the prediction results of the Portugal model for an individual wildfire time series. For this wildfire, the Portugal model achieved an above-average weighted macro-mean IoU (Level-2) of 0.57. Although significant overpredictions in the first two days are visible, the model was able to capture the general behavior of the fire and predicted the rapid increase in the burned area at the start of the time series.
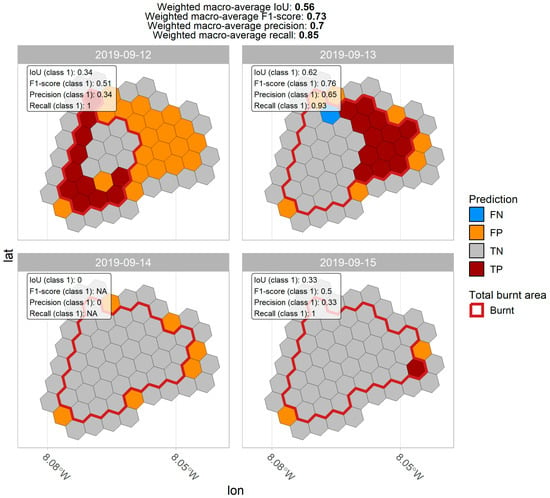
Figure 6.
Wildfire spread prediction of the Portugal model for an example test fire in 2019.
Comparing different fire seasons in Portugal, the model achieved similar median fire-weighted macro-mean accuracies (Level-2) over all fire seasons, ranging from 0.39 to 0.51 (see Figure 7). The fire seasons 2016, 2019, and 2022 showed the lowest accuracies with median fire-weighted macro-mean IoU values below 0.45. The best and most robust results were achieved with wildfires from the 2018 and 2021 fire seasons with median IoU values of 0.49 and 0.51, respectively.
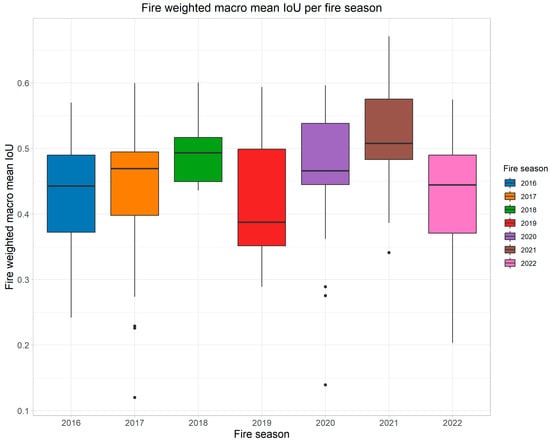
Figure 7.
Overall performance of the Portugal model per fire season.
The training process of the Mediterranean model was interrupted after 1834 epochs due to a stagnation of the loss (see Figure S4). Overall accuracy metrics showed similar but slightly worse accuracies compared to the Portugal model’s results with 0.59 (precision), 0.67 (recall), 0.55 (F1-score), and 0.36 (IoU) (see Table 4). Despite some regional performance differences, the Mediterranean model predicted the spread of wildfires in most fire-active countries with robust accuracies (see Figure 8). The best results were achieved on wildfires in Spain with an overall weighted macro-mean IoU (Level-3) of 0.44, closely followed by the fire-prone countries of Greece (0.43), France (0.39), and Portugal (0.39). Wildfire spread in Italy and Eastern European countries (e.g., Bosnia Herzegovina, Montenegro, Albania, Serbia, Romania, and Moldova) could only be predicted with lower accuracies with IoU values below 0.34. Compared to the overall weighted macro-mean IoU of the Portugal model (0.37), the Mediterranean model could predict Portuguese wildfires with slightly higher accuracies of 0.39.
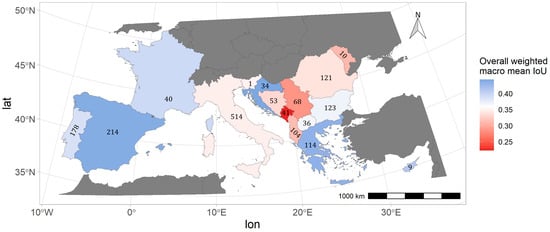
Figure 8.
Overall performance of the Mediterranean model per country. The number in each country refers to the respective number of wildfires in the Mediterranean reference dataset.
Like the Portugal model, the Mediterranean model achieved similar performances for all fire seasons for each country (see Figure 9). No particular fire season showed a significant increase or decrease in the model’s performance. Most wildfires in the fire-prone countries of Spain, France, Greece, Italy, and Portugal could be predicted with an overall weighted macro-mean IoU (Level-3) between 0.4 and 0.6 independent of the fire season.
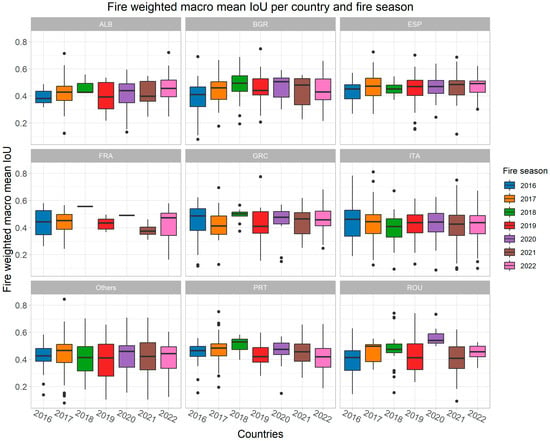
Figure 9.
Overall model performance of the Mediterranean model per country and fire season.
4.2. Model Performances Based on Spatial and Temporal Wildfire Dimensions
The Portugal model showed increasing accuracies up to a daily spread size of approx. 50 H3 cells (approx. 5 km2) (see Figure 10a). After this optimum fire spread size, a significant decrease in IoU values was observed. However, the small total number of extremely large wildfire spread days (>100 H3 cells) prevents any clear statement about the model performance on such wildfire spread events. The same increase, until an optimum daily wildfire spread size of approx. 50 H3 cells, was also visible in the results of the Mediterranean model (see Figure 10b). However, after this optimum size, the Mediterranean model predictions did not show a decrease in the prediction accuracies and stagnated around 0.6. For both the Portugal and Mediterranean results, both models achieved the lowest IoU values on days without any wildfire spread, confirming a significant overprediction bias until an optimum of approx. 50 H3 cells. The same trend was also visible when evaluating the daily Mediterranean model performance on a country level (see Figure S5).
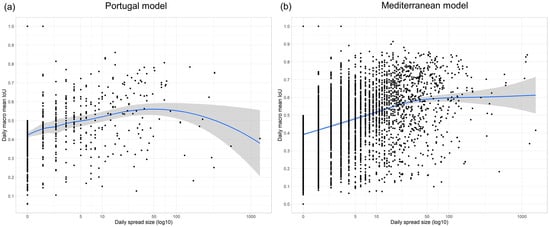
Figure 10.
Model performance per daily wildfire spread size (number of new burned H3 cells). Each predicted wildfire is represented as a point. The blue line represents the trend line with the 95% confidence level interval (grey). (a) Portugal model. (b) Mediterranean model.
Additionally, the Portugal and Mediterranean model predictions of an entire individual wildfire time series (fire-weighted macro-mean IoU, Level-2) were compared to the total burned areas of a wildfire. For both models, no significant trends in performance changes regarding the burned area could be identified (see Figure S6). This suggests that the final burned area of a wildfire does not influence the model’s predictive ability.
The effect of a wildfire’s temporal behavior was assessed by comparing the daily macro mean IoU (Level-1) of the Portugal and Mediterranean models with the subsequent prediction days of a wildfire time series. In Figure 11a, the distribution of the daily macro-mean IoU values for all tested Portuguese wildfires is displayed over the four prediction days. The Portugal model achieved the lowest median IoU values (approx. 0.4) on the first prediction day. After this, the prediction accuracies increasingly improved to approx. 0.45 on the second day, approx. 0.47 on the third day, and approx. 0.48 on the fourth day. The same trend is visible for the Mediterranean model, achieving a similar range of median macro-mean IoU values over the four prediction days (see Figure 11b). Overall, the results indicate that, with an ongoing prediction time series, both models tend to predict the wildfire spread more accurately. This trend is also confirmed when comparing the results of the Mediterranean model in individual European countries (see Figure S7).
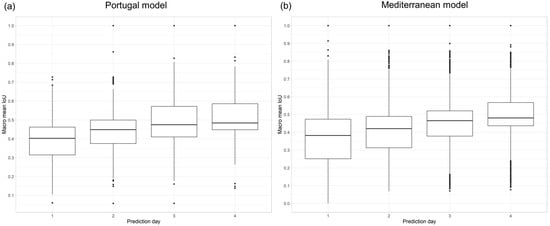
Figure 11.
Model performance per prediction day. (a) Portugal model. (b) Mediterranean model.
5. Discussion
5.1. Performance of the Spatiotemporal Graph Neural Network
Overall, the Portugal and Mediterranean STGNN models did not achieve satisfactory accuracies measured by the precision, recall, F1-score, and IoU (see Table 4). Despite capturing the general spread trend for most test wildfires (e.g., see Figure 6), major inaccuracies in the exact predictions of the wildfire expansion occurred. However, both models could achieve relatively high overall weighted macro-mean recall values (Portugal model: 0.69, Mediterranean model: 0.67) (see Table 4), showing that the models’ abilities to avoid false negative predictions are good. This is crucial, as missed wildfire spread detections can have serious consequences, while false positive predictions can be adjusted without any serious consequences [18]. Both models’ lower overall weighted macro-mean precision values (0.59) (see Table 4) indicate a significant overprediction bias. In comparison to other operationally used wildfire spread models, which often suffer from a serious underprediction bias [62], the overprediction errors of the STGNN are potentially less severe.
The reasons for the low overall accuracies are also partially related to the evaluation method. The implemented weighting technique emphasizes the model’s ability to detect large wildfire spread events, as precise information about such days is crucial for wildfire suppression strategies [11]. However, this weighting procedure also decreases the overall accuracy metrics, as frequently occurring overpredictions are strongly penalized. The temporal accuracy of the predictions is also difficult to assess. For many wildfires, the Portugal and Mediterranean models correctly predicted the newly burned cells with a time lag of one day (e.g., see Figure 6). Although this scenario produces low statistical performance metrics, the predictions can still be useful for wildfire suppression assessments, as the model was able to predict that the correct cells will burn eventually. This behavior is, however, not accounted for in the accuracy assessment. Similar problems were also experienced in the study of Radke et al. [24], underlining that the statistical evaluation of spatiotemporal wildfire spread models is not entirely representative of their usability.
A fair quantitative comparison of the STGNN model results to other wildfire spread models is difficult. Most DL-based studies produce no comparable outputs (e.g., numerical rate of spread predictions [28,29]) or were developed in small study areas and are difficult to transfer to the Mediterranean environment [23,24,25,26,29]. A comparison to other conventional wildfire spread models (e.g., semi-empirical, empirical, or simulation models) is also difficult as these models need highly specialized input data [15,18] which are not available for larger study regions like Portugal or the Mediterranean.
The performance assessment of the Portugal and Mediterranean wildfire spread models should be considered in the broader context of the research field. In general, state-of-the-art wildfire spread models contain significant uncertainties and overall results do not compare to other modeling problems in terms of accuracy. A benchmark of operationally used semi-empirical and empirical wildfire spread models highlighted that, out of all the tested models, only 3% produce exact results with a mean absolute percentage error (MAPE) < 2.5%, with some models reaching a MAPE of up to 310% [62]. A more recent benchmark compared newer conventional modeling approaches to established wildfire spread models, reporting an overall increase in the newer models’ accuracy. However, all models still resulted in a MAPE of >33% in various fuel environments [20]. These benchmarks put this study’s results into context. Although the overall accuracy metrics of the Portugal and Mediterranean models seem low, they are within the expected ranges of this research domain. Comparable studies using DL methods [24,25,31] or semi-empirical and empirical modeling approaches [20,62] achieved similar accuracy measures. This highlights the need for more research on this modeling problem, although Alexander and Cruz [18] remark that the complexity of the wildfire spread process might prevent future models from reaching accuracies as high as in other modeling domains. Despite their accuracy limitations, wildfire spread models are still useful in the operational context providing more of a guideline instead of being used as an absolute decision-making tool [18].
Given this stated complexity and non-linearity of the wildfire spread process [10,13,55], future modeling approaches based on DL techniques might be advantageous. Studies using spatially adapted DL models (e.g., CNNs) [24,25] or time series DL models (e.g., LSTM, GRU) [26,27,28] could outperform standard Machine Learning or simulation models but still did not achieve high overall accuracies. The low overall performances might result from the focus of their models on either the spatial or temporal dimension of a wildfire. Although the developed STGNN model did not outperform all of these studies, the equal influence of the spatial and temporal dimension of a wildfire has a non-negligible effect on the model performance which has been demonstrated in this study and was also mentioned in the study of Burge et al. [30]. Alternatively, compared to spatiotemporal adapted GNNs, Burge et al. [30] showed that using a spatiotemporal ConvRNN can produce promising results with high IoU values > 0.84. However, this performance was only achieved on artificially simulated wildfire data.
Using other STGNN architectures might have resulted in enhanced results in this study. Within the traffic forecasting domain, spatial convolutions achieved superior results over spectral convolutions [35], whereas the latter was implemented in the used TGCN [58]. Also, attention-based GNNs showed improved performances compared to GCN-based methods, but mostly for long-term forecasting problems [35,36]. As this work features the first usage of STGNNs for the application of wildfire spread modeling, no significant statements about performance-enhancing STGNN architectures for this specific modeling problem can be given. Future work should therefore focus on systematic tests to find optimal STGNN components, which could lead to an enhancement of wildfire spread model performances.
5.2. Influence of Dimensions of a Wildfire
The spatial dimensions of the wildfire spread showed an effect on the Portugal and Mediterranean model performances, where the daily macro-mean IoU increased with larger daily wildfire spread sizes up to an optimum of approx. 50 H3 cells (approx. 5 km2) (see Figure 10). Similar results were also reported by Radke et al. [24]. Regarding the expected intensification of the Mediterranean fire regime [6,11], this ability proves suitable for future applications. The reported overprediction bias was especially visible on days without any or with only a small wildfire spread. These results align with other empirical [63] or DL-based [24] wildfire spread models. Analyzing the density distribution of the daily spread sizes reveals that for both the Portugal and Mediterranean reference datasets, days with a spread size of less than five H3 cells are the predominantly occurring situation, while days without any wildfire spread are the most common scenario (see Figure S8). This is explainable by the natural behavior of wildfires, which tend to spread significantly on a small number of days while on the majority of days only small or no spread is observable [63]. Furthermore, the high total number of days with very small or no wildfire spread can also result from missed burned area detections by the S3 burned area monitoring system due to clouds or smoke. The large uncertainties of the Portugal and Mediterranean model on days with small wildfire spread size combined with the high frequency of such days potential explains the overall low accuracy metrics.
The Portugal and Mediterranean models showed a clear performance increase with continued prediction days (see Figure 11) highlighting the temporal influence on the models’ performances. As anticipated, this behavior aligns with the hypothesis that the STGNN model improves its predictive ability throughout a wildfire time series as it receives more input data with each new prediction day. Since technical restrictions in this study only allowed predicting the future four days of a wildfire time series, further work should test if this behavior continues on longer wildfire time series. However, the trend that the model continuously improves its predictive ability over time is counterproductive to the usability of such a model in an operational context, where emergency responders need accurate information about the wildfire’s propagation just after the ignition when containment measures are still the most effective [32].
5.3. Transferability
A significant challenge in operationally used wildfire spread models is the transferability to other environments, as semi-empirical and empirical models are highly dependent on the environment in which they were calibrated [15,18]. The Mediterranean model tried to address this issue by generalizing the wildfire spread over all Mediterranean fire regions. Although the model could only achieve mediocre overall accuracies, model performance between different countries with differing environmental conditions and fire regimes was similar (see Figure 8). The best performances of the Mediterranean model were achieved in Spain, France, and Portugal (see Figure 8 and Figure 9). These countries also experienced the largest average wildfire sizes [56] and the highest fire spread rates [64] over the last decade. These observations align with the model’s ability to predict larger wildfire spread rates more precisely.
The lowest performances were observed in Italy and the Balkan region. One explanation for this is the high number of agricultural fires, which are the most frequent type of wildfire in, e.g., Italy [56]. These prescribed burnings are mostly controlled, small in size, and do not experience large spread rates [65]. For the Mediterranean reference dataset, Italy showed the highest number of wildfires while also having one of the smallest median burned areas over all fire seasons (see Figures S9 and S10). As the Mediterranean model suffers from an overprediction bias on days with small wildfire spread, this might explain the lower overall accuracies in the countries that experienced many but very small fires.
Surprisingly, the Mediterranean model could outperform the Portugal model in predicting the spread of Portuguese wildfires, achieving an overall weighted macro-mean IoU of 0.39 compared to 0.37, respectively. This might be an effect of the larger training dataset available for the Mediterranean model which helped the model to see a larger variety in the data.
Results of the Mediterranean model also showed no significant performance differences comparing different wildfire seasons of Mediterranean countries (see Figure 9) despite large differences in their fire activity and fire sizes (see Figures S9 and S10). A qualitative comparison of different environmental conditions between Mediterranean countries also showed no clear model performance trends. The Mediterranean model performed best in Spain, Greece, and Portugal with overall weighted macro-mean IoU values of 0.44, 0.43 and 0.39, respectively. The similar performance in Spain and Portugal might result from the resemblance in the forest structure and dominant species in central and northern Portugal and the northwestern and northern parts of Spain, where large, homogenous stands of Eucalyptus globulus and other pine species are found [66,67]. However, Greece shows large differences to the environmental characteristics of Portugal or Spain, experiencing much hotter and drier summers while being covered predominantly by sparsely populated forest stands with mixed-in shrubland vegetation [9]. The fact that the model performed similarly well in Greece highlights the promising potential of data-driven methods to overcome the current transferability issues of wildfire spread models by exploiting the generalization abilities of spatiotemporal DL architectures.
It needs to be noted that the exact effects of vegetational or climatic characteristics in different Mediterranean regions on the model performance can not be assessed at country-level. However, this study adapted the national classification of the Copernicus EMS—European Forest Fire Information System (EFFIS) [56] to compare the model performances between Mediterranean countries. Quantitative estimations of the effects of environmental conditions on the performance of a generalized wildfire spread model would require analysis on a much smaller geographic scale, which was beyond the scope of this study.
5.4. Dataset Limitations
Although recent advances in the availability and capability of Earth observation data translated into improvements in newer wildfire spread models [19,20], the quality and availability of reference data are still the main limitations for currently used operational models [18]. High-quality reference data are still notoriously scarce while ground truth on the behavior of wildfires at an adequate spatial and temporal resolution does not exist [16,19]. Therefore, satellite-derived burned area mapping products are the most common source for large-scale wildfire spread reference data [64]. However, these sources do not represent true ground truth data and come with other limitations regarding the spatial and temporal resolution. Due to the lack of reference data, many studies try to evaluate their models using the outputs of operationally used semi-empirical or empirical models as a reference [23,24,31]. While this approach is reasonable given the limited availability of ground truth data, it remains highly questionable, especially when considering the significant uncertainties in all operational products (MAPE > 33%) [20]. For this reason, the results and evaluation of wildfire spread models should always be read carefully and within context.
In this study, we created a historic wildfire time series dataset of European wildfires from satellite-derived burned area perimeters and multiple relevant wildfire driver variables. Comparable datasets exist but do not incorporate all relevant wildfire driver variables or provide burned areas in a lower spatial resolution [25,64]. In contrast to other studies that focused on small study areas with varying environmental conditions (e.g., [24,28]) or relied on experimental or simulated wildfire datasets (e.g., [29,30]), the used reference dataset stands out because it includes the satellite-derived daily burned area of real-world historical wildfires spanning the entire Mediterranean region from 2016 to 2022. Nevertheless, the reference dataset has some limitations that may have affected the performance of the model.
The developed STGNN models are biased towards the S3 mapped burned area perimeters which served as the target variable. Although Nolde et al. [40] showed good agreement of the S3 burned area perimeters with other burned area products, the transferability of the model onto another burned area dataset from a different imaging source is not given and should be tested. Furthermore, the dataset did not contain any information on the type of wildfire. Therefore, it was not possible to differentiate between surface fires, crown fires, or prescribed agricultural burnings, which could have been beneficial to the learning process of the STGNN.
Moreover, noise contained in the burned area time series is probably one of the main reasons for the low statistical accuracies. Time series without a consecutive spread over multiple days are frequent in the burned area dataset. This introduced data gaps which had to be filled artificially to assure equal-length input sequences for the STGNN model. Such data gaps can result from missed burned area detections due to cloud and smoke cover. If consecutive days of cloud or smoke contamination are present in the S3 imagery, then the burned area perimeter of the next cloud-free observation is usually bolstered by the accumulated undetected burned area expansion of the previous cloudy days. This can lead to confusion for a model because the data indicates that a large wildfire spread occurred within one day although it was the product of multiple previous days. Such a problem was also reported by Radke et al. [24], which was solved by only using wildfires with consecutive daily burned areas. To retain a high number of data samples, we use a copying procedure which is encoded in the dataset by the “no_observation” variable (see Table 1). A more sophisticated solution for this problem would be the incorporation of daily cloud coverage information into the dataset. However, days without wildfire spread do not automatically result from missed detections due to cloud contamination of the satellite scene. Wildfires tend to grow in a non-linear manner, which can result in only a few large spread events during the wildfire activity [63]. However, such non-linear wildfire spread events are highly correlated to the prevailing weather conditions and fuel availability [13,63], which are encoded in the reference dataset. Moreover, the relatively high recall values (Portugal model 0.69, Mediterranean model 0.67) and the increasing predictive accuracy with larger daily wildfire spread sizes (see Figure 10) suggest that the model adequately accounts for this behavior.
Some wildfires within the reference dataset contain noise in the form of multiple independent burning cells, resulting in the heterogeneous growth of the burned area over time. Figure S11 displays an example fire where, on the second day of the time series, an independent burned area occurs that is not connected to the burned area perimeter of the previous day. This can result from spotting, where burned residuals can be transported by wind or flames and ignite a new fire ahead of the current flaming front [13]. Spotting fires are very difficult to model [16] and frequently lead to underprediction errors within wildfire spread models [18]. Another reason for the heterogenous burned area could result from near-simultaneous ignitions at different locations due to anthropogenic activity (e.g., arson). It is also possible that the two individual burned area perimeters are part of a larger, homogenous burned area perimeter which is partially covered by clouds and smoke and therefore cannot be correctly derived by the S3 mapping processer. Such cases, although occurring infrequently within the dataset, are not accounted for during the modeling process and potentially lead to confusion in the predictions.
The spatial resolution of the STGNN model is defined by the H3 cell resolution 9 (approx. 350 m cell diameter), which was selected since it matched the spatial resolution of the burned area perimeters derived by S3. This can suppress small-scale variations in the landscape variables. For instance, the cell aggregation of the CLC classes is performed using the most frequent class within each H3 cell. This leads to the suppression of underrepresented LULC classes that may influence the wildfire spread, e.g., streets or rivers that can act as fire barriers [32,52]. To include these features while maintaining the selected cell resolution, proxy variables, like street density per cell, can be included. The street density also shows a suppressing influence on the total burned area of wildfires [46], which highlights the importance of such small-scale features for wildfire behavior. The weather variables (e.g., temperature, relative humidity, precipitation) and FWI should not be affected by the H3 cell resolution, since weather phenomena usually occur on larger geographic scales. However, local wind systems or orographic channeling can influence wildfire behavior [13], an aspect which is not accounted for in the wildfire time series dataset.
Additional variables containing information about fuel characteristics can enhance the modeling performance. In this study, only a cell’s predominant fuel class from an existing fuel classification product [51] is included in the reference dataset. Fuel characteristic variables like canopy bulk density, canopy cover, or crown height have been successfully used for modeling wildfire spread [30]. Furthermore, many studies also include spectral indices derived from Earth observation data, e.g., NDVI or Normalized Burn Ratio (NBR), in wildfire spread models [24,25].
6. Conclusions
This study developed a data-driven, Deep Learning (DL)-based wildfire spread modeling approach by using a Spatiotemporal Graph Neural Network (STGNN) trained on a comprehensive wildfire time series dataset of European wildfires from 2016 to 2022. In a research field where current operational models contain large uncertainties and the usage of data-driven methods is only slowly being adopted, the proposed methodology provides a novel approach to account for the spatiotemporal nature of the wildfire spread process.
Overall, the models for Portugal and the Mediterranean region were only able to model the next day’s wildfire spread with mediocre accuracy. While being able to predict the general trend of wildfire expansions, the models suffered from significant overprediction bias, especially on days with smaller or no wildfire spread. A fair quantitative comparison to other studies could not be made due to differences in modeling outputs and the adaptation of other models to a specific region or dataset. However, based on a qualitative comparison, the achieved accuracies were in line with other DL-based modeling approaches and are within the expected ranges of this modeling domain, where large uncertainties still prevail in the state-of-the-art wildfire spread models. This highlighted the need for more research to understand the complex wildfire spread process and find solutions to translate this knowledge into advanced models.
This study demonstrated that both the spatial and temporal dimensions of wildfire spread can have a strong influence on a model’s predictive capability. Results showed that the STGNN was able to predict larger wildfire spread up to an optimum spread size of 50 H3 cells (approx. 5 km2) with increasing accuracy. Regarding the expected increase in wildfire size and intensity in the Mediterranean, the ability to accurately predict larger wildfire spread is beneficial. Furthermore, this study showed that the temporal evolution of a wildfire had a positive effect on the model performance. However, more research is needed to find alternative modeling frameworks that can predict the wildfire spread with high accuracies at the start of a wildfire time series, as this would provide crucial information for effective wildfire suppression measurements.
While not intended to replace established and operationally used wildfire spread models, this study addressed their prevailing transferability issues by developing a continental-scale, data-driven modeling approach. Since the STGNN model could achieve similar performances in various fire-prone Mediterranean countries, this showed that a data-driven modeling approach might produce more robust results when applied to varying environmental conditions. This helped form a promising methodology for developing more comprehensive and transferable wildfire spread models. However, more research is needed to assess the effects of local-scale environmental conditions on the performance of such generalized wildfire spread models.
The availability and quality of reference data seem to be the most limiting factors for the application of data-driven wildfire spread models. For this modeling problem, basically no ground truth data are available, while large-scale reference datasets, mostly derived from Earth observation data, come with many quality deficits regarding the spatial and temporal resolution. The developed historic wildfire time series reference dataset has proven to be a comprehensive dataset for modeling the behavior of wildfires on a daily and continental scale. However, inaccuracies in the satellite-based burned area perimeters or spatial data aggregations introduce noise into the dataset, which is probably the main reason for the insufficient overall accuracies of the developed STGNN models. Supported by these findings, future research must therefore focus on further improving the availability and quality of wildfire-related data products to provide a solid foundation for modeling wildfire spread based on promising data-driven methodologies that could potentially overcome the prevailing accuracy and transferability problems of established wildfire spread models.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fire7060207/s1.
Author Contributions
Conceptualization, M.R. and M.N.; methodology, M.R. and M.N.; software, M.R.; validation, M.R.; formal analysis, M.R.; investigation, M.R.; data curation, M.R.; writing—original draft preparation, M.R.; writing—review and editing, M.N., T.R. and T.U.; visualization, M.R.; supervision, M.N., T.R. and T.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All data generated in this study is available upon request from the corresponding author. The Sentinel-3 burned area perimeters can be accessed and visualized at https://services.zki.dlr.de/fire (accessed on 12 June 2024). The ERA5-Land and FWI datasets can be accessed and downloaded from the Copernicus Climate Data Store (ERA5-Land: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land (accessed on 12 June 2024); FWI: https://cds.climate.copernicus.eu/cdsapp#!/dataset/cems-fire-historical-v1 (accessed on 12 June 2024)). Hotspot data is available through FIRMS (https://firms.modaps.eosdis.nasa.gov/active_fire/ (accessed on 12 June 2024)). The global fuel classification can be downloaded from the respective publication (https://doi.org/10.5194/bg-13-2061-2016 (accessed on 12 June 2024)). CLC is available for download from the CLMS (https://land.copernicus.eu/en/products/corine-land-cover/clc2018 (accessed on 12 June 2024)). The Copernicus DEM is provided by ESA (https://spacedata.copernicus.eu/de/collections/copernicus-digital-elevation-model (accessed on 12 June 2024)).
Acknowledgments
We kindly thank Florian Fichtner and Marc Wieland for their advice during the development of the reference dataset and model.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bowman, D.M.J.S.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; D’Antonio, C.M.; DeFries, R.S.; Doyle, J.C.; Harrison, S.P.; et al. Fire in the Earth System. Science 2009, 324, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Lam, S.S.; Waugh, C.; Peng, W.; Sonne, C. Wildfire Puts Koalas at Risk of Extinction. Science 2020, 367, 750. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Guan, D.; Zhu, S.; Kinnon, M.M.; Geng, G.; Zhang, Q.; Zheng, H.; Lei, T.; Shao, S.; Gong, P.; et al. Economic Footprint of California Wildfires in 2018. Nat. Sustain. 2021, 4, 252–260. [Google Scholar] [CrossRef]
- Haque, M.K.; Azad, M.A.K.; Hossain, M.Y.; Ahmed, T.; Uddin, M.; Hossain, M.M. Wildfire in Australia during 2019-2020, Its Impact on Health, Biodiversity and Environment with Some Proposals for Risk Management: A Review. J. Environ. Prot. 2021, 12, 391–414. [Google Scholar] [CrossRef]
- Haynes, K.; Short, K.; Xanthopoulos, G.; Viegas, D.; Ribeiro, L.M.; Blanchi, R. Wildfires and WUI Fire Fatalities. In Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires; Manzello, S.L., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 1–16. [Google Scholar]
- Jones, M.W.; Abatzoglou, J.T.; Veraverbeke, S.; Andela, N.; Lasslop, G.; Forkel, M.; Smith, A.J.P.; Burton, C.; Betts, R.A.; Werf, G.R.v.d.; et al. Global and Regional Trends and Drivers of Fire Under Climate Change. Rev. Geophys. 2022, 60, e2020RG000726. [Google Scholar] [CrossRef]
- Ruffault, J.; Curt, T.; Moron, V.; Trigo, R.M.; Mouillot, F.; Koutsias, N.; Pimont, F.; Martin-StPaul, N.; Barbero, R.; Dupuy, J.L.; et al. Increased Likelihood of Heat-Induced Large Wildfires in the Mediterranean Basin. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Turco, M.; Llasat, M.C.; von Hardenberg, J.; Provenzale, A. Climate Change Impacts on Wildfires in a Mediterranean Environment. Clim. Chang. 2014, 125, 369–380. [Google Scholar] [CrossRef]
- Fernandez-Anez, N.; Krasovskiy, A.; Müller, M.; Vacik, H.; Baetens, J.; Hukić, E.; Solomun, M.K.; Atanassova, I.; Glushkova, M.; Bogunović, I.; et al. Current Wildland Fire Patterns and Challenges in Europe: A Synthesis of National Perspectives. Air Soil Water Res. 2021, 14, 11786221211028185. [Google Scholar] [CrossRef]
- Perry, G.L.W. Current Approaches to Modelling the Spread of Wildland Fire: A Review. Prog. Phys. Geogr. Earth Environ. 1998, 22, 222–245. [Google Scholar] [CrossRef]
- Cardil, A.; Monedero, S.; Schag, G.; de-Miguel, S.; Tapia, M.; Stoof, C.R.; Silva, C.A.; Mohan, M.; Cardil, A.; Ramirez, J. Fire Behavior Modeling for Operational Decision-Making. Curr. Opin. Environ. Sci. Health 2021, 23, 100291. [Google Scholar] [CrossRef]
- Sullivan, A.L. Inside the Inferno: Fundamental Processes of Wildland Fire Behaviour: Part 1: Combustion Chemistry and Heat Release. Curr. For. Rep. 2017, 3, 132–149. [Google Scholar] [CrossRef]
- Sullivan, A.L. Inside the Inferno: Fundamental Processes of Wildland Fire Behaviour: Part 2: Heat Transfer and Interactions. Curr. For. Rep. 2017, 3, 150–171. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 1: Physical and Quasi-Physical Models. Int. J. Wildland Fire 2009, 18, 349. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 2: Empirical and Quasi-Empirical Models. Int. J. Wildland Fire 2009, 18, 369. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland Surface Fire Spread Modelling, 1990–2007. 3: Simulation and Mathematical Analogue Models. Int. J. Wildland Fire 2009, 18, 387. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Res. Pap. INT-115; U.S. Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972.
- Alexander, M.E.; Cruz, M.G. Limitations on the Accuracy of Model Predictions of Wildland Fire Behaviour: A State-of-the-Knowledge Overview. For. Chron. 2013, 89, 370–381. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A Review of Machine Learning Applications in Wildfire Science and Management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Sullivan, A.L.; Gould, J.S.; Kilinc, M. Assessing Improvements in Models Used to Operationally Predict Wildland Fire Rate of Spread. Environ. Model. Softw. 2018, 105, 54–63. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Qiao, Y.; Jiang, W.; Su, G.; Jiang, J.; Li, X.; Wang, F. A Transformer-Based Neural Network for Ignition Location Prediction from the Final Wildfire Perimeter. Environ. Model. Softw. 2024, 172, 105915. [Google Scholar] [CrossRef]
- Hodges, J.L.; Lattimer, B.Y. Wildland Fire Spread Modeling Using Convolutional Neural Networks. Fire Technol. 2019, 55, 2115–2142. [Google Scholar] [CrossRef]
- Radke, D.; Hessler, A.; Ellsworth, D. FireCast: Leveraging Deep Learning to Predict Wildfire Spread. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, Macao, 10–16 August 2019; pp. 4575–4581. [Google Scholar]
- Huot, F.; Hu, R.L.; Goyal, N.; Sankar, T.; Ihme, M.; Chen, Y.F. Next Day Wildfire Spread: A Machine Learning Dataset to Predict Wildfire Spreading from Remote-Sensing Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4412513. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, M.; Wang, H. A Neural Network Model for Wildfire Scale Prediction Using Meteorological Factors. IEEE Access 2019, 7, 176746–176755. [Google Scholar] [CrossRef]
- Perumal, R.; Zyl, T.L.V. Comparison of Recurrent Neural Network Architectures for Wildfire Spread Modelling. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020. [Google Scholar]
- Li, X.; Zhang, M.; Zhang, S.; Liu, J.; Sun, S.; Hu, T.; Sun, L. Simulating Forest Fire Spread with Cellular Automation Driven by a LSTM Based Speed Model. Fire 2022, 5, 13. [Google Scholar] [CrossRef]
- Li, Z.; Huang, Y.; Li, X.; Xu, L. Wildland Fire Burned Areas Prediction Using Long Short-Term Memory Neural Network with Attention Mechanism. Fire Technol. 2021, 57, 1–23. [Google Scholar] [CrossRef]
- Burge, J.; Bonanni, M.R.; Hu, R.L.; Ihme, M. Recurrent Convolutional Deep Neural Networks for Modeling Time-Resolved Wildfire Spread Behavior. Fire Technol. 2023, 59, 3327–3354. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, F.; Su, G.; Li, X.; Wang, G.; Zheng, X.; Wang, T.; Meng, Q. Modeling Wildfire Spread with an Irregular Graph Network. Fire 2022, 5, 185. [Google Scholar] [CrossRef]
- Yemshanov, D.; Liu, N.; Thompson, D.K.; Parisien, M.A.; Barber, Q.E.; Koch, F.H.; Reimer, J. Detecting Critical Nodes in Forest Landscape Networks to Reduce Wildfire Spread. PLoS ONE 2021, 16, e0258060. [Google Scholar] [CrossRef]
- Ge, X.; Yang, Y.; Peng, L.; Chen, L.; Li, W.; Zhang, W.; Chen, J. Spatio-Temporal Knowledge Graph Based Forest Fire Prediction with Multi Source Heterogeneous Data. Remote Sens. 2022, 14, 3496. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y.; Peng, L.; Chen, L.; Ge, X. Knowledge Graph Representation Learning-Based Forest Fire Prediction. Remote Sens. 2022, 14, 4391. [Google Scholar] [CrossRef]
- Bui, K.H.N.; Cho, J.; Yi, H. Spatial-Temporal Graph Neural Network for Traffic Forecasting: An Overview and Open Research Issues. Appl. Intell. 2022, 52, 2763–2774. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Y.; Dou, X.; Wang, X.; Guo, M.; Zhang, R.; Li, H. Advances in Spatiotemporal Graph Neural Network Prediction Research. Int. J. Digit. Earth 2023, 16, 2034–2066. [Google Scholar] [CrossRef]
- Farahmand, H.; Xu, Y.; Mostafavi, A. A Spatial–Temporal Graph Deep Learning Model for Urban Flood Nowcasting Leveraging Heterogeneous Community Features. Sci. Rep. 2023, 13, 6768. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Xiang, J.; Huang, S. Classification and Prediction of Typhoon Levels by Satellite Cloud Pictures through GC–LSTM Deep Learning Model. Sensors 2020, 20, 5132. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Reichard-Flynn, W.; Zhang, M.; Hirn, M.; Lin, Y. Spatiotemporal Graph Convolutional Networks for Earthquake Source Characterization. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024401. [Google Scholar] [CrossRef] [PubMed]
- Nolde, M.; Plank, S.; Riedlinger, T. An Adaptive and Extensible System for Satellite-Based, Large Scale Burnt Area Monitoring in Near-Real Time. Remote Sens. 2020, 12, 2162. [Google Scholar] [CrossRef]
- Brodsky and Contributors H3—Hexagonal Hierarchical Geospatial Indexing System 2018. Available online: https://h3geo.org/ (accessed on 12 June 2024).
- Sahr, K. Hexagonal Discrete Global Grid Systems for Geospatial Computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Hernández Encinas, L.; Hoya White, S.; Martín del Rey, A.; Rodríguez Sánchez, G. Modelling Forest Fire Spread Using Hexagonal Cellular Automata. Appl. Math. Model. 2007, 31, 1213–1227. [Google Scholar] [CrossRef]
- Flannigan, M.; Stocks, B.; Weber, M. Fire Regimes and Climatic Change in Canadian Forests. In Fire and Climatic Change in Temperate Ecosystems of the Western Americas; Veblen, T.T., Baker, W.L., Montenegro, G., Swetnam, T.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 160, pp. 97–119. [Google Scholar]
- Hernandez, C.; Drobinski, P.; Turquety, S.; Dupuy, J.L. Size of Wildfires in the Euro-Mediterranean Region: Observations and Theoretical Analysis. Nat. Hazards Earth Syst. Sci. 2015, 15, 1331–1341. [Google Scholar] [CrossRef]
- Aldersley, A.; Murray, S.J.; Cornell, S.E. Global and Regional Analysis of Climate and Human Drivers of Wildfire. Sci. Total Environ. 2011, 409, 3472–3481. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A State-of-the-Art Global Reanalysis Dataset for Land Applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Vitolo, C.; Giuseppe, F.D.; Barnard, C.; Coughlan, R.; San-Miguel-Ayanz, J.; Libertá, G.; Krzeminski, B. ERA5-Based Global Meteorological Wildfire Danger Maps. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Stocks, B.J.; Lawson, B.D.; Alexander, M.E.; Wagner, C.E.V.; McAlpine, R.S.; Lynham, T.J.; Dubé, D.E. The Canadian Forest Fire Danger Rating System: An Overview. For. Chron. 1989, 65, 450–457. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m Active Fire Detection Data Product: Algorithm Description and Initial Assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Pettinari, M.L.; Chuvieco, E. Generation of a Global Fuel Data Set Using the Fuel Characteristic Classification System. Biogeosciences 2016, 13, 2061–2076. [Google Scholar] [CrossRef]
- Moreira, F.; Viedma, O.; Arianoutsou, M.; Curt, T.; Koutsias, N.; Rigolot, E.; Barbati, A.; Corona, P.; Vaz, P.; Xanthopoulos, G.; et al. Landscape—Wildfire Interactions in Southern Europe: Implications for Landscape Management. J. Environ. Manag. 2011, 92, 2389–2402. [Google Scholar] [CrossRef] [PubMed]
- European Environmental Agency (EEA) CORINE Land Cover (CLC) 2018. Available online: https://land.copernicus.eu/en/products/corine-land-cover/clc2018 (accessed on 12 June 2024). [CrossRef]
- European Space Agency (ESA) Copernicus DEM—Global and European Digital Elevation Model (COP-DEM) 2023. Available online: https://spacedata.copernicus.eu/collections/copernicus-digital-elevation-model (accessed on 12 June 2024). [CrossRef]
- Cruz, M.G.; Alexander, M.E. Modelling the Rate of Fire Spread and Uncertainty Associated with the Onset and Propagation of Crown Fires in Conifer Forest Stands. Int. J. Wildland Fire 2017, 26, 413–426. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Maianti, P.; Liberta, G.; Jacome Felix Oom, D.; Branco, A.; De Rigo, D.; Suarez-Moreno, M.; Ferrari, D.; et al. Forest Fires in Europe, Middle East and North Africa 2022; EU Publications: Luxembourg, 2023. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks 2017. Preprint. arXiv 2017, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Cho, K.; Merriënboer, B.V.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the EMNLP 2014—2014 Conference on Empirical Methods in Natural Language Processing, Proceedings of the Conference, Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Rozemberczki, B.; Scherer, P.; He, Y.; Panagopoulos, G.; Riedel, A.; Astefanoaei, M.; Kiss, O.; Beres, F.; López, G.; Collignon, N.; et al. PyTorch Geometric Temporal: Spatiotemporal Signal Processing with Neural Machine Learning Models. In Proceedings of the International Conference on Information and Knowledge Management, Proceedings, Online, 1–5 November 2021; pp. 4564–4573. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Uncertainty Associated with Model Predictions of Surface and Crown Fire Rates of Spread. Environ. Model. Softw. 2013, 47, 16–28. [Google Scholar] [CrossRef]
- Podur, J.; Wotton, B.M. Defining Fire Spread Event Days for Fire-Growth Modelling. Int. J. Wildland Fire 2011, 20, 497–507. [Google Scholar] [CrossRef]
- Artés, T.; Oom, D.; Rigo, D.d.; Durrant, T.H.; Maianti, P.; Libertà, G.; San-Miguel-Ayanz, J. A Global Wildfire Dataset for the Analysis of Fire Regimes and Fire Behaviour. Sci. Data 2019, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xanthopoulos, G.; Caballero, D.; Galante, M.; Alexandrian, D.; Rigolot, E.; Marzano, R. Forest Fuels Management in Europe. In Proceedings of the Fuels Management—How to Measure Success: Conference Proceedings, Portland, OR, USA, 28–30 March 2006. [Google Scholar]
- Mateus, P.; Fernandes, P.M. Forest Fires in Portugal: Dynamics, Causes and Policies. In Forest Context and Policies in Portugal: Present and Future Challenges; Reboredo, F., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 97–115. [Google Scholar]
- Rodrigues, M.; Jiménez-Ruano, A.; Riva, J. de la Fire Regime Dynamics in Mainland Spain. Part 1: Drivers of Change. Sci. Total Environ. 2020, 721, 135841. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).