Investigation of the Coupling Schemes between the Discrete and the Continuous Phase in the Numerical Simulation of a 60 kWth Swirling Pulverised Solid Fuel Flame under Oxyfuel Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Studies
2.2. Numerical Approach
2.2.1. Gas Phase Modelling
2.2.2. Particle Phase Modelling
Particle Dynamics
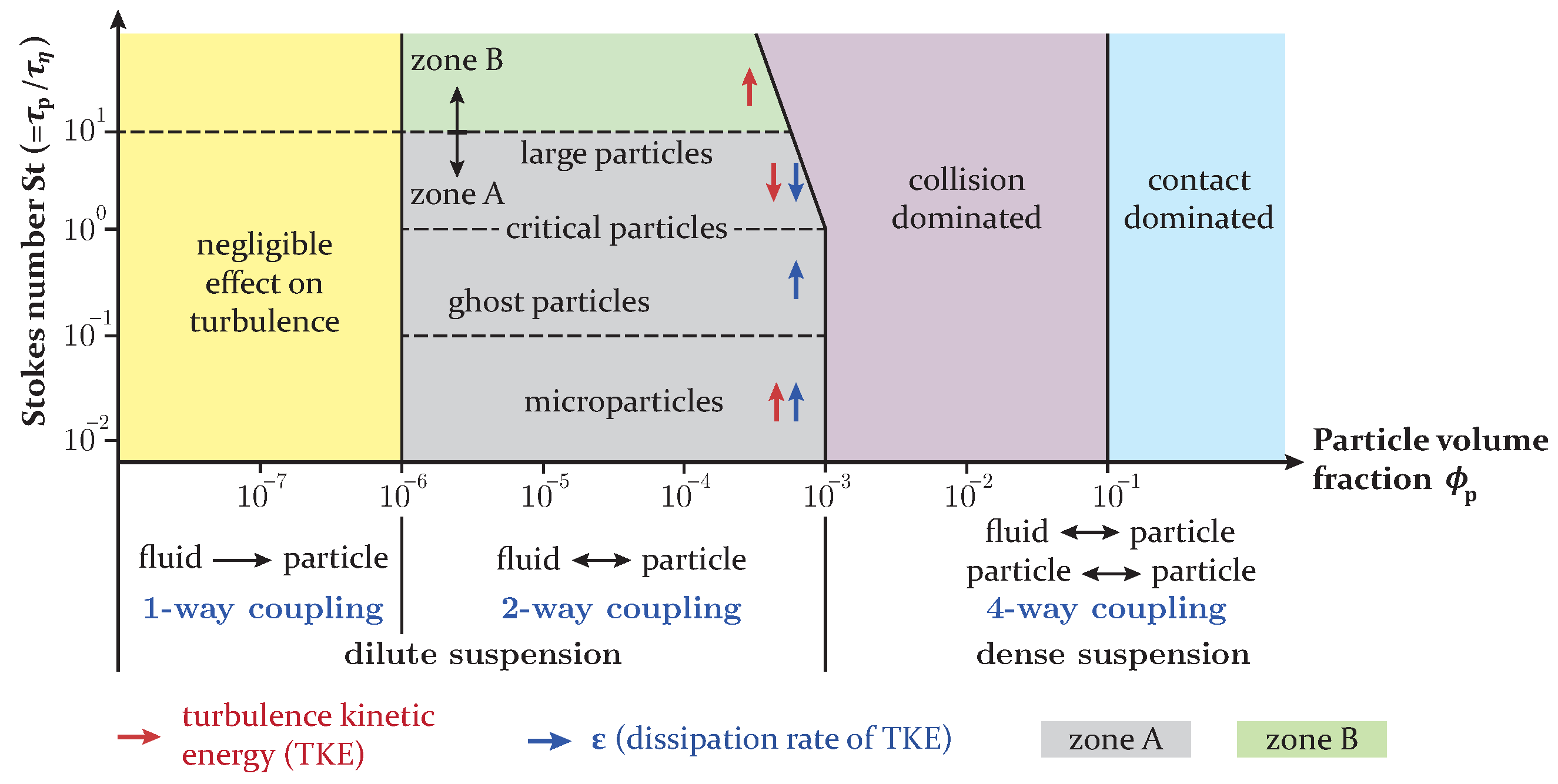
Turbulence Modulation by Particles
Particle Heat Transfer
Particle Reaction Kinetics
Particle Devolatilisation
Char Conversion
2.2.3. Radiation Modelling
2.2.4. Developed Numerical Solver
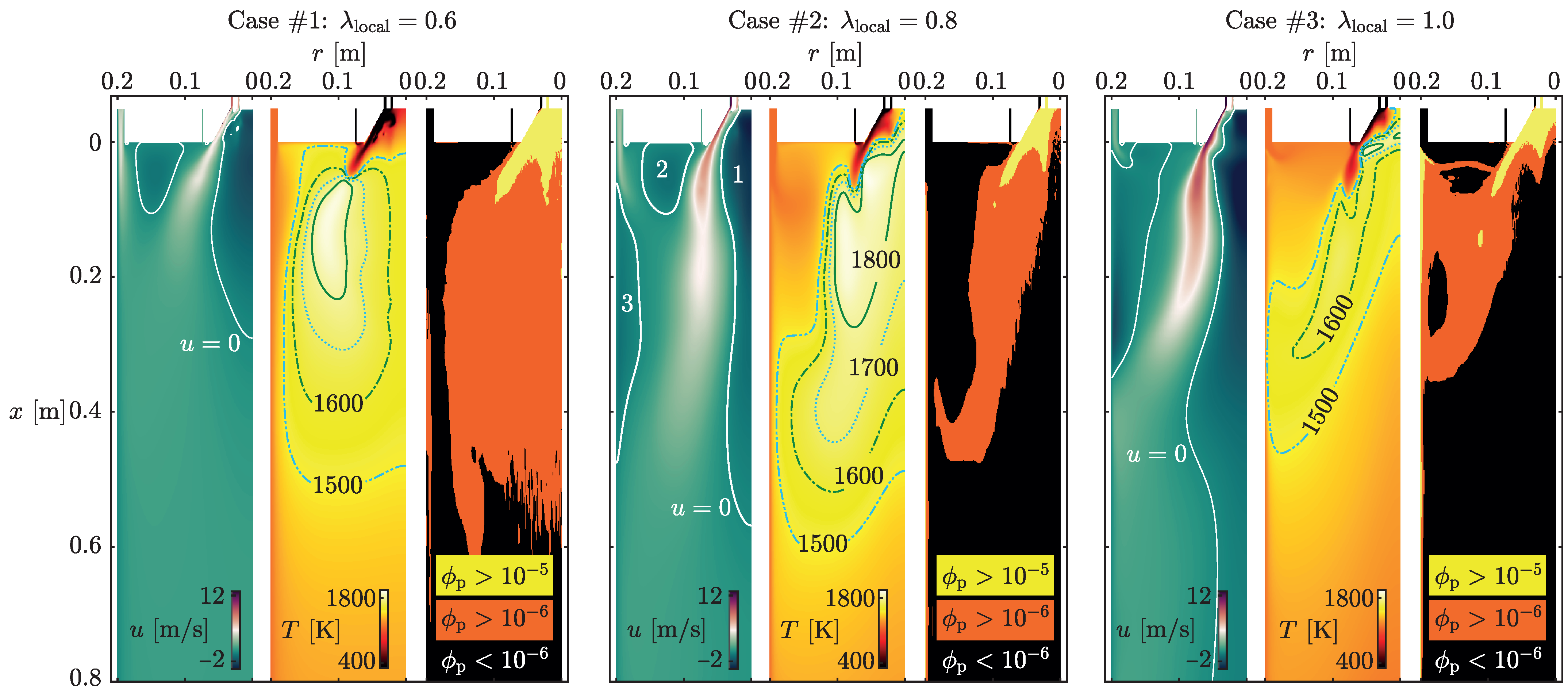
3. Results
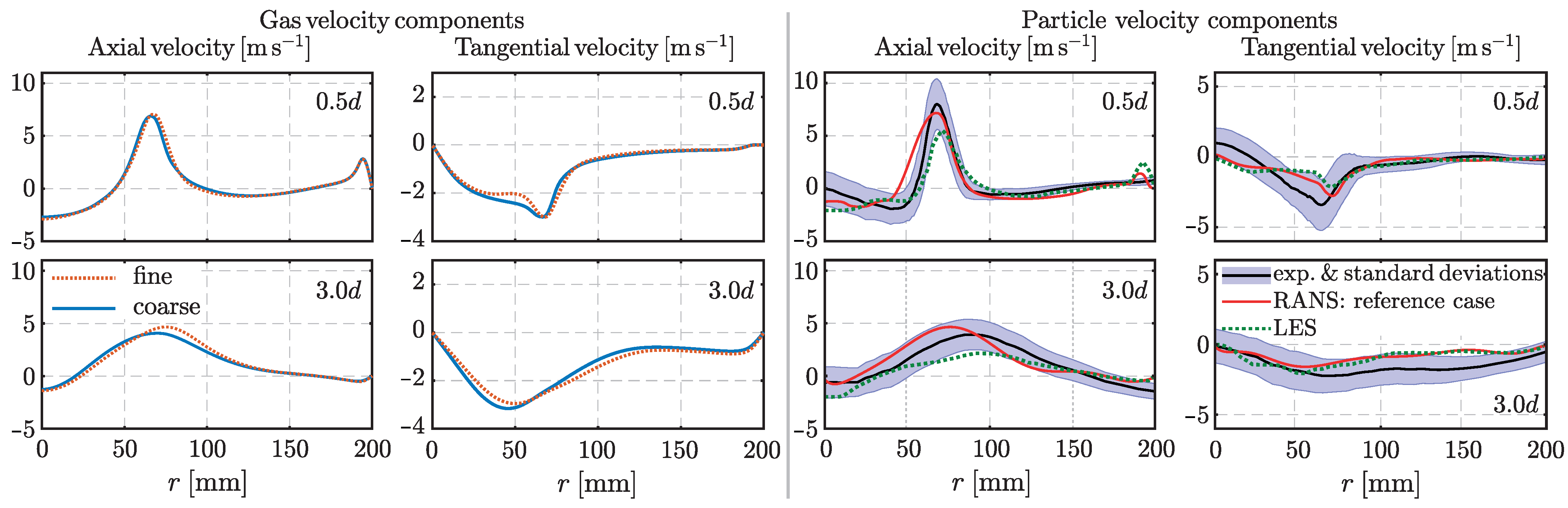
3.1. Verification and Validation
3.2. Solution of the Case Studies
3.2.1. Case #1,
3.2.2. Case #2,
3.2.3. Case #3,
4. Discussion
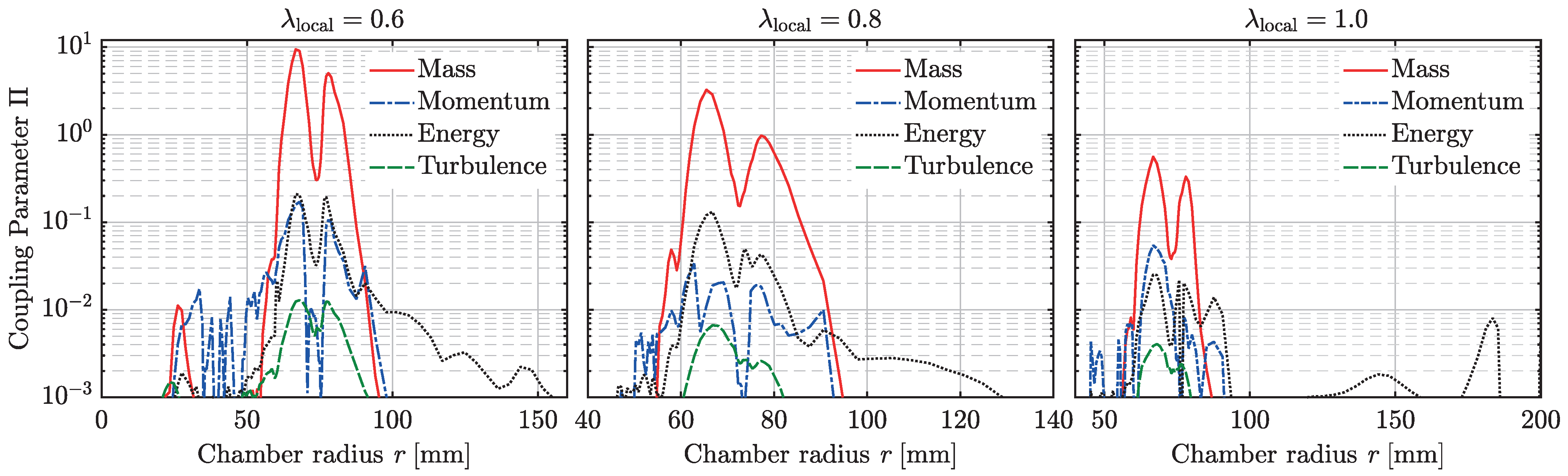
4.1. Coupling Parameters
- Mass Coupling
- Momentum Coupling
- Energy Coupling
- Turbulence Coupling
4.2. Evaluation of the Coupling Parameters
4.3. One-Way versus Two-Way Coupling
- The influence of the one-way coupling scheme for momentum on the results is hardly recognisable both for the near-burner (d) and the downstream (d) regions, comparing the red dashed line with the green solid line. This is due to the small differences between particle and gas velocities.
- The influence of the one-way coupling for turbulence on the results obtained for the downstream region (d) is negligible, comparing the black dotted line with the red dashed line. One of the reasons is the higher viscosity of the hot flue gas in the downstream region compared to the viscosity of the gas in the near-burner region.
- Neglecting the two-way coupling approach for turbulence results in small deviations between the scenarios in the near-burner region due to the high particle volume fraction. These deviations are negligible for the axial and tangential velocity components, but slightly larger for temperature and turbulence kinetic energy (TKE). This is due to the differences in the calculated effective viscosity and thermal conductivity, which directly influence the velocity and temperature of the gas phase.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNS | Direct numerical simulation; |
| EDC | Eddy dissipation concept; |
| HHV | Higher heating value; |
| LES | Large-eddy simulation; |
| OXY25 | 60 kWth Oxyfuel flame (oxidiser composition of a ratio of 25/75 vol% of O2/CO2); |
| PVF | Particle volume fraction; |
| RANS | Reynolds-averaged Navier–Stokes; |
| RBK | Rhenish lignite (Rheinische Braunkohle); |
| RHS | Right-hand side; |
| RNG | Renormalisation group; |
| RTE | Radiative transfer equation; |
| RZ | Recirculation zone; |
| SFOR | Single first-order reaction; |
| TKE | Turbulence kinetic energy; |
| UDF | User-defined function; |
| WSGGM | Weighted-sum-of-gray-gases model. |
Nomenclature
| Pre-exponetial factor [J m−1 K−1] | Boussinesq approximation [kg m−1 s−2] | ||
| A | Surface area [m2] | Viscous dissipation rate [m2 s−3] | |
| Amplitude ratio [-] | Emissivity [-] | ||
| c | Specific heat capacity [s−1] | Radiation temperature [K] | |
| C | Drag coefficient [-] | Phase lag angle between fluid | |
| d | Diameter [m] | Radiation temperature [K] | |
| D | Effective diffusion rate [s m−1] | Phase lag angle between fluid and particle flactuations [Rad] | |
| E | Total enthalpy [m2 s−2] | ||
| External body forces [N] | Wavenumber in Equation (7) [m−1], and Absorption coefficient in Equation (12) [m−1] | ||
| f | Scattering factor [-], and is the fraction of heat absorbed by particles [-] | Oxygen ratio [-] | |
| Gravitational acceleration [m s−2] | Dynamic viscosity [kg m−1 s−1] | ||
| Turbulence generation [W m−3] | Kinematic viscosity [m2 s−1] | ||
| G | Incident radiation over all solid angles [W] | Density [kg m−3] | |
| h | Sensible enthalpy [m2 s−2] | Density ratio (particle to fluid) [-] | |
| H | Reaction enthalpy [m2 s−2] | Scattering coefficient in Equation (12) [m−1], and Stefan–Boltzmann constant in Equations (8) and (12) [W m−2 K−4] | |
| Identity matrix [-] | |||
| I | Radiation intensity [W m−2] | ||
| Diffusion flux [kg m−2 s−1] | Relaxation time/time scale [s] | ||
| k | Thermal conductivity Equation (3) [W m−1 K−1] Turbulent kinetic energy Equation (4) [m2 s−2] | Stress tensor [Pa] | |
| Volume fraction [-] | |||
| Arrhenius kinetic rate [s−1] | Phase function [-] | ||
| m | Mass [kg] | Solid angle [Steradian] | |
| M | Molar mass [kg mol−1] | ||
| n | Refractive index [-] | Subscripts | |
| Total number of particles | Constants in Equation (5) | ||
| p | Pressure [Pa] | a | Activation energy |
| P | Fraction of TKE associated with the wavenumber [-] | c | Continuous phase |
| d | Discrete | ||
| Position vector [m] | D | Drag | |
| R | Universal gas constant Equation (11) [J mol−1] Net rate of species production in Equation (6) [kg s−1 m−3] | eff | Effective |
| g | Gas | ||
| h | Heat source | ||
| Ratio of the fluctuating relative velocity to that of the continuous phase [-] | h | Heat absorbed by particles in Equation (8) | |
| i, j | Counter | ||
| Direction vector [m] | k | Turbulent kinetic energy | |
| S | Source term | Wavenumber Equation (7) | |
| Time-averaged rate of deformation tensor [s−1] | m | Mass source | |
| p | Pressure | ||
| m | Mass | s | Direction, Equation (8) |
| p | Particle [T] | TP | Two-phase |
| U | Axial velocity [m s−1] | T | Turbulence |
| Velocity vector [m s−1] | Species | ||
| V | Volume of a computational cell [m3] | ||
| W | Particle weight concentration | Dimensionless numbers | |
| Compressibility effects [W m−3] | Nu | Nusselt number | |
| Y | Oxidant mass fraction [-] | Pr | Prandtl number |
| Re | Reynolds number | ||
| Greek | letters | Sc | Schmidt number |
| Convective heat transfer coefficient [W m−2 K−1] | St | Stokes number | |
References
- Hoque, M.M.; Joshi, J.B.; Evans, G.M.; Mitra, S. A critical analysis of turbulence modulation in particulate flow systems: A review of the experimental studies. Rev. Chem. Eng. 2023, 40, 511–544. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1906, 324, 289–306. [Google Scholar] [CrossRef]
- Eirich, F.; Bunzl, M.; Margaretha, H. Untersuchungen über die Viskosität von Suspensionen und Lösungen. 4. Über die Viskosität von Kugelsuspensionen. Kolloid Z. 1936, 74, 276–285. [Google Scholar] [CrossRef]
- Al Taweel, A.M.; Landau, J. Turbulence modulation in two-phase jets. Int. J. Multiph. Flow 1977, 3, 341–351. [Google Scholar] [CrossRef]
- Hetsroni, G. Particles-turbulence interaction. Int. J. Multiph. Flow 1989, 15, 735–746. [Google Scholar] [CrossRef]
- Crowe, C.T. On models for turbulence modulation in fluid–particle flows. Int. J. Multiph. Flow 2000, 26, 719–727. [Google Scholar] [CrossRef]
- Elgobashi, S. An updated classification map of particle-laden turbulent flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow; Fluid Mechanics and Its Applications; Balachandar, S., Prosperetti, A., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 81, pp. 3–10. [Google Scholar] [CrossRef]
- Crowe, C.T. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- M Kuerten, J.G. Point-particle DNS and LES of particle-laden turbulent flow—A state-of-the-art review. Flow Turbul. Combust. 2016, 97, 689–713. [Google Scholar] [CrossRef] [PubMed]
- Elghobashi, S.; Abou-Arab, T.; Rizk, M.; Mostafa, A. Prediction of the particle-laden jet with a two-equation turbulence model. Int. J. Multiph. Flow 1984, 10, 697–710. [Google Scholar] [CrossRef]
- Gore, R.A.; Crowe, C.T. Effect of particle size on modulating turbulent intensity. Int. J. Multiph. Flow 1989, 15, 279–285. [Google Scholar] [CrossRef]
- Farazi, S.; Sayadi, T.; Pitsch, H. Numerical analysis of the drag force acting on the reactive single char particle under oxy-fuel condition. In Proceedings of the China National Symposium on Combustion, Ma’anshan, China, 21–23 October 2016. [Google Scholar]
- Fröhlich, K.; Schneiders, L.; Meinke, M.; Schröder, W. Validation of Lagrangian two-way coupled point-particle models in large-eddy simulations. Flow Turbul. Combust. 2018, 101, 317–341. [Google Scholar] [CrossRef]
- Jayawickrama, T.R.; Haugen, N.E.L.; Babler, M.U.; Chishty, M.A.; Umeki, K. The effect of Stefan flow on the drag coefficient of spherical particles in a gas flow. Int. J. Multiph. Flow 2019, 117, 130–137. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, K.; Haugen, N.E.L.; Mao, C.; Fan, J. Drag force for a burning particle. Combust. Flame 2020, 217, 188–199. [Google Scholar] [CrossRef]
- Llamas, Á.D.G.; Guo, N.; Li, T.; Gebart, R.; Umeki, K. Rapid change of particle velocity due to volatile gas release during biomass devolatilization. Combust. Flame 2022, 238, 111898. [Google Scholar] [CrossRef]
- Du, S.; Zhao, L.; Chen, X.; Yang, B.; Zhou, Q. Effect of Stefan flow on the drag force of single reactive particle surrounded by a sea of inert particles. Chem. Eng. Sci. 2022, 253, 117546. [Google Scholar] [CrossRef]
- Hasse, C.; Debiagi, P.; Wen, X.; Hildebrandt, K.; Vascellari, M.; Faravelli, T. Advanced modeling approaches for CFD simulations of coal combustion and gasification. Prog. Energy Combust. Sci. 2021, 86, 100938. [Google Scholar] [CrossRef]
- Toporov, D.; Bocian, P.; Heil, P.; Kellermann, A.; Stadler, H.; Tschunko, S.; Förster, M.; Kneer, R. Detailed investigation of a pulverized fuel swirl flame in CO2/O2 atmosphere. Combust. Flame 2008, 155, 605–618. [Google Scholar] [CrossRef]
- Sadiki, A.; Agrebi, S.; Chrigui, M.; Doost, S.; Knappstein, R.; Di Mare, F.; Janicka, J.; Maßmeyer, A.; Zabrodiec, D.; Hees, J.; et al. Analyzing the effects of turbulence and multiphase treatments on oxy-coal combustion process predictions using LES and RANS. Chem. Eng. Sci. 2017, 166, 283–302. [Google Scholar] [CrossRef]
- Nicolai, H.; Wen, X.; Miranda, F.; Zabrodiec, D.; Maßmeyer, A.; Di Mare, F.; Dreizler, A.; Hasse, C.; Kneer, R.; Janicka, J. Numerical investigation of swirl-stabilized pulverized coal flames in air and oxy-fuel atmospheres by means of large eddy simulation coupled with tabulated chemistry. Fuel 2020, 287, 119429. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Nicolai, H.; Zabrodiec, D.; Pielsticker, S.; Hasse, C.; Kneer, R.; Maßmeyer, A. Numerische Untersuchung zur Relevanz von Teilmodellen für Pyrolyse und Koksabbrand in turbulenten drallbehafteten Flammen unter Oxyfuel-Bedingungen. In Proceedings of the 30. Deutscher Flammentag, Hannover, Germany, 28–29 September 2021. [Google Scholar] [CrossRef]
- Russo, E.; Kuerten, J.G.M.; Geurts, B.J. Delay of biomass pyrolysis by gas–particle interaction. J. Anal. Appl. Pyrolysis 2014, 110, 88–99. [Google Scholar] [CrossRef]
- Zabrodiec, D.; Becker, L.; Hees, J.; Maßmeyer, A.; Habermehl, M.; Hatzfeld, O.; Dreizler, A.; Kneer, R. Detailed analysis of the velocity fields from 60 kW swirl-stabilized coal flames in CO2/O2- and N2/O2-atmospheres by means of laser Doppler velocimetry and Particle Image Velocimetry. Combust. Sci. Technol. 2017, 189, 1751–1775. [Google Scholar] [CrossRef]
- Becker, L.; Kosaka, H.; Böhm, B.; Doost, S.; Knappstein, R.; Habermehl, M.; Kneer, R.; Janicka, J.; Dreizler, A. Experimental investigation of flame stabilization inside the quarl of an oxyfuel swirl burner. Fuel 2017, 201, 124–135. [Google Scholar] [CrossRef]
- Schneider, H.; Valentiner, S.; Vorobiev, N.; Böhm, B.; Schiemann, M.; Scherer, V.; Kneer, R.; Dreizler, A. Investigation on flow dynamics and temperatures of solid fuel particles in a gas-assisted oxy-fuel combustion chamber. Fuel 2021, 286, 119424. [Google Scholar] [CrossRef]
- Özer, B.; Zabrodiec, D.; Kneer, R.; Maßmeyer, A. Experimental investigation of 40 kWth methane-assisted and self-sustained pulverized biomass flames. Proc. Combust. Inst. 2023, 39, 3343–3351. [Google Scholar] [CrossRef]
- Axt, C.; Maßmeyer, A.; Pielsticker, S.; Kneer, R. Spatially-resolved experimental investigations of combustion characteristics in a solid fuel doped methane swirl flame and the influence on the formation of ultrafine particulate matter. Combust. Flame 2022, 244, 112223. [Google Scholar] [CrossRef]
- Chigier, N.A.; Beeé, J.M. Velocity and static-pressure distributions in swirling air jets issuing from annular and divergent nozzles. J. Basic Eng. 1964, 86, 788–796. [Google Scholar] [CrossRef]
- Habermehl, M.; Hees, J.; Maßmeyer, A.; Zabrodiec, D.; Hatzfeld, O.; Kneer, R. Comparison of flame stability under air and oxy-fuel conditions for an aerodynamically stabilized pulverized coal swirl flame. J. Energy Res. Technol. 2016, 138, 042209. [Google Scholar] [CrossRef]
- Bordbar, M.H.; Węcel, G.; Hyppänen, T. A line by line based weighted sum of gray gases model for inhomogeneous CO2–H2O mixture in oxy-fired combustion. Combust. Flame 2014, 161, 2435–2445. [Google Scholar] [CrossRef]
- ANSYS Fluent 17.1 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2016.
- Pozrikidis, C. Fluid Dynamics: Theory, Computation, and Numerical Simulation; Springer Science+Business Media: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Magnussen, B. On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow. In Proceedings of the 19th Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981; p. 42. [Google Scholar]
- Askarizadeh, H.; Koch, M.; Nicolai, H.; Pielsticker, S.; Kneer, R.; Hasse, C.; Maßmeyer, A. Influence of gas radiation, particle radiation interactions, and conversion-dependent particle radiative properties on pulverized solid fuel combustion. In Proceedings of the 31. Deutscher Flammentag, Berlin, Germany, 27–28 September 2023. [Google Scholar]
- Benim, A.C.; Deniz Canal, C.; Boke, Y.E. A validation study for RANS based modelling of swirling pulverized fuel flames. Energies 2021, 14, 7323. [Google Scholar] [CrossRef]
- Boyd, R.K.; Kent, J.H. Three-dimensional furnace computer modelling. Symp. (Int.) Combust. 1988, 21, 265–274. [Google Scholar] [CrossRef]
- Frössling, N. Über die Verdunstung fallender Tropfen. Gerlands Beitr. Geophys. 1938, 52, 170–216. [Google Scholar]
- Ranz, W.E.; Marshall, W.R., Jr. Evaporation from drops. Part I and Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Nicolai, H. Towards Predictive Simulations of Low-Emission Reactive Solid Fuel Systems. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2022. [Google Scholar] [CrossRef]
- Nicolai, H.; Debiagi, P.; Wen, X.; Dressler, L.; Maßmeyer, A.; Janicka, J.; Hasse, C. Flamelet LES of swirl-stabilized oxy-fuel flames using directly coupled multi-step solid fuel kinetics. Combust. Flame 2022, 241, 112062. [Google Scholar] [CrossRef]
- Nicolai, H.; Debiagi, P.; Janicka, J.; Hasse, C. Flamelet LES of oxy-fuel swirling flames with different O2/CO2 ratios using directly coupled seamless multi-step solid fuel kinetics. Fuel 2023, 344, 128089. [Google Scholar] [CrossRef]
- Badzioch, S.; Hawksley, P.G.W. Kinetics of thermal decomposition of pulverized coal particles. Ind. Eng. Chem. Process Des. Dev. 1970, 9, 521–530. [Google Scholar] [CrossRef]
- Baum, M.M.; Street, P.J. Predicting the combustion behaviour of coal particles. Combust. Sci. Technol. 1971, 3, 231–243. [Google Scholar] [CrossRef]
- Field, M.A.; Gill, D.W.; Morgan, B.B.; Hawksley, P.G.W. Combustion of Pulverised Coal; B.C.U.R.A.: London, UK, 1967. [Google Scholar]
- Gövert, B.; Pielsticker, S.; Kreitzberg, T.; Habermehl, M.; Hatzfeld, O.; Kneer, R. Measurement of reaction rates for pulverized fuel combustion in air and oxyfuel atmosphere using a novel fluidized bed reactor setup. Fuel 2017, 201, 81–92. [Google Scholar] [CrossRef]
- Guo, J.; Hu, F.; Jiang, X.; Li, P.; Liu, Z. Effects of gas and particle radiation on IFRF 2.5 MW swirling flame under oxy-fuel combustion. Fuel 2020, 263, 116634. [Google Scholar] [CrossRef]
- Backreedy, R.I.; Fletcher, L.M.; Ma, L.; Pourkashanian, M.; Williams, A. Modelling pulverised coal combustion using a detailed coal combustion model. Combust. Sci. Technol. 2006, 178, 763–787. [Google Scholar] [CrossRef]
- Al-Abbas, A.H.; Naser, J.; Dodds, D. CFD modelling of air-fired and oxy-fuel combustion of lignite in a 100 kW furnace. Fuel 2011, 90, 1778–1795. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Huang, X.; Zhang, T.; Luo, W.; Hu, F.; Li, P.; Zheng, C. Experimental and numerical investigations on oxy-coal combustion in a 35 MW large pilot boiler. Fuel 2017, 187, 315–327. [Google Scholar] [CrossRef]
- Yin, C. On gas and particle radiation in pulverized fuel combustion furnaces. Appl. Energy 2015, 157, 554–561. [Google Scholar] [CrossRef]
- Kim, T.K.; Lee, H.S. Radiative transfer in two-dimensional anisotropic scattering media with collimated incidence. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 225–238. [Google Scholar] [CrossRef]
- Jendoubi, S.; Lee, H.S.; Kim, T.K. Discrete ordinates solutions for radiatively participating media in a cylindrical enclosure. J. Thermophys Heat Transf. 1993, 7, 213–219. [Google Scholar] [CrossRef]
- Zabrodiec, D.; Hees, J.; Maßmeyer, A.; vom Lehn, F.; Habermehl, M.; Hatzfeld, O.; Kneer, R. Experimental investigation of pulverized coal flames in CO2/O2- and N2/O2-atmospheres: Comparison of solid particle radiative characteristics. Fuel 2017, 201, 136–147. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193. [Google Scholar] [CrossRef]
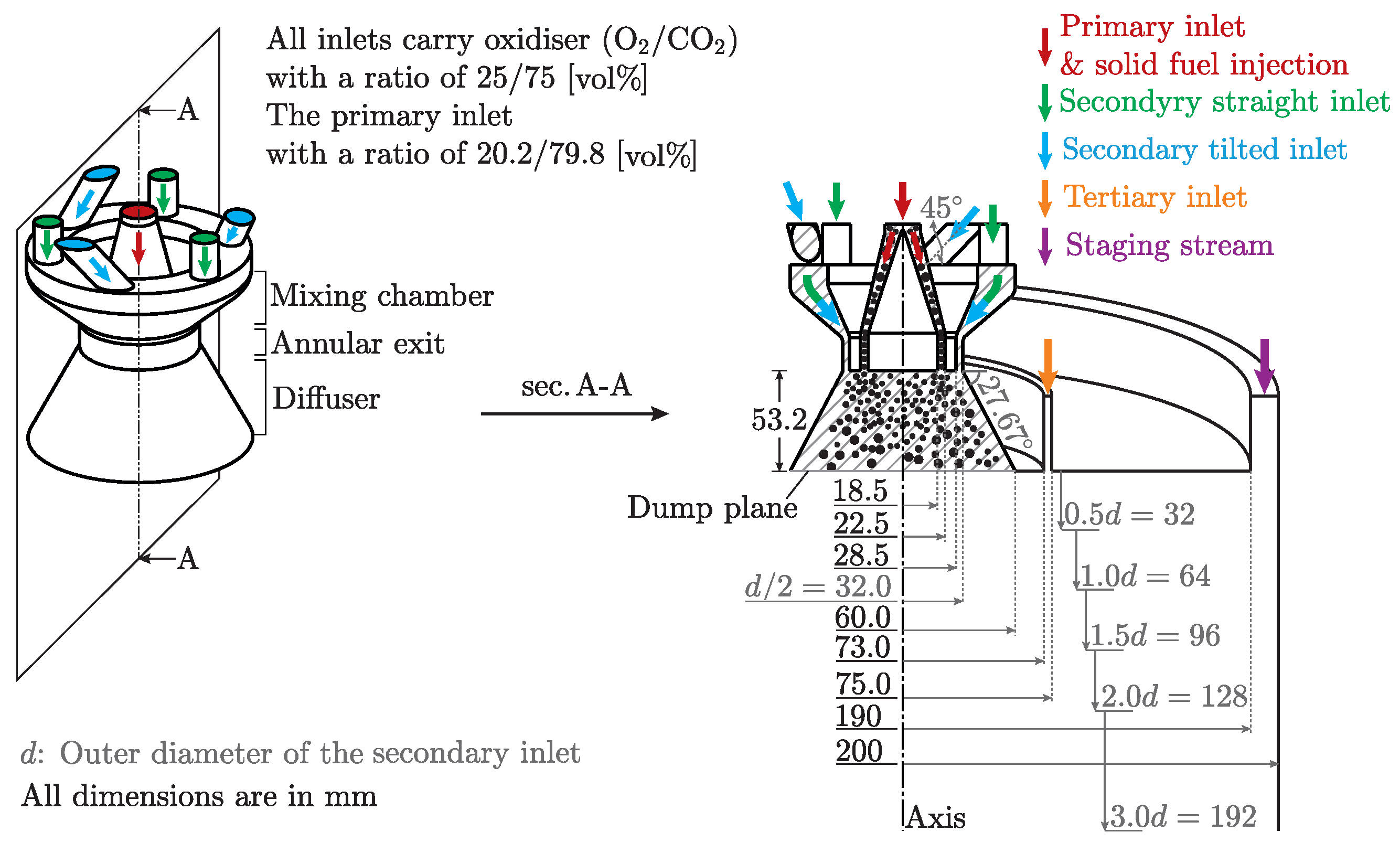
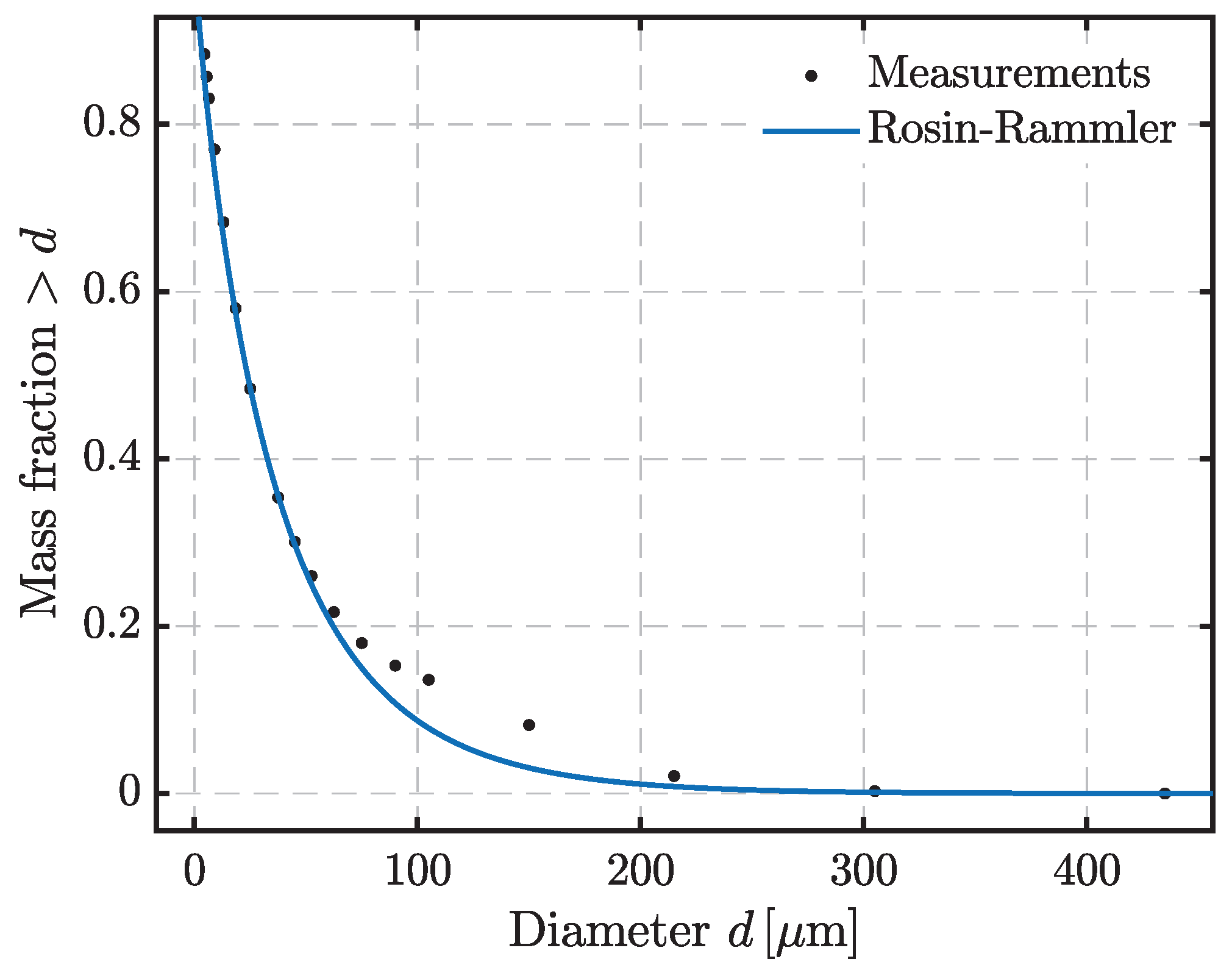


| Ultimate Analysis a | [wt%] | Proximate Analysis b | [wt%] |
|---|---|---|---|
| C | 69.05 | Ash | 5.440 |
| H | 4.830 | Water | 12.15 |
| N | 0.690 | Volatiles | 42.42 |
| S | 0.300 | Char | 39.99 |
| O | 25.13 | HHV c [MJ/kg] | 22.153 |
| Inlet | T [°C] | a [m3/h] | O2/CO2 [vol %] | ||
|---|---|---|---|---|---|
| Case #1 | Case #2 | Case #3 | |||
| Primary | 25 | 9.4 | 9.4 | 9.4 | 20.2/79.8 |
| Secondary | 40 | 16.2 | 23.8 | 31.3 | 25/75 |
| Tertiary | 40 | 2.9 | 4.2 | 5.5 | 25/75 |
| Staging | 900 | 31.3 | 22.2 | 13.3 | 25/75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askarizadeh, H.; Pielsticker, S.; Nicolai, H.; Kneer, R.; Hasse, C.; Maßmeyer, A. Investigation of the Coupling Schemes between the Discrete and the Continuous Phase in the Numerical Simulation of a 60 kWth Swirling Pulverised Solid Fuel Flame under Oxyfuel Conditions. Fire 2024, 7, 185. https://doi.org/10.3390/fire7060185
Askarizadeh H, Pielsticker S, Nicolai H, Kneer R, Hasse C, Maßmeyer A. Investigation of the Coupling Schemes between the Discrete and the Continuous Phase in the Numerical Simulation of a 60 kWth Swirling Pulverised Solid Fuel Flame under Oxyfuel Conditions. Fire. 2024; 7(6):185. https://doi.org/10.3390/fire7060185
Chicago/Turabian StyleAskarizadeh, Hossein, Stefan Pielsticker, Hendrik Nicolai, Reinhold Kneer, Christian Hasse, and Anna Maßmeyer. 2024. "Investigation of the Coupling Schemes between the Discrete and the Continuous Phase in the Numerical Simulation of a 60 kWth Swirling Pulverised Solid Fuel Flame under Oxyfuel Conditions" Fire 7, no. 6: 185. https://doi.org/10.3390/fire7060185
APA StyleAskarizadeh, H., Pielsticker, S., Nicolai, H., Kneer, R., Hasse, C., & Maßmeyer, A. (2024). Investigation of the Coupling Schemes between the Discrete and the Continuous Phase in the Numerical Simulation of a 60 kWth Swirling Pulverised Solid Fuel Flame under Oxyfuel Conditions. Fire, 7(6), 185. https://doi.org/10.3390/fire7060185






